Abstract
In the paper, a new class of dynamic game models with a moving information horizon or dynamic updating is studied. In this class of games, players do not have full information about the game structure (motion equations, payoff functions) on the interval on which the game is defined. It is supposed that the players at each stage of the dynamic game have only truncated information about the game structure defined by the information horizon. Cooperative and noncooperative settings are considered in the paper. Results are illustrated using the oligopoly advertising game model, and comparison between the solution in the initial game model and in the game model with moving information horizon is presented. Simulation results are presented.
1. Introduction
Noncooperative game theory deals with strategic interactions among multiple decision makers with the objective functions depending on the choices of all the players. It is supposed that the players do not cooperate, and it is important to model their behavior using some optimality principal. There are many results that have been obtained in the field of noncooperative game theory; for a general description. see the fundamental book [1]. In the papers [2,3], the solution concept called the Nash equilibrium was proposed; in the current paper, this solution concept is used, but for a dynamic setting. The following book [4] can be used to study the main recent results in the field of dynamic cooperative game theory, which is a focus of the current paper.
The cooperative dynamic game theory offers socially convenient and group efficient solutions to different decision problems involving strategic actions. One of the fundamental questions in the theory of cooperative dynamic games is to define the allocation rule for cooperative payoff or set of imputations based on the optimal behavior of players, and the notation of characteristic function is used for that, which shows the strength of coalition S. In this paper, it is defined as in [5] as a total payoff of players from coalition S in Nash equilibrium in the game with the following set of players: coalition S (acting as one player) and players from the set N∖S. To compute the feedback Nash equilibrium, we analyze [4]. A set of imputations or solutions of the game is determined using the characteristic function at the beginning of each subinterval. In the paper [6], Haurie noted the problem of time inconsistency for the Nash bargaining solution in one differential game model. The notion of time consistency was formalized mathematically by Petrosyan in the paper [7]. In the next paper on time consistency [8], L. Petrosyan defined the notion of the Imputation Distribution Procedure (IDP), which is used to compose a time consistent cooperative solution or single imputation. Later on, L. Petrosyan defined the notion of strong time consistency in the paper [9]. See the recent publications on this topic in [10,11,12]. In order to determine a solution for the game model with dynamic updating, it is necessary to combine partial solutions and their IDP on subintervals. The theories of time consistency and strong time consistency introduced by L. Petrosyan in [7,9] are also studied for the offered solution.
Classical dynamic game models assume that the game structure does not change in the interval on which the game is defined or that the players have all information about the change of the game structure. However, if we consider a long term process, then these assumptions cannot cope with the reality. In the class of games with continuous updating, it is supposed that the players have or use only information about motion equations and payoff functions defined on the interval with a length equal to the value of the information horizon. This information is updated as the current time evolves, see Figure 1. In order to define the best possible behavior for players in this type of dynamic game, it is necessary to use a special approach, which is called the Looking Forward Approach (LFA).
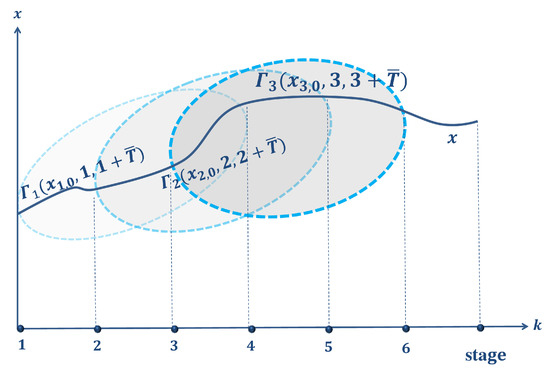
Figure 1.
The behavior of players in the game with truncated information can be modeled using a series of truncated subgames
The concept of the looking forward approach was introduced in [13] for differential games, where a new class of games was presented and the foundation for further study of games with dynamic updating or a moving information horizon was laid. To get more information about the approach, one may consider the following papers [13,14,15,16,17,18,19,20]. In the paper [13], the looking forward approach was applied to the cooperative differential game with a finite horizon. The paper [17] was focused on studying the looking forward approach with stochastic forecast and dynamic adaptation. In the paper [15], the looking forward approach was applied to a cooperative differential game of pollution control. In the paper [16], the looking forward approach was applied to the cooperative differential game with an infinite horizon. The paper [14] was devoted to studying the cooperative differential games with an infinite horizon and different types of forecasts and information structures. The last papers on the looking forward approach [18,21] were devoted to either studying the looking forward approach for cooperative differential games with nontransferable utility and real-life application of the looking forward approach to economic simulation. The class of differential games with continuous updating was considered in the papers [19,20]; here, it was supposed that the updating process evolves continuously in time. In the paper [19], the system of Hamilton–Jacobi–Bellman equations was derived for the Nash equilibrium in the game with continuous updating. In the paper [20], the class of linear-quadratic differential games with continuous updating was considered, and the explicit form of the Nash equilibrium was derived. In this paper, we apply the looking forward approach to the class of games with dynamic updating. The importance of the results of this paper is supported by the applicability of dynamic models to real-life processes, the more simple structure of dynamic models, and the dynamic nature of numerical model predictive control. In the papers described above, we studied differential games. Another important thing is that in this paper, we study the dynamic oligopoly marketing model of advertising, where we apply the looking forward approach. This result is essentially new.
In order to demonstrate the looking forward approach, we present the dynamic marketing model of advertising with a finite horizon. We refrain from reviewing the literature on advertising models, given that there are recent surveys on this topic. Huang, Leng, and Liang [22] gave an extensive and comprehensive survey of dynamic advertising competition since 1994, their coverage starting where the previous survey in Feichtinger, Hartl, and Sethi [23] stopped. Jørgensen and Zaccour [24] covered advertising models in oligopolies (horizontal strategic interactions) and in marketing channels (vertical strategic interactions), whereas He, Prasad, Gutierrez, and Sethi [25] focused on Stackelberg differential game models in supply chains and marketing channels that include advertising. Finally, Aust and Buscher [26] and Jørgensen and Zaccour [27] concentrated on cooperative advertising in marketing channels. This model was based on the model presented by Naik, Prasad, and Sethi in [28]. The model in [28] is the extension of the Sethi model for awareness of auto brands with the churn term, which is the extension of the decay market share term in monopoly models capturing forgetting and noise. The closed-loop Nash equilibrium concept is used to obtain the optimal advertising expenditure for the noncooperative game model. Considering the applications of game theory in different fields of research, many subjects from society modeling have been covered, for example see [29]. In this paper, the looking forward approach is applied to the dynamic case of the model presented in [28]. Both noncooperative and cooperative models are considered.
The paper is structured as follows. In Section 2 , a description of the looking forward approach is presented for a general dynamic game model, and a solution for a game with dynamic updating is presented for both fixed and random information horizons. In Section 3, the looking forward approach is applied to a dynamic oligopoly marketing model of advertising for noncooperative game and cooperative game models, respectively. In Section 4, simulation results for a marketing game model are presented.
2. Looking Forward Approach
Information plays one of the main roles in game theory. Generally, classical differential game models consider only the complete information, which means the information about the game structure is known and will not change during the whole game. This paper focuses on, however, the case that when information updates dynamically, players use only the truncated information and update it at each stage. In order to model the behavior of players when information updates dynamically, a novel approach called the looking forward approach in [13] is introduced.
Consider a general N-stage n-person nonzero-sum discrete-time dynamic game [30] with initial state . The state dynamics of the game is defined by the following difference equation:
where is the control vector of player i at stage k, is the state of the game, and
The payoff function of player i is:
where r is the discount rate.
This game is a complete information game; however, in real-life-like games, players do not have full information about the game structure on the interval on which the game is defined. We apply the looking forward approach in order to model the behavior of players when information about the game updates dynamically.
2.1. Truncated Subgame
Assume that at each stage k, players have full information about the motion equations and payoff functions within k + stages, where is a fixed value, namely the information horizon. At the stage k, information about the game is updated. At the stage k + 1, players have full information about the game structure on the interval until the stage , see Figure 1.
Definition 1.
Let . Truncated subgame is defined on the interval . The motion equation and payoff function of truncated subgame on the stage interval coincide with that of the initial game on the same stage interval. The motion equation and initial condition of truncated subgame have the following form:
(denote for the truncated subgame ).
The payoff function of firm i in truncated subgame has the form:
for .
2.2. Noncooperative Outcomes in the Game Model with a Moving Information Horizon
Considering each truncated subgame, let , be a vector of strategies that provides a feedback Nash equilibrium solution for the truncated subgame , and by , denote the payoff of player in feedback Nash equilibrium in the subgame defined on the interval , :
Theorem 1.
Denote the strategies obtained by maximization the right hand side of (5) by , . By , denote the trajectory obtained with strategies involved. The presented solution is valid only for a truncated subgame, not for the whole game defined on the interval . It is also impossible to construct the Nash equilibrium using the classical approaches, since information about the game updates dynamically, and it is different on different intervals. In order to construct the resulting equilibrium strategies and corresponding trajectory for a class of games with dynamic updating, we introduce the notion of the resulting strategies and corresponding resulting trajectory:
Definition 2.
The resulting feedback Nash equilibrium strategies are constructed in the following way:
Definition 3.
The resulting noncooperative trajectory is a combination of for each truncated subgame :
Along the resulting noncooperative trajectory, players receive a payoff according to the following formula:
2.3. Cooperative Game Model with a Moving Information Horizon
The theory of cooperative dynamic games offers socially convenient and group efficient solutions to different decision problems involving strategic actions. One of the fundamental problems in the theory of cooperative dynamic games is the formulation of optimal or cooperative behavior for players and the definition of the allocation rule or cooperative solution, which is the set of imputations chosen by the players in the game. We suppose that the players decide to cooperate in each truncated subgame. By , we denote a truncated cooperative subgame defined on the interval with the initial condition . The maximal joint payoff of all players in this game can be defined by maximizing functional:
subject to:
Assume that the Bellman function for each truncated subgame has the following form [32]:
where .
Theorem 2.
Definition 4.
The resulting cooperative strategies are constructed in the following way:
In a similar way, we define the resulting cooperative trajectory. By , denote the optimal strategies obtained by maximization of the right hand side of (12). The corresponding trajectory is defined by .
Definition 5.
The resulting cooperative trajectory is a combination of cooperative trajectories for each truncated cooperative subgame defined on the successive intervals :
On the interval , the resulting cooperative trajectory coincides with the cooperative trajectory in the truncated cooperative subgame . At the stage k + 1, information about the game structure updates. On the interval , trajectory coincides with cooperative trajectory in the truncated cooperative subgame , etc.
The characteristic function of the coalition is an essential concept in the theory of cooperative games. In this paper, it is defined as in [5] as a total payoff of players from coalition in Nash equilibrium in the game with the following set of players: coalition S (acting as one player) and players from the set I∖S(acting as individuals). For each coalition , define the values of the characteristic function for each truncated subgame as was done in [16]:
where is defined as the total payoff of players from coalition in feedback Nash equilibrium in the game with the following set of players: coalition S (acting as one player) and players from the set , i.e., in the game with players. For , the cooperative case turns into the noncooperative case. In other cases, players from coalition S act as one player maximizing their total payoff.
2.4. Resulting Cooperative Solution and Theoremerties
An imputation for each truncated cooperative subgame is defined as an arbitrary vector satisfying the conditions:
Denote the set of all possible imputations for each truncated subgame by . Suppose that for each truncated subgame, a non-empty cooperative solution is defined by:
it can be a core, nucleus, or Shapley value.
In order to guarantee time consistency Theoremerty [30] in each cooperative truncated subgame, it is necessary to use the notion of the imputation distribution procedure. The Theoremerty of time consistency was introduced in 1977 by L. Petrosyan [33].
Following the continuous time analysis of Yeung and Petrosyan [34] for cooperative differential games, we formulate a discrete time version of the imputation distribution procedure [8] so that the agreed upon imputations will be time consistent. By , denote the payment that firm i receives in stage k under the cooperative agreement along the cooperative trajectory . The payment scheme involving constitutes an IDP in the sense that the imputation of firm i over the stages from k to N can be expressed as:
Definition 6.
Solution is called time consistent, if for any imputation , there exists IDP such that for , this satisfies:
The agreed-upon optimality principle or cooperative solution is time consistent, if the condition (6) is maintained at any time instant throughout the game along the cooperative trajectory.
In order to construct the resulting cooperative solution or cooperative solution in the game with dynamic updating , it is necessary to use a special approach, because the standard approach can only be applied to each truncated subgame with dynamic updating defined on the interval . IDP also provides the time consistency Theoremerty of the new solution concept and the ability to determine solutions within the interval .
Suppose that in each truncated subgame , cooperative solution along the cooperative trajectory is selected. Suppose that the imputation:
and corresponding IDP for are selected in a way so as to guarantee the time consistency Theoremerty:
The corresponding IDP can be obtained in the following form [30]:
where .
However, the time consistency only holds on the interval for each truncated subgame , . In order to guarantee time consistency for the whole interval , we introduce the resulting IDP.
Definition 7.
The resulting IDP is defined for a set of chosen imputations in each truncated subgame using the corresponding as follows:
Using the resulting IDP , we define the following vector:
Definition 8.
The resulting imputation is a vector defined using the resulting IDP in the following way, for stage :
in particular .
Using the notion of resulting imputation, it is possible to define the allocation rule for the joint payoff:
Definition 9.
Resulting solution is the set of resulting imputations for all possible resulting IDPs, (defined by different imputations in each truncated subgame).
Any resulting imputation and corresponding resulting IDP allocate the total payoff of players along the resulting cooperative trajectory in the initial game with prescribed duration or the following condition holds:
The resulting solution is time consistent by construction. However, it can also be proven that an arbitrary resulting cooperative solution is strong time consistent in the game model with dynamic updating. By an arbitrary solution, we understand a solution that for example is composed of some vectors from the core in the first stage, the Shapley value in the second stage, etc.
Definition 10.
Cooperative solution is called strong time consistent, if for and every , the corresponding IDP satisfies the condition:
where .
Theorem 3.
The arbitrary resulting cooperative solution is strong time consistent in the game model with dynamic updating.
2.5. Construction of the Characteristic Function in the Game Model with Dynamic Updating
In the previous section, we defined the notion of the resulting cooperative solution or we defined a way for allocating cooperative payoff along the chosen trajectory in the game with dynamic updating. However, we did not show that the constructed set was a set of imputations or was a set of vectors satisfying individual and group rationality Theoremerties. In order to justify the resulting cooperative solution, we need to define the characteristic function for the game model with dynamic updating.
Definition 11.
The resulting characteristic function , in the game with dynamic updating was the function calculated using the values of characteristic functions in every truncated subgame along the resulting cooperative trajectory for :
Using the resulting characteristic function, we can show that the resulting imputation was the imputation in the game with dynamic updating:
Theorem 4.
The resulting imputation is the imputation in the game with dynamic updating, if for , the following condition is satisfied:
where .
The proof of Theorems 4, 5, 6, 8, 9, 10, 11 in the paper can be found in the Appendix A.
2.6. Relationship of the Solutions in Truncated Subgames and Resulting Solutions
In this section, it is shown that if the players choose imputations based on for , in every truncated subgame by the same rule, then the resulting imputation corresponds to the imputation chosen by the same rule using the resulting characteristic function , . Further, we prove it for the number of classical optimality principals.
We assume that if in every truncated subgame , players choose Shapley value as the imputation, then the corresponding resulting imputation coincides with the Shapley value calculated using the resulting characteristic function , , .
Theorem 5.
Suppose that in every truncated subgame :
where , then corresponding resulting imputation coincides with :
where is the Shapley value, calculated using the resulting characteristic function , .
Suppose that in every truncated subgame , players choose the core as the cooperative solution, then each resulting imputation belongs to the core, defined using the resulting characteristic function .
Theorem 6.
Suppose that in every truncated subgame :
where then for every , the following is satisfied:
where is the core, calculated using the resulting characteristic function , , if this condition holds:
2.7. Random Information Horizon
In this section, we consider a case when the length of the information horizon is not fixed; this means that the players may have certain information on truncated intervals , but the length of intervals is a random variable (see Figure 2). By , we denote the length of the information horizon in the stage k. can take values from the interval , where is the realization of random horizon in the previous truncated subgame, in particular . It is worth mentioning that once , then the updating procedure stops. is a discrete random variable. At the initial position , the following probabilities are defined for realization on the interval : . In the position (second position), the probabilities are recalculated in the following way:
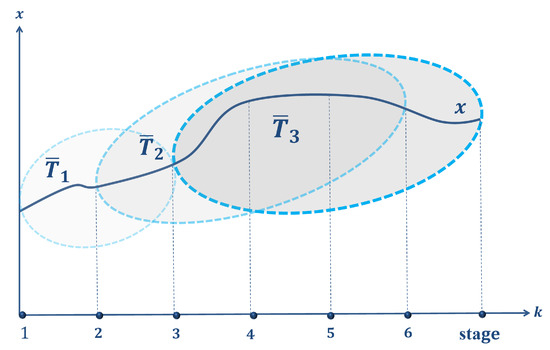
Figure 2.
The length of each blue oval is the realization of the infinite horizon.
The motion equation on the interval is:
The payoff function of player for the truncated subgame is:
Consider the noncooperative game model. In order to define the feedback Nash equilibrium in this game, denote the Bellman function for the truncated subgame as follows:
with the set of strategies , then:
where
As in the theorem in [35], a feedback Nash equilibrium in the noncooperative case of each truncated subgame with random horizon can be characterized as follows.
Theorem 7.
Consider the case when all players agree to cooperate in each truncated subgame. To maximize their expected joint payoff for the truncated subgame, we need to solve the following discrete time dynamic programming problem:
subject to (25).
Corollary 1.
Using the set of optimal strategies, can be generated from (25), and we obtain the corresponding cooperative trajectory.
3. Dynamic Oligopoly Marketing Model of Advertising
3.1. Initial Game Model
Consider an n-firm dynamic oligopoly marketing model of advertising defined on the closed time interval . The solution for the noncooperative case of this model in differential form was presented in [28]. In this paper, the model is transformed to the dynamic setting and studied for not only the noncooperative case, but mainly for the cooperative case [36]. Advertising efforts as strategies are used by firms to compete on the oligopoly market, and each firm tries to increase its market share while competitors try to minimize it using their advertising efforts. Denote by the market share of firm at stage k. The full list of notations is presented in the Table 1. The dynamic oligopoly marketing model of advertising is defined as follows. Motion equation of firm or its market share:
where is a positive constant.

Table 1.
List of variables and parameters.
The payoff function of firm in the dynamic game model or the profit of firm :
Unlike the motion Equation (2) in the model example, here we use the discount rate . The main reason is that we do not want to complicate the result of the model and show the difference between the looking forward approach and the initial differential game first. The next thing is that we may model the advertising process on the short time interval, i.e., with a small value of T.
In the table, the list of parameters of the model is presented.
The initial marketing game model is defined on the interval [0,N]. As in Section 2, suppose that players have full information about the motion equations and payoff functions on the interval . In order to construct a solution in the game model with dynamic updating, we use the notion of truncated subgame .
The payoff function of firm in truncated subgame has the form:
In Expression (30), there is a logical consistency requirement that the market shares should satisfy:
3.2. Noncooperative Outcomes in a Truncated Subgame
Firstly, we consider the noncooperative case for each truncated subgame , with the initial condition . According to Theorem 1, the set of strategies {, for , and }, provides a feedback Nash equilibrium solution to the game (30), (32) if there exist functions , for , and in each truncated subgame , such that the following recursive relations are satisfied, for each :
Theorem 8.
The payoff of players for each truncated subgame in feedback Nash equilibrium on the interval has the following form:
where are determined from the relations:
with initial conditions , where , , .
The corresponding feedback Nash equilibrium strategies are:
Consider now the case of a random horizon for a truncated subgame. Suppose that the players know certain information about the game structure, but the duration of this information being right (or not changed) is unknown. Suppose that the probabilities are symmetric on the interval , . In our model, the first truncated subgame starts at Stage 0. Invoking Theorem 7 for the truncated subgame, if there exist continuously differentiable functions , , , and for , such that the following recursive relations are satisfied:
then strategies , that maximize the right hand side of System (35) constitute the feedback Nash equilibrium. The corresponding Bellman functions can be obtained as follows:
Theorem 9.
The Bellman functions for the feedback Nash equilibrium of the truncated subgame in (35) are:
- 1.
- 2.
- with initial conditions , , , , for and ,
3.3. Cooperative Outcomes in a Truncated Subgame
In this section, we focus on the cooperative setting, where all firms agree to cooperate in each truncated subgame. Denote by the truncated cooperative subgame on the interval with the initial condition . All firms aim to maximize their joint payoff:
Suppose that the set of strategies {, for , and }, provides an optimal control to the game (30), (38). Invoking Theorem 2.2, if there exist functions , for , and in each truncated subgame , then the following recursive relations are satisfied:
Theorem 10.
The maximum joint payoff of players for each truncated subgame has the following form:
where , , , , satisfy the relations:
with initial conditions , and .
The optimal cooperative strategies for each truncated subgame have the form:
Denote the solution of (39) with optimal strategies involved with the cooperative trajectory, , . The cooperative trajectory in each truncated subgame can be calculated using (30) as follows, :
So far, we have formalized the case when all firms cooperate in the game model with dynamic updating and fixed information horizon. Hence, we start to study the case when the information horizon is random, where has symmetric probabilities on the interval , . In the cooperative truncated subgame, if there exist functions for , , and for , such that the following recursive relations are satisfied:
then the strategies {, for , and } are optimal.
The value function can be obtained as follows:
Theorem 11.
The Bellman functions of the cooperative truncated subgame in (40) are:
- 1.
- 2.
- with initial conditions , , , , .
3.4. Characteristic Function in a Truncated Subgame
Using the characteristic function formula (14), we define the characteristic function for each truncated subgame:
where is defined as the total payoff of players from coalition S in feedback Nash equilibrium in the game with the following set of players: coalition S (acting as one player) and players from the set , i.e., in the game with players.
Suppose that the Bellman function for coalition and players in truncated subgame has the following form:
then the corresponding system of Bellman equations will have the form:
4. Numerical Simulation for a Dynamic Advertising Game Model with Updating
We consider a specific three firm oligopoly case n the stage interval N = 8, with fixed information horizon . In order to illustrate our model, let the parameters for each firm be and with the initial conditions
Figure 3 and Figure 4 show the feedback Nash equilibrium strategies for each firm in the noncooperative case and cooperative strategies in the cooperative case respectively for both the initial game model and the game model with the looking forward approach.
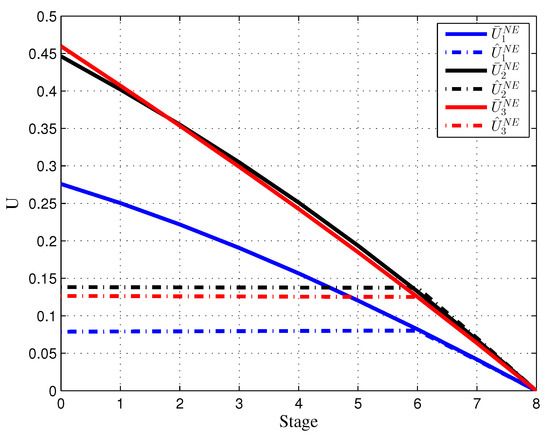
Figure 3.
The feedback Nash equilibrium of the noncooperative case in the initial game (solid line) and the feedback Nash equilibrium of noncooperative case in the game model with dynamic updating (dashed line).
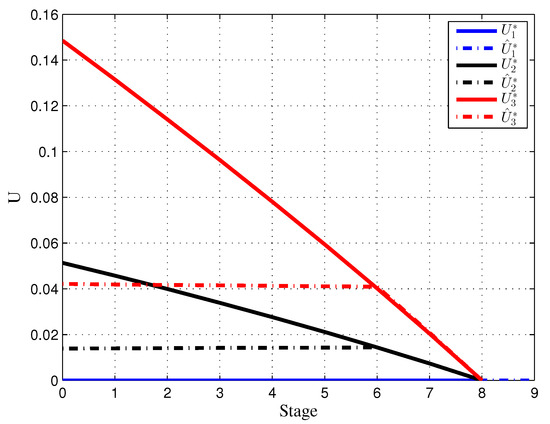
Figure 4.
Optimal cooperative strategies in the cooperative case of the initial game (solid line) and optimal cooperative strategies in the cooperative game model with dynamic updating (dashed line).
Figure 5 and Figure 6 show the dynamics of players’ market shares corresponding to the feedback Nash equilibrium strategies for each firm in the noncooperative case and the dynamics of market shares corresponding to the optimal cooperative strategies in the cooperative case respectively for both the initial game and the game model with dynamic updating.
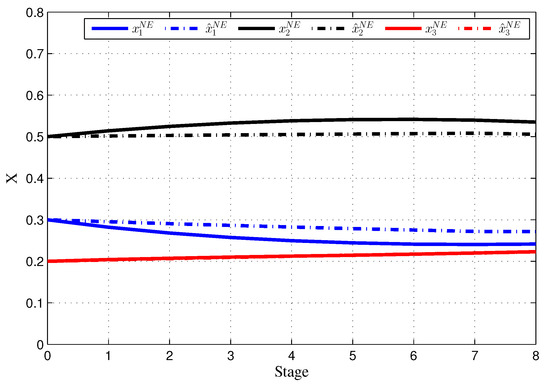
Figure 5.
Noncooperative trajectory in the initial game (solid line) and resulting noncooperative trajectory (dashed line) in the game model with dynamic updating.
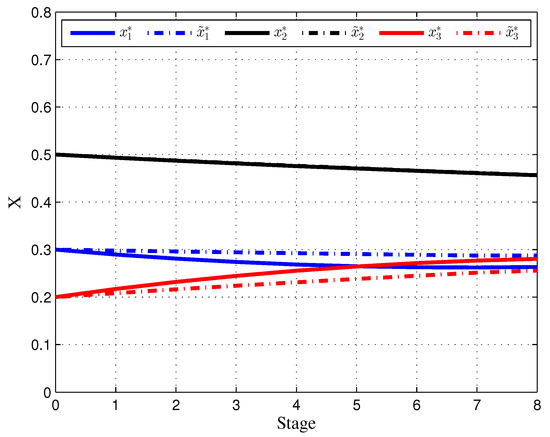
Figure 6.
Cooperative trajectory in the initial game (solid line) and resulting cooperative trajectory (dashed line) in the game model with dynamic updating.
Figure 7 and Figure 8 show the optimal payoff of each firm in the noncooperative case and the characteristic function of the cooperative case for coalitions: , , and , respectively, for both the initial game model and the game model with dynamic updating.
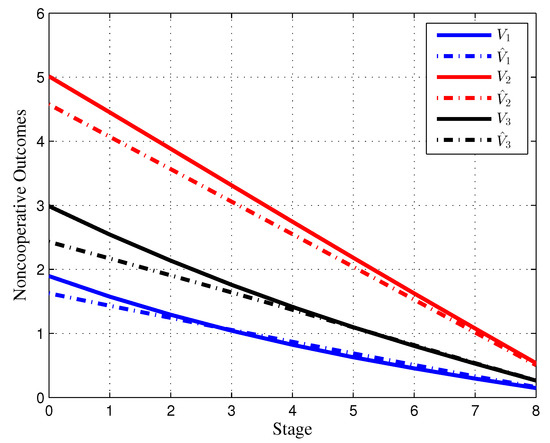
Figure 7.
Noncooperative outcomes in the initial game (solid line) and resulting noncooperative outcomes (dashed line) in the game model with dynamic updating.
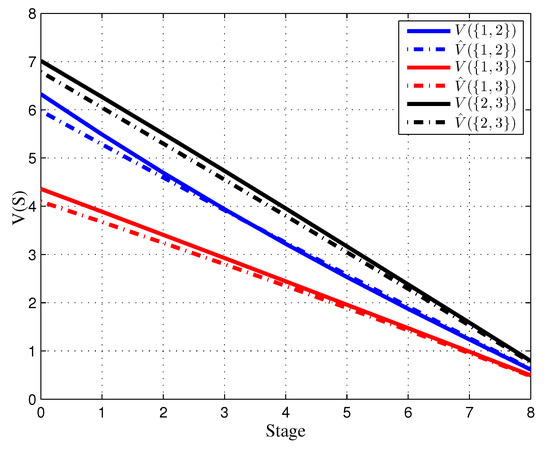
Figure 8.
Characteristic function in the initial game model (solid line) and resulting characteristic function (dashed line) in the game model with dynamic updating.
Figure 9 shows the difference between the resulting Shapley value and the Shapley value in the initial game model. As we can see from above, the resulting Shapley value of the game with moving information horizon changed more steadily over stages rather than the Shapley value of the initial game. It can be seen that the competition among the companies was more fierce in the initial game rather than in the game with a moving information horizon, considering market shares in Figure 6 and advertising expenditure in Figure 7. The Shapley value of each company barely changed in the last stage, which means that the profit of each company did not change much, as is shown in Figure 9.
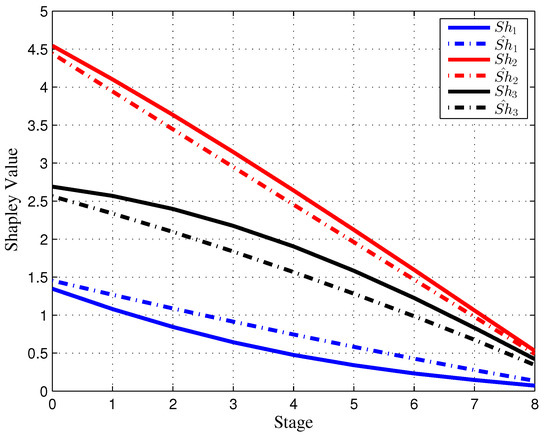
Figure 9.
Shapley value in the initial game model (solid line) and the resulting Shapley value (dashed line) in the game model with dynamic updating.
Suppose that the realization of the game information horizon: , , . Figure 10 shows the difference of the resulting noncooperative trajectory with a fixed information horizon and a random information horizon, respectively.
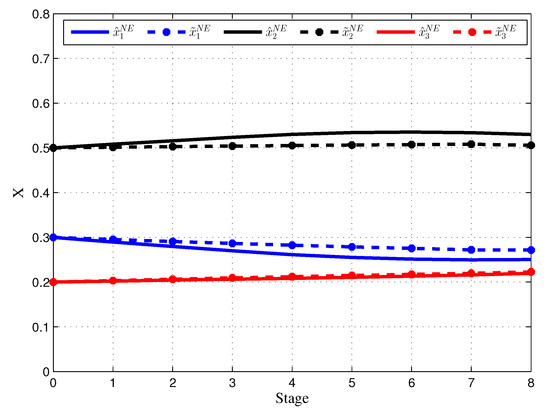
Figure 10.
The resulting noncooperative trajectory with a fixed information horizon (dashed line) and the resulting noncooperative trajectory with a random information horizon (solid line).
Figure 11 shows the difference between the resulting noncooperative outcomes of each firm in the noncooperative case with the fixed information horizon and random information horizon approaches.
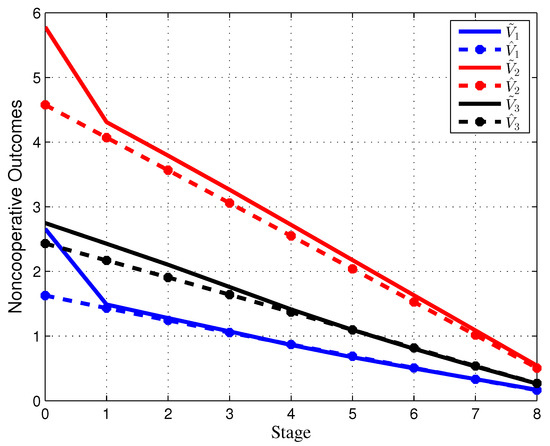
Figure 11.
The resulting noncooperative outcomes with a fixed information horizon (dashed line) and the resulting noncooperative outcomes with a random information horizon (solid line).
Figure 12 shows the difference between the resulting cooperative trajectory with fixed and random information horizons.
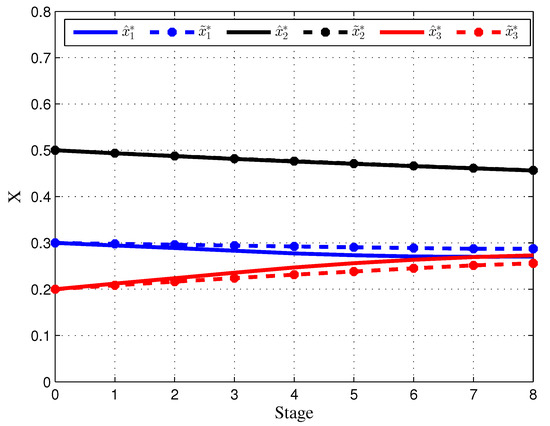
Figure 12.
The resulting cooperative trajectory with a fixed information horizon (dashed line) and the resulting cooperative trajectory with a random information horizon (solid line).
5. Conclusions
In this paper, a novel approach was presented for defining the solution in the dynamic game model, where information updated dynamically. Here, players did not have full information about the game structure through the whole time interval on which the game was defined, but they had certain information about the game structure on a fixed interval, namely the information horizon. As the time evolved, information about the game structure updated. Moreover, a random information horizon was considered for this approach. Therefore, the approach can be used to perform more realistic modeling of real-life conflict processes.
The dynamic oligopoly marketing model of advertising was considered, and the corresponding numerical example was used to illustrate the comparison between the initial dynamic marketing model and the corresponding model with dynamic updating. Besides, the comparison between the looking forward approach with a fixed information horizon and the looking forward approach with a random information horizon was presented.
Author Contributions
Methodology, O.P.; formal analysis, L.S.; investigation, Y.L.; supervision, H.G.
Funding
The work of first author is supported by Postdoctoral International Exchange Program of China and funded by Russian Foundation for Basic Research (RFBR) according to the research project No. 18-00-00727 (18-00-00725). The work of last author is supported by National Natural Science Foundation of China (71571108).
Acknowledgments
Great thanks to Lihong Shi who while working in Huawei found time to contribute to this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Proof of Theorem 4
It is necessary to prove that the following conditions are satisfied:
Denote function
According to Definition 8, the right hand side of (A1) can be rewritten as:
The right hand side of (A3) is equal to according to Definition 11; therefore, (A1) is correct. Now, consider (A2), where the left hand side can be rewritten as:
(A2) is fulfilled for each stage, if for , the following condition is satisfied:
Fulfillment of Condition (A5) implies the fulfillment of the condition for each truncated subgame :
The theorem is proven.
Appendix A.2. Proof of Theorem 5
Appendix A.3. Proof of Theorem 6
The statement of the theorem is satisfied when the following two statements are true:
- 1.
- If players in every truncated subgame choose the imputation calculated using for then the resulting imputation belongs to core , calculated using the resulting characteristic function .
- 2.
- Core should not contain imputation , for which it is impossible to find the set of imputations in truncated subgame .
For the first statement, if the set of imputations satisfies the system of inequalities:
for , then the resulting imputation satisfies the system of inequalities:
Substitute the expression for into the left hand side of (A10). To the right hand side of (A10), substitute (22). It shows that for every , , the fulfillment of (24) leads to the fulfillment of (A9); hence, (A10) is satisfied. The first statement is proven.
For the second statement, any , , the following inequalities are satisfied in the set of imputations ,,:
If there exists one set of imputations , , in (A11) for which the inequalities (A9) are not satisfied, this unsatisfied inequalities will lead to the following condition for being satisfied:
which contradicts (24), so the theorem is proven.
Appendix A.4. Proof of Theorem 8
The Bellman equation for firm is given by:
Invoking (30) and for , and , the above Bellman equation becomes:
Performing the indicated maximization in the above yields:
for , and , then the feedback Nash equilibrium strategy of firm can be obtained in the form:
Anticipating that the controls will be shown to be positive, substituting it into (A13), collecting the terms together, then the parameters and can be expressed as:
where , ,
Appendix A.5. Proof of Theorem 9
Consider the Bellman function in the last stage, in the stage N. Performing the indicated maximization in it yields:
Invoking (36) and , the second equation in (35) becomes:
Performing the indicated maximization in the above yields:
for and , then the feedback Nash equilibrium strategy of firm can be obtained in the form:
Anticipating that the controls will be shown to be positive, substituting it into the second equation in (35), collecting the terms together, the parameters and can be expressed as:
In the stage , performing the indicated maximization in the third equation in (35) yields:
Anticipating that the controls will be shown to be positive, substituting it into the third equation in (35), collecting the terms together, then the parameters and can be expressed as:
where , ,
Appendix A.6. Proof of Theorem 10
The Bellman equation for the cooperative setting is given by:
Substituting (39) into (A14):
Substitute the right hand side of (30) to (A15). Performing the indicated maximization in (A15) yields:
Optimal cooperative strategies can be obtained in the form:
for , and
Anticipating the cooperative strategies will be shown to be positive, substituting it into (A15), hence and are defined as:
Appendix A.7. Proof of Theorem 11
Consider the Bellman function in the last stage, that is in the stage N. Performing the indicated maximization in it yields:
Invoking (41) and , then the second equation in (40) becomes:
Performing the indicated maximization in the above yields:
for and , then the feedback Nash equilibrium strategy of firm can be obtained in the form:
Anticipating that the controls will be shown to be positive, substituting this into the second equation in (40), collecting the terms together, then the parameters and can be expressed as:
For stage , performing the indicated maximization in third equation of (40) yields:
Anticipating that the controls will be shown to be positive, substituting this into the third equation in (40), collecting the terms together, then the parameters and can be expressed as:
where , ,
References
- Owen, G. Game Theory; Emerald Group Publishing Limited: Bingley, UK, 2013. [Google Scholar]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.F. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Basar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory; SIAM: Philadelphia, PA, USA, 1999; Volume 23. [Google Scholar]
- Chander, P.; Tulkens, H. A core-theoretic solution for the design of cooperative agreements on transfrontier pollution. In Public Goods, Environmental Externalities and Fiscal Competition; Springer: Berlin/Heidelberg, Germany, 2006; pp. 176–193. [Google Scholar]
- Haurie, A. A note on nonzero-sum differential games with bargaining solution. J. Optim. Theory Appl. 1976, 18, 31–39. [Google Scholar] [CrossRef]
- Petrosyan, L. Time-consistency of solutions in multi-player differential games. Vestn. Leningr. State Univ. 1977, 4, 46–52. [Google Scholar]
- Petrosyan, L.; Danilov, N. Stability of solutions in non-zero sum differential games with transferable payoffs. Vestn. Leningr. Univ. 1979, 1, 52–59. [Google Scholar]
- Petrosyan, L. Strongly time-consistent differential optimality principles. Vestn. St. Petersburg Univ. Math. 1993, 26, 40–46. [Google Scholar]
- Petrosyan, L.; Yeung, D.W.K. Dynamically stable cooperative solutions in randomly furcating differential games. Proc. Steklov Inst. Math. 2006, 253, S208–S220. [Google Scholar] [CrossRef]
- Jørgensen, S.; Yeung, D.W. Inter-and intragenerational renewableresource extraction. Ann. Oper. Res. 1999, 88, 275–289. [Google Scholar] [CrossRef]
- Jørgensen, S.; Martin-Herran, G.; Zaccour, G. Agreeability and time consistency in linear-state differential games. J. Optim. Theory Appl. 2003, 119, 49–63. [Google Scholar] [CrossRef]
- Petrosian, O. Looking Forward Approach in Cooperative Differential Games. Int. Game Theory Rev. 2016, 18, 1640007. [Google Scholar]
- Yeung, D.; Petrosian, O. Infinite Horizon Dynamic Games: A New Approach via Information Updating. Int. Game Theory Rev. 2017, 19, 1–16. [Google Scholar] [CrossRef]
- Gromova, E.; Petrosian, O. Control of information horizon for cooperative differential game of pollution control. In Proceedings of the International Conference on Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy’s Conference), Moscow, Russia, 1–3 June 2016; pp. 1–4. [Google Scholar]
- Petrosian, O.L. Looking Forward Approach in Cooperative Differential Games with Infinite-Horizon Vestn. St. Petersburg Univ. Math. 2016, 10, 18–30. [Google Scholar]
- Petrosian, O.; Barabanov, A. Looking Forward Approach in Cooperative Differential Games with Uncertain Stochastic Dynamics. J. Optim. Theory Appl. 2017, 172, 328–347. [Google Scholar] [CrossRef]
- Petrosian, O.; Nastych, M.; Volf, D. Differential game of oil market with moving informational horizon and non-transferable utility. In Proceedings of the Constructive Nonsmooth Analysis and Related Topics (Dedicated to the Memory of VF Demyanov) (CNSA), St. Petersburg, Russia, 22–27 May 2017; pp. 1–4. [Google Scholar]
- Petrosian, O.; Tur, A. Hamilton-Jacobi-Bellman Equations for Non-cooperative Differential Games with Continuous Updating. Commun. Comput. Inf. Sci. 2019. to be published. [Google Scholar]
- Kuchkarov, I.; Petrosian, O. On Class of Linear Quadratic Non-cooperative Differential Games with Continuous Updating. Lect. Notes Comput. Sci. 2019. to be published. [Google Scholar]
- Petrosian, O.; Nastych, M.; Volf, D. Non-cooperative Differential Game Model of Oil Market with Looking Forward Approach. Frontiers of Dynamic Games, Game Theory and Management, St. Petersburg, 2017; Petrosyan, L.A., Mazalov, V.V., Zenkevich, N., Eds.; Birkhäuser: Basel, Switzerland, 2018. [Google Scholar]
- Huang, J.; Leng, M.; Liang, L. Recent developments in dynamic advertising research. Eur. J. Oper. Res. 2012, 220, 591–609. [Google Scholar] [CrossRef]
- Feichtinger, G.; Hartl, R.F.; Sethi, S.P. Dynamic optimal control models in advertising: Recent developments. Manag. Sci. 1994, 40, 195–226. [Google Scholar] [CrossRef]
- Jorgensen, S.; Zaccour, G. Differential Games in Marketing. International Series in Quantitative Marketing; Springer: New York, NY, USA, 2004. [Google Scholar]
- He, X.; Prasad, A.; Sethi, S.P.; Gutierrez, G.J. A survey of Stackelberg differential game models in supply and marketing channels. J. Syst. Sci. Syst. Eng. 2007, 16, 385–413. [Google Scholar] [CrossRef]
- Aust, G.; Buscher, U. Vertical cooperative advertising in a retailer duopoly. Comput. Ind. Eng. 2014, 72, 247–254. [Google Scholar] [CrossRef]
- Jørgensen, S.; Zaccour, G. A survey of game-theoretic models of cooperative advertising. Eur. J. Oper. Res. 2014, 237, 1–14. [Google Scholar] [CrossRef]
- Prasad, A.; Sethi, S.P.; Naik, P.A. Optimal Control of an Oligopoly Model of Advertising. IFAC Proc. Vol. 2009, 42, 91–96. [Google Scholar] [CrossRef]
- Helbing, D.; Brockmann, D.; Chadefaux, T.; Donnay, K.; Blanke, U.; Woolley-Meza, O.; Moussaid, M.; Johansson, A.; Krause, J.; Schutte, S.; et al. Saving Human Lives: What Complexity Science and Information Systems can Contribute. Phys. Soc. 2015, 158, 735–781. [Google Scholar] [CrossRef] [PubMed]
- Yeung, D.W.; Petrosyan, L.A. Subgame Consistent Economic Optimization: An Advanced Cooperative Dynamic Game Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Yeung, D. On differential games with a feedback Nash equilibrium. J. Optim. Theory Appl. 1994, 82, 181–188. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Petrosjan, L.A. Differential Pursuit Games; World Scientific Publishing Co Pte Ltd.: Singapore, 1993. [Google Scholar]
- Yeung, D.W.; Petrosjan, L.A. Cooperative Stochastic Differential Games; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yeung, D.W.; Petrosyan, L.A. Subgame consistent cooperative solution of dynamic games with random horizon. J. Optim. Theory Appl. 2011, 150, 78–97. [Google Scholar] [CrossRef]
- Shi, L.; Petrosian, O. A Dynamic Oligopoly Marketing Model of Advertising. In Proceedings of the 2017 International Conference on Eleventh International Conference “Game Theory and Management”, St. Petersburg, Russia, 28–30 June 2017; pp. 207–223. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).