On Inverses of the Dirac Comb
Abstract
1. Introduction
2. Notation
2.1. Equality between Generalized Functions
2.2. Vector-Valued Generalized Functions
2.3. Spaces of Generalized Functions
2.4. Smooth Functions versus Generalized Functions
2.5. Finite, Entire, Local and Regular Functions
2.6. Cross-Inverses
3. Preliminaries
3.1. Convolution-Multiplication Duality
3.2. Periodization-Discretization Duality
4. Cross-Inverses of the Dirac Comb
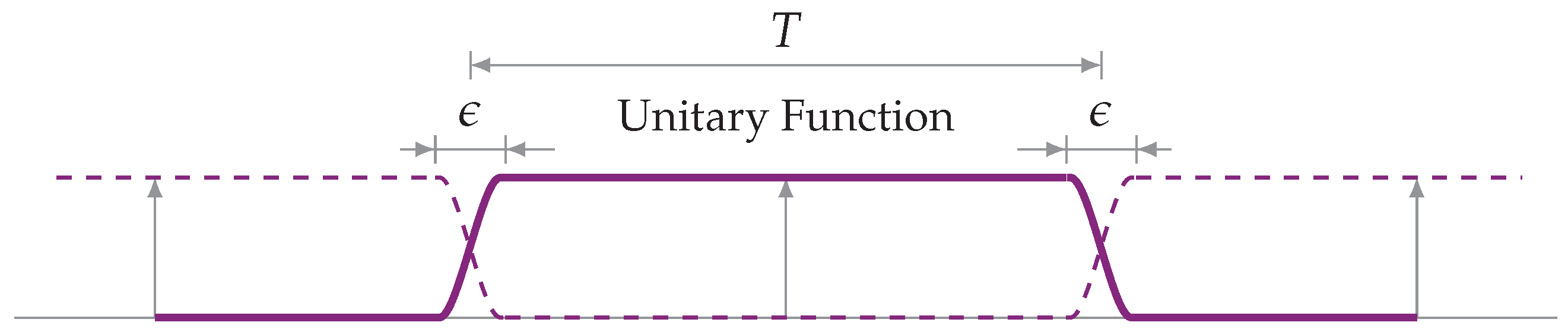
4.1. Single-Sided Partitions of Unity
4.2. Double-Sided Smooth Partitions of Unity
4.3. Operations Interpretation
4.4. Applications
4.5. Self-Reciprocity
5. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Construction of Unitary Functions
Appendix A.1. Construction via Integration
Appendix A.2. Construction via Regularization
References
- Schwartz, L. Théorie des Distributions, Tome I; Hermann: Paris, France, 1950. [Google Scholar]
- Schwartz, L. Théorie des Distributions, Tome II; Hermann: Paris, France, 1951. [Google Scholar]
- Halperin, I.; Schwartz, L. Introduction to the Theory of Distributions; University of Toronto Press, Scholarly Publishing: Toronto, ON, Canada, 1952. [Google Scholar]
- Temple, G. The Theory of Generalized Functions. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1955, 228, 175–190. [Google Scholar]
- Lighthill, M.J. An Introduction to Fourier Analysis and Generalised Functions; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Erdélyi, A. Operational Calculus and Generalized Functions; Holt, Rinehart and Winston, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Gel’fand, I.M.; Vilenkin, N.Y. Generalized Functions: Applications of Harmonic Analysis; Academic Press: New York, NY, USA, 1964; Volume 4. [Google Scholar]
- Zemanian, A. Distribution Theory And Transform Analysis—An Introduction to Generalized Functions, with Applications; McGraw-Hill Inc.: New York, NY, USA, 1965. [Google Scholar]
- Horváth, J. Topological Vector Spaces and Distributions; Addison-Wesley Publishing Company: Reading, MA, USA, 1966. [Google Scholar]
- Jones, D. The Theory of Generalized Functions; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Trèves, F. Topological Vector Spaces, Distributions and Kernels: Pure and Applied Mathematics; Dover Publications Inc.: Mineola, NY, USA, 1967; Volume 25. [Google Scholar]
- Zemanian, A. An Introduction to Generalized Functions and the Generalized Laplace and Legendre Transformations. SIAM Rev. 1968, 10, 1–24. [Google Scholar] [CrossRef]
- Zemanian, A.H. Generalized Integral Transformations; Dover Publications Inc.: Mineola, NY, USA, 1968. [Google Scholar]
- Gel’fand, I.; Schilow, G. Verallgemeinerte Funktionen (Distributionen), Teil I-II; Deutscher Verlag der Wissenschaften: Berlin, Germany, 1969. [Google Scholar]
- Ehrenpreis, L. Fourier Analysis in Several Complex Variables; John Wiley & Sons, Inc.: Mineola, NY, USA, 1970. [Google Scholar]
- Vladimirov, V.S. Gleichungen der Mathematischen Physik; Deutscher Verlag der Wissenschaften: Berlin, Germany, 1972. [Google Scholar]
- Barros-Neto, J. An Introduction to the Theory of Distributions; Marcel Dekker Inc.: New York, NY, USA, 1973. [Google Scholar]
- Peterson, B.E. Introduction to the Fourier Transform and Pseudo-Differential Operators; Pitman Publishing Inc.: Marshfield, MA, USA, 1983. [Google Scholar]
- Hörmander, L. The Analysis of Linear Partial Differential Operators I, Die Grundlehren der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Hoskins, R.F.; Pinto, J.S. Distributions, Ultradistributions and Other Generalized Functions; Woodhead Publishing Ltd.: Cambridge, UK, 1994. [Google Scholar]
- Walter, W. Einführung in die Theorie der Distributionen; BI-Wissenschaftsverlag, Bibliographisches Institut & FA Brockhaus: Mannheim, Germany, 1994. [Google Scholar]
- Zayed, A.I. Handbook of Function and Generalized Function Transformations; CRC Press Inc.: Boca Raton, FL, USA, 1996. [Google Scholar]
- Vladimirov, V.S. Methods of the Theory of Generalized Functions; CRC Press Inc.: Boca Raton, FL, USA, 2002. [Google Scholar]
- Strichartz, R.S. A Guide to Distribution Theory and Fourier Transforms; World Scientific Publishing Co. Pte Ltd.: Singapore, 2003. [Google Scholar]
- Rahman, M. Applications of Fourier Transforms to Generalized Functions; WIT Press: Southampton, UK, 2011. [Google Scholar]
- Mikusiński, J. On the square of the Dirac delta-distribution. Bull. de l’Acad. Pol. Sci. Sér. Sci. Math. Astr. Phys. 1966, 14, 511–513. [Google Scholar]
- Koh, E.; Li, C. On defining the generalized functions δα(z) and δn(x). Int. J. Math. Math. Sci. 1993, 16, 749–754. [Google Scholar] [CrossRef]
- Özçağ, E. Defining the k-th Powers of the Dirac-Delta Distribution for Negative Integers. Appl. Math. Lett. 2001, 14, 419–423. [Google Scholar] [CrossRef]
- Li, C. A Review on the Products of Distributions. In Mathematical Methods in Engineering; Springer: Dordrecht, The Netherlands, 2007; pp. 71–96. [Google Scholar]
- Accardi, L.; Boukas, A. Powers of the Delta Function. In Quantum Probability and Infinite Dimensional Analysis; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2007; pp. 33–44. [Google Scholar]
- Kiliçman, A. Note on the Products of Distributions. Math Dig. Res. Bull. Inst. Math. Res. 2008, 1, 1–5. [Google Scholar]
- Li, C. The Powers of the Dirac Delta Function by Caputo Fractional Derivatives. J. Fract. Calc. Appl. 2016, 7, 12–23. [Google Scholar]
- Özçağ, E. Results on Compositions Involving Dirac-Delta Function; AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2017; Volume 1895, p. 050007. [Google Scholar]
- Özçağ, E. On Powers of the Compositions Involving Dirac-Delta and Infinitely Differentiable Functions. Results Math. 2018, 73, 6. [Google Scholar] [CrossRef]
- Dirac, P. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Córdoba, A. Dirac Combs. Lett. Math. Phys. 1989, 17, 191–196. [Google Scholar] [CrossRef]
- Oberguggenberger, M.B. Multiplication of Distributions and Applications to Partial Differential Equations; Longman Scientific & Technical: Harlow, UK, 1992; Volume 259. [Google Scholar]
- Friedrichs, K.O. On the Differentiability of the Solutions of Linear Elliptic Differential Equations. Commun. Pure Appl. Math. 1953, 6, 299–326. [Google Scholar] [CrossRef]
- Schechter, M. Modern Methods in Partial Differential Equations, An Introduction; McGraw-Hill Book Company: New York, NY, USA, 1977. [Google Scholar]
- Gasquet, C.; Witomski, P. Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets; Springer Science & Business Media: New York, NY, USA, 1999; Volume 30. [Google Scholar]
- Simon, B. Distributions and their Hermite Expansions. J. Math. Phys. 1971, 12, 140–148. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. II: Fourier Analysis, Self-Adjointness; Academic Press Inc.: New York, NY, USA, 1975; Volume II. [Google Scholar]
- Folland, G.B. Harmonic Analysis in Phase Space; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Messiah, A. Quantum Mechanics—Two Volumes Bound as One; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Mund, J.; Schroer, B.; Yngvason, J. String-Localized Quantum Fields from Wigner Representations. Phys. Lett. B 2004, 596, 156–162. [Google Scholar] [CrossRef][Green Version]
- Glimm, J.; Jaffe, A. Quantum Physics: A Functional Integral Point of View; Springer-Verlag Inc.: New York, NY, USA, 2012. [Google Scholar]
- de Costa Campos, L.M.B. Generalized Calculus with Applications to Matter and Forces; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Bahns, D.; Doplicher, S.; Morsella, G.; Piacitelli, G. Quantum Spacetime and Algebraic Quantum Field Theory. In Advances in Algebraic Quantum Field Theory; Springer: Cham, Switzerland, 2015; pp. 289–330. [Google Scholar]
- Li, C.; Li, C.; Humphries, T.; Plowman, H. Remarks on the Generalized Fractional Laplacian Operator. Mathematics 2019, 7, 320. [Google Scholar] [CrossRef]
- Dierolf, P. The Structure Theorem for Linear Transfer Systems. Note Mat. 1991, 11, 119–125. [Google Scholar]
- Osgood, B. The Fourier Transform and Its Applications; EE 261 Lecture Notes; Stanford University: Stanford, CA, USA, 2007. [Google Scholar]
- Süße, H.; Rodner, E. Bildverarbeitung und Objekterkennung; Springer: Wiesbaden, Germany, 2014. [Google Scholar]
- Smith, D.C. An Introduction to Distribution Theory for Signals Analysis. Digit. Signal Process. 2006, 16, 419–444. [Google Scholar] [CrossRef]
- Burger, W.; Burge, M.J. Digital Image Processing: An Algorithmic Introduction Using Java; Springer-Verlag: London, UK, 2016. [Google Scholar]
- Lützen, J. The Prehistory of the Theory of Distributions; Vol. 7, Studies in the History of Mathematics and Physical Sciences; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Debnath, L. A Short Biography of Paul A M Dirac and Historical Development of Dirac Delta Function. Int. J. Math. Educ. Sci. Technol. 2013, 44, 1201–1223. [Google Scholar] [CrossRef]
- Fischer, J.V. On the Duality of Discrete and Periodic Functions. Mathematics 2015, 3, 299–318. [Google Scholar] [CrossRef]
- Fischer, J.V. On the Duality of Regular and Local Functions. Mathematics 2017, 5, 41. [Google Scholar] [CrossRef]
- Fischer, J.V. Four Particular Cases of the Fourier Transform. Mathematics 2018, 6, 335. [Google Scholar] [CrossRef]
- Bracewell, R.N. Fourier Transform and its Applications; McGraw-Hill Book Company: New York, NY, USA, 1986. [Google Scholar]
- Kammler, D.W. A First Course in Fourier Analysis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Sebastião e Silva, J. Les fonctions analytiques comme ultra-distributions dans le calcul opérationnel. Math. Ann. 1958, 136, 58–96. [Google Scholar] [CrossRef]
- Bengel, G. Das Weylsche Lemma in der Theorie der Hyperfunktionen. Math. Z. 1967, 96, 373–392. [Google Scholar] [CrossRef]
- Bényi, Á.; Grafakos, L.; Gröchenig, K.; Okoudjou, K. A Class of Fourier Multipliers for Modulation Spaces. Appl. Comput. Harmon. Anal. 2005, 19, 131–139. [Google Scholar] [CrossRef]
- Bényi, Á.; Gröchenig, K.; Okoudjou, K.A.; Rogers, L.G. Unimodular Fourier Multipliers for Modulation Spaces. J. Funct. Anal. 2007, 246, 366–384. [Google Scholar] [CrossRef]
- Cordero, E.; Trapasso, S.I. Linear Perturbations of the Wigner Distribution and the Cohen’s Class. arXiv 2018, arXiv:1811.07795. [Google Scholar]
- Bayer, D.; Cordero, E.; Gröchenig, K.; Trapasso, S.I. Linear Perturbations of the Wigner Transform and the Weyl Quantization. arXiv 2019, arXiv:1906.02503. [Google Scholar]
- Kaplan, W. Operational Methods for Linear Systems; Addison-Wesley Pub. Co.: Boston, MA, USA, 1962. [Google Scholar]
- Chandrasekharan, K. Classical Fourier Transforms; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Fischer, J. Anwendung der Theorie der Distributionen auf ein Problem in der Signalverarbeitung. Diploma Thesis, Ludwig-Maximillians-Universität München, Fakultät für Mathematik, Munich, Germany, 1997. [Google Scholar]
- Forster, O. Analysis 3, Integralrechnung im IRn mit Anwendungen, 3. Auflage; Vieweg: Wiesbaden, Germany, 1984. [Google Scholar]
- Hasumi, M. Note on the n-dimensional Tempered Ultra-Distributions. Tohoku Math. J. Second Ser. 1961, 13, 94–104. [Google Scholar] [CrossRef]
- Kiliçman, A. Generalized Functions Using the Neutrix Calculus. Ph.D. Thesis, University of Leicester, Leicester, UK, 1995. [Google Scholar]
- Berenstein, C.A.; Gay, R. Exponential Polynomials. In Complex Analysis and Special Topics in Harmonic Analysis; Springer: New York, NY, USA, 1995. [Google Scholar]
- Mikusiński, J. Irregular Operations on Distributions. Stud. Math. 1961, 20, 163–169. [Google Scholar] [CrossRef]
- Kamiński, A. Convolution, Product and Fourier Transform of Distributions. Stud. Math. 1982, 74, 83–96. [Google Scholar] [CrossRef]
- Gruber, M. Proofs of the Nyquist-Shannon Sampling Theorem. Bachelor’s Thesis, University Konstanz, Konstanz, Germany, 2013. [Google Scholar]
- Woodward, P.M. Probability and Information Theory, with Applications to Radar; Pergamon Press Ltd.: Oxford, UK, 1953. [Google Scholar]
- Campbell, L. Sampling Theorems for the Fourier Transform of a Distribution with Bounded Support. SIAM J. Appl. Math. 1968, 16, 626–636. [Google Scholar] [CrossRef]
- Lüke, H.D. The Origins of the Sampling Theorem. IEEE Commun. Mag. 1999, 37, 106–108. [Google Scholar] [CrossRef]
- Unser, M. Sampling-50 Years after Shannon. Proc. IEEE 2000, 88, 569–587. [Google Scholar] [CrossRef]
- Boyd, J.P. Construction of Lighthill’s Unitary Functions: The Imbricate Series of Unity. Appl. Math. Comput. 1997, 86, 1–10. [Google Scholar] [CrossRef]
- Boyd, J.P. Asymptotic Fourier Coefficients for a C∞ Bell (Smoothed-”Top-Hat”) & the Fourier Extension Problem. J. Sci. Comput. 2006, 29, 1–24. [Google Scholar]
- Termonia, P.; Voitus, F.; Degrauwe, D.; Caluwaerts, S.; Hamdi, R. Application of Boyd’s Periodization and Relaxation Method in a Spectral Atmospheric Limited-Area Model. Part I: Implementation and Reproducibility Tests. Mon. Weather Rev. 2012, 140, 3137–3148. [Google Scholar] [CrossRef]
- Bodmann, B.G.; Hoffman, D.K.; Kouri, D.J.; Papadakis, M. Hermite Distributed Approximating Functionals as Almost-Ideal Low-Pass Filters. Sampl. Theory Signal Image Process. 2008, 7, 15. [Google Scholar]
- Feichtinger, H.G. Banach Convolution Algebras of Wiener Type. Funct. Ser. Oper. Proc. Conf. Bp. 1980, 38, 509–524. [Google Scholar]
- Ionescu-Tira, M. Time-Frequency Analysis in the Unit Ball. arXiv 2019, arXiv:1905.03178. [Google Scholar]
- Bogolyubov, N.N.; Shirkov, D. Introduction to the Theory of Quantized Fields. Intersci. Monogr. Phys. Astron. 1980, 3, 1–720. [Google Scholar] [CrossRef]
- Accardi, L.; Boukas, A. The Emergence of the Virasoro and w∞ Algebras through the Renormalized Higher Powers of Quantum White Noise. arXiv 2006, arXiv:math-ph/0607062. [Google Scholar]
- Accardi, L.; Boukas, A. Renormalized Higher Powers of White Noise (RHPWN) and Conformal Field Theory. Infinite Dimens. Anal. Quantum Probab. Relat. Top. 2006, 9, 353–360. [Google Scholar] [CrossRef]
- Accardi, L.; Boukas, A. Quantum Probability, Renormalization and Infinite Dimensional ∗–Lie Algebras. Symm. Integrab. Geom. Methods Appl. 2009, 5, 056. [Google Scholar] [CrossRef][Green Version]
- Hardy, G.H.; Titchmarsh, E. Self-Reciprocal Functions. Q. J. Math. 1930, 9, 196–231. [Google Scholar] [CrossRef]
- Born, M. A Suggestion for Unifying Quantum Theory and Relativity. J. Chem. Phys. 1938, 3, 439–444. [Google Scholar] [CrossRef]
- Born, M. Reciprocity Theory of Elementary Particles. Rev. Mod. Phys. 1949, 21, 463. [Google Scholar] [CrossRef]
- Cowley, J.; Moodie, A. Fourier Images: II-The Out-of-focus Patterns. Proc. Phys. Soc. Sect. B 1957, 70, 497. [Google Scholar] [CrossRef]
- de Branges, L. Self-Reciprocal Functions. J. Math. Anal. Appl. 1964, 9, 433–457. [Google Scholar] [CrossRef]
- Wei, G. Quasi Wavelets and Quasi Interpolating Wavelets. Chem. Phys. Lett. 1998, 296, 215–222. [Google Scholar] [CrossRef]
- Wei, G.W.; Gu, Y. Conjugate Filter Approach for Solving Burgers’ Equation. J. Comput. Appl. Math. 2002, 149, 439–456. [Google Scholar] [CrossRef]


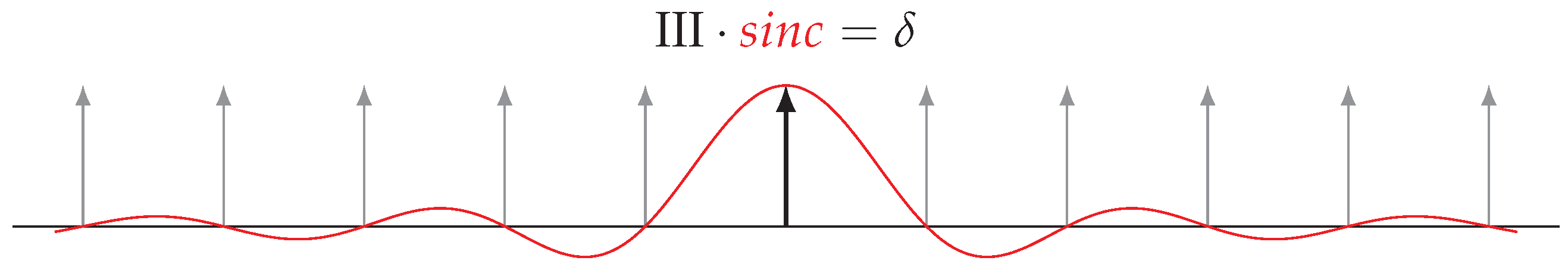
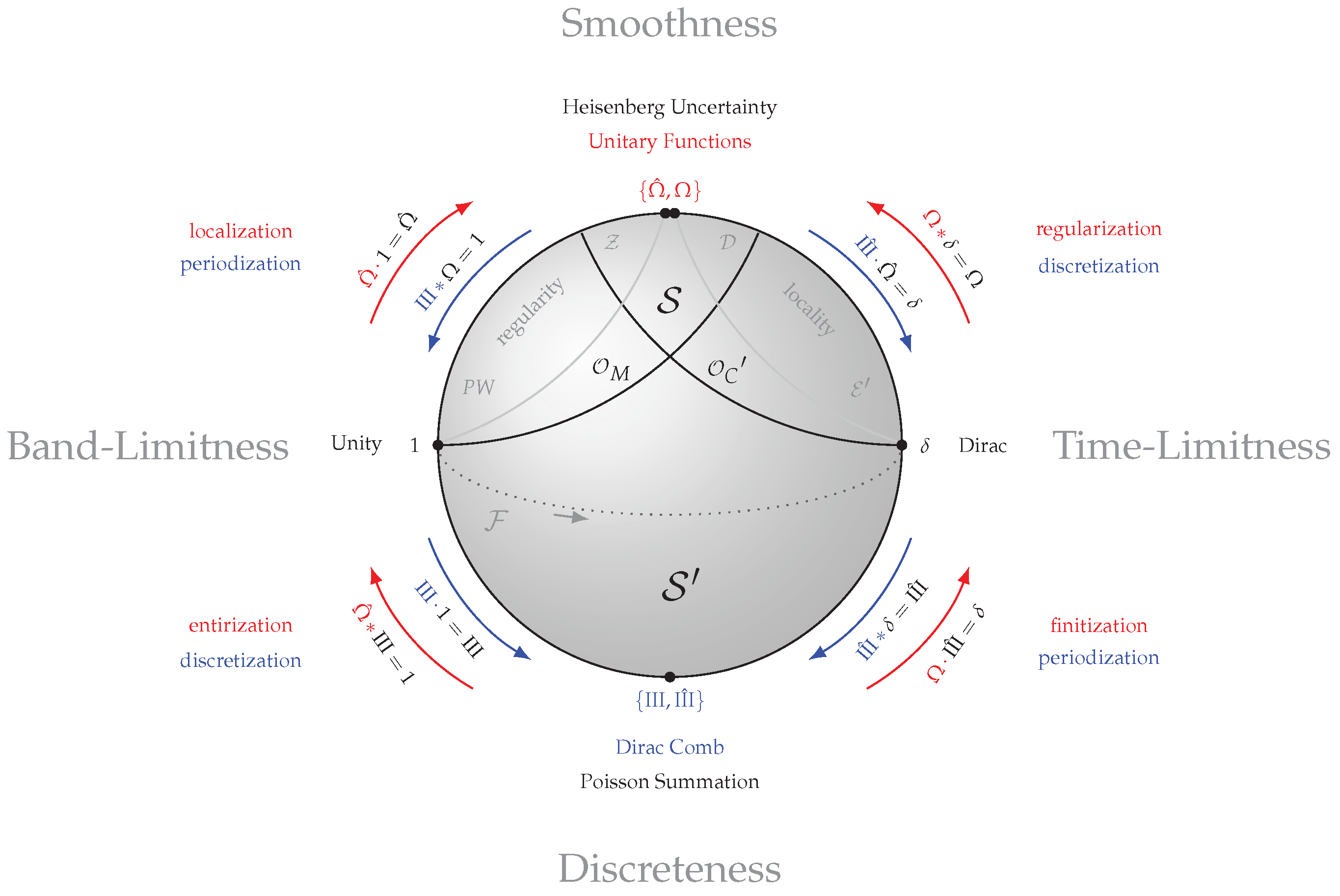
| No | Operation | Domain | Definition | Goal | Result | Function |
|---|---|---|---|---|---|---|
| I | Discretization | Discreteness (time) | discrete | |||
| II | Periodization | Discreteness (freq) | periodic | |||
| (i) | Regularization | Smoothness (time), smooth | regular | |||
| (ii) | Localization | Smoothness (freq), smooth | local | |||
| [i] | Finitization | Smoothness (freq), sharp | finite | |||
| [ii] | Entirization | Smoothness (time), sharp | entire |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, J.V.; Stens, R.L. On Inverses of the Dirac Comb. Mathematics 2019, 7, 1196. https://doi.org/10.3390/math7121196
Fischer JV, Stens RL. On Inverses of the Dirac Comb. Mathematics. 2019; 7(12):1196. https://doi.org/10.3390/math7121196
Chicago/Turabian StyleFischer, Jens V., and Rudolf L. Stens. 2019. "On Inverses of the Dirac Comb" Mathematics 7, no. 12: 1196. https://doi.org/10.3390/math7121196
APA StyleFischer, J. V., & Stens, R. L. (2019). On Inverses of the Dirac Comb. Mathematics, 7(12), 1196. https://doi.org/10.3390/math7121196







