Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method
Abstract
1. Introduction
2. Fractional Calculus and CAS Wavelets
2.1. Function Approximations
2.2. CAS Wavelet Operational Matrix
3. Approximate Solutions of BVP via Green-CAS Wavelet Method
Numerical Procedure to Fractional Linear Differential Equations
4. Existence and Uniqueness
5. Applications
5.1. Linear Case
5.2. Non-Linear Case
6. Error Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, J.H. A new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 1997, 2, 230–235. [Google Scholar] [CrossRef]
- He, J.H. Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 1998, 167, 57–68. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Anh, V.V.; Leonenko, N.N. Spectral analysis of fractional kinetic equations with random data. J. Stat. Phys. 2001, 104, 1349–1387. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Ciesielski, M.; Klimek, M.; Leszczynski, J. Numerical solution of fractional oscillator equation. Appl. Math. Comput. 2011, 218, 2480–2488. [Google Scholar] [CrossRef]
- Khan, N.A.; Ara, A.; Ali, S.A.; Mahmood, A. Analytical study of Navier-Stokes equation with fractional orders using He’s homotopy perturbation and variational iteration methods. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 1127–1134. [Google Scholar] [CrossRef]
- Schulz, B.M.; Schulz, M. Numerical investigations of anomalous diffusion effects in glasses. J. Non-Cryst. Solids 2006, 352, 4884–4887. [Google Scholar] [CrossRef]
- Burgos, C.; Cortés, J.C.; Villafuerte, L.; Villanueva, R.J. Mean square calculus and random linear fractional differential equations: Theory and applications. Appl. Math. Nonlinear Sci. Appl. Math. Nonl. Sci. 2017, 2, 317–328. [Google Scholar] [CrossRef]
- Youssef, I.K.; el Dewaik, M.H. Solving Poisson’s Equations with fractional order using Haarwavelet. Appl. Math. Nonlinear Sci. Appl. Math. Nonlinear Sci. 2017, 2, 271–284. [Google Scholar] [CrossRef]
- Guirao, J.L.G.; Bayram, M. Computational Methods in Applied Analysis and Mathematical Modeling; MDPI: Basel, Switzerland, 2019; ISSN 2227-7390. [Google Scholar]
- He, J.H. Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol. Soc. 1999, 15, 86–90. [Google Scholar]
- Magin, R.L. Fractional calculus in bioengineering. Redd. Begell House 2006, 32, 105–194. [Google Scholar]
- Engheta, N. On fractional calculus and fractional multipoles in electromagnetism. IEEE Trans. Antennas Propag. 1996, 44, 554–566. [Google Scholar] [CrossRef]
- Sierociuk, D.; Dzielinski, A.; Sarwas, G.; Petras, I.; Podlubny, I.; Skovranek, T. Modelling heat transfer in heterogeneous media using fractional calculus. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120146. [Google Scholar] [CrossRef] [PubMed]
- Cosenza, P.; Korosak, D. Secondary consolidation of clay as an anomalous diffusion process. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1231–1246. [Google Scholar] [CrossRef]
- Pagnini, G. Erdelyi-Kober fractional diffusion. Fract. Calc. Appl. Anal. 2012, 15, 117–127. [Google Scholar] [CrossRef]
- Martinez-Garcia, M.; Gordon, T. Human control of systems with fractional order dynamics. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016. [Google Scholar]
- Martinez-Garcia, M.; Gordon, T.; Shu, L. Extended crossover model for human-control of fractional order plants. IEEE Access 2017, 5, 27622–27635. [Google Scholar] [CrossRef]
- Li, B.C.; Luo, J.S. Wavelet Analysis and Its Application; Electronic Industrial Publication: Beijing, China, 2005. [Google Scholar]
- Yousefi, S.; Banifatemi, A. Numerical solution of Fredholm integral equations by using CAS wavelets. Appl. Math. Comput. 2006, 183, 458–463. [Google Scholar] [CrossRef]
- Yi, M.; Huang, J. CAS wavelet method for solving the fractional integro-differential equation with a weakly singular kernel. Int. J. Comput. Math. 2014, 92, 1715–1728. [Google Scholar] [CrossRef]
- Shamooshaky, M.M.; Assari, P.; Adibi, H. CAS wavelet method for the numerical solution of boundary integral equations with logarithmic singular kernels. Int. J. Math. Model. Comput. 2014, 4, 377–987. [Google Scholar]
- Saeedi, H.; Moghadam, M.M. Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1216–1226. [Google Scholar] [CrossRef]
- Saeed, U. CAS Picard method for fractional nonlinear differential equation. Appl. Math. Comput. 2017, 307, 102–112. [Google Scholar] [CrossRef]
- Aziz, I.; Khan, W. Numerical integration of multi-dimensional highly oscillatory, gentle oscillatory and non-oscillatory integrands based on wavelets and radial basis functions. Eng. Anal. Bound. Elem. 2012, 36, 1284–1295. [Google Scholar]
- Aziz, I.; Fayyaz, M. A new approach for numerical solution of integro-differential equations via Haar wavelets. Int. J. Comput. Math. 2013, 90, 1971–1989. [Google Scholar]
- Saeed, U.; Rehman, M. Haar wavelet-quasilinearization technique for fractional nonlinear differential equations. Appl. Math. Comput. 2013, 220, 630–648. [Google Scholar] [CrossRef]
- Wu, J.L. A wavelet operational method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2009, 214, 31–40. [Google Scholar] [CrossRef]
- Lepik, Ü. Numerical solution of evolution equations by the Haar wavelet method. Appl. Math. Comput. 2007, 185, 695–704. [Google Scholar] [CrossRef]
- Rehman, M.; Khan, R.A. A numerical method for solving boundary value problems for fractional differential equations. Appl. Math. Model. 2012, 36, 894–907. [Google Scholar] [CrossRef]
- Diaz, L.A.; Martin, M.T.; Vampa, V. Daubechies wavelet beam and plate finite elements. Finite Elem. Anal. Des. 2009, 45, 200–209. [Google Scholar] [CrossRef]
- Dehghan, M.; Lakestani, M. Numerical solution of nonlinear system of second-order boundary value problems using cubic B-spline scaling functions. Int. J. Comput. Math. 2008, 85, 1455–1461. [Google Scholar] [CrossRef]
- Rehman, M.; Khan, R.A. The Legendre wavelet method for solving fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4163–4173. [Google Scholar] [CrossRef]
- Wang, X.T. Numerical solution of time-varying systems with a stretch by general Legendre wavelets. Appl. Math. Comput. 2008, 198, 613–620. [Google Scholar] [CrossRef]
- Khan, H.; Arif, M.; Mohyud-Din, S.T. Numerical Solution of Fractional Boundary Value Problems by Using Chebyshev Wavelet. Matrix Sci. Math. 2019, 3, 13–26. [Google Scholar] [CrossRef]
- Akgül, A.; Akgül, E.K. A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems. Fractal Fract. 2019, 3, 33. [Google Scholar] [CrossRef]
- Gholami, S.; Babolian, E.; Javidi, M. Fractional pseudospectral integration/differentiation matrix and fractional differential equations. Appl. Math. Comput. 2019, 343, 314–327. [Google Scholar] [CrossRef]
- Patricio, M.F.S.; Ramos, H.; Patricio, M. Solving initial and boundary value problems of fractional ordinary differential equations by using collocation and fractional powers. J. Comput. Appl. Math. 2019, 354, 348–359. [Google Scholar] [CrossRef]
- Khan, R.A. Generalized approximation method for heat radiation equations. Appl. Math. Comput. 2009, 212, 287–295. [Google Scholar] [CrossRef]
- Saeed, U. Assessment of Haar wavelet-quasilinearization technique in heat convection-radiation equations. Appl. Comput. Intell. Soft Comput. 2014. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics 2004; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Kilicman, A.; al Zhour, Z.A.A. Kronecker operational matrices for fractional calculus and some applications. Appl. Math. Comput. 2007, 187, 250–265. [Google Scholar] [CrossRef]
- Conte, S.D.; de Boor, C. Elementary Numerical Analysis; SIAM: Philadelphia, PA, USA, 2018. [Google Scholar]
- Diethelm, K. An extension of the well-posedness concept for fractional differential equations of Caputo’s type. Appl. Anal. 2014, 93, 2126–2135. [Google Scholar] [CrossRef]
- Su, X.; Zhang, S. Solutions to boundary-value problems for nonlinear differential equations of fractional order. Electr. J. Differ. Equ. 2009, 2009, 1–15. [Google Scholar]
- Su, X. Boundary value problem for a coupled system of nonlinear fractional differential equations. Appl. Math. Lett. 2009, 22, 64–69. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Li, X.F. Approximate solution of linear ordinary differential equations with variable coefficients. Math. Comput. Simul. 2007, 75, 113–125. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier Publishing Company: New York, NY, USA, 1965. [Google Scholar]
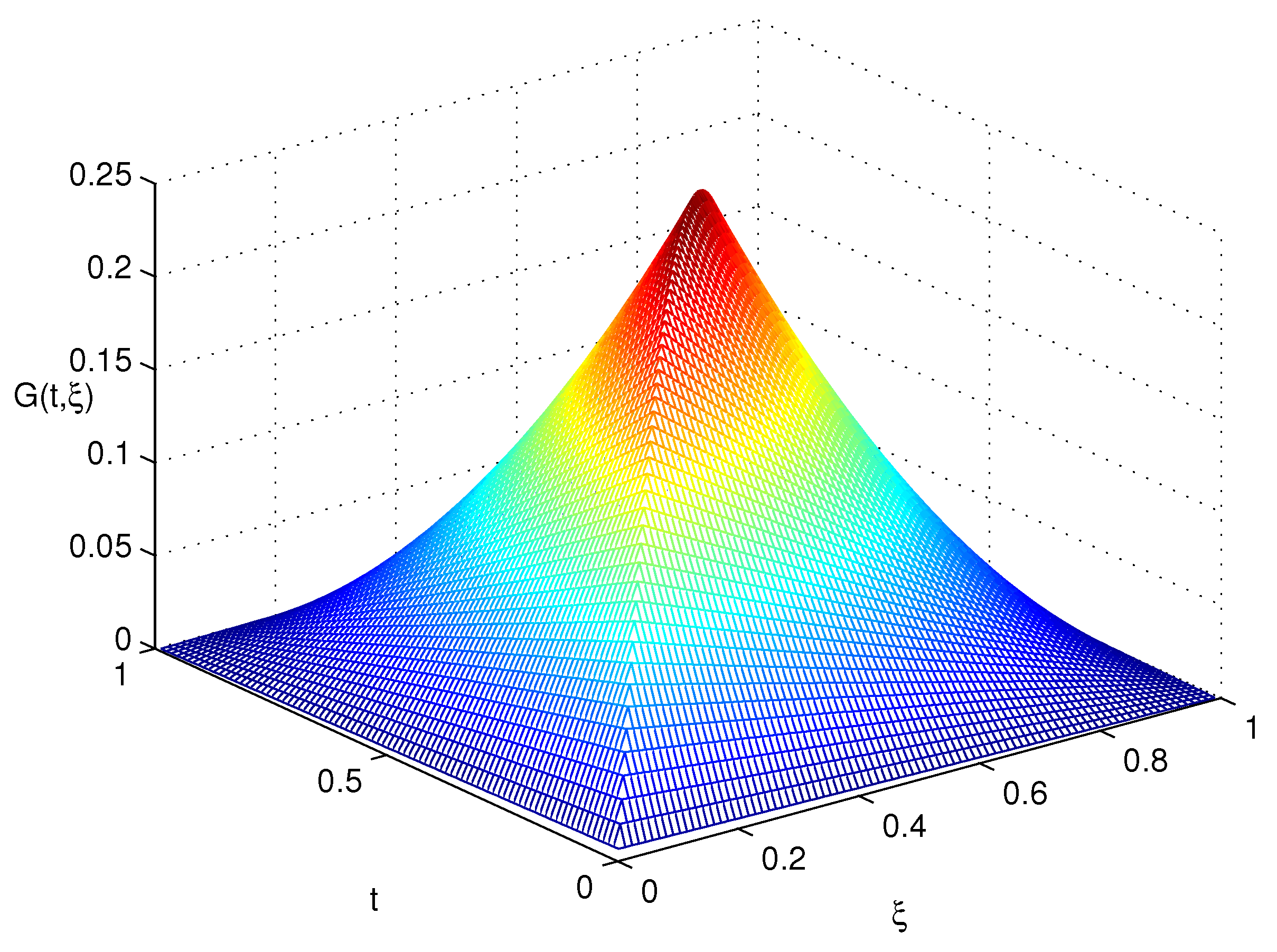
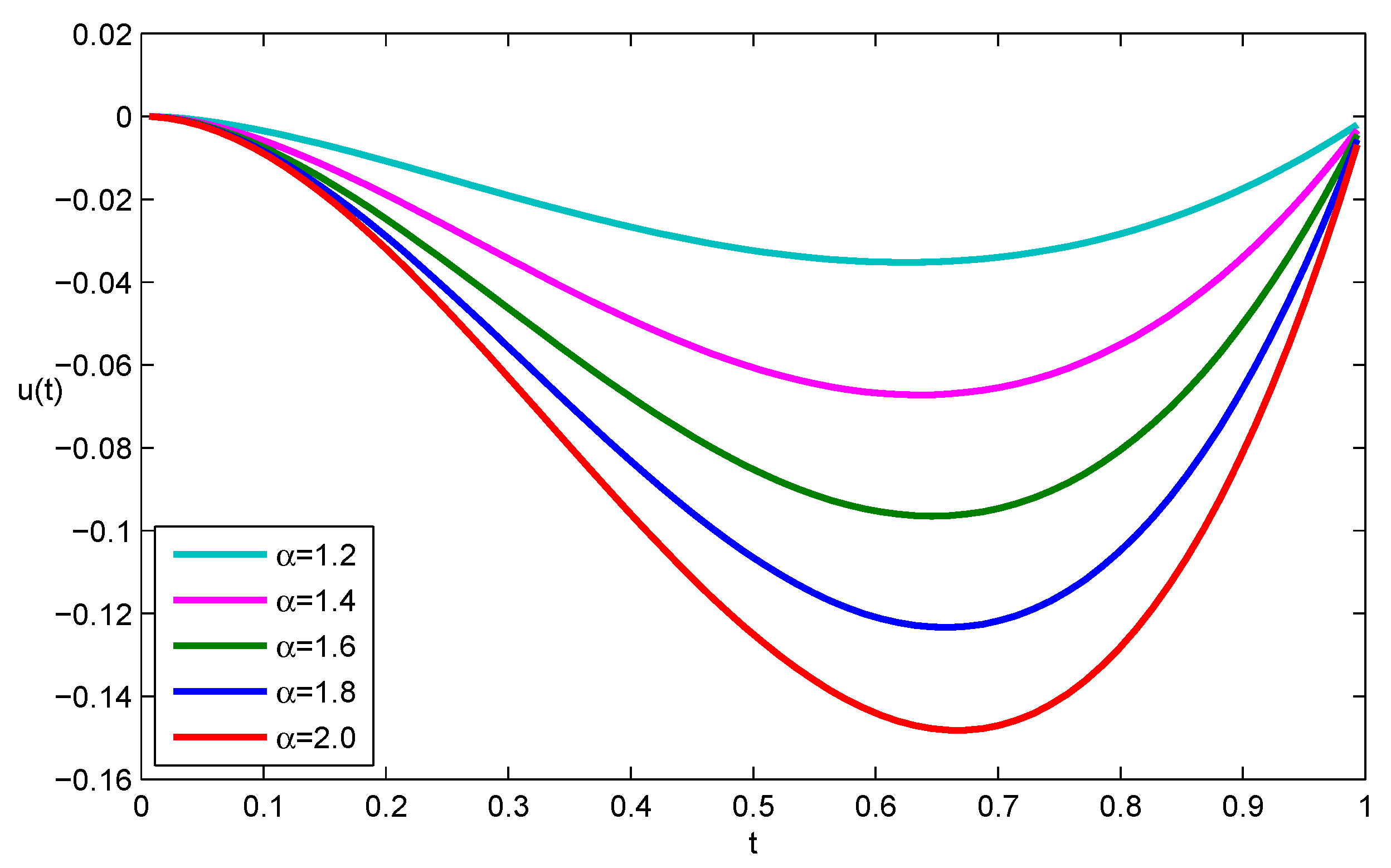
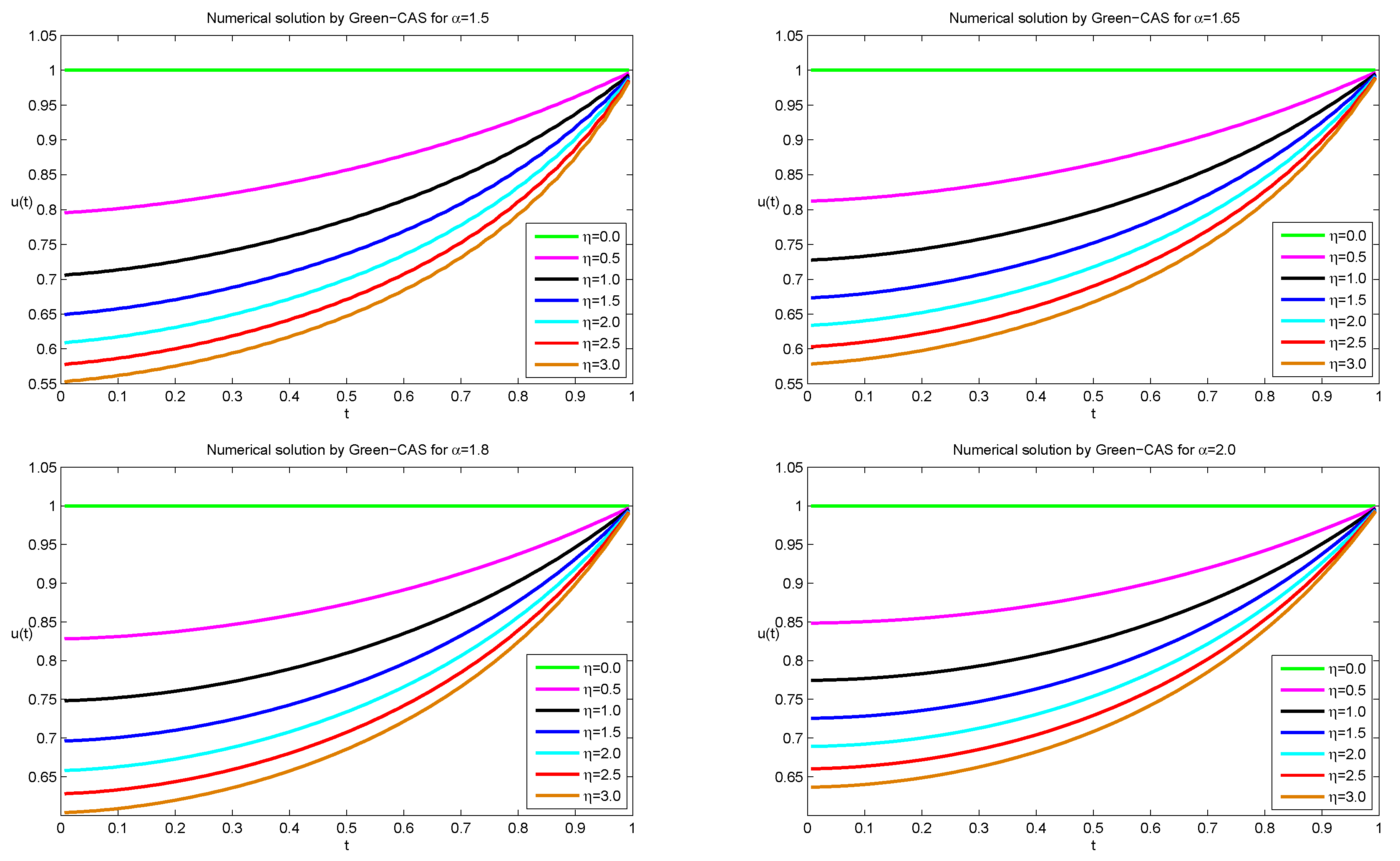
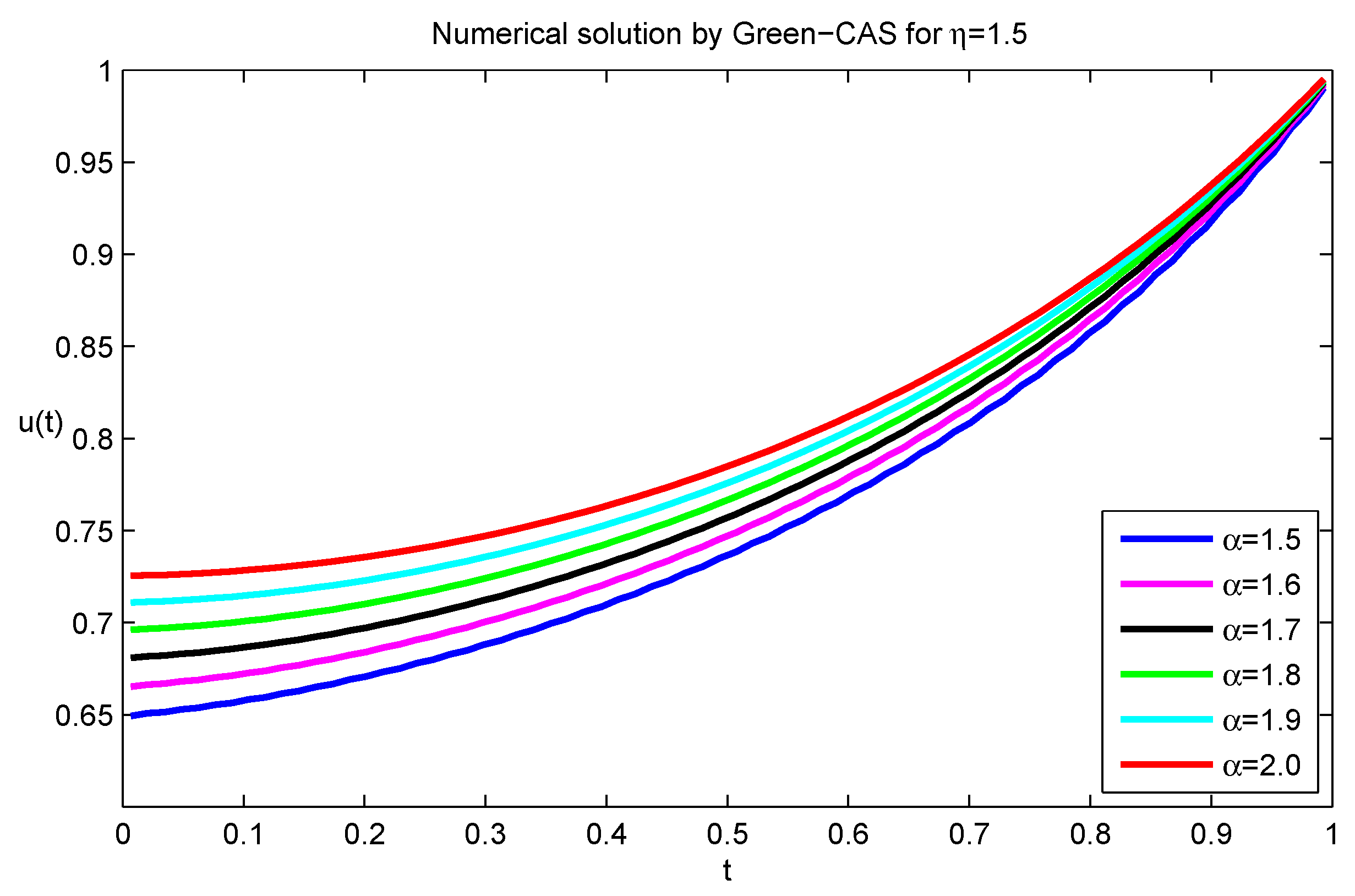
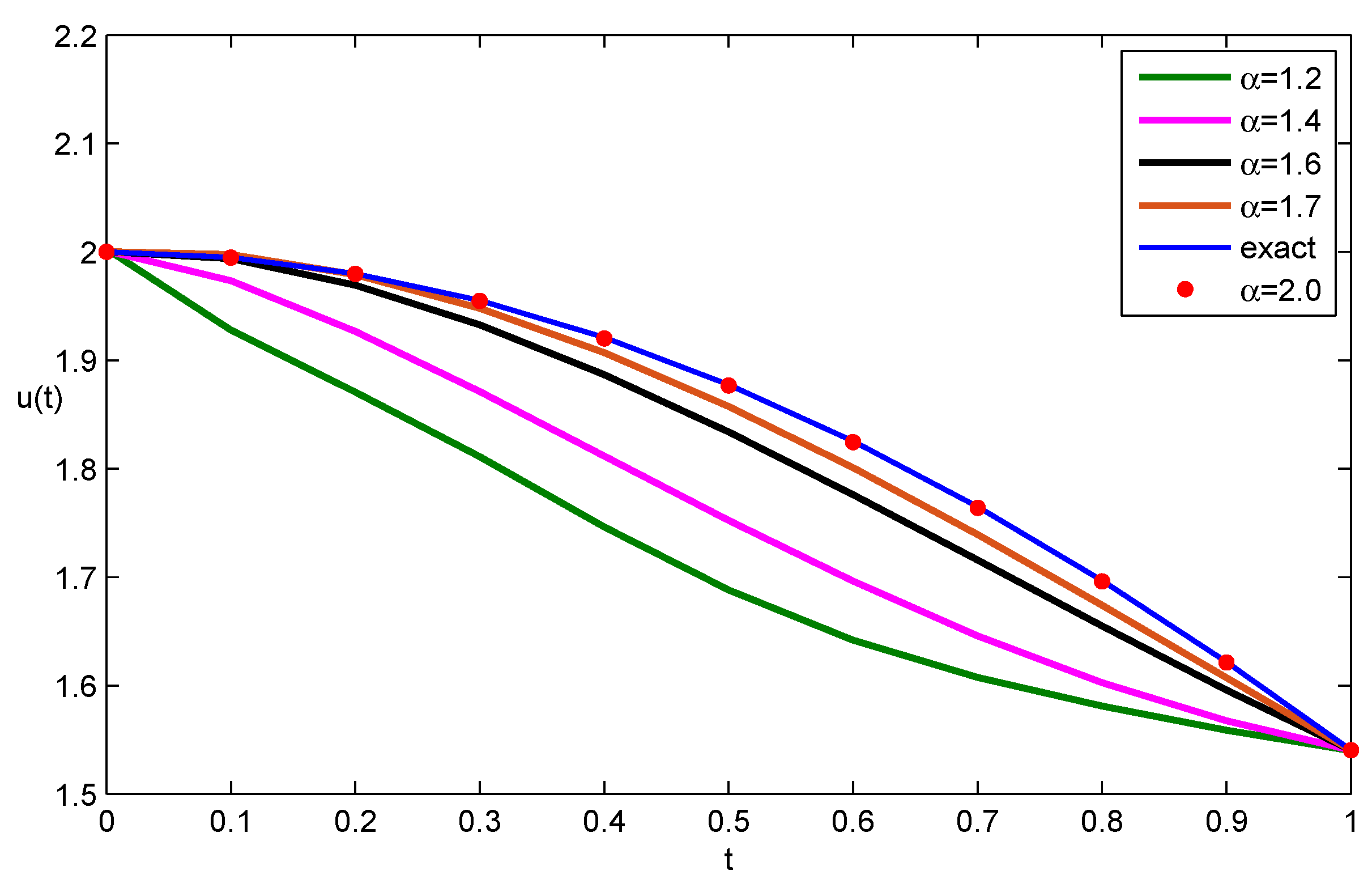
| t | |||||
|---|---|---|---|---|---|
| t | ||||
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, M.; Saeed, U.; Alzabut, J.; ur Rehman, M. Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method. Mathematics 2019, 7, 1164. https://doi.org/10.3390/math7121164
Ismail M, Saeed U, Alzabut J, ur Rehman M. Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method. Mathematics. 2019; 7(12):1164. https://doi.org/10.3390/math7121164
Chicago/Turabian StyleIsmail, Muhammad, Umer Saeed, Jehad Alzabut, and Mujeeb ur Rehman. 2019. "Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method" Mathematics 7, no. 12: 1164. https://doi.org/10.3390/math7121164
APA StyleIsmail, M., Saeed, U., Alzabut, J., & ur Rehman, M. (2019). Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method. Mathematics, 7(12), 1164. https://doi.org/10.3390/math7121164






