Abstract
A Pythagorean fuzzy set (PFS) is one of the extensions of the intuitionistic fuzzy set which accommodate more uncertainties to depict the fuzzy information and hence its applications are more extensive. In the modern decision-making process, aggregation operators are regarded as a useful tool for assessing the given alternatives and whose target is to integrate all the given individual evaluation values into a collective one. Motivated by these primary characteristics, the aim of the present work is to explore a group of interactive hybrid weighted aggregation operators for assembling Pythagorean fuzzy sets to deal with the decision information. The proposed aggregation operators include interactive the hybrid weighted average, interactive hybrid weighted geometric and its generalized versions. The major advantages of the proposed operators to address the decision-making problems are (i) to consider the interaction among membership and non-membership grades of the Pythagorean fuzzy numbers, (ii) it has the property of idempotency and simple computation process, and (iii) it possess an adjust parameter value and can reflect the preference of decision-makers during the decision process. Furthermore, we introduce an innovative multiple attribute decision making (MADM) process under the PFS environment based on suggested operators and illustrate with numerous numerical cases to verify it. The comparative analysis as well as advantages of the proposed framework confirms the supremacies of the method.
1. Introduction
Multiple attribute decision making (MADM) is one of the processes to find the most desirable alternative among all given alternatives in the light of finite attributes or criteria. In the decision-making process, it is commonly supposed that the evaluation information of alternatives for attributes described by decision-makers (DMs) is precise numbers. However, due to the indeterminacy of the practical environment and human cognition, DMs are usually do not find it easy to use crisp numbers to express their preferences. An appropriate way to deal with such problems is to adopt uncertain evaluations rather than crisp ones, for instance, an intuitionistic fuzzy set (IFS) [1] and fuzzy set (FS) [2]. As a successful extension of the notions of IFS and FS, the Pythagorean fuzzy set (PFS) was put forward by Yager [3,4]. Similar to the IFS, the PFS is still depicted by the membership and non-membership degrees, but their square sum within interval (0, 1). Thus, PFS is more versatile than IFS. For instance, if the membership grade is given as 0.4 by DM, while the non-membership grade is 0.8, it can be seen that , so IFS cannot solve this issue, but since , then the PFS can easily deal with it. Therefore, in some cases, the PFS can settle a large number of problems, while the IFS cannot. Since PFS appeared, it has become a useful technique for modeling vagueness and indeterminacy of the MADM issues or multiple attribute group decision making (MAGDM) issues [5,6,7,8,9,10,11,12]. Some evaluation methods in the light of PFS are given to solve Pythagorean fuzzy MADM problems. For instance, Rani et al. [13] extended traditional TOPSIS (technique for an order of preference by similarity to ideal solution) approach to Pythagorean fuzzy numbers (PFNs) and studied the selection of a sustainable recycling partner. Considering DM’s psychological characteristics, in the light of the prospect and regret theories, Peng and Dai [14] explored a stochastic decision approach under Pythagorean fuzzy setting. Ren et al. [15] extended traditional TODIM (an acronym in Portuguese of interactive and multiple attribute decision making) approach to PFNs. Chen [16] introduced a Pythagorean fuzzy VIKOR (vlseKriterijumska optimizacija I Kompromisno Resenje in Serbian) approach for MADM. Zhang [17] expanded the hierarchical QUALIFLEX (qualitative flexible multiple criteria method) algorithm to the interval-valued PFSs, and employed it to investigate the industries’ risk evaluation.
The way of evaluation methods in Pythagorean fuzzy decision-making problems is only one aspect, the other significant aspect is to aggregate these evaluation values. Aggregation operators (AOs) can integrate all the given individual evaluation values into a collective one, which is regarded as a useful tool for assessing alternatives. Now AOs are investigated more broadly under the Pythagorean fuzzy environment, and the research related to AOs are from general categories:
- (1)
- The operation of AOs defined by classical operational rules with PFSs [12]. Wei and Lu [18] developed six power AOs in Pythagorean fuzzy setting and also discussed desirable properties of them. Ma and Xu [19] employed the symmetric Pythagorean fuzzy AOs to settle MADM problems. Garg [20,21] defined exponential operation and logarithms operations for PFSs and discussed their relevant aggregation operators. In the light of the Einstein t-norm operations, Garg [22,23] introduced a series of generalized Pythagorean averaging and geometric AOs. With the aid of the Hamacher operations, Wu and Wei [24] introduced several Hamacher AOs for managing Pythagorean fuzzy MADM problems. Yu et al. [25] presented a kind of new Pythagorean fuzzy distance AOs. Wang and Li [26] developed four continuous interval-valued Pythagorean fuzzy AOs in MAGDM. Taking the relationship of aggregated PFNs into account, Qin [27] introduced the generalized form of Pythagorean fuzzy Maclaurin symmetric means. With the aid of the traditional Bonferroni mean (BM), Liang et al. [28] discussed a Pythagorean fuzzy geometric BM (PFGBM) operator. After that, a partitioned PFGBM operator was introduced by Liang et al. [29]. Wei and Lu [30] defined the Pythagorean fuzzy Maclaurin symmetric mean AOs for PFNs. Li et al. [31] proposed a series of Hamy mean operators under a Pythagorean fuzzy context. Li et al. [32] investigated two Pythagorean fuzzy power Muirhead mean AOs along with their properties and applied them to deal with the evaluation of domestic airlines.
- (2)
- The operation of AOs defined by the interactive operational rules with PFSs [33]. It is more reasonable in some situations, because it captures the interactive influence over the membership and non-membership grades of PFNs. For example, Let and be two PFNs, if membership degrees and , then in the light of operational rules [12], we get membership degree , which implies that has no effect on the result . Similarly, if non-membership degrees and , then has no effect on the result non-membership degree . To overcome this issue, Wei [33] introduced the interactive operation for PFNs and also some corresponding interactive AOs were developed. They are Pythagorean fuzzy interactive weighted average (PFIWA), ordered weighted average (PFIOWA), hybrid average (PFIHA), weighted geometric (PFIWG), ordered weighted geometric (PFIOWG) and hybrid geometric (PFIHG) operators. Garg [34,35] presented the concept of neutrality operational laws for PFNs and the AOs for solving the group decision making problems. Gao et al. [36] defined some interactive power AOs for PFNs. Yang and Pang [37] presented interactive Maclaurin symmetric mean AOs and corresponding weighted forms using the different PFNs for dealing with MADM problems. Garg [38] presented the generalized interactive weighted Einstein AOs for PFNs and hence solved the decision-making problems. Yang et al. [39] extended the traditional BM operator to a Pythagorean fuzzy environment and proposed some interactive partitioned BM operators as well as their interesting properties.
From these above analyses, we can see that different aggregation operators have different features and application aspects. The PFIWA and the PFIWG AOs can weigh only the significance of PFNs themselves, while the PFIOWA and the PFIOWG AOs can weigh the ordered positions of given PFNs but cannot weigh the PFNs themselves. Moreover, the PFIHA and the PFIHG operators may weigh all aggregated PFNs and correspond ordered positions of them. Therefore, the PFIHA and the PFIHG operators have some superiority over the operators described above. However, these two operators have a drawback that the aggregated value of some identical integrated PFNs relies on the weight values, that is they do not possess the property of idempotency. It was pointed out by Liao and Xu [40], hybrid aggregation operators should satisfy the basic property of idempotency, so they presented a group of hybrid operators under a hesitant fuzzy environment. However, these aggregation operators are not available to tackle the Pythagorean fuzzy MADM problems. PFS, a valuable generalization of IFSs, has been shown as a successful means to deal with the indeterminacy and fuzziness which appear in many real decision problems. The presented research concentrated on the Pythagorean fuzzy setting. Therefore, it was worth putting forward some novel Pythagorean fuzzy interactive hybrid operators. Inspired by this idea, the motivation and objective of this manuscript were to
- (1)
- explore novel Pythagorean fuzzy interactive hybrid weighted average (PFIHWA) and geometric (PFIHWG) operators, discuss some interesting properties and particular cases;
- (2)
- propose novel generalized PFIHWA (GPFIHWA) and generalized PFIHWG (GPFIHWG) operators, also study their desirable properties and special cases;
- (3)
- introduce some steps for MADM and MAGDM by using the proposed operators;
- (4)
- demonstrate the availability and flexibility of the proposed MADM and MAGDM methods through some practical examples.
The remaining paper is arranged as follows: Some fundamental notions about PFSs and the AOs are introduced in Section 2. Novel PFIHWA and PFIHWG operators along with their properties are given in Section 3. Generalized forms of the AOs are provided in Section 4. In Section 5, we use the presented AOs to tackle the MADM problems and MAGDM problems, and the availability as well as flexibility of the proposed methods is illustrated with some real examples. Section 6 summarizes the paper.
2. Preliminaries
We briefly review some fundamental notions about PFS and Pythagorean fuzzy AOs in this part.
2.1. Pythagorean Fuzzy Sets
Definition 1
[12]. Let be a universal set, a PFS is defined as:
where meet the condition: . define degrees of membership and non-membership for every , respectively. Indeterminacy degree is .
Zhang and Xu [12] called as a PFN, meets the condition and . denotes all Pythagorean fuzzy numbers (PFNs).
Some fundamental operational rules for PFNs given by Zhang and Xu [12] as follows:
Definition 2
[12]. Let and be three PFNs, then their operational laws are shown as follows:
where denotes complement operation of . and denote addition and multiplication between and , respectively.
Definition 3
[33]. Let and be three PFNs, then the interactive operational laws are given as follows:
Definition 4
[12]. Let be a PFN, and denote the score and the accuracy degree of , respectively. For two PFNs , we have
- (1)
- If, then;
- (2)
- If, then:
- (a)
- If, then;
- (b)
- If, then.
2.2. Interactive Aggregation Operators for PFNs
With the aid of interactive operational rules given as Definition 3, Wei [33] proposed some interactive aggregation operators for PFNs:
Definition 5
[33]. Suppose that are a family of PFNs and is the collection relevant vector of , with , . Then
(1) A PFIWA operator is a function, and
(2) A PFIWG operator is a function, and
Definition 6
[33]. Suppose that are a family of PFNs and is the collection relevant vector of , with , . means any permutation of satisfies . Then
(1) A PFIOWA operator is a function, and
(2) A PFIOWG operator is a function, and
Especially, if, then the PFIOWA (PFIOWG)operator becomes the PFIWA(PFIWG) operator.
Definition 7
[33]. Suppose that are a family of PFNs and is the collection relevant vector of , with , . means any permutation of satisfies . denotes the weight vector of with , . Thus
(1) A PFIHA operator is a function, and
in which,is the-th largest value of weighted PFNs,indicates the balancing coefficient.
(2) A PFIHG operator is a function, and
in which,is the-th largest value of weighted PFNs,indicates the balancing coefficient.
Especially, if, then the PFIHA (PFIHG)operator becomes the PFIWA (PFIWG)operator. If, then the PFIHA(PFIHG)operator becomes the PFIOWA (PFIOWG) operator.
3. Some Novel Pythagorean Fuzzy Interactive Hybrid Weighted Aggregation Operators
Although PFIHA (PFIHG) possesses both the advantages of the PFIWA (PFIWG) operator and the PFIOWA (PFIOWG) operator, have a shortcoming which is that the AOs do not meet the prominent property, that is idempotency.
3.1. Shortcoming of the Existing Operators
In the below example, we illustrate with a numerical example that the existing aggregation operators do not own the feature of the idempotency.
Example 1.
Let,,be three PFNs, the corresponding weight vector is. is the aggregation associated vector. From Definition 3, we have
Based on Definition 4, we obtain,,, Since,, then. From Equation (6) in Definition 7, we obtain
Similarly,
Based on Definition 4, we have,,, since,, then. From Equation (7) in Definition 7, we obtain
Idempotency is a very significant feature for every operator [40], but the PFIHA (PFIHG) operator does not have this fundamental property. Hence, it is worth presenting some novel interactive hybrid AOs which also can reflect the significance of the given PFNs as well as ordered positions of them. Motivated by the work in Reference [40], in the following, we will present some new interactive hybrid AOs.
3.2. New Proposed Hybrid Aggregation Operators
In this part, we have presented some novel hybrid AOs for Pythagorean fuzzy sets to settle the deficiencies of the existing AOs.
Definition 8.
Suppose thatare a family of PFNs, a PFIHWA operator is a function:with associated weightingsatisfies,, and
wheremeans any permutation ofsatisfiesis the-th largest value of collective values. Theis weight vector of PFNsmeets,.
Theorem 1.
For a family of PFNs, then the output via employing PFIHWA operator remains a PFN, and
whereis anassociated weighting vector ofwith,. Thestands for weight vector ofsuch that,.
Proof.
On the basis of Definition 3, for every we have
Then, based on Equation (2), we can calculate that
Hence, the Theorem 1 holds. □
Like the characteristic of the PFIHA operator, if , then the PFIHWA operator becomes PFIWA operator. If , then the PFIHWA operator becomes the PFIOWA operator.
Example 2.
Let,,be the three PFNs, the aggregation associated vector isandis the weight vector. In line with Definition 4, we obtain,,. Since,, then. Hence, further,. According to Equation (9), we obtain
Theorem 2
(Idempotency). If allare equal to, then
Proof.
From Equation (9), we obtain
Hence, the Theorem 2 holds. □
Example 3.
Let us employ the PFIHWA operator in Definition 8 to recalculate Example 1. We obtain
In what follows, we shall present the novel interactive hybrid weighted geometric AOs for PFNs.
Definition 9.
Suppose thatare a family of PFNs, a PFIHWG operator is a function:with associated weightingand,, such that
whereandare the same as in Definition 8.
Theorem 3.
For a family of PFNs, then the output via employing the PFIHWG operator remains a PFN, and
whereis the associated weighting vector ofwith,. Thestands for the weight vector ofmeeting,.
Proof.
Based on Definition 3, for every , we obtain
Then, on the basis of Equation (3), we obtain
Hence, the Theorem 3 holds. □
Like the character of the PFIHG operator, if , then the PFIHWG operator becomes the PFIWG operator. If , then the PFIHWG operator becomes the PFIOWG operator.
Example 4.
Let us employ PFIHWG operator to compute Example 2. According to Equation (12), we obtain
Theorem 4
(Idempotency).If allare equal to, then
Proof.
From Equation (12), we obtain
Therefore, the statement of Theorem 4 holds. □
Example 5.
Let us employ the PFIHWG operator in Definition 9 to recalculate Example 1. We obtain
4. Generalized Pythagorean Fuzzy Interactive Hybrid Weighted Aggregation Operators
Yang and Pang [37] presented the generalized PFIWA (GPFIWA) and the generalized PFIWG (GPFIWG) operators. Next, we can extend the PFIHWA and PFIHWG operators into generalized forms.
Definition 10.
Letbe a group of PFNs, a GPFIHWA operator is a function:with associated weighting vectorand,, such that
wherethe weight vector ofsatisfies,.
Theorem 5.
For a family of PFNs, then the output via employing the GPFIHWA operator remains a PFN, and
where. Theis the associated weighting vector ofand satisfies,. Theis the weight vector ofandmeets,.
Proof.
Since , then from Definition 3, we have
Let , then
Based on Equation (2), we have
Further, we get
Therefore
Hence, the Theorem 5 holds. □
Theorem 6
(Idempotency).If allare equal to, then
Proof.
Since , so , . According to Equation (15), we have
Therefore, the Theorem 6 holds. □
In what follows, by choosing a different parameter , we explored some particular cases of the GPFIHWA operator.
Remark 1.
(1) If, then the GPFIHWA operator becomes the GPFIWA operator [33].
(2) If, then the GPFIHWA operator becomes
We call it a generalized PFIOWA (GPFIOWA) operator.
(3) If, then the GPFIHWA operator becomes the PFIHWG operator.
(4) If, then the GPFIHWA operator becomes the PFIHWA operator.
(5) Ifand, then the GPFIHWA operator becomes the PFIWG operator as given in Definition 5.
(6) Ifand, then the GPFIHWA operator becomes the PFIWA operator as given in Definition 5.
(7) Ifand, then the GPFIHWA operator becomes the PFIOWG as given in Definition 6.
(8) Ifand, then the GPFIHWA operator becomes t e PFIOWA operator as given in Definition 6.
Definition 11.
Suppose thatare a family of PFNs, a GPFIHWG operator is a function:with associated weighting vectorand,, such that
where, thestands forthe weight vector ofmeeting,.
Theorem 7.
For a family of PFNs, then the output via employing the GPFIHWG operator remains a PFN, and
where. Thestands for the weight vector ofmeeting,.
Proof.
Analogous to Theorem 5, the proof is omitted. □
Theorem 8
(Idempotency).If allare equal to, then
Proof.
Analogous to Theorem 6, the proof is omitted. □
In the following, by choosing a different parameter , we explored some particular cases of the GPFIHWG operator.
Remark 2.
(1) If, then the GPFIHWG operator becomes the GPFIWG operator.
(2) If, then the GPFIHWG operator becomes
We call it a generalized PFIOWG(GPFIOWG) operator.
(3) If, then the GPFIHWG operator becomes the PFIHWA operator.
(4) If, then the GPFIHWG operator becomes the PFIHWG operator.
(5) Ifand, then the GPFIHWG operator becomes thePFIWA operator as given in Definition 5.
(6) Ifand, then the GPFIHWG operator becomes the PFIWG operator as given in Definition 5.
(7) Ifand, then the GPFIHWG operator becomes thePFIOWA operator as given in Definition 6.
(8) Ifand, then the GPFIHWG operator becomes the PFIOWG operator as given in Definition 6.
Example 6.
Let us employ the GPFIHWA and GPFIHWG operators to recalculate Example 2. Without loss of generality, suppose. In the light of Equation (15) we can obtain
and, , .
Then
Similarly, with the aid of Equation (18), we can derive
5. MADM Approach with PFNs by Employing the Presented AOs
In this section, we adopted our developed PFIHWA, PFIHWAG, GPFIHWA and GPFIHWG operators to handle multiple attribute single person decision making and MAGDM based on PFNs, respectively.
5.1. MADM Method by Using the PFIHWA and the PFIHWG Operators
For a Pythagorean fuzzy MADM issue. Suppose is a group of decision alternatives. Assume is a group of attributes, stands for the weight of meeting ,. is the aggregation associated vector for , . The decision information matrix takes the form of provided by the DM, where expresses the grade that alternative meets attribute , expresses the grade that alternative doesnot meet attribute . , and . Then, the procedure of the MADM problem (Algorithm 1) is listed below:
| Algorithm 1. The procedure of the MADM problem using PFIHWA and PFIHWG operators. |
| Step 1. Compute the normalized decision information matrix of . The transformation is given as follows [41]:
|
| Step 2. Aggregate whole attribute values to the comprehensive values with the PFIHWA operator
|
| Step 3. Compute the scores and accuracy degrees in light of Definition 4. |
| Step 4. Sort whole alternatives and hence obtain the optimal one(s) based on and . |
Remark 3.
In MADM issues, attribute information is often divided into benefit and cost types. In order to facilitate calculation, some methods are needed to standardize the attribute information [41].
Example 7.

Consider that an organization wants to evaluate emerging technology enterprises (adapted from Reference [18]), the experts of the organization are given five potential alternatives . After careful analysis, the experts evaluate the five potential alternatives in accordance with the four attributes . represents technical advancement; represents the likely market and market risk; represents the financial conditions and human resources; represents the science and technology development and employment creation. Suppose is the weight vector. stands for the associated weight vector of four attributes, which assigns more weight to the attribute obtained for the optimal performance. The decision values take the form of PFNs, as listed in Table 1.

Table 1.
Pythagorean fuzzy decision matrix .
5.1.1. Process of MADM based on the PFIHWA Operator
To choose the optimal emerging technology enterprise, the following procedures are summarized:
Step 1. Since every attribute is a benefit type, no transformation is needed. The evaluation matrix is , described in Table 1.
Step 2. Utilizethe PFIHWA operator to acquire the comprehensive values :
From Definition 4, we obtain ,,, . Since, , so , then . Further , , , . According to Equation (9), we obtain , similarly, , , , .
Step 3. Acquire the scores of PFNs :
Step 4. Since , then we obtain
Thus, the optimal emerging technology enterprise is .
5.1.2. Process of MADM based on the PFIHWG Operator
In order to choose the optimal one(s) based on the PFIHWG operator, the following procedures of the proposed approach are summarized as below.
Step 1. It is identical with Step 1 in Section 5.1.1.
Step 2. Utilizethe PFIHWG operator to obtain the comprehensive values .
On the basis of Definition 4, we have ,,, . Since, , so , then . Further , , , . From Equation (12), we obtain , similarly, , , , .
Step 3. Acquire the scores of PFNs .
Step 4. Since , then we obtain
Then, the optimal emerging technology enterprise is .
5.1.3. Comparison and Discussion
To demonstrate the feasibility of the presented approach, we compare our methods with the PFIHA and PFIHG operators developed by Wei [33], the SPFWA (symmetric Pythagorean fuzzy weighted averaging) and SPFWG(symmetric Pythagorean fuzzy weighted geometric) operators developed by Ma and Xu [19], and the PFEWA(Pythagorean fuzzy Einstein weighted averaging) and PFEWG(Pythagorean fuzzy Einstein weighted geometric) operators developed by Garg [22] and Garg [23], respectively. These methods were used to solve the above example, and the aggregating values and sort outcomes are given in Table 2.

Table 2.
The aggregating and ranking results by different operators.
The content of Table 2 implies the aggregating results are different from each other, the ranking of alternative and is slightly different in the SPFWA, SPFWG, PFEWA and PFEWG operators, but the optimal emerging technology enterprise is still in all operators. Therefore, our methods are effective and feasible. However, comparing with the PFIHA and PFIHG operators [33] our methods are simple from the computational point of view. For instance, in the PFIHWA operator, are crisp numbers, we only compute the Pythagorean fuzzy value . However, in the PFIHA operator [33], we should first compute Pythagorean fuzzy value , then compute the Pythagorean fuzzy value .
From Figure 1, we observe that the Spearman correlation of SPFWA [19], SPFWG [19], PFEWA [22] and PFEWG [23] are all −0.6, whereas, the Spearman correlation of proposed operator (PFIHWA, PFIHWG), PFIHA [33] and PFIHG [33] are all 1. Comparing with PFIHA [33] and PFIHG [33], the typical characteristics of our techniques are that they possess a small amount of computation and idempotency. It further indicates that our approaches are superior. Therefore, our approach is suitable for settling some practical multiple attribute decision problems with Pythagorean fuzzy information.
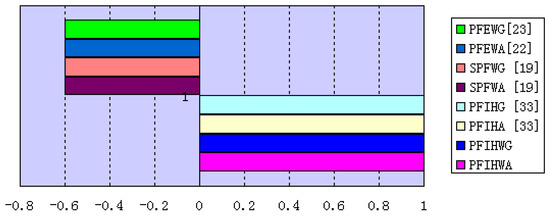
Figure 1.
Spearman correlation: proposed methods vs. others.
5.2. MAGDM Method by Using GPFIHWA and GPFIHWG Operators
Plenty of practical decision-making problems usually demand multiple DMs rather than a single DM. PFSs have the successful capacity to handle the indeterminacy under the MAGDM environment [8,17,25,26,27,28,29,31].
In what follows, we will employ GPFIHWA and GPFIHWG operators to tackle MAGDM problems with PFNs. Assume and are respectively the group of alternatives and attributes. The is the weight vector, that meets ,. Suppose is the associated vector for , . is the group of experts, is the corresponding weight vector that satisfies , . is the assessment matrix, in which is a PFN offered by the expert for the alternative relevant to the attribute . and means the grade that alternative meets attribute and doesnot meet attribute offered by the expert , respectively. Where , . Then, the procedure of the MAGDM problem (Algorithm 2) is listed below:
| Algorithm 2. The procedure of the MAGDM problem using GPFIHWA and GPFIHWG operators. |
| Step 1. It is identical with Step 1 in Algorithm 1. |
| Step 2. Utilize the PFIWA operator and decision matrixes to get the group decision matrix , where |
| Step 3. Utilize the assessment matrix and the GPFIHWA operator |
| Step 4. It is identical with Step 3 in Algorithm 1. |
| Step 5. It is identical with Step 4 in Algorithm 1. |
Example 8.



Suppose a company intends to implement the ERP (Enterprise Resource Planning) system (revised from Reference [28]). Three expertsfrom different departments form a project team to make the evaluations, including a CIO(Chief Information Officer) and two senior representatives, whose weight vector is. Assume that we have five latent ERP systems, and four assessment attributeswere selected,stands for the technology and function;stands for the strategic adaptability;stands for competence of vendor andstands for renown of vendor. Assumeis the importance degree of attributes. The associated weight vector given by the project team as, which assigns more weight to the attribute obtaining the optimal performance. The five potential ERP systemsare appraised by PFNs, and are summarized in Table 3, Table 4 and Table 5.

Table 3.
The Pythagorean fuzzy decision matrix .

Table 4.
The Pythagorean fuzzy decision matrix .

Table 5.
The Pythagorean fuzzy decision matrix .
5.2.1. Process of MAGDM based on the GPFIHWA Operator
Step 1. Since every attribute is a benefit type, no transformation is needed. The decision matrix , is described in Table 3, Table 4 and Table 5.
Step 2. Utilize the PFIWA operator, we get the group decision matrix , see Table 6.

Table 6.
The group integrated decision matrix .
Step 3. Utilize the decision matrix and the GPFIHWA operator (suppose ), from Definition 4, we obtain ,,, . Since, , so , then . Further, ,, , . According to Equation (15), we obtain , similarly, ,,, .
Step 4. Compute the scores of PFNs .
Step 5. Since , then we obtain
Hence, the optimal ERP system is .
5.2.2. Process of MAGDM based on the GPFIHWG Operator
Step 1–2. It is the same as Step 1–2 in Section 5.2.1.
Step 3. Utilize the decision matrix and the GPFIHWG operator (suppose ), by Definition 4, we obtain ,,, . Since, , so , then . Further, ,, , . Based on Equation (18), we get , similarly,,,,.
Step 4. Compute the scores of PFNs .
Step 5., therefore we get
Hence, the optimal ERP system is .
5.2.3. Comparison and Discussion
In Step 3 of Section 5.2.2, if we employ the PFIHA and PFIHG operators [33], then the decision result is . If we use the SPFWA [19], SPFWG [19], PFEWA [22] and PFEWG [23] operators, we obtain the following result: . We can obtain that the decision outcomes by the PFIHA operator [33] and PFIHG operator [33] are the same as our GPFIHWG operator, and are slightly different with our GPFIHWA operator, but the most desirable alternative by the PFIHA and PFIHG operators [33] coincide with the proposed operator results, i.e., alternative . The most desirable alternative determined by SPFWA [19], SPFWG [19], PFEWA [22] and PFEWG [23] operators is for all, the reason is that these AOs do not consider the interaction among membership and non-membership grades. Therefore, it is available and feasible in the proposed approaches. Moreover, our approaches are simple from the computational point of view compared with the PFIHA and PFIHG operators [33]. Further contrast effect can be reflected in Figure 2.
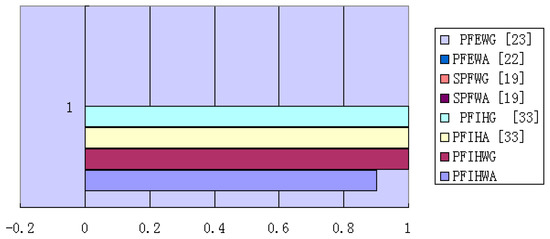
Figure 2.
Spearman correlation: presented methods vs. others.
As provided in Figure 2, the Spearman correlations of SPFWA [19], SPFWG [19], PFEWA [22] and PFEWG [23] are all 0, which shows that our methods are superior. The main features of the proposed GPFIHWA and GPFIHWG operators are that: (1) it considers the interaction among membership and non-membership grades for PFNs, and are more suitable to address actual MADM issues in some special situations; (2) it has the property of idempotency and simple computation process; (3) it possess an adjust parameter value and can reflect the preference of DMs during the decision process.
5.2.4. Sensitivity Analysis
Parameter plays a significant influence in the decision-making process; it can reflect the mentality of the DMs. For this, we chose different values of from 0 to 30 in Algorithm 2 to solve Example 8, so as to investigate the flexibility and sensitivity of different . The scores as well as decision results are listed in Table 7 and Table 8.

Table 7.
The scores and ranking results by the generalized Pythagorean fuzzy interactive hybrid weighted average (GPFIHWA) operator with different parameter .

Table 8.
The scores and ranking results by the generalized Pythagorean fuzzy interactive hybrid weighted geometric (GPFIHWG) operator with different parameter .
Table 7 indicates that the scores in the GPFIHWA operator become bigger with parameter increasing. Therefore, the DMs with optimistic attitude should take larger values of . Moreover, the ranking results are different by using different values of , but the best alternative is always . Furthermore, we can find that
- (1)
- (1) when , the ranking is .
- (2)
- when , the ranking is .
- (3)
- when , the ranking is .
Table 8 indicates that the scores in the GPFIHWG operator become smaller with parameter increasing. Therefore, the DMs with optimistic attitude should take smaller values of . Moreover, the ranking results are also different by employing different values of , and the best alternative is from to , then from to with parameter increasing. Furthermore, we can find that
- (1)
- when , the ranking is ,
- (2)
- when , the ranking is ,
- (3)
- when , the ranking is ,
- (4)
- when , the ranking is ,
- (5)
- when , the ranking is ,
- (6)
- when , the ranking is ,
- (7)
- when , the ranking is ,
- (8)
- when , the ranking is .
Therefore, the approach by using the GPFIHWA operator is relatively stable. In the actual decision environment, the DMs may select a different parameter in line with their preferences.
To better distinguish the presented approach with the existing approaches [19,22,23,33,37,38,39], we summarize the differences of them in Table 9. Based on Table 9, we can obtain that the presented approaches possess the property of idempotency, and also embody the interactions among membership and non-membership during the information aggregation process. Therefore, the novel approaches can obtain more reasonable ranking results.

Table 9.
Characteristic comparisons of different methods.
6. Conclusions
In this study, the authors have presented a group of novel Pythagorean fuzzy interactive hybrid weighted AOs, such as the PFIHWA, PFIHWG, GPFIHWA and GPFIHWG operators. It can be seen that these novel developed operators have the feature of idempotency, which indicated that the proposed AOs could overcome the shortcomings of the PFIHA and the PFIHG operators. It was also shown that some other existing AOs [33,35] were the particular cases of our presented AOs. In addition, our approaches were simple in view of computational cost and also captured the interaction over membership and non-membership grades. Afterward, two algorithms to MADM and MAGDM by the proposed operators were provided. Lastly, we verified the validity and flexibility with two practical examples.
In future research work, we can expand the explored operators to neutrosophic set [42,43,44], q-rung orthopair fuzzy set [45,46,47] and other uncertain environments [48,49,50,51,52,53,54,55,56].
Author Contributions
L.W. and N.L. conceived and worked together to achieve this work; H.G. studied the numerical example and investigation; L.W. and N.L. wrote the initial draft paper; L.W., H.G. revised the manuscript. Finally, all the authors read and approved the final manuscript.
Funding
The work was supported by the Scientific Research Funds Project of Liaoning Province Education Department (No. LJ2019QL014).
Acknowledgments
The authors would like to thank anonymous referees for their helpful remarks.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, AB, Canada, 24–28 June 2013. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Akram, M.; Ilyas, F.; Garg, H. Multi-criteria group decision making based on ELECTRE-I method on Pythagorean fuzzy information. Soft Comp. 2019, 1–29. [Google Scholar] [CrossRef]
- Garg, H. A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision making processes. Int. J. Intell. Syst. 2016, 31, 1234–1252. [Google Scholar] [CrossRef]
- Chen, T. An effective correlation-based compromise approach for multiple criteria decision analysis with Pythagorean fuzzy information. Int. J. Intell. Syst. 2018, 35, 3529–3541. [Google Scholar] [CrossRef]
- Peng, X.D.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Garg, H. A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multi-attribute decision making problem. J. Intell. Fuzzy Syst. 2016, 31, 529–540. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multi attribute decision making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Garg, H. A novel improved accuracy function for interval valued Pythagorean fuzzy sets and its applications in decision making process. Int. J. Intell. Syst. 2017, 31, 1247–1260. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multiple attribute decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Rezaei, C.; Liao, H.; Mardani, A. Extended Pythagorean fuzzy TOPSIS method based on similarity measure for sustainable recycling partner selection. Int. J. Fuzzy Syst. 2019, 1–13. [Google Scholar] [CrossRef]
- Peng, X.D.; Dai, J.G. Approaches to Pythagorean fuzzy stochastic multi-criteria decision making based on prospect theory and regret theory with new distance measure and score function. Int. J. Intell. Syst. 2017, 32, 1187–1214. [Google Scholar] [CrossRef]
- Ren, P.; Xu, Z.; Gou, X. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Chen, T.Y. Remoteness index-based Pythagorean fuzzy VIKOR methods with a generalized distance measure for multiple criteria decision analysis. Inf. Fusion 2018, 41, 129–150. [Google Scholar] [CrossRef]
- Zhang, X.L. Multi-attribute Pythagorean fuzzy decision analysis: a hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf. Sci. 2016, 330, 104–124. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 169–186. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric Pythagorean fuzzy weighted geometric/averaging operators and their application in multi-attribute decision-making problems. Int. J. Intell. Syst. 2016, 31, 1198–1219. [Google Scholar] [CrossRef]
- Garg, H. New exponential operational laws and their aggregation operators for interval-valued Pythagorean fuzzy multi-criteria decision-making. Int. J. Intell. Syst. 2018, 33, 653–683. [Google Scholar] [CrossRef]
- Garg, H. New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int. J. Intell. Syst. 2019, 34, 82–106. [Google Scholar] [CrossRef]
- Garg, H. A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multi-criteria decision making process. Int. J. Intell. Syst. 2017, 32, 597–630. [Google Scholar] [CrossRef]
- Wu, S.J.; Wei, G.W. Pythagorean fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Int. J. Knowl. Intell. Eng. Syst. 2017, 21, 189–201. [Google Scholar] [CrossRef]
- Yu, L.; Zeng, S.; Merigó, J.M.; Zhang, C. A new distance measure based on the weighted induced method and its application to Pythagorean fuzzy multiple attribute group decision making. Int. J. Intell. Syst. 2019, 34, 1440–1454. [Google Scholar] [CrossRef]
- Wang, L.; Li, N. Continuous interval-valued Pythagorean fuzzy aggregation operators for multiple attribute group decision making. J. Intell. Fuzzy Syst. 2019, 36, 6245–6263. [Google Scholar] [CrossRef]
- Qin, J. Generalized Pythagorean fuzzy maclaurin symmetric means and its application to multiple attribute SIR group decision model. Int. J. Fuzzy Syst. 2018, 20, 943–957. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S.; Darko, A.P. Projection model for fusing the information of Pythagorean fuzzy multicriteria group decision making based on geometric Bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Liang, D.C.; Darko, A.P.; Xu, Z.S. Pythagorean fuzzy partitioned geometric Bonferroni mean and its application to multi-criteria group decision making with grey relational analysis. Int. J. Fuzzy Syst. 2019, 21, 115–128. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1043–1070. [Google Scholar] [CrossRef]
- Li, Z.; Wei, G.; Lu, M. Pythagorean fuzzy Hamy mean operators in multiple attribute group decision making and their application to supplier selection. Symmetry 2018, 10, 505. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Wang, J.; Zhu, X.; Xing, Y. Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 2035–2050. [Google Scholar] [CrossRef]
- Wei, G.W. Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 2119–2132. [Google Scholar] [CrossRef]
- Garg, H. Neutrality operations-based Pythagorean fuzzy aggregation operators and its applications to multiple attribute group decision-making process. J. Ambient Intell. Human. Comput. 2019, 1–21. [Google Scholar] [CrossRef]
- Garg, H. Novel neutrality operations based Pythagorean fuzzy geometric aggregation operators for multiple attribute group decision analysis. Int. J. Intell. Syst. 2019, 34, 2459–2489. [Google Scholar] [CrossRef]
- Gao, H.; Lu, M.; Wei, G.W.; Wei, Y. Some novel Pythagorean fuzzy interaction aggregation operators in multiple attribute decision making. Fund Inform. 2018, 159, 385–428. [Google Scholar] [CrossRef]
- Yang, W.; Pang, Y. New Pythagorean fuzzy interaction Maclaurin symmetric mean operators and their application in multiple attribute decision making. IEEE Access. 2018, 6, 39241–39260. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean fuzzy geometric interactive aggregation operators using Einstein operations and their application to decision making. J. Exp. Artif. Intell. 2018, 30, 763–794. [Google Scholar] [CrossRef]
- Yang, W.; Shi, J.; Liu, Y.; Pang, Y.; Lin, R. Pythagorean fuzzy interaction partitioned Bonferroni mean operators and their application in multiple attribute decision-making. Complexity 2018. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S. Some new hybrid weighted aggregation operators under hesitant fuzzy multi-criteria decision making environment. J. Intell. Fuzzy Syst. 2014, 26, 1601–1617. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, H. Projection models for intuitionistic fuzzy multiple attribute decision making. Int. J. Inf. Technol. Decis. 2010, 9, 267–280. [Google Scholar] [CrossRef]
- Peng, X.D.; Dai, J.G. Approaches to single-valued neutrosophic MADM based on MABAC, TOPSIS and new similarity measure with score function. Neural Comput. Appl. 2018, 9, 939–954. [Google Scholar] [CrossRef]
- Nancy; Garg, H. A novel divergence measure and its based TOPSIS method for multi criteria decision-making under single-valued neutrosophic environment. J. Intell. Fuzzy Syst. 2019, 36, 101–115. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Linguistic single-valued neutrosophic power aggregation operators and their applications to group decision-making problems. IEEE/CAA J. Autom. Sin. 2019, 1–13. [Google Scholar] [CrossRef]
- Peng, X.D.; Liu, L. Information measures for q-rung orthopair fuzzy sets. Int. J. Intell. Syst. 2019, 34, 1795–1834. [Google Scholar] [CrossRef]
- Liu, P.; Liu, W. Multiple-attribute group decision-making based on power Bonferroni operators of linguistic q-rung orthopair fuzzy numbers. Int. J. Intell. Syst. 2019, 34, 652–689. [Google Scholar] [CrossRef]
- Wang, L.; Garg, H.; Li, N. Interval-valued q-rung orthopair 2-tuple linguistic aggregation operators and their applications to decision making process. IEEE Access. 2019, 7, 131962–131977. [Google Scholar] [CrossRef]
- Garg, H. Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision-making process. Int. J. Intell. Syst. 2019, 34, 601–626. [Google Scholar] [CrossRef]
- Wang, L.; Li, N. Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2019. [Google Scholar] [CrossRef]
- Blanco-Mesa, F.; Merigó, J.M.; Gil-Lafuente, A.M. Fuzzy decision making: a bibliometric-based review. J. Intell. Fuzzy Syst. 2017, 32, 2033–2050. [Google Scholar] [CrossRef]
- Merigó, J.M. Fuzzy decision making with immediate probabilities. Comput. Ind. Eng. 2010, 58, 651–657. [Google Scholar] [CrossRef]
- Nilashi, M.; Mardani, A.; Liao, H.; Ahmadi, H.; Manaf, A.A.; Almukadi, W. A hybrid method with TOPSIS and machine learning techniques for sustainable development of green hotels considering online reviews. Sustainability 2019, 11, 6013. [Google Scholar] [CrossRef]
- Hafezalkotob, A.; Hafezalkotob, A.; Liao, H.; Herrera, F. An overview of MULTIMOORA for multi-criteria decision-making: theory, developments, applications, and challenges. Inf. Fusion 2019, 51, 145–177. [Google Scholar] [CrossRef]
- Atanassov, K.; Szmidt, E.; Kacprzyk, J. Shrinking operators over interval-valued intuitionistic fuzzy sets. Notes Int. Fuzzy Sets 2018, 24, 20–28. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some Results on Information measures for complex intuitionistic fuzzy sets. Int. J. Intell. Syst. 2019, 34, 2319–2363. [Google Scholar] [CrossRef]
- Yager, R.R.; Xu, Z. The continuous ordered weighted geometric operator and its application to decision making. Fuzzy Sets Syst. 2006, 157, 1393–1402. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).