Topologies on Z n that Are Not Homeomorphic to the n-Dimensional Khalimsky Topological Space

Abstract

The present paper deals with two types of topologies on the set of integers, $\mathbb{Z}$: a quasi-discrete topology and a topology satisfying the $T_{\frac{1}{2}}$-separation axiom. Furthermore, for each $n\in \mathbb{N}$, we develop countably many topologies on ${\mathbb{Z}}^n$ which are not homeomorphic to the typical n-dimensional Khalimsky topological space. Based on these different types of new topological structures on ${\mathbb{Z}}^n$, many new mathematical approaches can be done in the fields of pure and applied sciences, such as fixed point theory, rough set theory, and so on.

1. Introduction

The present paper concerns the existence problem of the topologies on ${\mathbb{Z}}^n$ that are not homeomorphic to the typical n-dimensional Khalimsky topology. More precisely, after establishing many topologies on $\mathbb{Z}$ that are not homeomorphic to the Khalimsky line topology, we will extend this approach to the set ${\mathbb{Z}}^n$, where $n\in \mathbb{N}$, and $\mathbb{N}$ is the set of natural numbers. Namely, how many topologies on ${\mathbb{Z}}^n$ are not homoeomorphic to the typical n-dimensional Khalimsky topological space? Since we will often use the term “Khalimsky” in this paper, hereafter, we will use the notation “$K$-” for short instead of the “Khalimsky” if there is no danger of ambiguity. In this paper we will often use the notation “$:=$” to introduce new notions without proving the fact.

Several kinds of digital topologies [1,2,3,4,5,6], such as digital topology using digital adjacencies [7], K-topology [8], Marcus–Wyse (M-, for short) topology [3], and generalized M-topology [9], have played important roles in pure and applied topologies. More precisely, digital images can be considered as subsets of ${\mathbb{Z}}^n$ with some structures, such as a digital adjacency (or the digital connectivity in the Rosenfeld model), the Khalimsky, the Marcus–Wyse, the H-topological, and the Alexandroff structures [10,11]. In particular, these structures play important roles in the fields of digital homotopy theory, fixed point theory, digital topological rough set theory, digital geometry, information theory, and so forth [12,13,14,15,16]. Thus, an intensive development of new topologies on ${\mathbb{Z}}^n$, which are different from the well-known topologies on ${\mathbb{Z}}^n$, can facilitate the study of pure and applied sciences including computer science. Indeed, the present paper aims at developing new topologies that are different from the K-product topology on ${\mathbb{Z}}^n$ (or (${\mathbb{Z}}^n,{\kappa }^n)$) and are not homeomorphic to $({\mathbb{Z}}^n,{\kappa }^n)$. Based on these kinds of new topologies on ${\mathbb{Z}}^n$, we can further establish several kinds of homotopies for various types of continuous maps on the newly-established topological spaces. In addition, we can introduce new types of homotopic thinnings using these homotopies on ${\mathbb{Z}}^n$.

The rest of the paper is organized as follows: Section 2 refers to some notions relating to homeomorphism for Alexandroff spaces and comparisons among topological spaces. Section 3 proposes countably many subbases $S_k$ on $\mathbb{Z}$ for establishing the corresponding topological spaces $(\mathbb{Z},T_k),k\in \mathbb{Z}$, where $T_k:=T_{S_k}$ is the topology generated by $S_k$ as a subbase. In addition, we prove that the topology $T_0:=T_{S_0}$ is not a Kolmogorov space and the topology $T_k$ satisfies the $T_{\frac{1}{2}}$-separation axiom, $k\ne 1$. Section 4 proposes two kinds of topologies on $\mathbb{Z}$: a quasi-discrete (clopen) topology and a topology equipped with the $T_{\frac{1}{2}}$-separation axiom. In addition, they are proved to be Alexandroff spaces. Section 5 corrects a certain inappropriate comment proposed by Boxer et al. in the paper [17]. Section 6 concludes the paper.

2. Homeomorphisms for Alexandroff Spaces

In this section we refer to several concepts and definitions which are used in this paper.

Definition 1.

[10,11] We say that a topological space $(X,T)$ is an Alexandroff (topological) space if every point $x\in X$ has the smallest (or minimal) open neighborhood in $(X,T)$.

As an Alexandroff space, the Khalimsky nD space was established and the study of its properties includes the papers [8,18,19,20,21].

Let us now recall basic notions from the K-topology on ${\mathbb{Z}}^n$.

Definition 2.

The Khalimsky line topology on $\mathbb{Z}$, denoted by $(\mathbb{Z},\kappa )$, is induced by the set $\{{[2n-1,2n+1]}_{\mathbb{Z}}|n\in \mathbb{Z}\}$ as a subbase [8], where for $a,b\in \mathbb{Z}$, ${[a,b]}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|a\le x\le b\}$.

The product topology on ${\mathbb{Z}}^n$ induced by $(\mathbb{Z},\kappa )$ is called the Khalimsky product topology on ${\mathbb{Z}}^n$ (or the Khalimsky nD space), denoted by $({\mathbb{Z}}^n,{\kappa }^n)$.

Hereafter, for a subset $X\subseteq {\mathbb{Z}}^n$ we will denote the subspace induced by $({\mathbb{Z}}^n,{\kappa }^n)$ with $(X,{\kappa }_X^n)$, $n\ge 1$, and we call it a K-topological space. As usual, we denote the cardinality of a denumerable set with ${\aleph }_0$. In particular, we denote a Khalimsky interval with $({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$ (or ${[a,b]}_{\mathbb{Z}}$ for short, if there is no danger of ambiguity). In addition, we will often use the following notations in this paper: ${(m,n)}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|m⪇x⪇n\}$, ${[m,n)}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|m\le x⪇n\}$, ${[m,+\infty )}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|m\le x\}$, and ${(-\infty ,n]}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|x\le n\}$. Depending on the situation, we may use the intervals with the K-topology or without topology, i.e., just a set.

Let us now recall certain notions and basic structures of $({\mathbb{Z}}^n,{\kappa }^n)$. A point $x={(x_i)}_{i\in {[1,n]}_{\mathbb{Z}}}\in {\mathbb{Z}}^n$ is pure open if all coordinates, say $x_i,i\in {[1,n]}_{\mathbb{Z}}$, are odd, pure closed if each of the coordinates is even, and the other points in ${\mathbb{Z}}^n$ are called mixed [20]. In addition, these points are shown by using the following symbols, i.e., ■ and • mean a pure closed point and a pure open point, respectively. Motivated by these notations, in order to describe certain points in the newly-established topological spaces in this paper such as $T_k$, $T_k^{\prime }$, we will also use the symbols ■ and • for showing a closed point and a pure open point, respectively, in the topologies (see Figure 1 and Figure 2). Regarding the further statement of a mixed point in $({\mathbb{Z}}^2,{\kappa }^2)$, for the points $p=(2m,2n+1)$ (resp. $p=(2m+1,2n)$), we call the point p closed-open (resp. open-closed).

Figure 1. Configuration of the closedness of the singleton $\{2n\}$ in the topological space $(\mathbb{Z},T_1)$, e.g., $2n=8$.

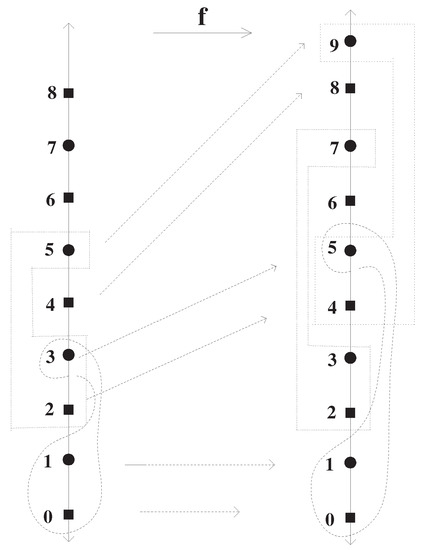
Figure 2. Non-homeomorphism between $T_1$ and $T_2$. In particular, see the elements 2, 3, 6, and 7 in $(\mathbb{Z},T_2)$, and so on.

With this perspective, in $({\mathbb{Z}}^2,{\kappa }^2)$ we clearly observe that for the point $p=(p_1,p_2)$ of ${\mathbb{Z}}^2$ the smallest (open) neighborhood of the point, denoted by $S{N}_K(p)\subset {\mathbb{Z}}^2$, is the following [10,11,18]:

$$S{N}_K(p)=\left\{\begin{array}{l}\{p\}\mathrm{if}p\mathrm{is}\mathrm{pure}\mathrm{open},\\ \{(p_1-1,p_2),p,(p_1+1,p_2)\}\mathrm{if}p\mathrm{is}\mathrm{closed-open},\\ \{(p_1,p_2-1),p,(p_1,p_2+1)\}\mathrm{if}p\mathrm{is}\mathrm{open-closed},\\ N_8(p)\mathrm{if}p:=(2m,2n),m,n\in \mathbb{Z},\mathrm{i}.\mathrm{e}.,\mathrm{pure}\mathrm{closed},\\ \mathit{where}{\mathit{N}}_{\mathit{8}}(\mathit{p}):={[\mathit{2}\mathit{m}-\mathit{1},\mathit{2}\mathit{m}+\mathit{1}]}_{\mathbb{Z}}\times {[\mathit{2}\mathit{n}-\mathit{1},\mathit{2}\mathit{n}+\mathit{1}]}_{\mathbb{Z}}.\end{array}\right\}$$

(1)

Hereafter, in $(X,{\kappa }_X^n)$, we denote the smallest open set containing a point x with $S{N}_X(x):=S{N}_K(x)\cap X$ for short or $SN(x)$ [22] if there is no danger of confusion.

Definition 3.

A topology T is called a quasi-discrete topology [23] (or clopen or pseudo-discrete topology [24]) if every open set in T is closed.

Remark 1.

(1) In view of (1), any infinite set of $({\mathbb{Z}}^n,{\kappa }^n)$ is not compact in $({\mathbb{Z}}^n,{\kappa }^n)$.

(2) Due to the connectedness of $(\mathbb{Z},\kappa )$ [20], $({\mathbb{Z}}^n,{\kappa }^n)$ is clearly connected.

In the category of Alexandroff spaces, for two Alexandroff spaces $A_1$ and $A_2$, it is clear that a map $f:A_1\to A_2$ is continuous if, and only if, for each point $a_1\in A_1$, $f(SN(a_1))\subseteq SN(f(a_1))$, where $SN(x)$ means the smallest open set containing the point x in the given Alexandroff space. In addition, for two Alexandroff spaces $A_1$ and $A_2$, a map $h:A_1\to A_2$ is called an Alexandroff homeomorphism if h is a continuous bijection, and further, $h^{-1}:A_2\to A_1$ is continuous.

For instance, in $({\mathbb{Z}}^n,{\kappa }^n)$, let us now recall the notion of K-continuity of a map between two K-topological spaces [8] as follows: For two K-topological spaces $(X,{\kappa }_X^{n_0}):=X$ and $(Y,{\kappa }_Y^{n_1}):=Y$, a function $f:X\to Y$ is said to be K-continuous at a point $x\in X$ if f is continuous at the point x from the viewpoint of K-topology. Further, we say that a map $f:X\to Y$ is K-continuous if it is K-continuous at every point $x\in X$. Indeed, since $({\mathbb{Z}}^n,{\kappa }^n)$ is an Alexandroff space (see (1)), the above X and Y are Alexandroff spaces. Thus we can represent the K-continuity of f at a point $x\in X$ [18], as follows

$$f(S{N}_K(x))\subseteq S{N}_K(f(x)).$$

(2)

Based on this approach, a map $h:X\to Y$ is called a K-homeomorphism if h is a K-continuous bijection and further, $h^{-1}:Y\to X$ is K-continuous.

We say that a topological space satisfies the separation axiom $T_{\frac{1}{2}}$ [25,26,27] if every singleton of $({\mathbb{Z}}^2,\gamma )$ is either an open or a closed set. Then, we call it a $T_{\frac{1}{2}}$-space.

For two topologies, ${\top }_1$ and ${\top }_2$, on a set X, in the case ${\top }_1$ is coarser (weaker) than ${\top }_2$ and ${\top }_2$ is finer (stronger) than ${\top }_1$ [28], we use the notation ${\top }_1\le {\top }_2$. If additionally ${\top }_1\ne {\top }_2$, then we say that ${\top }_1$ is strictly coarser than ${\top }_2$ and ${\top }_2$ is strictly finer than ${\top }_1$ [28]. In this case we use the notation ${\top }_1⪇{\top }_2$. In examining the case ${\top }_1\le {\top }_2$, we can equivalently take the following approach. Let $B_i$ be bases for the topologies ${\top }_i,i\in \{1,2\}$. Then, it is clear that

$${\top }_1\le {\top }_2\iff \forall b_1\in B_1\mathrm{and}\forall x\in b_1,\exists b_2\in B_2\mathrm{such}\mathrm{that}x\in b_2\subseteq b_1.$$

(3)

3. Various Types of Topologies on $\mathbb{Z}$ Generated by Certain Subbases ${\mathit{S}}_{\mathit{k}},\mathit{K}$ $\in \mathbb{Z}$

In this section, many types of subbases, say $S_k,k\in \mathbb{Z}$, are introduced for establishing topologies of $\mathbb{Z}$. Then, we intensively explore the topological features of $T_{S_k},k\in \mathbb{Z}$, with respect to separation axioms and an Alexandroff space structure. As mentioned previously, each element ${[2n-1,2n+1]}_{\mathbb{Z}}$ of the subbase of the K-line topology consists of three consecutive elements. Indeed, the topology on $\mathbb{Z}$ generated by the set $\{{[2n,2n+2]}_{\mathbb{Z}}|n\in \mathbb{Z}\}$ as a subbase is homeomorphic to $(\mathbb{Z},\kappa )$. Thus, we now consider other types of elements which are not consecutive, such as for a given number $k\in \mathbb{Z}$, $\{\{2n,2n+1,2n+2k+1\},n\in \mathbb{Z}\}$, $\{\{2n,2n+1,2n+2k\},n\in \mathbb{Z}\}$ and so forth.

Let us now investigate various properties of the topologies generated by certain subbases $S_k,k\in \mathbb{Z}$.

Lemma 1.

Given a number $k\in \mathbb{Z}$, assume the set

$$S_k:=\{S_{k,n}|S_{k,n}:=\{2n,2n+1,2n+2k+1\},n\in \mathbb{Z}\}.$$

(4)

Consider a topology on $\mathbb{Z}$ generated by $S_k$ as a subbase, denoted by $T_{S_k}$. Then, $(\mathbb{Z},T_{S_k})$ is an Alexandroff space.

Before proving this claim, as the set $S_k$ is totally determined by the number $k\in \mathbb{Z}$, hereafter, the topology $T_{S_k}$ of Lemma 1 will be denoted by $T_k$ for simplicity, i.e., $T_k:=T_{S_k}$.

Proof. 

Given a number $k\in \mathbb{Z}$, a topology generated by the given subbase $S_k$ is obtained in terms of the following process.

$$S_k\to B_{S_k}\to T_{B_{S_k}}:=T_k,$$

(5)

where $B_{S_k}$ is the base induced by the subbase $S_k$ and $T_k$ is the topology generated by the set $B_{S_k}$ as a base. Since

$$B_{S_k}=S_k\cup \{\{2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\},$$

$T_k$ is an Alexandroff space. □

Example 1.

(1) The topology $T_{-1}:=T_{S_{-1}}$ is generated by the set $S_{-1}=\{\{2n-1,2n,2n+1\}|n\in \mathbb{Z}\}$ as a subbase. Thus, for any $n\in \mathbb{Z}$, we obtain

$$SN(2n)={[2n-1,2n+1]}_{\mathbb{Z}}\mathrm{and}SN(2n+1)=\{2n+1\},$$

from which $T_{-1}$ is proved to be an Alexandroff space.

(2) The topology $T_0:=T_{S_0}$ is generated by the set $S_0=\{\{2n,2n+1\}|n\in \mathbb{Z}\}$ as a subbase. Thus, for any $n\in \mathbb{Z}$ we obtain

$$SN(2n)=SN(2n+1)=\{2n,2n+1\},$$

which implies that $T_0$ is an Alexandroff space.

(3) The topology $T_1:=T_{S_1}$ is generated by the set $S_1=\{\{2n,2n+1,2n+3\}|n\in \mathbb{Z}\}$ as a subbase. Thus, for any $n\in \mathbb{Z}$ we obtain

$$SN(2n)=\{2n,2n+1,2n+3\}\mathrm{and}SN(2n+1)=\{2n+1\},$$

which means that $T_1$ is an Alexandroff space.

Lemma 2.

For distinct numbers $k_1,k_2\in \mathbb{Z}$, we obtain the following:

(1) $S_{k_1}\cap S_{k_2}=\varnothing$.

(2) $B_{S_{k_1}}\ne B_{S_{k_2}}$.

Proof. 

(1) (Case 1) Consider the case of which either of $k_1$ and $k_2$ is equal to 0. Without loss of generality, let us assume $k_1=0$. Then, due to the subbase given in (4) (see also Example 1(2)), we observe that whereas each member of $S_0$ has cardinality 2, that of $S_{k_2}$ has cardinality 3, which clearly implies that $S_0\cap S_{k_2}=\varnothing$.

(Case 2) In the case neither of $k_1$ and $k_2$ is equal to 0 and further, $k_1\ne k_2$, each member of $S_{k_1}$ is different from any element of $S_{k_2}$ because

$$\left\{\begin{array}{l}\{2m,2m+1,2m+2k_1+1\}(\in S_{k_1})\ne \{2n,2n+1,2n+2k_2+1\}(\in S_{k_2})\\ \mathrm{if}{k}_1\ne k_2,\end{array}\right.$$

which implies that $S_{k_1}\cap S_{k_2}=\varnothing$.

(2) The bases $B_{S_{k_i}}$, induced by the subbases $S_{k_i},i\in \{1,2\}$, are finally obtained, as follows:

$$\left\{\begin{array}{l}{B}_{S_{k_1}}=S_{k_1}\cup \{\{2m+1\}|m\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}\mathrm{and}\\ B_{S_{k_2}}=S_{k_2}\cup \{\{2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}.\end{array}\right\}$$

(6)

According to the property $S_{k_1}\cap S_{k_2}=\varnothing$ (see the proof of (1) of Lemma 2), (6) supports the assertion. □

Theorem 1.

For a number $k\in \mathbb{Z}\backslash \{0\}$, we obtain

(1) $(\mathbb{Z},T_0)$ is not a Kolmogorov space.

(2) $(\mathbb{Z},T_k)$ is a $T_{\frac{1}{2}}$-space, $k\in \mathbb{Z}\backslash \{0\}$.

Proof. 

(1) Since $B_{S_0}=\{\{2n,2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}$, by Example 1(2), the proof is completed. To be precise, due to the smallest open sets $SN(2n)$ and $SN(2n+1)$ in $(\mathbb{Z},T_0)$ (see Example 1(2)), $(\mathbb{Z},T_0)$ is not a Kolmogorov space.

(2) Due to the bases on (6), we obtain $B_{S_1}=S_1\cup \{\{2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}$. Thus, in the topological space $(\mathbb{Z},T_1)$, it is clear that every singleton consisting of an odd number is open. Let us now prove that every singleton consisting of an even number is closed. Namely, let us prove that for each element $2n\in \mathbb{Z}$, the singleton $\{2n\}$ is a closed set in $T_1$. For the sake of doing this work, let us take a hard look at the topological structure of $T_1$. Due to the topology $T_1:=T_{S_1}$ generated by the set $S_1:=\{S_{1,n}:=\{2n,2n+1,2n+3\}|n\in \mathbb{Z}\}$ as a subbase, it is clear that for each $2n+1\in \mathbb{Z}$, the singleton $\{2n+1\}\in B_{S_1}\subset T_1$. Let us now consider the complement of $\{2n\}$ in $\mathbb{Z}$, denoted by ${\{2n\}}^C$. For the set

$${\{2n\}}^C={(-\infty ,2n-1]}_{\mathbb{Z}}\cup {[2n+1,\infty )}_{\mathbb{Z}},$$

for convenience, put $A_1:={(-\infty ,2n-1]}_{\mathbb{Z}}$ and $A_2:={[2n+1,\infty )}_{\mathbb{Z}}$. Then, the set $A_2$ can be represented in the following way, say $A_2:=\{2n+1\}\cup {[2n+2,\infty )}_{\mathbb{Z}}$. Since the singleton $\{2n+1\}(\subset A_2)$ belongs to $B_{S_1}\subset T_1$ and further, ${[2n+2,\infty )}_{\mathbb{Z}}\in T_1$, it is clear that the set $A_2\in T_1$. Considering the topology $T_1$, let us now examine if each element of $A_1$ is an interior point of ${\{2n\}}^C$. Indeed, $A_1$ is represented by

$$A_1:={(-\infty ,2n-3]}_{\mathbb{Z}}\cup \{2n-2,2n-1\}.$$

Based on the subbase $S_1$ of (4), whereas the subset ${(-\infty ,2n-3]}_{\mathbb{Z}}\cup \{2n-1\}(\subset A_1)$ is an open set in $T_1$, there is no element $b_1(\in S_1\subset B_{S_1})$ containing the remaining element $2n-2\in A_1$, where $b_1\subset A_1$. Thus, $A_1\notin T_1$. However, there is a member $\{2n-2,2n-1,2n+1\}(\ni 2n-2)$ in $S_1$. Thus, $2n-2(\in \mathbb{Z})$ is an interior point of ${\{2n\}}^C$. Hence, although $\{2n-2,2n-1,2n+1\}(\in S_1)$ is not a subset of $A_1$, it is a subset of ${\{2n\}}^C$. Finally, we conclude that ${\{2n\}}^C$ is an open set in $T_1$.

For instance, we can confirm that the singleton $\{8\}$ of Figure 1 is proved a closed set in $T_1$ in the following way. The set

$${\{8\}}^C={(-\infty ,7]}_{\mathbb{Z}}\cup {[9,\infty )}_{\mathbb{Z}}$$

is represented by $A_1:={(-\infty ,7]}_{\mathbb{Z}}$ and $A_2:={[9,\infty )}_{\mathbb{Z}}$. Although $A_1:={(-\infty ,5]}_{\mathbb{Z}}\cup \{6,7\}$ is not an open set in $T_1$, we observe that $A_2\in T_1$. Since each of the sets $\{6,7,9\}$, ${(-\infty ,5]}_{\mathbb{Z}}$, and ${[9,\infty )}_{\mathbb{Z}}$ belongs to $T_1$ (for $2n=8$, see Figure 1), we conclude that ${\{8\}}^C$ is an open set in $T_1$.

Finally, according to (4) and using a method similar to the proof of being a $T_{\frac{1}{2}}$-space of $(\mathbb{Z},T_1)$, we obtain that $(\mathbb{Z},T_i)$ is also a $T_{\frac{1}{2}}$-space, $i\in \mathbb{Z}\backslash \{0\}$. Then this is true since every singleton consisting of an odd number is an open set in $T_i,i\in \mathbb{Z}\backslash \{0\}$. □

Some further studies of the structures of $(\mathbb{Z},T_i),i\in \mathbb{Z}$, will intensively be done in Section 4 (see Theorem 2).

4. Countably Many Types of Topologies on $\mathbb{Z}$ Generated by the Subbases ${\mathit{S}}_{\mathit{k}},\mathit{K}$ $\in \mathbb{Z}$

In this section, we now intensively characterize the topological spaces $(\mathbb{Z},T_k),k\in \mathbb{Z}$. One important thing is that we can observe several types of topological features on $\mathbb{Z}$ depending on the given subbases $S_k,k\in \mathbb{Z}$, such as a quasi-discrete, the K-topological, and Alexandroff topological structures. Furthermore, for $i\ne j$, $i,j\in \mathbb{Z}$, we find that $T_i\ne T_j$ and further, $T_i$ is not homeomorphic to $T_j$ either.

Theorem 2.

For the topological spaces $(\mathbb{Z},T_k),k\in \mathbb{Z}$, we obtain the following properties, where $T_k:=T_{S_k}$.

(1) $(\mathbb{Z},T_0)$ is a quasi-discrete (not discrete) topological space.

(2) $(\mathbb{Z},T_0)$ is not connected.

(3) $(\mathbb{Z},T_{-1})$ is the K-topological line.

(4) $T_i\ne T_j$ if $i\ne j$, and $i,j\in \mathbb{Z}$.

(5) For distinct numbers $i,j\in \mathbb{Z}$, $T_i$ is not homeomorphic to $T_j$.

Proof. 

(1) Since $S_0=\{\{2n,2n+1\}|n\in \mathbb{Z}\}$, we have $B_{S_0}=S_0\cup \{\varnothing ,\mathbb{Z}\}$. Hence, with the topology $T_0:=T_{S_0}$ (see (5)), the smallest open set containing an even number $2n(\in \mathbb{Z})$ or an odd number $2n+1(\in \mathbb{Z})$ is exactly the set $\{2n,2n+1\}$ (see Example 1(2)). Thus, each open set in $T_0$, denoted by $O(\in T_0)$, can be represented by

$$O=\bigcup _{n\in M\subseteq \mathbb{Z}}\{2n,2n+1\}.$$

(7)

Therefore, the closure of $O(\in T_0)$ is equal to itself, which completes the proof.

(2) Owing to Theorem 2 (1), the proof is completed. Namely, for any $n\in \mathbb{Z}$, $\{\{2n,2n+1\},{\{2n,2n+1\}}^C\}$ is a separation of $(\mathbb{Z},T_0)$.

(3) Since the topology $T_{-1}$ is generated by the set $\{\{2n-1,2n,2n+1\}|n\in \mathbb{Z}\}$ as a subbase, it is equal to the K-line topology $\kappa$ on $\mathbb{Z}$.

(4) (Case 1) For distinct numbers $i,j\in \mathbb{Z}$, assume that either of i and j is equal to 0. Without loss of generality, we may take $i=0$ and $j\ne 0$. Since $S_0=\{\{2m,2m+1\}|m\in \mathbb{Z}\}$, we obtain $B_{S_0}=S_0\cup \{\varnothing ,\mathbb{Z}\}$. Meanwhile, for each $j\in \mathbb{Z}\backslash \{0\}$, the base

$$B_{S_j}=S_j\cup \{\{2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}(\mathrm{see}(6)),$$

is induced by the subbase $S_j=\{\{2n,2n+1,2n+2j+1\}|n\in \mathbb{Z}\}$. According to (3), we obtain that $T_j$ is not comparable with $T_0$. Namely, $T_0\nleqq T_j$ and $T_j\nleqq T_0$. To be precise, based on (3), consider an arbitrary member of $B_{S_0}$, say $b_0\in B_{S_0}=\{\{2m,2m+1\}|m\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}$, and take an element $2m\in b_0\in B_{S_0}$. Then, there is no element

$$b_j\in B_{S_j}$$

such that $2m\in b_j\subseteq b_0$, which implies that $T_0\nleqq T_j$.

Conversely, consider an arbitrary member of $B_{S_j}$, say $b_j\in B_{S_j}$, and take an element $2n+1\in b_j$. For convenience, we may put $b_j=\{2n+1\}$. Then, there is no element

$$b_0\in B_{S_0}=\{\{2n,2n+1\}|n\in \mathbb{Z}\}\cup \{\varnothing ,\mathbb{Z}\}$$

such that $2n+1\in b_0\subseteq b_j$, which implies that $T_j\nleqq T_0$.

(Case 2) For $i,j\in \mathbb{Z}\backslash \{0\}$ and $i\ne j$, let us compare two topologies $T_i$ and $T_j$ according to (3). Then, we prove that $T_i$ is not comparable with $T_j$, i.e., $T_i\nleqq T_j$ and $T_j\nleqq T_i$. Let us take any $b_i\in B_{S_i}$, e.g., $b_i:=\{2n,2n+1,2n+2i+1\}$ and further, an element $2n\in b_i$. Then, by Lemma 2, there is no member $b_j\in B_{S_j}$ such that $2n\in b_j\subseteq b_i$, which implies that $T_j$ is not finer than $T_i$.

Meanwhile, using a method similar to the proof of this approach, we can also prove that $T_i$ is not finer than $T_j$ either, which completes the proof.

(5) (Case 1) Owing to Theorem 1, it is clear that $T_0$ is not homeomorphic to $T_i,i\in \mathbb{Z}\backslash \{0\}$.

(Case 2) For two numbers $i,j\in \mathbb{Z}\backslash \{0\}$, without loss of generality, we may assume $i⪇j$. Then we prove that $T_i$ is not homeomorphic to $T_j$. Before proving this assertion, we observe that for the topologies $T_i,T_j$, in view of (3) and Theorem 1 (2), each singleton consisting of an odd (resp. an even) number is an open (resp. a closed) set in both $T_i$ and $T_j$.

Using the reductio ad absurdum, suppose there is a homeomorphism

$$f:(\mathbb{Z},T_i)\to (\mathbb{Z},T_j).$$

(8)

At this moment, we need to recall the following.

• By Lemma 1, both $T_i$ and $T_j$ are Alexandroff topological structures, in which every point in these topological spaces has its smallest open set with finite cardinality.
• Owing to the continuities of the bijections f and $f^{-1}$ and the Alexandroff topological structures of $T_i$ and $T_j$, it is clear that

  $$f(S{N}_i(x))=S{N}_j(f(x)),$$

  (9)

  where $S{N}_i(x)$ is the smallest open set of x in $(\mathbb{Z},T_i)$ and $S{N}_j(f(x))$ is the smallest open set of $f(x)$ in $(\mathbb{Z},T_j)$.
• Owing to the bases $B_{S_i}$ and $B_{S_j}$ (see (6)), for the even or odd numbers in $(\mathbb{Z},T_i)$ and $(\mathbb{Z},T_j)$, we obtain the following.

  $$\mathrm{in}(\mathbb{Z},T_i),\left\{\begin{array}{l}(1)S{N}_i(2n)=\{2n,2n+1,2n+2i+1\},\mathrm{and}\\ (2)S{N}_i(2n+1)=\{2n+1\}.\end{array}\right\}$$

  (10)

  $$\mathrm{in}(\mathbb{Z},T_j),\left\{\begin{array}{l}(3)S{N}_j(2m)=\{2m,2m+1,2m+2j+1\},\mathrm{and}\\ (4)S{N}_j(2m+1)=\{2m+1\}.\end{array}\right\}$$

  (11)
• The homeomorphism of f implies that

  $$\mathrm{for}\mathrm{any}{s}_j\in S_j(\mathrm{see}(4)),\mathrm{we}\mathrm{should}\mathrm{obtain}{f}^{-1}(s_j)\in T_i.$$

Namely, $f^{-1}(s_j)={\cup }_{i\in M}{b}_i$, where $b_i\in B_{S_i}=S_i\cup \{(2n+1|n\in \mathbb{Z}\}$. In other words, any element $x\in f^{-1}(s_j)$ should be an interior point of $f^{-1}(s_j)$ in $T_i$. Put $x=2n\in {\mathbb{Z}}_0$, where ${\mathbb{Z}}_0$ (resp. ${\mathbb{Z}}_1$) is the set of even (resp. odd) integers. Then, owing to (10), $2n\in S{N}_i(2n)\subset f^{-1}(s_j)$.

Based on this observation, we now proceed to the proof. Since f is a continuous bijection, in view of (9), (10), and (11), in $(\mathbb{Z},T_j)$ we obtain

$$f(2n)=2m\in s_j=\{2m,2m+1,2m+2j+1\}=S{N}_j(2m).$$

More precisely, owing to (9), (10), and (11), we obviously obtain that

$$f(2n)\in {\mathbb{Z}}_0,\mathrm{and}f(2n+1)\in {\mathbb{Z}}_1.$$

(12)

Hence, using the smallest open sets in $T_i$ and $T_j$ (see (10) and (11)), for some $m,n\in \mathbb{Z}$, we may assume $f(2n)=2m$. Then, the other elements $2n+1$ and $2n+2i+1$ in $S{N}_i(2n)$ should be mapped by the map f as follows:

$$\left\{\begin{array}{l}(1)f(2n+1)=2m+1,\mathrm{and}\\ (2)f(2n+2i+1)=2m+2j+1.\end{array}\right\}$$

(13)

Indeed, regarding the maps in (13), we observe $f(2n+1)\ne 2m+2j+1$ according to the continuities of f and $f^{-1}$ (see the continuity of $f^{-1}$ at $2m+2j$) because

$$\left\{\begin{array}{l}f(S{N}_i(2n))=S{N}_j(f(2n))\mathrm{and}\\ f(2n)\in {\mathbb{Z}}_0,S{N}_j(2m+2j)=\{2m+2j,2m+2j+1,2m+2j+5\}.\end{array}\right\}$$

Then, owing to (1) and (2) of (13), we have a contradiction with respect to the bijection of f because f is not a bijection at least what concerns the elements $2m+2,2m+3,2m+6,2m+7$, and so on in $(\mathbb{Z},T_j)$. Thus it turns out that $T_i$ is not homeomorphic to $T_j$.

For instance, without loss of generality, we may take $j=i+1$. Then consider the map f of (8) with $j=i+1$, i.e.,

$$f:(\mathbb{Z},T_i)\to (\mathbb{Z},T_{i+1}).$$

In practice, considering the topologies $T_i$ (resp. $T_{i+1}$) as $T_1$ (resp. $T_2$), we suffice to prove that $T_1$ and $T_2$ are not homeomorphic, as follows:

Following the reductio ad absurdum, recall the homeomorphism in (8)

$$f:(\mathbb{Z},T_1)\to (\mathbb{Z},T_2).$$

Furthermore, without loss of generality, we may assume $f(0)=0$ according to (12) and (13). Then $f(1)=1$, because $S{N}_1(0)=\{0,1,3\}$ and $S{N}_2(f(0))=S{N}_2(0)=\{0,1,5\}$ (see (4) and (5)) and further, $f(S{N}_1(0))=S{N}_2(f(0))=\{0,1,5\}$ so that $f(1)\in \{1,5\}$. Suppose $f(1)=5$ instead of $f(1)=1$. Then, since the smallest open set of 4 in $(\mathbb{Z},T_2)$ is $S{N}_2(4)=\{4,5,9\}$, and $f^{-1}$ should be also continuous at 4 in $(\mathbb{Z},T_2)$. Thus $f^{-1}(S{N}_2(4))$ should contain the element 1 and further, $|f^{-1}(S{N}_2(4))|=3$, where $|·|$ means the cardinality of the given set. Hence we obtain $f^{-1}(4)=0$, which invokes a contradiction to being a map of f at 0, i.e., $f(0)=0$ and $f(0)=4$ (see this process in Figure 2). Thus we must have $f(1)=1$ and further, $f(3)=5$. Owing to the mapping $f(3)=5$ and $S{N}_1(2)=\{2,3,5\}$, we obtain $f(S{N}_1(2))=S{N}_2(f(2))$ (see (9)). Then $f^{-1}(S{N}_2(4))=S{N}_1(f^{-1}(4))=S{N}_1(2)$ (see (12)) so that we have $f(2)=4$ and $f(5)=9$.

Owing to the mapping $f(5)=9$, we have $f(S{N}_1(4))=S{N}_2(f(4))$, where $S{N}_1(4)=\{4,5,7\}$. In addition, $f^{-1}(S{N}_2(8))=S{N}_1(f^{-1}(8))$ so that we have $f^{-1}(8)=4$, i.e., $f(4)=8$ and further, $f(5)=9$ and $f(7)=13$.

Using this process, we conclude that there are no elements in $(\mathbb{Z},T_1)$ mapping to the elements 2, 3, 6, 7 and so on, which invokes a contradiction to the bijection of f. □

Corollary 1.

Each $T_i$ is connected if $i\in \mathbb{Z}\backslash \{0\})$.

Proof. 

By Theorems 1 and 2 ((3), and (5)), the proof is completed. □

Up to now we have studied the structures of the topologies $T_k$ generated by the subbase $S_k,k\in \mathbb{Z}$ in terms of the process of (5). As proven in Theorem 2, it turns out that there are countably many topologies $T_k,k\in \mathbb{Z}\backslash \{-1\}$, on $\mathbb{Z}$ which are not homeomorphic to the K-line topology $(\mathbb{Z},\kappa )$.

Let us now replace the subbase $S_k$ of (4) by the set $S_k^{\prime }$ (see (9)), where

$$S_k^{\prime }:=\{S_{k,n}^{\prime }|S_{k,n}^{\prime }=\{2n,2n+1,2n+2k\},n\in \mathbb{Z}\}.$$

(14)

Then, what happens on the topology $T_{S_k^{\prime }}$ using the process of (5) (see also (15) below)? Based on this query, we now investigate certain structures of $T_{S_k^{\prime }}$. Before proceeding to this work, we can recognize some similarities and differences between $S_k$ of (4) and $S_k^{\prime }$, as follows:

$$\left\{\begin{array}{l}(1)|S_{k,n}|=|S_{k,n}^{\prime }|\mathrm{for}k,n\in \mathbb{Z},\\ (2)|S_k|={\aleph }_0=\left|S_k^{\prime }\right|\mathrm{for}k\in \mathbb{Z},\mathrm{and}\\ (3)\mathrm{the}\mathrm{only}\mathrm{difference}\mathrm{between}{S}_{k,n}\mathrm{and}{S}_{k,n}^{\prime }\\ \mathrm{are}\mathrm{the}\mathrm{two}\mathrm{distinct}\mathrm{numbers}2n+2k+1\mathrm{and}2n+2k.\end{array}\right\}$$

Lemma 3.

Given a number $k\in \mathbb{Z}$, consider the set $S_k^{\prime }$ of (14). Then, $S_k^{\prime }$ is a subbase for a topology on $\mathbb{Z}$. The topology generated by $S_k^{\prime }$ as a subbase is denoted by $T_{S_k^{\prime }}$. Thus, we have $(\mathbb{Z},T_{S_k^{\prime }})$ as an Alexandroff space.

Since the set $S_k^{\prime }$ is totally determined by the number $k\in \mathbb{Z}$, hereafter, the topology $T_{S_k^{\prime }}$ of Lemma 3 will be denoted by $T_k^{\prime }:=T_{S_k^{\prime }}$ for simplicity. Thus, given a number $k\in \mathbb{Z}$, with the process given in (5), consider the topology generated by the given subbase $S_k^{\prime }$ of Lemma 3 in the following way.

$$S_k^{\prime }\to B_{S_k^{\prime }}\to T_{B_{S_k^{\prime }}}:=T_k^{\prime },$$

(15)

where $B_{S_k^{\prime }}$ is the base generated by the subbase $S_k^{\prime }$ and $T_k^{\prime }$ is the topology generated by the set $B_{S_k^{\prime }}$ as a base. According to the process of (15), we observe that for $k\in \mathbb{Z}\backslash \{0\}$ each singleton consisting of even (resp. odd) number is an open (resp. a closed) set.

Using a method similar to the proof of Theorem 2, we obtain the following:

Corollary 2.

For the topological spaces $(\mathbb{Z},T_i^{\prime }),i\in \mathbb{Z}$, we obtain the following:

(1) $(\mathbb{Z},T_0^{\prime })$ is a quasi-discrete (not discrete) topological space.

(2) $T_0^{\prime }$ is not connected.

(3) Although $(\mathbb{Z},T_1^{\prime })$ is not the K-topological line, it is homoeomorphic to $(\mathbb{Z},\kappa )$.

(4) $T_i^{\prime }\ne T_j^{\prime }$ if $i\ne j$, and $i,j\in \mathbb{Z}$.

(5) For distinct numbers $i,j\in \mathbb{Z}$, $T_i^{\prime }$ is not homeomorphic to $T_j^{\prime }$ if $i,j\in \mathbb{Z}$.

Proof. 

(1) Due to the structure of $S_0^{\prime }$ and the process of (15), the smallest open set of $2n$ or $2n+1$ is the set $\{2n,2n+1\}$.

(2) Due to (1) above, the proof is completed.

(3) Consider the map $h:(\mathbb{Z},T_1^{\prime })\to (\mathbb{Z},T_{-1})$ defined as $h(x)=x+1$. Then, it is a homeomorphism.

(4) Due to (15), for any distinct numbers $k_1,k_2\in \mathbb{Z}$, using a method similar to the proof of Lemma 2, we obtain

$$S_{k_1}^{\prime }\cap S_{k_2}^{\prime }=\varnothing \mathrm{and}{B}_{S_{k_1}}^{\prime }\ne B_{S_{k_2}}^{\prime }.$$

Further, in terms of a method similar to the proof of Theorem 2 (3), the proof is completed.

(5) With the topology $T_i^{\prime },i\in \mathbb{Z}$, using a method similar to the proof of Theorem 2 (5), we complete the proof. □

In view of Theorem 2 and Corollary 2, we obtain the following:

Remark 2.

For each $k\in \mathbb{Z}$ we obtain

(1) $T_0=T_0^{\prime }$.

(2) $T_0\ne T_k^{\prime },k\in \mathbb{Z}\backslash \{0\}$.

(3) $T_k$ is not homeomorphic to $T_k^{\prime }$ if $k\in \mathbb{Z}\backslash \{0\}$.

Let us now consider some topologies on ${\mathbb{Z}}^2$ generated by certain Cartesian products of the sets $S_k$, $S_k^{\prime }$ as subbases. To be precise, using the process similar to that of (5), we may consider many types of the Cartesian products, such as $S_k\times S_k$, $S_k\times S_k^{\prime }$, and so forth. Then, we denote by $({\mathbb{Z}}^2,T_{S_k\times S_k})$ and $({\mathbb{Z}}^2,T_{S_k\times S_k^{\prime }})$ generated by the above Cartesian products as subbases. Based on Theorem 2 and Corollary 2, we obtain the following:

Corollary 3.

There are countably many topologies $T_{S_k\times S_k}$, $T_{S_k\times S_k^{\prime }}$, and so on, $k\in \mathbb{Z}\backslash \{0\}$ which are not homeomorphic to the 2-dimensional K-topological plane, i.e., $({\mathbb{Z}}^2,{\kappa }^2)$.

Using the method given in Corollary 3, for the set ${\mathbb{Z}}^n$, we can also obtain countably many topologies generated by certain n-tuple Cartesian products of $S_k$ and $S_k^{\prime }$. Further, each of these topologies need not be homeomorphic to the n-dimensional K-topological space, i.e., $({\mathbb{Z}}^n,{\kappa }^n)$.

5. Further Remarks and Work

Recently, there have been many works regarding fixed point theory from the viewpoint of digital topology, including the papers [1,2,15,17]. We say that a non-empty digital image $(X,k)$ has the almost (or approximate) fixed point property (AFPP) if, for every k-continuous self-map f of $(X,k)$, there is a point $x\in X$, such that $f(x)=x$ or $f(x)$ is k-adjacent to x (see Theorem 4.1 of [7]). Indeed, the paper [7] started the AFPP for digital images. Regarding the previous part of Example 2.12 in [17], Boxer et al. pointed out in [1] that there is a certain wrong attribution of the AFPP of a finite digital plane (or a finite digital picture) in [7]. However, Rosenfeld indeed proved that a finite digital plane $(Y,8)$ has the AFPP. Thus the paper [1] just cited this fact in the following way. “Every digital image $(Y,8)$ has the AFPP [7].” Then we strongly need to stress that in [7], the above digital image, $(Y,8)$, certainly means only a finite digital plane (or a finite digital picture) instead of a general digital image. Despite this situation, misunderstanding it, the authors of [17] stated an irrelevant comment.

Remark 3.

As a general case instead of the finite digital plane, we can state that “not every digital image $(Y,8)$ has the AFPP (see Remark 6.2 of [1] in details)”. Boxer et al. [17] mentioned that a simple closed 8-curve with l elements in ${\mathbb{Z}}^2$, say $S{C}_8^{2,l}:={(x_i)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ does not have the AFPP in the category of digital topological space (or DTC). Indeed, one important thing is that every $S{C}_k^{n,l}:={(x_i)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ does not have the AFPP in DTC. For instance, consider the self-map f of $S{C}_k^{n,l}$ with $f(x_i)=x_{i+2(modl)}$.

Using a method similar to the AFPP in DTC in Remark 3, we can refer to the AFPP for simple closed curves under K- or Marcus-Wyse topology, as follows:

Remark 4.

In the category of K- or Marcus–Wyse topological spaces, every simple closed curve with l element does not have the AFPP (see [9,29,30,31]).

As a further work, we can study the following:

• As proven in Theorem 2, since there are many kinds of connected topological spaces $(\mathbb{Z},T_i),i\in \mathbb{Z}\backslash \{0\}$, which are different from the K-line topology $(\mathbb{Z},T_{-1})$, we can further explore the fixed point property (FPP) or the AFPP for connected subspaces of these topological spaces in the given topological categories.
• As mentioned in Corollary 3, based on the new topological spaces $({\mathbb{Z}}^2,T_{S_k\times S_k})$ and $({\mathbb{Z}}^2,T_{S_k\times S_k^{\prime }})$, we can further study the FPP or the AFPP for connected subspaces of these topological spaces.

6. Concluding Remarks

We have shown countably many topologies on the set $\mathbb{Z}$ which are not homeomorphic to the K-line topology. Further, in proceeding with this work, another two types of topologies, a quasi-discrete topology and a topology satisfying the $T_{\frac{1}{2}}$-separation axiom have been discussed. In addition, many types of topologies on ${\mathbb{Z}}^n$ which are not homeomorphic to the n-dimensional K-topological space were also proposed. Based on these newly-established topological structures, we can explore the FPP or the AFPP for connected subspaces of these topological spaces.