Modelling the Relation between Managers, Shadow Cost of External Finance and Corporate Investment
Abstract
1. Introduction
2. Theory
2.1. Corporate Investment in a Perfect Capital Market
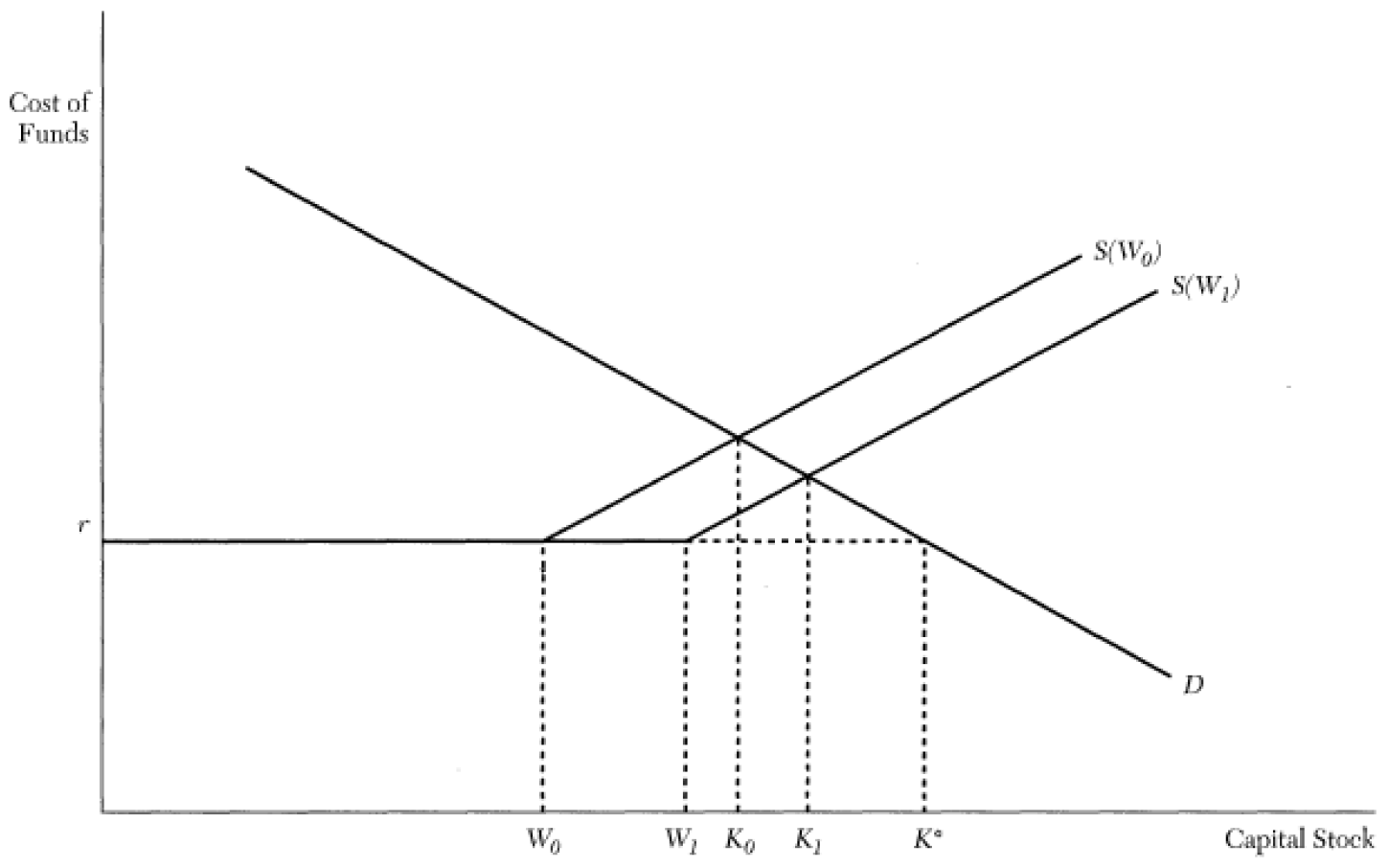
2.2. Corporate Investment in Presence of Misaligned Managers
3. Conclusions
Funding
Conflicts of Interest
References
- Hall, R.; Jorgenson, D.W. Tax policy and investment behavior. Am. Econ. Rev. 1967, 57, 391–414. [Google Scholar]
- Jorgenson, W.D. Capital theory and investment behavior. Am. Econ. Rev. 1963, 53, 247–259. [Google Scholar]
- Tobin, J. A general equilibrium approach to monetary theory. J. Money Credit Bank. 1969, 1, 265–293. [Google Scholar] [CrossRef]
- Hayashi, F. Tobin’s marginal q and average q: A neoclassical interpretation. Econometrica 1982, 50, 213–224. [Google Scholar] [CrossRef]
- Akerlof, G. The market for lemons: Quality and the market mechanism. Q. J. Econ. 1970, 84, 488–500. [Google Scholar] [CrossRef]
- Jaffee, D.M.; Russell, T. Imperfect information, uncertainty, and credit rationing. Q. J. Econ. 1976, 90, 651–666. [Google Scholar] [CrossRef]
- Myers, S.; Majluf, N. Corporate financing decisions when firms have investment information that investors do not. J. Financ. Econ. 1984, 13, 187–221. [Google Scholar] [CrossRef]
- Stiglitz, J.E.; Weiss, A. Credit rationing and markets with imperfect information. Am. Econ. Rev. 1981, 71, 393–411. [Google Scholar]
- Jensen, M.C. Agency costs of free cash flow, corporate finance, and takeovers. Am. Econ. Rev. 1986, 76, 323–329. [Google Scholar]
- Jensen, M.C. The modern industrial revolution, exit, and the failure of internal control systems. J. Financ. 1993, 48, 831–880. [Google Scholar] [CrossRef]
- Harris, M.; Raviv, A. Capital structure and the informational role of debt. J. Financ. 1990, 45, 321–350. [Google Scholar] [CrossRef]
- Hart, O.; Moore, J. Property rights and the nature of the firm. J. Political Econ. 1990, 98, 1119–1158. [Google Scholar] [CrossRef]
- Stulz, R. Managerial discretion and optimal financing policies. J. Financ. Econ. 1990, 26, 3–27. [Google Scholar] [CrossRef]
- Shleifer, A.; Vishny, R.W. Management entrenchment: The case of manager-specific investments. J. Financ. Econ. 1989, 25, 123–139. [Google Scholar] [CrossRef]
- Narayanan, M.P. Managerial incentives for short–term results. J. Financ. 1985, 40, 1469–1484. [Google Scholar] [CrossRef]
- Bertrand, M.; Mullainathan, S. Enjoying the quiet life? Corporate governance and managerial control. J. Political Econ. 2003, 111, 1043–1075. [Google Scholar] [CrossRef]
- Iona, A. Managers’ empire preservation behaviour and corporate investment. Phys. Life Rev. 2017, 22, 32–34. [Google Scholar] [CrossRef]
- Heaton, J.B. Managerial Optimism and Corporate Finance; Working Paper; University of Chicago: Chicago, IL, USA, 1998. [Google Scholar]
- Aiello, F.; Iona, A.; Leonida, L. Regional infrastructure and firm investment. Theory and empirical evidence for Italy. Empir. Econ. 2012, 42, 835–862. [Google Scholar] [CrossRef]
- Baum, C.F.; Caglayan, M.; Talavera, O. Uncertainty determinants of firm investment. Econ. Lett. 2008, 98, 282–287. [Google Scholar] [CrossRef][Green Version]
- Love, I. Financial development and financing constraints: International evidence from a structural investment model. Rev. Financ. Stud. 2003, 16, 765–791. [Google Scholar] [CrossRef]
- Hubbard, R.G. Capital market imperfections and investment. J. Econ. Lit. 1998, 36, 193–225. [Google Scholar]
- Fazzari, S.M.; Hubbard, R.G.; Petersen, B.C. Financing constraints and corporate investment. Brook. Pap. Econ. Act. 1988, 1, 141–195. [Google Scholar] [CrossRef]
- Fazzari, S.M.; Hubbard, R.G.; Petersen, B.C. Investment-cash flow sensitivities are useful: A comment on Kaplan and Zingales. Q. J. Econ. 2000, 115, 695–705. [Google Scholar] [CrossRef]
- Adelino, M.; Lewellen, K.; Sundaram, A. Investment decisions of nonprofit firms: Evidence from hospitals. J. Financ. 2015, 70, 1583–1628. [Google Scholar] [CrossRef]
- Ağca, Ş.; Mozumdar, A. Investment–cash sensitivity: Fact or fiction? J. Financ. Quant. Anal. 2017, 52, 1111–1141. [Google Scholar] [CrossRef]
- Bond, S.R.; Söderbom, M. Conditional investment–cash flow sensitivities and financing constraints. J. Eur. Econ. Assoc. 2013, 11, 112–136. [Google Scholar] [CrossRef][Green Version]
- Cleary, S. The relationship between firm investment and financial status. J. Financ. 1999, 54, 673–692. [Google Scholar] [CrossRef]
- Cleary, S.; Povel, P.; Raith, M. The u–shaped investment curve: Theory and evidence. J. Financ. Quant. Anal. 2007, 42, 1–39. [Google Scholar] [CrossRef]
- Kaplan, S.N.; Zingales, L. Do investment–cash flow sensitivities provide useful measures of financing constraints? Q. J. Econ. 1997, 112, 169–215. [Google Scholar] [CrossRef]
- Kaplan, S.N.; Zingales, L. Investment–cash flow sensitivities are not valid measures of financing constraints. Q. J. Econ. 2000, 115, 707–712. [Google Scholar] [CrossRef]
- Lewellen, J.; Lewellen, K. Investment and cash flow: New evidence. J. Financ. Quant. Anal. 2016, 51, 1135–1164. [Google Scholar] [CrossRef]
- Iona, A.; Leonida, L.; Ventouri, A. Does executive ownership lead to excess target cash? The case of U.K. firms. Corp. Gov. 2017, 17, 876–895. [Google Scholar] [CrossRef]
- Iona, A.; Leonida, L. Suboptimal financial policies and executive ownership in the UK. Evidence from a pre-crisis. Corp. Gov. 2016, 16, 187–210. [Google Scholar] [CrossRef]
- Davies, J.R.; Hillier, D.; McColgan, P. Ownership structure, managerial behavior and corporate value. J. Corp. Financ. 2005, 11, 645–660. [Google Scholar] [CrossRef]
- Holmström, B.; Tirole, J. Financial intermediation, loanable funds, and the real sector. Q. J. Econ. 1997, 112, 663–691. [Google Scholar] [CrossRef]
- Lundstrum, L.L. Entrenchment, management, capital structure changes and firm value. J. Econ. Financ. 2009, 33, 161–175. [Google Scholar] [CrossRef]
- Hart, O.; Moore, J. Debt and seniority: An analysis of the role of hard claims in constraining management. Am. Econ. Rev. 1995, 85, 567–585. [Google Scholar]
- Myers, S.C. Determinants of corporate borrowing. J. Financ. Econ. 1977, 5, 147–175. [Google Scholar] [CrossRef]
- Myers, S.C. The Capital structure puzzle. J. Financ. 1984, 39, 575–592. [Google Scholar] [CrossRef]
- Myers, S.C. Outside equity. J. Financ. 2000, 55, 1005–1037. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iona, A. Modelling the Relation between Managers, Shadow Cost of External Finance and Corporate Investment. Mathematics 2019, 7, 1050. https://doi.org/10.3390/math7111050
Iona A. Modelling the Relation between Managers, Shadow Cost of External Finance and Corporate Investment. Mathematics. 2019; 7(11):1050. https://doi.org/10.3390/math7111050
Chicago/Turabian StyleIona, Alfonsina. 2019. "Modelling the Relation between Managers, Shadow Cost of External Finance and Corporate Investment" Mathematics 7, no. 11: 1050. https://doi.org/10.3390/math7111050
APA StyleIona, A. (2019). Modelling the Relation between Managers, Shadow Cost of External Finance and Corporate Investment. Mathematics, 7(11), 1050. https://doi.org/10.3390/math7111050



