A Mollification Regularization Method for the Inverse Source Problem for a Time Fractional Diffusion Equation
Abstract
1. Introduction
2. Some Auxiliary Results
3. The Priori Parameter Choice
The Inverse Source Problem
4. The Discrepancy Principle
- (a)
- is a continous function.
- (b)
- .
- (c)
- .
- (d)
- is a strictly increasing function.
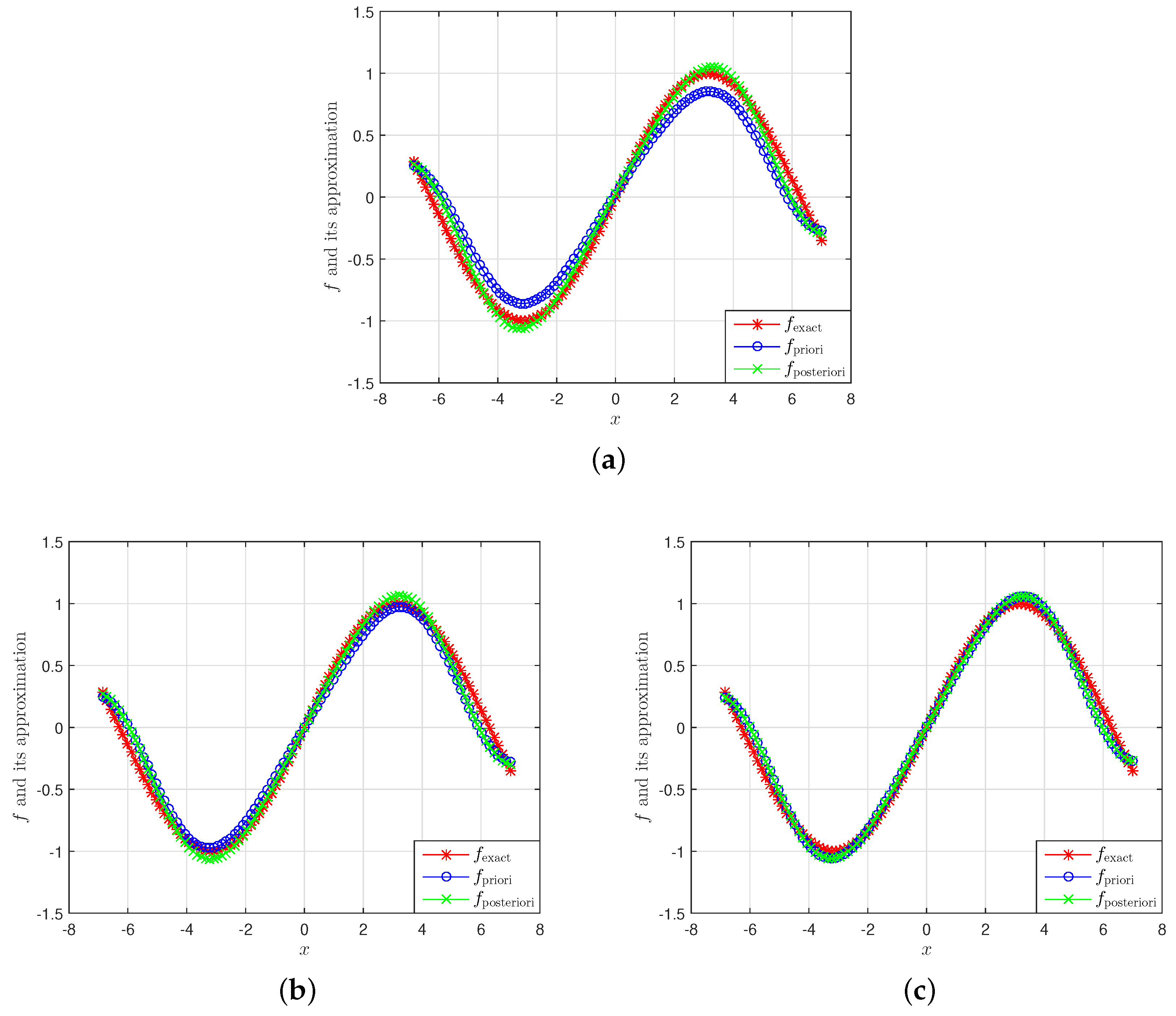
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Malyshev, I. An inverse source problem for heat equation. J. Math. Anal. Appl. 1989, 142, 206–218. [Google Scholar] [CrossRef]
- Geng, F.; Lin, Y. Application of the variational iteration method to inverse heat source problems. Comput. Math. Appl. 2009, 58, 2098–2102. [Google Scholar] [CrossRef]
- Shidfar, A.; Babaei, A.; Molabahrami, A. Solving the inverse problem of identifying an unknown source term in a parabolic equation. Comput. Math. Appl. 2010, 60, 1209–1213. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 2000, 61, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Chaves, A. Fractional diffusion equation to describe Levy flights. Phys. Lett. A 1998, 239, 13–16. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F.; Scalas, E.; Raberto, M. Fractional calculus and continuoustime finance, the diffusion limit. In Mathematical Finance. Trends in Mathematics; Birkhuser: Basel, Switzerland, 2001; pp. 171–180. [Google Scholar]
- Sakamoto, K.; Yamamoto, M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Wei, T. Identifying an unknown source in time-fractional diffusion equation by a truncation method. Appl. Math. Comput. 2013, 219, 5972–5983. [Google Scholar] [CrossRef]
- Yang, F.; Fu, C.L. The quasi-reversibility regularization method for identifying the unknown source for time fractional diffusion equation. Appl. Math. Modell. 2015, 39, 1500–1512. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. A modified Quasi-Boundary Value method for an inverse source problem of the time fractional diffusion equation. Appl. Numer. Math. 2014, 78, 95–111. [Google Scholar] [CrossRef]
- Yang, F.; Fu, C.L.; Li, X.X. A mollification regularization method for identifying the time-dependent heat source problem. J. Engine Math. 2016, 100, 67–80. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. Quasi-reversibility method to identify a space-dependent source for the time-fractional diffusion equation. Appl. Math. Modell. 2015, 39, 6139–6149. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Le, D.L.; Nguyen, V.T. Regularized solution of an inverse source problem for the time fractional diffusion equation. Appl. Math. Modell. 2016, 40, 8244–8264. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Application; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Yang, F.; Fu, C.L. A mollification regularization method for the inverse spatial-dependent heat source problem. J. Comput. Appl. Math. 2014, 255, 555–567. [Google Scholar] [CrossRef]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problem; Applied Mathematical Sciences; Springer Science Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Podlubny, I.; Kacenak, M. Mittag-Leffler Function. The MATLAB Routine. 2006. Available online: http://www.mathworks.com/matlabcentral/fileexchange (accessed on 19 September 2019).
- Mathai, A.M.; Haubold, H.J. Mittag Leffler function and Fractional Calculus. In Special Functions for Applied Scientists; Springer: New York, NY, USA, 2008; Chapter 2. [Google Scholar]
- Meerschaert, M.; Tadjeran, C. Finite difference approximations for two-sided spacefractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Bu, W.; Liu, X.; Tang, Y.; Jiang, Y. Finite element multigrid method for multiterm time fractional advection-diffusion equations. Int. J. Model. Simul. Sci. Comput. 2015, 6, 1540001. [Google Scholar] [CrossRef]
| 0.1 | 0.279660141830880 | 0.163452531664322 | 0.188256991900635 | 0.110030273632189 |
| 0.01 | 0.167130513450332 | 0.146077554813055 | 0.112506156619184 | 0.098334073898654 |
| 0.001 | 0.144054212078375 | 0.144599158066180 | 0.096972033479447 | 0.097338871212350 |
| 0.2 | 0.156401672575436 | 0.176079016470940 | 0.078962919638416 | 0.092189970426402 |
| 0.4 | 0.146364358305196 | 0.165153671589525 | 0.073895354649786 | 0.086469770247512 |
| 0.6 | 0.136338164832119 | 0.153413164488168 | 0.068833404246973 | 0.080322774289912 |
| 0.8 | 0.124692172130227 | 0.140316883268202 | 0.062953661590221 | 0.073465933522836 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, L.D.; Zhou, Y.; Thanh Binh, T.; Can, N. A Mollification Regularization Method for the Inverse Source Problem for a Time Fractional Diffusion Equation. Mathematics 2019, 7, 1048. https://doi.org/10.3390/math7111048
Long LD, Zhou Y, Thanh Binh T, Can N. A Mollification Regularization Method for the Inverse Source Problem for a Time Fractional Diffusion Equation. Mathematics. 2019; 7(11):1048. https://doi.org/10.3390/math7111048
Chicago/Turabian StyleLong, Le Dinh, Yong Zhou, Tran Thanh Binh, and Nguyen Can. 2019. "A Mollification Regularization Method for the Inverse Source Problem for a Time Fractional Diffusion Equation" Mathematics 7, no. 11: 1048. https://doi.org/10.3390/math7111048
APA StyleLong, L. D., Zhou, Y., Thanh Binh, T., & Can, N. (2019). A Mollification Regularization Method for the Inverse Source Problem for a Time Fractional Diffusion Equation. Mathematics, 7(11), 1048. https://doi.org/10.3390/math7111048





