Abstract
A new mathematical model of a general autoimmune disease is presented. Basic information about autoimmune diseases is given and illustrated with examples. The model is developed by using ideas from the kinetic theory describing individuals expressing certain functions. The modeled problem is formulated by ordinary and partial equations involving a variable for a functional state. Numerical results are presented and discussed from a medical view point.
1. Introduction
Among the tasks of the human immune system is the defence and protection of the organism from the invasion of foreign pathogens (viruses, bacteria, helminths, fungi, protozoa, etc.), the neutralization of extracellular invaders, the destruction of infected and degenerated own cells and so forth. In order to function properly, the immunological system should discriminate between own cells and foreign agents. The defend system must not attack healthy own cells, tissues and organs. This feature is known as “immune tolerance” [1,2].
However sometimes the mechanisms of immunological tolerance fail. Then the defence system attacks and destroys some of its own healthy cells and other structures. This can result in a disorder called autoimmune disease. Depending on the organs attacked by the immune system, more than 80 autoimmune diseases are known. Among them are insulin-dependent diabetes, rheumatoid arthritis (RA) and psoriatic arthritis, disseminated sclerosis (known also as multiple sclerosis (MS)), myocarditis, autoimmune hemolytic anemia, psoriasis, pancreatitis, lupus (known also as systemic lupus erythematosus (SLE)), Crohn’s disease, ulcerative colitis, celiac sprue (gluten-sensitive enteropathy), autoimmune thyroid diseases—Graves’ disease (thyroid overactivity), Hashimoto’s thyroiditis (thyroid underactivity) and many others [2,3].
The opinion of the contemporary medicine concerning the causes of the autoimmune diseases is that they are multifactorial. It is believed that the autoimmune diseases are determined by multifaceted factors. They include environmental triggers (chemicals, heavy metals, bacterial and viral infections, mold etc.), genetic predispositions, sedentary habits, socioeconomic and emotional stress, drugs and so forth [3,4,5]. Many authors mention also the possible role of diet (the food quality, gluten consumption, vitamin D deficiency etc.) and gut dysbiosis for the development of autoimmune disorders [3,6,7,8,9].
Numerous immunological studies have been devoted to clarification of the role of infections in processes related to the failure of the self-tolerance of the immune system. Various pathogenic agents such as viruses, bacteria, fungi, parasites and so forth have been shown to participate in the development of autoimmunity [3,10]. For example, Streptococcus pyogenes bacteria has been associated with rheumatic fever [11,12], enteroviruses—with insulin-dependent diabetes [11,13], the hepatitis C virus has been shown to be able to trigger chronic liver disease and mixed cryoglobulinemia [14,15,16], the Epstein–Barr virus—to induce SLE, RA, juvenile idiopathic arthritis, type 1 diabetes, MS, celiac disease and inflammatory bowel disease [14,17,18,19].
Over the last decades a rapid growth of autoimmune diseases was observed in the developed countries. This led D. Strachan to a controversial idea called the “hygiene hypothesis” [11,14,20,21]. The idea consists in associating the rise of autoimmune disease incidence with the following from the better personal cleanliness lower rates of childhood infections. The hypothesis states that the immune system needs to be trained by multiple interactions with pathogenic agents in order to function correctly.
There is evidence that various natural and acquired immune components and mechanisms are involved in the processes of autoimmune diseases. For example, the infiltration of non-specific monocytes and macrophages in diseased tissues is often observed in the course of autoimmune diseases as well as the participation of specific antibodies, B and T cells and so forth [22,23,24].
This paper presents a new model of a general autoimmune disease for studying some mechanisms of autoimmune diseases, particularly the pathogenic role of viruses. The proposed model is a nonlinear system of Boltzmann-type equations.
During the last decades many mathematical models have been proposed for studying the mechanisms of the interactions between immune system and infectious agents. Some of them are related to autoimmune disorders, see among others the models in References [25,26,27,28,29,30] and references therein. The model presented in Reference [29] is developed within the framework of idiotypic networks. Most of the remaining deterministic models use ordinary differential equations describing populations which are assumed to be homogeneous. Taking into account immunological evidence that often the populations involved in interactions during the autoimmune reactions are heterogeneous [11,21,23,31], in the presented model the activity of interacting individuals is also considered.
2. Mathematical Model
2.1. Kinetic-Type Models
2.1.1. General Description
The presented model of a general autoimmune disease is developed by the use of ideas from the kinetic theory of active particles (in short KTAP)). It uses mathematical structures similar to statistical mechanics and phenomenological theory of gases, in particular Boltzmann-type equations. Within this framework a system of one or several large populations of interacting individuals characterized by an additional continuous or discrete variable describing their functional state, is considered. The introduction of this inner characteristic of the interacting entities makes this approach very suitable for describing the non-homogeneity often observed in complex living systems, see for example References [32,33,34,35,36] and references cited therein. In many cases the space and velocity variables of the modeled systems are homogeneously distributed or have no relevant meaning for the interactions [32,33,36].
Often it is possible to divide the system under consideration into several subsystems where the individuals have the same functional state [37,38].
2.1.2. Examples
The KTAP has been actively used for modeling phenomena not only in physics (see e.g., Reference [39,40]) but also in many other areas of applied and life sciences, for example in the political [41], economic and social [42,43,44,45,46,47] systems, psychological interactions [48], the dynamics of crowds [49,50,51,52,53,54] and swarms [55,56,57,58,59,60,61], traffic flow [62,63,64,65,66,67,68] and so forth.
Examples of applications of KTAP in biology are modeling of wound healing and disease [69,70,71,72,73,74], cancer dynamics [75,76,77,78,79] and multi-cellular dynamics [80,81].
Some of these models are formulated within the so-called thermostatted KTAP developed recently in a series of papers, see for example, References [36,82,83,84,85,86,87,88,89,90] and the references therein.
2.1.3. Functional State of Active Particles
The variable describing the inner functional states of the interacting individuals represents the function, strategy, type of behaviour, purpose or activity expressed by the interacting entities (particles). Often it is named “state of activity” (or “activation state”), which explains the term KTAP. The introduction of the microscopic functional states allows to account for heterogeneity of the corresponding subsystems. The functional states describe specific characteristics of the system (or its subsystems) under study.
For example, in models describing pedestrian/crowd dynamics, the functional (activation) state can be related to walking ability or walking strategy of pedestrians [50,51,53,67] depending on such characteristics of the environment as the quality of the road, light, interactions with other pedestrians, possible danger and so forth and their own emotional and physical state (including stress, panic, etc).
One of the first applications of KTAP to biology was the model by Jäger and Segel [91] describing the interactions between a general population of insects. The functional state there is the dominance governing their social dynamics and depending on the results of their encounters.
As an example of a decomposition of a complex system into several interacting functional subsystems can be considered can be considered. The model [69] describing fibrosis disease and in particular the process of keloid formation represents an example how a decomposition of a system into several interacting functional subsystems can be performed. In this model, the activity of normal-fibroblast cells and keloid fibroblast cells describes their ability to proliferate. The functional state of activated viruses refers to the value of their aggressiveness in regard to their proliferative capability. The functional state of immune cells describes their degree of activity and of responsiveness to pathogens. The activity of malignant cells refers to the magnitude of their progression capability.
Another example of a decomposition of a complex system into several interacting functional subsystems is the model [28] describing the development of autoimmune diseases. The model describes the competition between host cells, foreign cells, antigen presenting cells (APC) that do not expose any antigen on their surface, APC that expose a certain antigen on their surface, naive and active T cells. It is assumed that the population of APC that are not exposing any antigen are homogeneous with respect to their activation state. The functional state of the host cells and of the foreign cells refers to their antigenic expression. The activity of the structured population of APC denotes the antigen exposed by them. The functional state of the non-active T lymphocytes identifies their cognate antigen. The activity of the activated T cells stands for their target antigens.
2.2. Kinetic-Type Model of Autoimmune Disease
2.2.1. The Main Biological Assumptions
The main goal of the proposed mathematical model is to investigate the pathogenic impact of viruses and damaged cells for the autoimmune disorders.
One of the main mechanisms leading to such autoimmune diseases as type 1 diabetes, MS, primary biliary cirrhosis, SLE and so forth is the so-called molecular (or antigenic or epitopic) mimicry due to viral infection [12,25,26].
This phenomenon may occur when the peptides of foreign pathogens are similar to those of the host peptides. Such similarity can trigger an immune response not only to the pathogens but also to the host constituents with similar protein structure or shape. Thus we observe a cross-reaction of the immune system with self-antigens which can lead to damaging of self cells. The damaged cells can release other sequestered antigens that can be attacked by immune cells. Thus the autoimmune response can be enhanced leading to a prolonged disorder due to the continuous production of self-antigens becoming targets for the immune cells.
In order to analyse some pathogenic properties of viral infections for autoimmunity, the presented model describes the interactions between the following three populations:
- host cells, denoted by the subscript h;
- immune cells, denoted by the subscript i;
- viral particles with molecular mimicry, denoted by the subscript v.
In the model it is supposed that certain viral infection leads to damage of some healthy host cells. This triggers a cross-reactive immune response. Specific immune cells are produced and activated, which can attack and destroy healthy cells possessing an antigen similar to the antigen presented by the viruses. In the model it is assumed that the healthy host cells can be produced from sources within the organism, for example in the thymus as well as due to the proliferation of existing healthy cells. It is supposed that the proliferation of existing healthy host cells is described by a logistic-like gain term. Immune cells are able to damage healthy cells, which also decay due to their natural death.
The immune cells can be produced due to self-antigens presented by damaged host cells as well as due to the presence of viral agents. It is assumed that it is more probably that the newly produced immune cells are with low activation states and they need some time in order to be activated. Immune cells are supposed also to be able to destroy virus particles.
2.2.2. Description of the Kinetic Model of Autoimmune Disease
It is assumed, that the general process of autoimmunity is modeled by a system consisting of three functional subsystems interacting with each other. They correspond to the populations described in the previous subsection. Due to the observations that the particular viral populations are homogeneous with respect to their ability to trigger an immune response, in the model it is supposed that the functional subsystem of the viruses is unstructured.
The remaining two functional subsystems of the host cells and of the immune cells are assumed to be structured, that is, to be able to express a specific biological function. The functional state of the population of the host cells is represented by the discrete variable , whose value is equal to 1 if the corresponding host cell is healthy and is equal to 0 if the corresponding host cell is damaged.
The functional state of the population of immune cells is represented by the continuous variable that spans the interval . The activation states of the immune cells refer to their capability to damage healthy host cells. Increasing values of the activity denote the capability to damage more healthy cells. The assumption the activities of the immune cells to be represented by a continuous variable is due to the large number of active individuals participated in the functional subsystem of immune cells. The macroscopic state of the unstructured population of the viral particles is characterized, at time t, by their concentration
The states of the structured populations are modeled, at time t, by their probability density functions and
The concentrations of the structured populations can be determined from the relations
The present model is a modification of the kinetic model of autoimmune diseases proposed in Reference [92]. Here, the populations of target cells and damaged cells are described as only one population of host cells. The functional state of host cells may either be healthy or damaged.
Following the general suggestions for creating models within the KTAP [33], the dynamics of the system under consideration is modeled through derivation of evolution equations for the probability density functions of the structured subsystems as well as for the density of the unstructured subsystem.
To model the interactions between active particles belonging to the subsystems one can equate the variation rates of the numbers of active particles with the sums of inlet flux rates due to the proliferative interactions and outlet flow rates due to the destructive interactions described in the previous subsection. In addition, conservative interactions allowing the time change of the variable should be taken into account.
As a result, the following system of ordinary and partial integro-differential equations is obtained for the present model:
with non-negative initial conditions
Equation (2) describes the time change of the distribution density of the host cells. The participating parameters have the following meaning:
- models the birth rate of healthy host cells from sources within the organism: it is assumed that their production is limited by the amount of healthy cells present in the organism;
- characterizes the proliferation rate of the healthy host cells;
- refers to the concentration of the healthy cells at which their proliferation turns off;
- describes the natural mortality rate of the healthy cells;
- describes the rate of damaging of the healthy cells by the immune cells;
- is the natural mortality rate of the damaged host cells.
Equation (3) describes the evolution of the distribution density of the immune cells. The participating parameters have the following meaning:
- is the birth rate of immune cells due to the presence of self-antigens presented by damaged host cells;
- is the birth rate of immune cells due to the presence of viruses;
- is the natural mortality rate of the immune cells;
- the factor is related to the assumption that the state of activity of the newly produced immune cells is low and they need time for activation;
- Due to the viral infection and certain cytokines and chemokines released by the damaged cells the activity of the immune cells can increase. The raising of the functional state of the immune cells is described by the conservative term which do not change the concentration of the immune cells.
Equation (4) describes the evolution of the the concentration of the viral particles. The participating parameters have the following meaning:
- is the rate of replication of viruses;
- is the rate of destruction of the viruses due to the immune response;
- is the natural mortality rate of the viruses.
Consider the following spaces:
By the use of standard arguments it is easy to verify the validity of the following statement:
3. Results of Simulations
The computational algorithm for solving the Cauchy problem corresponding to (2)–(4) includes the discretization of Equation (3) regarding the activation state by uniform mesh. The included integrals are calculated by using the Simpson’s rule.
The corresponding system of ordinary differential equations has been solved for various parameter sets by the use of the Matlab ODE suite [93].
The assumption for the initial conditions has been that there is a certain amount of healthy host cells and small amounts of immune cells with equally distributed states of activity:
The following values of parameters have been used:
and various values of parameter describing the rate of production of immune cells due to damaged cells.
The numerical experiments have been aimed at studying the effects of damaging ability of the immune cells activated against healthy self-cells by viral infection.
First, the case without virus infection is considered setting and assuming that there is no damaged cells before the infection and . The dynamics of the concentrations of the healthy cells is shown in Figure 1. After initial growth, the healthy cells remains at high levels due to the absence of autoimmune reaction in this case.
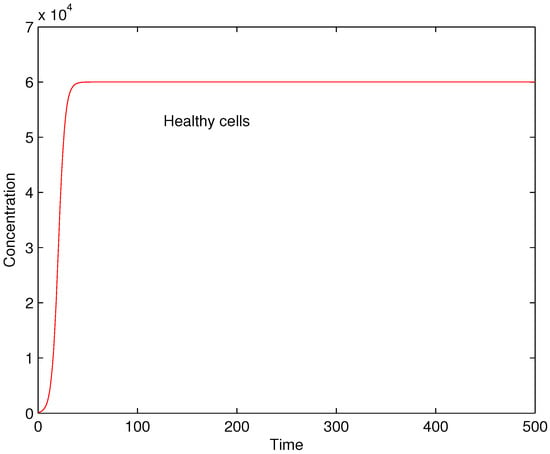
Figure 1.
Concentrations of healthy cells for , and .
In the further considerations it is assumed that initially small amounts of damaged host cells and viruses are present in the organism, by setting:
The results of numerical experiments show that for low values of the rate of production of immune cells due to damaged cells the autoimmune reaction is weak and the concentration of healthy cells remains at high levels, see Figure 2 where . In such cases autoimmune disorders are not observed or are very mild.
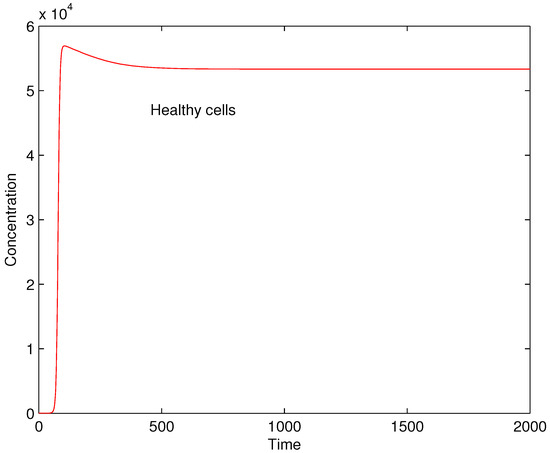
Figure 2.
Concentrations of healthy cells for .
The results of numerical experiments show that for higher values of parameter the cross-reaction of the immune system with self-antigens becomes very strong and damages a large amount of healthy cells. The result for is shown in Figure 3. One can see that in this case almost the half of the population of healthy cells is damaged. Such situation corresponds to a very severe autoimmune disease with possible lethal effect.
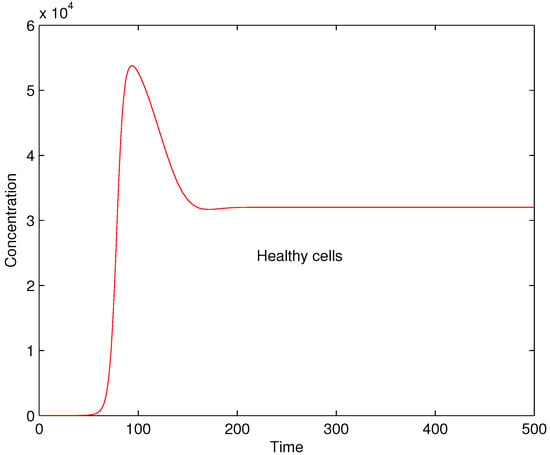
Figure 3.
Concentrations of healthy cells for .
The performed numerical experiments show that is a bifurcation parameter. It separates two different dynamics of the solutions. When the value of is lower or equal to the solution is stable and tends to equilibrium while when it is greater than the value the solution is oscillating. In Figure 4 and Figure 5 the concentrations of healthy cells for values and are shown for illustration.
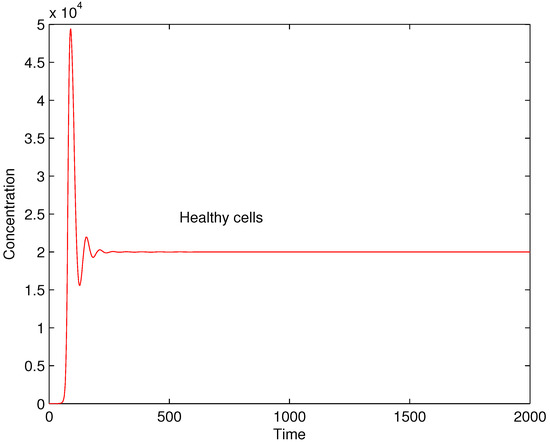
Figure 4.
Concentrations of healthy cells for .
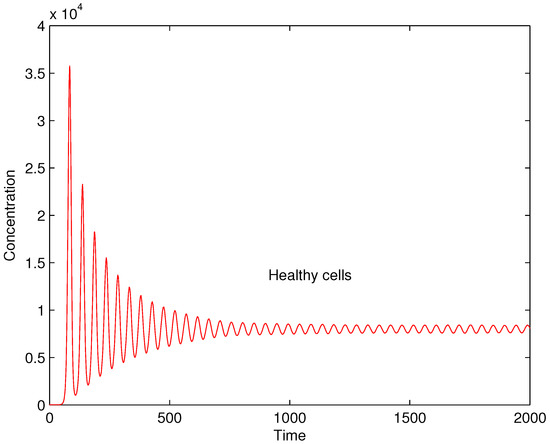
Figure 5.
Concentrations of healthy cells for .
The cases with periodic flare ups can be considered autoimmune diseases characterized with repeated periods of dormancy of the autoaggressive immune cells and their flare ups triggered by spreading pathogenic proteins, possible failure of regulatory immune cells to control the destructive reaction of effector immune cells against host constituents and so forth. An example of repeated flare ups is the MS [25,94]. The numerous repeated periods when large amounts of healthy cells are damaged can lead to serious tissue or organ destruction and even lethal result for the patients.
4. Concluding Remarks
In this paper, a kinetic type model of general autoimmune disease is presented. The modeled problem is solved numerically. The numerical solutions represent several typical dynamics of autoimmune diseases resulting from viral infection (absence of disease, mild symptoms, chronic disease, flare ups and severe autoimmune disease).
The presented results and further development of the model can be useful for the better understanding of the group of autoimmune diseases. The results confirm the evidence that the viral infections and damaged cells can be very potent pro-inflammatory triggers and sources for self-antigens for specific immune cells thus leading to chronic or severe autoimmune diseases [25,94].
Funding
This research received no external funding
Acknowledgments
The author wishes to express his gratitude to M. Lachowicz for the useful discussions on the mathematical model as well as to the anonymous referees for the helpful comments and remarks that led to the improvements in the presentation of the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Anderson, C.C.; Bretscher, P.; Corthay, A.; Dembic, Z.; Havele, C.; Nagy, Z.A.; Øynebraten, I. Immunological Tolerance: Part I of a Report of a Workshop on Foundational Concepts of Immune Regulation. Scand. J. Immunol. 2017, 85, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Janeway, C.; Travers, P.; Walport, M.; Shlomchik, M. Immunobiology: The Immune System in Health and Disease; Garland: New York, NY, USA, 2006. [Google Scholar]
- Campbell, A.W. Autoimmunity and the Gut. Autoimmune Dis. 2014, 2014, 152428. [Google Scholar] [CrossRef] [PubMed]
- Vojdani, A. A potential link between environmental triggers and autoimmunity. Autoimmune Dis. 2013, 2013, 437231. [Google Scholar] [CrossRef] [PubMed]
- Ceccarelli, F.; Agmon-Levin, N.; Perricone, C. Genetic factors of autoimmune diseases 2017. J. Immunol. Res. 2017, 2017, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Pelajo, C.F.; Lopez-Benitez, J.M.; Miller, L.C. Vitamin D and autoimmune rheumatologic disorders. Autoimmun. Rev. 2010, 9, 507–510. [Google Scholar] [CrossRef] [PubMed]
- Agmon-Levin, N.; Theodor, E.; Segal, R.; Shoenfeld, Y. Vitamin D in systemic and organ-specific autoimmune diseases. Clin. Rev. Allergy Immunol. 2013, 45, 256–266. [Google Scholar] [CrossRef] [PubMed]
- Syage, J.; Kelly, C.; Dickason, M.; Ramirez, A.C.; Leon, F.; Dominguez, R.; Sealey-Voyksner, J. Determination of gluten consumption in celiac disease patients on agluten-free diet. Am. J. Clin. Nutr. 2018, 107, 201–207. [Google Scholar] [CrossRef]
- Lebwohl, B.; Ludvigsson, J.F.; Green, P.H.R. Celiac disease and non-celiac gluten sensitivity. Autoimmune Dis. 2015, 351, h4347. [Google Scholar] [CrossRef]
- Abbas, A.; Lichtman, A.; Pillai, S. Cellular and Molecular Immunology; Elsevier: Philadelphia, PA, USA, 2018. [Google Scholar]
- Kivity, S.; Agmon-Levin, N.; Blank, M.; Shoenfeld, Y. Infections and autoimmunity: Friends or foes? Trends Immunol. 2009, 30, 409–414. [Google Scholar] [CrossRef]
- Rose, N. Introduction. In Infection and Autoimmunity; Shoenfeld, Y., Agmon-Levin, N., Rose, N., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 1–12. [Google Scholar]
- Richardson, S.J.; Willcox, A.; Bone, A.J.; Foulis, A.K.; Morgan, N.G. The prevalence of enteroviral capsid protein vp1 immunostaining in pancreatic islets in human type 1 diabetes. Diabetologia 2009, 52, 1143–1151. [Google Scholar] [CrossRef]
- Martinelli, M.; Agmon-Levin, N.; Amital, H.; Shoenfeld, Y. Infections and autoimmune diseases: An interplay of pathogenic and protective links. In Infection and Autoimmunity; Shoenfeld, Y., Agmon-Levin, N., Rose, N., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 13–23. [Google Scholar]
- Lidar, M.; Lipschitz, N.; Agmon-Levin, N.; Langevitz, P.; Barzilai, O.; Ram, M.; Porat-Katz, B.S.; Bizzaro, N.; Damoiseaux, J.; Tervaert, J.W.; et al. Infectious serologies and autoantibodies in hepatitis C and autoimmune disease-associated mixed cryoglobulinemia. Clin. Rev. Allergy Immunol. 2012, 42, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Fabrizi, F.; Dixit, V.; Messa, P. Antiviral therapy of symptomatic HCV-associated mixed cryoglobulinemia: Meta-analysis of clinical studies. J. Med. Virol. 2013, 85, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Harley, J.B.; Chen, X.; Pujato, M.; Miller, D.; Maddox, A.; Forney, C.; Magnusen, A.F.; Lynch, A.; Chetal, K.; Yukawa, M.; et al. Transcription factors operate across disease loci, with EBNA2 implicated in autoimmunity. Nat. Genet. 2018, 50, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Afrasiabi, A.; Parnell, G.P.; Fewings, N.; Schibeci, S.D.; Basuki, M.A.; Chandramohan, R.; Zhou, Y.; Taylor, B.; Brown, D.A.; Swaminathan, S.; et al. Evidence from genome wide association studies implicates reduced control of Epstein-Barr virus infection in multiplesclerosis susceptibility. Genome Med. 2019, 11, 26–38. [Google Scholar] [CrossRef]
- Li, Z.X.; Zeng, S.; Wu, H.X.; Zhou, Y. The risk of systemic lupus erythematosus associated with Epstein–Barr virus infection: A systematic review and meta-analysis. Clin. Exp. Med. 2019, 19, 23–36. [Google Scholar] [CrossRef]
- Strachan, D.P. Hay fever, hygiene, and household size. BMJ 1989, 229, 1259–1260. [Google Scholar] [CrossRef]
- Davies, T.F. Infection and autoimmune thyroid disease. J. Clin. Endocrinol. Metab. 2008, 93, 674–676. [Google Scholar] [CrossRef]
- Navegantes, K.C.; de Souza Gomes, R.; Pereira, P.A.T.; Czaikoski, P.G.; Azevedo, C.H.M.; Monteiro, M.C. Immune modulation of some autoimmune diseases: The critical role of macrophages and neutrophils in the innate and adaptive immunity. J. Transl. Med. 2017, 15, 36. [Google Scholar] [CrossRef]
- Ma, W.T.; Gao, F.; Gu, K.; Chen, D.K. The Role of Monocytes and Macrophages in Autoimmune Diseases: A Comprehensive Review. Front. Immunol. 2019, 10, 1140. [Google Scholar] [CrossRef]
- McInnes, I.B.; Schett, G. The pathogenesis of rheumatoid arthritis. New Engl. J. Med. 2011, 365, 2205–2219. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Miura, Y.; Sasaki, T.; Kajiwara, T. Dynamical properties of autoimmune disease models: Tolerance, flare-up, dormancy. J. Theor. Biol. 2007, 246, 646–659. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Iwamoto, K.; Naruo, Y.; Yasukawa, T. A mathematical design of vector vaccine against autoimmune disease. J. Theor. Biol. 2009, 256, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, D.; Kerr, E.; Jepps, O.; Nicholson, L. Modelling experimental uveitis: Barrier effects in autoimmune disease. Inflamm. Res. 2012, 61, 759–773. [Google Scholar] [CrossRef] [PubMed]
- Delitala, M.; Dianzani, U.; Lorenzi, T.; Melensi, M. A mathematical model for immune and autoimmune response mediated by T-cells. Comput. Math. Appl. 2013, 66, 1010–1023. [Google Scholar] [CrossRef]
- Landmann, S.; Preuss, N.; Behn, U. Self-tolerance and autoimmunity in a minimal model of the idiotypic network. J. Theor. Biol. 2017, 426, 17–39. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Roy, A.K.; Roy, P.K.; Grigorieva, E. Mathematical insights on psoriasis regulation: Role of Th1 and Th2 cells. Math. Biosci. Eng. 2018, 15, 717–738. [Google Scholar]
- Sakaguchi, S.; Wing, K.; Miyara, M. Regulatory T cells: A brief history and perspective. Eur. J. Immunol. 2007, 37, S116–S123. [Google Scholar] [CrossRef]
- Romanczuk, P.; Bar, M.; Ebeling, W.; Linder, B.; Schimansky-Geier, L. Active Brownian particles, from individual to collective stochastic dynamics. Eur. Phys. J. 2012, 202, 1–162. [Google Scholar]
- Bianca, C.; Bellomo, N. Towards a Mathematical Theory of Multiscale Complex Biological Systems; World Scientific: Singapore, 2011. [Google Scholar]
- Bellomo, N.; Brezzi, F. Challenges in active particles methods: Theory and applications. Math. Model. Methods Appl. Sci. 2018, 28, 1627–1633. [Google Scholar] [CrossRef]
- Bellomo, N.; Brezzi, F. Towards a multiscale vision of active particles. Math. Model. Methods Appl. Sci. 2019, 29, 581–588. [Google Scholar] [CrossRef]
- Bianca, C. Thermostatted kinetic equations as models for complex systems in physics and life sciences. Phys. Life Rev. 2012, 9, 359–399. [Google Scholar] [CrossRef] [PubMed]
- Bianca, C. Modeling complex systems by functional subsystems representation and thermostatted-KTAP methods. Appl. Math. Inf. Sci. 2012, 6, 495–499. [Google Scholar]
- Bellomo, N.; Bianca, C.; Delitala, M. Complexity analysis and mathematical tools towards the modelling of living systems. Phys. Life Rev. 2009, 6, 144–175. [Google Scholar] [CrossRef] [PubMed]
- Degond, P.; Pareschi, L.; Russo, G. (Eds.) Modeling and Computational Methods for Kinetic Equations; Springer Science+Bussiness Media: New York, NY, USA, 2004; pp. 219–258. [Google Scholar]
- Bianca, C.; Dogbe, C. On the Boltzmann gas mixture equation: Linking the kinetic and fluid regimes. Commun. Nonlinear Sci. Numer. Simulat. 2015, 29, 240–256. [Google Scholar] [CrossRef]
- Schiavo, M.L. The modelling of political dynamics by generalized kinetic (Boltzmann) models. Math. Comput. Model. 2003, 37, 261–281. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Delitala, M. Conservation laws and asymptotic behavior of a model of social dynamics. Nonlinear Anal. Real World Appl. 2008, 9, 183–196. [Google Scholar] [CrossRef]
- Ajmone Marsan, G.; Bellomo, N.; Gibelli, L. Stochastic evolutionary differential games toward a systems theory of behavioral social dynamics. Math. Model. Methods Appl. Sci. 2016, 26, 1051–1093. [Google Scholar] [CrossRef]
- Dolfin, M.; Leonida, L.; Outada, N. Modelling human behaviour in economics and social science. Phys. Life Rev. 2017, 22–23, 1–21. [Google Scholar] [CrossRef]
- Bellomo, N.; Brezzi, F.; Pulvirenti, M. Modeling behavioral social systems. Math. Model. Methods Appl. Sci. 2017, 27, 1–11. [Google Scholar] [CrossRef]
- Bianca, C.; Kombargi, A. On the inverse problem for thermostatted kinetic models with application to the financial market. Appl. Math. Inf. Sci. 2017, 11, 1463–1471. [Google Scholar] [CrossRef]
- Bianca, C.; Kombargi, A. On the modeling of the stock market evolution by means of the information-thermostatted kinetic theory. Nonlinear Stud. 2017, 24, 935–944. [Google Scholar]
- Bellomo, N.; Carbonaro, B. On the complexity of multiple interactions with additional reasoning about Kate, Jules and Jim. Math. Comput. Model. 2008, 47, 168–177. [Google Scholar] [CrossRef]
- Bellomo, N.; Bianca, C.; Coscia, V. On the modeling of crowd dynamics: An overview and research perspectives. Bol. Soc. Esp. Mat. Apl. 2011, 54, 25–46. [Google Scholar] [CrossRef]
- Bellomo, N.; Bellouquid, A. On multiscale models of pedestrian crowds - from mesoscopic to macroscopic. Commun. Math. Sci. 2015, 13, 1649–1664. [Google Scholar] [CrossRef]
- Bellomo, N.; Gibelli, L. Toward a mathematical theory of behavioural-social dynamics for pedestrian crowds. Math. Model. Methods Appl. Sci. 2015, 25, 2417–2437. [Google Scholar] [CrossRef]
- Elaiw, A.; Al-Turki, Y.; Alghamdi, M. A critical analysis of behavioural crowd dynamics—From a modelling strategy to kinetic theory methods. Symmetry 2019, 11, 851. [Google Scholar] [CrossRef]
- Bellomo, N.; Gibelli, L. Behavioral human crowds. In Crowd Dynamics, Volume 1—Theory, Models, and Safety Problems. Modeling and Simulation in Science, Engineering, and Technology; Bellomo, N., Gibelli, L., Eds.; Birkhäuser: New York, NY, USA, 2018; pp. 1–14. [Google Scholar]
- Bellomo, N.; Gibelli, L.; Outada, N. On the interplay between behavioral dynamics and social interactions in human crowds. Kinet. Relat. Mod. 2019, 12, 397–409. [Google Scholar] [CrossRef]
- Cucker, F.; Smale, S. Emergent behavior in flocks. IEEE Trans. Automat. Control 2007, 52, 852–862. [Google Scholar] [CrossRef]
- Ha, S.-Y.; Tadmor, E. From particle to kinetic and hydrodynamic description of flocking. Kinet. Relat. Model. 2008, 1, 415–435. [Google Scholar]
- Bellomo, N.; Bellouquid, A.; Gibelli, L.; Outada, N. A Quest Towards a Mathematical Theory of Living Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Bellomo, N.; Ha, S.-Y. A quest toward a mathematical theory of the dynamics of swarms. Math. Model. Methods Appl. Sci. 2017, 27, 745–770. [Google Scholar] [CrossRef]
- Degond, P.; Frouvelle, A.; Merino-Aceituno, S. A new flocking model through body attitude coordination. Math. Model. Methods Appl. Sci. 2017, 27, 1005–1049. [Google Scholar] [CrossRef]
- Lachowicz, M.; Leszczynski, H.; Parisot, M. Blow-up and global existence for a kinetic equation of swarm formation. Math. Model. Methods Appl. Sci. 2017, 27, 1153–1175. [Google Scholar] [CrossRef]
- Poyato, D.; Soler, J. Euler-type equations and commutators in singular and hyperbolic limits of kinetic Cucker–Smale models. Math. Model. Methods Appl. Sci. 2017, 27, 1089–1152. [Google Scholar] [CrossRef]
- Delitala, M.; Tosin, A. Mathematical modelling of vehicular traffic: A discrete kinetic theory approach. Math. Model. Methods Appl. Sci. 2007, 17, 901–932. [Google Scholar] [CrossRef]
- Klar, A.; Wegener, R. Traffic flow: Models and numerics. In Modeling and Computational Methods for Kinetic Equations; Degond, P., Pareschi, L., Russo, G., Eds.; Springer Science+Bussiness Media: New York, NY, USA, 2004; pp. 219–258. [Google Scholar]
- Bianca, C.; Coscia, V. On the coupling of steady and adaptive velocity grids in vehicular traffic modelling. Appl. Math. Lett. 2011, 24, 149–155. [Google Scholar] [CrossRef]
- Bianca, C. Mathematical modeling of crowds dynamics: Complexity and kinetic approach. Nonlinear Stud. 2012, 19, 345–354. [Google Scholar]
- Bianca, C.; Dogbe, C. A mathematical model for crowd dynamics: Multiscale analysis, fluctuations and random noise. Nonlinear Stud. 2013, 20, 281–305. [Google Scholar]
- Bianca, C.; Mogno, C. A thermostatted kinetic theory model for event-driven pedestrian dynamics. Eur. Phys. J. Plus 2018, 133, 213. [Google Scholar] [CrossRef]
- Bianca, C.; Mogno, C. Modelling pedestrian dynamics into a metro station by thermostatted kinetic theory methods. Math. Comput. Model. Dyn. Syst. 2018, 24, 207–235. [Google Scholar] [CrossRef]
- Bianca, C. Mathematical modelling for keloid formation triggered by virus: Malignant effects and immune system competition. Math. Model. Methods Appl. Sci. 2011, 21, 389–419. [Google Scholar] [CrossRef]
- Bianca, C.; Fermo, L. Bifurcation diagrams for the moments of a kinetic type model of keloid-immune system competition. Comput. Math. Appl. 2011, 61, 277–288. [Google Scholar] [CrossRef]
- Bianca, C.; Delitala, M. On the modelling of genetic mutations and immune system competition. Comput. Math. Appl. 2011, 61, 2362–2375. [Google Scholar] [CrossRef]
- Bianca, C.; Riposo, J. Mimic therapeutic actions against keloid by thermostatted kinetic theory methods. Eur. Phys. J. Plus 2015, 130, 159. [Google Scholar] [CrossRef]
- Ben Amar, M.; Bianca, C. Towards a unified approach in the modelling of fibrosis: A review with research perspectives. Phys. Life Rev. 2016, 16, 61–85. [Google Scholar]
- Ben Amar, M.; Bianca, C. Multiscale modeling of fibrosis—What’s next? Phys. Life Rev. 2016, 16, 118–123. [Google Scholar]
- Bianca, C. How do mutative events modify moments evolution in thermostatted kinetic models? Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2155–2159. [Google Scholar] [CrossRef]
- Bianca, C.; Dogbe, C.; Lemarchand, A. Mimic therapeutic actions against keloid by thermostatted kinetic theory methods. Eur. Phys. J. Plus 2016, 131, 41. [Google Scholar] [CrossRef][Green Version]
- Bianca, C.; Lemarchand, A. Miming the cancer-immune system competition by kinetic Monte Carlo simulations. J. Chem. Phys. 2016, 145, 154108. [Google Scholar] [CrossRef]
- Masurel, L.; Bianca, C.; Lemarchand, A. On the learning control effects in the cancer-immune system competition. Phys. A Stat. Mech. Its Appl. 2018, 506, 462–475. [Google Scholar] [CrossRef]
- Aylaj, B. Qualitative analysis and simulation of a nonlinear integro-differential system modeling tumor-immune cells competition. Int. J. Biomath. 2018, 11, 1850104. [Google Scholar] [CrossRef]
- Bianca, C.; Lemarchand, A. Density evolution by the low-field limit of kinetic frameworks with thermostat and mutations. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 14–23. [Google Scholar] [CrossRef]
- Bianca, C.; Brezin, L. Modeling the antigen recognition by B-cell and T-cell receptors through thermostatted kinetic theory methods. Int. J. Biomath. 2017, 10, 1750072. [Google Scholar] [CrossRef]
- Bianca, C. Kinetic theory for active particles modelling coupled to Gaussian thermostats. Appl. Math. Sci. 2012, 6, 651–660. [Google Scholar]
- Bianca, C. An existence and uniqueness theorem for the Cauchy problem for thermostatted-KTAP models. Int. J. Math. Anal. 2012, 6, 813–824. [Google Scholar]
- Bianca, C. Thermostatted kinetic models for complex systems under microscopic external fields. Math. Eng. Sci. Aerosp. 2012, 3, 225–238. [Google Scholar]
- Bianca, C. Onset of nonlinearity in thermostatted active particles models for complex systems. Nonlinear Anal. Real World Appl. 2012, 13, 2593–2608. [Google Scholar] [CrossRef]
- Bianca, C. Thermostatted models - Multiscale analysis and tuning with real-world systems data. J. Appl. Comput. Math. 2012, 9, 418–425. [Google Scholar] [CrossRef]
- Bianca, C.; Ferrara, M.; Guerrini, L. Thermostatted models - Multiscale analysis and tuning with real-world systems data. J. Glob. Optim. 2014, 58, 389–404. [Google Scholar] [CrossRef]
- Bianca, C.; Dogbe, C. Kinetic models coupled with Gaussian thermostats: Macroscopic frameworks. Nonlinearity 2014, 27, 2771–2803. [Google Scholar] [CrossRef][Green Version]
- Bianca, C.; Menale, M. Existence and uniqueness of nonequilibrium stationary solutions in discrete thermostatted models. Commun. Nonlinear Sci. Numer. Simulat. 2019, 73, 25–34. [Google Scholar] [CrossRef]
- Bianca, C.; Menale, M. On the interaction domain reconstruction in the weighted thermostatted kinetic framework. Eur. Phys. J. Plus 2019, 134, 143. [Google Scholar] [CrossRef]
- Jäger, E.; Segel, L. On the distribution of dominance in a population of interacting anonymous organisms. SIAM J. Appl. Math. 1992, 52, 1442–1468. [Google Scholar] [CrossRef]
- Kolev, M.; Nikolova, I. A mathematical model of some viral-induced autoimmune diseases. Math. Appl. 2018, 46, 97–108. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The Matlab ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Vadasz, Z.; Toubi, E. Acute and chronic infections: Their role in immune thrombocytopenia. In Infection and Autoimmunity; Shoenfeld, Y., Agmon-Levin, N., Rose, N., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 859–876. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).