Abstract
Suppose that G is a simple undirected connected graph. Denote by the distance matrix of G and by the diagonal matrix of the vertex transmissions in G, and let . The generalized distance matrix is defined as , where . If are the eigenvalues of ; we define the generalized distance Estrada index of the graph G as where denotes for the Wiener index of G. It is clear from the definition that and , where denotes the distance Estrada index of G and denotes the distance signless Laplacian Estrada index of G. This shows that the concept of generalized distance Estrada index of a graph G merges the theories of distance Estrada index and the distance signless Laplacian Estrada index. In this paper, we obtain some lower and upper bounds for the generalized distance Estrada index, in terms of various graph parameters associated with the structure of the graph G, and characterize the extremal graphs attaining these bounds. We also highlight relationship between the generalized distance Estrada index and the other graph-spectrum-based invariants, including generalized distance energy. Moreover, we have worked out some expressions for of some special classes of graphs.
Keywords:
generalized distance matrix (spectrum); distance (signless Laplacian) Estrada index; distance (signless Laplacian) matrix; generalized distance Estrada index; generalized distance energy MSC:
05C50, 05C12, 15A18
1. Introduction
In this paper, we are concerned only with simple, finite, connected and undirected graphs with vertex set and edge set . The order and the size of G is, respectively, the number of vertices and the number of edges of G. The degree of a vertex v, denoted by (or simply ) is the cardinality of the set of vertices adjacent to v in a graph G. The distance between two vertices , denoted by , represents the number of edges in a shortest path between these two end nodes in G. The diameter of G is the maximum distance between any pair of vertices of G. The distance matrix of a graph G is a square symmetric matrix defined as . The transmission of a vertex v, denoted by , is defined as the sum of the distances from v to all other vertices in G, in other words, . A graph G is referred to as k-transmission regular when the matrix has the constant row sum equal to k. The Wiener index (also called the transmission) of a graph G, denoted by , is the sum of distances between all unordered pairs of vertices in G. Apparently, . For any vertex , the transmission is also called the transmission degree, shortly denoted by , and the sequence is called the transmission degree sequence of the graph G.
Let be the diagonal matrix of vertex transmissions of G. Following Aouchiche and Hansen [1,2], the distance Laplacian matrix and the distance signless Laplacian matrix of a graph G are defined, respectively, as and . Recently, the spectral properties of the distance Laplacian matrix, distance matrix, as well as distance signless Laplacian matrix have attracted attention of the many researchers and a large number of papers have been published regarding their spectral properties, like spectral radius, energy, Estrada index, second largest eigenvalue, smallest eigenvalue, etc. For some recent works, we refer to [3,4,5] and the references cited therein.
Motivated by [6], Cui et al. [7] introduced the generalized distance matrix as a convex combinations of and , defined as , for . Noting that , and , any result regarding the spectral properties of generalized distance matrix has its counterpart for each of these particular graph matrices, and these counterparts following immediately from a single proof. In fact, this matrix reduces to merging the distance Laplacian spectral, distance spectral, as well as distance signless Laplacian spectral theories. As the matrix is real symmetric, all its eigenvalues are real. Therefore, we can arrange them as . The largest eigenvalue of the matrix is called the generalized distance spectral radius of G (We will denote by ).
Based upon some geometric characteristics of biomolecules, Ernesto Estrada [8,9] investigated an expression taking the form
where represent all eigenvalues of the adjacency matrix of a molecular graph G. Analytical studies on this quantity was performed later in [10] and the name “Estrada index” was proposed in [11]. The properties of the Estrada index have been intensively explored, see, for example [11,12,13,14]. There exists a vast literature related to Estrada index and its bounds and we refer the reader to the nice surveys [15,16].
This graph-spectrum-based invariant has also an important role in chemistry, biology, as well as network science. It has been applied for instance to gauge the extent of folding of long chain polymeric molecules, encompassing some proteins [8,17,18]. It has found a number of applications in complex networks and characterizes the centrality [9]. offers a unique metric to characterize the robustness of complex networks [19]; namely, it is a monotonic measure with respect to the edge deletion and addition. For more applications of the Estrada index in network science, see the monograph in [20] and papers [19,21].
The pioneering papers [8,9] further investigate varied versions of Estrada index with respect to other graph associated matrices. Because of the evident success of the graph Estrada index, this proposal has been put into effect, and Estrada index-based on the eigenvalues of more graph matrices have been introduced subsequently: Estrada index-based invariant with respect to distance matrix [22], Estrada index-based invariant with respect to Laplacian matrix [23,24], Estrada index-based invariant with respect to signless Laplacian matrix [25,26], and Estrada index-based invariant with respect to distance signless Laplacian matrix [27] have been introduced and studied. For some other interesting papers, we direct the reader to works [28,29,30,31].
The distance matrix graph has shown its importance in a wide range of areas across science and engineering. The distance matrix contains information on the number of walks and self-avoiding walks of chemical graphs, which adjacency matrix fails to show. Distance matrix has been used to calculate many topological indices, including the Wiener index, and thermodynamic properties involving temperature and pressure coefficients. In the design of communication infrastructure network, molecular stability, and graph embedding theory, distance matrix has played an important role. Distance eigenvalues of graphs have attracted huge attention for mathematicians for decades. For more information regarding distance spectrum, we refer to the survey [1] and the references therein.
We observe that the distance matrix and its eigenvalues are of importance not only from a chemistry point of view, but also because they are very useful in other branches of science and social science. Clearly, the information one gets regarding the graph from the distance matrix is also visible from the distance Laplacian and the distance signless Laplacian matrices of a graph. As these matrices use more structural properties of a graph than the distance matrix, these matrices may contain a wealth of information about the graph. In addition to its formal analogy to the Estrada index, the distance and the distance signless Laplacian Estrada indices are arguably of prominent significance in physical chemistry. Distance turns out to be rooted deeply in the molecular graphs.
Therefore, here we define the generalized distance Estrada index , based on the generalized distance matrix of the graph G, as
where are the eigenvalues of (the generalized distance eigenvalues of a graph G).
It follows from the definition that and , where denotes the distance Estrada index of a graph G and denotes the distance signless Laplacian Estrada index of a graph G. This shows that the concept of generalized distance Estrada index of a graph G merges the theories of distance Estrada index and the distance signless Laplacian Estrada index of a graph G. Let
Then, and Recalling the power series expansion of , we can write the generalized distance Estrada index as
The rest of the paper is structured as follows. In Section 2, we mention some preliminary results which will be helpful throughout the paper. In Section 3, we obtain some lower bounds for the generalized distance Estrada index , in terms of various graph parameters associated with structure of the graph G, and identify the extremal graphs attaining these bounds. In Section 4, we obtain some upper bounds for the generalized distance Estrada index and delineate the extremal graphs. In Section 5, we derive some relations between the generalized distance Estrada index and the generalized distance energy of G. Finally, in Section 6, we obtain some results about generalized distance Estrada index of some elementary graphs and give an expression for of a (transmission) regular graph G, in terms of the distance eigenvalues as well as adjacency eigenvalues of G, and describe the generalized distance Estrada index of some graphs obtained by operations.
2. Preliminary Results
In this section, we give some preliminary results which will be utilized in the subsequent sections. The following lemma can be found in [7].
Lemma 1
([7]). Suppose that G is a connected graph of order n. We have
where the equality holds if and only if G is transmission regular.
By a similar way as used in the proof of ([32], Lemma 2), we can prove the following lemma.
Lemma 2.
A connected graph G admits two distinct generalized distance eigenvalues if and only if G is a complete graph.
The proof of the following lemma is similar to that of ([4], Theorem 2.2) and is omitted here.
Lemma 3.
Let the transmission degree sequence of G be . Then,
where the equality holds if and only if G is transmission regular.
Given two nonincreasing real sequences and of length n, is said to be majorized by or majorizes , denoted by if
The relation means that and is not the rearrangement of .
The following observation can be found in [23].
Lemma 4
([23]). Let and be nonincreasing sequences of real numbers of length n. If , then for any convex function ψ, we have . Equality holds if and only if for all . In addition, when and ψ is strictly convex, holds.
The majorization relation between the spectrum and diagonal elements of Hermitian matrices perfectly links the spectrum of a generalized distance matrix with majorization. The relation given below immediately follows.
Lemma 5.
Assume that G is a connected graph of order n admitting generalized distance eigenvalues and transmission degrees . Then,
Theorem 1.
Assume that G is any connected graph of order with transmission degree sequence .
- (i)
- If or , then ;
- (ii)
- If , then .
Equality occurs in both parts, if and only if for .
Proof.
(i) For , it follows that the function is a convex function if or . Let and . By Lemma 5, we have . It then follows by Lemma 4 that
Therefore, by Lemma 4, equality occurs in the inequality (3) if and only if That is, if and only if for all .
(ii) For , it follows that the function is a convex function if . Therefore, proceeding similarly as in part (i), we arrive at part (ii). □
3. Lower Bounds for the Generalized Distance Estrada Index of Graphs
In this section, we obtain some lower bounds for the generalized distance Estrada index of a connected graph G. These bounds are characterized in terms of the order n, the Wiener index , the transmission degree and the parameter . We also investigate the extremal graph attaining these bounds.
Our first result gives a lower bound for the generalized distance Estrada index , in terms of the order n, the transmission degrees and the parameter .
Theorem 2.
Suppose G is a connected graph of order n. Then,
with equality if and only if .
Proof.
Starting with Equation (1), we have
Thanks to the arithmetic–geometric mean inequality, we have
Using a power-series expansion, and as , and , we get
We apply a multiplier to arrive at
where we have used the fact that for since , for and for when .
The function
monotonically decreases for . Consequently, the best lower bound for is attained for . This gives us the first part of the proof.
From the derivation of (4), we observe readily that the equality holds if and only if G has no non-zero -eigenvalues. Recall that G is connected. Therefore, this can only happen when . The proof is then complete. □
The following result is an immediate consequence of Theorem 2.
Corollary 1.
Assume that G is a connected graph of order n. We have
where the equality holds if and only if .
Proof.
As from the lower bound of Theorem 2, we obtain
Thus, the result, □
The next result gives a complementary lower bound for the generalized distance Estrada index . The bound is characterized by the order n of graph, its Wiener index as well as the parameter .
Theorem 3.
Suppose that G is a connected graph of order n. Then,
where the equality holds if and only if .
Proof.
Consider the following function,
for . We have
for It is not difficult to see that is increasing for . Using Equation (10) and Lemma 1, we obtain
Moreover, from the derivation of (8), it is clear that equality holds if and only if the equality holds in the inequality (9). Also, equality holds in (9) if and only if . Therefore, G has exactly two distinct generalized distance eigenvalues; then, by Lemma 2, we see that G is the complete graph .
Conversely, it is easy to see that the equality holds in (8) for . □
We will make use of the following lemma in our next results.
Lemma 6
([33]). Let be non-negative numbers. Then,
Let be the geometric mean of the transmission degrees sequence. Clearly, , and equality is attained if and only if (i.e., G is a transmission regular graph).
Our next result gives a lower bound for in terms of the order n, the Wiener index , the geometric mean of the transmission degrees sequence and the parameter . It also gives an upper bound for in terms of the order n, the diameter d and the parameter .
Theorem 4.
Assume that G is a connected graph of order with diameter d. Then,
Proof.
We will deal with the left part inequality first. Thanks to the arithmetic–geometric mean inequality, we arrive at
By Lemma 3, . Setting in Lemma 6, we get
Combining this with Lemma 3 yields
Clearly, and so
Similar to Theorem 3, we obtain the desired result. If , we have , and Therefore, and the equality holds.
Conversely, assume that the equality holds true. In view of (13), we have Clearly, if and only if From (14), it follows that for Thus, G has exactly two distinct generalized distance eigenvalues, and so Lemma implies that G is the complete graph .
Next, we prove the right inequality. We have
As for and there are pairs of vertices in we have , so that
Therefore, we arrive at the right-hand side of the inequality (12).
In the above proof, it can be seen that the equality holds if and only if G has no non-zero -eigenvalues. Recall that G is connected. This can only happen when . The proof is complete. □
Remark 1.
In view of the inequality we obtain
Given a k-transmission regular graph G, we have and . Therefore, the following result follows immediately from Theorem 4.
Corollary 2.
Suppose that G is k-transmission regular. We have
where the equality holds if and only if .
The next result provides a lower bound for involving the order n and the Wiener index .
Theorem 5.
Suppose that G is a connected graph of order n. We have
Proof.
Applying the Cauchy–Schwartz inequality we have , therefore
It follows again by the Cauchy–Schwartz inequality that
Consequently, we have
□
Corollary 3.
Suppose that G is connected with order n. We have
Proof.
As for and there are pairs of vertices in by Theorem 5, we obtain
and the result follows. □
4. Upper Bounds for the Generalized Distance Estrada Index of Graphs
In this section, we obtain some upper bounds for the generalized distance Estrada index of a connected graph G involving the order n, the Wiener index , the transmission degrees as well as the parameter . We also characterize the extremal graphs attaining these bounds.
The next result gives an upper bound for the generalized distance Estrada index using the order n, the Wiener index , the transmission degrees as well as the parameter .
Theorem 6.
Suppose that G is connected with order n. For any integer ,
where the equality holds if and only if
Proof.
Remark 2.
Notice that we have
where the second inequality can be derived from the following fact:
For non-negative integers and integer ,
Therefore, . Then,
It follows from Theorem 6 that
Putting , we get the following upper bound for the distance Estrada index,
Remark 3.
The following upper bound for the distance Estrada index was obtained in [22]. Let G be a connected graph of order n and diameter d. Then,
The last upper bound is as follows.
Theorem 7.
Suppose that G is connected with order n. For any integer ,
where with equality if and only if
Proof.
Notice that
Using the inequality (17), we have
where by the power-series expansion of , we have
and the last equality holds. This completes the proof. □
5. Relationship between the Generalized Distance Estrada Index and Generalized Distance Energy of Graphs
The energy of a graph G, first introduced in [34], is defined as the sum of absolute values of eigenvalues of the adjacency matrix of G. Since then, has found a wide range of applications in chemical mathematics and has been investigated extensively by mathematicians. In addition to adjacency matrix, the energy of Laplacian, distance Laplacian, signless Laplacian as well as distance signless Laplacian has also been studied; see works [4,32,33,35,36,37] and the references therein for more details. Recently, the authors of [38] considered a novel energy with respect to the generalized distance matrix of a graph. The generalized distance energy, denoted by , is defined as
It is clear from the definition that and , where and denotes, respectively, the distance energy and the distance signless Laplacian energy of a graph G. This shows that the concept of generalized distance energy of a graph G merges the theories of distance energy and the distance signless Laplacian energy of a graph G. Therefore, it will be interesting to study the quantity and explore some properties like the bounds, the dependence on the structure of graph G, and the dependence on the parameter and its relation with other graph-spectrum-based invariants. The authors of [38] give some bounds for and have investigated its dependence on the graph topology as well as the parameter . Our aim in this section is to explore the relationship between generalized distance Estrada index and generalized distance energy of a simple connected graph G.
Theorem 8.
Proof.
Starting with Equation (2), we have
Taking into account the definition of the generalized distance energy, we obtain
which leads to
Notice that the function monotonically increases for . Therefore, the minimum upper bound for is attained for and we have
Another way to obtain the relation between and is as follows,
implying
Theorem 9.
Assume that G is connected with order n and Then,
where the equality holds if and only if
Proof.
Notice that it holds and . From the definition of , we get
with equality attained if and only if holds for all integers i.e., if and only if at most one of for is positive and all others are equal to zero, i.e., As then , which is in contradiction with . Therefore , and the proof is complete. □
Remark 4.
The following upper bound for the distance Estrada index was obtained in [22],
Putting in the upper bound of Theorem 9, we can easily see that the resulting upper bound for the distance Estrada index is better than the upper bound given by (23).
Theorem 10.
Assume that G is connected with order n. We have
where t means the number of eigenvalues with . Furthermore, the equality holds on both sides of (24) if and only if .
Proof.
We will first prove the left inequality. Suppose that t is an integer such that and . As equality holds if and only if and equality holds if and only if We have
Next, we want to prove the right inequality. Since monotonically increases in the interval , we obtain
We observe that the equality holds on both sides of (24) if and only if . This only happens when since G is a connected graph. □
6. Examples
In this section, we obtain some results about the generalized distance Estrada index of some typical graphs. This would be instrumental in interpreting this measure further in the case of more complex graphs. We also give an expression for of a (transmission) regular graph G, in terms of the distance eigenvalues as well as adjacency eigenvalues of G, and describe the generalized distance Estrada index of some graphs obtained by operations.
As mentioned in introduction of the paper, for the generalized distance matrix is equivalent to the distance matrix and for , twice the generalized distance matrix is the same as the distance signless Laplacian matrix . Therefore, if in particular we put and in all the results obtained in this paper, we obtain the corresponding bounds for the distance Estrada index and the distance signless Laplacian Estrada index , respectively.
Theorem 11.
Suppose that G is a k-transmission regular graph of order n having distance eigenvalues Then,
Proof.
Note that the generalized distance spectrum of the graph G consists of where is the distance spectrum of Also, it is easy to see that Then, □
Theorem 12.
Let G be an r-regular graph of order n, size m and diameter at most 2. If are the eigenvalues of the adjacency matrix of then
Proof.
The transmission of each vertex can be computed as and the Wiener index of G becomes Also,
where J is the all ones matrix. Then,
□
We denote by the cartesian product of two graphs G and H. It is the graph with vertex set and two vertices and are adjacent if and only if and or and
Corollary 4.
Let G be an r-regular graph of diameter at most 2 with an adjacency matrix A and . Then, the generalized distance Estrada index of is
Proof.
Let , . As , we see that all vertices of H have the same transmission and . So . Then Note that has distance spectrum (see in [37]) for
Then,
□
The graph is obtained by joining each vertex of G to each vertex of a second copy of G.
Corollary 5.
Let G be an r-regular graph with an adjacency matrix A and . Then, the generalized distance Estrada index of is
Proof.
For it is easy to see that Then, is a transmission regular graph and Note that the has distance spectrum (see in [37]) for Then,
□
Next, we study the generalized distance Estrada index of the lexicographic product of two graphs G and H. The lexicographic product of G and H can be defined as follows.
Definition 1
([39]). Let G and H be two graphs on vertex sets and , respectively. Their lexicographic product is a graph defined by , the cartesian product of , and , where is adjacent to if and only if either
- (a)
- is adjacent to in G, or
- (b)
- and is adjacent to in G.
Theorem 13.
Given a k-transmission regular graph G of order p. If H is an r-regular graph of order n with adjacency eigenvalues , then
where are the eigenvalues of the distance matrix .
Proof.
For it is easy to see that Then is a transmission regular graph and Note that has distance spectrum (see [40]) for and Then,
□
Example 1.
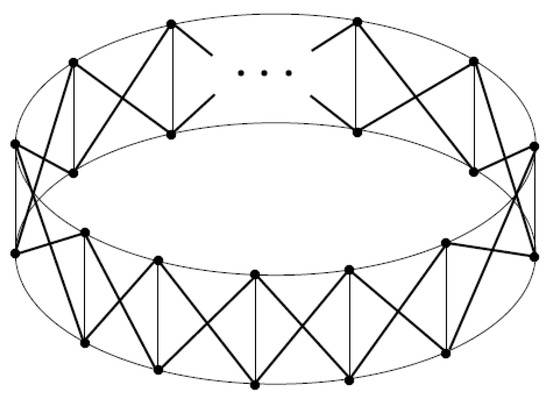
Let be a cycle of order n and be the complete graph of order 2. Then, the closed fence graph is defined as , and depicted in Figure 1. Applying Theorem 13, we will be able to compute the generalized distance Estrada index of closed fence . It is well known ([41], Theorem 3) that is a k-transmission regular graph, with . It is also clear tht the adjacency spectrum of the graph is . Then, applying Theorem 13, the generalized distance Estrada index of closed fence , according to the parity of n, is as follows.

Figure 1.
The closed fence graph.
If (i.e., n is even), then following [2] the distance spectrum of is
Thus, applying Theorem 13 we have
If (i.e., n is odd), then following [2] the distance spectrum of is

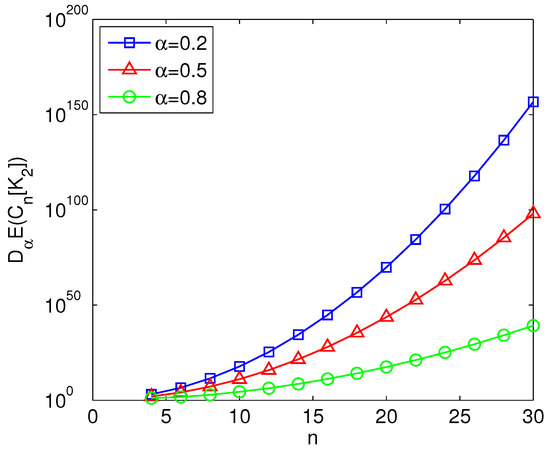
Figure 2.
versus n for different values of .
7. Conclusions
The concept of Estrada index of a graph was first motivated by Ernesto Estrada in [9] as the sum of the exponential of the eigenvalues of adjacency matrix assigned to graphs. In recent years, because of the apparent success of the graph Estrada index, many variations of Estrada index have been proposed and varied Estrada indices based on the eigenvalues of other graph matrices have, one-by-one, been introduced: Estrada index-based invariant with respect to distance matrix, Laplacian matrix, signless Laplacian matrix, distance Laplacian matrix and also distance signless Laplacian matrix, etc.
As the distance and distance signless Laplacian matrices of graphs play an essential role in mathematics and are more informative than ordinary adjacency matrix, in this paper, the Estrada index of generalized distance matrix is firstly defined and investigated. In fact, this is a natural generalization of distance Estrada and distance signless Laplacian Estrada indices. Thus all properties about them can be handled by this new index, and any result regarding the spectral properties of generalized distance Estrada index, has its counterpart for each of these particular indices, and these counterparts follow immediately from a single proof. As characterization of turns out to be highly desirable in mathematics as well as engineering, it is interesting to study the quantity and explore some properties including the bounds, the dependence on the structure of graph G, and the dependence on the parameter . We established some bounds for the generalized distance Estrada index of a connected graph G, in terms of the different graph parameters including the order n, the Wiener index , the transmission degree, and the parameter . We have also characterized the extremal graphs attaining these bounds. We worked out some expressions for of some special classes of graphs.
Author Contributions
Conceptualization, A.A. and M.B.; formal analysis, A.A., M.B. and Y.S.; writing–original draft preparation, A.A and M.B.; writing–review and editing, A.A., M.B. and Y.S.; project administration, A.A.; funding acquisition, A.A. and Y.S.
Funding
The research of A. Alhevaz was in part supported by a grant from Shahrood University of Technology. Y. Shang was supported by UoA Flexible Fund No. 201920A1001 from Northumbria University.
Acknowledgments
The authors would like to thank the academic editor and the three anonymous referees for their detailed constructive comments that helped improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aouchiche, M.; Hansen, P. Two Laplacians for the distance matrix of a graph. Linear Algebra Appl. 2013, 439, 21–33. [Google Scholar]
- Aouchiche, M.; Hansen, P. On the distance signless Laplacian of a graph. Linear Multilinear Algebra 2016, 64, 1113–1123. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Hashemi, E.; Ramane, H.S. On the distance signless Laplacian spectrum of graphs. Bull. Malay. Math. Sci. Soc. 2019, 42, 2603–2621. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Paul, S. On the distance signlees Laplacian spectral radius and the distance signless Laplacian energy of graphs. Discrete Math. Algorithms Appl. 2018, 10, 1850035. [Google Scholar] [CrossRef]
- Xing, R.; Zhou, B.; Li, J. On the distance signless Laplacian spectral radius of graphs. Linear Multilinear Algebra 2014, 62, 1377–1387. [Google Scholar] [CrossRef]
- Nikiforov, V. Merging the A- and Q-spectral theories. Appl. Anal. Discrete Math. 2017, 11, 81–107. [Google Scholar] [CrossRef]
- Cui, S.Y.; He, J.X.; Tian, G.X. The generalized distance matrix. Linear Algebra Appl. 2019, 563, 1–23. [Google Scholar] [CrossRef]
- Estrada, E. Characterization of the folding degree of proteins. Bioinformatics 2002, 18, 697–704. [Google Scholar] [CrossRef]
- Estrada, E. Characterization of the amino acid contribution to the folding degree of proteins. Proteins 2004, 54, 727–737. [Google Scholar] [CrossRef]
- Gutman, I.; Estrada, E.; Rodriguez-Velázquez, J.A. On a graph-spectrum-based structure descriptor. Croat. Chem. Acta 2007, 80, 151–154. [Google Scholar]
- De la Pe na, J.A.; Gutman, I.; Rada, J. Estimating the Estrada index. Linear Algebra Appl. 2007, 427, 70–76. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Shang, Y. On generalized distance Gaussian Estrada index of graphs. Symmetry 2019, 11, 1276. [Google Scholar] [CrossRef]
- Bozkurt, B.Ş.; Adiga, C.; Bozkurt, D. On the energy and Estrada index of strongly quotient graphs. Indian J. Pure Appl. Math. 2012, 43, 25–36. [Google Scholar] [CrossRef]
- Shang, Y. Estrada index of general weighted graphs. Bull. Aust. Math. Soc. 2013, 88, 106–112. [Google Scholar] [CrossRef]
- Deng, H.; Radenković, S.; Gutman, I. The Estrada index. In Applications of Graph Spectra; Cvetković, D., Gutman, I., Eds.; Mathematical Institute: Belgrade, Serbia, 2009; pp. 123–140. [Google Scholar]
- Gutman, I.; Deng, H.; Radenković, S. The Estrada index: An updated survey. In Selected Topics on Applications of Graph Spectra; Cvetković, D.M., Gutman, I., Eds.; Matematički Institut SANU: Beograd, Serbia, 2011; pp. 155–174. [Google Scholar]
- Estrada, E. Characterization of 3-D molecular structure. Chem. Phys. Lett. 2000, 319, 713–718. [Google Scholar] [CrossRef]
- Estrada, E.; Rodriguez-Velázguez, J.A.; Randić, M. Atomic branching in molecules. Int. J. Quantum Chem. 2006, 106, 823–832. [Google Scholar] [CrossRef]
- Shang, Y. Local natural connectivity in complex networks. Chin. Phys. Lett. 2011, 28, 068903. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks-Theory and Applications; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Shang, Y. Perturbation results for the Estrada index in weighted networks. J. Phys. A Math. Theor. 2011, 44, 075003. [Google Scholar] [CrossRef]
- Güngör, A.D.; Bozkurt, Ḃ. On the distance Estrada index of graphs. Hacet. J. Math. Stat. 2009, 38, 277–283. [Google Scholar]
- Liu, J.; Liu, B. A Laplacian-energy-like invariant of a graph. MATCH Commun. Math. Comput. Chem. 2008, 59, 355–372. [Google Scholar]
- Shang, Y. More on the normalized Laplacian Estrada index. Appl. Anal. Discrete Math. 2014, 8, 346–357. [Google Scholar] [CrossRef]
- Ayyaswamy, S.K.; Balachandran, S.; Venkatakrishnan, Y.B.; Gutman, I. Signless Laplacian Estrada index. MATCH Commun. Math. Comput. Chem. 2011, 66, 785–794. [Google Scholar]
- Gutman, I.; Medina, C.L.; Pizarro, P.; Robbiano, M. Graphs with maximum Laplacian and signless Laplacian Estrada index. Discrete Math. 2016, 339, 2664–2671. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Pirzada, S. On distance signless Laplacian Estrada index and energy of graphs. Kragujevac J. Math. 2021, 45, 837–858. [Google Scholar]
- Shang, Y. Distance Estrada index of random graphs. Linear Multilinear Algebra 2015, 63, 466–471. [Google Scholar] [CrossRef]
- Shang, Y. Bounds of distance Estrada index of graphs. Ars Comb. 2016, 128, 287–294. [Google Scholar]
- Shang, Y. Estimating the distance Estrada index. Kuwait J. Sci. 2016, 43, 14–19. [Google Scholar]
- Shang, Y. Further results on distance Estrada index of random graphs. Bull. Malay. Math. Sci. Soc. 2018, 41, 537–544. [Google Scholar] [CrossRef]
- Indulal, G. Sharp bounds on the distance spectral radius and the distance energy of graphs. Linear Algebra Appl. 2009, 430, 106–113. [Google Scholar] [CrossRef]
- Zhou, B.; Gutman, I.; Aleksić, T. A note on Laplacian energy of graphs. MATCH Commun. Math. Comput. Chem. 2008, 60, 441–446. [Google Scholar]
- Gutman, I. The energy of a graph. Ber. Math. Statist. Sekt. Forschungsz. Graz 1978, 103, 1–22. [Google Scholar]
- Das, K.C.; Aouchiche, M.; Hansen, P. On (distance) Laplacian energy and (distance) signless Laplacian energy of graphs. Discrete Appl. Math. 2018, 243, 172–185. [Google Scholar] [CrossRef]
- Gutman, I.; Zhou, B. Laplacian energy of a graph. Linear Algebra Appl. 2006, 414, 29–37. [Google Scholar] [CrossRef]
- Indulal, G.; Gutman, I.; Vijayakumar, A. On distance energy of graphs. MATCH Commun. Math. Comput. Chem. 2008, 60, 461–472. [Google Scholar]
- Alhevaz, A.; Baghipur, M.; Ganie, H.A.; Shang, Y. On the generalized distance energy of graphs. 2019, submitted. [Google Scholar]
- Cvetković, D.M.; Doob, M.; Sachs, H. Spectra of Graphs. Theory and Application; Pure and Applied Mathematics, 87; Academic Press, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Indulal, G. The distance spectrum of graph compositions. Ars. Math. Contemp. 2009, 2, 93–100. [Google Scholar]
- Abiad, A.; Brimkov, B.; Erey, A.; Leshock, L.; Rivera, X.M.; O, S.; Song, S.Y.; Williford, J. On the Wiener index, distance cospectrality and transmission-regular graphs. Discrete Appl. Math. 2017, 230, 1–10. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).