Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors
Abstract
1. Introduction
2. The Lagrange–d’Alembert Principle and the Forced Euler–Poincaré Equation
2.1. The Lagrange–d’Alembert Principle
2.2. The Forced Euler–Poincaré Equation
3. Rigid-Body Equations
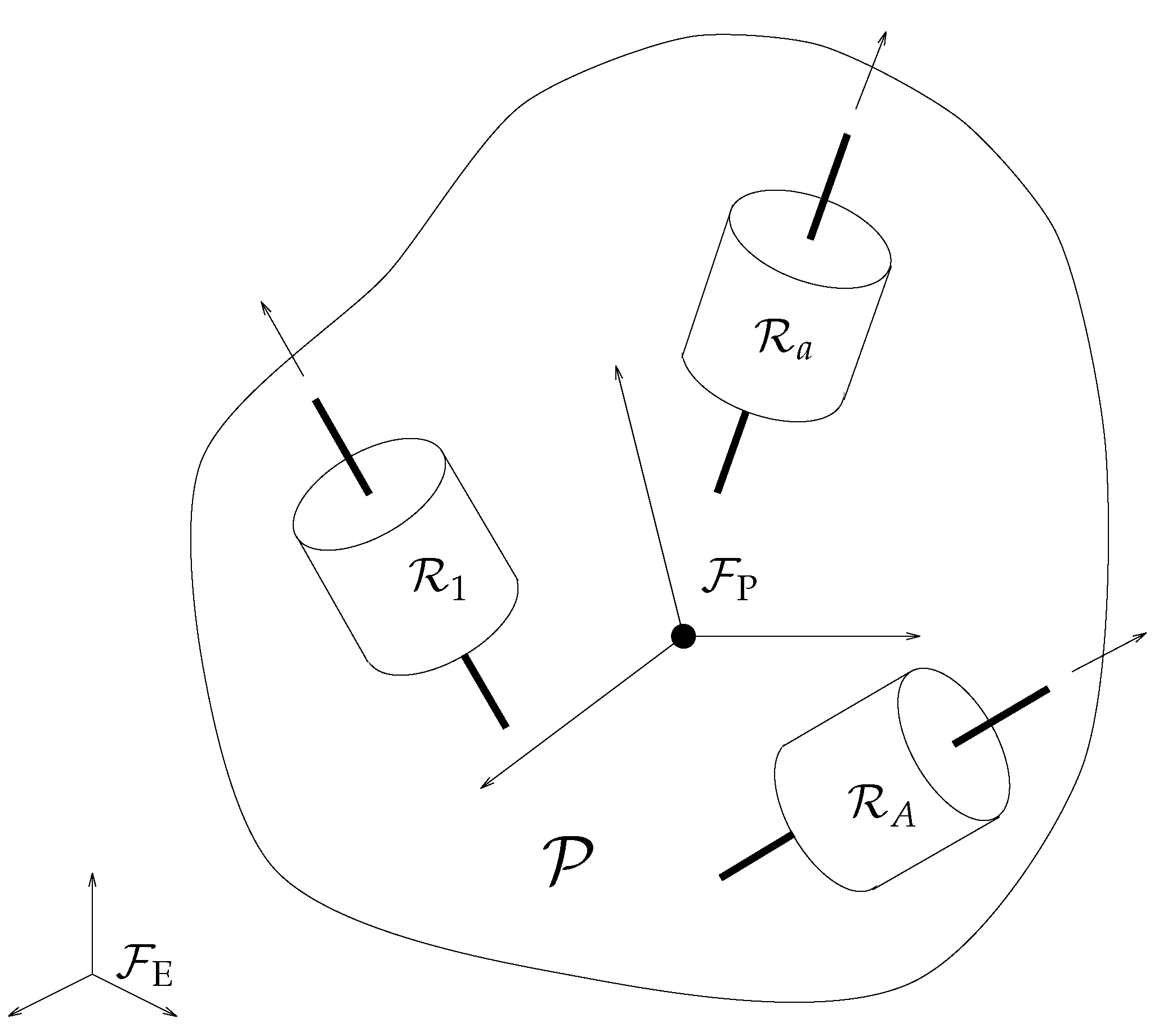
3.1. Satellite Gyrostat
3.1.1. Frictionless Gyrostat with Blocked Rotors
3.1.2. Frictionless Gyrostat with Spinning Rotors
3.1.3. Friction Gyrostat with Spinning Rotors
3.1.4. Friction Gyrostat with Spinning Rotors and Feedback Control
3.1.5. Explicit State-Space Form of Gyrostat Equations
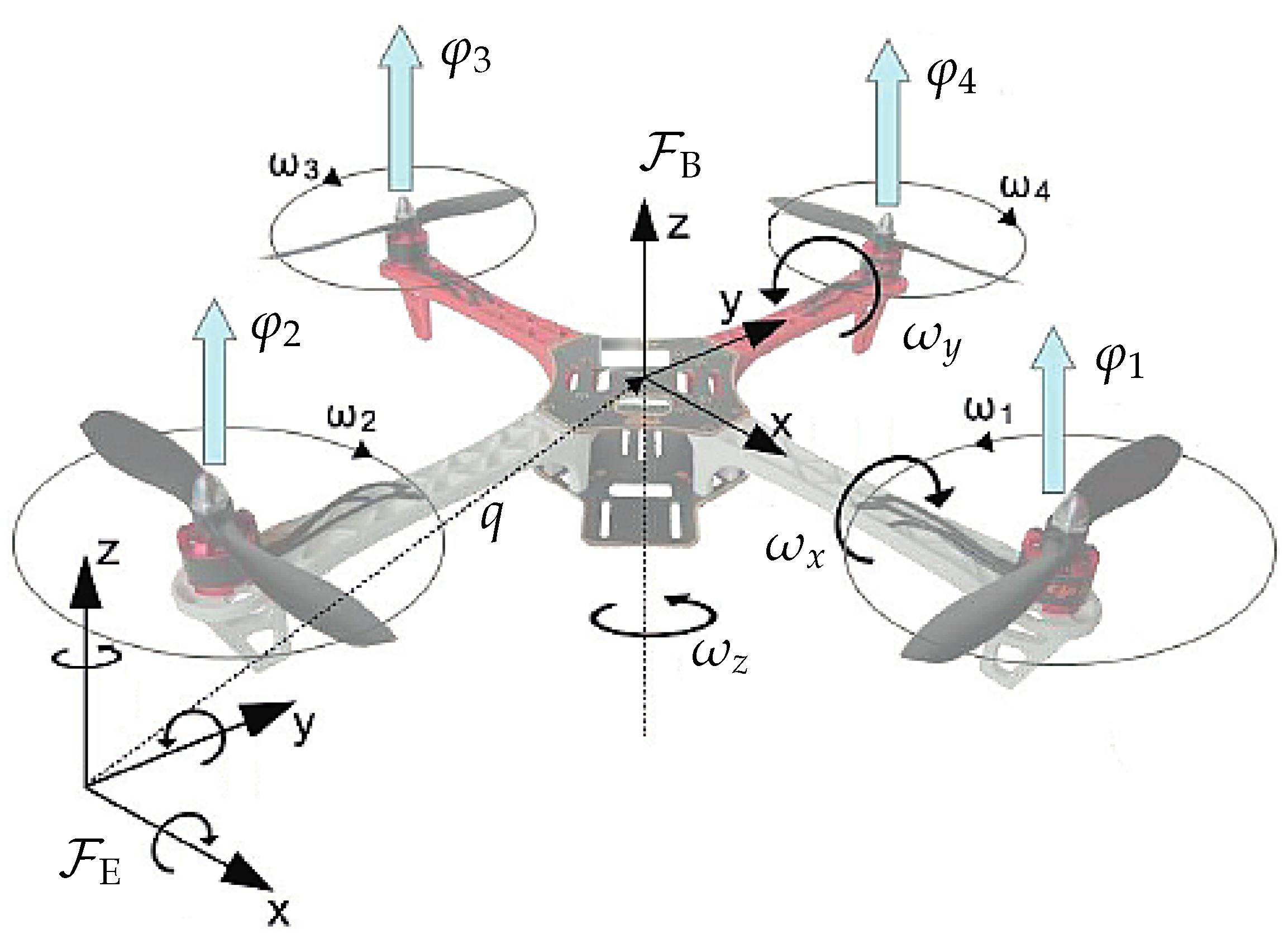
3.2. Quadrotor Drone
3.2.1. Total Kinetic Energy
3.2.2. Equations for the Rotational Component of Motion
3.2.3. Equations for the Translational Component of Motion
3.2.4. Explicit State-Space Form of Quadcopter Equations
4. Numerical Integration of Initial Value Problems
4.1. Numerical Schemes in
4.1.1. Forward Euler Scheme
4.1.2. Explicit Fourth-Order Runge–Kutta Scheme on
4.2. Extension of fEul and eRK4 Schemes to Smooth Manifolds
4.2.1. Forward Euler Scheme on a Smooth Manifold
4.2.2. Explicit Fourth-Order Runge–Kutta Scheme on a Smooth Manifold
- The first stage of the eRK4 scheme is defined as . We can extend this calculation directly to a smooth manifold to get the first stage of the eRK4M scheme by . Notice that . The tangent vector represents an estimation of the tangent vector field at .
- The second stage of the eRK4 scheme is defined as . As we already know, the inner sum is not necessarily legitimate on a manifold but may be extended by means of a retraction operator as . Therefore, we define the second stage of a eRK4M scheme asThe tangent vector represents an estimation of the tangent vector field at the midpoint .
- The third stage of the eRK4 scheme is defined as . Now, this definition cannot be made legitimate just by replacing the inner sum with a retraction because . Before applying a retraction, it is necessary to take a preliminary step, namely, to transport the local estimation of the vector field to the space . For the sake of notation conciseness, let us define the intermediate point(the notation for the subscript is standard in numerical calculus). Notice now that . The third stage in the eRK4M scheme is defined asThe tangent vector represents a further estimation of the tangent vector field at the midpoint , as required by the original eRK4 scheme.
- The fourth stage of the eRK4 scheme is defined as . Again, before applying a retraction, it is necessary to transport the local estimation of the vector field to the space . Let us define the intermediate pointand notice that . The fourth stage in the eRK4M scheme is defined as
- In the original eRK4 scheme, the four stages are combined together as . We already know that, on a curved manifold, the four stages belong to different tangent spaces and cannot, therefore, be combined together as they stand. In particular, the second increment needs to be transported to the tangent space by means of parallel transport to give , the third stage needs to be replaced by , and the fourth stage by , where . The four stages may be combined together with the retraction map to give the next point in the sequence as
5. Numerical Integration of Rigid-Body Equations
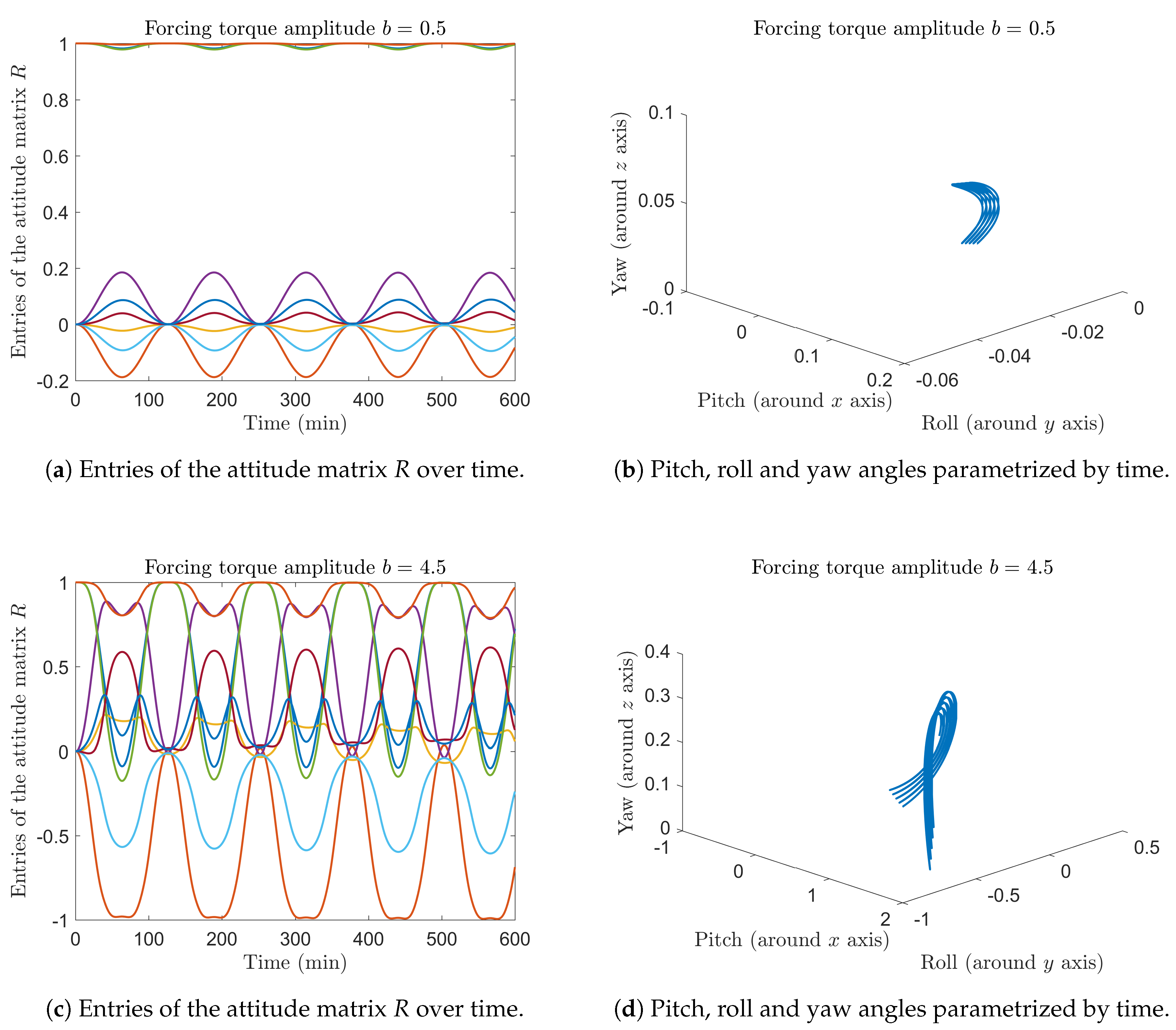
5.1. Numerical Integration of A Gyrostat Satellite Equations on
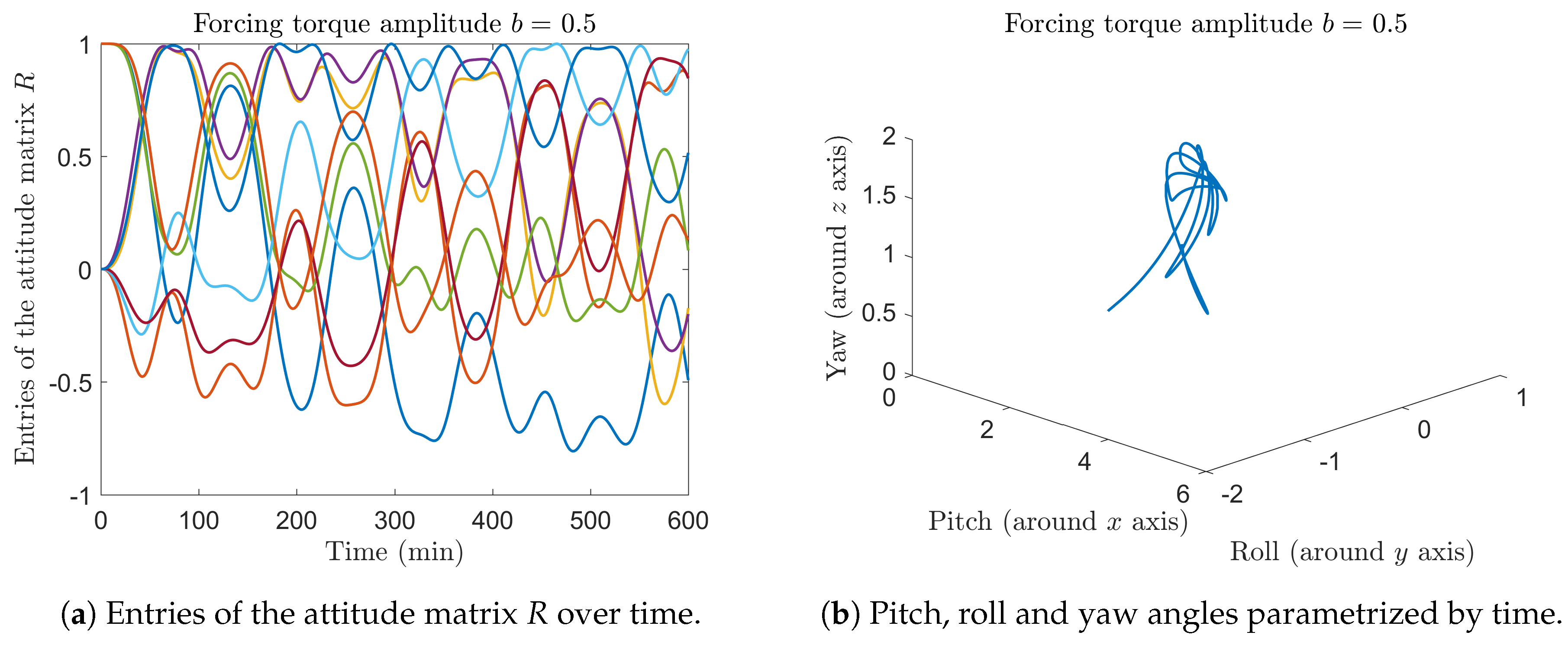
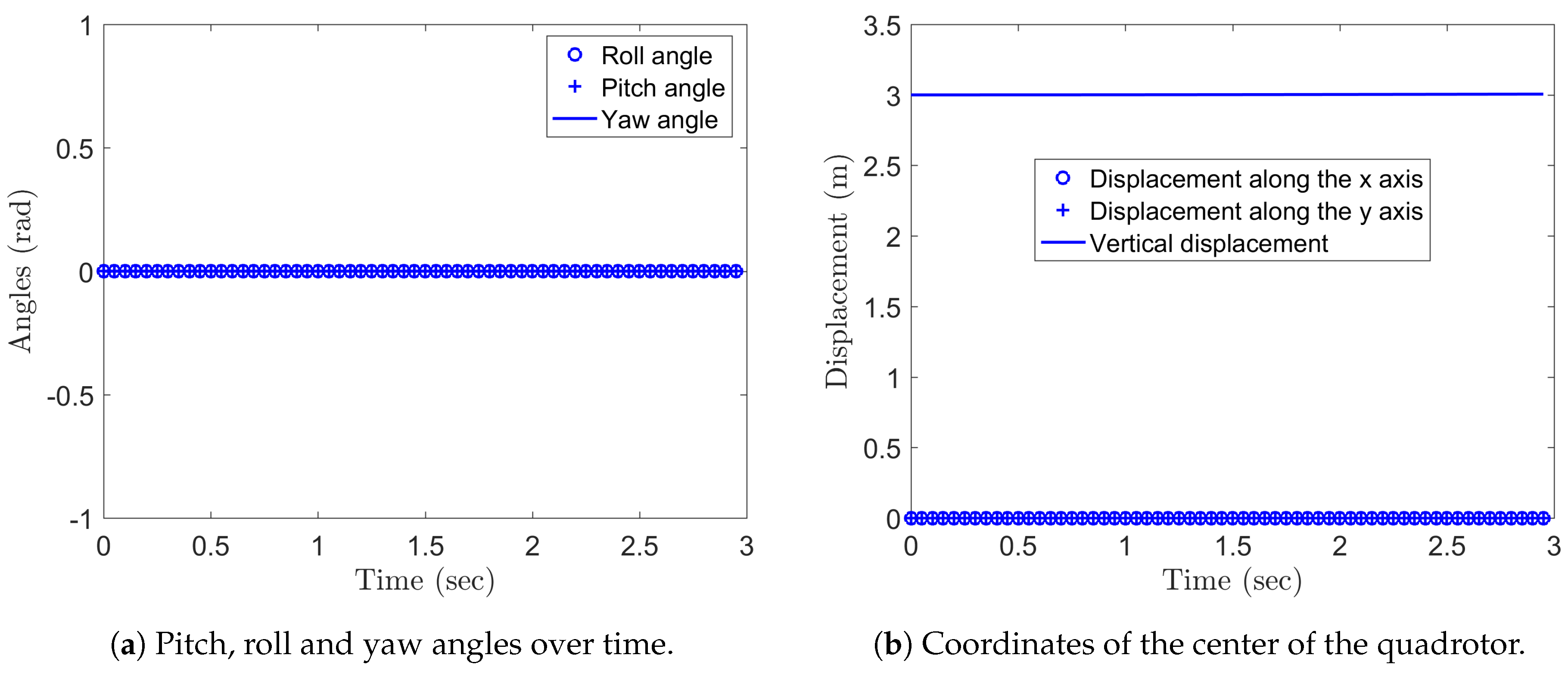
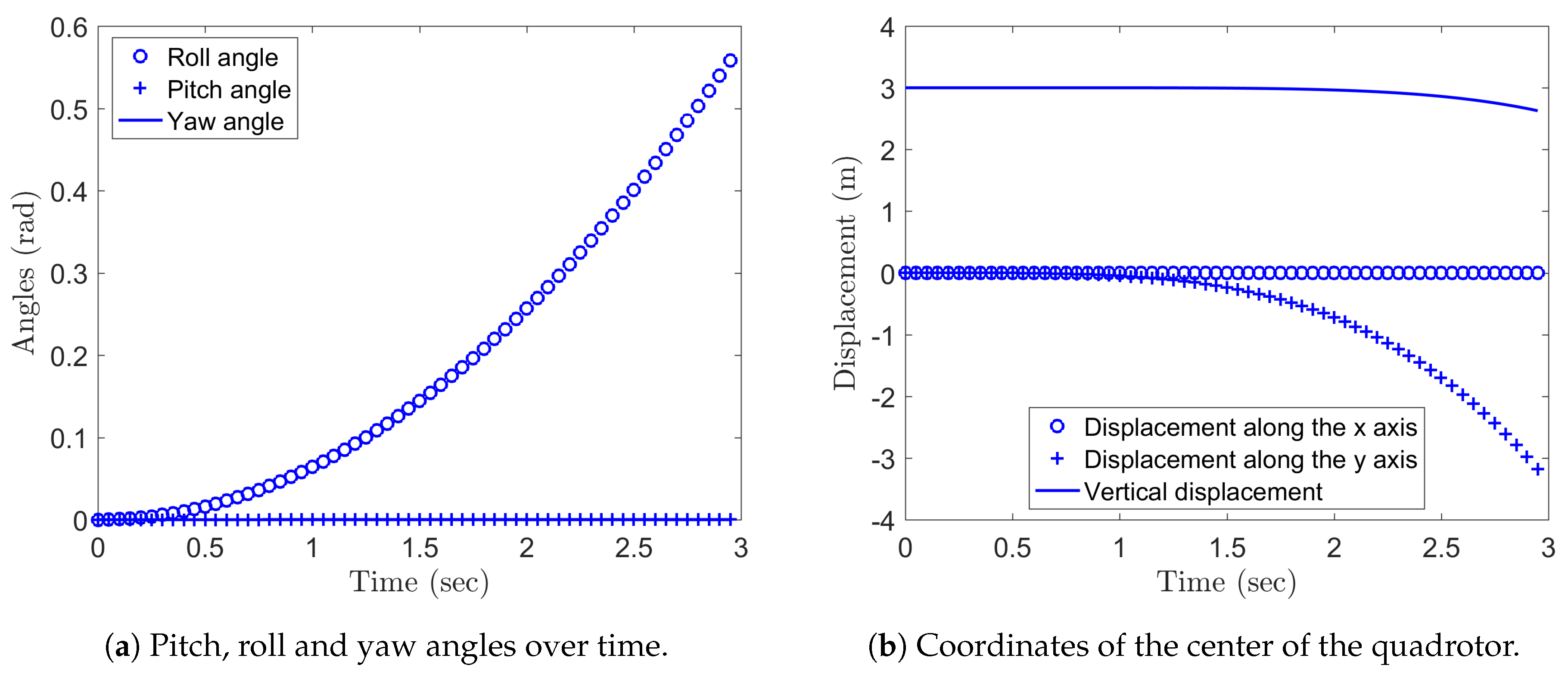
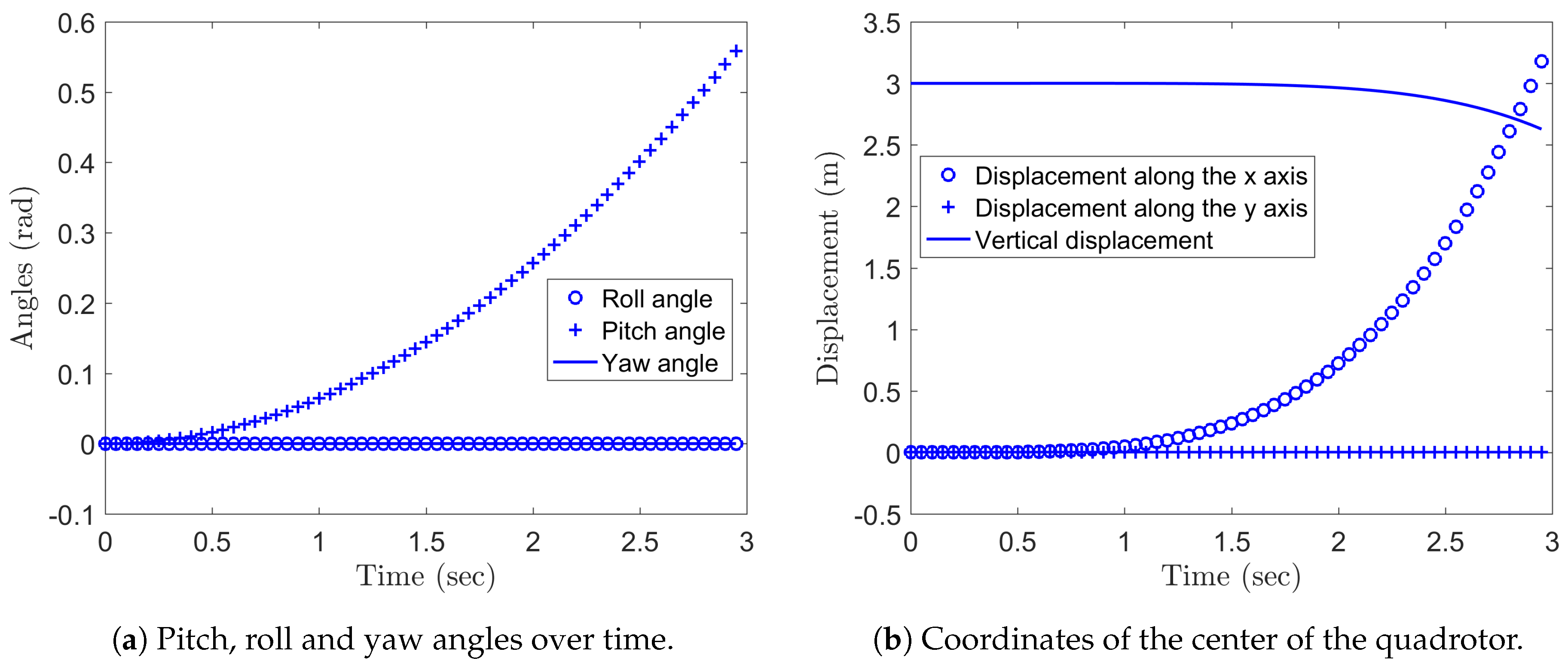
5.2. Integration of the Quadrotor Drone Equations on
6. Conclusions
- The problem about the order of the numerical schemes, which may be studied either analytically and by means of numerical experiments. The present author has started an analysis of the order of some numerical schemes which rely on ad-hoc Taylor-series-like expansions [46]. It would also be informative to use examples for which the analytic solution is known, and then compare the two numerical solutions to the analytic solution individually. This would also allow for the error order of the Runge–Kutta method to be evaluated numerically. While it is true that closed-form solutions of ODEs on nonlinear spaces cannot be obtained in general, the solutions are available in special cases, as shown in [47].
- The problem of the convergence of the numerical schemes, which is quite involved, being the algorithms considered in this paper of complex non-linear nature. The numerical schemes were stable in the numerical simulations performed in the course of this study. In general, it is expected that they would enjoy/suffer from the same advantages/drawbacks of their precursors.
- An accurate evaluation of the computational complexity of the forward Euler method and of the Runge–Kutta integration method.
- It would be very interesting to design more model-based experimental settings to survey the behavior of the studied satellite gyrostat. For example, it would be interesting to study a control strategy to see if it is possible to set the inputs so as to make the satellite gain a prescribed attitude with respect to the earth-fixed reference frame. On the same line, it would be interesting to enrich the model (119) with a (possibly differential) equation that describes the relationship between the motors control voltages and the rotors rotation speed, in order to make the control scheme more realistic.
Funding
Acknowledgments
Conflicts of Interest
References
- Arnol’d, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1989; (Originally published by Nauka, Moscow, 1974. Translated by A. Weinstein and K. Vogtmann). [Google Scholar]
- Abraham, R.; Marsden, J.E.; Ratiu, T.S. Manifolds, Tensor Analysis, and Applications; Springer: New York, NY, USA, 1988; (Originally published by Addison-Wesley Publishing Company, 1983). [Google Scholar]
- Bullo, F.; Lewis, A.D. Geometric Control of Mechanical Systems: Modeling, Analysis, and Design for Mechanical Control Systems; Springer: New York, NY, USA, 2005. [Google Scholar]
- Fiori, S. Nonlinear damped oscillators on Riemannian manifolds: Fundamentals. J. Syst. Sci. Complex. 2016, 29, 22–40. [Google Scholar] [CrossRef]
- Fiori, S. Nonlinear damped oscillators on Riemannian manifolds: Numerical simulation. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 207–222. [Google Scholar] [CrossRef]
- Bloch, A.; Krishnaprasad, P.S.; Marsden, J.E.; Ratiu, T.S. The Euler–Poincaré equations and double bracket dissipation. Commun. Math. Phys. 1996, 175, 1–42. [Google Scholar] [CrossRef]
- Ge, Z.-M.; Lin, T.-N. Chaos, chaos control and synchronization of a gyrostat system. J. Sound Vib. 2002, 251, 519–542. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry—A Basic Exposition of Classical Mechanical Systems, 2nd ed.; Texts in Applied Mathematics (Book 17); Springer: New York, NY, USA, 2002. [Google Scholar]
- Holm, D.D. Geometric Mechanics—Part I: Dynamics and Symmetry, 2nd rev. ed.; Imperial College Press: London, UK, 2011. [Google Scholar]
- Holm, D.D. Geometric Mechanics—Part II: Rotating, Translating And Rolling, 2nd ed.; Imperial College Press: London, UK, 2011. [Google Scholar]
- Aslanov, V. Behavior of a free dual-spin gyrostat with different ratios of inertia moments. Adv. Math. Phys. 2015, 2015, 323714. [Google Scholar] [CrossRef]
- Tong, C. Lord Kelvin’s gyrostat and its analogs in physics, including the Lorenz model. Am. J. Phys. 2009, 77, 526. [Google Scholar] [CrossRef]
- Hall, C.D. Momentum transfer in two-rotors gyrostat. J. Guid. Control. Dyn. 1996, 19, 1157–1161. [Google Scholar] [CrossRef]
- Yu, W.; Pan, Z. Dynamical equations of multibody systems on Lie groups. Adv. Mech. Eng. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Tong, X.; Tabarrok, B.; Rimrott, F.P.J. Chaotic motion of an asymmetric gyrostat in the gravitational field. Int. J. Non-Linear Mech. 1995, 30, 191–203. [Google Scholar] [CrossRef]
- Bezglasnyi, S. Stabilization of gyrostat motion with cavity filled with viscous fluid. In Proceedings of the World Congress on Engineering (WCE 2015), London, UK, 1–3 July 2015; Volume 1. [Google Scholar]
- Hamm, A.; Lin, Z. “Why drones for ordinary people?” Digital representations, topic clusters, and techno-nationalization of drones on Zhihu. Information 2019, 10, 256. [Google Scholar] [CrossRef]
- Moskalenko, V.; Moskalenko, A.; Korobov, A.; Semashko, V. The model and training algorithm of compact drone autonomous visual navigation system. Data 2019, 4, 4. [Google Scholar] [CrossRef]
- Lynskey, J.; Thar, K.; Oo, T.Z.; Hong, C.S. Facility location problem approach for distributed drones. Symmetry 2019, 11, 118. [Google Scholar] [CrossRef]
- Benić, Z.; Piljek, P.; Kotarski, D. Mathematical modelling of unmanned aerial vehicles with four rotors. Interdiscip. Descr. Complex Syst. 2016, 14, 88–100. [Google Scholar]
- Goodarzi, F.A.; Lee, D.; Lee, T. Geometric control of a quadrotor UAV transporting a payload connected via flexible cable. Int. J. Control. Autom. Syst. 2015, 13, 1486–1498. [Google Scholar] [CrossRef]
- Becker, M.; Sampaio, R.C.B.; Bouabdallah, S.; de Perrot, V.; Siegwart, R. In-flight collision avoidance controller based only on OS4 embedded sensors. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 294–307. [Google Scholar] [CrossRef]
- Lambert, J.D.; Lambert, D. Numerical Methods for Ordinary Differential Systems: The Initial Value Problem; Wiley: New York, NY, USA, 1991; Chapter 5. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 2006. [Google Scholar]
- Cear, C.W. Numerical Initial Value Problems in Ordinary Differential Equations; Prentice-Hall: Upper Saddle River, NJ, USA, 1973. [Google Scholar]
- Milne, W.E. Numerical integration of ordinary differential equations. Am. Math. Mon. 1926, 33, 455–460. [Google Scholar] [CrossRef]
- Euler, L. Institutionum Calculi Integralis. Volumen Secundum (1769); Kowalewski, G., Ed.; Opera Omnia Series 1; Opera Mathematica; 1914; Available online: http://sites.mathdoc.fr/cgi-bin/oeitem?id=OE_EULER_1_12_1_0 (accessed on 3 August 2019).
- Henrici, P. Discrete Variable Methods in Ordinary Differential Equations; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations, I. Nonstiff Problems; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Lambert, J.D. Computational Methods In Ordinary Differential Equations; Wiley: London, UK, 1973. [Google Scholar]
- Dekker, K.; Verwer, J.G. Stability of Runge–Kutta Methods for Stiff Nonlinear Differential Equations; CWI Monographs, 2; North-Holland: Amsterdam, The Natherlands, 1984. [Google Scholar]
- Butcher, J.C. The Numerical Analysis of Ordinary Differential Equations. Runge–Kutta and General Linear Methods; Wiley-Interscience: New York, NY, USA, 1987. [Google Scholar]
- Stetter, H.J. Analysis of Discretization Methods for Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Obrechkoff, N. Neue Kwadraturformuln; Abh. Preuss. Akad. Wiss. Math.-Nat. Kl.: Berlin, Germany, 1940; Volume 4. [Google Scholar]
- Merson, R.H. An operational method for the study of integration processes. In Proceedings of the Symposium in Weapons Research Establishment, Salisbury, Australia, 3–8 June 1957; pp. 110–125. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis, 3rd ed.; Springer-Verlag: Berlin, Germany; New York, NY, USA, 2002. [Google Scholar]
- Fiori, S. Gyroscopic signal smoothness assessment by geometric jolt estimation. Math. Methods Appl. Sci. 2017, 40, 5893–5905. [Google Scholar] [CrossRef]
- Celledoni, E.; Fiori, S. Neural learning by geometric integration of reduced ‘rigid-body’ equations. J. Comput. Appl. Math. 2004, 172, 247–269. [Google Scholar] [CrossRef]
- Bobenko, A.I.; Suris, Y.B. Discrete time Lagrangian mechanics on Lie groups, with an application to the Lagrange top. Commun. Math. Phys. 1999, 204, 147–188. [Google Scholar] [CrossRef]
- Marsden, J.E.; Pekarsky, S.; Shkoller, S. Discrete Euler–Poincaré and Lie-Poisson equations. Nonlinearity 1999, 12, 1647–1662. [Google Scholar] [CrossRef]
- Marsden, J.E.; Pekarsky, S.; Shkoller, S. Symmetry reduction of discrete Lagrangian mechanics on Lie groups. J. Geom. Phys. 2000, 36, 140–151. [Google Scholar] [CrossRef]
- Bou-Rabee, N.; Marsden, J.E. Hamilton–Pontryagin Integrators on Lie Groups Part I: Introduction and Structure-Preserving Properties. Found. Comput. Math. 2009, 9, 197–219. [Google Scholar] [CrossRef]
- Kobilarov, M.; Crane, K.; Desbrun, M. Lie group integrators for animation and control of vehicles. ACM Trans. Graph. 2009, 28, 16. [Google Scholar] [CrossRef]
- Huang, H.; Hoffmann, G.M.; Waslander, S.L.; Tomlin, C.J. Aerodynamics and control of autonomous quadrotor helicopters in aggressive maneuvering. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3277–3282. [Google Scholar]
- Shahid, F.; Kadri, M.B.; Jumani, N.A.; Pirwani, Z. Dynamical modeling and control of quadrotor. Trans. Mach. Des. 2016, 4, 50–63. [Google Scholar]
- Fiori, S. A closed-form expression of the instantaneous rotational lurch index to evaluate its numerical approximation. Symmetry 2019, 11, 1208. [Google Scholar] [CrossRef]
- Markdahl, J.; Hu, X. Exact solutions to a class of feedback systems on SO(n). Automatica 2016, 63, 138–147. [Google Scholar] [CrossRef]
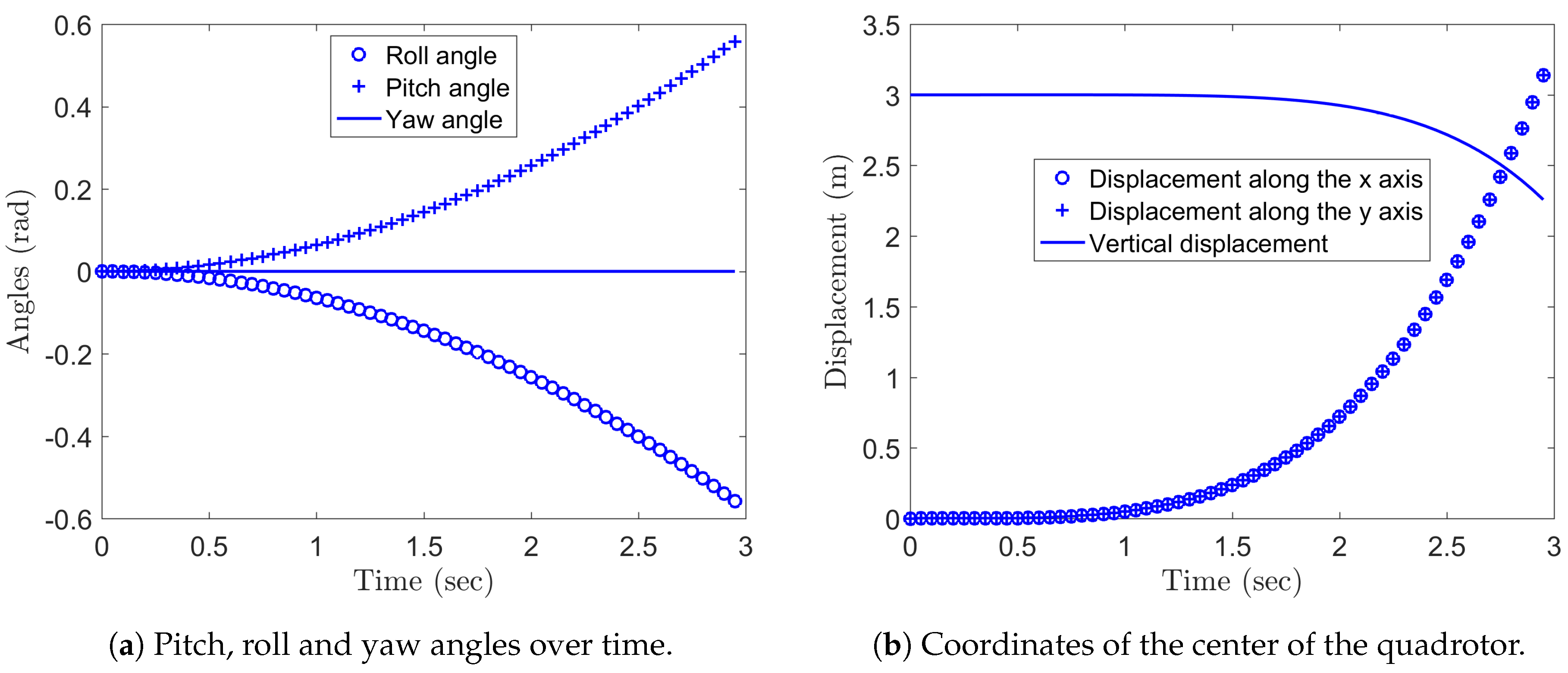
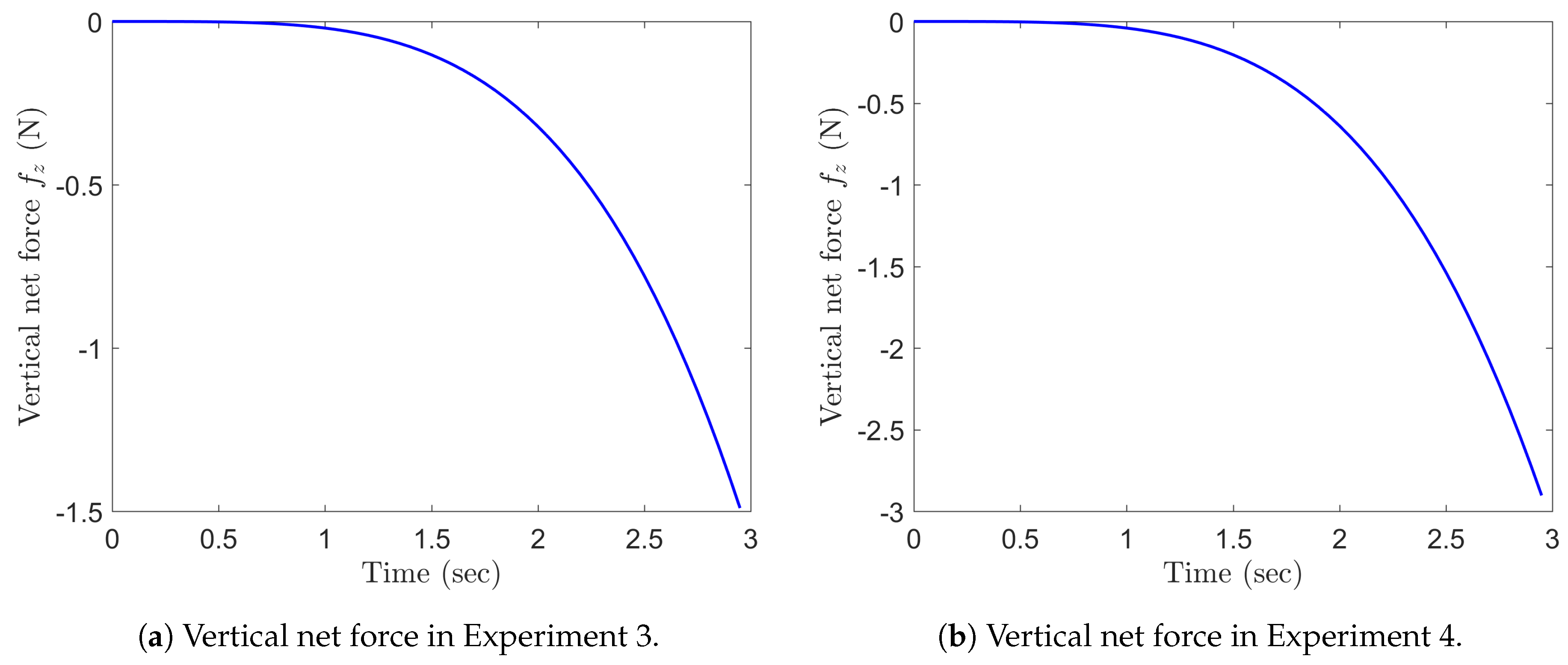
| Experiment | Rotors RPM | |||
|---|---|---|---|---|
| First | 3048 | 3048 | 3048 | 3048 |
| Second | 3048 | 3047 | 3048 | 3049 |
| Third | 3047 | 3048 | 3049 | 3048 |
| Fourth | 3047 | 3049 | 3049 | 3047 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiori, S. Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors. Mathematics 2019, 7, 935. https://doi.org/10.3390/math7100935
Fiori S. Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors. Mathematics. 2019; 7(10):935. https://doi.org/10.3390/math7100935
Chicago/Turabian StyleFiori, Simone. 2019. "Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors" Mathematics 7, no. 10: 935. https://doi.org/10.3390/math7100935
APA StyleFiori, S. (2019). Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors. Mathematics, 7(10), 935. https://doi.org/10.3390/math7100935





