Gradient Methods with Selection Technique for the Multiple-Sets Split Equality Problem
Abstract
1. Introduction
2. Preliminaries
3. Main Results
| Algorithm 1: Gradient method 1 |
| Take arbitrarily and compute |
| Algorithm 2: Gradient method 2 |
| Take and initial point . Compute |
4. Numerical Experiments
Author Contributions
Funding
Conflicts of Interest
References
- Censor, Y.; Elfving, T. A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Yao, Y.H.; Postolache, M.; Qin, X.L.; Yao, J.C. Iterative algorithms for the proximal split feasibility problem. UPB Sci. Bull. Ser. A Appl. Math. Phys. 2018, 80, 37–44. [Google Scholar]
- Bauschke, H.H.; Borwein, J.M. On projection algorithms for solving convex feasibility problems. SIAM Rev. 1996, 38, 367–426. [Google Scholar] [CrossRef]
- Byrne, C. Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 2002, 18, 441–453. [Google Scholar] [CrossRef]
- Takahashi, W. The split feasibility problem in Banach spaces. J. Nonlinear Convex Anal. 2014, 15, 1349–1355. [Google Scholar]
- Wang, F.; Xu, H.K. Cyclic algorithms for split feasibility problems in Hilbert spaces. Nonlinear Amal. 2011, 74, 4105–4111. [Google Scholar] [CrossRef]
- Xu, H.K.; Alghamdi, M.A.; Shahzad, N. An unconstrained optimization approach to the split feasibility problem. J. Nonlinear Convex Anal. 2017, 18, 1891–1899. [Google Scholar]
- Ceng, L.C.; Wong, N.C.; Yao, J.C. Hybrid extragradient methods for finding minimum-norm solutions of split feasibility problems. J. Nonlinear Convex Anal. 2015, 16, 1965–1983. [Google Scholar]
- Yao, Y.H.; Postolache, M.; Zhu, Z.C. Gradient methods with selection technique for the multiple-sets split feasibility problem. Optimization 2019. [Google Scholar] [CrossRef]
- Moudafi, A. Alternating CQ algorithm for convex feasibility and split fixed point problems. J. Nonlinear Convex Anal. 2013, 15, 809–818. [Google Scholar]
- Shi, L.Y.; Chen, R.D.; Wu, Y.J. Strong convergence of iterative algorithms for the split equality problem. J. Inequal. Appl. 2014, 2014, 478. [Google Scholar] [CrossRef]
- Dong, Q.L.; He, S.N.; Zhao, J. Solving the split equality problem without prior knowledge of operator norms. Optimization 2015, 64, 1887–1906. [Google Scholar] [CrossRef]
- Tian, D.L.; Shi, L.Y.; Chen, R.D. Strong convergence theorems for split inclusion problems in Hilbert spaces. J. Fixed Point Theory Appl. 2017, 19, 1501–1514. [Google Scholar] [CrossRef]
- Cegielski, A. General method for solving the split common fixed point problem. J. Optim. Theory Appl. 2015, 165, 385–404. [Google Scholar] [CrossRef]
- Kraikaew, P.; Saejung, S. On split common fixed point problems. J. Math Anal. Appl. 2014, 415, 513–524. [Google Scholar] [CrossRef]
- Moudafi, A. The split common fixed-point problem for demicontractive mappings. Inverse Probl. 2010, 26, 055007. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, W. The split common fixed point problem and strong convergence theorems by hybrid methods in two Banach spaces. J. Nonlinear Convex Anal. 2016, 17, 1051–1067. [Google Scholar]
- Takahashi, W.; Wen, C.F.; Yao, J.C. An implicit algorithm for the split common fixed point problem in Hilbert spaces and applications. Appl. Anal. Optim. 2017, 1, 423–439. [Google Scholar]
- Yao, Y.H.; Qin, X.L.; Yao, J.C. Self-adaptive step-sizes choice for split common fixed point problems. J. Nonlinear Convex Anal. 2018, 11, 1959–1969. [Google Scholar]
- Xu, H.K. A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 2006, 22, 2021–2034. [Google Scholar] [CrossRef]
- Goebel, K.; Reich, S. Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. In Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker: New York, NY, USA, 1984; pp. 1–170. [Google Scholar]
- Aoyama, K.; Kimura, Y.; Takahashi, W.; Toyoda, M. Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Anal. Theory Methods Appl. 2007, 67, 2350–2360. [Google Scholar] [CrossRef]
- Browder, F.E. Fixed point theorems for noncompact mappings in Hilbert spaces. Proc. Natl. Acad. Sci. USA 1965, 53, 1272–1276. [Google Scholar] [CrossRef] [PubMed]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 595–597. [Google Scholar] [CrossRef]
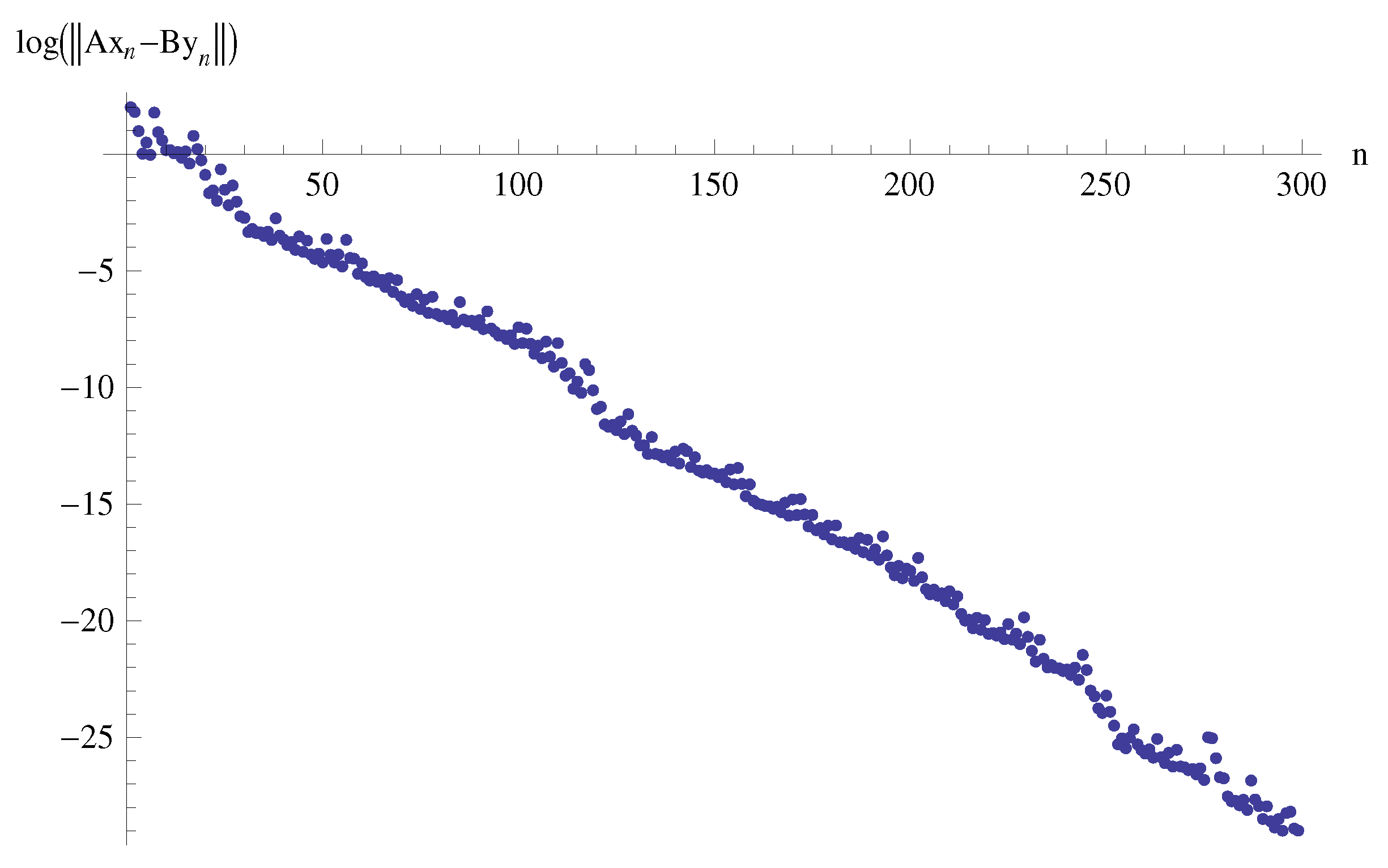

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, D.; Jiang, L.; Shi, L. Gradient Methods with Selection Technique for the Multiple-Sets Split Equality Problem. Mathematics 2019, 7, 928. https://doi.org/10.3390/math7100928
Tian D, Jiang L, Shi L. Gradient Methods with Selection Technique for the Multiple-Sets Split Equality Problem. Mathematics. 2019; 7(10):928. https://doi.org/10.3390/math7100928
Chicago/Turabian StyleTian, Dianlu, Lining Jiang, and Luoyi Shi. 2019. "Gradient Methods with Selection Technique for the Multiple-Sets Split Equality Problem" Mathematics 7, no. 10: 928. https://doi.org/10.3390/math7100928
APA StyleTian, D., Jiang, L., & Shi, L. (2019). Gradient Methods with Selection Technique for the Multiple-Sets Split Equality Problem. Mathematics, 7(10), 928. https://doi.org/10.3390/math7100928




