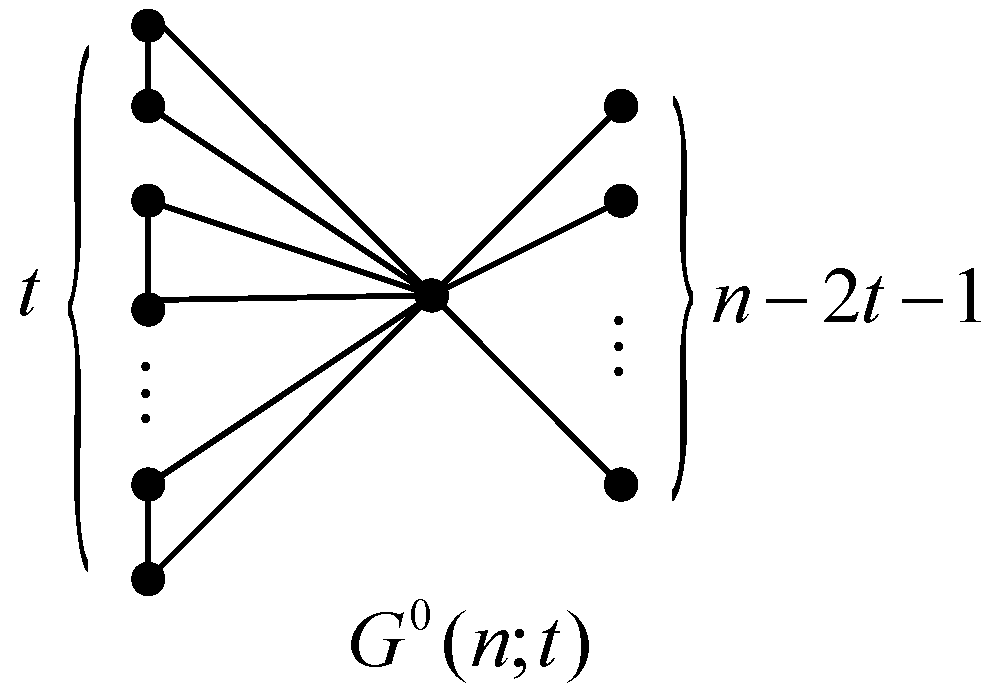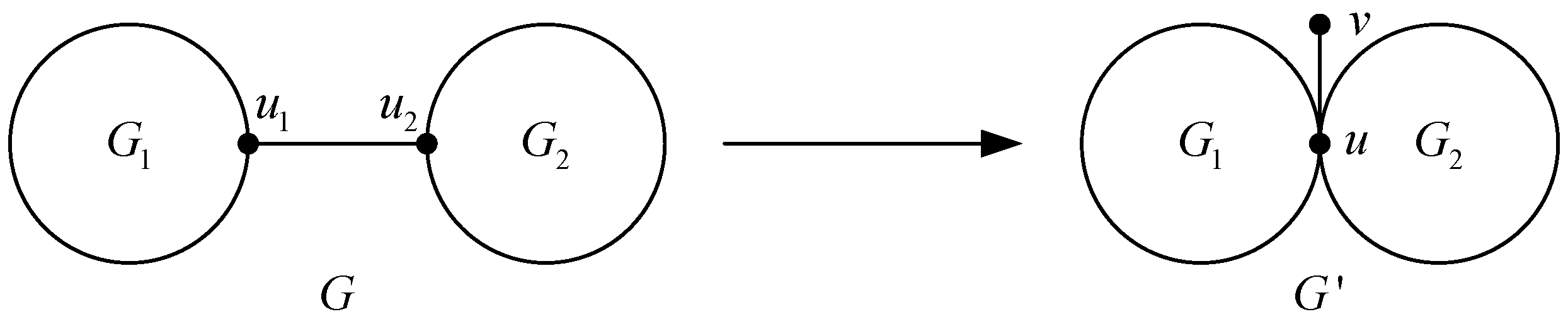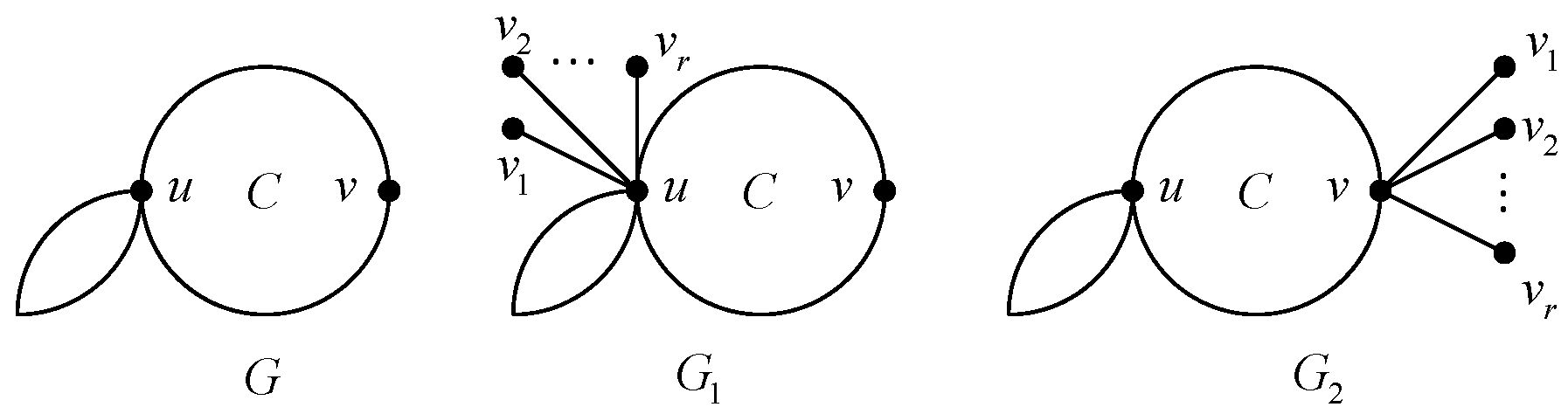The Extremal Cacti on Multiplicative Degree-Kirchhoff Index

Abstract

For a graph G, the resistance distance $r_G(x,y)$ is defined to be the effective resistance between vertices x and y, the multiplicative degree-Kirchhoff index $R^{\ast }(G)={\sum }_{\{x,y\}\subset V(G)}{d}_G(x)d_G(y)r_G(x,y)$, where $d_G(x)$ is the degree of vertex x, and $V(G)$ denotes the vertex set of G. L. Feng et al. obtained the element in $Cact(n;t)$ with first-minimum multiplicative degree-Kirchhoff index. In this paper, we first give some transformations on $R^{\ast }(G)$, and then, by these transformations, the second-minimum multiplicative degree-Kirchhoff index and the corresponding extremal graph are determined, respectively.

1. Introduction

Throughout this paper, we consider finite, undirected simple graphs. Let $G=(V(G),E(G))$ be a graph with vertex set $V(G)$ (or V) and edge set $E(G)$. For a graph G, the distance between vertices x and y, denoted by $d_G(x,y)$, is the length of a shortest path between them.

For distance, Harold Wiener in 1947 defined a famous index $W(G)$ [1], named Wiener index, where $W(G)={\sum }_{x,y\in V}{d}_G(x,y)$. It is the earliest and one of the most thoroughly studied distance-based graph invariants. Later, Dobrynin and Kochetova [2] gave a modified version of the Wiener index $D^{+}(G)={\sum }_{x,y\in V}(d_G(x)+d_G(y))d_G(x,y)$. It is called degree distance and has attracted much attention (see [3,4,5,6]). For a graph G, the degree distance $D^{+}(G)$ is the essential part of the molecular topological index $MTI(G)$ introduced by Schultz [7], which is defined as $MTI(G)={\sum }_{x\in V}{d}_G^2(x)+D^{+}(G)$, where ${\sum }_{x\in V}{d}_G^2(x)$ is the well-known first Zagreb index [8]. Klein et al. [9] discovered the relation between degree distance and Wiener index for a tree G on n vertices:

$$\begin{array}{c}\hfill D^{+}(G)=4W(G)-n(n-1).\end{array}$$

The Gutman index of a connected graph G is defined as $D^{\ast }(G)={\sum }_{x,y\in V}{d}_G(x)d_G(y)d_G(x,y)$. It was introduced in [10] and has been studied extensively (see, e.g., [11,12]). For a tree G on n vertices, Gutman [10] showed that

$$\begin{array}{c}\hfill D^{\ast }(G)=4W(G)-(n-1)(2n-1).\end{array}$$

In 1993, Klein and Randić [13] introduced a distance function named resistance distance on a graph. They viewed a graph G as an electrical network such that each edge of G is assumed to be a unit resistor, and the resistance distance between the vertices x and y of the graph G, denoted by $r_G(x,y)$, is then defined to be the effective resistance between the vertices x and y in G. The Kirchhoff index $Kf(G)$ of G is defined as

$$\begin{array}{c}\hfill Kf(G)=\sum _{x,y\in V}{r}_G(x,y).\end{array}$$

The index has been widely studied in mathematical, physical and chemical aspects; for details on the Kirchhoff index, the readers are referred to [14,15,16,17,18]. In 1996, Gutman and Mohar [19] obtained the result by which a relationship is established between the Kirchhoff index and the Laplacian spectrum: $Kf(G)=n{\sum }_{i=1}^{n-1}\frac{1}{{\mu }_i}$, where ${\mu }_1\ge {\mu }_2\ge \dots \ge {\mu }_n=0$ are the eigenvalues of the Laplacian matrix of a connected graph G with n vertices.

Similarly, if the distance is replaced by resistance distance in the expression for the degree distance and Gutman index, respectively, then one arrives at the following indices

$$\begin{array}{ccc}\hfill R^{+}(G)& =& \sum _{x,y\in V}(d_G(x)+d_G(y))r_G(x,y),\hfill \\ \hfill R^{\ast }(G)& =& \sum _{x,y\in V}{d}_G(x)d_G(y)r_G(x,y).\hfill \end{array}$$

$R^{+}(G)$ and $R^{\ast }(G)$ are called the additive degree-Kirchhoff index and multiplicative degree- Kirchhoff index, respectively, and were introduced by Gutman et al. [20] and Chen et al. [21], respectively. The indices have been well studied in both mathematical and chemical literature. In [22] some properties of $R^{+}(G)$ are determined and the extremal graph of cacti with minimum $R^{+}$-value characterized. Bianchi et al. [23] studied some upper and lower bounds for $G^{+}(G)$ whose expressions do not depend on the resistance distances. Feng et al. [24] characterized n-vertex unicyclic graphs having maximum, second maximum, minimum, and second minimum multiplicative degree-Kirchhoff index. Palacios [25] studied some interplay of the three Kirchhoff indices and found lower and upper bounds for the additive degree-Kirchhoff index. Yang and Klein [26] derived a formula for $R^{\ast }(G)$ of subdivisions and triangulations of graphs. To simplify the calculation of $R^{\ast }(G)$, the present authors [27] also obtained a formula for $R^{\ast }(G)$ with respect to the subgraph of G. For more work on the topological indices, we refer the reader to [13,21,22,28,29,30,31].

In this paper, we study the multiplicative degree-Kirchhoff index of cacti. To state our results, we introduce some notation and terminology. For graph-theoretical terms that are not defined here, we refer to Bollobás’ book [32]. Let $P_n,C_n$ and $S_n$ be the path, the cycle and the star on n vertices, respectively. We denote by $G\cong H$ if graph G is isomorphic to graph H. Let $N_G(x)=\{y|yx\in E\}$. Denote by $d_G(x)=\left|N_G(x)\right|$ the degree of the vertex x of G. If $E_0\subset E$, we denote by $G-E_0$ the subgraph of G obtained by deleting the edges in $E_0$. If $E_1$ is the subset of the edge set of the complement of G, $G+E_1$ denotes the graph obtained from G by adding the edges in $E_1.$ Similarly, if $W\subset V(G)$, we denote by $G-W$ the subgraph of G obtained by deleting the vertices of W and the edges incident with them and $G[W]$ the subgraph of G induced by W. If $E=\{xy\}$ and $W=\{x\}$, we write $G-xy$ and $G-x$ instead of $G-\{xy\}$ and $G-\{x\}$, respectively.

A graph G is called a cactus if each block of G is either an edge or a cycle. Denote by $Cact(n;t)$ the set of cacti possessing n vertices and t cycles. Let $G\in Cact(n;t),t\ge 2$, a cycle $C=v_1{v}_2\cdots v_k{v}_1$ of G is said to be an end cycle if all vertices $v_1,\cdots ,v_{k-1}$ are of degree two, and the degree of vertex $v_k$ is greater than two. The vertex $v_k\in V(C)$ is called the anchor of C. Let $G^0(n;t)$ be the graph shown in Figure 1. In this paper, we first give some transformations on $R^{\ast }(G)$, and then, by these transformations, we determine the first-minimum and second-minimum multiplicative degree-Kirchhoff index in $Cact(n;t)$ and characterize the corresponding extremal graphs, respectively.

Figure 1. The graph $G^0(n;t)$.

Now, we give some lemmas that are used in the proof of our main results.

Lemma 1.

Ref. [13] Let u be a cut vertex of a connected graph G and x and y be vertices occurring in different components which arise upon deletion of u, then $r_G(x,y)=r_G(x,u)+r_G(u,y).$

Lemma 2.

Ref. [27] Let $G_1$ and $G_2$ be connected graphs with disjoint vertex sets, with $m_1$ and $m_2$ edges, respectively. Let $u_1\in V(G_1),u_2\in V(G_2)$. Constructing the graph G by identifying the vertices $u_1$ and $u_2$, and denote the so obtained vertex by u. Then,

$$R^{\ast }(G)=R^{\ast }(G_1)+R^{\ast }(G_2)+2m_2\sum _{x\in V(G_1)}{d}_{G_1}(x)r_{G_1}(u,x)+2m_1\sum _{y\in V(G_2)}{d}_{G_2}(y)r_{G_2}(u,y).$$

For completeness, we also give the proof in this paper.

Proof. 

Let $V_1=V(G_1)-u$, $V_2=V(G_2)-u$. Note that $\forall x\in V_i,d_G(x)=d_{G_i}(x)$ for $i=1,2$, and $d_G(u)=d_{G_1}(u)+d_{G_2}(u)$. By the definition of $R^{\ast }(G)$ and Lemma 1, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)& =& \frac{1}{2}\sum _{x,y\in V_1}{d}_G(x)d_G(y)r_G(x,y)+\frac{1}{2}\sum _{x,y\in V_2}{d}_G(x)d_G(y)r_G(x,y)+\sum _{x\in V_1}{d}_G(x)d_G(u)r_G(x,u)+\hfill \\ & & \sum _{y\in V_2}{d}_G(y)d_G(u)r_G(u,y)+\sum _{x\in V_1,y\in V_2}{d}_G(x)d_G(y)r_G(x,y)\hfill \\ & =& [R^{\ast }(G_1)-\sum _{x\in V_1}{d}_{G_1}(x)d_{G_1}(u)r_{G_1}(x,u)]+[R^{\ast }(G_2)-\sum _{y\in V_2}{d}_{G_2}(y)d_{G_2}(u)r_{G_2}(u,y)]+\hfill \\ & & \sum _{x\in V_1}{d}_{G_1}(x)d_G(u)r_G(x,u)+\sum _{y\in V_2}{d}_{G_2}(y)d_G(u)r_G(u,y)+\hfill \\ & & \sum _{x\in V_1,y\in V_2}{d}_{G_1}(x)d_{G_2}(y)[r_{G_1}(x,u)+r_{G_2}(u,y)]\hfill \end{array}$$

Because $d_G(u)=d_{G_1}(u)+d_{G_2}(u)$ and $r_G(x,u)=r_{G_1}(x,u)$ for $x\in V_1$, $r_G(u,y)=r_{G_2}(u,y)$ for $y\in V_2$, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)& =& [R^{\ast }(G_1)+d_{G_2}(u)\sum _{x\in V_1}{d}_{G_1}(x)r_{G_1}(x,u)]+[R^{\ast }(G_2)+d_{G_1}(u)\sum _{y\in V_2}{d}_{G_2}(y)r_{G_2}(u,y)]+\hfill \\ & & \sum _{y\in V_2}\sum _{x\in V_1}{d}_{G_1}(x)d_{G_2}(y)r_{G_1}(x,u)+\sum _{x\in V_1}\sum _{y\in V_2}{d}_{G_1}(x)d_{G_2}(y)r_{G_2}(u,y)\hfill \\ & =& [R^{\ast }(G_1)+d_{G_2}(u)\sum _{x\in V_1}{d}_{G_1}(x)r_{G_1}(x,u)]+[R^{\ast }(G_2)+d_{G_1}(u)\sum _{y\in V_2}{d}_{G_2}(y)r_{G_2}(u,y)]+\hfill \\ & & \sum _{y\in V_2}{d}_{G_2}(y)·\sum _{x\in V_1}{d}_{G_1}(x)r_{G_1}(x,u)+\sum _{x\in V_1}{d}_{G_1}(x)·\sum _{y\in V_2}{d}_{G_2}(y)r_{G_2}(u,y)\hfill \\ & =& [R^{\ast }(G_1)+d_{G_2}(u)\sum _{x\in V_1}{d}_{G_1}(x)r_{G_1}(x,u)]+[R^{\ast }(G_2)+d_{G_1}(u)\sum _{y\in V_2}{d}_{G_2}(y)r_{G_2}(u,y)]+\hfill \\ & & [2m_2-d_{G_2}(u)]\sum _{x\in V_1}{d}_{G_1}(x)r_{G_1}(x,u)+[2m_1-d_{G_1}(u)]\sum _{y\in V_2}{d}_{G_2}(y)r_{G_2}(u,y)\hfill \\ & =& R^{\ast }(G_1)+R^{\ast }(G_2)+2m_2\sum _{x\in V(G_1)}{d}_{G_1}(x)r_{G_1}(u,x)+2m_1\sum _{y\in V(G_2)}{d}_{G_2}(y)r_{G_2}(u,y),\hfill \end{array}$$

since $r_{G_i}(u,u)=0$ for $i=1,2$. □

Lemma 3.

Ref. [27] Let $G\in {\mathcal{U}}_n$, then $R^{\ast }(G)\ge R^{\ast }(G^0(n;1))$, where ${\mathcal{U}}_n$ is the class of unicyclic graphs. The equality holds if and only if $T\cong G^0(n;1)$.

2. Transformations

In this section, we give some transformations that decrease $R^{\ast }(G)$.

Transformation 1.

Let $u_1{u}_2$ be a cut-edge of G, but not an pendent edge, $G_1,G_2$ be the connected components of $G-u_1{u}_2$ , where $u_1\in V(G_1),u_2\in V(G_2)$ . Constructing the graph $G^{\prime }$ from G by deleting $u_1{u}_2$ and identifying the vertices $u_1,u_2$ , denote the so obtained vertex by u, adding an pendent edge $uv$ (as shown in Figure 2).

Figure 2. The graphs G and $G^{\prime }$ in Transformation 1.

Lemma 4.

Let $G,G^{\prime }$ be the graphs described in Transformation 1, then $R^{\ast }(G)>R^{\ast }(G^{\prime })$.

Proof. 

Let $|V(G_1)|=n_1,\left|V(G_2)\right|=n_2$ and $|E(G_1)|=m_1,\left|E(G_2)\right|=m_2$, where $m_1,m_2\ge 1$. Let H be the graph obtained by attaching to the vertex $u_1$ of $G_1$ the pendent vertex $u_2$, then $\left|V(H)\right|=n_1+1,\left|E(H)\right|=m_1+1$. By Lemma 2, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)& =& R^{\ast }(H)+R^{\ast }(G_2)+2m_2\sum _{x\in V(H)}{d}_H(x)r_H(u_2,x)+2(m_1+1)\sum _{y\in V(G_2)}{d}_{G_2}(y)r_{G_2}(u_2,y),\hfill \\ \hfill R^{\ast }(G^{\prime })& =& R^{\ast }(H)+R^{\ast }(G_2)+2m_2\sum _{x\in V(H)}{d}_H(x)r_H(u,x)+2(m_1+1)\sum _{y\in V(G_2)}{d}_{G_2}(y)r_{G_2}(u,y).\hfill \end{array}$$

Note that $r_{G_2}(u_2,y)=r_{G_2}(u,y)$, then

$$\begin{array}{ccc}\hfill R^{\ast }(G)-R^{\ast }(G^{\prime })& =& 2m_2[\sum _{x\in V(H)}{d}_H(x)r_H(u_2,x)-\sum _{x\in V(H)}{d}_H(x)r_H(u,x)]\hfill \\ & =& 2m_2\left\{\sum _{x\in V(G_1)}{d}_H(x)[r_H(u_1,x)+1]-[\sum _{x\in V(G_1)}{d}_H(x)r_H(u,x)+1]\right\}\hfill \\ & =& 2m_2[2(m_1+1)-1-1]=4m_1{m}_2>0,\hfill \end{array}$$

so $R^{\ast }(G)>R^{\ast }(G^{\prime })$. □

Let ${\mathcal{G}}_n$ be the class of connected graphs on n vertices. By Transformation 1 and Lemma 4, we have the following result.

Corollary 1.

Let $G_0$ be a graph with the smallest multiplicative degree-Kirchhoff index in ${\mathcal{G}}_n$, then all cut-edges are pendent edges.

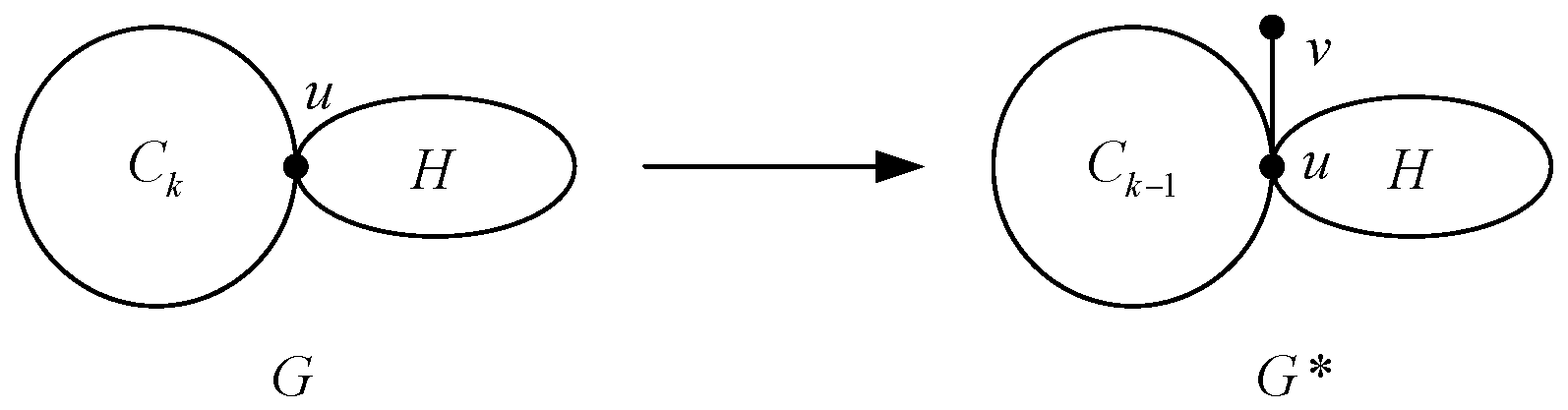
Transformation 2.

For $G\in Cact(n;t)$, let $C_k$ be a cycle with $k(\ge 4)$ vertices, contained in G. Let there be a unique vertex $u\in C_h$ which is adjacent to a vertex in $V(G)-V(C)$. Assuming that $uv,vw\in E(C)$, construct a new graph $G^{\ast }=G-vw+uw$ (as shown in Figure 3).

Figure 3. The graphs G and $G^{\ast }$ in Transformation 2.

For $u\in V(C_k)$, by direct calculation, we have

$$\begin{array}{ccc}\hfill R^{\ast }(C_k)& =& \frac{k^3-k}{3}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \sum _{y\in V(C_k)}{r}_{C_k}(u,y)& =& \frac{k^2-1}{6}\hfill \end{array}$$

(2)

Lemma 5.

Let $G,G^{\ast }$ be the graphs described in Transformation 2, then $R^{\ast }(G)>R^{\ast }(G^{\ast })$.

Proof. 

Let S be the graph obtained by attaching to the vertex u of $C_{k-1}$ the pendent vertex v. By Lemma 1, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)& =& R^{\ast }(H)+R^{\ast }(C_k)+2k\sum _{x\in V(H)}{d}_H(x)r_H(u,x)+2\left|E(H)\right|\sum _{y\in V(C_k)}{d}_{C_k}(y)r_{C_k}(u,y),\hfill \\ \hfill R^{\ast }(G^{\ast })& =& R^{\ast }(H)+R^{\ast }(S)+2k\sum _{x\in V(H)}{d}_H(x)r_H(u,x)+2\left|E(H)\right|\sum _{y\in V(S)}{d}_S(y)r_S(u,y).\hfill \end{array}$$

Further by Equations (1) and (2), then

$$\begin{array}{ccc}\hfill R^{\ast }(G)-R^{\ast }(G^{\ast })& =& [R^{\ast }(C_k)-R^{\ast }(S)]+2\left|E(H)\right|[\sum _{y\in V(C_k)}{d}_{C_k}(y)r_{C_k}(u,y)-\sum _{y\in V(S)}{d}_S(y)r_S(u,y)]\hfill \\ & =& [\frac{k^3-k}{3}-(\frac{(k-1)(k^2+2)}{3}+2k-1)]+2\left|E(H)\right|·\frac{2k-4}{3}\hfill \\ & \ge & \frac{k^2-5k+3}{3}+\frac{4k-8}{3}=\frac{k^2-k-5}{3}>0,\hfill \end{array}$$

since $k\ge 4,|E(H)|\ge 1$. □

Transformation 3.

Let $G\in Cact(n;t),t\ge 2$, be a cactus without cut edges. Let C be an end cycle of G and u be its anchor. Let v be a vertex of C different from u. The graphs $G_1$ and $G_2$ are constructed by adding r pendent edges to the vertices u and v of G respectively (as shown in Figure 4).

Figure 4. The graphs G, $G_1$ and $G_3$ in Transformation 3.

Lemma 6.

Let $G,G_1,G_2$ be the graphs described in Transformation 3, then $R^{\ast }(G_2)>R^{\ast }(G_1)$.

Proof. 

Let $H=G[V(G)-V(C)],H_1=G[V(G_1)\setminus (V(G)-u)]$ and $H_2=G[V(G_2)\setminus (V(G)-v)]$, then $H_1\cong H_2\cong K_{1,r}$. By Lemma 2, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G_1)& =& R^{\ast }(G)+R^{\ast }(K_{1,r})+2r\sum _{x\in V(G)}{d}_G(x)r_G(u,x)+2\left|E(G)\right|\sum _{y\in V(K_{1,r})}{d}_{K_{1,r}}(y)r_{K_{1,r}}(u,y),\hfill \\ \hfill R^{\ast }(G_2)& =& R^{\ast }(G)+R^{\ast }(K_{1,r})+2r\sum _{x\in V(G)}{d}_G(x)r_G(v,x)+2\left|E(G)\right|\sum _{y\in V(K_{1,r})}{d}_{K_{1,r}}(y)r_{K_{1,r}}(v,y).\hfill \end{array}$$

Note that $r_G(u,u)=r_G(v,v)=0$, $V(G)=V(H)\cup \{V(C)-u\}\cup \{u\}$ and $r_G(v,x)=r_G(x,u)+r_G(v,u)$ for $x\in V(H)$, then

$$\begin{array}{ccc}\hfill R^{\ast }(G_2)-R^{\ast }(G_1)& =& 2r[\sum _{x\in V(G)}{d}_G(x)r_G(v,x)-\sum _{x\in V(G)}{d}_G(x)r_G(u,x)]\hfill \\ & =& 2r\{[\sum _{x\in V(H)}{d}_G(x)(r_G(x,u)+r_G(v,u))+\sum _{x\in V(C)-u}{d}_G(x)r_G(v,x)+d_G(u)r_G(v,u)]\hfill \\ & & -[\sum _{x\in V(H)}{d}_G(x)r_G(u,x)+\sum _{x\in V(C)-u}{d}_G(x)r_G(u,x)]\}\hfill \end{array}$$

Considering that $d_G(u)=d_H(u)+d_C(u)$ and ${\sum }_{x\in V(C)-u}{d}_G(x)r_G(u,x)={\sum }_{x\in V(C)-u}{d}_G(x)r_G(v,x)+d_C(u)r_G(v,u)]$, we obtain

$$R^{\ast }(G_2)-R^{\ast }(G_1)=2r[\sum _{x\in V(H)}{d}_G(x)r_G(v,u)+d_G(u)r_G(v,u)]>0.$$

This completes the proof. □

Transformation 4.

Let $C=v_1{v}_2{v}_3{v}_1$ be a cycle of the graph G, C is called a pendant triangle if $d_G(v_1)=d_G(v_2)=2$ and $d_G(v_3)>2$. Suppose that G is a cactus graph and $u,v\in V(G)$ are two vertices, such that $u{x}_i{y}_{i}u$ $(i=1,2,\dots ,s)$ and $v{p}_j{q}_{j}v$ $(j=1,2,\dots ,t)$ are pendant triangles with the anchor u and v, respectively. We form two new graphs A and B according to the following transformation.

$$\begin{array}{ccc}\hfill A& =& G-{\cup }_{i=1}^s\{u{x}_i,u{y}_i\}+{\cup }_{i=1}^s\{v{x}_i,v{y}_i\},\hfill \\ \hfill B& =& G-{\cup }_{i=1}^t\{v{p}_i,v{q}_i\}+{\cup }_{i=1}^t\{u{p}_i,u{q}_i\}.\hfill \end{array}$$

Lemma 7.

Let $G,A,B$ be the graphs described in Transformation 4, then either $R^{\ast }(G)>R^{\ast }(A)$ or $R^{\ast }(G)>R^{\ast }(B)$.

Proof. 

Let $M=\{x_1,y_1,\dots ,x_s,y_s\}$, $N=\{p_1,q_1,\dots ,p_t,q_t\}$ and $H=V(G)-M-N-\{u,v\}$. Because of $V(G)=M\cup N\cup H\cup \{u,v\}$, by Lemma 2, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)& =& [\sum _{\{x,y\}\subset M}+\sum _{\{x,y\}\subset N}+\sum _{\{x,y\}\subset H}]d_G(x)d_G(y)r_G(x,y)+\sum _{x\in H,y\in M}{d}_G(x)d_G(y)r_G(x,y)+\hfill \\ & & \sum _{x\in H,y\in N}{d}_G(x)d_G(y)r_G(x,y)+\sum _{x\in M,y\in N}{d}_G(x)d_G(y)r_G(x,y)+d_G(u)d_G(v)r_G(u,v)\hfill \\ & & +\sum _{x\in H}{d}_G(x)d_G(u)r_G(x,u)+\sum _{x\in H}{d}_G(x)d_G(v)r_G(x,v)+\sum _{x\in M}{d}_G(x)d_G(u)r_G(x,u)+\hfill \\ & & \sum _{x\in M}{d}_G(x)d_G(v)r_G(x,v)+\sum _{x\in N}{d}_G(x)d_G(u)r_G(x,u)+\sum _{x\in N}{d}_G(x)d_G(v)r_G(x,v).\hfill \end{array}$$

and analogously

$$\begin{array}{ccc}\hfill R^{\ast }(A)& =& [\sum _{\{x,y\}\subset M}+\sum _{\{x,y\}\subset N}+\sum _{\{x,y\}\subset H}]d_A(x)d_A(y)r_A(x,y)+\sum _{x\in H,y\in M}{d}_A(x)d_A(y)r_A(x,y)+\hfill \\ & & \sum _{x\in H,y\in N}{d}_A(x)d_A(y)r_A(x,y)+\sum _{x\in M,y\in N}{d}_A(x)d_A(y)r_A(x,y)+d_A(u)d_A(v)r_A(u,v)\hfill \\ & & +\sum _{x\in H}{d}_A(x)d_A(u)r_A(x,u)+\sum _{x\in H}{d}_A(x)d_A(v)r_A(x,v)+\sum _{x\in M}{d}_A(x)d_A(u)r_A(x,u)+\hfill \\ & & \sum _{x\in M}{d}_G(x)d_A(v)r_A(x,v)+\sum _{x\in N}{d}_A(x)d_A(u)r_A(x,u)+\sum _{x\in N}{d}_A(x)d_A(v)r_A(x,v).\hfill \end{array}$$

Note that $d_G(x)=d_A(x)$ for $x\in V(G)-\{u,v\}$ and $r_G(x,y)=r_A(x,y)$ for $x,y\in M$ or $x,y\in N$ or $x,y\in H$, then

$$\begin{array}{ccc}\hfill a_0& =& [\sum _{\{x,y\}\subset M}+\sum _{\{x,y\}\subset N}+\sum _{\{x,y\}\subset H}]d_G(x)d_G(y)r_G(x,y),\hfill \\ \hfill b_0& =& [\sum _{\{x,y\}\subset M}+\sum _{\{x,y\}\subset N}+\sum _{\{x,y\}\subset H}]d_A(x)d_A(y)r_A(x,y),\hfill \\ \hfill a_0-b_0& =& 0\hfill \end{array}$$

(3)

Considering that $r(u,y)=\frac{2}{3}$ for $y\in M$ and $r(x,y)=r(x,u)+r(u,y)$, we get

$$\begin{array}{ccc}\hfill a_1=\sum _{x\in H,y\in M}{d}_G(x)d_G(y)r_G(x,y)& =& \sum _{x\in H,y\in M}{d}_G(x)d_G(y)[r_G(x,u)+\frac{2}{3}],\hfill \\ \hfill b_1=\sum _{x\in H,y\in M}{d}_A(x)d_A(y)r_A(x,y)& =& \sum _{x\in H,y\in M}{d}_G(x)d_G(y)[r_G(x,v)+\frac{2}{3}],\hfill \\ \hfill a_1-b_1& =& \sum _{x\in H,y\in M}{d}_G(x)d_G(y)[r_G(x,u)-r_G(x,v)]\hfill \end{array}$$

(4)

and analogously,

$$\begin{array}{ccc}\hfill a_2=\sum _{x\in H,y\in N}{d}_G(x)d_G(y)r_G(x,y)& =& \sum _{x\in H,y\in N}{d}_G(x)d_G(y)[r_G(x,v)+\frac{2}{3}],\hfill \\ \hfill b_2=\sum _{x\in H,y\in N}{d}_A(x)d_A(y)r_A(x,y)& =& \sum _{x\in H,y\in N}{d}_G(x)d_G(y)[r_G(x,v)+\frac{2}{3}],\hfill \\ \hfill a_2-b_2& =& 0\hfill \end{array}$$

(5)

Because $r_G(x,y)=r_G(x,u)+r_G(u,v)+r_G(v,y)=r_G(u,v)+\frac{4}{3}$ for $x\in M,y\in N$, then

$$\begin{array}{ccc}\hfill a_3=\sum _{x\in M,y\in N}{d}_G(x)d_G(y)r_G(x,y)& =& \sum _{x\in M,y\in N}{d}_G(x)d_G(y)[r_G(u,v)+\frac{4}{3}],\hfill \\ \hfill b_3=\sum _{x\in M,y\in N}{d}_A(x)d_A(y)r_A(x,y)& =& \frac{4}{3}\sum _{x\in M,y\in N}{d}_G(x)d_G(y),\hfill \\ \hfill a_3-b_3& =& \sum _{x\in M,y\in N}{d}_G(x)d_G(y)r_G(u,v)\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill a_4& =& d_G(u)d_G(v)r_G(u,v),\hfill \\ \hfill b_4=d_A(u)d_A(v)r_A(u,v)& =& [d_G(u)-2s][d_G(v)+2s]r_G(u,v),\hfill \\ \hfill a_4-b_4& =& 4s^2{r}_G(u,v)+2s{d}_G(v)r_G(u,v)-2s{d}_G(u)r_G(u,v)\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill a_5& =& \sum _{x\in H}{d}_G(x)d_G(u)r_G(x,u),\hfill \\ \hfill b_5=\sum _{x\in H}{d}_A(x)d_A(u)r_A(x,u)& =& \sum _{x\in H}{d}_G(x)[d_G(u)-2s]r_G(x,u),\hfill \\ \hfill a_5-b_5& =& \sum _{x\in H}2s{d}_G(x)r_G(x,u)\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill a_6& =& \sum _{x\in H}{d}_G(x)d_G(v)r_G(x,v),\hfill \\ \hfill b_6=\sum _{x\in H}{d}_A(x)d_A(v)r_A(x,v)& =& \sum _{x\in H}{d}_G(x)[d_G(v)+2s]r_G(x,v),\hfill \\ \hfill a_6-b_6& =& -\sum _{x\in H}2s{d}_G(x)r_G(x,v)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill a_7=\sum _{x\in M}{d}_G(x)d_G(u)r_G(x,u)& =& \frac{2}{3}\sum _{x\in M}{d}_G(x)d_G(u),\hfill \\ \hfill b_7=\sum _{x\in M}{d}_A(x)d_A(u)r_A(x,u)& =& \sum _{x\in M}{d}_G(x)[d_G(u)-2s][r_G(u,v)+\frac{2}{3}],\hfill \\ \hfill a_7-b_7& =& \sum _{x\in M}[(2s-d_G(u))d_G(x)r_G(u,v)+\frac{4}{3}s{d}_G(x)]\hfill \end{array}$$

(10)

Because $r_G(x,v)=r_G(u,v)+\frac{2}{3}$ for $x\in M$. After the transformation, the degree of the vertex v increases by $2s$, and $r_A(x,v)=\frac{2}{3}$ for $x\in M$.

$$\begin{array}{ccc}\hfill a_8=\sum _{x\in M}{d}_G(x)d_G(v)r_G(x,v)& =& \sum _{x\in M}{d}_G(x)d_G(v)[r_G(u,v)+\frac{2}{3}],\hfill \\ \hfill b_8=\sum _{x\in M}{d}_G(x)d_A(v)r_A(x,v)& =& \frac{2}{3}\sum _{x\in M}{d}_G(x)[d_G(v)+2s],\hfill \\ \hfill a_8-b_8& =& \sum _{x\in M}[d_G(x)d_G(v)r_G(u,v)-\frac{4}{3}s{d}_G(x)]\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill a_9=\sum _{x\in N}{d}_G(x)d_G(u)r_G(x,u)& =& \sum _{x\in N}{d}_G(x)d_G(u)[r_G(v,u)+\frac{2}{3}],\hfill \\ \hfill b_9=\sum _{x\in N}{d}_A(x)d_A(u)r_A(x,u)& =& \sum _{x\in N}{d}_G(x)[d_G(u)-2s][r_G(v,u)+\frac{2}{3}],\hfill \\ \hfill a_9-b_9& =& \sum _{x\in N}2s{d}_G(x)[r_G(v,u)+\frac{2}{3}]\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill a_{10}=\sum _{x\in N}{d}_G(x)d_G(v)r_G(x,v)& =& \frac{2}{3}\sum _{x\in N}{d}_G(x)d_G(v),\hfill \\ \hfill b_{10}=\sum _{x\in N}{d}_A(x)d_A(v)r_A(x,v)& =& \frac{2}{3}\sum _{x\in N}{d}_G(x)[d_G(v)+2s],\hfill \\ \hfill a_{10}-b_{10}& =& -\frac{4}{3}\sum _{x\in N}s{d}_G(x)\hfill \end{array}$$

(13)

By Equations (3)–(13), we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)-R^{\ast }(A)& =& 4s\sum _{x\in H}{d}_G(x)[r_G(x,u)-r_G(x,v)]+24st{r}_G(u,v)+6s{r}_G(u,v)[d_G(v)-d_G(u)]+\hfill \\ & & 12s^2{r}_G(u,v)+\sum _{x\in H}2s{d}_G(x)[r_G(x,u)-r_G(x,v)].\hfill \end{array}$$

Similarly, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)-R^{\ast }(B)& =& 4t\sum _{x\in H}{d}_G(x)[r_G(x,v)-r_G(x,u)]+24st{r}_G(u,v)+6t{r}_G(u,v)[d_G(u)-d_G(v)]+\hfill \\ & & 12t^2{r}_G(u,v)+2t\sum _{x\in H}{d}_G(x)[r_G(x,v)-r_G(x,u)].\hfill \end{array}$$

If $R^{\ast }(G)-R^{\ast }(A)\le 0,$ then

$$\begin{array}{cc}& 4\sum _{x\in H}{d}_G(x)[r_G(x,u)-r_G(x,v)]+6r_G(u,v)[d_G(v)-d_G(u)]+\sum _{x\in H}2d_G(x)[r_G(x,u)-r_G(x,v)]\hfill \\ \le & -(24t{r}_G(u,v)+12s{r}_G(u,v)).\hfill \end{array}$$

Further, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G)-R^{\ast }(B)& \ge & t(24t{r}_G(u,v)+12s{r}_G(u,v))+24st{r}_G(u,v)+12t^2{r}_G(u,v)>0.\hfill \end{array}$$

This completes the proof. □

Transformation 5.

Let u be a vertex of G such that there are s pendent vertices $u_1,u_2,\dots ,u_s$ attached to u, and v be another vertex of G such that there are t pendent vertices $v_1,v_2,\dots ,v_t$ attached to v. Let

$$\begin{array}{ccc}\hfill G_3& =& G-\{u{u}_1,u{u}_2,\dots ,u{u}_s\}+\{v{u}_1,v{u}_2,\dots ,v{u}_s\},\hfill \\ \hfill G_4& =& G-\{v{v}_1,v{v}_2,\dots ,v{v}_t\}+\{u{v}_1,u{v}_2,\dots ,u{v}_t\}.\hfill \end{array}$$

Similar to the proof of Lemma 7, we can prove the following result.

Lemma 8.

Let $G,G_3$ and $G_4$ be graphs as described in Transformation 5, then either $R^{\ast }(G)>R^{\ast }(G_3)$ or $R^{\ast }(G)>R^{\ast }(G_4)$.

3. Main Results

In this section, we determine the elements in $Cact(n;t)$ with first-minimum and second-minimum multiplicative degree-Kirchhoff index by the transformations that we have obtained. Note that the first-minimum multiplicative degree-Kirchhoff index has been obtained in [33]; for completeness, we also give the following proof.

Theorem 1.

Ref. [33] Let $G\in Cact(n;t)$, then $R^{\ast }(G)\ge 16t^2-8t+{(n-2t-1)}^2+(n-2t-1)(n-2t-2)+\frac{34}{3}t(n-2t-1)$. The equality holds if and only if $G\cong G^0(n,t)$.

Proof. 

Let $\tilde{G}$ be the unique graph having the minimum multiplicative degree-Kirchhoff index in $Cact(n;t)$.

Case 1. If $t=1$, $Cact(n;t)$ is the class of unicyclic graphs. By Lemma 3, we know the results hold.

Case 2. If $t=2$, $Cact(n;t)$ is the class of bicyclic graphs. By Lemma 4, we conclude that $\tilde{G}$ contains two cycles attached to a common vertex u, and all cut-edges are all pendent edges (if any). Further, by Lemmas 8 and 6, all pendent edges (if any) are also attached to u. Finally, by Lemma 5, the two cycles must be triangles, that is, $\tilde{G}\cong G^0(n,2)$. This obtains the desirable results.

Case 3. If $t\ge 3$, by Lemma 4, we conclude that all cut-edges are all pendent edges (if any) in $\tilde{G}$. Further, by Lemmas 8 and 6, $\tilde{G}$ has at least two end cycles. Repeated by Lemmas 5–8, we arrive at the conclusion $\tilde{G}\cong G^0(n,t)$

By direct calculation, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G^0(n;t))& =& 16t^2-8t+{(n-2t-1)}^2+(n-2t-1)(n-2t-2)+\frac{34}{3}t(n-2t-1).\hfill \end{array}$$

This completes the proof. □

Theorem 2.

Let $G\in Cact(n;t)\setminus G^0(n;t)$, then $R^{\ast }(G)\ge [16t^2+\frac{34t-22}{3}]+[{(n-2t-2)}^2+(n-2t-2)(n-2t-3)]+\frac{(16t+14)(n-2t-2)}{3}+2(3t+1)(n-2t-2)$. The equality holds if and only if $G\cong G_3^0$.

Proof. 

By Lemmas 4–8 and Theorem 1, one can conclude that G, which has the second-minimum multiplicative degree-Kirchhoff index in $Cact(n;t)$ must be one of the graphs $G_1^0,G_2^0,G_3^0$, as shown in Figure 5. By Lemma 2, we have

$$\begin{array}{ccc}\hfill R^{\ast }(G_1^0)& =& [16t^2-8t]+[2+4(n-2t-2)+7(n-2t-3)+(n-2t-2)(n-2t-3)+\hfill \\ & & (n-2t-3)(n-2t-4)]+\frac{16}{3}t(n-2t-1)+6t(n-2t+1),\hfill \\ \hfill R^{\ast }(G_2^0)& =& [16t^2+\frac{34}{3}t-7]+[{(n-2t-2)}^2+(n-2t-2)(n-2t-3)]+\frac{(16t+14)(n-2t-2)}{3}\hfill \\ & & +2(3t+1)(n-2t-2),\hfill \\ \hfill R^{\ast }(G_3^0)& =& [16t^2+\frac{34t-22}{3}]+[{(n-2t-2)}^2+(n-2t-2)(n-2t-3)]+\frac{(16t+14)(n-2t-2)}{3}\hfill \\ & & +2(3t+1)(n-2t-2).\hfill \end{array}$$

Figure 5. The graphs $G_1^0,G_2^0,G_3^0$.

Then,

$$\begin{array}{ccc}\hfill R^{\ast }(G_1^0)-R^{\ast }(G_3^0)& =& \frac{4n+4t+5}{3},\hfill \\ \hfill R^{\ast }(G_2^0)-R^{\ast }(G_3^0)& =& \frac{1}{3}.\hfill \end{array}$$

This completes the proof. □

By Theorems 1 and 2, we have

Corollary 2.

Among all graphs in $Cact(n;t)$, $G^0(n;t)$ and $G_3^0$ are the graphs with first-minimum and second-minimum multiplicative degree-Kirchhoff index.

According to the above discussion, we find that the extremal cacti for the index $R^{\ast }(G)$ are the same as the extremal cacti for the Kirchhoff index, the multiplicative degree-Kirchhoff index, the Wiener index and the other indices [22,29,34,35]. Based on the known results for these indices, we guess the element of $Cact(n;t)$ with maximum multiplicative degree-Kirchhoff index is isomorphic to the graph $C_{n,t}$ (as shown in Figure 6).

Figure 6. The graphs $C_{n,t}$.

Conjecture 1.

Let $C_{n,t}$ be the graph depicted in Figure 6, where $k=\lfloor \frac{t}{2}\rfloor$. Then, $C_{n,t}$ is the unique element of $Cact(n;t)$ having maximum multiplicative degree-Kirchhoff index.

In particular, for $Cat(n;t)$, if $t=1;0$, $Cat(n;1)$ and $Cat(n;0)$ are the set of unicyclic graphs and trees, respectively. For $G\in Cat(n;1)$, the graphs having maximum and minimum multiplicative degree-Kirchhoff index are given in [13], that is

$$R^{\ast }(G^0(n,1))\le R^{\ast }(G)\le R^{\ast }(U_3^n).$$

where $U_3^n$ consists of a cycle of size 3 to which a path with $n-3$ vertices is attached. For $G\in Cat(n;0)$, it is easy to get the result

$$R^{\ast }(S_n)\le R^{\ast }(G)\le R^{\ast }(P_n).$$

4. Conclusions

In this paper, we give some transformations on the multiplicative degree-Kirchhoff index. As applications, the second-minimum multiplicative degree-Kirchhoff index on $Cat(n;t)$ and the corresponding extremal graph are determined. We guess $C_{n,t}$ is the graph of $Cat(n;t)$ with maximum $R^{\ast }(G)$ value. For solving the problem, our approach would need to be modified; it would be interesting to continue studying the extremal graphs.