Tribonacci and Tribonacci-Lucas Sedenions

Abstract

The sedenions form a 16-dimensional Cayley-Dickson algebra. In this paper, we introduce the Tribonacci and Tribonacci-Lucas sedenions. Furthermore, we present some properties of these sedenions and derive relationships between them.

1. Introduction

The Tribonacci sequence ${\left\{T_n\right\}}_{n\ge 0}$ and the Tribonacci-Lucas sequence ${\left\{K_n\right\}}_{n\ge 0}$ are defined by the third-order recurrence relations:

$$T_n=T_{n-1}+T_{n-2}+T_{n-3},T_0=0,T_1=1,T_2=1,$$

(1)

and:

$$K_n=K_{n-1}+K_{n-2}+K_{n-3},K_0=3,K_1=1,K_2=3$$

(2)

respectively. The Tribonacci concept was introduced by 14-year-old student M.Feinberg [1] in 1963. The basic properties of it were given in [2,3,4,5,6,7,8,9,10,11,12], and Binet’s formula for the nth number was given in [13].

The sequences ${\left\{T_n\right\}}_{n\ge 0}$ and ${\left\{K_n\right\}}_{n\ge 0}$ can be extended to negative subscripts by defining:

$$T_{-n}=-T_{-(n-1)}-T_{-(n-2)}+T_{-(n-3)}$$

and:

$$K_{-n}=-K_{-(n-1)}-K_{-(n-2)}+K_{-(n-3)}$$

for $n=1,2,3,\dots$, respectively. Therefore, recurrences (1) and (2) hold for all integers $n.$

By writing $T_{n-1}=T_{n-2}+T_{n-3}+T_{n-4},$ substituting for $T_{n-2}$ in (1), and eliminating $T_{n-2}$ and $T_{n-3}$ between this recurrence relation and the recurrence relation (1), a useful alternative recurrence relation is obtained for $n\ge 4:$

$$T_n=2T_{n-1}-T_{n-4},T_0=0,T_1=T_2=1,T_3=2.$$

(3)

Extension of the definition of $T_n$ to negative subscripts can be proven by writing the recurrence relation (3) as:

$$T_{-n}=2T_{-n+3}-T_{-n+4}.$$

Note that $T_{-n}=T_{n-1}^2-T_{n-2}{T}_n$ (see [4]).

Next, we present the first few values of the Tribonacci and Tribonacci-Lucas numbers with positive and negative subscripts:

$$\begin{array}{ccccccccccccc}n& 0& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \dots \\ T_n& 0& 1& 1& 2& 4& 7& 13& 24& 44& 81& 149& \dots \\ T_{-n}& 0& 0& 1& -1& 0& 2& -3& 1& 4& -8& 5& \dots \\ K_n& 3& 1& 3& 7& 11& 21& 39& 71& 131& 241& 443& \dots \\ K_{-n}& 3& -1& -1& 5& -5& -1& 11& -15& 3& 23& -41& \dots \end{array}$$

It is well known that for all integers $n,$ the usual Tribonacci and Tribonacci-Lucas numbers can be expressed using Binet’s formulas:

$$T_n=\frac{{\alpha }^{n+1}}{(\alpha -\beta )(\alpha -\gamma )}+\frac{{\beta }^{n+1}}{(\beta -\alpha )(\beta -\gamma )}+\frac{{\gamma }^{n+1}}{(\gamma -\alpha )(\gamma -\beta )}$$

(4)

and:

$$K_n={\alpha }^n+{\beta }^n+{\gamma }^n$$

respectively, where $\alpha ,\beta$, and $\gamma$ are the roots of the cubic equation $x^3-x^2-x-1=0.$ Moreover,

$$\begin{array}{ccc}\hfill \alpha & =& \frac{1+\sqrt[3]{19+3\sqrt{33}}+\sqrt[3]{19-3\sqrt{33}}}{3},\hfill \\ \hfill \beta & =& \frac{1+\omega \sqrt[3]{19+3\sqrt{33}}+{\omega }^2\sqrt[3]{19-3\sqrt{33}}}{3},\hfill \\ \hfill \gamma & =& \frac{1+{\omega }^2\sqrt[3]{19+3\sqrt{33}}+\omega \sqrt[3]{19-3\sqrt{33}}}{3}\hfill \end{array}$$

where:

$$\omega =\frac{-1+i\sqrt{3}}{2}=exp(2\pi i/3),$$

is a primitive cube root of unity. Note that we have the following identities:

$$\begin{array}{ccc}\hfill \alpha +\beta +\gamma & =& 1,\hfill \\ \hfill \alpha \beta +\alpha \gamma +\beta \gamma & =& -1,\hfill \\ \hfill \alpha \beta \gamma & =& 1.\hfill \end{array}$$

The generating functions for the Tribonacci sequence ${\left\{T_n\right\}}_{n\ge 0}$ and Tribonacci-Lucas sequence ${\left\{K_n\right\}}_{n\ge 0}$ are:

$$\sum _{n=0}^{\infty }{T}_n{x}^n=\frac{x}{1-x-x^2-x^3}\mathrm{and}\sum _{n=0}^{\infty }{K}_n{x}^n=\frac{3-2x-x^2}{1-x-x^2-x^3}.$$

We now present some properties of the Tribonacci and Tribonacci-Lucas numbers.

• We have [3]:

  $$N^n=\left(\begin{array}{ccc}{T}_{n+1}& T_n& T_{n-1}\\ T_n+T_{n-1}& T_{n-1}+T_{n-2}& T_{n-2}+T_{n-3}\\ T_n& T_{n-1}& T_{n-2}\end{array}\right)$$

  and:

  $$\begin{array}{ccc}\hfill tr(N^n)& =& K_n=T_n+2T_{n-1}+3T_{n-2}=3T_{n+1}-2T_n-T_{n-1},\hfill \\ \hfill C_n& =& -T_n^2+2T_{n-1}^2+3T_{n-2}^2-2T_n{T}_{n-1}+2T_n{T}_{n-2}+4T_{n-1}{T}_{n-2}\hfill \end{array}$$

  where:

  $$N=\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 1& 0& 0\end{array}\right),$$

  $tr(.)$ is the trace operator and $C_n$ is defined by:

  $$C_n={\alpha }^n{\beta }^n+{\alpha }^n{\gamma }^n+{\beta }^n{\gamma }^n$$

  which is the sum of the determinants of the principal minors of order two of $N^n.$
• We have [4]:

  $$\begin{array}{ccc}\hfill T_{n-1}^3-1& =& 2T_{n-2}{T}_{n-1}{T}_n+T_{n-3}{T}_{n-1}{T}_{n+1}-T_{n-2}^2{T}_{n+1}-T_{n-3}{T}_n^2\hfill \\ & =& T_{n-2}(2T_{n-1}{T}_n-T_{n+1})+T_{n-3}(T_n^2-T_{n-1}{T}_{n+1}).\hfill \end{array}$$
• Tribonacci numbers satisfy the following equality [12]:

  $$T_{k+n}=T_k{K}_n-T_{k-n}{C}_n+T_{k-2n}.$$

In this paper, we define Tribonacci and Tribonacci-Lucas sedenions in the next section and give some properties of them. Before giving their definition, we present some information on Cayley-Dickson algebras.

The algebras $\mathbb{C}$ (complex numbers), $\mathbb{H}$ (quaternions), and $\mathbb{O}$ (octonions) are real division algebras obtained from the real numbers $\mathbb{R}$ by a doubling procedure called the Cayley-Dickson process (construction). By doubling $\mathbb{R}$ (dim $2^0=1$), we obtain the complex numbers $\mathbb{C}$ (dim $2^1=2$); then, $\mathbb{C}$ yields the quaternions $\mathbb{H}$ (dim $2^2=4$); and $\mathbb{H}$ produces octonions $\mathbb{O}$ (dim $2^3=8$). The next doubling process applied to $\mathbb{O}$ then produces an algebra $\mathbb{S}$ (dim $2^4=16$) called the sedenions. This doubling process can be extended beyond the sedenions to form what are known as the $2^n$-ions (see for example [14,15,16]).

Next, we explain this doubling process.

The Cayley-Dickson algebras are a sequence $A_0,A_1,\dots$ of non-associative $\mathbb{R}$-algebras with involution. The term “conjugation” can be used to refer to the involution because it generalizes the usual conjugation on the complex numbers. For a full explanation of the basic properties of Cayley-Dickson algebras, see [14]. Cayley-Dickson algebras are defined inductively. We begin by defining $A_0$ to be $\mathbb{R}.$ Given $A_{n-1},$ the algebra $A_n$ is defined additively to be $A_{n-1}\times A_{n-1}.$ Conjugation in $A_n$ is defined by:

$$\overline{(a,b)}=(\overline{a},-b)$$

multiplication is defined by:

$$(a,b)(c,d)=(ac-\overline{d}b,da+b\overline{c})$$

and addition is defined by componentwise as:

$$(a,b)+(c,d)=(a+c,b+d).$$

Note that $A_n$ has dimension $2^n$ as an $\mathbb{R}$-vector space. If we set, as usual, $∥x∥=\sqrt{\mathrm{Re}(x\overline{x})}$ for $x\in A_n$, then $x\overline{x}=\overline{x}x={∥x∥}^2.$

Now, suppose that $B_{16}=\{e_i\in \mathbb{S}:i=0,1,2,\dots ,15\}$ is the basis for $\mathbb{S}$, where $e_0$ is the identity (or unit) and $e_1,e_2,\dots ,e_{15}$ are called imaginaries. Then, a sedenion $S\in \mathbb{S}$ can be written as:

$$S=\sum _{i=0}^{15}{a}_i{e}_i=a_0+\sum _{i=1}^{15}{a}_i{e}_i$$

where $a_0,a_1,\dots ,a_{15}$ are all real numbers. Here, $a_0$ is called the real part of S, and ${\sum }_{i=1}^{15}{a}_i{e}_i$ is called its imaginary part.

The addition of sedenions is defined as componentwise, and multiplication is defined as follows: if $S_1,S_2\in \mathbb{S}$, then we have:

$$S_1{S}_2=\left(\sum _{i=0}^{15}{a}_i{e}_i\right)\left(\sum _{i=0}^{15}{b}_i{e}_i\right)=\sum _{i,j=0}^{15}{a}_i{b}_j(e_i{e}_j).$$

(5)

By setting $i\equiv e_i$ where $i=0,1,2,\dots ,15,$ the multiplication rule of the base elements $e_i\in B_{16}$ can be summarized as in the following Figure 1 (see [17,18]).

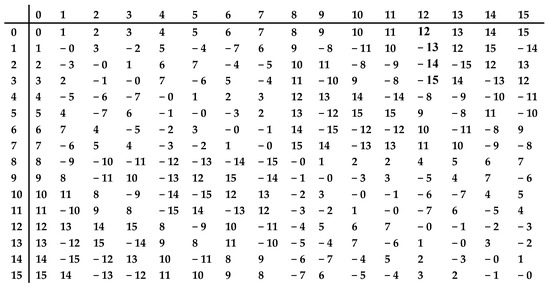
Figure 1. Multiplication table for sedenions’ imaginary units.

From the above table, we can see that:

$e_0{e}_i=e_i{e}_0=e_i;$$e_i{e}_i=-e_0$ for $i\ne 0;$ $e_i{e}_j=-e_j{e}_i$ for $i\ne j$ and $i,j\ne 0.$

The operations requiring the multiplication in (5) are quite a few. The computation of a sedenion multiplication (product) using the naive method requires 256 multiplications and 240 additions, while an algorithm, which was given in [19], can compute the same result in only 122 multiplications (or multipliers, in the hardware implementation case) and 298 additions (for more details, see [19]).

Using direct multiplication, the numbers of the operations requiring for the multiplication of two $2^n$-ions are presented in the following Table 1.

Table 1. Direct multiplication.

$2^{\mathit{n}}\text{-}\mathbf{Ions}$	Computational Method	Multiplications	Additions
Quaternions	Based on expression (5)	16	12
Octonions	Based on expression (5)	64	56
Sedenions	Based on expression (5)	256	240

Efficient algorithms for the multiplication of quaternions, octonions, and sedenions with a reduced number of real multiplications already exist, and the results of synthesizing an efficient algorithm of computing the two $2^n$-ions product are given in the following Table 2.

Table 2. Efficient algorithms for the multiplication.

$2^{\mathit{n}}\text{-}\mathbf{Ions}$	Computational Method	Multiplications	Additions
Quaternions	Algorithm in [20]	8	-
Octonions	Algorithm in [21]	32	88
Sedenions	Algorithm in [19]	122	298

The problem with the Cayley-Dickson process is that each step of the doubling process results in a progressive loss of structure. $\mathbb{R}$ is an ordered field, and it has all the nice properties we are so familiar with in dealing with numbers like: the associative property, commutative property, division property, self-conjugate property, etc. When we double $\mathbb{R}$ to have $\mathbb{C}$, $\mathbb{C}$ loses the self-conjugate property (and is no longer an ordered field); next, $\mathbb{H}$ loses the commutative property, and $\mathbb{O}$ loses the associative property. When we double $\mathbb{O}$ to obtain $\mathbb{S}$; $\mathbb{S}$ loses the division property. It means that $\mathbb{S}$ is non-commutative, non-associative, and has a multiplicative identity element $e_0$ and multiplicative inverses, but it is not a division algebra because it has zero divisors; this means that two non-zero sedenions can be multiplied to obtain zero: an example is $(e_3+e_{10})(e_6-e_{15})=0$, and the other example is $(e_2-e_{14})(e_3+e_{15})=0$ (see [18]).

The algebras beyond the complex numbers go by the generic name hypercomplex number. All hypercomplex number systems after sedenions that are based on the Cayley-Dickson construction contain zero divisors.

Note that there is another type of sedenions, which is called conic sedenions or sedenions of Charles Muses, as they are also known; see [22,23,24] for more information. The term sedenion is also used for other 16-dimensional algebraic structures, such as a tensor product of two copies of the biquaternions, or the algebra of four by four matrices over the reals.

In the past, non-associative algebras and related structures with zero divisors have not been given much attention because they did not appear to have any useful applications in most mathematical subjects. Recently, theoretical physicists have centered much attention on the Cayley-Dickson algebras $\mathbb{O}$ (octonions) and $\mathbb{S}$ (sedenions) because of their increasing usefulness in formulating many of the new theories of elementary particles. In particular, the octonions $\mathbb{O}$ (which is the only non-associative normed division algebra over the reals; see for example [25,26]) has been found to be involved in many unexpected areas (such as topology, quantum theory, Clifford algebras, etc.), and sedenions appear in many areas of science like linear gravity and electromagnetic theory.

Briefly, $\mathbb{S}$, the algebra of sedenions, has the following properties:

• $\mathbb{S}$ is a 16-dimensional non-associative and non-commutative (Cayley-Dickson) algebra over the reals,
• $\mathbb{S}$ is not a composition algebra or division algebra because of its zero divisors,
• $\mathbb{S}$ is a non-alternative algebra, i.e., if $S_1$ and $S_2$ are sedenions, the rules $S_1^2{S}_2=S_1(S_1{S}_2)$ and $S_1{S}_2^2=(S_1{S}_2)S_2$ do not always hold,
• $\mathbb{S}$ is a power-associative algebra, i.e., if S is a sedenion, then $S^n{S}^m=S^{n+m}.$

2. The Tribonacci and Tribonacci-Lucas Sedenions, Their Generating Functions, and Binet’s Formulas

In this section, we define Tribonacci and Tribonacci-Lucas sedenions and give generating functions and Binet formulas for them. First, we give some information about quaternion sequences, octonion sequences, and sedenion sequences from the literature.

Horadam [27] introduced nth Fibonacci and nth Lucas quaternions as:

$$Q_n=F_n+F_{n+1}{e}_1+F_{n+2}{e}_2+F_{n+3}{e}_3=\sum _{s=0}^3{F}_{n+s}{e}_s$$

and:

$$R_n=L_n+L_{n+1}{e}_1+L_{n+2}{e}_2+L_{n+3}{e}_3=\sum _{s=0}^3{L}_{n+s}{e}_s$$

respectively, where $F_n$ and $L_n$ are the nth Fibonacci and Lucas numbers, respectively. He also defined the generalized Fibonacci quaternion as:

$$P_n=H_n+H_{n+1}{e}_1+H_{n+2}{e}_2+H_{n+3}{e}_3=\sum _{s=0}^3{H}_{n+s}{e}_s$$

where $H_n$ is the nth generalized Fibonacci number (which is now called the Horadam number) by the recursive relation $H_1=p,$ $H_2=p+q,$ $H_n=H_{n-1}+H_{n-2}$ (p and q are arbitrary integers). Many other generalizations of Fibonacci quaternions have been given; see for example Halici and Karataş [28] and Polatlı [29].

Cerda-Morales [30] defined and studied the generalized Tribonacci quaternion sequence that includes the previously-introduced Tribonacci, Padovan, Narayana, and third-order Jacobsthal quaternion sequences. She defined the generalized Tribonacci quaternion as:

$$Q_{v,n}=V_n+V_{n+1}{e}_1+V_{n+2}{e}_2+V_{n+3}{e}_3=\sum _{s=0}^3{V}_{n+s}{e}_s$$

where $V_n$ is the nth generalized Tribonacci number defined by the third-order recurrence relations:

$$V_n=r{V}_{n-1}+s{V}_{n-2}+t{V}_{n-3}.$$

Here, $V_0=a,V_1=b,V_2=c$ are arbitrary integers and $r,s,t$ are real numbers.

Various families of octonion number sequences (such as Fibonacci octonion, Pell octonion, Jacobsthal octonion, and third-order Jacobsthal octonion) have been defined and studied by a number of authors in many different ways. For example, Keçilioglu and Akkuş [31] introduced the Fibonacci and Lucas octonions as:

$$Q_n=\sum _{s=0}^7{F}_{n+s}{e}_s$$

and:

$$R_n=\sum _{s=0}^7{L}_{n+s}{e}_s$$

respectively, where $F_n$ and $L_n$ are the nth Fibonacci and Lucas numbers, respectively. In ref. [32], Çimen and İpek introduced Jacobsthal octonions and Jacobsthal-Lucas octonions. In ref. [33], Cerda-Morales introduced third-order Jacobsthal octonions, and also in ref. [34], she defined and studied Tribonacci-type octonions.

A number of authors have defined and studied sedenion number sequences (such as second-order sedenions: Fibonacci sedenion, k-Pell and k-Pell-Lucas sedenions, Jacobsthal and Jacobsthal-Lucas sedenions). For example, Bilgici, Tokeşer, and Ünal [17] introduced the Fibonacci and Lucas sedenions as:

$${\widehat{F}}_n=\sum _{s=0}^{15}{F}_{n+s}{e}_s$$

and:

$${\widehat{L}}_n=\sum _{s=0}^{15}{L}_{n+s}{e}_s$$

respectively, where $F_n$ and $L_n$ are the nth Fibonacci and Lucas numbers, respectively. In ref. [35], Catarino introduced k-Pell and k-Pell-Lucas sedenions. In ref. [36], Çimen and İpek introduced Jacobsthal and Jacobsthal-Lucas sedenions.

Gül [37] introduced the k-Fibonacci and k-Lucas trigintaduonions as:

$$T{F}_{k,n}=\sum _{s=0}^{31}{F}_{k,n+s}{e}_s$$

and:

$$T{L}_{k,n}=\sum _{s=0}^{31}{L}_{k,n+s}{e}_s$$

respectively, where $F_{k,n}$ and $L_{k,n}$ are the nth k-Fibonacci and k-Lucas numbers, respectively.

We now define Tribonacci and Tribonacci-Lucas sedenions over the sedenion algebra $\mathbb{S}$. The nth Tribonacci sedenion is:

$${\widehat{T}}_n=\sum _{s=0}^{15}{T}_{n+s}{e}_s=T_n+\sum _{s=1}^{15}{T}_{n+s}{e}_s$$

(6)

and the nth Tribonacci-Lucas sedenion is:

$${\widehat{K}}_n=\sum _{s=0}^{15}{K}_{n+s}{e}_s=K_n+\sum _{s=1}^{15}{K}_{n+s}{e}_s.$$

(7)

It can be easily shown that:

$${\widehat{T}}_n={\widehat{T}}_{n-1}+{\widehat{T}}_{n-2}+{\widehat{T}}_{n-3}$$

(8)

and:

$${\widehat{K}}_n={\widehat{K}}_{n-1}+{\widehat{K}}_{n-2}+{\widehat{K}}_{n-3}.$$

(9)

Note that:

$${\widehat{T}}_{-n}=-{\widehat{T}}_{-(n-1)}-{\widehat{T}}_{-(n-2)}+{\widehat{T}}_{-(n-3)}$$

and:

$${\widehat{K}}_{-n}=-{\widehat{K}}_{-(n-1)}-{\widehat{K}}_{-(n-2)}+{\widehat{K}}_{-(n-3)}.$$

The conjugate of ${\widehat{T}}_n$ and ${\widehat{K}}_n$ are defined by:

$$\overline{{\widehat{T}}_n}=T_n-\sum _{s=1}^{15}{T}_{n+s}{e}_s=T_n-T_{n+1}{e}_1-T_{n+2}{e}_2-\dots -T_{n+15}{e}_{15}$$

and:

$$\overline{{\widehat{K}}_n}=K_n-\sum _{s=1}^{15}{K}_{n+s}{e}_s=K_n-K_{n+1}{e}_1-K_{n+2}{e}_2-\dots -K_{n+15}{e}_{15}$$

respectively. The norms of nth Tribonacci and Tribonacci-Lucas sedenions are:

$${∥{\widehat{T}}_n∥}^2=N^2({\widehat{T}}_n)={\widehat{T}}_n\overline{{\widehat{T}}_n}=\overline{{\widehat{T}}_n}{\widehat{T}}_n=T_n^2+T_{n+1}^2+\dots +T_{n+15}^2$$

and:

$${∥{\widehat{K}}_n∥}^2=N^2({\widehat{K}}_n)={\widehat{K}}_n\overline{{\widehat{K}}_n}=\overline{{\widehat{K}}_n}{\widehat{K}}_n=K_n^2+K_{n+1}^2+\dots +K_{n+15}^2$$

respectively.

To calculate the norms of ${\widehat{T}}_n$ and ${\widehat{K}}_n,$ we need the following Lemma.

Lemma 1

([38]). The following formulas are valid:

$$\begin{array}{ccc}\hfill \sum _{i=1}^n{T}_i^2& =& \frac{1+4T_n{T}_{n+1}-{(T_{n+1}-T_{n-1})}^2}{4},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \sum _{i=1}^n{K}_i^2& =& \frac{-K_{n+1}^2-K_{n-1}^2+K_{2n+3}+K_{2n-2}}{2}-2.\hfill \end{array}$$

(11)

We can now calculate the norms of ${\widehat{T}}_n$ and ${\widehat{K}}_n.$

Theorem 1.

The norms of nth Tribonacci and Tribonacci-Lucas sedenions are given as:

$$\begin{array}{ccc}\hfill {∥{\widehat{T}}_n∥}^2& =& \frac{4(T_{n+15}{T}_{n+16}-T_{n-1}{T}_n)+{(T_n-T_{n-2})}^2-{(T_{n+16}-T_{n+14})}^2}{4},\hfill \\ \hfill {∥{\widehat{K}}_n∥}^2& =& \frac{-K_{n+16}^2-K_{n+14}^2+K_n^2+K_{n-2}^2+K_{2n+33}+K_{2n+28}-K_{2n+1}-K_{2n-4}}{2}.\hfill \end{array}$$

Proof. 

We obtain the results from the following calculations:

$$\begin{array}{ccc}\hfill {∥{\widehat{T}}_n∥}^2& =& \sum _{i=n}^{n+15}{T}_i^2=\sum _{i=1}^{n+15}{T}_i^2-\sum _{i=1}^{n-1}{T}_i^2\hfill \\ & =& \frac{1+4T_{n+15}{T}_{n+16}-{(T_{n+16}-T_{n+14})}^2}{4}-\frac{1+4T_{n-1}{T}_n-{(T_n-T_{n-2})}^2}{4}\hfill \\ & =& \frac{4(T_{n+15}{T}_{n+16}-T_{n-1}{T}_n)+{(T_n-T_{n-2})}^2-{(T_{n+16}-T_{n+14})}^2}{4}\hfill \end{array}$$

and:

$$\begin{array}{ccc}\hfill {∥{\widehat{K}}_n∥}^2& =& \sum _{i=n}^{n+15}{K}_i^2=\sum _{i=1}^{n+15}{K}_i^2-\sum _{i=1}^{n-1}{K}_i^2\hfill \\ & =& (\frac{-K_{n+16}^2-K_{n+14}^2+K_{2n+33}+K_{2n+28}}{2}-2)\hfill \\ & & -(\frac{-K_n^2-K_{n-2}^2+K_{2n+1}+K_{2n-4}}{2}-2)\hfill \\ & =& \frac{-K_{n+16}^2-K_{n+14}^2-K_{2n+1}-K_{2n-4}+K_{2n+33}+K_n^2+K_{n-2}^2+K_{2n+28}}{2}.\hfill \end{array}$$

 □

Now, we will state Binet’s formula for the Tribonacci and Tribonacci-Lucas sedenions, and in the rest of the paper, we fixed the following notations.

$$\begin{array}{ccc}\hfill \widehat{\alpha }& =& \sum _{s=0}^{15}{\alpha }^s{e}_s,\hfill \\ \hfill \widehat{\beta }& =& \sum _{s=0}^{15}{\beta }^s{e}_s,\hfill \\ \hfill \widehat{\gamma }& =& \sum _{s=0}^{15}{\gamma }^s{e}_s.\hfill \end{array}$$

Theorem 2.

For any integer $n,$ the nth Tribonacci sedenion is:

$${\widehat{T}}_n=\frac{\widehat{\alpha }{\alpha }^{n+1}}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }{\beta }^{n+1}}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^{n+1}}{(\gamma -\alpha )(\gamma -\beta )}$$

(12)

and the nth Tribonacci-Lucas sedenion is:

$${\widehat{K}}_n=\widehat{\alpha }{\alpha }^n+\widehat{\beta }{\beta }^n+\widehat{\gamma }{\gamma }^n.$$

(13)

Proof. 

Repeated use of (4) in (6) enables us to write for $\widehat{\alpha }={\sum }_{s=0}^{15}{\alpha }^s{e}_s,$ $\widehat{\beta }={\sum }_{s=0}^{15}{\beta }^s{e}_s$ and $\widehat{\gamma }={\sum }_{s=0}^{15}{\gamma }^s{e}_s:$

$$\begin{array}{ccc}\hfill {\widehat{T}}_n& =& \sum _{s=0}^{15}{T}_{n+s}{e}_s=\sum _{s=0}^{15}\left(\frac{{\alpha }^{n+1+s}{e}_s}{(\alpha -\beta )(\alpha -\gamma )}+\frac{{\beta }^{n+1+s}{e}_s}{(\beta -\alpha )(\beta -\gamma )}+\frac{{\gamma }^{n+1+s}{e}_s}{(\gamma -\alpha )(\gamma -\beta )}\right)\hfill \\ & =& \frac{\widehat{\alpha }{\alpha }^{n+1}}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }{\beta }^{n+1}}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^{n+1}}{(\gamma -\alpha )(\gamma -\beta )}.\hfill \end{array}$$

Similarly, we can obtain (13). □

The next theorem gives us an alternative proof of Binet’s formula for the Tribonacci and Tribonacci-Lucas sedenions. For this, we need the quadratic approximation of ${\left\{T_n\right\}}_{n\ge 0}$ and ${\left\{K_n\right\}}_{n\ge 0}$:

Lemma 2.

For all integers $n,$ we have:

(a) 

$$\begin{array}{ccc}\hfill \alpha {\alpha }^{n+2}& =& T_{n+2}{\alpha }^2+(T_{n+1}+T_n)\alpha +T_{n+1},\hfill \\ \hfill \beta {\beta }^{n+2}& =& T_{n+2}{\beta }^2+(T_{n+1}+T_n)\beta +T_{n+1},\hfill \\ \hfill \gamma {\gamma }^{n+2}& =& T_{n+2}{\gamma }^2+(T_{n+1}+T_n)\gamma +T_{n+1}.\hfill \end{array}$$

(b) 

$$\begin{array}{ccc}\hfill P{\alpha }^{n+2}& =& K_{n+2}{\alpha }^2+(K_{n+1}+K_n)\alpha +K_{n+1},\hfill \\ \hfill Q{\beta }^{n+2}& =& K_{n+2}{\beta }^2+(K_{n+1}+K_n)\beta +K_{n+1},\hfill \\ \hfill R{\gamma }^{n+2}& =& K_{n+2}{\gamma }^2+(K_{n+1}+K_n)\gamma +K_{n+1},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill P& =& 3-(\beta +\gamma )+3\beta \gamma ,\hfill \\ \hfill Q& =& 3-(\alpha +\gamma )+3\alpha \gamma ,\hfill \\ \hfill R& =& 3-(\alpha +\beta \gamma )+3\alpha \beta .\hfill \end{array}$$

Proof. 

See [39] or [34].

Alternative proof of Theorem 2:

Note that:

$$\begin{array}{cc}& {\alpha }^2{\widehat{T}}_{n+2}+\alpha ({\widehat{T}}_{n+1}+{\widehat{T}}_n)+{\widehat{T}}_{n+1}\hfill \\ =& {\alpha }^2(T_{n+2}+T_{n+3}{e}_1+\dots +T_{n+17}{e}_{15})\hfill \\ & +\alpha ((T_{n+1}+T_n)+(T_{n+2}+T_{n+1})e_1+\dots +(T_{n+16}+T_{n+15})e_{15})\hfill \\ & +(T_{n+1}+T_{n+2}{e}_1+\dots +T_{n+16}{e}_{15})\hfill \\ =& {\alpha }^2{T}_{n+2}+\alpha (T_{n+1}+T_n)+T_{n+1}+({\alpha }^2{T}_{n+3}+(T_{n+2}+T_{n+1})+T_{n+2})e_1\hfill \\ & +({\alpha }^2{T}_{n+4}+(T_{n+3}+T_{n+2})+T_{n+3})e_2\hfill \\ & ⋮\hfill \\ & +({\alpha }^2{T}_{n+17}+(T_{n+16}+T_{n+15})+T_{n+16})e_{15}.\hfill \end{array}$$

From the identity ${\alpha }^{n+3}=T_{n+2}{\alpha }^2+(T_{n+1}+T_n)\alpha +T_{n+1}$ for the nth Tribonacci number $T_n,$ we have:

$${\alpha }^2{\widehat{T}}_{n+2}+\alpha ({\widehat{T}}_{n+1}+{\widehat{T}}_n)+{\widehat{T}}_{n+1}=\widehat{\alpha }{\alpha }^{n+3}.$$

(14)

Similarly, we obtain:

$${\beta }^2{\widehat{T}}_{n+2}+\beta ({\widehat{T}}_{n+1}+{\widehat{T}}_n)+{\widehat{T}}_{n+1}=\widehat{\beta }{\beta }^{n+3}$$

(15)

and:

$${\gamma }^2{\widehat{T}}_{n+2}+\gamma ({\widehat{T}}_{n+1}+{\widehat{T}}_n)+{\widehat{T}}_{n+1}=\widehat{\gamma }{\gamma }^{n+3}.$$

(16)

Subtracting (15) from (14), we have:

$$(\alpha +\beta ){\widehat{T}}_{n+2}+({\widehat{T}}_{n+1}+{\widehat{T}}_n)=\frac{\widehat{\alpha }{\alpha }^{n+3}-\widehat{\beta }{\beta }^{n+3}}{\alpha -\beta }.$$

(17)

Similarly, subtracting (16) from (14), we obtain:

$$(\alpha +\gamma ){\widehat{T}}_{n+2}+({\widehat{T}}_{n+1}+{\widehat{T}}_n)=\frac{\widehat{\alpha }{\alpha }^{n+3}-\widehat{\gamma }{\gamma }^{n+3}}{\alpha -\gamma }.$$

(18)

Finally, subtracting (18) from (17), we get:

$$\begin{array}{ccc}\hfill {\widehat{T}}_{n+2}& =& \frac{1}{\alpha -\beta }\left(\frac{\widehat{\alpha }{\alpha }^{n+3}-\widehat{\beta }{\beta }^{n+3}}{\alpha -\beta }-\frac{\widehat{\alpha }{\alpha }^{n+3}-\widehat{\gamma }{\gamma }^{n+3}}{\alpha -\gamma }\right)\hfill \\ & =& \frac{\widehat{\alpha }{\alpha }^{n+3}}{(\alpha -\beta )(\alpha -\gamma )}-\frac{\widehat{\beta }{\beta }^{n+3}}{(\alpha -\beta )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^{n+3}}{(\gamma -\alpha )(\gamma -\beta )}\hfill \\ & =& \frac{\widehat{\alpha }{\alpha }^{n+3}}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }{\beta }^{n+3}}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^{n+3}}{(\gamma -\alpha )(\gamma -\beta )}.\hfill \end{array}$$

Therefore, this proves (12). Similarly, we obtain (13). □

Next, we present generating functions.

Theorem 3.

The generating functions for the Tribonacci and Tribonacci-Lucas sedenions are:

$$g(x)=\sum _{n=0}^{\infty }{\widehat{T}}_n{x}^n=\frac{{\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+{\widehat{T}}_{-1}{x}^2}{1-x-x^2-x^3}$$

(19)

and:

$$g(x)=\sum _{n=0}^{\infty }{\widehat{K}}_n{x}^n=\frac{{\widehat{K}}_0+({\widehat{K}}_1-{\widehat{K}}_0)x+{\widehat{K}}_{-1}{x}^2}{1-x-x^2-x^3}$$

(20)

respectively.

Proof. 

Define $g(x)={\sum }_{n=0}^{\infty }{\widehat{T}}_n{x}^n.$ Note that:

$$\begin{array}{ccccccccc}g(x)& =& {\widehat{T}}_0+& {\widehat{T}}_{1}x+& {\widehat{T}}_2{x}^2+& {\widehat{T}}_3{x}^3+& {\widehat{T}}_4{x}^4+& {\widehat{T}}_5{x}^5+\dots +& {\widehat{T}}_n{x}^n+\dots \\ xg(x)& =& & {\widehat{T}}_{0}x+& {\widehat{T}}_1{x}^2+& {\widehat{T}}_2{x}^3+& {\widehat{T}}_3{x}^4+& {\widehat{T}}_4{x}^5+\dots +& {\widehat{T}}_{n-1}{x}^n+\dots \\ x^{2}g(x)& =& & & {\widehat{T}}_0{x}^2+& {\widehat{T}}_1{x}^3+& {\widehat{T}}_2{x}^4+& {\widehat{T}}_3{x}^5+\dots +& {\widehat{T}}_{n-2}{x}^n+\dots \\ x^{3}g(x)& =& & & & {\widehat{T}}_0{x}^3+& {\widehat{T}}_1{x}^4+& {\widehat{T}}_2{x}^5+\dots +& {\widehat{T}}_{n-3}{x}^n+\dots \end{array}$$

Using the above table and the recurrence relation ${\widehat{T}}_n={\widehat{T}}_{n-1}+{\widehat{T}}_{n-2}+{\widehat{T}}_{n-3}$, we have:

$$\begin{array}{cc}& g(x)-xg(x)-x^{2}g(x)-x^{3}g(x)\hfill \\ =& {\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+({\widehat{T}}_2-{\widehat{T}}_1-{\widehat{T}}_0)x^2+({\widehat{T}}_3-{\widehat{T}}_2-{\widehat{T}}_1-{\widehat{T}}_0)x^3+\hfill \\ & ({\widehat{T}}_4-{\widehat{T}}_3-{\widehat{T}}_2-{\widehat{T}}_1)x^4+\dots +({\widehat{T}}_n-{\widehat{T}}_{n-1}-{\widehat{T}}_{n-2}-{\widehat{T}}_{n-3}+)x^n+\dots \hfill \\ =& {\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+({\widehat{T}}_2-{\widehat{T}}_1-{\widehat{T}}_0)x^2.\hfill \end{array}$$

It follows that:

$$g(x)=\frac{{\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+({\widehat{T}}_2-{\widehat{T}}_1-{\widehat{T}}_0)x^2}{1-x-x^2-x^3}.$$

Since ${\widehat{T}}_2-{\widehat{T}}_1-{\widehat{T}}_0={\widehat{T}}_{-1},$ the generating function for the Tribonacci sedenion is:

$$g(x)=\frac{{\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+{\widehat{T}}_{-1}{x}^2}{1-x-x^2-x^3}.$$

Similarly, we can obtain (20). □

In the following theorem, we present another forms of Binet’s formulas for the Tribonacci and Tribonacci-Lucas sedenions using generating functions.

Theorem 4.

For any integer $n,$ the nth Tribonacci sedenion is:

$$\begin{array}{ccc}\hfill {\widehat{T}}_n& =& \frac{(({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1}){\alpha }^n}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}+\frac{(({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1}){\beta }^n}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}\hfill \\ & & +\frac{(({\gamma }^2-\gamma ){\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}){\gamma }^n}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}\hfill \end{array}$$

and the nth Tribonacci-Lucas sedenion is:

$$\begin{array}{ccc}\hfill {\widehat{K}}_n& =& \frac{(({\alpha }^2-\alpha ){\widehat{K}}_0+\alpha {\widehat{K}}_1+{\widehat{K}}_{-1}){\alpha }^n}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}+\frac{(({\beta }^2-\beta ){\widehat{K}}_0+\beta {\widehat{K}}_1+{\widehat{K}}_{-1}){\beta }^n}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}\hfill \\ & & +\frac{(({\gamma }^2-\gamma ){\widehat{K}}_0+\gamma {\widehat{K}}_1+{\widehat{K}}_{-1}){\gamma }^n}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}.\hfill \end{array}$$

Proof. 

We can use generating functions. Since the roots of the equation $1-x-x^2-x^3=0$ are $\alpha \beta ,\beta \gamma ,\alpha \gamma$ and:

$$1-x-x^2-x^3=(1-\alpha x)(1-\beta x)(1-\gamma x)$$

we can write the generating function of ${\widehat{T}}_n$ as:

$$\begin{array}{cc}& g(x)=\frac{{\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+{\widehat{T}}_{-1}{x}^2}{1-x-x^2-x^3}=\frac{{\widehat{T}}_0+({\widehat{T}}_1-{\widehat{T}}_0)x+{\widehat{T}}_{-1}{x}^2}{(1-\alpha x)(1-\beta x)(1-\gamma x)}\hfill \\ =& \frac{A}{(1-\alpha x)}+\frac{B}{(1-\beta x)}+\frac{C}{(1-\gamma x)}\hfill \\ =& \frac{A(1-\beta x)(1-\gamma x)+B(1-\alpha x)(1-\gamma x)+C(1-\alpha x)(1-\beta x)}{(1-\alpha x)(1-\beta x)(1-\gamma x)}\hfill \\ =& \frac{(A+B+C)+(-A\beta -A\gamma -B\alpha -B\gamma -C\alpha -C\beta )x+(A\beta \gamma +B\alpha \gamma +C\alpha \beta )x^2}{(1-\alpha x)(1-\beta x)(1-\gamma x)}.\hfill \end{array}$$

We need to find $A,B$, and C, so the following system of equations should be solved:

$$\begin{array}{ccc}\hfill A+B+C& =& {\widehat{T}}_0\hfill \\ \hfill -A\beta -A\gamma -B\alpha -B\gamma -C\alpha -C\beta & =& {\widehat{T}}_1-{\widehat{T}}_0\hfill \\ \hfill A\beta \gamma +B\alpha \gamma +C\alpha \beta & =& {\widehat{T}}_{-1}\hfill \end{array}$$

We find that:

$$\begin{array}{ccc}\hfill A& =& \frac{-\alpha {\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1}+{\alpha }^2{\widehat{T}}_0}{{\alpha }^2-\alpha \beta -\alpha \gamma +\beta \gamma }=\frac{(({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1})}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)},\hfill \\ \hfill B& =& \frac{-\beta {\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1}+{\beta }^2{\widehat{T}}_0}{{\beta }^2-\alpha \beta +\alpha \gamma -\beta \gamma }=\frac{(({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1})}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)},\hfill \\ \hfill C& =& \frac{-\gamma {\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}+{\gamma }^2{\widehat{T}}_0}{{\gamma }^2+\alpha \beta -\alpha \gamma -\beta \gamma }=\frac{(({\gamma }^2-\gamma ){\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1})}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}.\hfill \end{array}$$

and:

$$\begin{array}{ccc}\hfill g(x)& =& \frac{(({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1})}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}\sum _{n=0}^{\infty }{\alpha }^n{x}^n+\frac{(({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1})}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}\sum _{n=0}^{\infty }{\beta }^n{x}^n\hfill \\ & & +\frac{(-\gamma {\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}+{\gamma }^2{\widehat{T}}_0)}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}\sum _{n=0}^{\infty }{\gamma }^n{x}^n\hfill \\ & =& \sum _{n=0}^{\infty }\left(\begin{array}{c}\frac{(({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1}){\alpha }^n}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}+\frac{(({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1}){\beta }^n}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}\\ +\frac{(({\gamma }^2-\gamma ){\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}){\gamma }^n}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}\end{array}\right)x^n.\hfill \end{array}$$

Thus, Binet’s formula of the Tribonacci sedenion is:

$$\begin{array}{ccc}\hfill {\widehat{T}}_n& =& \frac{(({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1}){\alpha }^n}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}+\frac{(({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1}){\beta }^n}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}\hfill \\ & & +\frac{(({\gamma }^2-\gamma ){\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}){\gamma }^n}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}.\hfill \end{array}$$

Similarly, we can obtain Binet’s formula of the Tribonacci-Lucas sedenion. □

If we compare Theorem 2 and Theorem 4 and use the definition of ${\widehat{T}}_n,$ ${\widehat{K}}_n,$ we have the following remark showing relations between ${\widehat{T}}_{-1},{\widehat{T}}_0,{\widehat{T}}_1;{\widehat{K}}_{-1},{\widehat{K}}_0,{\widehat{K}}_1$ and $\widehat{\alpha },\widehat{\beta },\widehat{\gamma }.$ We obtain (b) and (d) after solving the system of equations in (a) and (c), respectively.

Remark 1.

We have the following identities:

(a) 

$$\begin{array}{ccc}\hfill \frac{({\alpha }^2-\alpha ){\widehat{T}}_0+\alpha {\widehat{T}}_1+{\widehat{T}}_{-1}}{\alpha }& =& \widehat{\alpha }\hfill \\ \hfill \frac{({\beta }^2-\beta ){\widehat{T}}_0+\beta {\widehat{T}}_1+{\widehat{T}}_{-1}}{\beta }& =& \widehat{\beta }\hfill \\ \hfill \frac{({\gamma }^2-\gamma ){\widehat{T}}_0+\gamma {\widehat{T}}_1+{\widehat{T}}_{-1}}{\gamma }& =& \widehat{\gamma }\hfill \end{array}$$

(b) 

$$\begin{array}{ccc}\hfill \sum _{s=0}^{15}{T}_{-1+s}{e}_s& =& {\widehat{T}}_{-1}=\frac{\widehat{\alpha }}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }}{(\gamma -\alpha )(\gamma -\beta )}\hfill \\ \hfill \sum _{s=0}^{15}{T}_s{e}_s& =& {\widehat{T}}_0={\displaystyle \frac{\widehat{\alpha }\alpha }{(\alpha -\beta )(\alpha -\gamma )}}+{\displaystyle \frac{\widehat{\beta }\beta }{(\beta -\alpha )(\beta -\gamma )}}+{\displaystyle \frac{\widehat{\gamma }\gamma }{(\gamma -\alpha )(\gamma -\beta )}}\hfill \\ \hfill \sum _{s=0}^{15}{T}_{1+s}{e}_s& =& {\widehat{T}}_1=\frac{\widehat{\alpha }{\alpha }^2}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }{\beta }^2}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^2}{(\gamma -\alpha )(\gamma -\beta )}\hfill \end{array}$$

(c) 

$$\begin{array}{ccc}\hfill {\displaystyle \frac{(({\alpha }^2-\alpha ){\widehat{K}}_0+\alpha {\widehat{K}}_1+{\widehat{K}}_{-1})}{\left(\alpha -\gamma \right)\left(\alpha -\beta \right)}}& =& \widehat{\alpha }\hfill \\ \hfill {\displaystyle \frac{(({\beta }^2-\beta ){\widehat{K}}_0+\beta {\widehat{K}}_1+{\widehat{K}}_{-1})}{\left(\beta -\gamma \right)\left(\beta -\alpha \right)}}& =& \widehat{\beta }\hfill \\ \hfill {\displaystyle \frac{(({\gamma }^2-\gamma ){\widehat{K}}_0+\gamma {\widehat{K}}_1+{\widehat{K}}_{-1})}{\left(\gamma -\beta \right)\left(\gamma -\alpha \right)}}& =& \widehat{\gamma }\hfill \end{array}$$

(d) 

$$\begin{array}{ccc}\hfill \sum _{s=0}^{15}{K}_{-1+s}{e}_s& =& {\widehat{K}}_{-1}=\widehat{\alpha }{\alpha }^{-1}+\widehat{\beta }{\beta }^{-1}+\widehat{\gamma }{\gamma }^{-1}\hfill \\ \hfill \sum _{s=0}^{15}{K}_s{e}_s& =& {\widehat{K}}_0=\widehat{\alpha }+\widehat{\beta }+\widehat{\gamma }\hfill \\ \hfill \sum _{s=0}^{15}{K}_{1+s}{e}_s& =& {\widehat{K}}_1=\widehat{\alpha }\alpha +\widehat{\beta }\beta +\widehat{\gamma }\gamma .\hfill \end{array}$$

Using the above remark, we can find ${\widehat{T}}_2,$ ${\widehat{K}}_2$ as follows:

$$\sum _{s=0}^{15}{T}_{2+s}{e}_s={\widehat{T}}_2={\widehat{T}}_1+{\widehat{T}}_0+{\widehat{T}}_{-1}=\frac{\widehat{\alpha }{\alpha }^3}{(\alpha -\beta )(\alpha -\gamma )}+\frac{\widehat{\beta }{\beta }^3}{(\beta -\alpha )(\beta -\gamma )}+\frac{\widehat{\gamma }{\gamma }^3}{(\gamma -\alpha )(\gamma -\beta )}$$

(21)

and:

$$\sum _{s=0}^{15}{K}_{2+s}{e}_s={\widehat{K}}_2={\widehat{K}}_1+{\widehat{K}}_0+{\widehat{K}}_{-1}=\widehat{\alpha }{\alpha }^2+\widehat{\beta }{\beta }^2+\widehat{\gamma }{\gamma }^2.$$

(22)

Of course, (21) and (22) can be found directly from (12) and (13).

Now, we present the formulas, which give the summation of the first n Tribonacci and Tribonacci-Lucas numbers.

Lemma 3.

For every integer $n\ge 0,$ we have:

$$\sum _{i=0}^n{T}_i=T_0+{\displaystyle \frac{1}{2}}(T_{n+2}+T_n-1)={\displaystyle \frac{1}{2}}(T_{n+2}+T_n-1)$$

(23)

and:

$$\sum _{i=0}^n{K}_i={\displaystyle \frac{K_{n+2}+K_n}{2}}.$$

(24)

Proof. 

(23) and (24) can be easily proven by mathematical induction. For a proof of (23) with a telescopic sum method, see [40], or with a matrix diagonalization proof, see [41], or see also [30].

For a proof of (24), see [42]. Since $K_0=3$ and ${\displaystyle \sum _{i=1}^n}{K}_i={\displaystyle \frac{K_{n+2}+K_n-6}{2}},$ it follows that ${\displaystyle \sum _{i=0}^n}{K}_i={\displaystyle \frac{K_{n+2}+K_n}{2}}.$ □

There is also a formula of the summation of the first n negative Tribonacci numbers:

$$\sum _{i=1}^n{T}_{-i}={\displaystyle \frac{1}{2}}(1-T_{-n-1}-T_{-n+1}).$$

For a proof of the above formula, see Kuhapatanakul and Sukruan [43].

Next, we present the formulas that give the summation of the first n Tribonacci and Tribonacci-Lucas sedenions.

Theorem 5.

The summation formulas for Tribonacci and Tribonacci-Lucas sedenions are

$$\sum _{i=0}^n{\widehat{T}}_i={\displaystyle \frac{1}{2}}({\widehat{T}}_{n+2}+{\widehat{T}}_n+c_1)$$

(25)

and:

$$\sum _{i=0}^n{\widehat{K}}_i={\displaystyle \frac{1}{2}}({\widehat{K}}_{n+2}+{\widehat{K}}_n+c_2)$$

(26)

respectively, where:

$$\begin{array}{ccc}\hfill c_1& =& -1-e_1-3e_2-5e_3-9e_4-17e_5-31e_6-57e_7-105e_8-193e_9\hfill \\ & & -355e_{10}-653e_{11}-1201e_{12}-2209e_{13}-4063e_{14}-7473e_{15}\hfill \end{array}$$

and:

$$\begin{array}{ccc}\hfill c_2& =& -6e_1-8e_2-14e_3-28e_4-50e_5-92e_6-170e_7-312e_8-574e_9\hfill \\ & & -1056e_{10}-1842e_{11}-3572e_{12}-6570e_{13}-12084e_{14}-22226e_{15}.\hfill \end{array}$$

Proof. 

Using (6) and (23), we obtain:

$$\begin{array}{ccc}\hfill \sum _{i=0}^n{\widehat{T}}_i& =& \sum _{i=0}^n{T}_i+e_1\sum _{i=0}^n{T}_{i+1}+e_2\sum _{i=0}^n{T}_{i+2}+\dots +e_{15}\sum _{i=0}^n{T}_{i+15}\hfill \\ & =& (T_0+\dots +T_n)+e_1(T_1+\dots +T_{n+1})\hfill \\ & & +e_2(T_2+\dots +T_{n+2})+\dots +e_{15}(T_{15}+\dots +T_{n+15}).\hfill \end{array}$$

and:

$$\begin{array}{ccc}\hfill 2\sum _{i=0}^n{\widehat{T}}_i& =& (T_{n+2}+T_n-1)+e_1(T_{n+3}+T_{n+1}-1-2T_0)\hfill \\ & & +e_2(T_{n+4}+T_{n+3}-1-2(T_0+T_1))\hfill \\ & & ⋮\hfill \\ & & +e_{15}(T_{n+17}+T_{n+15}-1-2(T_0+T_1+\dots +T_{14}))\hfill \\ & =& {\widehat{T}}_{n+2}+{\widehat{T}}_n+c_1\hfill \end{array}$$

where $c_1=-1+e_1(-1-2T_0)+e_2(-1-2(T_0+T_1))+\dots +e_{15}(-1-2(T_0+\dots +T_{14})).$ Hence:

$$\sum _{i=0}^n{\widehat{T}}_i=\frac{1}{2}({\widehat{T}}_{n+2}+{\widehat{T}}_n+c_1).$$

We can compute $c_1$ as:

$$\begin{array}{ccc}\hfill c_1& =& -1-e_1-3e_2-5e_3-9e_4-17e_5-31e_6-57e_7-105e_8-193e_9\hfill \\ & & -355e_{10}-653e_{11}-1201e_{12}-2209e_{13}-4063e_{14}-7473e_{15}.\hfill \end{array}$$

This proves (25). Similarly, we can obtain (26). □

3. Some Identities for the Tribonacci and Tribonacci-Lucas Sedenions

In this section, we give identities about Tribonacci and Tribonacci-Lucas sedenions.

Theorem 6.

For $n\ge 1,$ the following identities hold:

(a) 

${\widehat{K}}_n=3{\widehat{T}}_{n+1}-2{\widehat{T}}_n-{\widehat{T}}_{n-1},$

(b) 

${\widehat{T}}_n+\overline{{\widehat{T}}_n}=2T_n,$${\widehat{K}}_n+\overline{{\widehat{K}}_n}=2K_n,$

(c) 

${\widehat{T}}_{n+1}+{\widehat{T}}_n={\displaystyle \frac{\widehat{\alpha }\left(\alpha +1\right){\alpha }^{n+1}}{(\alpha -\beta )(\alpha -\gamma )}}+{\displaystyle \frac{\widehat{\beta }\left(\beta +1\right){\beta }^{n+1}}{(\beta -\alpha )(\beta -\gamma )}}+{\displaystyle \frac{\widehat{\gamma }\left(\gamma +1\right){\gamma }^{n+1}}{(\gamma -\alpha )(\gamma -\beta )}},$

(d) 

${\widehat{K}}_{n+1}+{\widehat{K}}_n=\widehat{\alpha }\left(\alpha +1\right){\alpha }^n+\widehat{\beta }\left(\beta +1\right){\beta }^n+\widehat{\gamma }\left(\gamma +1\right){\gamma }^n,$

(e) 

${\displaystyle \sum _{i=0}^n}\left(\genfrac{}{}{0pt}{}{n}{i}\right){\widehat{F}}_i={\displaystyle \frac{\widehat{\alpha }\alpha {(1+\alpha )}^n}{(\alpha -\beta )(\alpha -\gamma )}}+{\displaystyle \frac{\widehat{\beta }\beta {(1+\beta )}^n}{(\beta -\alpha )(\beta -\gamma )}}+{\displaystyle \frac{\widehat{\gamma }\gamma {(1+\gamma )}^n}{(\gamma -\alpha )(\gamma -\beta )}},$

(f) 

${\displaystyle \sum _{i=0}^n}\left(\genfrac{}{}{0pt}{}{n}{i}\right){\widehat{K}}_i=\widehat{\alpha }{(1+\alpha )}^n+\widehat{\beta }{(1+\beta )}^n+\widehat{\gamma }{(1+\gamma )}^n.$

Proof. 

(a) follows from the recurrence relation $K_n=3T_{n+1}-2T_n-T_{n-1}$ (see for example [39]). The others can be easily established. □

Theorem 7.

For $n\ge 0,$ $m\ge 3$, we have:

(a) 

${\widehat{T}}_{m+n}=T_{m-1}{\widehat{T}}_{n+2}+(T_{m-2}+T_{m-3}){\widehat{T}}_{n+1}+T_{m-2}{\widehat{T}}_n,$

(b) 

${\widehat{T}}_{m+n}=T_{m+2}{\widehat{T}}_{n-1}+(T_{m+1}+T_m){\widehat{T}}_{n-2}+T_{m+1}{\widehat{T}}_{n-3},$

(c) 

${\widehat{K}}_{m+n}=K_{n-1}{\widehat{T}}_{m+2}+({\widehat{T}}_{m+1}+{\widehat{T}}_m)K_{n-2}+K_{n-3}{\widehat{T}}_{m+1},$

(d) 

${\widehat{K}}_{m+n}=K_{m+2}{\widehat{T}}_{n-1}+(K_{m+1}+K_m){\widehat{T}}_{n-2}+K_{m+1}{\widehat{T}}_{n-3}.$

Proof. 

(a) and (d) can be proven by strong induction on m, and (c) can be proven by strong induction on $n.$ For (b), replace n by $n-3$ and m by $m+3$ in (a). □

Note that in fact, the results of the above theorem are true for all integers n and m, and taking $n=2$ in (c), we obtain:

$${\widehat{K}}_{m+2}={\widehat{T}}_{m+2}+2{\widehat{T}}_{m+1}+3{\widehat{T}}_m$$

and taking $m=-4$ in (d):

$${\widehat{K}}_{n-4}=-{\widehat{T}}_{n-1}+5{\widehat{T}}_{n-3}.$$

Note also that since, for all integers $n,$ $T_{-n}=2T_{-n+3}-T_{-n+4}$, it follows that:

$${\widehat{T}}_{-n}=2{\widehat{T}}_{-n+3}-{\widehat{T}}_{-n+4}.$$

Theorem 8.

For all integers $n,$ the following identities hold:

(a) 

${\widehat{T}}_{n+6}=7{\widehat{T}}_{n+3}-5{\widehat{T}}_n+{\widehat{T}}_{n-3}$

(b) 

${\widehat{T}}_{n+8}=11{\widehat{T}}_{n+4}+5{\widehat{T}}_n+{\widehat{T}}_{n-4}$

(c) 

${\widehat{T}}_{n+10}=21{\widehat{T}}_{n+5}+{\widehat{T}}_n+{\widehat{T}}_{n-5}$

(d) 

${\widehat{K}}_{n+6}=2{\widehat{K}}_{n+3}+{\widehat{K}}_n+{\widehat{K}}_{n-3}$

(e) 

${\widehat{K}}_{n+8}=4{\widehat{K}}_{n+4}+{\widehat{K}}_{n-4}$

(f) 

${\widehat{K}}_{n+10}=7{\widehat{K}}_{n+5}-2{\widehat{K}}_n+{\widehat{K}}_{n-5}.$

Proof. 

For all integers n and m, we have $T_{n+2m}=K_m{T}_{n+m}-K_{-m}{T}_n+T_{n-m}$ and $K_{n+2m}=T_m{K}_{n+m}-T_{-m}{K}_n+K_{n-m}$ (see [44]). Giving some value for $m,$ we obtain the results. □

4. Matrices and Determinants Related to Tribonacci and Tribonacci-Lucas Sedenions

Define the $4\times 4$ determinants $D_n$ and $E_n,$ for all integers $n,$ by:

$$D_n=\left|\begin{array}{cccc}{T}_n& K_n& K_{n+1}& K_{n+2}\\ T_2& K_2& K_3& K_4\\ T_1& K_1& K_2& K_3\\ T_0& K_0& K_1& K_2\end{array}\right|,E_n=\left|\begin{array}{cccc}{K}_n& T_n& T_{n+1}& T_{n+2}\\ K_2& T_2& T_3& T_4\\ K_1& T_1& T_2& T_3\\ K_0& T_0& T_1& T_2\end{array}\right|$$

Theorem 9.

The following statements are true.

(a) 

$D_n=0$ and $E_n=0$ for all integers $n.$

(b) 

$44{\widehat{T}}_n=10{\widehat{K}}_{n+2}-6{\widehat{K}}_{n+1}-8{\widehat{K}}_n.$

(c) 

${\widehat{K}}_n=-{\widehat{T}}_{n+2}+4{\widehat{T}}_{n+1}-{\widehat{T}}_n.$

Proof. 

(a) is a special case of a result in [45]. Expanding $D_n$ along the top row gives $44T_n=10K_{n+2}-6K_{n+1}-8K_n$, and now, (b) follows. Expanding $E_n$ along the top row gives $K_n=-T_{n+2}+4T_{n+1}-T_n$, and now, (c) follows. □

Consider the sequence $\left\{U_n\right\}$, which is defined by the third-order recurrence relation:

$$U_n=U_{n-1}+U_{n-2}+U_{n-3},U_0=U_1=0,U_2=1.$$

Note that some authors call $\left\{U_n\right\}$ a Tribonacci sequence instead of $\left\{T_n\right\}$. The numbers $U_n$ can be expressed using Binet’s formula:

$$U_n=\frac{{\alpha }^n}{(\alpha -\beta )(\alpha -\gamma )}+\frac{{\beta }^n}{(\beta -\alpha )(\beta -\gamma )}+\frac{{\gamma }^n}{(\gamma -\alpha )(\gamma -\beta )}$$

and the negative numbers $U_{-n}$ $(n=1,2,3,\dots )$ satisfy the recurrence relation:

$$U_{-n}=\left|\begin{array}{cc}{U}_{n+1}& U_{n+2}\\ U_n& U_{n+1}\end{array}\right|=U_{n+1}^2-U_{n+2}{U}_n.$$

The matrix method is a very useful method in order to obtain some identities for special sequences. We define the square matrix M of order three as:

$$M=\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)$$

such that $detM=1.$ Note that:

$$M^n=\left(\begin{array}{ccc}{U}_{n+2}& U_{n+1}+U_n& U_{n+1}\\ U_{n+1}& U_n+U_{n-1}& U_n\\ U_n& U_{n-1}+U_{n-2}& U_{n-1}\end{array}\right).$$

(27)

For a proof of (27), see [46]. Matrix formulation of $T_n$ and $K_n$ can be given as:

$$\left(\begin{array}{c}{T}_{n+2}\\ T_{n+1}\\ T_n\end{array}\right)={\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)}^n\left(\begin{array}{c}{T}_2\\ T_1\\ T_0\end{array}\right)$$

(28)

and:

$$\left(\begin{array}{c}{K}_{n+2}\\ K_{n+1}\\ K_n\end{array}\right)={\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)}^n\left(\begin{array}{c}{K}_2\\ K_1\\ K_0\end{array}\right).$$

(29)

The matrix M was defined and used in [47]. For the matrix formulations (28) and (29), see [48,49].

Now, we define the matrices $M_T$ and $M_K$ as:

$$M_T=\left(\begin{array}{ccc}{\widehat{T}}_4& {\widehat{T}}_3+{\widehat{T}}_2& {\widehat{T}}_3\\ {\widehat{T}}_3& {\widehat{T}}_2+{\widehat{T}}_1& {\widehat{T}}_2\\ {\widehat{T}}_2& {\widehat{T}}_1+{\widehat{T}}_0& {\widehat{T}}_1\end{array}\right)\mathrm{and}{M}_K=\left(\begin{array}{ccc}{\widehat{K}}_4& {\widehat{K}}_3+{\widehat{K}}_2& {\widehat{K}}_3\\ {\widehat{K}}_3& {\widehat{K}}_2+{\widehat{K}}_1& {\widehat{K}}_2\\ {\widehat{K}}_2& {\widehat{K}}_1+{\widehat{K}}_0& {\widehat{K}}_1\end{array}\right).$$

These matrices $M_T$ and $M_K$ can be called the Tribonacci sedenion matrix and Tribonacci-Lucas sedenion matrix, respectively.

Theorem 10.

For $n\ge 0,$ the following are valid:

(a) 

$$M_T{\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)}^n=\left(\begin{array}{ccc}{\widehat{T}}_{n+4}& {\widehat{T}}_{n+3}+{\widehat{T}}_{n+2}& {\widehat{T}}_{n+3}\\ {\widehat{T}}_{n+3}& {\widehat{T}}_{n+2}+{\widehat{T}}_{n+1}& {\widehat{T}}_{n+2}\\ {\widehat{T}}_{n+2}& {\widehat{T}}_{n+1}+{\widehat{T}}_n& {\widehat{T}}_{n+1}\end{array}\right)$$

(30)

(b) 

$$M_K{\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)}^n=\left(\begin{array}{ccc}{\widehat{K}}_{n+4}& {\widehat{K}}_{n+3}+{\widehat{K}}_{n+2}& {\widehat{K}}_{n+3}\\ {\widehat{K}}_{n+3}& {\widehat{K}}_{n+2}+{\widehat{K}}_{n+1}& {\widehat{K}}_{n+2}\\ {\widehat{K}}_{n+2}& {\widehat{K}}_{n+1}+{\widehat{K}}_n& {\widehat{K}}_{n+1}\end{array}\right)$$

(31)

Proof. 

We prove (a) by mathematical induction on $n.$ If $n=0$, then the result is clear. Now, we assume it is true for $n=k,$ that is:

$$M_T{M}^k=\left(\begin{array}{ccc}{\widehat{T}}_{k+4}& {\widehat{T}}_{k+3}+{\widehat{T}}_{k+2}& {\widehat{T}}_{k+3}\\ {\widehat{T}}_{k+3}& {\widehat{T}}_{k+2}+{\widehat{T}}_{k+1}& {\widehat{T}}_{k+2}\\ {\widehat{T}}_{k+2}& {\widehat{T}}_{k+1}+{\widehat{T}}_k& {\widehat{T}}_{k+1}\end{array}\right).$$

If we use (8), then for $k\ge 3,$ we have ${\widehat{T}}_{k+3}={\widehat{T}}_{k+2}+{\widehat{T}}_{k+1}+{\widehat{T}}_k.$ Then, by induction hypothesis, we obtain:

$$\begin{array}{ccc}\hfill M_T{M}^{k+1}& =& (M_T{M}^k)M\hfill \\ & =& \left(\begin{array}{ccc}{\widehat{T}}_{k+4}& {\widehat{T}}_{k+3}+{\widehat{T}}_{k+2}& {\widehat{T}}_{k+3}\\ {\widehat{T}}_{k+3}& {\widehat{T}}_{k+2}+{\widehat{T}}_{k+1}& {\widehat{T}}_{k+2}\\ {\widehat{T}}_{k+2}& {\widehat{T}}_{k+1}+{\widehat{T}}_k& {\widehat{T}}_{k+1}\end{array}\right)\left(\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)\hfill \\ & =& \left(\begin{array}{ccc}{\widehat{T}}_{k+2}+{\widehat{T}}_{k+3}+{\widehat{T}}_{k+4}& {\widehat{T}}_{k+4}+{\widehat{T}}_{k+3}& {\widehat{T}}_{k+4}\\ {\widehat{T}}_{k+1}+{\widehat{T}}_{k+2}+{\widehat{T}}_{k+3}& {\widehat{T}}_{k+3}+{\widehat{T}}_{k+2}& {\widehat{T}}_{k+3}\\ {\widehat{T}}_{k+1}+{\widehat{T}}_{k+2}+{\widehat{T}}_k& {\widehat{T}}_{k+2}+{\widehat{T}}_{k+1}& {\widehat{T}}_{k+2}\end{array}\right)\hfill \\ & =& \left(\begin{array}{ccc}{\widehat{T}}_{k+5}& {\widehat{T}}_{k+4}+{\widehat{T}}_{k+3}& {\widehat{T}}_{k+4}\\ {\widehat{T}}_{k+4}& {\widehat{T}}_{k+3}+{\widehat{T}}_{k+2}& {\widehat{T}}_{k+3}\\ {\widehat{T}}_{k+3}& {\widehat{T}}_{k+2}+{\widehat{T}}_{k+1}& {\widehat{T}}_{k+2}\end{array}\right).\hfill \end{array}$$

Thus, (30) holds for all non-negative integers $n.$

(31) can be similarly proven. □

Corollary 1.

For $n\ge 0,$ the following hold:

(a) 

${\widehat{T}}_{n+2}={\widehat{T}}_2{U}_{n+2}+({\widehat{T}}_1+{\widehat{T}}_0)U_{n+1}+{\widehat{T}}_1{U}_n$

(b) 

${\widehat{K}}_{n+2}={\widehat{K}}_2{U}_{n+2}+({\widehat{K}}_1+{\widehat{K}}_0)U_{n+1}+{\widehat{K}}_1{U}_n$

Proof. 

The proof of (a) can be seen by the coefficient (28) of the matrix $M_T$ and (27). The proof of (b) can be seen by the coefficient (29) of the matrix $M_K$ and (27).

Note that we have similar results if we replace the matrix M with the matrices N and O defined by:

$$N=\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 1& 0& 0\end{array}\right)\mathrm{and}O=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 1& 1\end{array}\right).$$

 □