On Soft Rough Topology with Multi-Attribute Group Decision Making

Abstract

Rough set approaches encounter uncertainty by means of boundary regions instead of membership values. In this paper, we develop the topological structure on soft rough set ($\mathcal{SR}$-set) by using pairwise $\mathcal{SR}$-approximations. We define $\mathcal{SR}$-open set, $\mathcal{SR}$-closed sets, $\mathcal{SR}$-closure, $\mathcal{SR}$-interior, $\mathcal{SR}$-neighborhood, $\mathcal{SR}$-bases, product topology on $\mathcal{SR}$-sets, continuous mapping, and compactness in soft rough topological space ($\mathcal{SRTS}$). The developments of the theory on $\mathcal{SR}$-set and $\mathcal{SR}$-topology exhibit not only an important theoretical value but also represent significant applications of $\mathcal{SR}$-sets. We applied an algorithm based on $\mathcal{SR}$-set to multi-attribute group decision making (MAGDM) to deal with uncertainty.

1. Introduction

The problem of imperfect knowledge has been the center of attention for many years. In the field of mathematics, computer science, and artificial intelligence, researchers have used different methods to tackle the problem of uncertain and incomplete data, including probability theory, fuzzy set [1], and rough set [2,3] and soft set techniques [4,5,6]. Molodstov [6] introduced soft set as an effective tool to manage imprecision; it includes a set of parameters to describe the set properly. Maji et al. (2002–2003) [4,5] extended some operations of soft set and effectively used this technique in a decision-making problem. Soft set with decision making have studied by many researchers [7,8,9,10,11]. In 2011, Shabir and Naz [12] and Cagman et al. [13] independently worked on the topological structure of soft set. Chen [14] presented a new definition related to the reduction of soft parameterization. The study of hybrid structures, having emerged from the fusion of soft sets with other mathematical approaches, is becoming an active topic for research nowadays. Aktas and Cagman (2007) [15] efficiently related the three concepts of soft set, rough set, and fuzzy set. Riaz et al. [16,17,18] established some results of soft algebra, soft metric spaces, and measurable soft mappings. Riaz and Masooma [19,20,21,22,23] introduced fuzzy parameterized fuzzy soft set ($\mathfrak{fpfs}$-set), $\mathfrak{fpfs}$-topology, and $\mathfrak{fpfs}$-compact spaces, with some important applications of $\mathfrak{fpfs}$-set to decision-making problems. They presented $\mathfrak{fns}$-mappings and fixed points of $\mathfrak{fns}$-mapping. Different researchers have tackled the problem of incomplete or uncertain information in the system in different ways. Shang worked on robust statistics, and he investigated the robustness of a system under different circumstances and analyzed the robustness properties of subgraphs under attack in complex networks [24,25]. The rough set concept presented by Pawlak presents a systematic approach for the classification of objects. It characterizes a set of objects by two exact concepts, known as its approximations. Here, vagueness is expressed in the form of a boundary region, where empty boundary region implies that the set is crisp, and a non-empty boundary region implies that our knowledge is insufficient to explain the set precisely. By using equivalence relations, Thivagar et al. [26] generated the topology on rough set which includes approximations and the boundary region. Equivalence relation plays an important role in Pawlak’s rough set model, and by replacing it with a soft set, soft rough set $\mathcal{SR}$-sets were introduced by Feng [27]. Feng et al. [28] presented some properties related to $\mathcal{SR}$-approximations. Xue et al. [29] presented some decision-making algorithms regarding hybrid soft models. Zou and Xiao [30] analyzed data in soft sets under incomplete information systems. There are mainly two streams of study connecting soft rough set theory and topology theory. At the same time, according to the topological properties on the topological $\mathcal{SR}$-space, some applications for image processing and some topological diagrams are introduced. The remainder of the paper is composed as follows. In Section 2, we briefly define the notions of rough set $\mathcal{R}$-set and soft rough set $\mathcal{SR}$-set. In Section 3, we present a novel topological structure of $\mathcal{SR}$-set. We present some new results of $\mathcal{SR}$-set theory and $\mathcal{SR}$-topology. A topological structure on soft rough set was defined by Bakier et al. [31]. Malik and Riaz [32,33] studied action of modular group on real quadratic fields. Soft sets, neutrosophic set and rough sets with decision making problems have studied by many researchers [34,35,36,37,38,39,40]. We define $\mathcal{SR}$-topology on soft rough set in the form of the pair ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$, where ${{\tau }_{\mathcal{SR}}}_{★}$ is the lower $\mathcal{SR}$-topology and ${{\tau }_{\mathcal{SR}}}^{★}$ is the upper $\mathcal{SR}$-topology on set $\mathcal{Y}$. This $\mathcal{SR}$-topology is more appropriate, as it looks like a natural soft rough topology on a soft rough set. In Section 4, continuity, homeomorphism, and projection mappings in $\mathcal{SR}$-set are discussed. Section 5 describes the compactness in $\mathcal{SR}$-set. 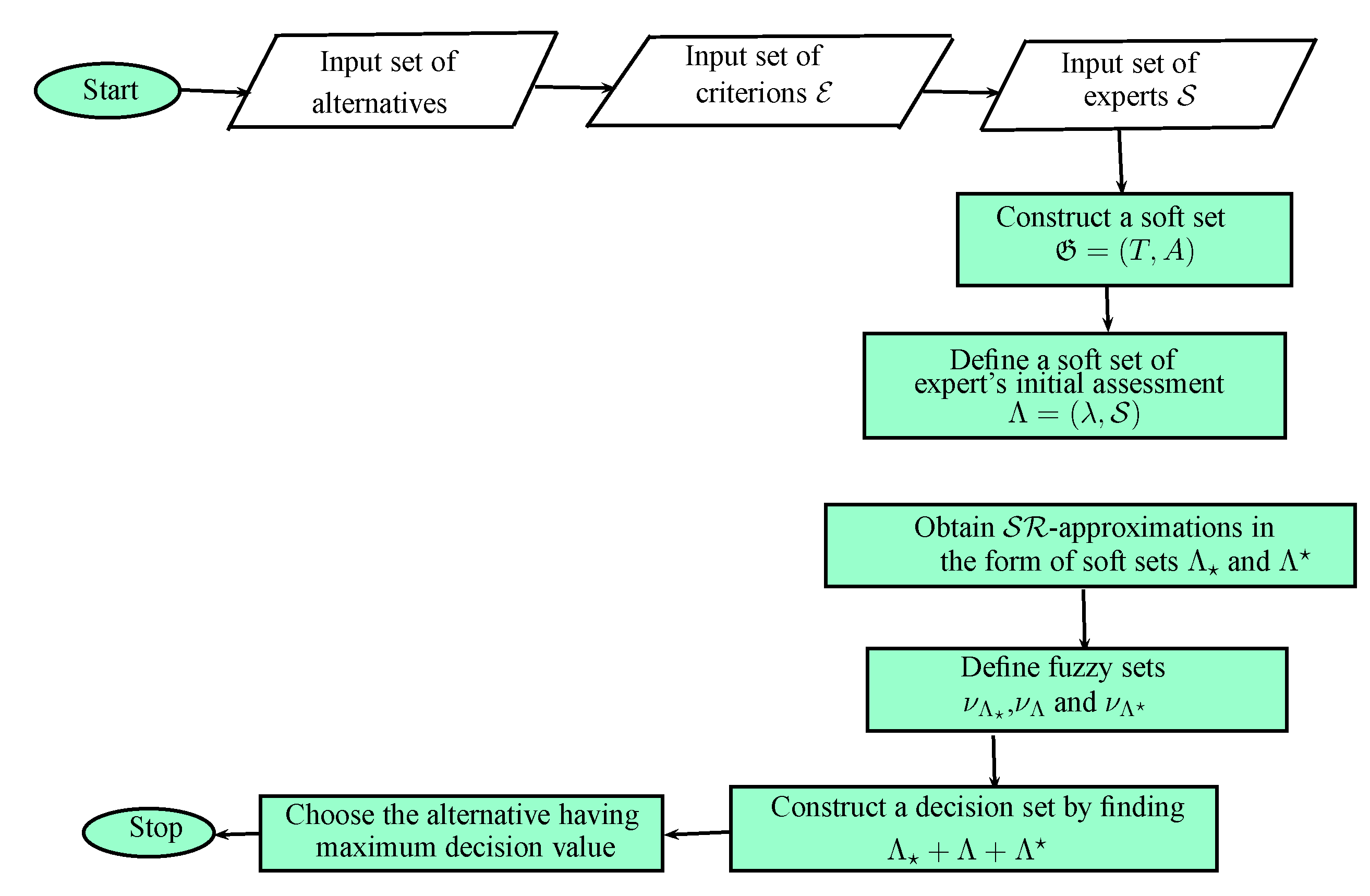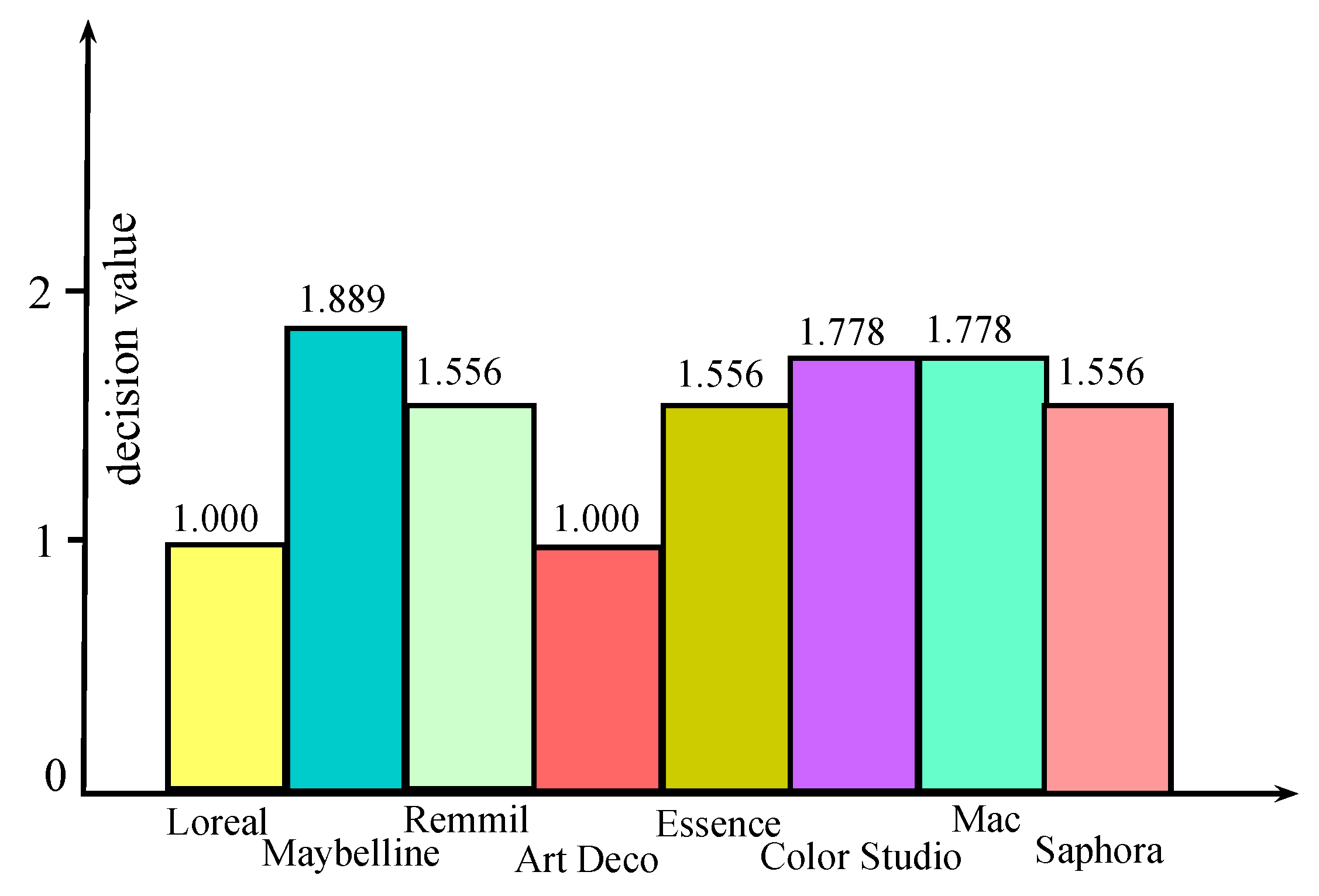In Section 6, $\mathcal{SR}$ approximations are employed to solve multi-attribute group decision-making problem.

2. Preliminaries

In this section, we illustrate some basic notions related to $\mathcal{SR}$-theory. First we define rough set $\mathcal{R}$-set and soft rough set $\mathcal{SR}$-set and then explain a few related operations on $\mathcal{SR}$-set.

Definition 1

([2]). Suppose we have an object set $\mathcal{V}$ known as universe, and an indiscernibility relation $\Re \subseteq \mathcal{V}\times \mathcal{V}$ which represents knowledge about elements of $\mathcal{V}$. We take ℜ as an equivalence relation and denote it by $\Re \left(y\right)$. The pair $(\mathcal{V},\Re )$ is called the approximation space. Let $\mathcal{Y}$ be any subset of $\mathcal{V}$. We characterize the set $\mathcal{Y}$ with respect to ℜ.

(1) The union of all granules which are entirely included in the set $\mathcal{Y}$ is called the lower approximation of the set $\mathcal{Y}$ w.r.t ℜ, mathematically defined as

$${\Re }_{★}\left(\mathcal{Y}\right)=\bigcup _{y\in \mathcal{V}}\{\Re \left(y\right):\Re \left(y\right)\subseteq \mathcal{Y}\}$$

(2) The union of all the granules having a non-empty intersection with the set $\mathcal{Y}$ is called the upper approximation of the set $\mathcal{Y}$ w.r.t ℜ, mathematically defined as

$${\Re }^{★}\left(\mathcal{Y}\right)=\bigcup _{y\in \mathcal{V}}\{\Re \left(y\right):\Re \left(y\right)\cap \mathcal{Y}\ne \varnothing \}$$

(3) The difference between the upper and lower approximations is called the boundary region of the set $\mathcal{Y}$ w.r.t ℜ, mathematically defined as

$$B_{\Re }\left(\mathcal{Y}\right)={\Re }^{★}\left(\mathcal{Y}\right)-{\Re }_{★}\left(\mathcal{Y}\right)$$

If ${\Re }^{★}\left(\mathcal{Y}\right)={\Re }_{★}\left(\mathcal{Y}\right)$, the set $\mathcal{Y}$ is said to be defined. If ${\Re }^{★}\left(\mathcal{Y}\right)\ne {\Re }_{★}\left(\mathcal{Y}\right)$, i.e., $B_R\left(\mathcal{Y}\right)\ne \varnothing$, the set $\mathcal{Y}$ is said to be a (imprecise) rough set w.r.t ℜ.

We denote a rough set $\mathcal{Y}$ by a pair comprising a lower approximation and upper approximation $\mathcal{Y}=({\Re }_{★}\left(\mathcal{Y}\right),{\Re }^{★}\left(\mathcal{Y}\right))$

Definition 2

([28]). Consider a soft set $\mathcal{S}=(\mathcal{T},\mathcal{A})$ over the universe $\mathcal{V}$, where $\mathcal{A}\subseteq \mathcal{E}$ and $\mathcal{T}$ is a mapping defined as $\mathcal{T}:\mathcal{A}\to \mathcal{P}\left(\mathcal{V}\right)$. Here, soft approximation space is the pair $\mathcal{P}=(\mathcal{V},\mathcal{S})$. Following the soft approximation space $\mathcal{P}$, we define two operations as follows:

$${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\{v\in \mathcal{V}:\exists a\in \mathcal{A},[v\in \mathcal{T}\left(a\right)\subseteq \mathcal{Y}]\},$$

$${{\Re }_P}^{★}\left(\mathcal{Y}\right)=\{v\in \mathcal{V}:\exists a\in \mathcal{A},[v\in \mathcal{T}\left(a\right)\cap \mathcal{Y}\ne \varnothing ]\}$$

regarding every subset $\mathcal{Y}\subseteq \mathcal{V}$, two sets ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, which are called the soft P-lower approximation and soft P-upper approximation of $\mathcal{Y}$, respectively. In general, we refer to ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$ as $\mathcal{SR}$-approximations of $\mathcal{Y}$ w.r.t $\mathit{P}$. If ${{\Re }_P}_{★}\left(\mathcal{Y}\right)={{\Re }_P}^{★}\left(\mathcal{Y}\right)$, then $\mathcal{Y}$ is said to be soft P-definable; otherwise, $\mathcal{Y}$ is a soft P-rough set. Then, $Bn{d}_P={{\Re }_P}^{★}\left(\mathcal{Y}\right)-{{\Re }_P}_{★}\left(\mathcal{Y}\right)$ is the $\mathcal{SR}$-boundary region.

We denote $\mathcal{SR}$-set ($\mathcal{SR}$-set) $\mathcal{Y}$ by a pair comprising $\mathcal{SR}$-lower approximation and $\mathcal{SR}$-upper approximation $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$.

Example 1.

Let $\mathcal{V}=\{s_1,s_2,s_3,s_4,s_5\}$ be the set of perfumes, and let $\mathcal{A}=\{{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4\}=\mathcal{E}$ be the qualities which Miss Amal wants in her perfume. Let $\mathcal{S}=(\mathcal{T},\mathcal{A})$ be a soft set over $\mathcal{V}$. $\mathcal{T}\left({\zeta }_1\right)=\{s_3,s_5\},\mathcal{T}\left({\zeta }_2\right)=\{s_2,s_4,s_5\},\mathcal{T}\left({\zeta }_3\right)=\{s_1,s_2,s_5\},\mathcal{T}\left({\zeta }_4\right)=\{s_2,s_3\}$ and the soft approximation space $\mathcal{P}=(\mathcal{V},\mathcal{S})$. The tabular form of soft set $(\mathcal{T},\mathcal{A})$ is given in

Table 1. Soft set $(\mathcal{T},\mathcal{A})$.

$(\mathcal{T},\mathcal{A})$	${\mathit{s}}_{\mathbf{1}}$	${\mathit{s}}_{\mathbf{2}}$	${\mathit{s}}_{\mathbf{3}}$	${\mathit{s}}_{\mathbf{4}}$	${\mathit{s}}_{\mathbf{5}}$
${\zeta }_1$	0	1	1	0	0
${\zeta }_2$	0	1	0	1	1
${\zeta }_3$	1	1	0	0	1
${\zeta }_4$	0	0	1	0	1

.

For $\mathcal{Y}=\{s_3,s_4,s_5\}\subseteq \mathcal{V}$, we have ${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\{s_3,s_5\}$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)=\{s_1,s_2,s_3,s_4,s_5\}$. Since ${{\Re }_P}_{★}\left(\mathcal{Y}\right)\ne {{\Re }_P}^{★}\left(\mathcal{Y}\right)$; therefore, $\mathcal{Y}$ is a soft P-rough set and is denoted by $\mathcal{Y}=\left(\{s_3,s_5\},\{s_1,s_2,s_3,s_4,s_5\}\right)$

Definition 3.

Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ and $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ be two arbitrary $\mathcal{SR}$-sets and $\mathcal{P}=(\mathcal{V},\mathcal{S})$ be soft approximation space. Then, $\mathcal{A}$ is a $\mathcal{SR}$-subset of $\mathcal{B}$ if ${{\Re }_P}_{★}\left(\mathcal{A}\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{B}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)\subseteq {{\Re }_P}^{★}\left(\mathcal{B}\right)$.

Example 2.

Suppose $\mathcal{V}=\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7,{\alpha }_8\}$ and $\mathcal{E}=\{{\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4\}$. Let $\mathcal{S}=(\mathcal{T},\mathcal{E})$ be a soft set over $\mathcal{V}$,

• $\mathcal{T}\left({\xi }_1\right)=\{{\alpha }_2,{\alpha }_8\}$
• $\mathcal{T}\left({\xi }_2\right)=\{{\alpha }_2,{\alpha }_3,{\alpha }_6,{\alpha }_8\}$
• $\mathcal{T}\left({\xi }_3\right)=\{{\alpha }_2,{\alpha }_5,{\alpha }_7\}$
• $\mathcal{T}\left({\xi }_4\right)=\{{\alpha }_3,{\alpha }_4,{\alpha }_6\}$

and $\mathcal{P}=(\mathcal{V},\mathcal{S})$ be soft approximation space. Consider $\mathcal{A}=\{{\alpha }_2,{\alpha }_4,{\alpha }_5,{\alpha }_7\}\subseteq \mathcal{V}$ and $\mathcal{B}=\{{\alpha }_3,{\alpha }_4\}$ then ${{\Re }_P}_{★}\left(\mathcal{A}\right)=\{{\alpha }_2,{\alpha }_5,{\alpha }_7\}$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)=\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7,{\alpha }_8\}$, while ${{\Re }_P}_{★}\left(\mathcal{B}\right)=\varnothing$ and ${{\Re }_P}^{★}\left(\mathcal{B}\right)=\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_6,{\alpha }_8\}$.

So we have two $\mathcal{SR}$-sets $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))=(\{{\alpha }_2,{\alpha }_5,{\alpha }_7\},\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7,{\alpha }_8\})$ and $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))=(\varnothing ,\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_6,{\alpha }_8\})$. Since ${{\Re }_P}_{★}\left(\mathcal{B}\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{B}\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{B}\right)$. Thus, $\mathcal{B}$ is $\mathcal{SR}$-subset of $\mathcal{A}$.

Definition 4.

Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$, $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ be taken as two arbitrary $\mathcal{SR}$ sets and let $(\mathcal{V},\mathcal{S})$ be soft approximation space. Then, the union of $\mathcal{A}$ and $\mathcal{B}$ is defined as $\mathcal{A}\cup \mathcal{B}=\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\cup {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cup {{\Re }_P}^{★}\left(\mathcal{B}\right)\right)$.

Definition 5.

Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$, $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ be taken as two arbitrary $\mathcal{SR}$ sets and $(\mathcal{V},\mathcal{S})$ be soft approximation space. Then, the intersection of $\mathcal{A}$ and $\mathcal{B}$ is defined as $\mathcal{A}\cap \mathcal{B}=\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right)\right)$.

Example 3.

By using Example 2, we obtain $\mathcal{A}\cup \mathcal{B}=\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\cup {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cup {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)=\left(\{{\alpha }_2,{\alpha }_5,{\alpha }_7\},\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7,{\alpha }_8\}\right)$ and$\mathcal{A}\cap \mathcal{B}=\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\cup {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cup {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)=\left(\varnothing ,\{{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_6,{\alpha }_8\}\right)$.

Definition 6

([31]). Let $\mathcal{V}$ be the universe of discourse and $\mathcal{P}=(\mathcal{V},\mathcal{S})$ is soft approximation space; then, $\mathcal{SR}$-topology is defined as

$${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)=\{\mathcal{V},\varnothing ,{{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right),\mathit{Bd}\left(\mathcal{Y}\right)\}$$

where $\mathcal{Y}\subseteq \mathcal{V}$. ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$ satisfies the following axioms:

(i) $\mathcal{V}$ and ∅ belong to ${\tau }_{\mathcal{SR}}\left(X\right)$.

(ii) Union of elements of any subcollection of ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$ belongs to ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$.

(iii) Intersection of elements of finite subcollection of ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$ belongs to ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$.

The topology defined by ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)$ on $\mathcal{V}$ is called $\mathcal{SR}$-topology on $\mathcal{V}$ w.r.t $\mathcal{Y}$ and $(\mathcal{V},{\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right),\mathcal{E})$ is said to be $\mathcal{SR}$-topological space. Soft rough set with the topology ${\tau }_{\mathcal{SR}}$ is called a topological $\mathcal{SR}$-set.

Example 4.

Let $\mathcal{V}=\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4,{\vartheta }_5,{\vartheta }_6\}$ be the set of cars under consideration, and let $\mathcal{E}=\{{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4,{\zeta }_5\}$ be the set of all parameters and $\mathcal{A}=\{{\zeta }_1,{\zeta }_2,{\zeta }_3\}\subseteq \mathcal{E}$. Consider the soft approximation $P=(\mathcal{V},\mathcal{S})$, where $\mathcal{S}=(\mathcal{T},\mathcal{A})$ is a soft set over $\mathcal{U}$ given by:$\mathcal{T}\left({\zeta }_1\right)=\{{\vartheta }_1,{\vartheta }_3\},\mathcal{T}\left({\zeta }_2\right)=\{{\vartheta }_1,{\vartheta }_3,{\vartheta }_6\}and\mathcal{T}\left({\zeta }_3\right)=\{{\vartheta }_2,{\vartheta }_4\}$.

For $\mathcal{Y}=\{{\vartheta }_2,{\vartheta }_3,{\vartheta }_4,{\vartheta }_6\}$, we obtain ${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\{{\vartheta }_2,{\vartheta }_4\}$, ${{\Re }_P}^{★}\left(\mathcal{Y}\right)=\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4,{\vartheta }_6\}$ and $Bd\left(\mathcal{Y}\right)=\{{\vartheta }_1,{\vartheta }_3,{\vartheta }_6\}$. Then,

$${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)=\{\mathcal{V},\varnothing ,\{{\vartheta }_2,{\vartheta }_4\},\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4,{\vartheta }_6\},\{{\vartheta }_1,{\vartheta }_3,{\vartheta }_6\}\}$$

is a $\mathcal{SR}$-topology.

Definition 7.

Let $(\mathcal{V},{\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right),\mathcal{E})$ be a $\mathcal{SR}$-topological space. Any subset $\mathcal{A}$ such that $\mathcal{A}\in {\tau }_{\mathcal{SR}}$ $\mathcal{A}$ is said to be $\mathcal{SR}$-open, and any subset $\mathcal{A}$ is $\mathcal{SR}$-closed if and only if ${\mathcal{A}}^c\in {\tau }_{\mathcal{SR}}$.

Example 5.

In Example 2, we can see that $\{{\vartheta }_2,{\vartheta }_4\},\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4,{\vartheta }_6\},\{{\vartheta }_1,{\vartheta }_3,{\vartheta }_6\}$ are $\mathcal{SR}$-open sets, and their relative complements $\{{\vartheta }_1,{\vartheta }_3,{\vartheta }_5,{\vartheta }_6\},\left\{{\vartheta }_5\right\},\{{\vartheta }_2,{\vartheta }_4,{\vartheta }_5\}$ are $\mathcal{SR}$-closed sets, while $\mathcal{V}$ and ∅ are both $\mathcal{SR}$-open and $\mathcal{SR}$-closed.

3. Topological Structure of $\mathcal{SR}$-Sets

In this section, we define a new topological structure on $\mathcal{SR}$-sets. We define $\mathcal{SR}$-open set, $\mathcal{SR}$-closed sets, $\mathcal{SR}$-closure, $\mathcal{SR}$-interior, $\mathcal{SR}$-neighborhood, and $\mathcal{SR}$-bases.

Definition 8.

Let $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ be a $\mathcal{SR}$-subset, where $\mathcal{P}=(\mathcal{V},\mathcal{S})$. Let ${{\tau }_{\mathcal{SR}}}_{★}$ and ${{\tau }_{\mathcal{SR}}}^{★}$ be two topologies which contain only exact subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively. Then, the pair ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$ is called a $\mathcal{SR}$-topology on the $\mathcal{SR}$-set $\mathcal{Y}$ and the pair $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ is known as a soft rough topological space (SRTS). Soft rough set $\mathcal{Y}$ with the topology ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$ is known as topological $\mathcal{SR}$-set. Also, in a $\mathcal{SR}$-topology, ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$, ${{\tau }_{\mathcal{SR}}}_{★}$ is the lower $\mathcal{SR}$-topology and ${{\tau }_{\mathcal{SR}}}^{★}$ is the upper $\mathcal{SR}$-topology on X.

Remark 1.

Since ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$ are only exactly defined sets in $\mathcal{SR}$-approximation space, we restrict the elements of ${\tau }_{★}$ and ${\tau }^{★}$ to the set of all exact or definable subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively. However, when they are grouped to form the $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$, indefinable sets can also be $\mathcal{SR}$-open. The point to be noted is that a subset of $\mathcal{Y}$, either exact or inexact, is $\mathcal{SR}$-open iff its lower approximation is in the lower $\mathcal{SR}$-topology and its upper approximation is in the upper $\mathcal{SR}$-topology.

Definition 9.

Let $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ be an SRTS, where ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ be any $\mathcal{SR}$-subset of $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$. Then, $\mathcal{A}$ is said to be lower $\mathcal{SR}$-open if the lower approximation of $\mathcal{A}$ belongs to the lower $\mathcal{SR}$-topology. That is, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$. Also, $\mathcal{A}$ is said to be upper $\mathcal{SR}$-open if the upper approximation of $\mathcal{A}$ belongs to the upper $\mathcal{SR}$-topology. That is, ${{\Re }_P}^{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$. $\mathcal{A}$ is said to be $\mathcal{SR}$-open iff $\mathcal{A}$ is both lower $\mathcal{SR}$-open and upper $\mathcal{SR}$-open, i.e., ${{\Re }_P}_{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$.

Theorem 1.

Consider an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let T be a collection of $\mathcal{SR}$-open subsets of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$. Then, T is a topology on $\mathcal{Y}$.

Proof. 

Consider $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$.

(i) We have $\varnothing \in {{\tau }_{\mathcal{SR}}}_{★}$ and $\varnothing \in {{\tau }_{\mathcal{SR}}}^{★}$. Therefore, $\varnothing (\varnothing ,\varnothing )\in T$. Also, ${{\Re }_P}_{★}\left(\mathcal{Y}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$ and, hence, $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))\in T$.

(ii) Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ and $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ be any two elements of T, implying that both $\mathcal{A}$ and $\mathcal{B}$ are $\mathcal{SR}$-open subsets of $\mathcal{Y}$. Therefore, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$, ${{\Re }_P}^{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$ and ${{\Re }_P}_{★}\left(\mathcal{B}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$, ${{\Re }_P}^{★}\left(\mathcal{B}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$. Being topologies, ${{\tau }_{\mathcal{SR}}}_{★}$ and ${{\tau }_{\mathcal{SR}}}^{★}$ are closed under finite intersection; therefore, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right)\in {{\tau }_{\mathcal{SR}}}^{★}$. Hence, $\mathcal{A}\cap \mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right))$ is an $\mathcal{SR}$-open subset of $\mathcal{Y}$, which shows that $\mathcal{A}\cap \mathcal{B}\in T$. Since $\mathcal{A}$ and $\mathcal{B}$ are arbitrary, T is closed under finite intersections.

(iii) Let $\{{\mathcal{A}}_{\mu }=({{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right),{{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right))|\mu \in \Omega \}$ be an arbitrary family of $\mathcal{SR}$-open subsets of $\mathcal{Y}$, and belongs to the subcollection T. ${\mathcal{A}}_{\mu }=({{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right),{{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right))\in T$ implies ${{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right)\in {{\tau }_{\mathcal{SR}}}^{★}$ for all $\mu \in \Omega$. Since ${{\tau }_{\mathcal{SR}}}_{★}$ and ${{\tau }_{\mathcal{SR}}}^{★}$ are closed under arbitrary union, we have ${\bigcup }_{\mu \in \Omega }{{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${\bigcup }_{\mu \in \Omega }{{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right)\in {{\tau }_{\mathcal{SR}}}^{★}$, which shows that ${\bigcup }_{\mu \in \Omega }{\mathcal{A}}_{\mu }=\left({\bigcup }_{\mu \in \Omega }{{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right),{\bigcup }_{\mu \in \Omega }{{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right)\right)$ is an $\mathcal{SR}$-open subset of $\mathcal{Y}$. Thus, T is closed under arbitrary union.

From (i), (ii), and (iii), the family T of $\mathcal{Y}$ forms a topology on $\mathcal{Y}$. □

Definition 10.

In any $\mathcal{SR}$-set $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$, define ${{\tau }_{\mathcal{SR}}}_{★}=\{\mathcal{A}\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)|\mathcal{A}isP-definable\}$ and ${{\tau }_{\mathcal{SR}}}^{★}=\{\mathcal{B}\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)/\mathcal{B}isP-definable\}$. Then, ${{\tau }_{\mathcal{SR}}}_{★}$ and ${{\tau }_{\mathcal{SR}}}^{★}$ are topologies on ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively, and the $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$ is known as the Discrete $\mathcal{SR}$-topology on $\mathcal{Y}$, and the topological space $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ is known as the Discrete $\mathcal{SR}$-Topological Space on $\mathcal{Y}$.

Definition 11.

In an $\mathcal{SR}$-set $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$, take ${{\tau }_{\mathcal{SR}}}_{★}=\left(\varnothing ,{{\Re }_P}_{★}\left(\mathcal{Y}\right)\right)$ and ${{\tau }_{\mathcal{SR}}}^{★}=\left(\varnothing ,{{\Re }_P}^{★}\left(\mathcal{Y}\right)\right)$, then ${{\tau }_{\mathcal{SR}}}_{★}$ and ${{\tau }_{\mathcal{SR}}}^{★}$ are topologies on ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively, and the $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$ on $\mathcal{Y}$ is known as the indiscrete $\mathcal{SR}$-topology on $\mathcal{Y}$, and $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ is known as the indiscrete $\mathcal{SR}$-topological space on $\mathcal{Y}$.

Definition 12.

In an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Consider a subcollection ${\beta }_{★}$ of subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$; if every element of ${{\tau }_{\mathcal{SR}}}_{★}$ can be expressed as the union of some elements of ${\beta }_{★}$, then ${\beta }_{★}$ is said to be a base for ${{\tau }_{\mathcal{SR}}}_{★}$. If every member of ${{\tau }_{\mathcal{SR}}}^{★}$ can be expressed as the union of some members of ${\beta }^{★}$ for another subcollection ${\beta }^{★}$ of subsets of ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, then ${\beta }^{★}$ is said to be a base for ${{\tau }_{\mathcal{SR}}}^{★}$. If the above conditions are satisfied, then the pair ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ is known as a $\mathcal{SR}$-base for the $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}$ on $\mathcal{Y}$.

Theorem 2.

Consider the SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ is an $\mathcal{SR}$-base for ${\tau }_{\mathcal{SR}}$ iff for any $\mathcal{SR}$-open set $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ and $(x,y)\in \mathcal{A}$ such that $x\in {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $y\in {{\Re }_P}^{★}\left(\mathcal{A}\right)$, then there exist ${\mathfrak{B}}_{★}\in {\beta }_{★}$ and ${\mathfrak{B}}^{★}\in {\beta }^{★}$ such that $x\in {\mathfrak{B}}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $y\in {\mathfrak{B}}^{★}\subseteq {{\Re }_P}^{★}\left(\mathcal{A}\right)$.

Proof. 

Consider the SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let ${\beta }_{★}$ and ${\beta }^{★}$ be families of subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$, respectively, such that ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ is a $\mathcal{SR}$-base for ${\tau }_{\mathcal{SR}}$. Also, consider any $\mathcal{SR}$-subset $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ and let $(x,y)\in \mathcal{A}$ be an arbitrary point such that $x\in {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $y\in {{\Re }_P}^{★}\left(\mathcal{A}\right)$. Now, $x\in {{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}_{★}\left(\mathcal{A}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and ${\beta }_{★}$ is a base for ${{\tau }_{\mathcal{SR}}}_{★}$, which implies that ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ can be written as the union of elements of ${\beta }_{★}$. Hence, $\exists {\mathfrak{B}}_{\mu }\in {\beta }_{★}$ such that $x\in {\mathfrak{B}}_{\mu }$ and ${\mathfrak{B}}_{\mu }\subseteq {{\Re }_P}^{★}\left(\mathcal{A}\right)$. Choose such a ${\mathfrak{B}}_{\mu }$ as ${\mathfrak{B}}_{★}$. Therefore, $x\in {\mathfrak{B}}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{A}\right)$.

Similarly, by the same argument, there exists ${\mathfrak{B}}^{★}\in {\beta }^{★}$ such that $y\in {\mathfrak{B}}^{★}\subseteq {{\Re }_P}^{★}\left(\mathcal{A}\right)$.

Conversely, suppose that ${\beta }_{★}$ and ${\beta }^{★}$ are families of subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively, such that for any $\mathcal{SR}$-open set $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, $(x,y)\in \mathcal{A}$, where $x\in {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $y\in {{\Re }_P}^{★}\left(\mathcal{A}\right)$; then, there exist ${\mathfrak{B}}_{★}\in {\beta }_{★}$ and ${\mathfrak{B}}^{★}\in {\beta }^{★}$ such that $x\in {\mathfrak{B}}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $y\in {\mathfrak{B}}^{★}\subseteq {{\Re }_P}^{★}\left(\mathcal{A}\right)$. Now, we have to prove that ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ is an $\mathcal{SR}$-base for ${\tau }_{\mathcal{SR}}$. Let $C=({{\Re }_P}_{★}\left(\mathcal{C}\right),{{\Re }_P}^{★}\left(\mathcal{C}\right))$ be any $\mathcal{SR}$-open subset of the SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$. By our assumption, for each $x\in {{\Re }_P}_{★}\left(\mathcal{C}\right)$, we have ${{\mathfrak{B}}_x}_{★}\in {\beta }_{★}$ such that $x\in {{\mathfrak{B}}_x}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{C}\right)$. Thus, ${{\Re }_P}_{★}\left(\mathcal{C}\right)={\bigcup }_{x\in {{\Re }_P}_{★}\left(\mathcal{C}\right)}{{\mathfrak{B}}_x}_{★}$. This implies that ${{\Re }_P}_{★}\left(\mathcal{C}\right)$ can be expressed as the union of some elements of ${\beta }_{★}$. Since $C=({{\Re }_P}_{★}\left(\mathcal{C}\right),{{\Re }_P}^{★}\left(\mathcal{C}\right))$ is taken arbitrarily, ${\beta }_{★}$ is a lower base for $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}$.

Similarly, by the same argument, ${{\Re }_P}^{★}\left(\mathcal{C}\right)$ can be expressed as the union of some members of ${\beta }^{★}$; therefore, ${\beta }^{★}$ is an upper base for the $\mathcal{SR}$-topology ${\tau }_{\mathcal{SR}}$. Hence, ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ is an $\mathcal{SR}$-base for ${\tau }_{\mathcal{SR}}$. □

Definition 13.

In an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. The collection $\mathcal{S}=({\mathcal{S}}_{★},{\mathcal{S}}^{★})$ of subsets of $\mathcal{Y}$, where ${\mathcal{S}}_{★}$ and ${\mathcal{S}}^{★}$ are a collection of subsets of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$. $\mathcal{S}$ is said to be an $\mathcal{SR}$-subbase for the topology ${\tau }_{\mathcal{SR}}$ iff the following conditions are satisfied:

(i) ${\mathcal{S}}_{★}\subset {{\tau }_{\mathcal{SR}}}_{★}$ and ${\mathcal{S}}^{★}\subset {{\tau }_{\mathcal{SR}}}^{★}$.

(ii) Finite intersection of elements of ${\mathcal{S}}_{★}$ gives a base for ${{\tau }_{\mathcal{SR}}}_{★}$ and finite intersection of elements of ${\mathcal{S}}^{★}$ gives a base for ${{\tau }_{\mathcal{SR}}}^{★}$.

Definition 14.

In an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ be any $\mathcal{SR}$-subset of $\mathcal{Y}$. Then, the lower closure of $\mathcal{A}$ is the closure of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ in $({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}_{★})$ and is defined as the intersection of all closed supersets of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$, and it is denoted by $C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)$. Also, the upper closure of ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ in $({{\Re }_P}^{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}^{★})$ is the intersection of all closed supersets of ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ and is denoted by $C{l}_{\mathcal{SR}}{{\Re }_P}^{★}\left(\mathcal{A}\right)$. Then, the $\mathcal{SR}$-closure of $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is defined as $C{l}_{\mathcal{SR}}\left(\mathcal{A}\right)=(C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right),C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right))$.

Definition 15.

In an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let $A=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ be any $\mathcal{SR}$-subset of $\mathcal{Y}$. Then, the lower interior of $\mathcal{A}$ is the interior of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ in $({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}_{★})$ and is defined as union of all $\mathcal{SR}$-open subsets of $({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}_{★})$ contained in ${{\Re }_P}_{★}\left(\mathcal{A}\right)$, and it is denoted by $In{t}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)$. Also, the upper interior of ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ in $({{\Re }_P}^{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}^{★})$ is the union of all $\mathcal{SR}$-open subsets of $({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\tau }_{\mathcal{SR}}}_{★})$ contained in ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ and is denoted by $In{t}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right)$. Then, the $\mathcal{SR}$-interior of $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ and is defined as $In{t}_{\mathcal{SR}}\left(\mathcal{A}\right)=(In{t}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right),In{t}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right))$.

Definition 16.

An $\mathcal{SR}$-subset $\mathcal{A}$ of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ is said to be dense in $\mathcal{Y}$ if $C{l}_{\mathcal{SR}}\left(\mathcal{A}\right)=\mathcal{Y}$, i.e., an $\mathcal{SR}$-subset $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is dense in $\mathcal{Y}$ if $C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)={{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and $C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right)={{\Re }_P}^{★}\left(\mathcal{Y}\right)$.

Theorem 3.

An $\mathcal{SR}$-subset $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ of SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ is dense in $\mathcal{Y}$ iff for every non-empty $\mathcal{SR}$-open set $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\ne \varnothing$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right)\ne \varnothing$.

Proof. 

Suppose $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is dense in $\mathcal{Y}$. Then, $C{l}_{\mathcal{SR}}\left(\mathcal{A}\right)=(C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right),$ $C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right))=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))=\mathcal{Y}$. Therefore, $C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)={{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and $C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right)={{\Re }_P}^{★}\left(\mathcal{Y}\right)$. Now, $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ be any non-empty $\mathcal{SR}$-open subset of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$. Then, $\mathcal{A}\cap \mathcal{B}=\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right)\right)$.

Suppose ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)=\varnothing$. Then, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\subseteq \left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)$, which implies $C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)\subseteq \left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)$, since ${{\Re }_P}_{★}\left(\mathcal{B}\right)\in {{\tau }_{\mathcal{SR}}}_{★}$ and, therefore, $\left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)$ is closed. However, $\left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {{\Re }_P}_{★}\left(\mathcal{B}\right)\right)$ is a proper subset of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$, which contradicts $C{l}_{\mathcal{SR}}{{\Re }_P}^{★}\left(\mathcal{A}\right)={{\Re }_P}^{★}\left(\mathcal{Y}\right)$. Hence, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\ne \varnothing$. Similarly, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\ne \varnothing$.

Conversely, suppose $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is a $\mathcal{SR}$-subset of $\mathcal{Y}$ such that for every non-empty $\mathcal{SR}$-open set $\mathcal{B}=({{\Re }_P}_{★}\left(\mathcal{B}\right),{{\Re }_P}^{★}\left(\mathcal{B}\right))$ of $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\ne \varnothing$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)\cap {{\Re }_P}^{★}\left(\mathcal{B}\right)\ne \varnothing$. Let $y\in {{\Re }_P}_{★}\left(\mathcal{Y}\right)$, since ${{\Re }_P}_{★}\left(\mathcal{A}\right)\cap {{\Re }_P}_{★}\left(\mathcal{B}\right)\ne \varnothing$; so, either $y\in {{\Re }_P}_{★}\left(\mathcal{A}\right)$ or it is a limit point of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$. That is, $y\in C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)$. Therefore, ${{\Re }_P}_{★}\left(\mathcal{Y}\right)\subseteq C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)$, which implies $C{l}_{\mathcal{SR}}\left({{\Re }_P}_{★}\left(\mathcal{A}\right)\right)={{\Re }_P}_{★}\left(\mathcal{Y}\right)$. By a similar argument, we can prove that $C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right)={{\Re }_P}^{★}\left(\mathcal{Y}\right)$. Hence $C{l}_{\mathcal{SR}}\left(\mathcal{A}\right)=\left(C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right),C{l}_{\mathcal{SR}}\left({{\Re }_P}^{★}\left(\mathcal{A}\right)\right)\right)=\left({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right)\right)=\mathcal{Y}$. So, $\mathcal{A}$ is dense in $\mathcal{Y}$. □

Definition 17.

In an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. If for $\gamma \in \mathcal{Y}$ there exist an open set ${\mathcal{V}}_1$ of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ such that $\gamma \in {\mathcal{V}}_1\subseteq {\mathcal{N}}_{★}$, where ${\mathcal{N}}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)$, then the subset ${\mathcal{N}}_{★}$ is called ${{\tau }_{\mathcal{SR}}}_{★}-neighborhood$. Similarly, if for $\gamma \in \mathcal{Y}$ there exist an open set ${\mathcal{V}}_2$ of ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$ such that $\gamma \in {\mathcal{V}}_2\subseteq {\mathcal{N}}^{★}$, where ${\mathcal{N}}^{★}\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)$, then the subset ${\mathcal{N}}^{★}$ is called ${{\tau }_{\mathcal{SR}}}^{★}-neighborhood$. If, at the same time, ${\mathcal{N}}_{★}\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${\mathcal{N}}^{★}\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)$, then ${\mathcal{N}}_{\mathcal{SR}}=({\mathcal{N}}_{★},{\mathcal{N}}^{★})$ is said to be a ${\tau }_{\mathcal{SR}}-neighborhood$ of $\gamma \in \mathcal{Y}$.

Proposition 1.

Consider an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ be an $\mathcal{SR}$-subset of $\mathcal{SR}$-set $\mathcal{Y}$ satisfying ${{\Re }_P}_{★}\left(\mathcal{A}\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)$. Then, $\mathcal{A}$ is $\mathcal{SR}$-open iff it is a neighborhood of each of its points.

Proof. 

Suppose that $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ as an open subset of $\mathcal{SR}$-set $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$. Then, for every $\mu \in {{\Re }_P}_{★}\left(\mathcal{A}\right)$, $\mu \in {{\Re }_P}_{★}\left(\mathcal{A}\right)\subset {{\Re }_P}_{★}\left(\mathcal{A}\right)$, and for every $\nu \in {{\Re }_P}^{★}\left(\mathcal{A}\right)$, $\nu \in {{\Re }_P}^{★}\left(\mathcal{A}\right)\subset {{\Re }_P}^{★}\left(\mathcal{A}\right)$. Hence, ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ satisfy the neighborhood definition and are neighborhoods of each point, and, hence, $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is a neighborhood of each of its points.

Conversely, suppose $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is a neighborhood of each of its points. Given the assumption ${{\Re }_P}_{★}\left(\mathcal{A}\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)$, if $\mathcal{A}=\varnothing$, then it is $\mathcal{SR}$-open. For $\mu \in \mathcal{A}$, then there exists an $\mathcal{SR}$-open set $\mathcal{V}=({{\mathcal{V}}_{\mu }}_{★},{{\mathcal{V}}_{\mu }}^{★})$ in $\mathcal{Y}$ such that $\mu \in {{\mathcal{V}}_{\mu }}_{★}\subset {{\Re }_P}_{★}\left(\mathcal{A}\right)$ and $\mu \in {{\mathcal{V}}_{\mu }}^{★}\subset {{\Re }_P}^{★}\left(\mathcal{A}\right)$. This implies ${{\Re }_P}_{★}\left(\mathcal{A}\right)=\bigcup \{{{\mathcal{V}}_{\mu }}_{★}/\mu \in {{\Re }_P}_{★}\left(\mathcal{A}\right)\}$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)=\bigcup \{{{\mathcal{V}}_{\mu }}^{★}/\mu \in {{\Re }_P}^{★}\left(\mathcal{A}\right)\}$. Hence, ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ are $\mathcal{SR}$-open, which implies $\mathcal{A}$ is open. □

4. Continuity in $\mathcal{SR}$-Sets

In this section, we discuss the continuity of functions in $\mathcal{SR}$-topological spaces, the continuous image of an $\mathcal{SR}$-closed set. The $\mathcal{SR}$-homeomorphism is the part of the conversation.

Definition 18.

Let $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ and $(\mathcal{Z},{\rho }_{\mathcal{SR}})$ be topological $\mathcal{SR}$-sets with topologies ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$ and ${\rho }_{\mathcal{SR}}=({{\rho }_{\mathcal{SR}}}_{★},{{\rho }_{\mathcal{SR}}}^{★})$, respectively. A function ${\phi }_1:{{\Re }_P}_{★}\left(\mathcal{Y}\right)\to {{\Re }_P}_{★}\left(\mathcal{Z}\right)$ is continuous at $\mu \in \mathcal{Y}$ iff every ${\rho }_1$-neighborhood ${\mathcal{H}}_1$ of ${\phi }_1\left(\mu \right)$ in ${{\Re }_P}_{★}\left(\mathcal{Z}\right)$ there exists a ${\tau }_1$-neighborhood ${\mathcal{G}}_1$ of μ in ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ such that ${\phi }_1\left({\mathcal{G}}_1\right)\subset {\mathcal{H}}_1$ and ${\phi }_2:{{\Re }_P}^{★}\left(\mathcal{Y}\right)\to {{\Re }_P}^{★}\left(\mathcal{Z}\right)$ is continuous at $\mu \in \mathcal{Z}$ iff every ${\rho }_2$-neighborhood ${\mathcal{H}}_2$ of ${\phi }_2\left(\mu \right)$ in ${{\Re }_P}_{★}\left(\mathcal{Z}\right)$ there exists a ${\tau }_2$-neighborhood ${\mathcal{G}}_2$ of μ in ${{\Re }_P}^{★}\left(\mathcal{Z}\right)$ such that ${\phi }_2\left({\mathcal{G}}_2\right)\subset {\mathcal{H}}_2$. Then, the function $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}\to \mathcal{Z}$ is said to be a continuous function at μ if both ${\phi }_1$ and ${\phi }_2$ are continuous functions at μ.

Example 6.

Assume that $\mathcal{V}=\{{\wp }_1,{\wp }_2,{\wp }_3,{\wp }_4\}$, $\mathcal{E}=\{{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4\}$, $\mathcal{A}=\{{\zeta }_1,{\zeta }_3,{\zeta }_4\}\subset \mathcal{E}$ and $\mathcal{G}=\{({\zeta }_1,({\wp }_1,{\wp }_4),({\zeta }_3,{\wp }_2),({\zeta }_4,{\wp }_3)\}$ is a soft set. Thus, we get $P=(\mathcal{V},\mathcal{G})$ as a soft approximation space. If we take $\mathcal{Y}\subset \mathcal{V}$, where $\mathcal{Y}=\{{\wp }_3,{\wp }_4\}$, then we have ${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\left\{{\wp }_3\right\}$, ${{\Re }_P}^{★}\left(\mathcal{Y}\right)=\{{\wp }_1,{\wp }_3,{\wp }_4\}$ and $Bn{d}_P=\{{\wp }_1,{\wp }_4\}$. Thus, ${\tau }_{\mathcal{SR}}\left(\mathcal{Y}\right)=\{\mathcal{V},\varnothing ,\left\{{\wp }_3\right\},\{{\wp }_1,{\wp }_3,{\wp }_4\},\{{\wp }_1,{\wp }_4\}\}$ is an $\mathcal{SR}$-topology.

Let $\mathcal{W}=\{{\varpi }_1,{\varpi }_2,{\varpi }_3,{\varpi }_4\}$ and $\mathcal{H}=\{({\zeta }_1,\left\{{\varpi }_1\right\}),({\zeta }_3,\{{\varpi }_2,{\varpi }_3\}),({\zeta }_4,\left\{{\varpi }_4\right\})\}$ be a soft set; then, we have $P^{\prime }=(\mathcal{W},\mathcal{H})$ as a soft approximation space. If we take $\mathcal{Z}\subset \mathcal{W}$, where $\mathcal{Z}=\{{\varpi }_3,{\varpi }_4\}$, then ${{\Re }_{P^{\prime }}}_{★}\left(\mathcal{Z}\right)=\left\{{\varpi }_4\right\}$, ${{\Re }_{P^{\prime }}}^{★}\left(\mathcal{Z}\right)=\{{\varpi }_2,{\varpi }_3,{\varpi }_4\}$ and $Bn{d}_{P^{\prime }}=\{{\varpi }_2,{\varpi }_3\}$, and ${\rho }_{\mathcal{SR}}=\{\mathcal{W},\varnothing ,\left\{{\varpi }_4\right\},\{{\varpi }_2,{\varpi }_3,{\varpi }_4\},\{{\varpi }_2,{\varpi }_3\}\}$ is another $\mathcal{SR}$-topology.

Define a function $\phi =({\phi }_1,{\phi }_2):\mathcal{V}\to \mathcal{W}$ such that $\phi \left({\wp }_1\right)={\phi }_2\left({\wp }_1\right)={\varpi }_2$, $\phi \left({\wp }_2\right)={\phi }_2\left({\wp }_2\right)={\varpi }_1$, $\phi \left({\wp }_3\right)={\phi }_1\left({\wp }_3\right)={\phi }_1\left({\wp }_1\right)={\varpi }_4$ and $\phi \left({\wp }_4\right)={\phi }_2\left({\wp }_4\right)={\varpi }_3$. Then, ${\phi }^{-1}\left(\{{\varpi }_2,{\varpi }_3,{\varpi }_4\}\right)=\{{\wp }_1,{\wp }_3,{\wp }_4\}$, ${\phi }^{-1}\left(\{{\varpi }_2,{\varpi }_3\}\right)=\{{\wp }_1,{\wp }_4\}$ and ${\phi }^{-1}\left(\left\{{\varpi }_4\right\}\right)=\left\{{\wp }_3\right\}$. Thus, φ is $\mathcal{SR}$-continuous, since the inverse image for each $\mathcal{SR}$-open set in $\mathcal{W}$ is $\mathcal{SR}$-open in $\mathcal{V}$.

Theorem 4.

Consider $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ and $(\mathcal{Z},{\rho }_{\mathcal{SR}})$ are topological $\mathcal{SR}$-sets and $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}\to \mathcal{Z}$. For every ρ-$\mathcal{SR}$-open set $\mathcal{V}=({\mathcal{V}}_1,{\mathcal{V}}_2),{{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)\subseteq {{\Re }_P}_{★}\left(\mathcal{Y}\right)\subseteq {{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)\subseteq {{\Re }_P}^{★}\left(\mathcal{Y}\right)$. Then, φ is a continuous function if and only if the inverse image of every $\mathcal{SR}$-open set in $\mathcal{Z}$ under φ is $\mathcal{SR}$-open in $\mathcal{Y}$.

Proof. 

Suppose $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}\to \mathcal{Z}$ is a continuous function and $\mathcal{V}=({\mathcal{V}}_1,{\mathcal{V}}_2)$ is an $\mathcal{SR}$-open set in $\mathcal{Z}$. We have to prove that ${\phi }^{-1}\left(\mathcal{V}\right)=\left({{\phi }_1}^{-1}\left({\mathcal{V}}_1\right),{{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)\right)$ is an $\mathcal{SR}$-open set in $\mathcal{Y}$. If ${{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)$ and ${{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)$ are empty, then the result is obvious.

Suppose $\mu \in {{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)\Rightarrow \mu \in {{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)$, that is, ${\phi }_1\left(\mu \right)\in {\mathcal{V}}_1$ and ${\phi }_2\left(\mu \right)\in {\mathcal{V}}_2$. By following the definition of continuity of ${\phi }_1$, there exists a neighborhood ${\mathcal{N}}_1$ of $\mu$ such that ${\phi }_1\left({\mathcal{N}}_1\right)\subset {\mathcal{V}}_1$; then, $\mu \in {\mathcal{N}}_1={{\phi }_1}^{-1}\left(\phi \left({\mathcal{N}}_1\right)\right)\subseteq {{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)$, which implies ${{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)$ is $\mathcal{SR}$-open. Similarly, ${{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)$ is also $\mathcal{SR}$-open. Hence, ${\phi }^{-1}\left(\mathcal{V}\right)$ is $\mathcal{SR}$-open.

Conversely, let ${\phi }^{-1}\left(\mathcal{V}\right)$ be $\mathcal{SR}$-open in $\mathcal{Y}$ for every $\mathcal{SR}$-open set $\mathcal{V}$ in $\mathcal{Z}$. We have to prove that $\phi$ is a continuous function.

Consider $\mu \in \mathcal{Y}$ as an arbitrary point, and ${\phi }_1\left(\mu \right)\in {\mathcal{V}}_1$ implies ${\phi }_2\left(\mu \right)\in {\mathcal{V}}_2$ (by hypothesis). Then, $\mu \in {{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)$ and $\mu \in {{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)$, which means ${\phi }_1\left({{\phi }_1}^{-1}\left({\mathcal{V}}_1\right)\right)\subset {\mathcal{V}}_1$ and ${\phi }_2\left({{\phi }_2}^{-1}\left({\mathcal{V}}_2\right)\right)\subset {\mathcal{V}}_2$ implies that ${\phi }_1$ and ${\phi }_2$ are continuous at $\mu$. Since we take $\mu$ as an arbitrary point, then ${\phi }_1$ and ${\phi }_2$ are continuous everywhere. Hence, $\phi$ is continuous. □

Corollary 1.

A function $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}\to \mathcal{Z}$ is continuous if and only if for every $\mathcal{SR}$-closed subset $\mathcal{C}$ in $\mathcal{Z}$, ${\phi }^{-1}\left(\mathcal{C}\right)$ is $\mathcal{SR}$-closed in $\mathcal{Y}$.

Proof. 

Consider $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))\to \mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ is a continuous function and $\mathcal{C}=({\mathcal{C}}_1,{\mathcal{C}}_2)$ is an arbitrary $\mathcal{SR}$-closed subset of $\mathcal{Z}$. Then, ${{\Re }_P}_{★}\left(\mathcal{Z}\right)\setminus {\mathcal{C}}_1$ and ${{\Re }_P}^{★}\left(\mathcal{Z}\right)\setminus {\mathcal{C}}_2$ are $\mathcal{SR}$-open in $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${{\phi }_1}^{-1}({{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {\mathcal{C}}_1)={{\Re }_P}_{★}\left(\mathcal{Y}\right)\setminus {{\phi }_1}^{-1}\left({\mathcal{C}}_1\right)$ and ${{\phi }_1}^{-1}({{\Re }_P}^{★}\left(\mathcal{Y}\right)\setminus {\mathcal{C}}_2)={{\Re }_P}^{★}\left(\mathcal{Y}\right)\setminus {{\phi }_1}^{-1}\left({\mathcal{C}}_2\right)$, which implies that ${{\phi }_1}^{-1}\left({\mathcal{C}}_1\right)$ and ${{\phi }_1}^{-1}\left({\mathcal{C}}_2\right)$ are closed in ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, respectively. Hence, ${\phi }^{-1}\left(\mathcal{C}\right)$ is $\mathcal{SR}$-closed in $\mathcal{Y}$.

Conversely, suppose that for any $\mathcal{SR}$-closed subset $\mathcal{C}=({\mathcal{C}}_1,{\mathcal{C}}_2)$ in $\mathcal{Z}$, ${\phi }^{-1}\left(\mathcal{C}\right)$ is $\mathcal{SR}$-closed in $\mathcal{Y}$. Let $\mathcal{V}=({\mathcal{V}}_1,{\mathcal{V}}_2)$ be any $\mathcal{SR}$-open subset of $\mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$. Then, $\mathcal{Z}\setminus \left(\mathcal{V}\right)=\left({{\Re }_P}_{★}\left(\mathcal{Z}\right)\setminus \left({\mathcal{V}}_1\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right)\setminus \left({\mathcal{V}}_2\right)\right)$ is $\mathcal{SR}$-closed and ${\phi }^{-1}(\mathcal{Z}\setminus \mathcal{V})=\left({{\phi }_1}^{-1}({{\Re }_P}_{★}\left(\mathcal{Z}\right)\setminus {\mathcal{V}}_1),{{\phi }_2}^{-1}({{\Re }_P}^{★}\left(\mathcal{Z}\right)\setminus {\mathcal{V}}_2)\right)$ = ${\phi }^{-1}\left(\mathcal{Z}\right)\setminus {\phi }^{-1}\left(\mathcal{V}\right)=\mathcal{Z}\setminus {\phi }^{-1}\left(\mathcal{V}\right)$ is $\mathcal{SR}$-closed in $\mathcal{Y}$, which implies ${\phi }^{-1}\left(\mathcal{V}\right)$ is $\mathcal{SR}$-open in $\mathcal{Y}$. Thus, $\phi$ is continuous. □

Remark 2.

1. Every restriction of a continuous mapping is also continuous.

Let $\psi =({\psi }_1,{\psi }_2):\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))\to \mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ be a continuous function and $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ be a $\mathcal{SR}$-subset of $\mathcal{Y}$. Then, the restriction ${\psi |}_{\mathcal{A}}={\psi }_{\mathcal{A}}:\mathcal{A}\to \mathcal{Z}$ of ψ to $\mathcal{A}$ is continuous. This is so because for each $\mathcal{SR}$-open subset W in $\mathcal{Z}$, ${{\psi }_{\mathcal{A}}}^{-1}\left(W\right)={\psi }^{-1}\left(W\right)\cap \mathcal{A}$, which is $\mathcal{SR}$-open in $\mathcal{A}$.

2. Consider ${\beta }_{\mathcal{SR}}=({\beta }_{★},{\beta }^{★})$ as a base for a $\mathcal{SR}$-topology on $\mathcal{Z}$. Then, the function $\psi :\mathcal{Y}\to \mathcal{Z}$ is continuous if and only if, for each $\mathcal{SR}$-basic open set in $\mathcal{Z}$, ${\psi }^{-1}\left(\beta \right)$ is $\mathcal{SR}$-open in $\mathcal{Y}$.

3. A function $\psi :\mathcal{Y}\to \mathcal{Z}$ is open if the image of every $\mathcal{SR}$-open set in $\mathcal{Y}$ is $\mathcal{SR}$-open.

4. A function $\psi :\mathcal{Y}\to \mathcal{Y}$ is closed if the image of every $\mathcal{SR}$-closed set in $\mathcal{Y}$ is $\mathcal{SR}$-closed.

Definition 19.

Let $(\mathcal{Y},{\tau }_{\mathcal{SR}})$ and $(\mathcal{Z},{\rho }_{\mathcal{SR}})$ be topological $\mathcal{SR}$-sets. A function $\phi =({\phi }_1,{\phi }_2):\mathcal{Y}\to \mathcal{Z}$ is known as $\mathcal{SR}$-homeomorphism if

(i) φ is $\mathcal{SR}$-bijective.

(ii) φ is $\mathcal{SR}$-continuous.

(iii) ${\phi }^{-1}$ is $\mathcal{SR}$-continuous.

Two soft rough topological spaces (SRTS) are said to be $\mathcal{SR}$-homeomorphic if there is a $\mathcal{SR}$-homeomorphism between $\mathcal{Y}$ and $\mathcal{Z}$.

Definition 20.

Consider $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and $\mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ as two topological $\mathcal{SR}$-sets with topologies ${\tau }_{\mathcal{SR}}=({\tau }_1,{\tau }_2)$ and ${\rho }_{\mathcal{SR}}=({\rho }_1,{\rho }_2)$, respectively, and $\mathcal{Y}\times \mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Y}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right))$ is the Cartesian product of $\mathcal{Y}$ and $\mathcal{Z}$. The topology ${\xi }_1$ on ${{\Re }_P}_{★}\left(\mathcal{Y}\right)\times {{\Re }_P}_{★}\left(\mathcal{Y}\right)$ containing a gathering of open sets of the form ${\mathcal{L}}_1\times {\mathcal{M}}_1$, where ${\mathcal{L}}_1$ is a ${\tau }_1-\mathcal{SR}$-open and ${\mathcal{M}}_1$ is a ${\rho }_1-\mathcal{SR}$-open, as basis, is known as the product topology. Similarly, the topology ${\xi }_2$ on ${{\Re }_P}^{★}\left(\mathcal{Y}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right)$ is the topology containing a gathering of open sets of the form ${\mathcal{L}}_2\times {\mathcal{M}}_2$, where ${\mathcal{L}}_2$ is a ${\tau }_2-\mathcal{SR}$-open and ${\mathcal{M}}_2$ is a ${\rho }_2-\mathcal{SR}$-open, as basis, is known as the product topology. Hence, the topology $\xi =({\xi }_1,{\xi }_2)$ is called thte product topology on $\mathcal{Y}\times \mathcal{Z}$.

Definition 21.

Consider $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and $\mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ as two topological $\mathcal{SR}$-sets with topologies ${\tau }_{\mathcal{SR}}=({\tau }_1,{\tau }_2)$ and ${\rho }_{\mathcal{SR}}=({\rho }_1,{\rho }_2)$, respectively. The mapping ${{\prod }_{\mu }}_{★}={{\Re }_P}_{★}\left(\mathcal{Y}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right)\to {{\Re }_P}_{★}\left(\mathcal{Y}\right)$ and ${{\prod }_{\mu }}^{★}={{\Re }_P}^{★}\left(\mathcal{Y}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right)\to {{\Re }_P}^{★}\left(\mathcal{Y}\right)$, defined as ${{\prod }_{\mu }}_{★}\left((\mu ,\nu )\right)=\mu ,\forall (\mu ,\nu )\in {{\Re }_P}_{★}\left(\mathcal{Y}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right)$ and ${{\prod }_{\mu }}^{★}\left((\mu ,\nu )\right)=\mu ,\forall (\mu ,\nu )\in {{\Re }_P}^{★}\left(\mathcal{Y}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right)$, respectively, are known as projection mappings. Then, ${\prod }_{\mu }=\left({{\prod }_{\mu }}_{★},{{\prod }_{\mu }}^{★}\right)$ is known as the projection mapping from $\mathcal{Y}\times \mathcal{Z}\to \mathcal{Y}$. Similarly, we can define the projection mapping ${\prod }_{\nu }=\left({{\prod }_{\nu }}_{★},{{\prod }_{\nu }}^{★}\right)$ from $\mathcal{Y}\times \mathcal{Z}\to \mathcal{Y}$.

Theorem 5.

Consider $\mathcal{Y}$ and $\mathcal{Z}$ as two topological $\mathcal{SR}$-sets and $\mathcal{Y}\times \mathcal{Z}$ as the product space. Then, the projections ${\prod }_{\mu }$ and ${\prod }_{\nu }$ are continuous mappings.

Proof. 

Suppose $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and $\mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ are two topological $\mathcal{SR}$-sets with topologies ${\tau }_{\mathcal{SR}}=({\tau }_1,{\tau }_2)$ and ${\rho }_{\mathcal{SR}}=({\rho }_1,{\rho }_2)$, respectively. Let $\xi$ be the product topology on $\mathcal{Y}\times \mathcal{Y}$ and $\mathcal{L}=({{\Re }_P}_{★}\left(\mathcal{L}\right),{{\Re }_P}^{★}\left(\mathcal{L}\right))$ be an $\tau -\mathcal{SR}$-open set. Then, ${{{\prod }_{\mu }}_{★}}^{-1}\left({{\Re }_P}_{★}\left(\mathcal{L}\right)\right)={{\Re }_P}_{★}\left(\mathcal{L}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right)$, where ${{\Re }_P}_{★}\left(\mathcal{L}\right)\in {\tau }_1$ and ${{\Re }_P}_{★}\left(\mathcal{Z}\right)\in {\rho }_1$ imply that ${{\Re }_P}_{★}\left(\mathcal{L}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right)$ belongs to the basis for ${\tau }_1$. Also, ${{{\prod }_{\mu }}^{★}}^{-1}\left({{\Re }_P}^{★}\left(\mathcal{L}\right)\right)={{\Re }_P}^{★}\left(\mathcal{L}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right)$, where ${{\Re }_P}^{★}\left(\mathcal{L}\right)\in {\tau }_2$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)\in {\rho }_2$ imply ${{\Re }_P}^{★}\left(\mathcal{L}\right)\times {{\Re }_P}^{★}\left(\mathcal{Y}\right)$ belongs to the basis for ${\tau }_2$, which implies that $\left({{\Re }_P}_{★}\left(\mathcal{L}\right)\times {{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{L}\right)\times {{\Re }_P}^{★}\left(\mathcal{Z}\right)\right)$. Thus, ${{\prod }_{\alpha }}_{★}$ and ${{\prod }_{\alpha }}^{★}$ are continuous mappings. Therefore, ${\prod }_{\alpha }=\left({{\prod }_{\mu }}_{★},{{\prod }_{\mu }}^{★}\right)$ is a continuous mapping. Similarly, we can show that ${\prod }_{\nu }=\left({{\prod }_{\nu }}_{★},{{\prod }_{\nu }}^{★}\right)$ is also a continuous mapping. □

5. Compactness in $\mathcal{SR}$-Set

In this section, we study the compactness of $\mathcal{SR}$-topological spaces, discuss images of $\mathcal{SR}$-compact spaces, and prove some basic results.

Definition 22.

Let $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ be a $\mathcal{SR}$-set. For any open covering ${\mathfrak{V}}_1=\{V_{\mu }/i\in \Omega \}$ of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$, if we get a finite subcovering ${{\mathfrak{V}}_1}^F=\{V_{\mu }/i=1,2,ߪ,m\}$, then ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ is said to be the compact lower approximation of $\mathcal{Y}$. Similarly, for any open covering ${\mathfrak{V}}_2=\{V_j/j\in \Omega \}$ of ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$, if we get a finite subcovering ${{\mathfrak{V}}_2}^F=\{V_j/j=1,2,ߪ,n\}$, then ${{\Re }_P}^{★}\left(\mathcal{Y}\right)$ is said to be the compact upper approximation of $\mathcal{Y}$. Then, the $\mathcal{SR}$-set $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ is known as a compact $\mathcal{SR}$-set.

Definition 23.

Suppose $\mathcal{A}=({{\Re }_P}_{★}\left(\mathcal{A}\right),{{\Re }_P}^{★}\left(\mathcal{A}\right))$ is an $\mathcal{SR}$ subset of $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$. If, for any open covering $\mathfrak{W}=\{W_j/j\in \Omega \}$ of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$, we get a finite subcovering ${\mathfrak{V}}^F=\{V_j/j=1,2,ߪ,n\}$ of ${{\Re }_P}_{★}\left(\mathcal{A}\right)$, then ${{\Re }_P}_{★}\left(\mathcal{A}\right)$ as the subset of ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ is said to be compact. If, at the same time, ${{\Re }_P}^{★}\left(\mathcal{A}\right)$ is also compact, then we call $\mathcal{A}$ a compact $\mathcal{SR}$-subset of $\mathcal{Y}$.

Theorem 6.

The continuous image of a compact topological $\mathcal{SR}$-set is compact.

Proof. 

Consider $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ as a compact $\mathcal{SR}$-set and suppose that $\psi =({\psi }_1,{\psi }_2):({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))\to ({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ is a continuous mapping. Then, ${\psi }_1:{{\Re }_P}_{★}\left(\mathcal{Y}\right)\to {{\Re }_P}_{★}\left(\mathcal{Z}\right)$ and ${\psi }_2:{{\Re }_P}^{★}\left(\mathcal{Y}\right)\to {{\Re }_P}^{★}\left(\mathcal{Z}\right)$ individually are continuous mappings. Let ${\mathcal{C}}_1=\{W_{\nu }/\nu \in \Omega \}$ be an open covering of ${{\Re }_P}_{★}\left(\mathcal{Z}\right)$. Then, ${{\psi }_1}^{-1}\left({\mathcal{C}}_1\right)=\{{{\psi }_1}^{-1}\left(W_{\nu }\right)/\nu \in \Omega \}$ is an open covering for ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$. Since ${{\Re }_P}_{★}\left(\mathcal{Y}\right)$ is compact, then, by definition of compactness, it has a finite subcovering, and there are indices ${\nu }_1{\nu }_2,...,{\nu }_m$ such that ${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\bigcup _{i=1}^m{{\psi }_1}^{-1}\left({\mathcal{C}}_1\right)$. ${\psi }_1\left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\right)\subseteq \bigcup _{i=1}^m\left({\mathcal{C}}_1\right)\subseteq {\psi }_1\left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\right)$. Therefore, $\{{W_{\nu }}_{\mu }/i=1,2,3,...,m\}$ is a finite subcovering of $\psi \left({{\Re }_P}_{★}\left(\mathcal{Y}\right)\right)={{\Re }_P}_{★}\left(\mathcal{Z}\right)$. So, ${{\Re }_P}_{★}\left(\mathcal{Z}\right)$ is also compact. Similarly, we can show that ${{\Re }_P}^{★}\left(\mathcal{Z}\right)$ is compact and, hence, $\mathcal{Z}=({{\Re }_P}_{★}\left(\mathcal{Z}\right),{{\Re }_P}^{★}\left(\mathcal{Z}\right))$ is a compact $\mathcal{SR}$-set. □

Corollary 2.

The homeomorphic image of a compact $\mathcal{SR}$-space is compact.

Remark 3.

In topological $\mathcal{SR}$-sets, compactness is a topological property.

Definition 24.

Consider an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$. Let $\Gamma =\{{\mathcal{A}}_{\mu }=({{\Re }_P}_{★}\left({\mathcal{A}}_{\mu }\right),{{\Re }_P}^{★}\left({\mathcal{A}}_{\mu }\right)):\mu \in \Lambda \}$ be a collection of $\mathcal{SR}$-subsets of $\mathcal{Y}$. If every finite subcollection of Γ has a non-empty intersection, which means that if we consider any finite subset ${\Lambda }_1$ of Λ, we get ${\bigcap }_{\nu \in {\Lambda }_1}{\mathcal{A}}_{\nu }\ne \varnothing$, then the finite intersection property holds in collection Γ.

Theorem 7.

Consider an SRTS $(\mathcal{Y},{\tau }_{\mathcal{SR}})$, where $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ and ${\tau }_{\mathcal{SR}}=({{\tau }_{\mathcal{SR}}}_{★},{{\tau }_{\mathcal{SR}}}^{★})$; $\mathcal{Y}$ is $\mathcal{SR}$-compact iff every collection of $\mathcal{SR}$-closed subsets in $\mathcal{Y}$ following the finite intersection property itself has non-empty intersections.

Proof. 

First, we suppose $\mathcal{Y}$ is $\mathcal{SR}$-compact and $\Gamma =\{{\mathcal{D}}_{\mu }=({{\Re }_P}_{★}\left({\mathcal{D}}_{\mu }\right),{{\Re }_P}^{★}\left({\mathcal{D}}_{\mu }\right)):\mu \in \Lambda \}$ is an arbitrary collection of $\mathcal{SR}$-closed sets satisfying the finite intersection property. We have to prove that the collection $\{{\mathcal{D}}_{\mu }=({{\Re }_P}_{★}\left({\mathcal{D}}_{\mu }\right),{{\Re }_P}^{★}\left({\mathcal{D}}_{\mu }\right)):\mu \in \Lambda \}$ itself has non-empty intersection. Suppose, on the contrary, that $\bigcap _{\mu \in \Lambda }{\mathcal{D}}_{\mu }=\varnothing$. By taking the complement ${\left(\bigcap _{\mu \in \Lambda }{\mathcal{D}}_{\mu }\right)}^{{}^{\prime }}={\varnothing }^{{}^{\prime }}$, we have $\mathcal{Y}=\bigcup _{\mu \in \Lambda }{\mathcal{D}}_{\mu }^{{}^{\prime }}$, which implies $\{{{\mathcal{D}}_{\mu }}^{{}^{\prime }}=({{\Re }_P}_{★}\left({{\mathcal{D}}_{\mu }}^{{}^{\prime }}\right),{{\Re }_P}^{★}\left({{\mathcal{D}}_{\mu }}^{{}^{\prime }}\right)):\mu \in \Lambda \}$ is an open cover for $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$. By our assumption, $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ is $\mathcal{SR}$-compact, and there are indices ${\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_k$ such that ${{\Re }_P}_{★}\left(\mathcal{Y}\right)=\bigcup _{\iota =1}^k{{\Re }_P}_{★}\left({{{\mathcal{D}}_{\mu }}_{\iota }}^{{}^{\prime }}\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)=\bigcup _{\iota =1}^k{{\Re }_P}^{★}\left({{{\mathcal{D}}_{\mu }}_{\iota }}^{{}^{\prime }}\right)$. Again, by taking the complement, we get $\bigcap _{\iota =1}^k{{\Re }_P}_{★}\left({{\mathcal{D}}_{\mu }}_{\iota }\right)=\varnothing$ and $\bigcap _{\iota =1}^k{{\Re }_P}^{★}\left({{\mathcal{D}}_{\mu }}_{\iota }\right)=\varnothing$, that is, $\bigcap _{\iota =1}^k{{\mathcal{D}}_{\mu }}_{\iota }=\left(\bigcap _{\iota =1}^k{{\Re }_P}_{★}\left({{\mathcal{D}}_{\mu }}_{\iota }\right),\bigcap _{\iota =1}^k{{\Re }_P}^{★}\left({{\mathcal{D}}_{\mu }}_{\iota }\right)\right)=\varnothing$, which contradicts the finite intersection property. So, our assumption is wrong and $\bigcap _{\mu \in \Lambda }{\mathcal{D}}_{\mu }\ne \varnothing$.

Conversely, suppose that every collection of $\mathcal{SR}$-closed sets satisfying the finite intersection property has a non-empty intersection itself. We now have to prove that $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ is $\mathcal{SR}$-compact. For this, let us consider $\{{\mathcal{V}}_{\epsilon }=({{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)):\epsilon \in {\rm Y}\}$ as an open cover of $\mathcal{Y}$, i.e., $\mathcal{Y}=\left({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right)\right)=\left(\bigcup _{\epsilon \in {\rm Y}}{{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),\bigcup _{\epsilon \in {\rm Y}}{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)\right)$. To prove that $\mathcal{Y}$ is $\mathcal{SR}$-compact, we have to show that this open cover has a finite subcover. On the contrary, suppose that there does not exist any finite subcover for this open cover. Then, for any finite subcover ${{\rm Y}}_1$ of ${\rm Y}$, $\bigcup _{ϵ\in {{\rm Y}}_1}{\mathcal{V}}_{ϵ}\ne \mathcal{Y}$, i.e., $\left(\bigcup _{ϵ\in {{\rm Y}}_1}{{\Re }_P}_{★}\left({\mathcal{V}}_{ϵ}\right),\bigcup _{ϵ\in {{\rm Y}}_1}{{\Re }_P}^{★}\left({\mathcal{V}}_{ϵ}\right)\right)\ne \left({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right)\right)$. This implies $\bigcap _{ϵ\in {{\rm Y}}_1}{{\mathcal{V}}_{ϵ}}^{{}^{\prime }}\ne \varnothing$. Now, $\{{{\mathcal{V}}_{\epsilon }}^{{}^{\prime }}=({{\Re }_P}_{★}\left({{\mathcal{V}}_{\epsilon }}^{{}^{\prime }}\right),{{\Re }_P}^{★}\left({{\mathcal{V}}_{\epsilon })}^{{}^{\prime }}\right):\epsilon \in {\rm Y}\}$ is a collection of $\mathcal{SR}$-closed sets satisfying the finite intersection property, so $\bigcap _{\epsilon \in {{\rm Y}}_1}{{\mathcal{V}}_{\epsilon }}^{{}^{\prime }}\ne \varnothing$ i.e., $\left(\bigcap _{\epsilon \in {\rm Y}}{{\Re }_P}_{★}\left({{\mathcal{V}}_{\epsilon }}^{{}^{\prime }}\right),\bigcap _{\epsilon \in {\rm Y}}{{\Re }_P}^{★}\left({{\mathcal{V}}_{\epsilon }}^{{}^{\prime }}\right)\right)\ne \varnothing$. By taking the complement, we get $\left(\bigcup _{\epsilon \in {\rm Y}}{{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),\bigcup _{\epsilon \in {\rm Y}}{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)\right)\ne \left({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right)\right)$, which contradicts our supposition that $\{{\mathcal{V}}_{\epsilon }=({{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)):\epsilon \in {\rm Y}\}$ is an open cover of $\mathcal{Y}$. Hence, $\{{\mathcal{V}}_{\epsilon }=({{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)):\epsilon \in {\rm Y}\}$ has a finite subcover, so $\mathcal{Y}$ is $\mathcal{SR}$-compact. □

Theorem 8.

Every $\mathcal{SR}$-closed subset of $\mathcal{SR}$-compact space is $\mathcal{SR}$-compact.

Proof. 

Let $\mathcal{Y}$ be an $\mathcal{SR}$-compact space and $\mathcal{D}=({{\Re }_P}_{★}\left(\mathcal{D}\right),{{\Re }_P}^{★}\left(\mathcal{D}\right))$ be a $\mathcal{SR}$-closed subset of $\mathcal{Y}$. Let $\{{\mathcal{V}}_{\epsilon }=({{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right),{{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)):\epsilon \in {\rm Y}\}$ be an open cover for $\mathcal{D}=({{\Re }_P}_{★}\left(\mathcal{D}\right),{{\Re }_P}^{★}\left(\mathcal{D}\right))$; there exist an $\mathcal{SR}$-open set ${\mathcal{W}}_{\epsilon }=({{\Re }_P}_{★}\left({\mathcal{W}}_{\epsilon }\right),{{\Re }_P}^{★}\left({\mathcal{W}}_{\epsilon }\right))$ in $\mathcal{Y}=({{\Re }_P}_{★}\left(\mathcal{Y}\right),{{\Re }_P}^{★}\left(\mathcal{Y}\right))$ such that ${\mathcal{V}}_{\epsilon }={\mathcal{W}}_{\epsilon }\cap \mathcal{D},\epsilon \in {\rm Y}$, i.e., ${{\Re }_P}_{★}\left({\mathcal{V}}_{\epsilon }\right)={{\Re }_P}_{★}\left({\mathcal{W}}_{\epsilon }\right)\cap {{\Re }_P}_{★}\left(\mathcal{D}\right)$ and ${{\Re }_P}^{★}\left({\mathcal{V}}_{\epsilon }\right)={{\Re }_P}^{★}\left({\mathcal{W}}_{\epsilon }\right)\cap {{\Re }_P}^{★}\left(\mathcal{D}\right)$. The collection $\{{\mathcal{D}}^{{}^{\prime }},{\mathcal{W}}_{\epsilon }:\epsilon \in {\rm Y}\}$ is an open cover for $\mathcal{Y}$. Since $\mathcal{Y}$ is compact, there exists a finite subcover $\{{\mathcal{D}}^{{}^{\prime }},{\mathcal{W}}_{\epsilon }:\epsilon \in {\rm Y}\}$ of $\mathcal{Y}$, that is, $\mathcal{Y}={\mathcal{D}}^{{}^{\prime }}\bigcup _{\iota =1}^k{{\mathcal{W}}_{\epsilon }}_{\iota }$, which implies ${{\Re }_P}_{★}\left(\mathcal{Y}\right)={{\Re }_P}_{★}\left({\mathcal{D}}^{{}^{\prime }}\right)\bigcup _{\iota =1}^k{{\Re }_P}_{★}\left({{\mathcal{W}}_{\epsilon }}_{\iota }\right)$ and ${{\Re }_P}^{★}\left(\mathcal{Y}\right)={{\Re }_P}^{★}\left({\mathcal{D}}^{{}^{\prime }}\right)\bigcup _{\iota =1}^k{{\Re }_P}^{★}\left({{\mathcal{W}}_{\epsilon }}_{\iota }\right)$. $\mathcal{D}=\mathcal{Y}\cap \mathcal{D}=\left({{\Re }_P}_{★}\left({\mathcal{D}}^{{}^{\prime }}\right)\cap \bigcup _{\iota =1}^k{{\Re }_P}_{★}({{\mathcal{W}}_{\epsilon }}_{\iota },{{\Re }_P}^{★}\left({\mathcal{D}}^{{}^{\prime }}\right)\cap \bigcup _{\iota =1}^k{{\Re }_P}^{★}({{\mathcal{W}}_{\epsilon }}_{\iota }\right)$ = $\left(\bigcup _{\iota =1}^k{{\Re }_P}_{★}\left({{\mathcal{V}}_{\epsilon }}_{\iota }\right),\bigcup _{\iota =1}^k{{\Re }_P}_{★}\left({{\mathcal{V}}_{\epsilon }}_{\iota }\right)\right)$, which indicates $\mathcal{D}=({{\Re }_P}_{★}\left(\mathcal{D}\right),{{\Re }_P}^{★}\left(\mathcal{D}\right))$ is $\mathcal{SR}$-compact. □

6. Application of $\mathcal{SR}$-Set in Multi-Attribute Group Decision Making

Decision-making performs a vital role in our daily life, and this process yields the best alternative among different choices. In this section, we present an application of an $\mathcal{SR}$-set in multi-attribute group decision making (MAGDM) for cosmetic brand selection. First, we present Algorithm 1 and its flowchart for multi-attribute group decision making.

Algorithm 1 The scheme of the algorithm is given as.

Step-1: Write the soft set $\mathfrak{G}=(\mathcal{T},\mathcal{A})$ which describes the given data.

Step-2: Based on initial assessment results of the group of analysts $\mathcal{S}$, define a soft set.

Step-3: Obtain an $\mathcal{SR}$-approximations in the form of soft sets ${\Lambda }_{★}=({\lambda }_{★},\mathcal{S})$ and ${\Lambda }^{★}=({\lambda }^{★},\mathcal{S})$.

Step-4: Define fuzzy sets ${{\nu }_{\Lambda }}_{★}$, ${\nu }_{\Lambda }$ and ${{\nu }_{\Lambda }}^{★}$ corresponding to the soft sets ${\Lambda }_{★}=({\lambda }_{★},\mathcal{S})$, $\Lambda =(\lambda ,\mathcal{S})$ and ${\Lambda }^{★}=({\lambda }^{★},\mathcal{S})$ defined by the formulas: $${{\nu }_{\Lambda }}_{★}\left({\alpha }_k\right)=\frac{1}{m}\sum _{\iota =1}^m{C}_{{\lambda }_{★}{D}_{\iota }}\left({\alpha }_k\right),$$

$${\nu }_{\Lambda }\left({\alpha }_k\right)=\frac{1}{m}\sum _{\iota =1}^m{C}_{\lambda D_{\iota }}\left({\alpha }_k\right),$$

$${{\nu }_{\Lambda }}^{★}\left({\alpha }_k\right)=\frac{1}{m}\sum _{\iota =1}^m{C}_{{\lambda }^{★}{D}_{\iota }}\left({\alpha }_k\right).$$

Step-6: Find the final decision set by adding ${\Lambda }_{★}$, $\Lambda$, and ${\Lambda }^{★}$, calculated as

$${\Lambda }_{★}+\Lambda +{\Lambda }^{★}={{\nu }_{\Lambda }}_{★}\left({\alpha }_k\right)+{\nu }_{\Lambda }\left({\alpha }_k\right)+{{\nu }_{\Lambda }}^{★}\left({\alpha }_k\right)-({{\nu }_{\Lambda }}_{★}\left({\alpha }_k\right)*{\nu }_{\Lambda }\left({\alpha }_k\right)*{{\nu }_{\Lambda }}^{★}\left({\alpha }_k\right))$$

Step-7: Finally, the alternative having the maximum decision value can be chosen as the optimal solution.

Now we present flow chart Algorithm 1 as given by Figure 1 and its flowchart for multi-attribute group decision making.

Example 7.

The trade of quality cosmetics is growing rapidly among the lower-middle class of developing countries like Pakistan and India. Assume that a popular departmental store of the city wants to make a contract with a multinational company for the production of cosmetics. The managing committee of the store consist of three managers, $\mathcal{S}=\{M_1,M_2,M_3\}$: the product manager, marketing manager, and accounts manager. The team of these three managers is elected to choose one brand which covers the major production of cosmetics. They consider seven brands: $\mathcal{V}=\{{\hslash }_1,{\hslash }_2,{\hslash }_3,{\hslash }_4,{\hslash }_5,{\hslash }_6,{\hslash }_7,{\hslash }_8\}$, where

${\hslash }_1$: Loreal,

${\hslash }_2$: Maybelline,

${\hslash }_3$: Remmil,

${\hslash }_4$: Art Deco,

${\hslash }_5$: Essence,

${\hslash }_6$: Color Studio,

${\hslash }_7$: Mac,

${\hslash }_8$: Sephora.

They define a set of criteria for the selection of a suitable brand for their store as follows, $\mathcal{E}=\{{\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,{\rho }_5,{\rho }_6,{\rho }_7,{\rho }_8\}$, where

${\rho }_1$: Product quality

${\rho }_2$: Relationship closeness (customer–brand relationship)

${\rho }_3$: Delivery performance

${\rho }_4$: Price stability

${\rho }_5$: Plans for major events

${\rho }_6$: Distribution plans (in-store furniture)

${\rho }_7$: Recovery services in case of damages

${\rho }_8$: Shopper marketing activities.

We construct a soft set $\mathfrak{G}=(\mathcal{T},\mathcal{A})$ which explains the qualities of the brands under consideration. The tabular form of the soft set is given in

Table 2. Soft set $(\mathcal{T},\mathcal{A})$.

$(\mathcal{T},\mathcal{A})$	${\mathit{\rho }}_{\mathbf{1}}$	${\mathit{\rho }}_{\mathbf{2}}$	${\mathit{\rho }}_{\mathbf{3}}$	${\mathit{\rho }}_{\mathbf{4}}$	${\mathit{\rho }}_{\mathbf{5}}$	${\mathit{\rho }}_{\mathbf{6}}$	${\mathit{\rho }}_{\mathbf{7}}$	${\mathit{\rho }}_{\mathbf{8}}$
${\hslash }_1$	1	0	1	1	0	1	0	0
${\hslash }_2$	1	0	1	1	1	1	0	1
${\hslash }_3$	0	1	0	1	0	0	1	0
${\hslash }_4$	0	1	0	1	0	0	0	0
${\hslash }_5$	1	0	1	0	0	1	0	1
${\hslash }_6$	0	1	1	1	0	0	0	0
${\hslash }_7$	1	0	1	1	0	1	1	0
${\hslash }_8$	0	1	0	1	0	0	1	0

.

Let $X_i$ be the initial assessment result of the manager team. We represent this evaluation by means of a soft set $\Lambda =(\lambda ,\mathcal{S})$ whose tabular representation is given by

Table 3. Soft set $(\lambda ,\mathcal{S})$.

	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{3}}$
${\hslash }_1$	1	0	1
${\hslash }_2$	1	0	1
${\hslash }_3$	0	1	0
${\hslash }_4$	0	1	0
${\hslash }_5$	0	0	1
${\hslash }_6$	1	0	1
${\hslash }_7$	1	0	1
${\hslash }_8$	0	1	0

.

From this soft set $\Lambda =(\lambda ,\mathcal{S})$, the primary evaluation result of experts is

$$\begin{array}{c}{\mathit{X}}_{\mathit{1}}=\lambda \left(D_1\right)=\{{\hslash }_1,{\hslash }_2,{\hslash }_6,{\hslash }_7\},\hfill \\ {\mathit{X}}_{\mathit{2}}=\lambda \left(D_2\right)=\{{\hslash }_3,{\hslash }_4,{\hslash }_7,{\hslash }_8\},\hfill \\ {\mathit{X}}_{\mathit{3}}=\lambda \left(D_3\right)=\{{\hslash }_1,{\hslash }_2,{\hslash }_5,{\hslash }_6\}\hfill \end{array}$$

Now, we find the $\mathcal{SR}$-approximations as

$$\begin{array}{c}{\lambda }_{★}\left(D_1\right)={{\Re }_P}_{★}\left({\mathit{X}}_{\mathit{1}}\right)=\left\{{\hslash }_1\right\},\hfill \\ {\lambda }_{★}\left(D_2\right)={{\Re }_P}_{★}\left({\mathit{X}}_{\mathit{2}}\right)=\{{\hslash }_3,{\hslash }_7,{\hslash }_8\},\hfill \\ {\lambda }_{★}\left(D_3\right)={{\Re }_P}_{★}\left({\mathit{X}}_{\mathit{3}}\right)=\{{\hslash }_2,{\hslash }_5\},\hfill \end{array}$$

and

$$\begin{array}{c}{\lambda }^{★}\left(D_1\right)={{\Re }_P}^{★}\left({\mathit{X}}_{\mathit{1}}\right)=\mathcal{V},\hfill \\ {\lambda }^{★}\left(D_2\right)={{\Re }_P}^{★}\left({\mathit{X}}_{\mathit{2}}\right)=\mathcal{V},\hfill \\ {\lambda }^{★}\left(D_3\right)={{\Re }_P}^{★}\left({\mathit{X}}_{\mathit{3}}\right)=\mathcal{V}.\hfill \end{array}$$

Following these $\mathcal{SR}$-approximations, we get two soft sets, ${\Lambda }_{★}=({\lambda }_{★},\mathcal{S})$ and ${\Lambda }^{★}=({\lambda }^{★},\mathcal{S})$, where ${\lambda }_{★}\left(D_i\right)={{\Re }_P}_{★}($ Xi) and ${\lambda }^{★}\left(D_i\right)={{\Re }_P}^{★}($ Xi). Tabular representation of these soft sets are given in

Table 4. Soft set ${\Lambda }_{★}$.

	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{3}}$
${\hslash }_1$	0	0	0
${\hslash }_2$	1	0	1
${\hslash }_3$	0	1	0
${\hslash }_4$	0	0	0
${\hslash }_5$	0	0	1
${\hslash }_6$	0	0	0
${\hslash }_7$	0	1	0
${\hslash }_8$	0	1	0

and

Table 5. Soft set ${\Lambda }^{★}$.

	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{3}}$
${\hslash }_1$	1	1	1
${\hslash }_2$	1	1	1
${\hslash }_3$	1	1	1
${\hslash }_4$	1	1	1
${\hslash }_5$	1	1	1
${\hslash }_6$	1	1	1
${\hslash }_7$	1	1	1
${\hslash }_8$	1	1	1

.

Now, we define a fuzzy set ${{\nu }_{\Lambda }}_{★}\left({\hslash }_k\right)$, ${\nu }_{\Lambda }\left({\hslash }_k\right)$, and ${{\nu }_{\Lambda }}^{★}\left({\hslash }_k\right)$ as follows:

$${{\nu }_{\Lambda }}_{★}\left({\hslash }_k\right)=\frac{1}{3}\sum _{i=1}^3{C}_{{\lambda }_{★}{D}_i}\left({\hslash }_k\right),$$

$${\nu }_{\Lambda }\left({\hslash }_k\right)=\frac{1}{3}\sum _{i=1}^3{C}_{\lambda D_i}\left({\hslash }_k\right),$$

$${{\nu }_{\Lambda }}^{★}\left({\hslash }_k\right)=\frac{1}{3}\sum _{i=1}^3{C}_{{\lambda }^{★}{D}_i}\left({\hslash }_k\right).$$

Thus, we have

$$\begin{array}{l}{{\nu }_{\Lambda }}_{★}\left({\hslash }_k\right)=\{({\hslash }_1,0),({\hslash }_2,2/3),({\hslash }_3,1/3),({\hslash }_4,0),({\hslash }_5,1/3),({\hslash }_6,0),({\hslash }_7,1/3),({\hslash }_8,1/3)\},\hfill \\ {\nu }_{\Lambda }\left({\hslash }_k\right)=\{({\hslash }_1,2/3),({\hslash }_2,2/3),({\hslash }_3,1/3),({\hslash }_4,1/3),({\hslash }_5,1/3),({\hslash }_6,2/3),({\hslash }_7,2/3),({\hslash }_8,1/3)\},\hfill \\ {{\nu }_{\Lambda }}^{★}\left({\hslash }_k\right)=\{({\hslash }_1,0),({\hslash }_2,2/3),({\hslash }_3,1/3),({\hslash }_4,0),({\hslash }_5,1/3),({\hslash }_6,0),({\hslash }_7,1/3),({\hslash }_8,1/3)\},\hfill \end{array}$$

Now, we find the decision set by adding ${\Lambda }_{★}$, Λ, and ${\Lambda }^{★}$. Then, we have

$${\nu }_{{\Lambda }_{★}+\Lambda +{\Lambda }^{★}}\left({\hslash }_k\right)={\nu }_{{\Lambda }_{★}}\left({\hslash }_k\right)+{\nu }_{\Lambda }\left({\hslash }_k\right)+{\nu }_{{\Lambda }^{★}}\left({\hslash }_k\right)-[{\nu }_{{\Lambda }_{★}}\left({\hslash }_k\right)*{\nu }_{\Lambda }\left({\hslash }_k\right)*{\nu }_{{\Lambda }^{★}}\left({\hslash }_k\right)].$$

Since ${\hslash }_2$ is the brand having the maximum decision value in

Table 6. Decision value table.

	Decision Value
${\hslash }_1$	1.000
${\hslash }_2$	1.889
${\hslash }_3$	1.556
${\hslash }_4$	1.000
${\hslash }_5$	1.556
${\hslash }_6$	1.778
${\hslash }_7$	1.778
${\hslash }_8$	1.556

, then ${\hslash }_2$ is selected by the the manager team as the major production brand for cosmetics in the departmental store.

In the proposed algorithm, we observe that the use of $\mathcal{SR}$-methodology filters the primary assessment results and permits the experts to choose the optimal alternative in a suitable manner. Particularly, the $\mathcal{SR}$-upper approximation can be used to add optimal objects possibly neglected by the selectors in the primary assessment, while the $\mathcal{SR}$-lower approximation can be used to remove the objects that are irregularly selected as optimal. Hence, $\mathcal{SR}$ reduces the error, to some extent, that is caused by the subjective nature of experts during group decision making.

Now we present bar chart as given by Figure 2 of the decision values.

7. Applications of the $\mathcal{SR}$-Topological Spaces in Image Processing

We know that a geometrical figure can be obtained by its part information and its topological structure properties. Similarly, according to the $\mathcal{SR}$-topological properties of the $\mathcal{SR}$-space, we can also restore the $\mathcal{SR}$-topological diagram for some incomplete diagram.

Example 8.

One of the best examples of an incomplete image is that of fingerprints. Figure 3 shows a portion of fingerprint information from a person; however, the fingerprint information is incomplete. We can obtain the real fingerprint image on the basis of this Figure 3 by using $\mathcal{SR}$-approximations and $\mathcal{SR}$-topological properties.

The development of these theories can form the theoretical basis for further applications of the $\mathcal{SR}$-set and $\mathcal{SR}$-topology in many science and engineering areas, such as image processing, protein structure prediction, target recognition, and gene structure prediction.

8. Conclusions

We established the topological structure on the $\mathcal{SR}$-set in a new way. We define various topological terms, define $\mathcal{SR}$-continuity, product topology in $\mathcal{SR}$-set, and compactness in $\mathcal{SR}$-sets by taking an $\mathcal{SR}$-set as a pair of sets corresponding to the lower and upper approximations. Furthermore, we present an algorithm to cope with uncertainties in multi-attribute group decision-making problems by utilizing $\mathcal{SR}$-sets. The effectiveness of the algorithm was verified by a case study for cosmetic brand selection. However, under topological transformation, some properties of the $\mathcal{SR}$-set and topological theory, like connectedness and separation axioms on the $\mathcal{SR}$-set, need to be further studied. If we combine the $\mathcal{SR}$-set with other soft computing methods, such as bipolar fuzzy, neutrosophic set, and other hybrid structures, and use them in image processing, expert systems, and cognitive maps, a high machine IQ and hybrid intelligent system can be designed, which will be a productive attempt.