Optimizing Three-Dimensional Constrained Ordered Weighted Averaging Aggregation Problem with Bounded Variables
Abstract
1. Introduction
2. Constrained OWA Aggregation Problem
3. Maximizing a Three-Dimensional Constrained OWA Aggregation Problem with Lower Bounded Variables for w1 ≥ w2 ≥ w3
4. Maximizing Three-Dimensional Constrained OWA Aggregation Problem with Lower Bounded Variables for l1 ≥ l2 ≥ l3
- (1)
- For or , the optimal solution is .
- (2)
- For , the optimal solution is
- (3)
- For , the optimal solution is
- (4)
- For , the optimal solution is
- (5)
- For , the optimal solution is
5. Minimizing Three-Dimensional Constrained OWA Aggregation Problem with Upper Bounded Variables
- (1)
- For , the optimal solution is
- (2)
- For , the optimal solution is
- (3)
- For , the optimal solution is
- (4)
- For , the optimal solution is
- (5)
- For and , the optimal solution is .
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Chaji, A.; Fukuyama, H.; Shiraz, R.K. Selecting a model for generating OWA operator weights in MAGDM problems by maximum entropy membership function. Comp. Ind. Eng. 2018, 124, 370–378. [Google Scholar] [CrossRef]
- De Miguel, L.; Sesma-Sara, M.; Elkano, M.; Asiain, M.; Bustince, H. An algorithm for group decision making using n-dimensional fuzzy sets, admissible orders and OWA operators. Inf. Fusion 2017, 37, 126–131. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Y. Interval neutrosophic prioritized OWA operator and its application to multiple attribute decision making. J. Syst. Sci. Complex. 2016, 29, 681–697. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M.; Zhou, L.G.; Chen, H.Y. Induced and linguistic generalized aggregation operators and their application in linguistic group decision making. Group Decis. Negot. 2012, 21, 531–549. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, H.; Liu, J. Generalized multiple averaging operators and their applications to group decision making. Group Decis. Negot. 2013, 22, 331–358. [Google Scholar] [CrossRef]
- Vigier, H.P.; Scherger, V.; Terceño, A. An application of OWA operators in fuzzy business diagnosis. Appl. Soft Comput. 2017, 54, 440–448. [Google Scholar] [CrossRef]
- Yager, R.R. On the analytic representation of the Leximin ordering and its application to flexible constraint propagation. Eur. J. Oper. Res. 1997, 102, 176–192. [Google Scholar] [CrossRef]
- Garg, B.; Garg, R. Enhanced accuracy of fuzzy time series model using ordered weighted aggregation. Appl. Soft Comput. 2016, 48, 265–280. [Google Scholar] [CrossRef]
- Mohammed, E.A.; Naugler, C.T.; Far, B.H. Breast tumor classification using a new OWA operator. Exp. Syst. Appl. 2016, 61, 302–313. [Google Scholar] [CrossRef]
- Yager, R.R.; Beliakov, G. OWA operators in regression problems. IEEE Trans. Fuzzy Syst. 2010, 18, 106–113. [Google Scholar] [CrossRef]
- Ogryczak, W.; Śliwiński, T. On solving linear programs with the ordered weighted averaging objective. Eur. J. Oper. Res. 2003, 148, 80–91. [Google Scholar] [CrossRef]
- Ameri, F.; Zoej, M.J.V.; Mokhtarzade, M. Multi-Criteria, Graph-Based Road Centerline Vectorization Using Ordered Weighted Averaging Operators. Photogramm. Eng. Remote Sens. 2016, 82, 107–120. [Google Scholar] [CrossRef]
- Chen, S.M.; Kuo, L.W. Autocratic decision making using group recommendations based on interval type-2 fuzzy sets, enhanced Karnik–Mendel algorithms, and the ordered weighted aggregation operator. Inf. Sci. 2017, 412, 174–193. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R. Maximal Entropy and Minimal Variability OWA Operator Weights: A Short Survey of Recent Developments. In Soft Computing Applications for Group Decision-Making and Consensus Modeling; Mikael, C., Janusz, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 187–199. [Google Scholar]
- Emrouznejad, A.; Marra, M. Ordered weighted averaging operators 1988–2014: A citation-based literature survey. Int. J. Intell. Syst. 2014, 29, 994–1014. [Google Scholar] [CrossRef]
- Yager, R.R.; Kacprzyk, J.; Beliakov, G. Recent Developments in the Ordered Weighted Averaging Operators: Theory and Practice; Springer: Berlin, Germany, 2011. [Google Scholar]
- Yager, R.R. Constrained OWA aggregation. Fuzzy Sets Syst. 1996, 81, 89–101. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R.; Majlender, P. A note on constrained OWA aggregation. Fuzzy Sets Syst. 2003, 139, 543–546. [Google Scholar] [CrossRef]
- Coroianu, L.; Fullér, R. On the constrained OWA aggregation problem with single constraint. Fuzzy Sets Syst. 2018, 332, 37–43. [Google Scholar] [CrossRef]
- Ahn, B.S. Parameterized OWA operator weights: An extreme point approach. Int. J. Approx. Reason. 2010, 51, 820–831. [Google Scholar] [CrossRef]
- Ahn, B.S. A New Approach to Solve the Constrained OWA Aggregation Problem. IEEE Trans. Fuzzy Syst. 2017, 25, 1231–1238. [Google Scholar] [CrossRef]
- Fernández, E.; Pozo, M.A.; Puerto, J.; Scozzari, A. Ordered Weighted Average optimization in Multiobjective Spanning Tree Problem. Eur. J. Oper. Res. 2017, 260, 886–903. [Google Scholar] [CrossRef]
- Fullér, R.; Majlender, P. On obtaining minimal variability OWA operator weights. Fuzzy Sets Syst. 2003, 136, 203–215. [Google Scholar] [CrossRef]
- Kasperski, A.; Zieliński, P. Using the WOWA operator in robust discrete optimization problems. Int. J. Approx. Reason. 2016, 68, 54–67. [Google Scholar] [CrossRef]
- Ogryczak, W.; Olender, P. Ordered median problem with demand distribution weights. Optim. Lett. 2016, 10, 1071–1086. [Google Scholar] [CrossRef]
- Ogryczak, W.; Śliwiński, T. On efficient WOWA optimization for decision support under risk. Int. J. Approx. Reason. 2009, 50, 915–928. [Google Scholar] [CrossRef]
- Chen, Y.F.; Tang, H.C. A Three Dimensional Constrained OWA Aggregation Problem with Lower Bounded Variables. Symmetry 2018, 10, 339. [Google Scholar] [CrossRef]
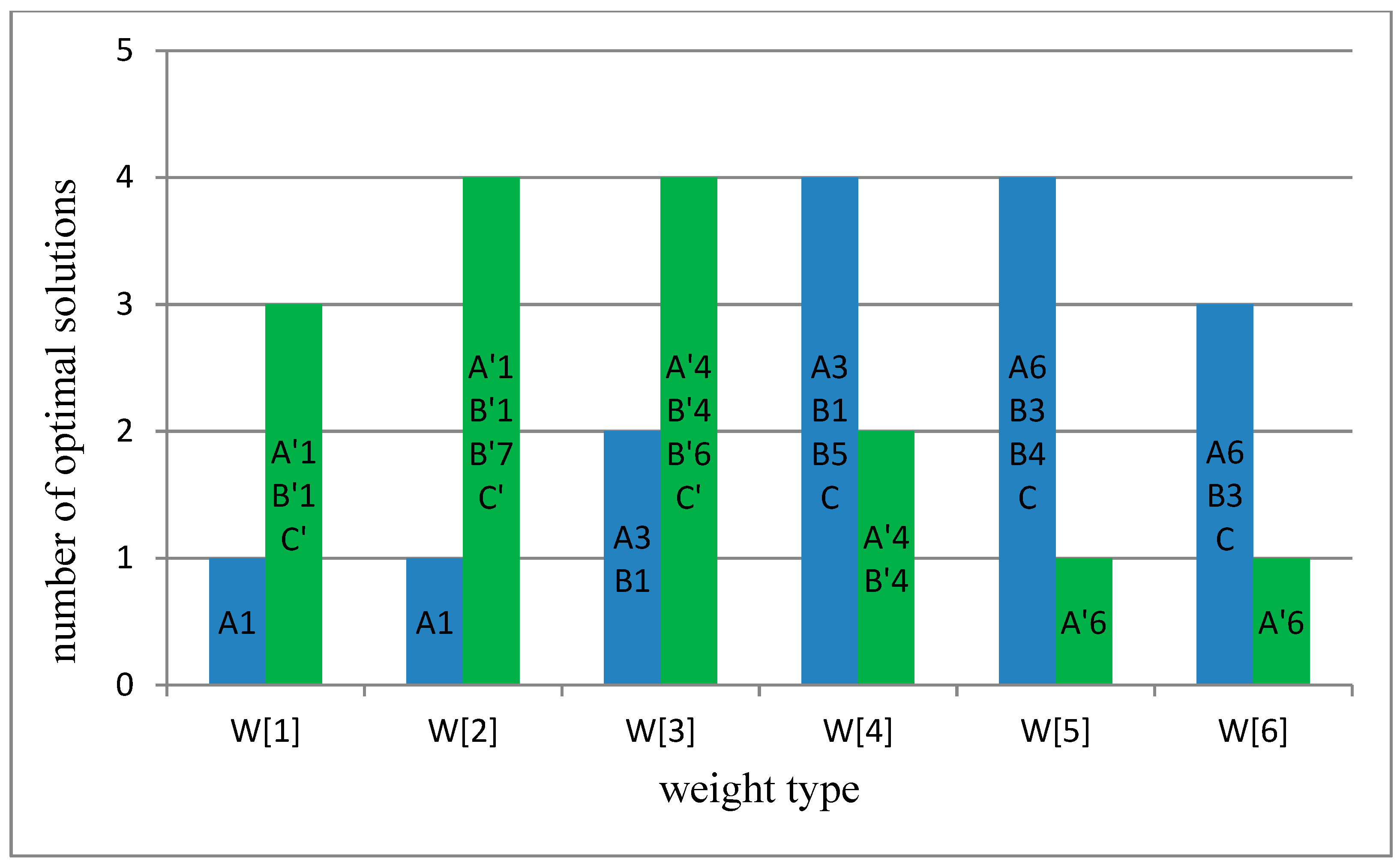
| A-1 | |||
| A-2 | , | ||
| A-3 | , , | ||
| B1-1 | |||
| B1-2 | |||
| B1-3 | |||
| B2-1 | |||
| B2-2 | |||
| B2-3 | |||
| B2-4 | |||
| B2-5 | |||
| B2-6 | |||
| C |
| Condition | |||||
|---|---|---|---|---|---|
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 | |||||
| A5 | |||||
| A6 | |||||
| B1 | , | ||||
| B2 | , | ||||
| B3 | , | ||||
| B4 | , | ||||
| B5 | , | ||||
| C | 1/3 | , , |
| Total | ||||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 8744 | 8744 | 0 | 0 | 0 | 0 | 17,488 | |
| A2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A3 | 0 | 0 | 1632 | 1632 | 0 | 0 | 3264 | |
| A4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A6 | 0 | 0 | 0 | 0 | 1920 | 1920 | 3840 | |
| B1 | 0 | 0 | 7112 | 5474 | 0 | 0 | 12,586 | |
| B2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B3 | 0 | 0 | 0 | 0 | 3026 | 3912 | 6938 | |
| B4 | 0 | 0 | 0 | 0 | 1614 | 0 | 1614 | |
| B5 | 0 | 0 | 0 | 910 | 0 | 0 | 910 | |
| C | 0 | 0 | 0 | 728 | 2184 | 2912 | 5824 |
| Total | ||||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 57,464 | 57,464 | 0 | 0 | 0 | 0 | 114,928 | |
| A2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A3 | 0 | 0 | 19,352 | 19,352 | 0 | 0 | 38,704 | |
| A4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A6 | 0 | 0 | 0 | 0 | 15,640 | 17,008 | 32,648 | |
| B1 | 0 | 0 | 38,112 | 29,004 | 0 | 0 | 67,116 | |
| B2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B3 | 0 | 0 | 0 | 0 | 19,566 | 28,312 | 47,878 | |
| B4 | 0 | 0 | 0 | 0 | 10,114 | 0 | 10,114 | |
| B5 | 0 | 0 | 0 | 5060 | 0 | 0 | 5060 | |
| C | 0 | 0 | 0 | 4048 | 12,144 | 12,144 | 28,336 |
| Condition | |||||
|---|---|---|---|---|---|
| A′1 | |||||
| A′2 | , | ||||
| A′3 | |||||
| A′4 | |||||
| A′5 | |||||
| A′6 | |||||
| B′1 | |||||
| B′2 | |||||
| B′3 | |||||
| B′4 | |||||
| B′5 | |||||
| B′6 | , | ||||
| B′7 | |||||
| C′ | 1/3 |
| Total | ||||||||
|---|---|---|---|---|---|---|---|---|
| A′1 | 624 | 624 | 0 | 0 | 0 | 0 | 1248 | |
| A′2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′4 | 0 | 0 | 912 | 888 | 0 | 0 | 1800 | |
| A′5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′6 | 0 | 0 | 0 | 0 | 1632 | 1632 | 3264 | |
| B′1 | 728 | 546 | 0 | 0 | 0 | 0 | 1274 | |
| B′2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′4 | 0 | 0 | 558 | 744 | 0 | 0 | 1302 | |
| B′5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′6 | 0 | 0 | 92 | 0 | 0 | 0 | 92 | |
| B′7 | 0 | 252 | 0 | 0 | 0 | 0 | 252 | |
| C′ | 280 | 210 | 70 | 0 | 0 | 0 | 560 |
| Total | ||||||||
|---|---|---|---|---|---|---|---|---|
| A′1 | 9184 | 9184 | 0 | 0 | 0 | 0 | 18,368 | |
| A′2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′4 | 0 | 0 | 13,472 | 13,328 | 0 | 0 | 26,800 | |
| A′5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A′6 | 0 | 0 | 0 | 0 | 26,352 | 26,352 | 52,704 | |
| B′1 | 11,728 | 8796 | 0 | 0 | 0 | 0 | 20,524 | |
| B′2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′4 | 0 | 0 | 9768 | 13,024 | 0 | 0 | 22,792 | |
| B′5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B′6 | 0 | 0 | 1752 | 0 | 0 | 0 | 1752 | |
| B′7 | 0 | 4292 | 0 | 0 | 0 | 0 | 4292 | |
| C′ | 5440 | 4080 | 1360 | 0 | 0 | 0 | 10,880 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.-C.; Yang, S.-T. Optimizing Three-Dimensional Constrained Ordered Weighted Averaging Aggregation Problem with Bounded Variables. Mathematics 2018, 6, 172. https://doi.org/10.3390/math6090172
Tang H-C, Yang S-T. Optimizing Three-Dimensional Constrained Ordered Weighted Averaging Aggregation Problem with Bounded Variables. Mathematics. 2018; 6(9):172. https://doi.org/10.3390/math6090172
Chicago/Turabian StyleTang, Hui-Chin, and Shen-Tai Yang. 2018. "Optimizing Three-Dimensional Constrained Ordered Weighted Averaging Aggregation Problem with Bounded Variables" Mathematics 6, no. 9: 172. https://doi.org/10.3390/math6090172
APA StyleTang, H.-C., & Yang, S.-T. (2018). Optimizing Three-Dimensional Constrained Ordered Weighted Averaging Aggregation Problem with Bounded Variables. Mathematics, 6(9), 172. https://doi.org/10.3390/math6090172






