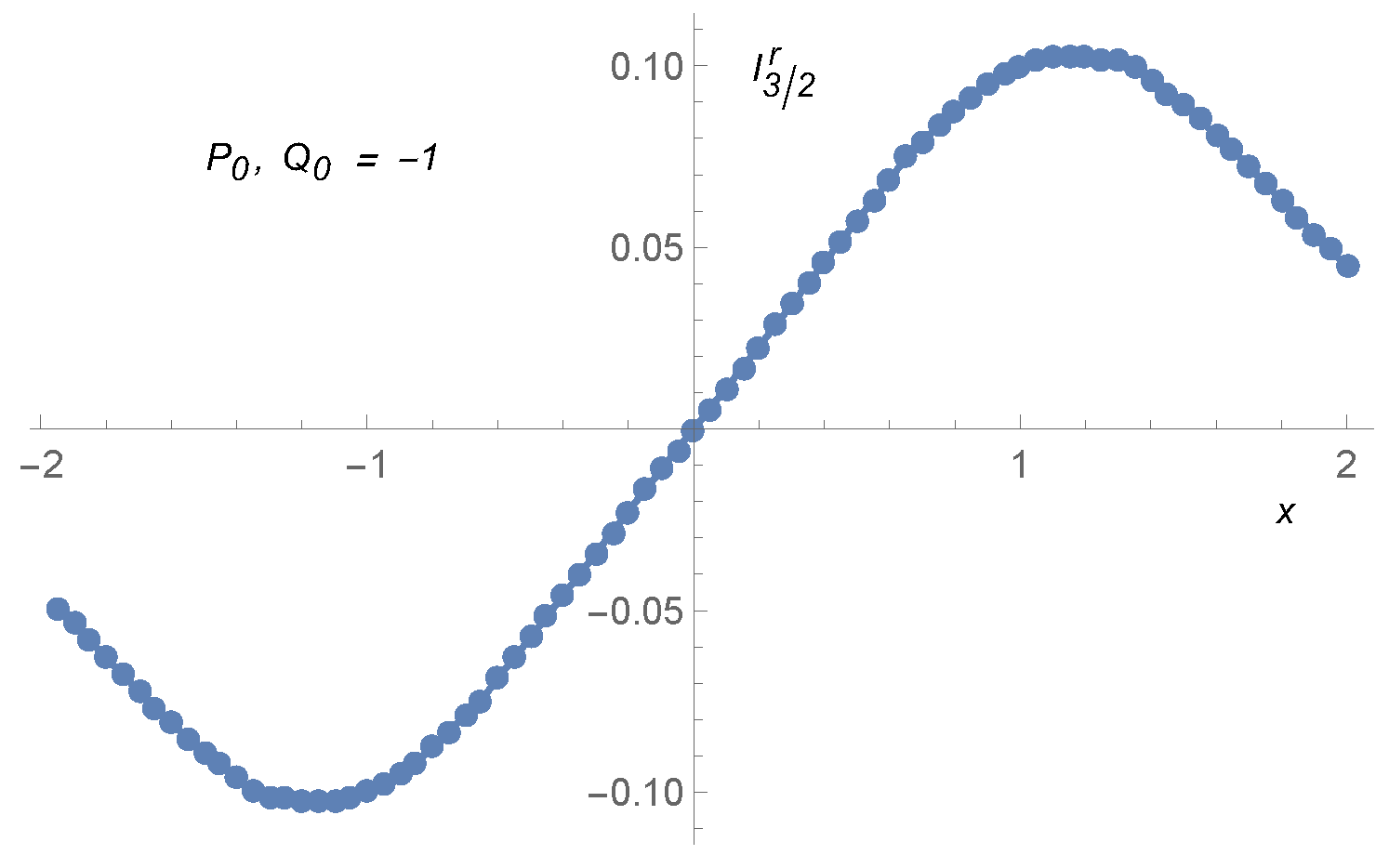1. Introduction
In most physical models, including those of elementary particles and condensed matter, the continuity equation, , is of fundamental importance, expressing the basic concept (or we could say the axiom) that the variation in time of the number of particles inside a certain region is opposite to the number of those crossing the boundary of that region in the same time. To visualize the essence of this statement it is also sufficient to think of a 1D system, like a fluid flowing in a pipe or charge carriers flowing in a wire, in which case the equation simply reads , where . For a stationary flow () this further simplifies, prescribing that must be independent of x.
We know that in quantum mechanics classical concepts like a particle’s trajectory, instant position and velocity, non-invasive measurements, arrival times, etc. lose their familiar meanings. Nevertheless, the continuity equation is recovered in a probabilistic sense, and one can usually resort to some classical limit in order to make contact with the corresponding classical concept. In other words, one can still imagine that the “bean counting” implied by the continuity equation is still meaningful, albeit in a statistical sense. This is actually true for the Schrödinger equation, the Dirac equation, and their extensions in quantum field theory. For example, for the Schrödinger equation,
, the continuity equation takes the form:
Conversely, we can regard the Schrödinger equation as a low energy limit of a Dirac or Klein–Gordon equation, and these in turn as consequences of a relativistic quantum field theory with local interactions. Here the local conservation of charge is mathematically implemented at a fundamental level, in the definition of the Lagrangian. Also note (and this is not a casual coincidence in our opinion) that in such a theory, space and time are essentially treated as two quantities of the same nature. The most radical expression of this equivalence between space and time is Euclidean quantum field theory, which gives the same results for physical observables as the Lorentzian theory [
1,
2]. In general, the formalism of elementary particle physics has a strong reductionist character, such that the concept of individual particles, even if weakened in a probabilistic sense, does not allow one to conceive exceptions to the law of local charge conservation. In the applications of quantum field theory to condensed matter this attitude is less pronounced but still present [
3].
However, when we detach ourselves a little bit from the paradigm of interactions between individual particles, some problems typical of quantum mechanics appear. One of these is the problem of the definition, calculation, and measurement of the tunneling time of a particle across a barrier. This motion does not have a classical analogue, so a correspondence limit of the continuity equation is not applicable. The tunneling time problem [
4,
5], and more generally the problem of arrival time in quantum mechanics [
6], has been early recognized and widely studied. Behind these issues lies the fundamental problem of the definition of a time operator in quantum mechanics [
7,
8].
The unification of quantum mechanics and special relativity attained in quantum field theory, though successful, inevitably requires a limitation of the scope of quantum mechanics [
9]. But in fact some useful quantum mechanical models exist, which are explicitly non-local. One of these is the fractional Schrödinger equation [
10,
11], where the kinetic energy operator is proportional to
,
, leading to a considerable change in the behavior of the wave function. Wei [
12] has recently shown that its continuity equation contains an anomalous source term, taking the form
, where
is called the “extra-current”. This property is related to the non-locality of the fractional Schrödinger equation [
13]. We shall discuss it in
Section 2.
The fractional Schrödinger equation has recently found novel important applications in optics, in particular concerning the behavior of wavepackets in a harmonic potential [
14]. The theory has further been extended to equations with a periodic
P-
T symmetric potential; this suggests that a real physical system, the honeycomb lattice, is a possible realization of the fractional Schrödinger equation ([
15] and references therein). Resonant mode conversions and Rabi oscillations in Gaussian and periodic potentials have been studied in Reference [
16]. While in our present calculations only free wave packets are considered, results in this field have potential applications in diffraction-free and self-healing optoelectronic devices.
Another well-known non-local wave equation of the Schrödinger kind is the equation:
It contains the non-local interaction kernel
U. Its solutions have been studied in References [
17,
18,
19]. Possible applications include the dissipative quantum transport processes in quantum dots [
20,
21]. We shall analyze Equation (
2) and compute the extra-current in
Section 3. Further applications concern long range interactions [
22], diffusion in active intracellular transport [
23], and nuclear scattering [
24,
25].
The Gorkov equation for the superconducting order parameter
also has a non-local form, namely:
In
Section 4 we shall see that this equation reduces to a local Ginzburg–Landau equation only under certain assumptions. It is not known yet whether the full non-local equation leads to an extra-current, because the form of the kernel
K varies considerably and depends on several microscopic assumptions. Nevertheless, this equation deserves further analysis because it can describe weak links in superconductors and Josephson junctions, which in our opinion are good candidates for an experimental observation of non-local electromagnetic coupling (
Section 5); this will be the subject of a forthcoming work.
In calculations of transport properties of nano-devices such as in density functional theory and non-equilibrium Green function theory, non-local potentials appear in several cases ([
26] and references therein).
More generally, non-local field theory is a wide subject. Non-local models can originate from coarse graining effective approximations of local models, or they can be conceived even at a more fundamental level than local theories. See on this point the work in Reference [
27], which we report on further in our conclusions. In this paper, we take a pragmatic stance about non-local wave equations. We do not require a derivation from an action principle or from a more fundamental underlying theory; we regard them just as effective phenomenological descriptions of certain systems. After all, quantum mechanics was born in this way and has always resisted “more fundamental” interpretations.
In
Section 5, we shall discuss the electromagnetic coupling of these wavefunctions, which requires an extension of Maxwell theory. Such an extension turns out to satisfy two crucial requirements: (1) It is fully compatible with special relativity; and (2) It has a censorship property, according to which the electromagnetic field of a source that is not locally conserved is the same as the field of a fictitious, equivalent (but different) locally conserved source. Thanks to these two properties, the non-local “quantum anomalies” that we have demonstrated do not spill over to classical electromagnetic fields, which thus remain a bedrock of special relativity.
3. The Non-Local Wave Equation by Lenzi et al.
The non-local wave Equation of Lenzi et al. [
17] has the form:
where
U is a non-local interaction kernel.
The continuity equation for Equation (
17) is found in Reference [
17] to be the following, where the argument of
, when missing, is understood to be
:
The term with the double integral is what we have called “extra-current
I” in the case of fractional quantum mechanics. According to Reference [
17], it is possible to prove that if
, with
a real and symmetric function, then the total probability is conserved. We shall restrict our attention to this case, which also excludes memory effects, due to the presence of
. We will compute the extra-current using the solution given in Reference [
17] for a potential of the form
, with
. The function
, defined as the Fourier transform in
x and Laplace transform in
t, is
, where
is a constant.
By applying a Fourier transform to Equation (
17), Lenzi et al. obtained the integral equation:
They then apply a Laplace transform to obtain the algebraic equation:
where
is the Fourier transform of the initial condition. The solution with the above choice for
U is:
With an inverse Laplace transform one arrives at:
The inverse Fourier transform of this equation can be written as a convolution with the Fox
H function. Figure 1 of Reference [
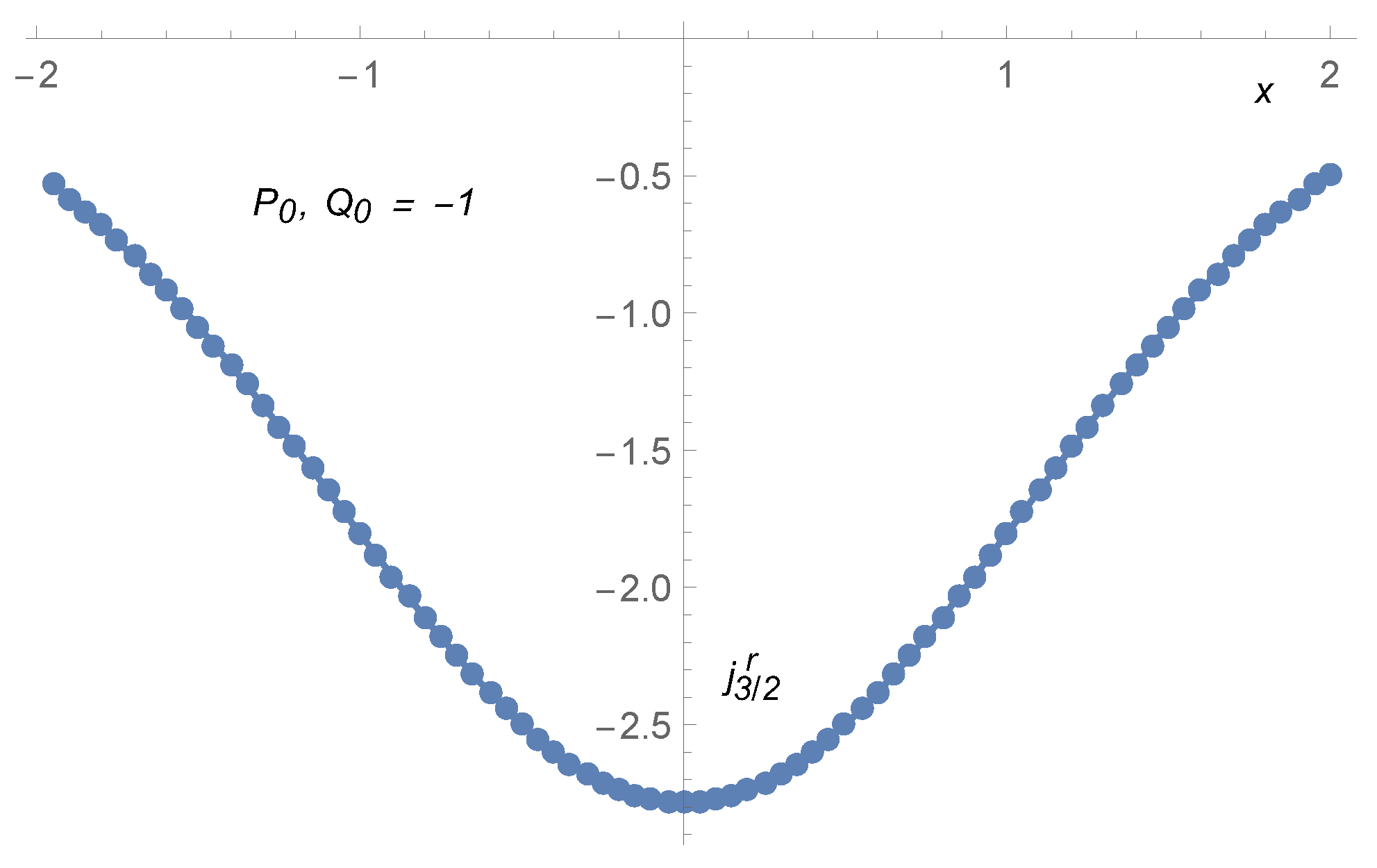
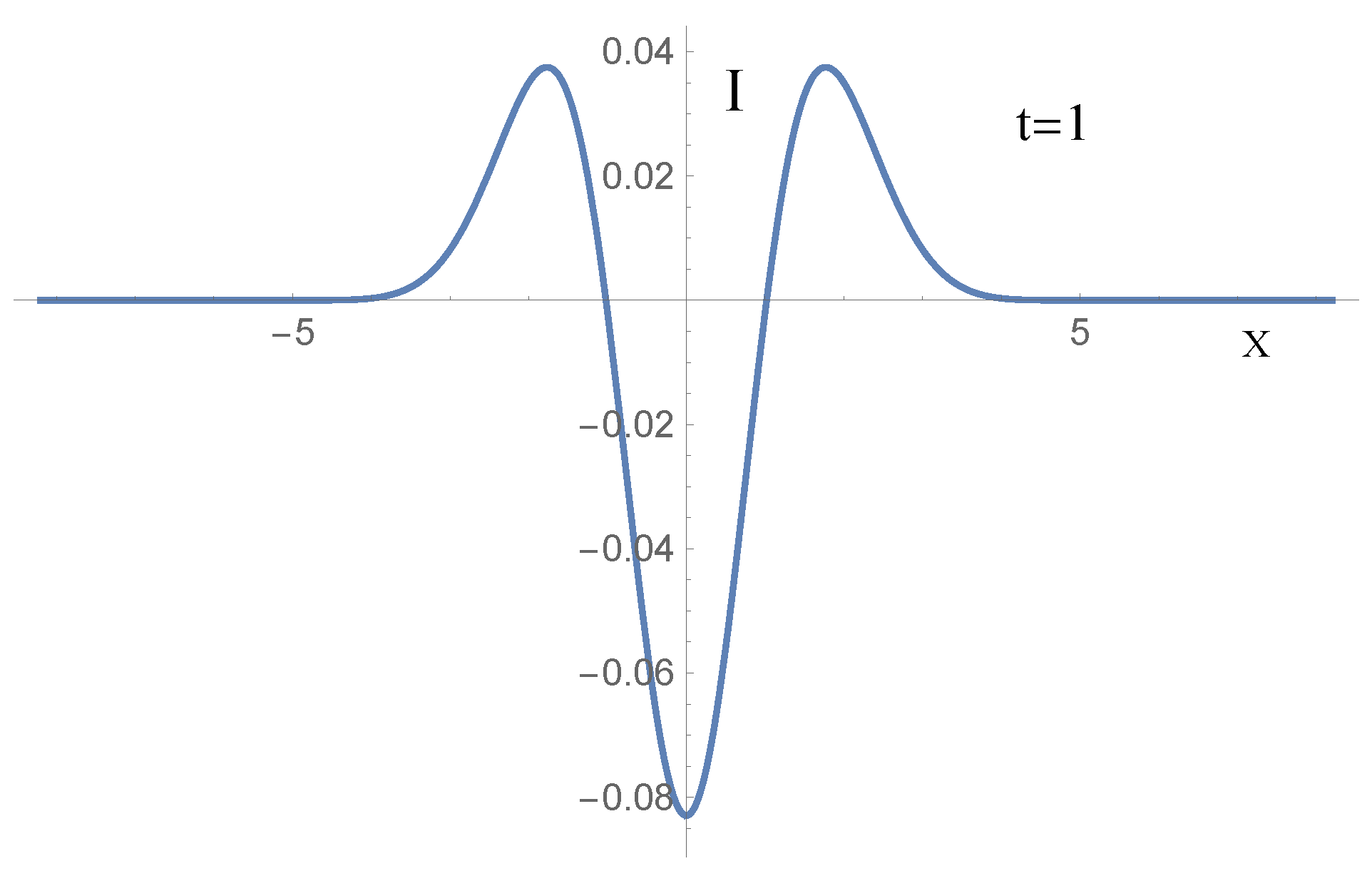
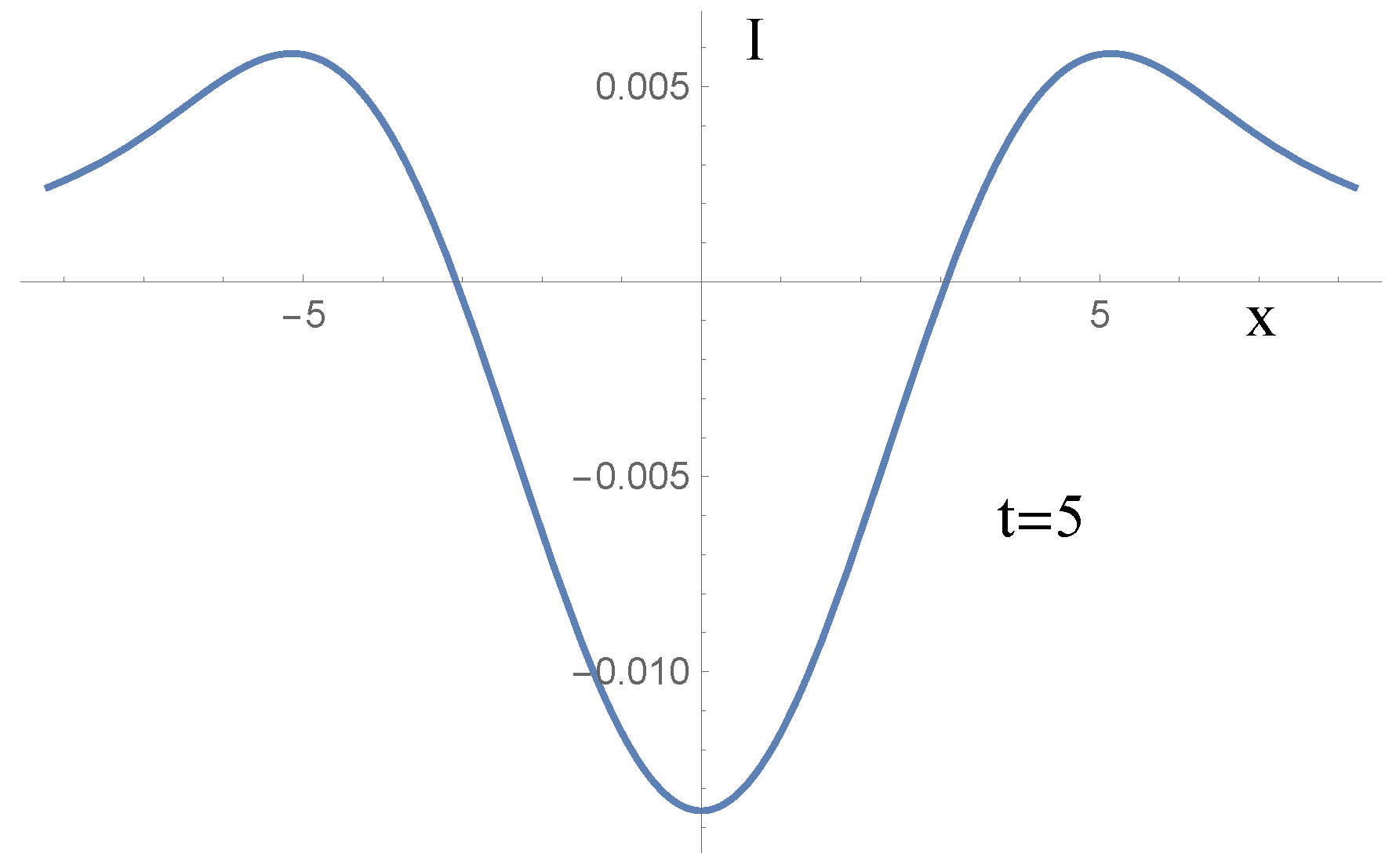
17] shows the behavior of
as a function of
x at the times
,
, and
; for the parameter choices of
,
,
,
, and the initial condition
. Our goal, however, is not to compute
, but to compute the corresponding extra-current, given by the formula:
In the following we turn to units such that
, and
. In Equation (
23) we express the two wavefunctions and
U as inverse transforms:
Thus we obtain:
Performing first the integral in
y we obtain
and through this
-function we can integrate in
v, replacing everywhere
v with
p. After also performing the integral in
we finally find:
Note that the integrals in
k and
p can be factorized. The two wavefunctions are known, having the explicit expression in Equation (
22). The integral
gives the wavefunction in the
x space, which Lenzi et al. have written formally in terms of the Fox function and plotted for some values of
t. Alternatively, one could numerically perform the two transforms, for some values of
t:
and plot the imaginary part of the result. We prefer, however, to make a first order expansion in the coupling
(see next subsection), which gives a relatively simple analytical result.
A useful check for the extra-current, Equation (
28), is to set
, which considerably simplifies the wavefunctions in momentum space;
is taken to be a Gaussian,
, whence:
The integral in
k gives a real Gaussian. Since we are interested in the imaginary part of the product, we consider only the imaginary part of the second factor, which is:
The latter integral is zero, and it follows that
.
4. Local Approximation of the Gorkov Equation
As mentioned in the Intoduction, the integral Gorkov Equation (
3) for superconductivity,
, can be approximated under certain conditions by a differential equation of the Ginzburg–Landau type, which has a locally conserved current. We recall that [
33]:
- (1)
The function represents an effective wavefunction and can be written as , where are the quantum field operators which create a particle with spin at , and is a measure of the effective local attraction of the electrons, such that the two-particle potential in the Hamiltonian is .
- (2)
The Gorkov equation can be derived from the Bogoliubov self-consistent equations, which in turn are obtained from a local quantum field theory plus a mean-field approximation.
We summarize here the local approximation procedure given by Waldram [
33,
34]. Let us suppose that the order parameter
F varies slowly in space (this is true for low-
superconductors, but not for high-
superconductors, which have a very short coherence length). Expanding
for
close to
, we can write:
Suppose that the kernel
is spherically symmetric, i.e. it depends only on
. Placing Equation (
33) into the integral equation, we find the approximated local equation:
where
If
was a really function of
and of nothing else, then after changing integration variable to
we could conclude that the quantities
A and
S are independent from
. However, in the examples of kernel given in References [
33,
34],
K “has a weak dependence on
F”. It follows that
A and
S also have a weak dependence on
F; however, disregarding this dependence Equation (
34) reduces to a familiar wave equation of the Ginzburg–Landau type. One can then look for non-local corrections to this equation, but they turn out to be quite complicated, and little progress has been made in this direction after Reference [
34] (for recent work see Reference [
35]).
The Gorkov equation has been used to analyze the proximity effect in superconductors (the diffusion of the order parameter into an adjacent normal material), especially for those cases where the microscopic BCS approach is not applicable. Both from physical and mathematical points of view, it might be interesting to consider cases in which the kernel is independent from
F, but cannot simply be approximated like in Equation (
33), i.e., there is a true non-locality. In that case, the form of the kernel should be postulated on phenomenological grounds. The extra-current
could then be computed along similar lines as done in the previous sections. Note that the Gorkov equation is time-independent, so the presence of an extra-current would mean that the stationary conservation law
becomes
.
5. Electromagnetic Coupling
It is known that the Maxwell equations are only compatible with a locally conserved current. In four-dimensional form, they are written as , in Gauss units. Since the tensor is antisymmetric, it follows as a necessary condition that . This is the covariant form of the continuity equation. The field equations for are obtained from the Lagrangian of the pure electromagnetic field, plus a current coupling of the form , with and . In quantum mechanics, the same coupling can be introduced through the principle of gauge invariance, whereby the momentum is replaced by and the energy by .
For quantum systems lacking a locally conserved current, one can employ an extension of Maxwell’s equations, first introduced by Aharonov and Bohm ([
36,
37] and references therein). In Reference [
38] a new version was given, where the degree of freedom
is explicitly removed and the field equations take the form:
here
is the usual localized physical current, of the form of Equation (
1), and
is a secondary, additional current, which is obtained by applying the non-local operator
to the term which breaks the local conservation:
In components, we can rewrite the secondary current as , and . Because of the antisymmetry of , the field equations automatically imply that . The reasoning can also be reversed; starting from the latter expression, define a current that compensates the non-conservation of .
We recently became aware of a work where this compensation procedure has been carried out, for the vector current density
, in order to recover local conservation in the stationary case [
26]. The authors of Reference [
26] consider a wavefunction which obeys a wave equation with a non-local potential. They write the total current in the form
, where
is the analogue of our
in Equation (
1) and
is a non-local current density defined as
. In turn,
is determined by solving the Poisson equation,
, and
is the term which breaks the continuity condition. The authors of Reference [
26] regard
as the true physical current density and prove an important property: by integrating this current density over an appropriate surface, one obtains the Landauer–Büttiker formula of the total current as computed in the quantum transport theory applied to the wavefunction they consider.
In our opinion, it is not clear yet whether the total current
has the same physical properties of the usual “
current” of Equation (
1), made with the local gradient of the wavefunction. In fact, the part
of the current
depends not only on the wavefunction in
, but on the wavefunction in all space at the same instant, even though it is clear that this dependence is causal and properly retarded in the full time-dependent expression of the secondary current, Equation (
37), obtained from the extended Maxwell equations. This can also have non-standard implications for dissipation, in the case when
“flows” at a different place than
.
We see here an example of a more general problem concerning non-local theories. Namely, what is the correct physical interpretation of the wavefunction, if we admit that the usual interpretation rule of quantum mechanics (Born rule) is only justified by a local conservation law?
In any case, from all the work cited above, it can be safely concluded that, at least for the wavefunctions considered in Reference [
26]:
- (1)
Conduction in the presence of non-locally-conserved currents satisfies the Landauer–Büttiker formula of quantum transport.
- (2)
The electromagnetic field generated by these currents is given by the extended Maxwell Equation (
36).
In the three-dimensional vector formalism, the extended equations without sources maintain the usual form, namely
,
. The extended equations with sources are written as follows [
32]:
where
I denotes the scalar quantity which breaks local charge conservation:
The extended Maxwell equations have an important “censorship” property [
38]; they imply that measurements of the field strength made with test particles cannot reveal any possible local non-conservation of the source. The apparent conservation is due to the secondary source, which however may be extended in space, outside the physical source. See our comments on this point in the Introduction.
Some solutions of Equations (
38) and (
39) have been given in References [
32,
38] and others will be presented in a forthcoming work. The explicit expressions for the extra-current found in this work serve as guidance for non-local quantum sources for these equations. More realistic sources could be obtained, as mentioned, from the Gorkov equation.
We finally note that changes in quantum electrodynamics following an extension of Maxwell theory with the Aharonov–Bohm Lagrangian have been extensively studied by Jiménez and Maroto ([
39] and references therein). However, they only consider coupling of the electromagnetic field to locally conserved currents. As a consequence, additional degrees of freedom like longitudinal wave components are decoupled from matter, but can have cosmological relevance.
6. Conclusions
The non-locality of the fractional Schrödinger equation and of the Schrödinger equation with a non-local interaction potential leads to a violation of the local conservation law of probability density (and of charge, in the case when the wave equation describes a charged particle). We have demonstrated this explicitly, both for 1D wave packets in motion and at rest, interpreting the extra-current, , as a physical consequence of a kind of super- or sub-diffusion, depending on the case. We have checked that at the microscopic level the order of magnitude order the extra-current is comparable to that of the current gradient , so that the effect cannot be disregarded as a minor correction. We have discussed the impact of these properties on the electromagnetic coupling of the wave functions considered, recalling the “censorship” property of extended electrodynamics, which to some extent prevents the non-locality of the wavefunctions from causing non-local behavior of the electromagnetic field. A brief discussion has been given of a possible application of these ideas to the Gorkov integral equation for the proximity effect in superconductors.
We recall that non-local field theories have been discussed by several authors, starting from early works by W. Pauli and others. The subject is wide and complex, because non-locality can occur in different ways and accordingly it can have different mathematical realizations. Substantial progress has recently been made by Kegeles and Oriti [
27]. They extend Nöther’s theorem to non-local field theories, thus finding a more general relation between symmetries of the action and conserved quantities. They consider a non-local action functional defined by a Lagrangian which mathematically depends on multiple copies of a jet bundle. Theories described by these kinds of actions are employed for many-particle systems in various branches of physics such as hydrodynamics, condensed matter, and solid state physics. An example is given by effective theories in which one disregards some microscopic degrees of freedom; the price to pay is often the emergence of non-locality. The general results of Reference [
27] are applied to model a complex scalar field with a non-local two-body interaction, which appears in the theory of Bose–Einstein condensates. A comparison of the currents of the local and non-local theories explicitly shows the appearance of a non-local correction term.
The scope of our work has been more limited. We have considered certain non-local wave equations as effective physical models, without postulating an underlying action. We have found some solutions that can be used as prototype sources for extended Maxwell equations, which automatically generate non-local corrections terms, while preserving the local covariant Lagrangian coupling . Results of the extended Maxwell equations, including a proposal of experimental verification, will be presented in a forthcoming work.