On the Role of Short-Term Animal Movements on the Persistence of Brucellosis
Abstract
1. Introduction
2. Materials and Methods
Modeling Framework
3. Results
3.1. Positivity and Boundedness of Solutions
3.2. Disease Dynamics for a Single Patch
3.3. The Reproduction Number
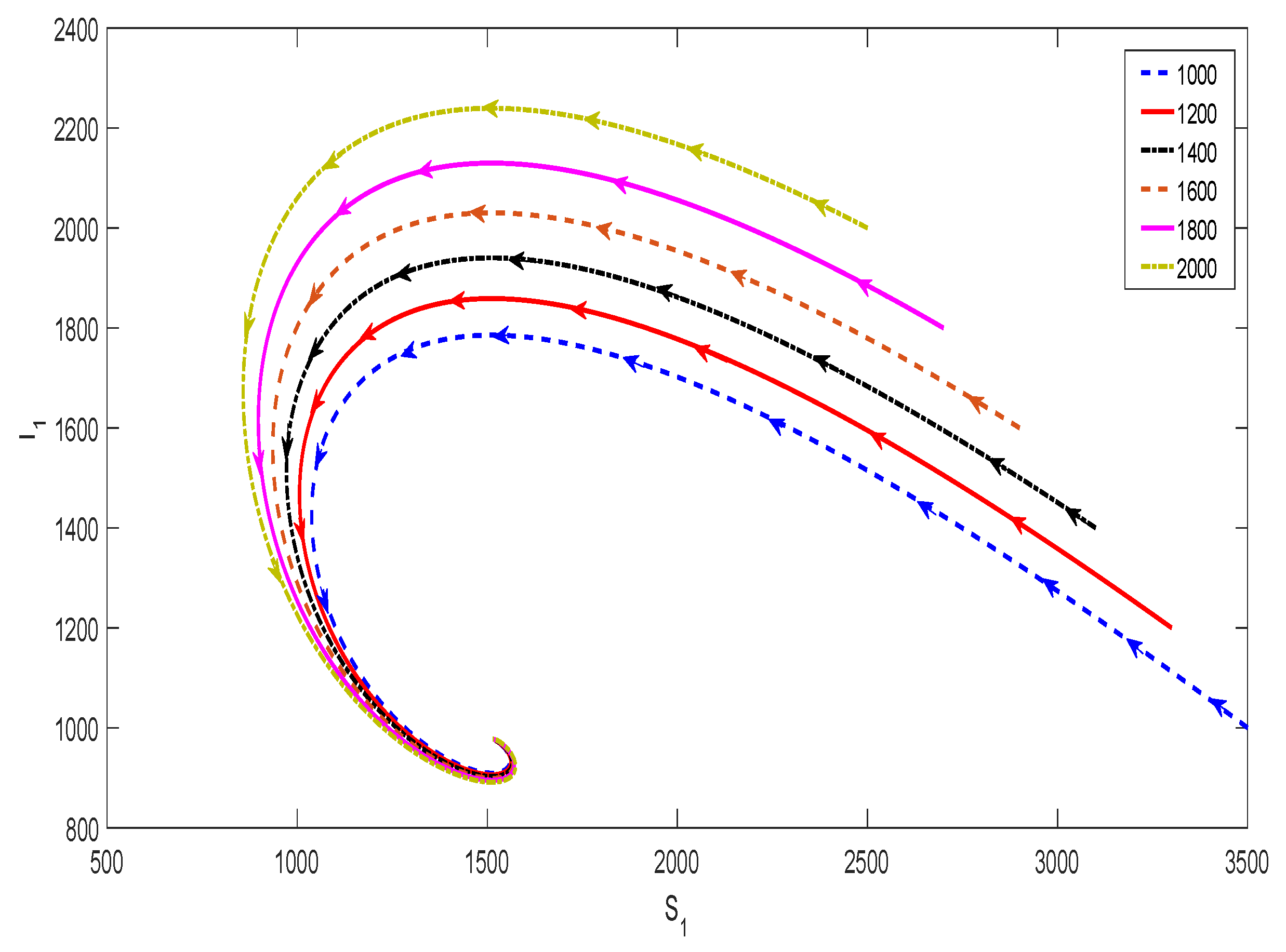
3.4. Disease Invasion and Persistence
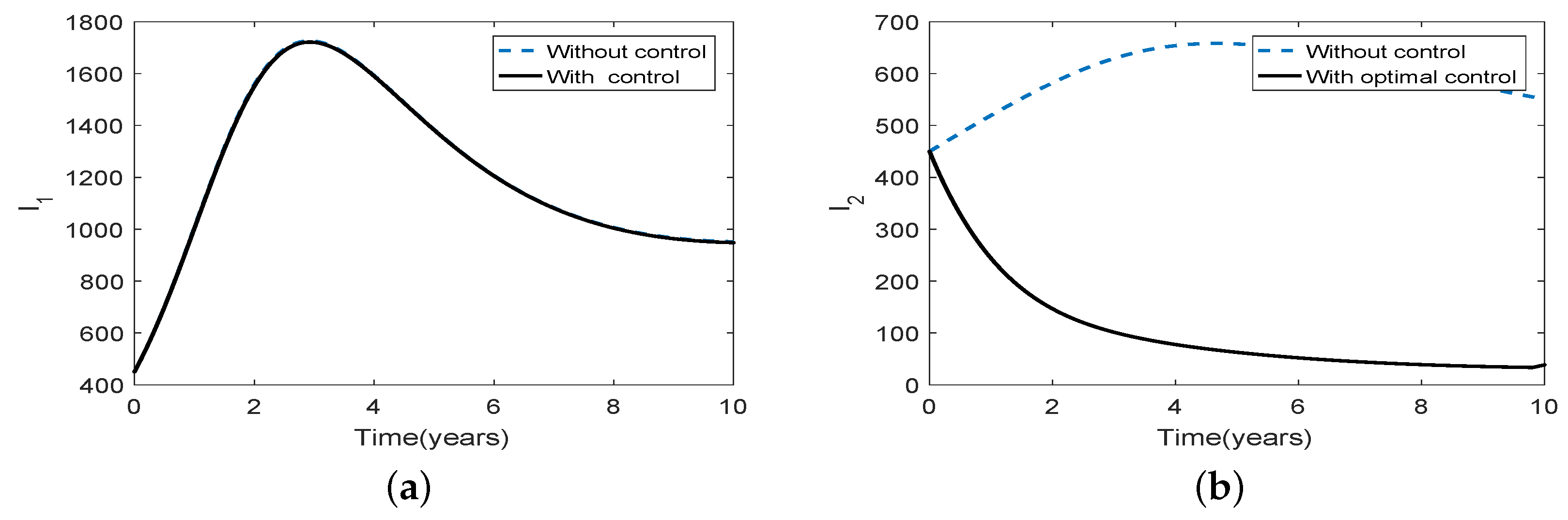
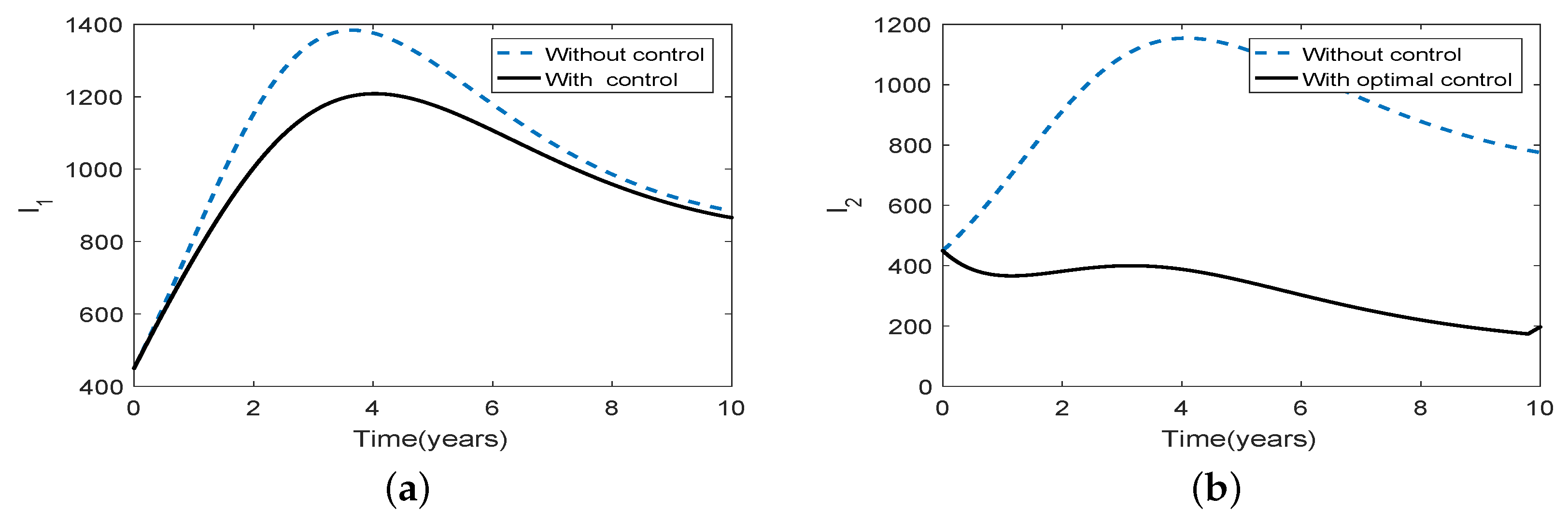
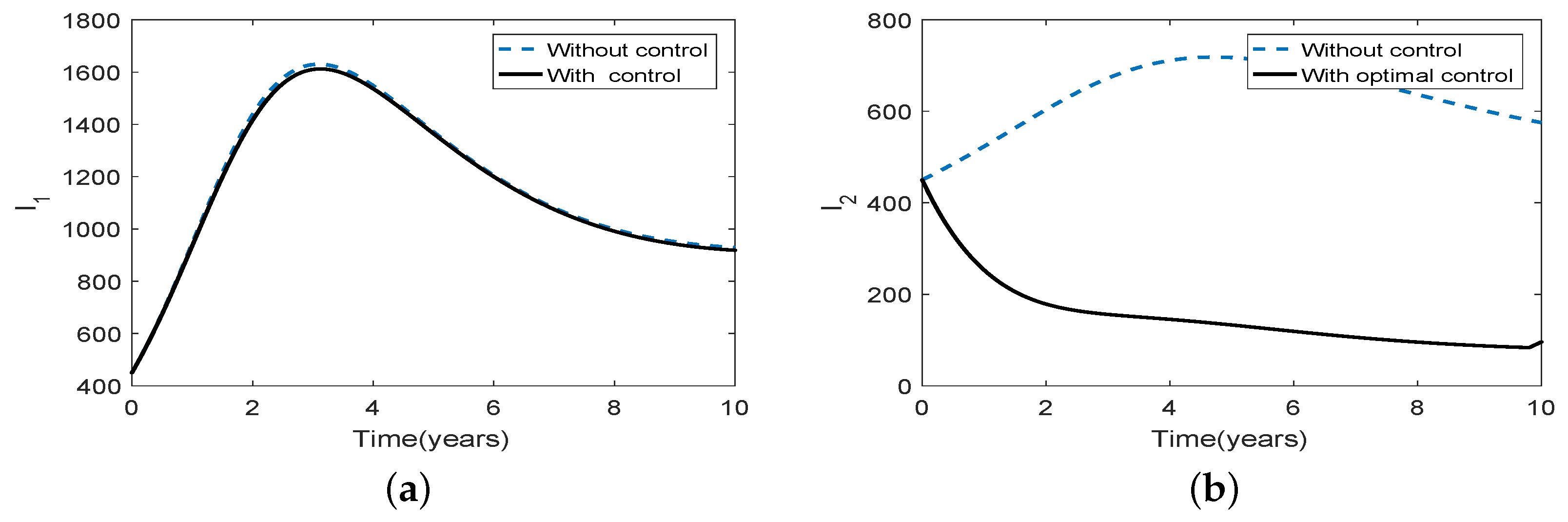
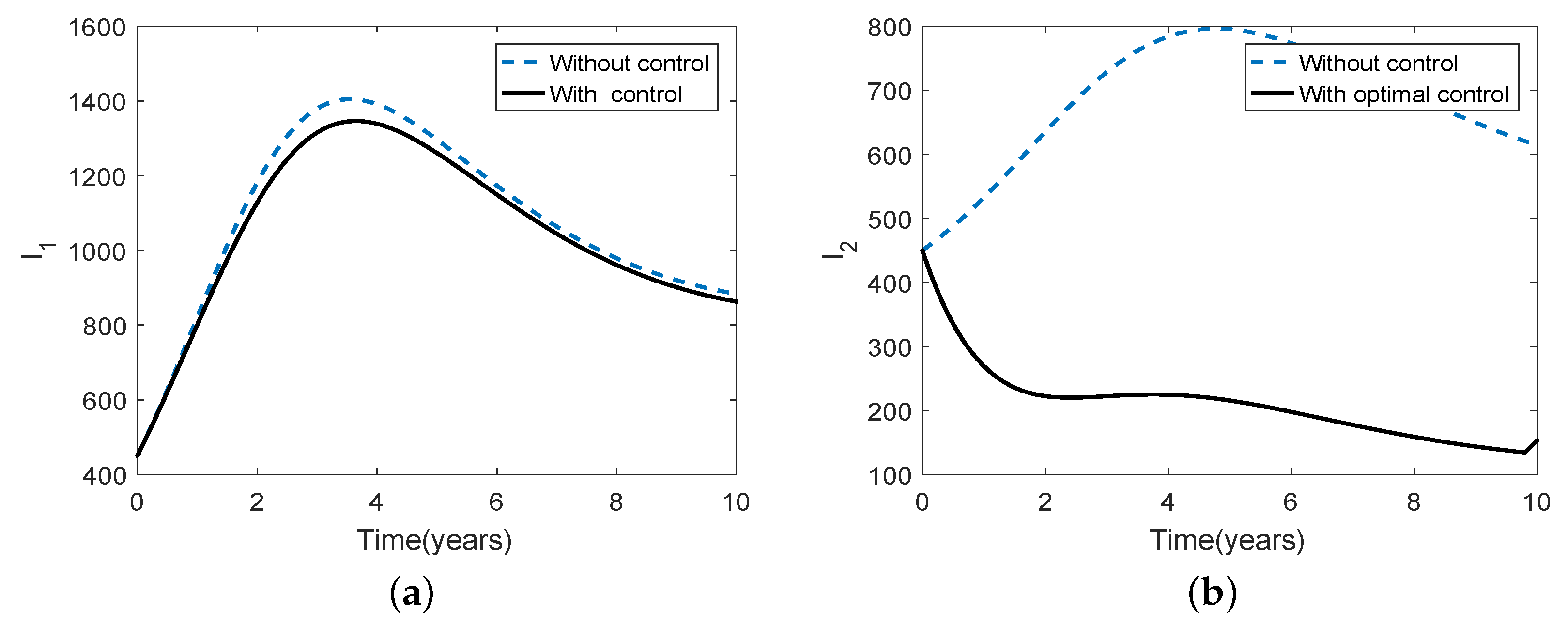
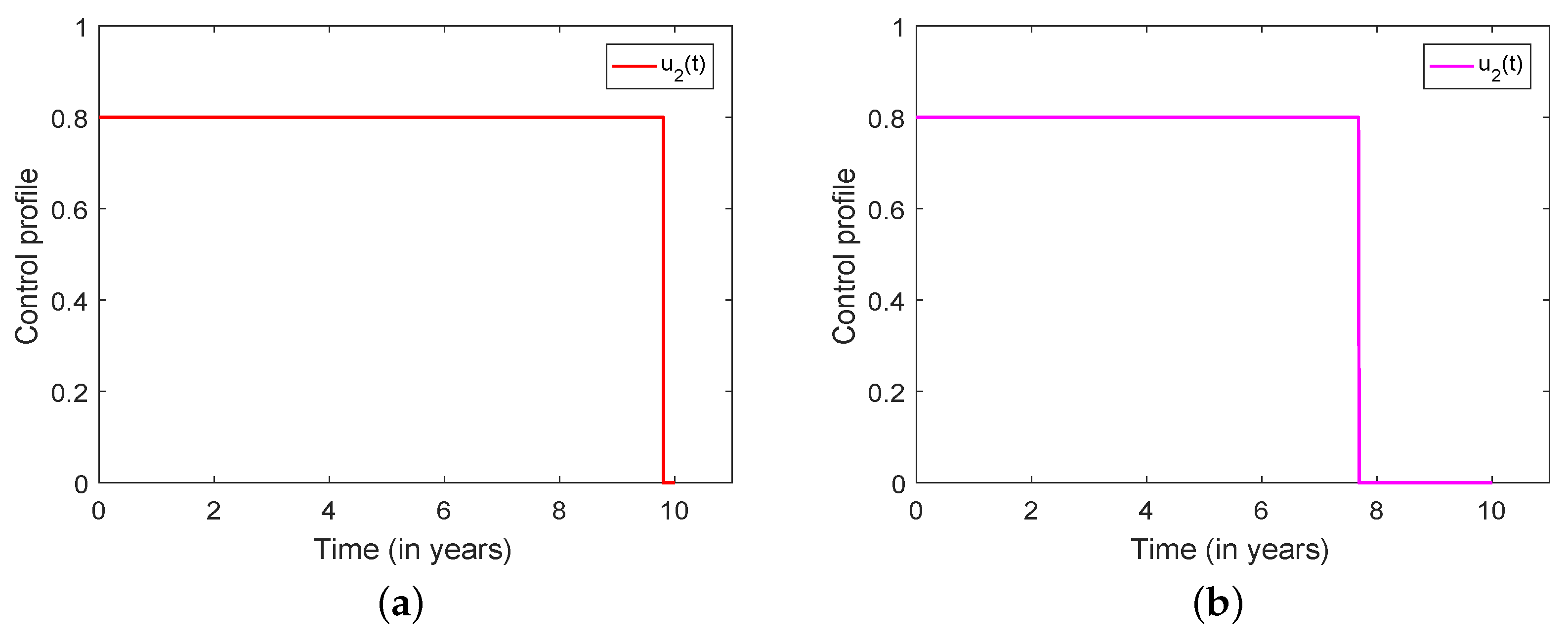
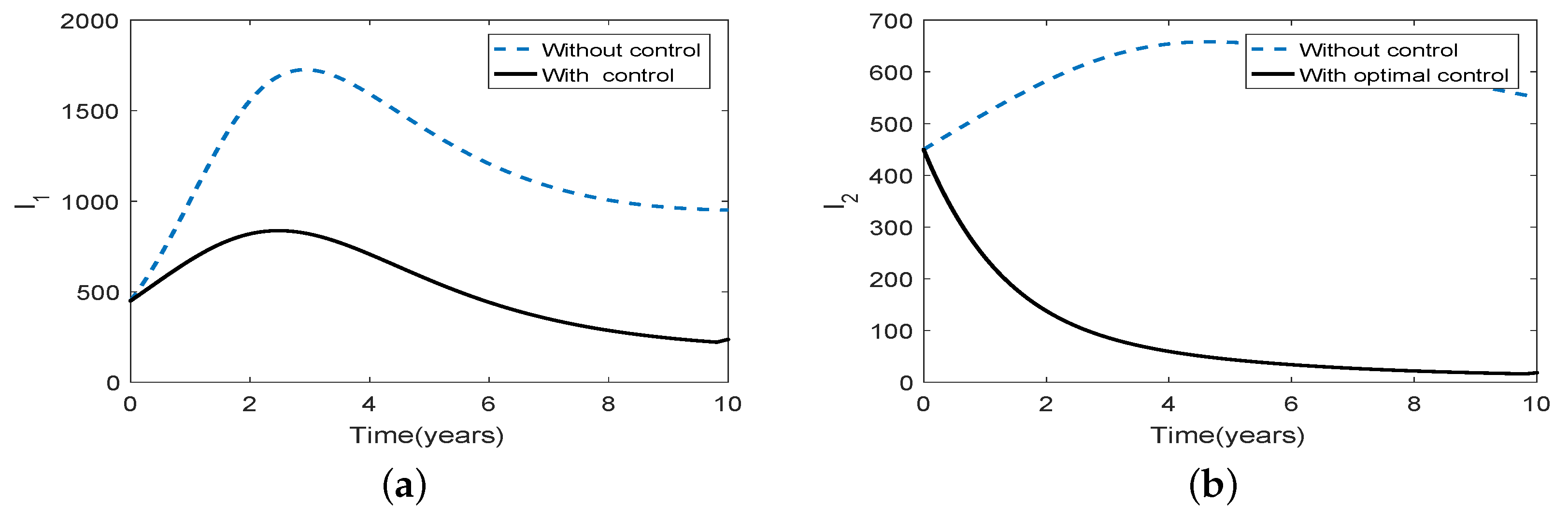
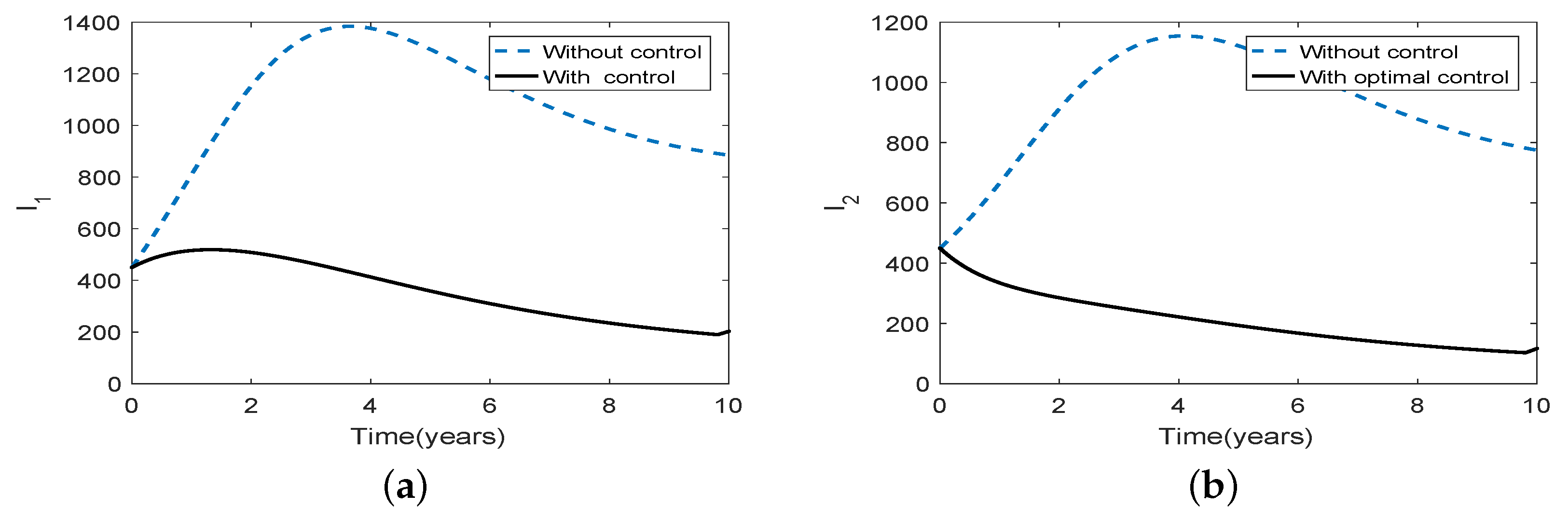
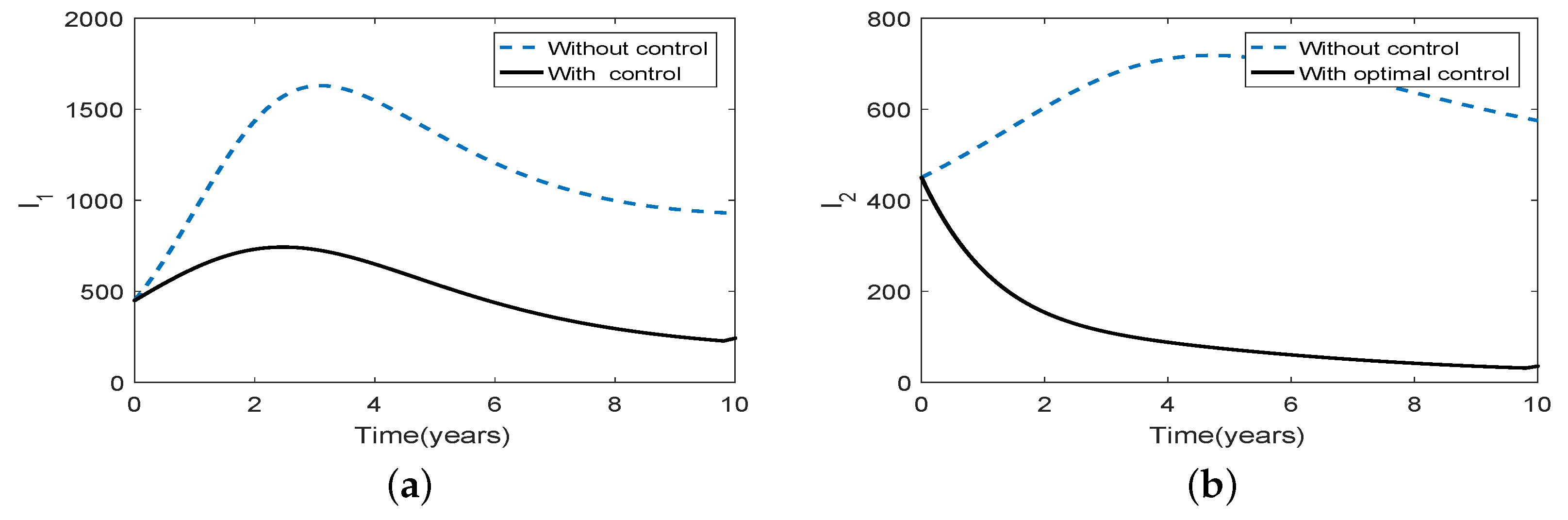
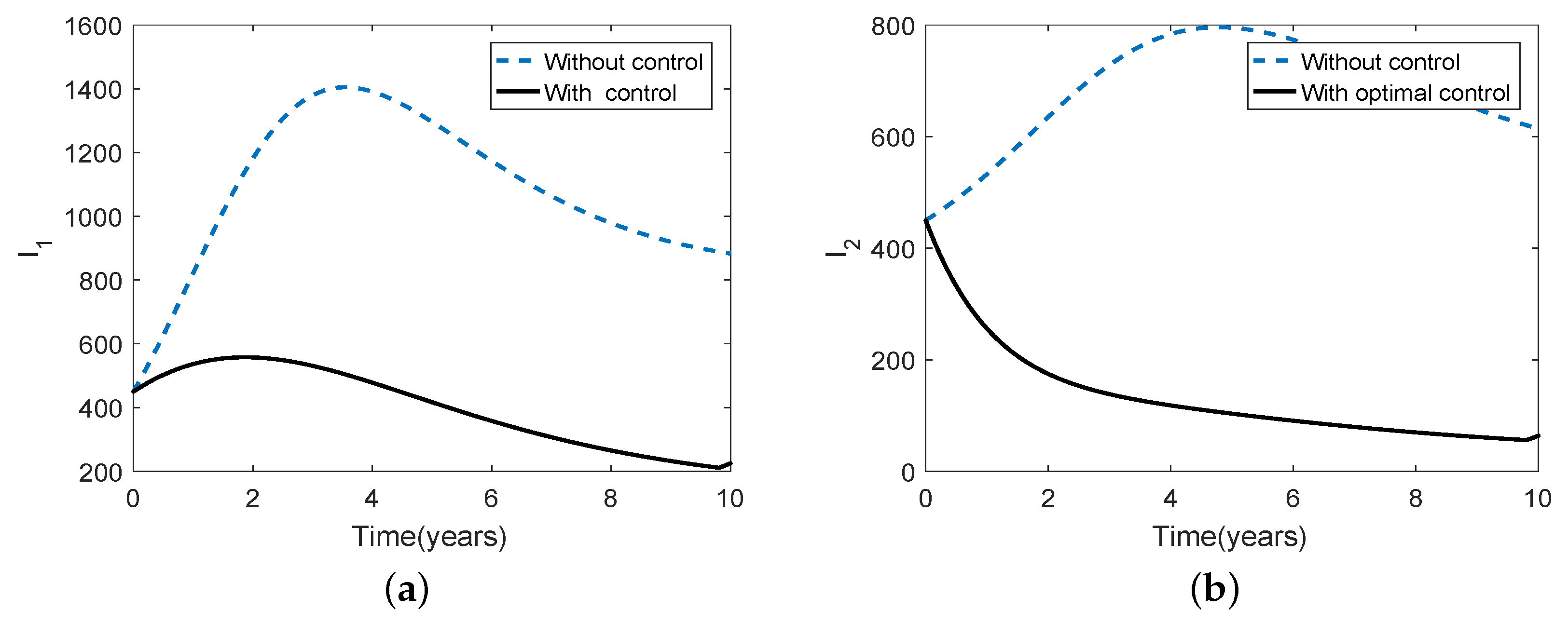
3.5. Optimal Culling
- (a)
- Scenario 1: No culling in high risk population (Patch 1), that is,
- (b)
- Scenario 2: Low intensity culling in high risk population,
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Derivation of Basic Reproduction Number
Appendix B. Stability of the Disease-Free Equilibrium
Appendix C. Uniform Persistence
Appendix D. Existence of a Unique Endemic Equilibrium Point
References
- Mufinda, F.C.; Boinas, F.; Nunes, C. Prevalence and factors associated with human brucellosis in livestock professionals. Revista Saúde Pública 2017, 57. [Google Scholar] [CrossRef] [PubMed]
- Shevtsova, E.; Shevtsov, A.; Mukanov, K.; Filipenko, M.; Kamalova, D.; Sytnik, I.; Syzdykov, M.; Kuznetsov, A.; Akhmetova, A.; Zharova, M.; et al. Epidemiology of brucellosis and genetic diversity of brucella abortus in Kazakhstan. PLoS ONE 2016, 11, e0167496. [Google Scholar] [CrossRef] [PubMed]
- Racloz, V.; Schelling, E.; Chitnis, N.; Roth, F. Persistence of brucellosis in pastoral systems. Rev. Sci. Tech. 2013, 32, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Mangen, M.J.; Otte, J.; Pfeiffer, D.; Chilonda, P. Bovine Brucellosis in Sub-Sahara Africa: Estimation of Sero-Prevalence and Impact on Meat and Milk Offtake Potential; Livestock Policy Discussion Paper No. 8; Food and Agriculture Organization of the United Nations (FAO) Livestock Information and Policy Branch: Rome, Italy, 2002. [Google Scholar]
- Yang, C.; Lolika, O.P.; Mushayabasa, S.; Wang, J. Modeling the spatiotempo- ral variations in brucellosis transmission. Nonlinear Anal. Real World Appl. 2017, 38, 49–67. [Google Scholar] [CrossRef]
- Dobson, A.; Meagher, M. The population dynamics of Brucellosis in the Yellowstone National Park. Ecology 1996, 77, 1026–1036. [Google Scholar] [CrossRef]
- Abatih, E.; Ron, L.; Speybroeck, N.; Williams, B.; Berkvens, D. Mathematical analysis of the transmission dynamics of brucellosis among bison. Math. Meth. Appl. Sci. 2015, 38, 3818–3832. [Google Scholar] [CrossRef]
- Li, M.; Sun, G.; Zhang, J.; Jin, Z.; Sun, X.; Wang, Y.; Huang, B.; Zheng, Y. Transmission dynamics and control for brucellosis model in Hingaan League Inner Mongolia, China. Math. Biosci. Eng. 2014, 11, 115–1137. [Google Scholar]
- Lolika, P.O.; Mushayabasa, S.; Bhunu, C.P.; Modnak, C.; Wang, J. Modeling and analyzing the effects of seasonality on brucellosis infection. Chaos Solitons Fractals 2017, 104, 338–349. [Google Scholar] [CrossRef]
- Lolika, P.O.; Modnak, C.; Mushayabasa, S. On the dynamics of brucellosis infection in bison population with vertical transmission and culling Mathematical Biosciences. Math Biosci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Lolika, P.O.; Mushayabasa, S. Dynamics and stability analysis of a brucellosis model with two discrete delays. Discrete Dyn. Nat. Soc. 2018, 2018, 6456107. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction number and subthreshold endemic equilibria for compartment models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: London, UK, 2007. [Google Scholar]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1975. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.T.; Gamkrelidze, R.V.; Mishcheuko, E.F. The Mathematical Theory of Optimal Processes; Wiley: Hoboken, NJ, USA, 1962. [Google Scholar]
- Meunier, N.V.; Sebulime, P.; White, R.G.; Kock, R. Wildlife-livestock interactions and risk areas for cross-species spread of bovine tuberculosis. Onderstepoort J. Vet. Res. 2017, 84, a1221. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Z.; Heesterbeek, J.A.P.; van den Driessche, P. Extending the type reproduction number to infectious disease control targeting contact between types. J. Math. Biol. 2013, 67, 1067–1082. [Google Scholar] [CrossRef] [PubMed]
- LaSalle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Zhao, X.-Q. Dynamical Systems in Population Biology; Springer Science and Business Media: New York, NY, USA, 2013. [Google Scholar]
- Hethcote, H.W.; Thieme, H.R. Stability of the endemic equilibrium in epidemic models with subpopulations. Math. Biosci. 1985, 75, 205–227. [Google Scholar] [CrossRef]
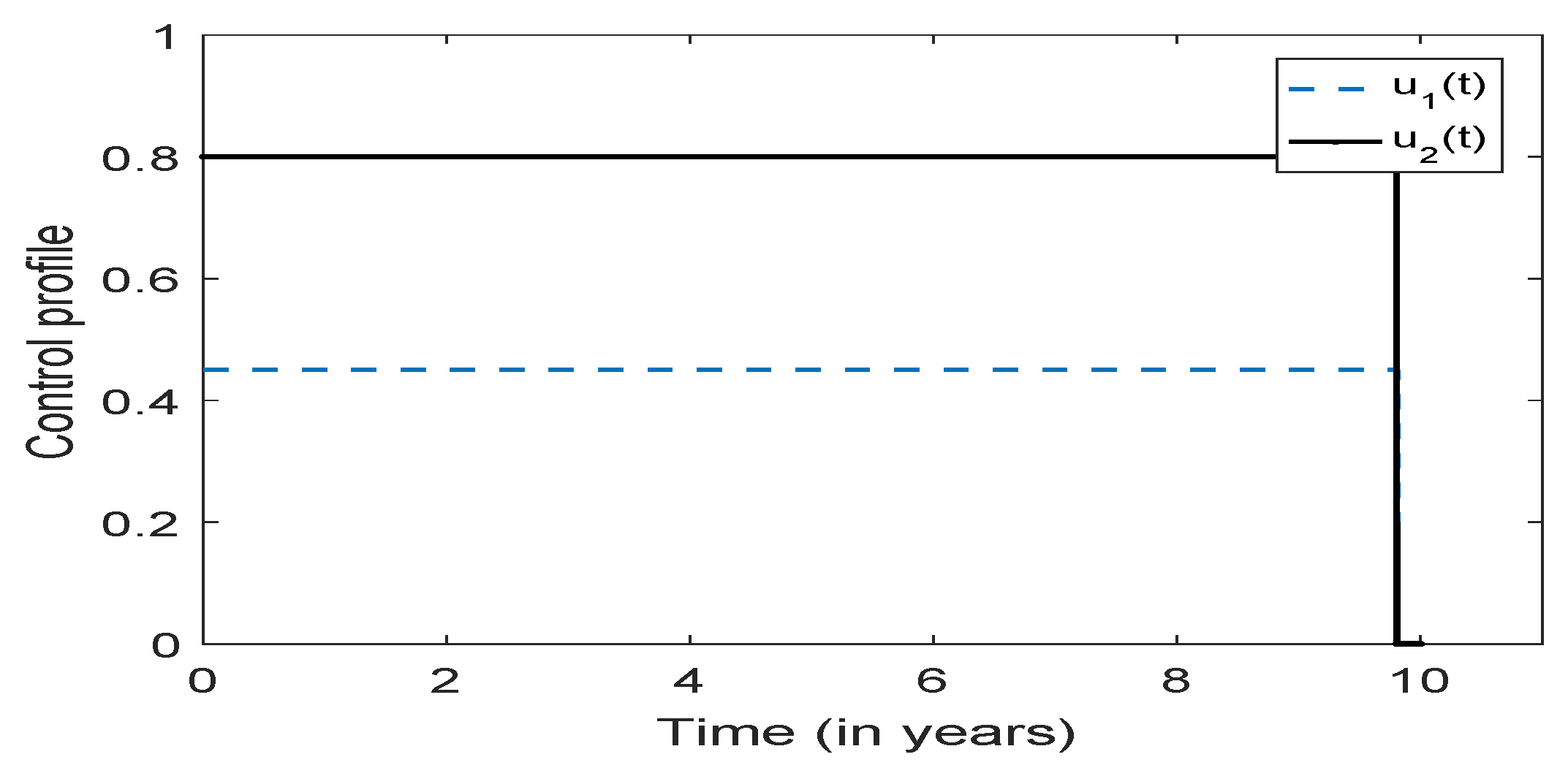
| Symbol | Definition | Units | Value | Source |
|---|---|---|---|---|
| Proportion of time that animals of Patch i spend in Patch j | unit-less | varies | ||
| Susceptibility to brucellosis invasion in Patch 1 | year | 1.63 | [7] | |
| Susceptibility to brucellosis invasion in Patch 2 | year | 0.75 | [7] | |
| Proportion of vertical transmission in Patch 1 | unit-less | 0.9 | [7] | |
| Proportion of vertical transmission in Patch 2 | unit-less | 0.4 | [7] | |
| Recruitment rate in Patch i | year | 0.04 | [7] | |
| Rate of loss of resistance in Patch i | year | 0.2 | [7] | |
| Recovery rate in Patch i | year | 0.5 | [7] | |
| Initial number of susceptible in Patch i | animals | 4050 | [7] | |
| Initial infected animals in Patch i | animals | 450 | [7] | |
| Initial recovered animals in Patch i | animals | 0 | [7] |
| Description | ||
|---|---|---|
| 1 | Weak symmetric coupling , , , | |
| 2 | Strong symmetric coupling , , , | |
| 3 | Weak asymmetric coupling , , , | |
| 4 | Strong asymmetric coupling , , , |
| J | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | ||||||
| 2 | 0 | ||||||
| 3 | 0 | ||||||
| 4 | 0 |
| J | |||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lolika, P.O.; Mushayabasa, S. On the Role of Short-Term Animal Movements on the Persistence of Brucellosis. Mathematics 2018, 6, 154. https://doi.org/10.3390/math6090154
Lolika PO, Mushayabasa S. On the Role of Short-Term Animal Movements on the Persistence of Brucellosis. Mathematics. 2018; 6(9):154. https://doi.org/10.3390/math6090154
Chicago/Turabian StyleLolika, Paride O., and Steady Mushayabasa. 2018. "On the Role of Short-Term Animal Movements on the Persistence of Brucellosis" Mathematics 6, no. 9: 154. https://doi.org/10.3390/math6090154
APA StyleLolika, P. O., & Mushayabasa, S. (2018). On the Role of Short-Term Animal Movements on the Persistence of Brucellosis. Mathematics, 6(9), 154. https://doi.org/10.3390/math6090154





