1. Introduction
All graphs considered here are finite, undirected, without loops or multiple edges. Denote by and the set of vertices and the set of edges of a graph G, respectively. Let and .
A labeling of a graph is any mapping that sends some set of graph elements to a set of numbers or colors. Graph labeling provides valuable information used in several application areas (see [
1]). It is interesting to consider labeling the elements of the graph by the elements of a finite field.
For a graph G, we characterize a labeling to be total k-labeling. A total k-labeling is characterized to be an edge irregular total labeling of the graph G if for each two distinct edges and their weights and are distinct. In addition, total k-labeling is characterized to be a vertex irregular total k-labeling of the graph G if for each two distinctive vertices r and s their weights and are distinct. Here, the weight of a vertex r in G is the sum of the label of r and the labels of all edges incident with the vertex r. The least k for which the graph G has an edge irregular total labeling is called the total irregularity strength of G, represented by . Analogously, the minimum k for which the graph G has a vertex irregular total labeling is called the total vertex irregularity strength of G, denoted by .
Chartrand et al. [
2] introduced two graph invariants namely irregular assignments and the irregularity strength. Baca et al. [
3] modified these graph invariants and introduced the concept of total edge irregularity strength and total vertex irregularity strength for a graph
G. A simple lower bound for
and
of a
—graph
G in terms of maximum degree
and the minimum degree
determine in the following theorems.
Theorem 1. [
3]
Let G be a finite graph with p vertices, q edges and having maximum degree , the upper square brackets represent the ceiling function, and then Theorem 2. [
3]
Let G be a finite graph with p vertices, q edges, minimum degree and maximum degree , the upper square brackets represent the ceiling function, and then In [
4], Ivančo and Jendroľ posed the following conjecture:
Conjecture 1. [4] Let G be a finite graph with p vertices, q edges, different from with minimum degree , maximum degree , the upper square brackets represent the ceiling function, and then In [
5], Nurdin et al. posed the following conjecture:
Conjecture 2. [5] Let G be a connected graph having vertices of degree , where δ and Δ
are the minimum and the maximum degree of G, respectively. Moreover, the upper square brackets represent the ceiling function, and then Conjecture 1 has been shown for complete graphs and complete bipartite graphs [
6,
7], for hexagonal grid graphs [
8] , for toroidal grid [
9], for generalized prism [
10], for strong product of cycles and paths [
11], for categorical product of two cycles [
12], for zigzag graphs [
13] and for strong product of two paths [
14].
Conjecture 2 has been verified for for circulant graphs [
15].
Combining both total edge irregularity strength and total vertex irregularity strength notions, Marzuki et al. [
16] introduced a new irregular total
k-labeling of a graph
G, which is required to be at the same time both vertex and edge irregular as follows:
Definition 1. A total labeling is called totally irregular total k-labeling of G if every two distinct vertices u and v in satisfy and every two distinct edges and in satisfy where and The minimum k for which a graph G has a totally irregular total k-labeling is called the total irregularity strength of G, denoted by
Marzuki, et al. [
16] gave a lower bond of
as follows:
Ramdani and Salman [
17] showed that the lower bound in Equation (
1) for some cartesian product graphs is tight. Besides that, they determined the total irregularity strength of cycles and paths. For more details, see [
18,
19,
20]. In [
21], Ahmad et al. found the exact value of total irregularity strength of generalized Petersen graph.
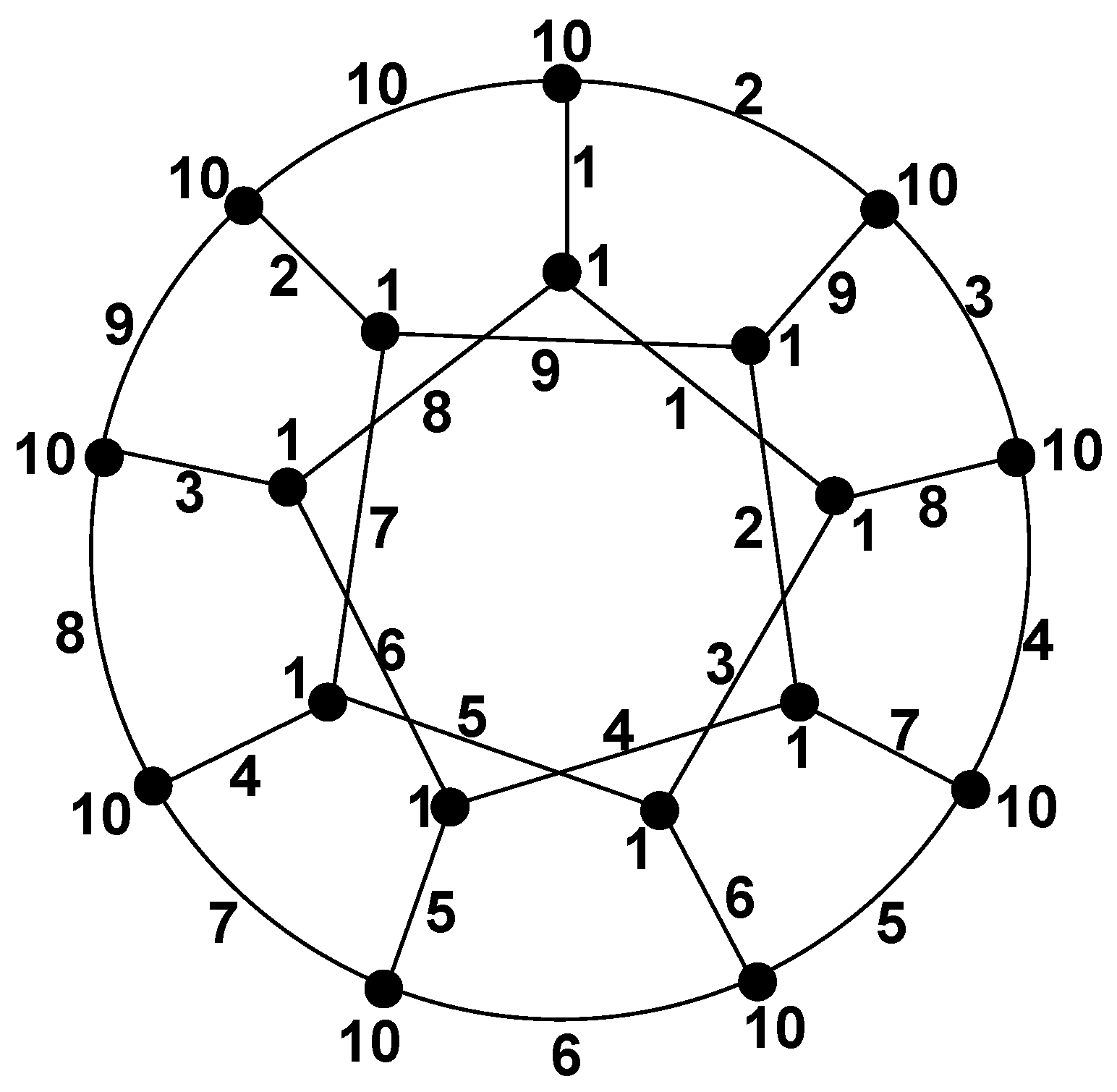
Example 1. For illustration, the concept of the totally irregular total k-labeling,
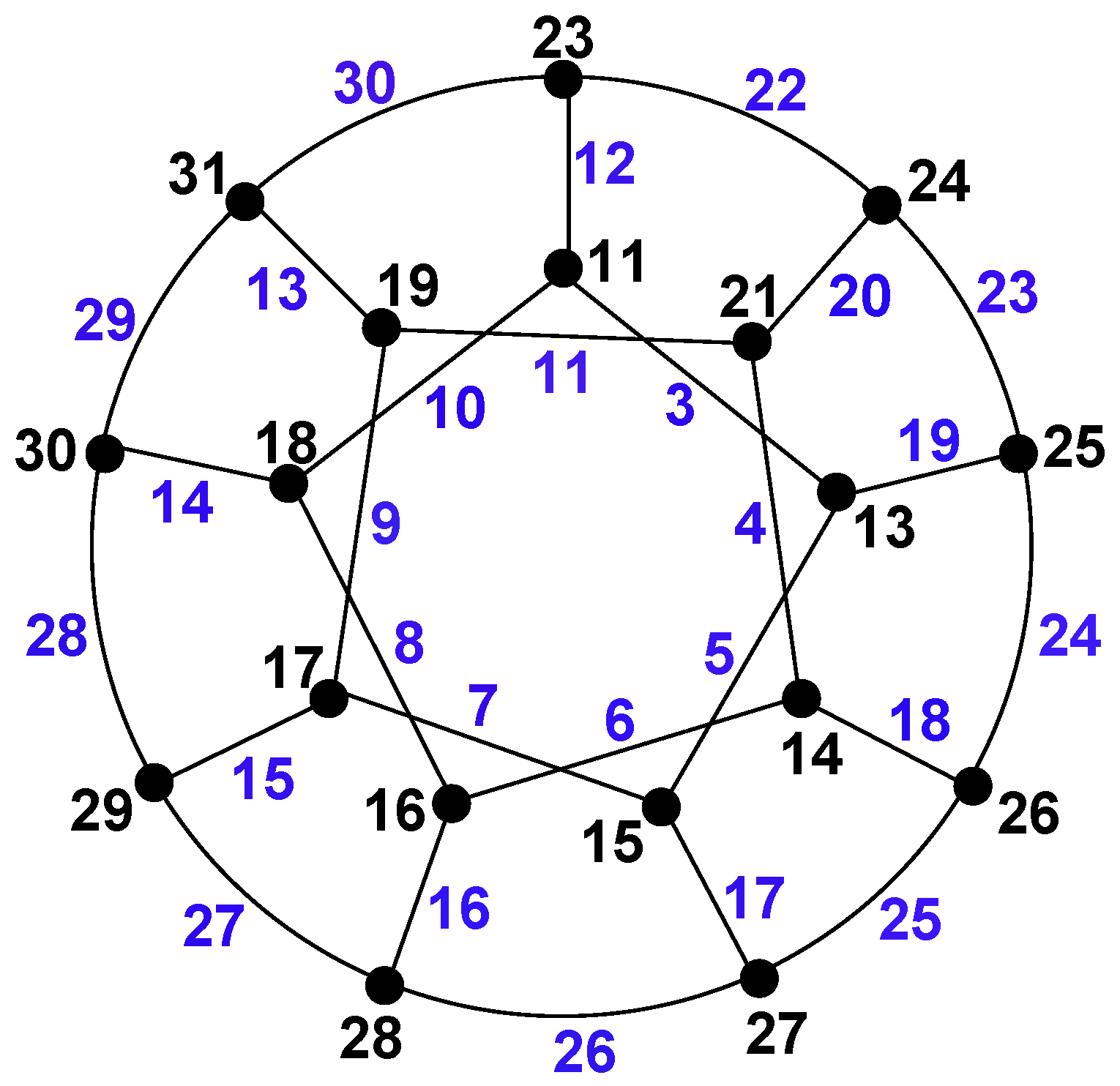
we give an example from our recent paper [21] in which we show the totally irregular total 10-labeling for generalized Petersen graph (see Figure 1). The weights for all vertices and the weights for all edges under the totally irregular total 10-labeling are given in
Figure 2.
Now, from
Figure 2, it is easy to check that edge weights are different and represented by blue. On the other hand, the vertex weights are different and represented by black.
In this paper, we investigate the total irregularity strength of planar graphs.
2. The Planar Graph
Siddiqui introduced the planar graph
in [
22] and computed the
. The planar graph
(see
Figure 3) is obtained from the planar graph
by adding new edges
and having the same vertex set. The planar graph
has
Clearly, the planar graph has vertices and edges. More preciously, we call the cycle induced by the inner cycle, cycle induced by the outer cycle, and the set vertices , the outer vertices. All subscripts are taken under modulo n. In the next theorem, we determine the total irregularity strength of the planar graph .
Theorem 3. Let , be a planar graph. Then, .
Proof. Since
, from Theorem 1,
. In addition,
has
n vertices of degree 2,
n vertices of degree 4, and
n vertices of degree 6; thus, from Theorem 2, we get
From Equation (
1), we get
Now, we show that
For this, we define a total labeling
from
into
and compute the vertex weight and edge weights in the following way. ☐
Let . For , we have
,
,
,
,
,
,
,
,
,
,
Now, the weight of the edges and vertices of under the labeling are distinct. It is easy to check that there are no two edges of the same weight and there are no two vertices of the same weight. Thus, is a totally irregular total labeling. We conclude that , which complete the proof.
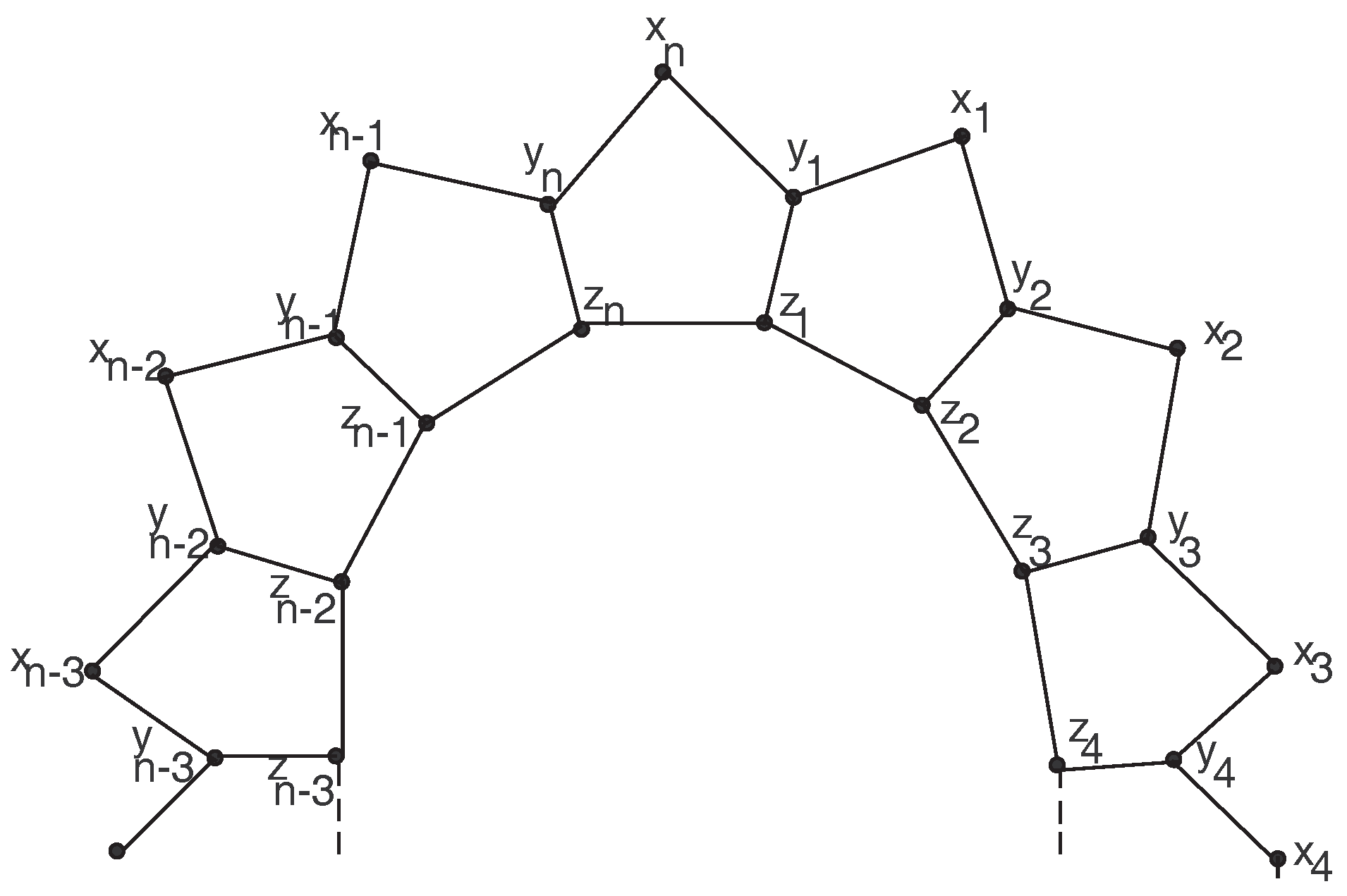
3. The Planar Graph (Pentagonal Circular Ladder)
In [
23], Bača defined the prism
(Circular ladder) for
. It is a cubic graph which can be defined as the cartesian product
on a path on two vertices with a cycle on
n vertices. Prism
is considered of
cycle
, an inner
cycle
, and a set of
n spokes
,
,
. The planar graph (pentagonal circular ladder)
(see
Figure 4) is obtained from the graph of prism
by adding a new vertex
between
and
, for
. The planar graph (pentagonal circular ladder)
has
For our purpose, we call the cycle induced by the inner cycle, and the cycle induced by the outer cycle. All subscripts are taken under modulo n. In the next theorem, we determine the total irregularity strength of the planar graph .
Theorem 4. Let , be a planar graph. Then, .
Proof. Since
, from Theorem 1,
. In addition,
has
n vertices of degree 2,
vertices of degree 3; thus, from Theorem 2, we get
From Equation (
1), we get
Now, we show that
For this, we define a total labeling
from
into
and compute the vertex weight and edge weights in the following way. ☐
Let and .
For , we have,
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
For , we have,
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
For , we have,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
For , we have,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
For
and
, we have
,
,
Case 1.when Case 2.when Case 3.when The weight of the edges and vertices under the labeling are distinct. It is easy to check that there are no two edges of the same weight and there are no two vertices of the same weight. Thus, is a totally irregular total labeling. We conclude that , which complete the proof.
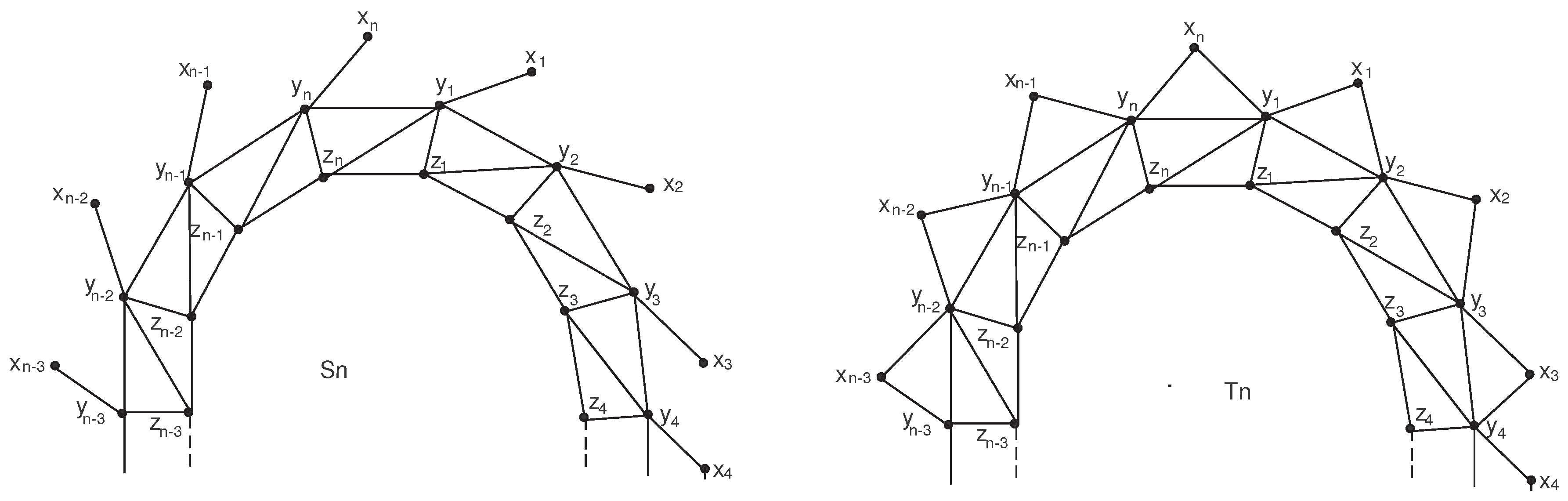
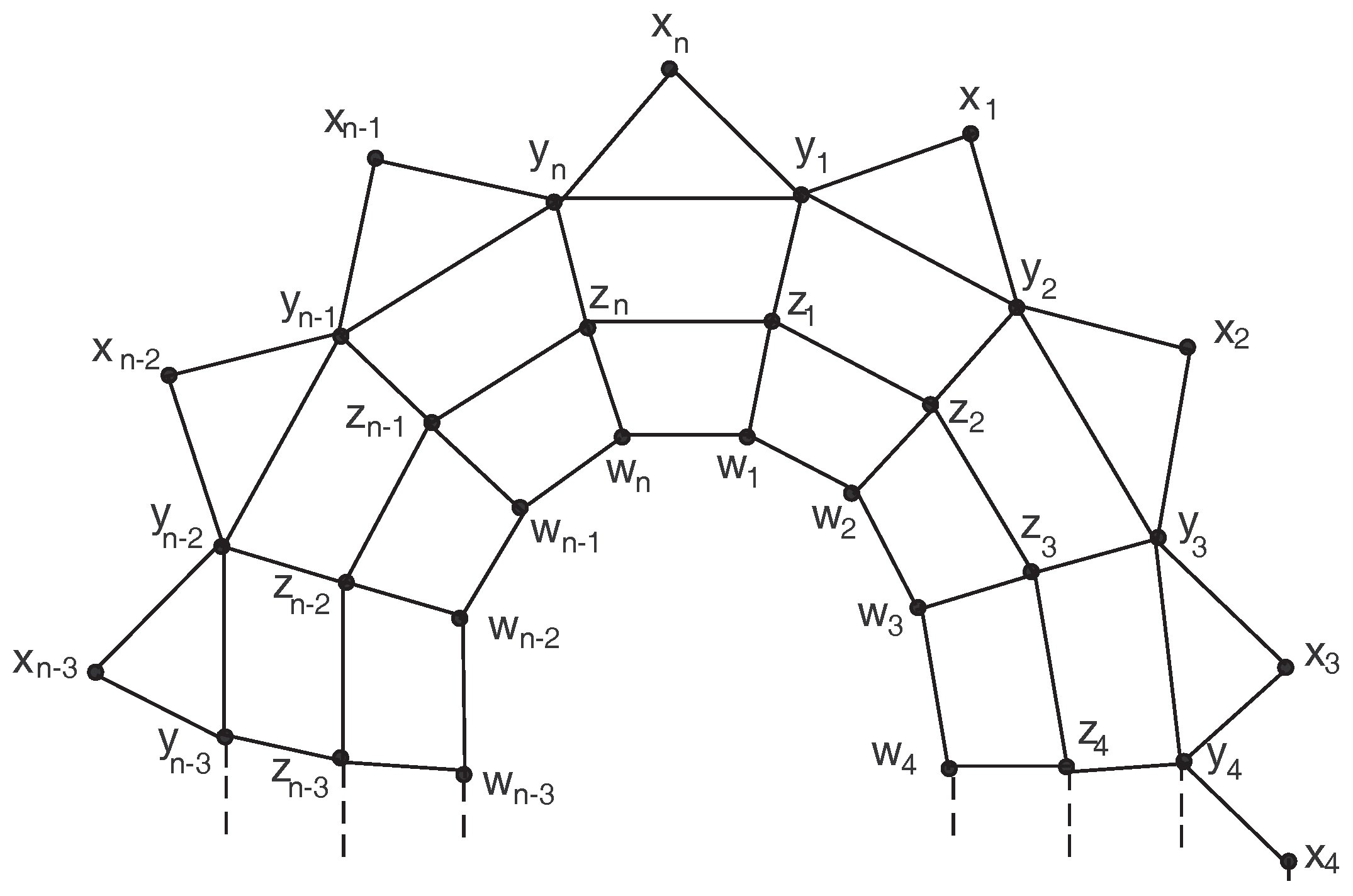
4. The Planar Graph
In [
23], Bača defined the planar graph (pentagonal circular ladder)
. The planar graph
(see
Figure 5) is obtained from the planar graph (pentagonal circular ladder)
by adding new edges
. The planar graph
has
The planar graph has vertices and edges. For our purpose, we call the cycle induced by the inner cycle, the cycle induced by the middle cycle, the cycle induced by the outer cycle, and the set of vertices the set of outer vertices. The subscript must be replaced by 1.
Theorem 5. Let , be a planar graph. Then,
Proof. Since
, from Theorem 1
. In addition,
has
n vertices of degree 2,
n vertices of degree 3,
n vertices of degree 4 and
n vertices of degree 5; thus, from Theorem 2, we get
From Equation (
1), we get
Now, we show that
For this, we define a total labeling
from
into
and compute the vertex weight and edge weights in the following way. ☐
Let and ,
,
,
,
,
,
,
,
,
,
Case 1.when and 1
,
,
,
,
,
,
Case 2.when 1 (mod 6) and 1
,
,
,
,
,
,
Case 3.when n ≡ 2 (mod 6) and 1 ≤ i ≤ n
,
,
,
,
,
,
Case 4.when 3 (mod 6) and 1
,
,
,
,
,
,
Case 5.when 4 (mod 6) and 1
,
,
,
,
,
,
Case 6.when 5 (mod 6) and 1
,
,
,
,
,
,
The weight of the edges and vertices of under the labeling ϕ are distinct. It is easy to check that there are no two edges of the same weight and there are no two vertices of the same weight. Thus, ϕ is a totally irregular total labeling. We conclude that , which completes the proof.
5. Conclusions
In this paper, we discus the total edge irregular k labeling, total vertex irregular k labeling and totally irregular total k labeling of planar graphs. We provide exact result of total irregularity strength for the planar graph , the planar graph (Pentagonal Circular Ladder) and the planar graph . In the future, we are interested in computing the total irregularity strength for the other planar graphs.