Energy of Pythagorean Fuzzy Graphs with Applications

Abstract

Pythagorean fuzzy sets (PFSs), an extension of intuitionistic fuzzy sets (IFSs), inherit the duality property of IFSs and have a more powerful ability than IFSs to model the obscurity in practical decision-making problems. In this research study, we compute the energy and Laplacian energy of Pythagorean fuzzy graphs (PFGs) and Pythagorean fuzzy digraphs (PFDGs). Moreover, we derive the lower and upper bounds for the energy and Laplacian energy of PFGs. Finally, we present numerical examples, including the design of a satellite communication system and the evaluation of the schemes of reservoir operation to illustrate the applications of our proposed concepts in decision making.

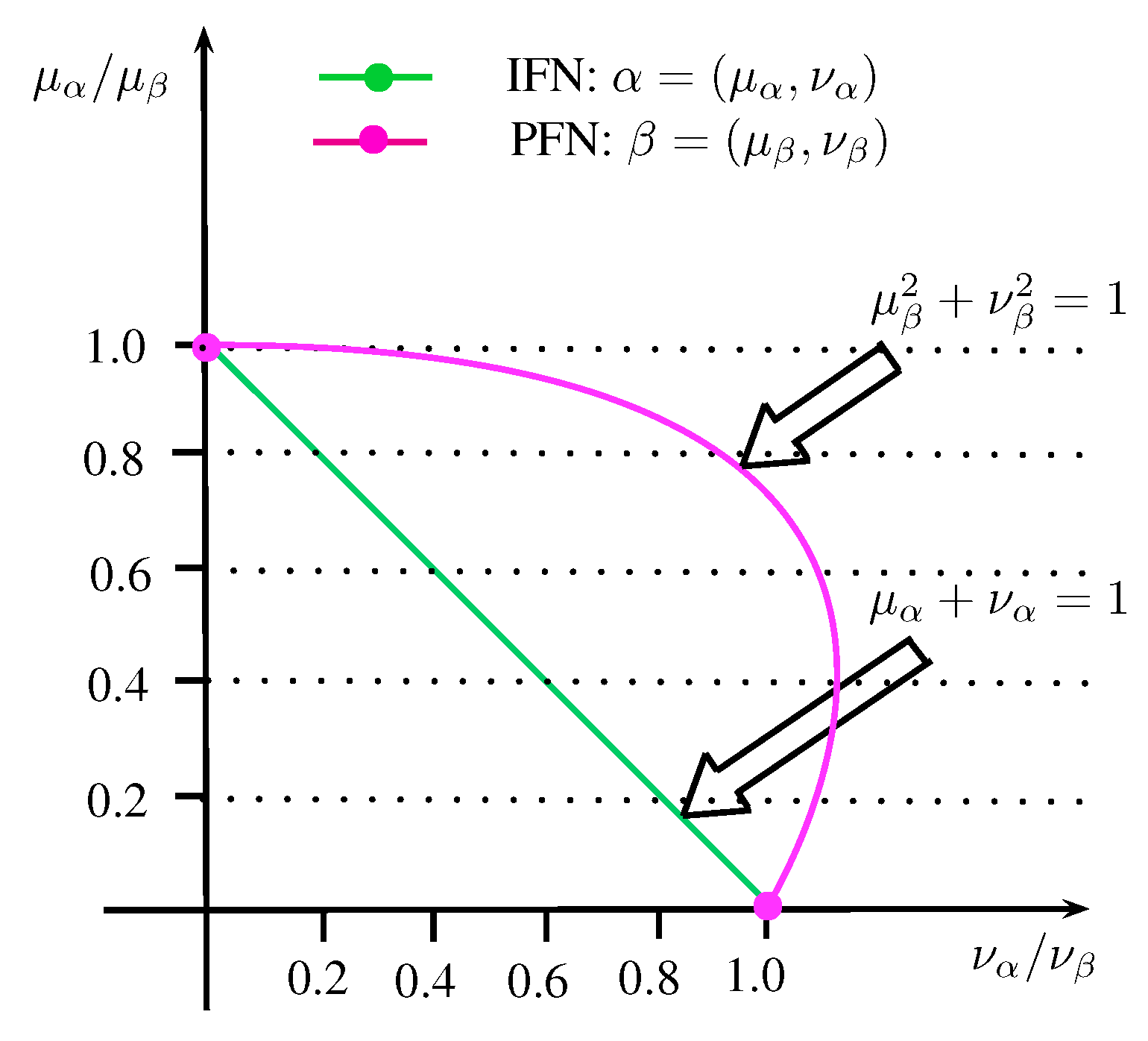
1. Introduction

Yager recently [1,2] introduced the concept of the Pythagorean fuzzy set (PFS) as a generalization of the intuitionistic fuzzy set (IFS) [3], to manage the complex impreciseness and uncertainty in practical decision-making problems. The prominent characteristic of the Pythagorean fuzzy model is to relax the condition that the sum of its membership degree and non-membership degree is no greater than one with the square sum of its membership degree and non-membership degree no greater than one. After the inception of PFS by Yager [2], Zhang and Xu [4] presented the mathematical form of the PFS and introduced the concept of the Pythagorean fuzzy number (PFN). Meanwhile, they presented a series of basic operational laws of PFNs and proposed the Pythagorean fuzzy aggregation operators. PFS, a novel class of the non-standard fuzzy set, has a wide range of applications in different fields, such as medical diagnosis [5], Internet stock investment [6], the service quality of domestic airlines [4] and the governor selection of the Asian Infrastructure Investment Bank [7].

Graph representations are generally used for dealing with structural information, in different domains such as operations research, networks, systems analysis, pattern recognition, economics and image interpretation. Gutman [8] introduced the notion of the energy of a graph in chemistry, because of its relevance to the total $\pi$-electron energy of certain molecules and found upper and lower bounds for the energy of graphs [9]. In chemistry, the energy of a given molecular graph is interesting because of its relation to the total $\pi$-electron energy of the molecule represented by that graph. A graph with all isolated vertices $K_n^c$ has zero energy, while the complete graph $K_n$ with n vertices has energy $2(n-1)$. Later, Gutman and Zhou [10] defined the Laplacian energy of a graph as the sum of the absolute values of the differences of the average vertex degree of G to the Laplacian eigenvalues of G. When there is obscureness in the description of the objects, or in their relations, or in both, the fuzzy graph model is put forward naturally. The concept of fuzzy graphs was initiated by Kaufmann [11], based on Zadeh’s fuzzy relations [12]. Rosenfeld [13] discussed the concept of the fuzzy graph and developed its structure. The energy of a fuzzy graph was investigated in [14] by Anjali and Mathew. The Laplacian energy of a fuzzy graph was defined by Sharbaf and Fayazi [15]. Parvathi and Karunambigai [16] generalized the concept of a fuzzy graph to an intuitionistic fuzzy graph (IFG). Later, IFGs were discussed by Akram and Davvaz [17]. Praba et al. [18] defined the energy of IFGs as an extension of [14]. Basha and Kartheek [19] generalized the concept of the Laplacian energy of a fuzzy graph to the Laplacian energy of an IFG. Akram et al. [20,21,22,23,24,25,26] put forward many new concepts concerning the extended structures of fuzzy graphs and provided their pertinent applications in decision-making. Recently, Naz et al. [27] proposed the concept of Pythagorean fuzzy graphs (PFGs), a generalization of the notion of Akram and Davvaz IFGs [17], along with its applications in decision-making. The Pythagorean fuzzy model is more flexible and practical than fuzzy and intuitionistic fuzzy models. Therefore, in this research study, we introduce certain novel concepts, including the energy and Laplacian energy of PFGs, as well as the energy and Laplacian energy of Pythagorean fuzzy digraphs (PFDGs). We illustrate these concepts with examples. We investigate some of their interesting properties. In particular, we solve decision-making problems concerning the design of a satellite communication system and the evaluation of the schemes of reservoir operation to illustrate the applicability and effectiveness of our proposed notions.

The paper is structured as follows: Section 2 proposes the concept of the energy of a PFG and investigates its properties. Section 3 puts forward the Laplacian energy of a PFG based on its Laplacian eigenvalues. Section 4 generalizes the concepts of energy and Laplacian energy to PFDGs. Section 5 is reserved for demonstrating the use of the proposed concepts of energy and Laplacian energy in decision-making, and finally, we draw conclusions in Section 6.

Throughout this paper, Z represents a crisp universe of generic elements, G stands for the crisp graph, $\mathcal{G}$ is the PFG and $\mathcal{D}$ is the PFDG.

Definition 1

([2,28]). Let Z be a fixed set. A PFS $\mathcal{P}$ in Z is expressed as the following mathematical symbol:

$$\mathcal{P}=\left\{⟨z,{\mu }_{\mathcal{P}}\left(z\right),{\nu }_{\mathcal{P}}\left(z\right)⟩\right|z\in Z\},$$

characterized by a membership function ${\mu }_{\mathcal{P}}$ and a non-membership function ${\nu }_{\mathcal{P}}$, where:

$$\begin{array}{cc}\hfill {\mu }_{\mathcal{P}}:Z\to [0,1],& z\in Z\to {\mu }_{\mathcal{P}}\left(z\right)\in [0,1]\hfill \\ \hfill {\nu }_{\mathcal{P}}:Z\to [0,1],& z\in Z\to {\nu }_{\mathcal{P}}\left(z\right)\in [0,1]\hfill \end{array}$$

such that $0\le {\mu }_{\mathcal{P}}^2\left(z\right)+{\nu }_{\mathcal{P}}^2\left(z\right)\le 1\mathrm{for}\mathrm{all}z\in Z.$ Moreover, for all $z\in Z,$ ${\pi }_{\mathcal{P}}\left(z\right)=\sqrt{1-{\mu }_{\mathcal{P}}^2\left(z\right)-{\nu }_{\mathcal{P}}^2\left(z\right)}$ is called a Pythagorean fuzzy index or degree of hesitancy of z in $\mathcal{P}$.

For computational convenience, $\beta =({\mu }_{\beta },{\nu }_{\beta })$ is called a PFN [4], where ${\mu }_{\beta },{\nu }_{\beta }\in [0,1],{\mu }_{\beta }^2+{\nu }_{\beta }^2\le 1$ and ${\pi }_{\beta }=\sqrt{1-{\mu }_{\beta }^2-{\nu }_{\beta }^2}$.

The key difference between the intuitionistic fuzzy number (IFN) [29] and PFN is their different constraint conditions, that is the constraint conditions of IFN and PFN are ${\mu }_{\alpha }+{\nu }_{\alpha }\le 1$ and ${\mu }_{\beta }^2+{\nu }_{\beta }^2\le 1$, respectively. Since for any point $(r,s)(r,s\in [0,1\left]\right)$, if $r+s\le 1$, then $r^2+s^2\le 1$, so the space of PFS’s membership degree is greater than the space of IFS’s membership degree, as shown in Figure 1.

Figure 1. Comparison of spaces of the IFNs and the Pythagorean fuzzy numbers (PFNs).

For more definitions and terminologies, the readers are referred to [30,31,32,33,34,35,36,37,38,39,40,41].

2. Energy of Pythagorean Fuzzy Graphs

In this section, we define the energy of a graph under Pythagorean fuzzy circumstances and investigate its properties.

Definition 2

([27]). A PFG on a non-empty set Z is a pair $\mathcal{G}=(\mathcal{P},\mathcal{Q})$, where $\mathcal{P}$ is a PFS on Z and $\mathcal{Q}$ is a Pythagorean fuzzy relation on Z such that:

$$\begin{array}{c}\hfill {\mu }_{\mathcal{Q}}\left(yz\right)\le min\{{\mu }_{\mathcal{P}}\left(y\right),{\mu }_{\mathcal{P}}\left(z\right)\},{\nu }_{\mathcal{Q}}\left(yz\right)\ge max\{{\nu }_{\mathcal{P}}\left(y\right),{\nu }_{\mathcal{P}}\left(z\right)\}\end{array}$$

and $0\le {\mu }_{\mathcal{Q}}^2\left(yz\right)+{\nu }_{\mathcal{Q}}^2\left(yz\right)\le 1$ for all $y,z\in Z.$ We call $\mathcal{P}$ and $\mathcal{Q}$ the Pythagorean fuzzy vertex set and the Pythagorean fuzzy edge set of $\mathcal{G}$, respectively. Here, $\mathcal{Q}$ is a symmetric Pythagorean fuzzy relation on $\mathcal{P}$. If $\mathcal{Q}$ is not symmetric on $\mathcal{P}$, then $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ is called PFDG.

Example 1.

Consider a graph $G=(V,E)$, where $V=\{z_1,z_2,z_3,z_4,z_5,z_6\}$ is the vertex set and $E=\{z_1{z}_2,z_1{z}_3,z_1{z}_4,z_1{z}_5,z_1{z}_6,z_2{z}_3,z_3{z}_4,z_4{z}_5,z_5{z}_6\}$ is the edge set of G. Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on V, as shown in Figure 2, defined by:

$$\begin{array}{ccc}\hfill \mathcal{P}& =& ⟨\left(\frac{z_1}{0.8},\frac{z_2}{0.7},\frac{z_3}{0.5},\frac{z_4}{0.8},\frac{z_5}{0.7},\frac{z_6}{0.4}\right),\left(\frac{z_1}{0.5},\frac{z_2}{0.4},\frac{z_3}{0.6},\frac{z_4}{0.3},\frac{z_5}{0.4},\frac{z_6}{0.3}\right)⟩,\hfill \\ \hfill \mathcal{Q}& =& ⟨\left(\frac{z_1{z}_2}{0.3},\frac{z_1{z}_3}{0.4},\frac{z_1{z}_4}{0.7},\frac{z_1{z}_5}{0.4},\frac{z_1{z}_6}{0.3},\frac{z_2{z}_3}{0.4},\frac{z_3{z}_4}{0.5},\frac{z_4{z}_5}{0.6},\frac{z_5{z}_6}{0.4}\right),\hfill \\ & & \left(\frac{z_1{z}_2}{0.8},\frac{z_1{z}_3}{0.7},\frac{z_1{z}_4}{0.6},\frac{z_1{z}_5}{0.5},\frac{z_1{z}_6}{0.6},\frac{z_2{z}_3}{0.9},\frac{z_3{z}_4}{0.7},\frac{z_4{z}_5}{0.6},\frac{z_5{z}_6}{0.9}\right)⟩.\hfill \end{array}$$

Figure 2. Pythagorean fuzzy graph.

Definition 3.

The adjacency matrix $A\left(\mathcal{G}\right)=(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right),A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right))$ of a PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is defined as a square matrix $A\left(\mathcal{G}\right)=\left[a_{ij}\right],$ $a_{ij}=({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right),{\nu }_{\mathcal{Q}}\left(z_i{z}_j\right))$, where ${\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)$ and ${\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)$ represent the strength of relationship and strength of non-relationship between $z_i$ and $z_j$, respectively.

Definition 4.

The spectrum of adjacency matrix of a PFG $A\left(\mathcal{G}\right)$ is defined as $(S,T)$, where S and T are the sets of eigenvalues of $A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)$ and $A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)$, respectively.

Definition 5.

The energy of a PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is defined as:

$$E\left(\mathcal{G}\right)=\left(E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right),E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)=\left({\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^n}|{\lambda }_i|,{\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^n}\left|{\zeta }_i\right|\right).$$

Example 2.

The adjacency matrix of a PFG given in Figure 2 is:

$A\left(\mathcal{G}\right)=\left[\begin{array}{cccccc}(0,0)& (0.3,0.8)& (0.4,0.7)& (0.7,0.6)& (0.4,0.5)& (0.3,0.6)\\ (0.3,0.8)& (0,0)& (0.4,0.9)& (0,0)& (0,0)& (0,0)\\ (0.4,0.7)& (0.4,0.9)& (0,0)& (0.5,0.7)& (0,0)& (0,0)\\ (0.7,0.6)& (0,0)& (0.5,0.7)& (0,0)& (0.6,0.6)& (0,0)\\ (0.4,0.5)& (0,0)& (0,0)& (0.6,0.6)& (0,0)& (0.4,0.9)\\ (0.3,0.6)& (0,0)& (0,0)& (0,0)& (0.4,0.9)& (0,0)\end{array}\right].$

The spectrum and the energy of a PFG $\mathcal{G}$, given in Figure 2, are as follows:

$$\begin{array}{c}Spec\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)=\{-0.9522,-0.5665,-0.3997,0.0031,0.4017,1.5137\},\hfill \\ Spec\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)=\{-1.3553,-0.9082,-0.8959,0.0534,0.9017,2.2044\}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill Spec\left(\mathcal{G}\right)& =& \left\{\right(-0.9522,-1.3553),(-0.5665,-0.9082),(-0.3997,-0.8959),(0.0031,0.0534),\hfill \\ & & (0.4017,0.9017),(1.5137,2.2044)\}.\hfill \end{array}$$

Now, $E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)=3.8369$ and $E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)=6.3190$.

Therefore, $E\left(\mathcal{G}\right)=(3.8369,6.3190)$.

Theorem 1.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG and $A\left(\mathcal{G}\right)$ be its adjacency matrix. If ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$ and ${\zeta }_1\ge {\zeta }_2\ge \dots \ge {\zeta }_n$ are the eigenvalues of $A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)$ and $A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)$, respectively, then:

(i) 

${\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^n}{\lambda }_i=0\mathrm{and}{\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^n}{\zeta }_i=0.$

(ii) 

${\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^n}{\lambda }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$ and ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^n}{\zeta }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$.

Proof. 

(i) 

Since $A\left(\mathcal{G}\right)$ is a symmetric matrix with zero trace, its eigenvalues are real with the sum equal to zero.

(ii) 

By the trace properties of a matrix, we have:

$$tr\left({\left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)}^2\right)={\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^n}{\lambda }_i^2$$

where:

$$\begin{array}{ccc}\hfill tr\left({\left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)}^2\right)& =& \left(0+{\left({\mu }_{\mathcal{Q}}\left(z_1{z}_2\right)\right)}^2+\dots +{\left({\mu }_{\mathcal{Q}}\left(z_1{z}_n\right)\right)}^2\right)\hfill \\ & & +\left({\left({\mu }_{\mathcal{Q}}\left(z_2{z}_1\right)\right)}^2+0+\dots +{\left({\mu }_{\mathcal{Q}}\left(z_2{z}_n\right)\right)}^2\right)\hfill \\ & & ⋮\hfill \\ & & +\left({\left({\mu }_{\mathcal{Q}}\left(z_n{z}_1\right)\right)}^2+{\left({\mu }_{\mathcal{Q}}\left(z_n{z}_2\right)\right)}^2+\dots +0\right)\hfill \\ & =& 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2.\hfill \end{array}$$

Hence:

$${\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^n}{\lambda }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2.$$

Analogously, we can show that ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^n}{\zeta }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$. ☐

Example 3.

Consider a PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ on $V=\{z_1,z_2,z_3,z_4,z_5,z_6\}$, as shown in Figure 2. Then:

$$\begin{array}{c}{\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^6}{\lambda }_i=0,{\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^6}{\zeta }_i=0.\hfill \\ {\displaystyle \sum _{\begin{array}{c}i=1\\ {\lambda }_i\in S\end{array}}^6}{\lambda }_i^2=3.8400=2\left(1.92\right)=2{\displaystyle \sum _{1\le i<j\le 6}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2,\hfill \\ {\displaystyle \sum _{\begin{array}{c}i=1\\ {\zeta }_i\in T\end{array}}^6}{\zeta }_i^2=9.1400=2\left(4.57\right)=2{\displaystyle \sum _{1\le i<j\le 6}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2.\hfill \end{array}$$

We now find upper and lower bounds of the energy of a PFG $\mathcal{G}$, in terms of the number of vertices and the sum of squares of membership and non-membership values of edges.

Theorem 2.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices and $A\left(\mathcal{G}\right)=(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right),A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right))$ be the adjacency matrix of $\mathcal{G}$. Then:

(i) 

$\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1){\left|\det \left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)\right|}^{\frac{2}{n}}}\le E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2};$

(ii) 

$\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1){\left|\det \left(A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)\right|}^{\frac{2}{n}}}\le E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}.$

Proof. 

(i) Upper bound:

Applying the Cauchy–Schwarz inequality to the vectors $(1,1,\dots ,1)$ and $\left(\right|{\lambda }_1|,|{\lambda }_2|,\dots ,|{\lambda }_n\left|\right)$ with n entries, we get:

$${\displaystyle \sum _{i=1}^n}\left|{\lambda }_i\right|\le \sqrt{n}\sqrt{{\displaystyle \sum _{i=1}^n}{\left|{\lambda }_i\right|}^2}$$

(1)

$${\left({\displaystyle \sum _{i=1}^n}{\lambda }_i\right)}^2={\displaystyle \sum _{i=1}^n}{\left|{\lambda }_i\right|}^2+2{\displaystyle \sum _{1\le i<j\le n}}{\lambda }_i{\lambda }_j$$

(2)

By comparing the coefficients of ${\lambda }^{n-2}$ in the characteristic polynomial:

$${\displaystyle \prod _{i=1}^n}(\lambda -{\lambda }_i)=|A\left(\mathcal{G}\right)-\lambda I|,$$

we have:

$${\displaystyle \sum _{1\le i<j\le n}}{\lambda }_i{\lambda }_j=-{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2.$$

(3)

Substituting (3) in (2), we obtain:

$${\displaystyle \sum _{i=1}^n}{\left|{\lambda }_i\right|}^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2.$$

(4)

Substituting (4) in (1), we obtain:

$${\displaystyle \sum _{i=1}^n}\left|{\lambda }_i\right|\le \sqrt{n}\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}=\sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}.$$

Therefore,

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}$$

Lower bound:

$$\begin{array}{ccc}\hfill {\left(E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)}^2& =& {\left({\displaystyle \sum _{i=1}^n}|{\lambda }_i|\right)}^2={\displaystyle \sum _{i=1}^n}|{\lambda }_i{|}^2+2{\displaystyle \sum _{1\le i<j\le n}}\left|{\lambda }_i{\lambda }_j\right|\hfill \\ & =& 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+\frac{2n(n-1)}{2}AM\left\{\right|{\lambda }_i{\lambda }_j\left|\right\}\hfill \end{array}$$

Since $AM\left\{\right|{\lambda }_i{\lambda }_j\left|\right\}\ge GM\left\{\right|{\lambda }_i{\lambda }_j\left|\right\}$, $1\le i<j\le n$, so,

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\ge \sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1)GM\left\{\right|{\lambda }_i{\lambda }_j\left|\right\}}$$

also since:

$$\begin{array}{ccc}\hfill GM\left\{\right|{\lambda }_i{\lambda }_j\left|\right\}={\left({\displaystyle \prod _{1\le i<j\le n}}\left|{\lambda }_i{\lambda }_j\right|\right)}^{\frac{2}{n(n-1)}}& =& {\left({\displaystyle \prod _{i=1}^n}{\left|{\lambda }_i\right|}^{n-1}\right)}^{\frac{2}{n(n-1)}}\hfill \\ & =& {\left({\displaystyle \prod _{i=1}^n}\left|{\lambda }_i\right|\right)}^{\frac{2}{n}}\hfill \\ & =& |\det \left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right){|}^{\frac{2}{n}}\hfill \end{array}$$

so,

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\ge \sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1){\left|\det \left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)\right|}^{\frac{2}{n}}}.$$

Thus, $\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1){\left|\det \left(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)\right|}^{\frac{2}{n}}}\le E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}.$

Analogously, we can show that

$\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2+n(n-1){\left|\det \left(A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\right)\right|}^{\frac{2}{n}}}\le E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}.$ ☐

The following result gives us the upper bound of the energy of a PFG, with the conditions $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$ and $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$.

Theorem 3.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices and $A\left(\mathcal{G}\right)=(A\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right),A\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right))$ be the adjacency matrix of $\mathcal{G}$. If $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$ and $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$, then:

(i) 

$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}+\sqrt{(n-1)\left\{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\left(\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}\right)}^2\right\}};$

(ii) 

$E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}+\sqrt{(n-1)\left\{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\left(\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}\right)}^2\right\}}.$

Proof. 

If $A={\left[a_{ij}\right]}_{n\times n}$ is a symmetric matrix with zero trace, then ${\lambda }_{max}\ge \frac{2{\displaystyle \sum _{1\le i<j\le n}}{a}_{ij}}{n},$ where, ${\lambda }_{max}$ is the maximum eigenvalue of A. If $A\left(\mathcal{G}\right)$ is the adjacency matrix of a PFG $\mathcal{G},$ then ${\lambda }_1\ge \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)}{n},$ where ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$. Moreover, since:

$${\displaystyle \sum _{i=1}^n}{\lambda }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$$

$${\displaystyle \sum _{i=2}^n}{\lambda }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\lambda }_1^2$$

(5)

Applying the Cauchy–Schwarz inequality to the vectors $(1,1,\dots ,1)$ and $\left(\right|{\lambda }_1|,|{\lambda }_2|,\dots ,|{\lambda }_n\left|\right)$ with $n-1$ entries, we get:

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)-{\lambda }_1={\displaystyle \sum _{i=2}^n}\left|{\lambda }_i\right|\le \sqrt{(n-1){\displaystyle \sum _{i=2}^n}{\left|{\lambda }_i\right|}^2}.$$

(6)

Substituting (5) in (6), we must have:

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)-{\lambda }_1\le \sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\lambda }_1^2\right)}$$

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le {\lambda }_1+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\lambda }_1^2\right)}.$$

(7)

Now, since the function:

$$F\left(z\right)=z+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-z^2\right)}$$

decreases on the interval:

$$\left(\sqrt{\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}},\sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}\right),$$

also $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$, $1\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}.$ Therefore,

$$\sqrt{\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}}\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)}{n}\le {\lambda }_1\le \sqrt{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}.$$

Therefore, Equation (7) implies:

$$E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}+\sqrt{(n-1)\left\{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\left(\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}\right)}^2\right\}}.$$

Analogously, we can show that:

$$E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}+\sqrt{(n-1)\left\{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2-{\left(\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2}{n}\right)}^2\right\}}.$$

 ☐

Theorem 4.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices. Then, $E\left(\mathcal{G}\right)\le \frac{n}{2}(1+\sqrt{n}).$

Proof. 

Suppose that $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is a PFG with n vertices. If $n\le 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2=2y$, then by routine calculus, it is easy to show that $f\left(y\right)=\frac{2y}{n}+\sqrt{(n-1)(2y-{(\frac{2y}{n})}^2)}$ is maximized when $y=\frac{n^2+n\sqrt{n}}{4}.$ Substituting this value of y in place of $y={\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)}^2$ in Theorem 3, we must have $E\left({\mu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{n}{2}(1+\sqrt{n}).$ Similarly, it is easy to show that $E\left({\nu }_{\mathcal{Q}}\left(z_i{z}_j\right)\right)\le \frac{n}{2}(1+\sqrt{n}).$ Hence, $E\left(\mathcal{G}\right)\le \frac{n}{2}(1+\sqrt{n}).$ ☐

3. Laplacian Energy of Pythagorean Fuzzy Graphs

This section defines and investigates the Laplacian energy of a PFG and provides its properties in detail.

Definition 6.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices. The degree matrix, $D\left(\mathcal{G}\right)=(D\left({\mu }_Q\left(z_i{z}_j\right)\right),D\left({\nu }_Q\left(z_i{z}_j\right)\right))=\left[d_{ij}\right],$ of $\mathcal{G}$ is a $n\times n$ diagonal matrix defined as:

$$d_{ij}=\left\{\begin{array}{cc}{d}_{\mathcal{G}}\left(z_i\right)\hfill & \mathrm{if}i=j,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Definition 7.

The Laplacian matrix of a PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is defined as $L\left(\mathcal{G}\right)=(L\left({\mu }_Q\left(z_i{z}_j\right)\right),L\left({\nu }_Q\left(z_i{z}_j\right)\right))=D\left(\mathcal{G}\right)-A\left(\mathcal{G}\right)$, where $A\left(\mathcal{G}\right)$ is an adjacency matrix and $D\left(\mathcal{G}\right)$ is a degree matrix of a PFG $\mathcal{G}$.

Example 4.

Consider a graph $G=(V,E)$, where $V=\{z_1,z_2,z_3,z_4,z_5,z_6,z_7,z_8\}$ and $E=\{z_1{z}_2,z_2{z}_3,z_3{z}_4,z_1{z}_4,z_2{z}_4,z_2{z}_8,z_4{z}_6,z_1{z}_8,z_4{z}_5,z_5{z}_6,z_6{z}_7,z_7{z}_8,z_5{z}_8,z_6{z}_8\}$. Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on V, as shown in Figure 3.

Figure 3. Pythagorean fuzzy graph.

The adjacency matrix, degree matrix and Laplacian matrix of the PFG shown in Figure 3 are as follows:

$A\left(\mathcal{G}\right)=\left[\begin{array}{cccccccc}(0,0)& (0.4,0.7)& (0,0)& (0.6,0.7)& (0,0)& (0,0)& (0,0)& (0.5,0.7)\\ (0.4,0.7)& (0,0)& (0.4,0.6)& (0.5,0.6)& (0,0)& (0,0)& (0,0)& (0.3,0.7)\\ (0,0)& (0.4,0.6)& (0,0)& (0.6,0.8)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0.6,0.7)& (0.5,0.6)& (0.6,0.8)& (0,0)& (0.4,0.7)& (0.6,0.8)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0.4,0.7)& (0,0)& (0.4,0.9)& (0,0)& (0.3,0.6)\\ (0,0)& (0,0)& (0,0)& (0.6,0.8)& (0.4,0.9)& (0,0)& (0.4,0.8)& (0.3,0.9)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0.4,0.8)& (0,0)& (0.2,0.6)\\ (0.5,0.7)& (0.3,0.7)& (0,0)& (0,0)& (0.3,0.6)& (0.3,0.9)& (0.2,0.6)& (0,0)\end{array}\right].$

$D\left(\mathcal{G}\right)=\left[\begin{array}{cccccccc}(1.5,2.1)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (1.6,2.6)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (1.0,1.4)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (2.7,3.6)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (1.1,2.2)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (1.7,3.4)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0.6,1.4)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (1.6,3.5)\end{array}\right].$

$L\left(\mathcal{G}\right)=\left[\begin{array}{cccccccc}(1.5,2.1)& (-0.4,-0.7)& (0,0)& (-0.6,-0.7)& (0,0)& (0,0)& (0,0)& (-0.5,-0.7)\\ (-0.4,-0.7)& (1.6,2.6)& (-0.4,-0.6)& (-0.5,-0.6)& (0,0)& (0,0)& (0,0)& (-0.3,-0.7)\\ (0,0)& (-0.4,-0.6)& (1.0,1.4)& (-0.6,-0.8)& (0,0)& (0,0)& (0,0)& (0,0)\\ (-0.6,-0.7)& (-0.5,-0.6)& (-0.6,-0.8)& (2.7,3.6)& (-0.4,-0.7)& (-0.6,-0.8)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (-0.4,-0.7)& (1.1,2.2)& (-0.4,-0.9)& (0,0)& (-0.3,-0.6)\\ (0,0)& (0,0)& (0,0)& (-0.6,-0.8)& (-0.4,-0.9)& (1.7,3.4)& (-0.4,-0.8)& (-0.3,-0.9)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (-0.4,-0.8)& (0.6,1.4)& (-0.2,-0.6)\\ (-0.5,-0.7)& (-0.3,-0.7)& (0,0)& (0,0)& (-0.3,-0.6)& (-0.3,-0.9)& (-0.2,-0.6)& (1.6,3.5)\end{array}\right].$

Definition 8.

The spectrum of Laplacian matrix of a PFG $L\left(\mathcal{G}\right)$ is defined as $(S_L,T_L)$, where $S_L$ and $T_L$ are the sets of Laplacian eigenvalues of $L\left({\mu }_Q\left(z_i{z}_j\right)\right)$ and $L\left({\nu }_Q\left(z_i{z}_j\right)\right)$, respectively.

Theorem 5.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG, and let $L\left(\mathcal{G}\right)$ be the Laplacian matrix of $\mathcal{G}$. If ${\vartheta }_1\ge {\vartheta }_2\ge \dots \ge {\vartheta }_n$ and ${\phi }_1\ge {\phi }_2\ge \dots \ge {\phi }_n$ are the eigenvalues of $L\left({\mu }_Q\left(z_i{z}_j\right)\right)$ and $L\left({\nu }_Q\left(z_i{z}_j\right)\right)$, respectively, then:

(i) 

${\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i=2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right),{\displaystyle \sum _{\begin{array}{c}i=1\\ {\phi }_i\in T_L\end{array}}^n}{\phi }_i=2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right).$

(ii) 

${\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{d}_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_i\right)$, ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\phi }_i\in T_L\end{array}}^n}{\phi }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{d}_{{\nu }_Q\left(z_i{z}_j\right)}^2\left(z_i\right)$.

Proof. 

(i) 

Since $L\left(\mathcal{G}\right)$ is a symmetric matrix with non-negative Laplacian eigenvalues, such that:

$${\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i=tr\left(L\left(\mathcal{G}\right)\right)={\displaystyle \sum _{i=1}^n}{d}_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)=2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right).$$

Therefore, ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i=2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)$.

Similarly, it is easy to show that, ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\phi }_i\in T_L\end{array}}^n}{\phi }_i=2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)$.

(ii) 

By the definition of Laplacian matrix, we have:

$L\left({\mu }_Q\left(z_i{z}_j\right)\right)=\left[\begin{array}{cccc}{d}_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_1\right)& -{\mu }_Q\left(z_1{z}_2\right)& \dots & -{\mu }_Q\left(z_1{z}_n\right)\\ -{\mu }_Q\left(z_2{z}_1\right)& d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_2\right)& \dots & -{\mu }_Q\left(z_2{z}_n\right)\\ ⋮& ⋮& \ddots & ⋮\\ -{\mu }_Q\left(z_n{z}_1\right)& -{\mu }_Q\left(z_n{z}_2\right)& \dots & d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_n\right)\end{array}\right].$

By the trace properties of a matrix, we have:

$$tr\left({\left(L\left({\mu }_Q\left(z_i{z}_j\right)\right)\right)}^2\right)={\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i^2$$

where:

$$\begin{array}{ccc}\hfill tr\left({\left(L\left({\mu }_Q\left(z_i{z}_j\right)\right)\right)}^2\right)& =& (d_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_1\right)+{\mu }_Q^2\left(z_1{z}_2\right)+\dots +{\mu }_Q^2\left(z_1{z}_n\right))\hfill \\ & & +({\mu }_Q^2\left(z_2{z}_1\right)+d_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_2\right)+\dots +{\mu }_Q^2\left(z_2{z}_n\right))\hfill \\ & & +\dots +({\mu }_Q^2\left(z_n{z}_1\right)+{\mu }_Q^2\left(z_n{z}_2\right)+\dots +d_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_n\right))\hfill \\ & =& 2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{d}_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_i\right).\hfill \end{array}$$

Therefore,

$${\displaystyle \sum _{\begin{array}{c}i=1\\ {\vartheta }_i\in S_L\end{array}}^n}{\vartheta }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{d}_{{\mu }_Q\left(z_i{z}_j\right)}^2\left(z_i\right).$$

Analogously, we can show that ${\displaystyle \sum _{\begin{array}{c}i=1\\ {\phi }_i\in T_L\end{array}}^n}{\phi }_i^2=2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{d}_{{\nu }_Q\left(z_i{z}_j\right)}^2\left(z_i\right)$. ☐

Definition 9.

The Laplacian energy of a PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is defined as:

$$LE\left(\mathcal{G}\right)=\left(LE\left({\mu }_Q\left(z_i{z}_j\right)\right),LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\right)=\left({\displaystyle \sum _{i=1}^n}|{\varrho }_i|,{\displaystyle \sum _{i=1}^n}\left|{\xi }_i\right|\right)$$

where:

$$\begin{array}{ccc}\hfill {\varrho }_i& =& {\vartheta }_i-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n},\hfill \\ \hfill {\xi }_i& =& {\phi }_i-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}.\hfill \end{array}$$

Theorem 6.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG, and let $L\left(\mathcal{G}\right)$ be the Laplacian matrix of $\mathcal{G}$. If ${\vartheta }_1\ge {\vartheta }_2\ge \dots \ge {\vartheta }_n$ and ${\phi }_1\ge {\phi }_2\ge \dots \ge {\phi }_n$ are the eigenvalues of $L\left({\mu }_Q\left(z_i{z}_j\right)\right)$ and $L\left({\nu }_Q\left(z_i{z}_j\right)\right)$, respectively, and ${\varrho }_i={\vartheta }_i-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}, {\xi }_i={\phi }_i-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n},$ then:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n}{\varrho }_i=0,{\displaystyle \sum _{i=1}^n}{\xi }_i=0,\hfill \\ {\displaystyle \sum _{i=1}^n}{\varrho }_i^2=2M_{\mu },{\displaystyle \sum _{i=1}^n}{\xi }_i^2=2M_{\nu },\hfill \end{array}$$

where:

$$\begin{array}{c}{M}_{\mu }={\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2,\hfill \\ M_{\nu }={\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2,\hfill \end{array}$$

Example 5.

The Laplacian spectrum and the Laplacian energy of a PFG $\mathcal{G}$, given in Figure 3, are as follows:

$$\begin{array}{c}\mathrm{Laplacian} \mathrm{Spec}\left({\mu }_Q\left(z_i{z}_j\right)\right)=\{0.0000,0.4877,0.8810,1.1086,1.9047,1.9763,2.0436,3.3981\},\hfill \\ \mathrm{Laplacian} \mathrm{Spec}\left({\nu }_Q\left(z_i{z}_j\right)\right)=\{0.0000,0.9099,1.6080,1.8014,3.1573,3.8148,3.8634,5.0453\}.\hfill \end{array}$$

Therefore, Laplacian Spec$\left(\mathcal{G}\right)=\left\{\right(0,0), (0.4877,0.9099), (0.8810,1.6080), (1.1086,1.8014), (1.9047,3.1573), (1.9763,3.8148), (2.0436,3.8634), (3.3981,5.0453\left)\right\}.$ Now,

$$\begin{array}{c}\hfill LE\left({\mu }_Q\left(z_i{z}_j\right)\right)=6.8454,LE\left({\nu }_Q\left(z_i{z}_j\right)\right)=11.5615.\end{array}$$

Therefore, $LE\left(\mathcal{G}\right)=(6.8454,11.5615)$.

Furthermore, we have:

$${\displaystyle \sum _{i=1}^8}{\varrho }_i=0,{\displaystyle \sum _{i=1}^8}{\xi }_i=0.$$

$$\begin{array}{c}{\displaystyle \sum _{i=1}^8}{\varrho }_i^2=8.0952=2\left(4.05\right)=2M_{\mu },\hfill \\ {\displaystyle \sum _{i=1}^8}{\xi }_i^2=20.5555=2\left(10.28\right)=2M_{\nu }.\hfill \end{array}$$

Theorem 7.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices, and let $L\left(\mathcal{G}\right)=(L\left({\mu }_Q\left(z_i{z}_j\right)\right),L\left({\nu }_Q\left(z_i{z}_j\right)\right))$ be the Laplacian matrix of $\mathcal{G}$. Then,

(i) 

$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+n{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2};$

(ii) 

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+n{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}.$

Proof. 

Applying the Cauchy–Schwarz inequality to the n numbers $1,1,\dots ,1$ and $|{\varrho }_1|,|{\varrho }_2|,\dots ,|{\varrho }_n|$, we have:

$${\displaystyle \sum _{i=1}^n}\left|{\varrho }_i\right|\le \sqrt{n}\sqrt{{\displaystyle \sum _{i=1}^n}{\left|{\varrho }_i\right|}^2}$$

$$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \sqrt{n}\sqrt{2M_{\mu }}=\sqrt{2n{M}_{\mu }}.$$

Since $M_{\mu }={\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2,$ therefore $LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+n{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}.$

Analogously, it is easy to show that

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \sqrt{2n{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+n{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}$. ☐

Theorem 8.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices, and let $L\left(\mathcal{G}\right)=(L\left({\mu }_Q\left(z_i{z}_j\right)\right),L\left({\nu }_Q\left(z_i{z}_j\right)\right))$ be the Laplacian matrix of $\mathcal{G}$. Then:

(i) 

$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\ge 2\sqrt{{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2};$

(ii) 

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\ge 2\sqrt{{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}.$

Proof. 

$${\left({\displaystyle \sum _{i=1}^n}|{\varrho }_i|\right)}^2={\displaystyle \sum _{i=1}^n}|{\varrho }_i{|}^2+2{\displaystyle \sum _{1\le i<j\le n}}\left|{\varrho }_i{\varrho }_i\right|\ge 4M_{\mu }$$

$$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\ge 2\sqrt{M_{\mu }}$$

Since $M_{\mu }={\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2,$ therefore $LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\ge 2\sqrt{{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}$.

Similarly, it is easy to show that

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\ge 2\sqrt{{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2}$. ☐

Theorem 9.

Let $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ be a PFG on n vertices, and let $L\left(\mathcal{G}\right)=(L\left({\mu }_Q\left(z_i{z}_j\right)\right),L\left({\nu }_Q\left(z_i{z}_j\right)\right))$ be the Laplacian matrix of $\mathcal{G}$.

Then:

(i) 

$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \left|{\varrho }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2-{\varrho }_1^2\right)};$

(ii) 

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \left|{\xi }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2-{\xi }_1^2\right)}.$

Proof. 

Using the Cauchy–Schwarz inequality, we get:

$${\displaystyle \sum _{i=1}^n}\left|{\varrho }_i\right|\le \sqrt{n{\displaystyle \sum _{i=1}^n}{\left|{\varrho }_i\right|}^2}$$

$${\displaystyle \sum _{i=2}^n}\left|{\varrho }_i\right|\le \sqrt{(n-1){\displaystyle \sum _{i=2}^n}{\left|{\varrho }_i\right|}^2}$$

$$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)-\left|{\varrho }_1\right|\le \sqrt{(n-1)(2M_{\mu }-{\varrho }_1^2)}$$

$$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \left|{\varrho }_1\right|+\sqrt{(n-1)(2M_{\mu }-{\varrho }_1^2)}$$

Since $M_{\mu }={\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2.$ Therefore:

$$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \left|{\varrho }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{\left(d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}\right)}^2-{\varrho }_1^2\right)}.$$

(8)

Similarly, we can show that $LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \left|{\xi }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{\left(d_{{\nu }_Q\left(z_i{z}_j\right)}\left(z_i\right)-\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\nu }_Q\left(z_i{z}_j\right)}{n}\right)}^2-{\xi }_1^2\right)}$. ☐

Theorem 10.

If the PFG $\mathcal{G}=(\mathcal{P},\mathcal{Q})$ is regular, then:

(i) 

$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \left|{\varrho }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2-{\varrho }_1^2\right)};$

(ii) 

$LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \left|{\xi }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2-{\xi }_1^2\right)}.$

Proof. 

Let $\mathcal{G}$ be a regular PFG, then:

$$d_{{\mu }_Q\left(z_i{z}_j\right)}\left(z_i\right)=\frac{2{\displaystyle \sum _{1\le i<j\le n}}{\mu }_Q\left(z_i{z}_j\right)}{n}$$

(9)

Substituting (9) in (8), we get

$LE\left({\mu }_Q\left(z_i{z}_j\right)\right)\le \left|{\varrho }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\mu }_Q\left(z_i{z}_j\right)\right)}^2-{\varrho }_1^2\right)}$.

Similarly, it is easy to show that $LE\left({\nu }_Q\left(z_i{z}_j\right)\right)\le \left|{\xi }_1\right|+\sqrt{(n-1)\left(2{\displaystyle \sum _{1\le i<j\le n}}{\left({\nu }_Q\left(z_i{z}_j\right)\right)}^2-{\xi }_1^2\right)}$. ☐

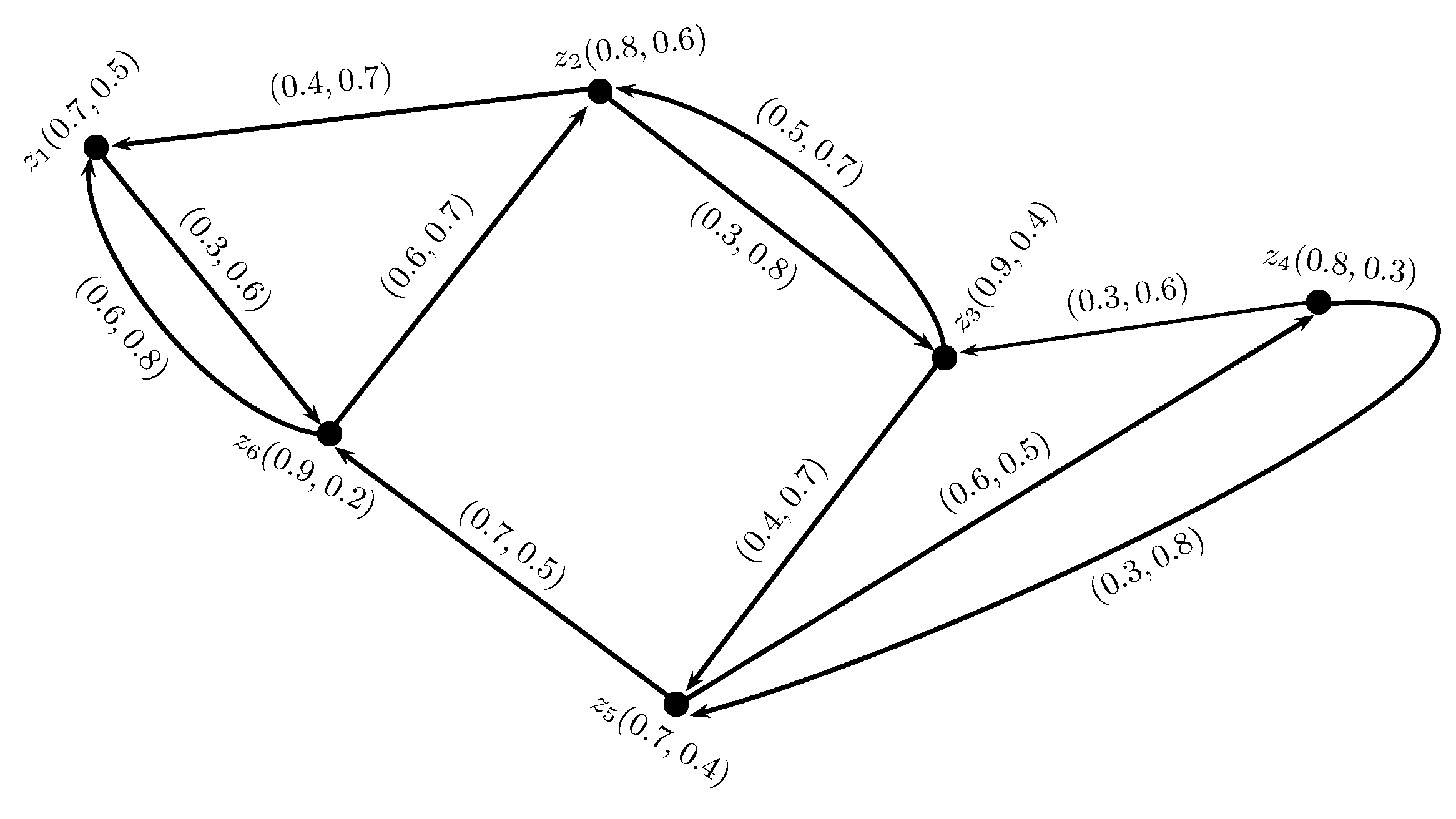
4. Energy and Laplacian Energy of Pythagorean Fuzzy Digraphs

This section generalizes the concept of energy to PFDGs. The eigenvalues of a PFDG may be complex numbers, as its adjacency matrix is not necessarily symmetric.

Definition 10.

The spectrum of the adjacency matrix of a PFDG $A\left(\mathcal{D}\right)$ is defined as $(\mathcal{S},\mathcal{T})$, where $\mathcal{S}$ and $\mathcal{T}$ are the sets of eigenvalues of $A\left({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)\right)$ and $A\left({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)\right)$, respectively.

Definition 11.

Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG on n vertices. The energy of $\mathcal{D}$ is defined as:

$$E\left(\mathcal{D}\right)=\left(E({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)),E({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))\right)=\left({\displaystyle \sum _{\begin{array}{c}i=1\\ t_i\in \mathcal{S}\end{array}}^n}|Re\left(t_i\right)|,{\displaystyle \sum _{\begin{array}{c}i=1\\ w_i\in \mathcal{T}\end{array}}^n}\left|Re\left(w_i\right)\right|\right)$$

where $Re\left(t_i\right)$ and $Re\left(w_i\right)$ represent the real part of eigenvalues $t_i$ and $w_i$, respectively.

Theorem 11.

Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG and $A\left(\mathcal{D}\right)$ be its adjacency matrix. If $t_1\ge t_2\ge \dots \ge t_n$ and $w_1\ge w_2\ge \dots \ge w_n$ are the eigenvalues of $A({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$ and $A({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$, respectively, then:

$${\displaystyle \sum _{\begin{array}{c}i=1\\ t_i\in \mathcal{S}\end{array}}^n}Re\left(t_i\right)=0\mathrm{and}{\displaystyle \sum _{\begin{array}{c}i=1\\ w_i\in \mathcal{T}\end{array}}^n}Re\left(w_i\right)=0.$$

(10)

Example 6.

Consider a digraph $D=(V,\overrightarrow{E})$, where $V=\{z_1,z_2,z_3,z_4,z_5,z_6\}$ and $\overrightarrow{E}=\{z_1{z}_4,z_1{z}_5,z_2{z}_4,z_2{z}_6,z_3{z}_5,z_3{z}_6,,z_4{z}_6\}$. Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG on V, as shown in Figure 4.

Figure 4. Pythagorean fuzzy digraph.

The adjacency matrix of a PFDG given in Figure 4 is:

$A\left(\mathcal{D}\right)=\left[\begin{array}{cccccc}(0,0)& (0,0)& (0,0)& (0.3,0.7)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0.5,0.8)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0.2,0.7)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0.4,0.6)\\ (0.2,0.9)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0.3,0.9)& (0.6,0.8)& (0,0)& (0,0)& (0,0)\end{array}\right].$

The spectrum and the energy of a PFDG $\mathcal{D}$ given in Figure 4 are:

$$\begin{array}{c}Spec({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=\{0.4237,-0.2281+0.3107i,-0.2281-0.3107i,0.0162+0.2133i,0.0162-0.2133i,0\},\hfill \\ Spec({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=\{0.8881,-0.5478+0.5900i,-0.5478-0.5900i,0.1037+0.5975i,0.1037-0.5975i,0\}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill Spec\left(\mathcal{D}\right)& =& \left\{\right(0.4237,0.8881),(-0.2281+0.3107i,-0.5478+0.5900i),(-0.2281-0.3107i,-0.5478-0.5900i),\hfill \\ & & (0.0162+0.2133i,0.1037+0.5975i),(0.0162-0.2133i,0.1037-0.5975i),(0,0)\}.\hfill \end{array}$$

Now, $E({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=0.9123$ and $E({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=2.1910$.

Therefore, $E\left(\mathcal{D}\right)=(0.9123,2.1910)$.

Furthermore,

$${\displaystyle \sum _{\begin{array}{c}i=1\\ t_i\in \mathcal{S}\end{array}}^6}Re\left(t_i\right)=0\mathrm{and}{\displaystyle \sum _{\begin{array}{c}i=1\\ w_i\in \mathcal{T}\end{array}}^6}Re\left(w_i\right)=0.$$

(11)

We now discuss the Laplacian energy of Pythagorean fuzzy digraphs.

Definition 12.

Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG on n vertices. The degree matrix, $D\left(\mathcal{D}\right)=(D({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)),D({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)))=\left[{\mathrm{d}}_{ij}\right],$ of $\mathcal{D}$ is a $n\times n$ diagonal matrix defined as:

$${\mathrm{d}}_{ij}=\left\{\begin{array}{cc}{\mathrm{d}}_{\mathcal{D}}^{\mathit{out}}\left(z_i\right)\hfill & \mathrm{if}i=j,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Definition 13.

The Laplacian matrix of a PFDG $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ is defined as $L\left(\mathcal{D}\right)=(L({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)),L({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)))=D^{\mathit{out}}\left(\mathcal{D}\right)-A\left(\mathcal{D}\right)$, where $A\left(\mathcal{D}\right)$ is an adjacency matrix and $D^{\mathit{out}}\left(\mathcal{D}\right)$ is an out-degree matrix of a PFDG $\mathcal{D}$.

Definition 14.

The spectrum of the Laplacian matrix of a PFDG $L\left(\mathcal{D}\right)$ is defined as $({\mathcal{S}}_L,{\mathcal{T}}_L)$, where ${\mathcal{S}}_L$ and ${\mathcal{T}}_L$ are the sets of Laplacian eigenvalues of $L({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$ and $L({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$, respectively.

Theorem 12.

Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG, and let $L\left(\mathcal{D}\right)$ be the Laplacian matrix of $\mathcal{D}$. If $g_1\ge g_2\ge \dots \ge g_n$ and $h_1\ge h_2\ge \dots \ge h_n$ are the eigenvalues of $L({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$ and $L({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$, respectively, then:

$$\begin{array}{c}\hfill {\displaystyle \sum _{\begin{array}{c}i=1\\ g_i\in {\mathcal{S}}_L\end{array}}^n}Re\left(g_i\right)={\displaystyle \sum _{1\le i<j\le n}}{\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right),{\displaystyle \sum _{\begin{array}{c}i=1\\ h_i\in {\mathcal{T}}_L\end{array}}^n}Re\left(h_i\right)={\displaystyle \sum _{1\le i<j\le n}}{\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right).\end{array}$$

Definition 15.

The Laplacian energy of a PFDG $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ is defined as:

$$LE\left(\mathcal{D}\right)=\left(LE({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)),LE({\nu }_{\overrightarrow{\mathcal{Q}}}(z_i{z}_j))\right)=\left({\displaystyle \sum _{i=1}^n}|r_i|,{\displaystyle \sum _{i=1}^n}\left|s_i\right|\right)$$

where:

$$\begin{array}{ccc}\hfill r_i& =& Re\left(g_i\right)-\frac{{\displaystyle \sum _{1\le i<j\le n}}{\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)}{n},\hfill \\ \hfill s_i& =& Re\left(h_i\right)-\frac{{\displaystyle \sum _{1\le i<j\le n}}{\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)}{n}.\hfill \end{array}$$

Theorem 13.

Let $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ be a PFDG, and let $L\left(\mathcal{D}\right)$ be the Laplacian matrix of $\mathcal{D}$. If $g_1\ge g_2\ge \dots \ge g_n$ and $h_1\ge h_2\ge \dots \ge h_n$ are the eigenvalues of $L({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$ and $L({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))$, respectively, and $r_i=Re\left(g_i\right)-\frac{{\displaystyle \sum _{1\le i<j\le n}}{\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)}{n},s_i=Re\left(h_i\right)-\frac{{\displaystyle \sum _{1\le i<j\le n}}{\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)}{n},$ then ${\displaystyle \sum _{i=1}^n}{r}_i=0,{\displaystyle \sum _{i=1}^n}{s}_i=0$.

Example 7.

Consider a PFDG $\mathcal{D}=(\mathcal{P},\overrightarrow{\mathcal{Q}})$ on $V=\{z_1,z_2,z_3,z_4,z_5,z_6\}$, as shown in Figure 5.

Figure 5. Pythagorean fuzzy digraph.

The adjacency matrix, out-degree matrix and Laplacian matrix of the PFDG shown in Figure 5 are as follows:

$A\left(\mathcal{D}\right)=\left[\begin{array}{cccccc}(0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (0.3,0.6)\\ (0.4,0.7)& (0,0)& (0.3,0.8)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0.5,0.7)& (0,0)& (0,0)& (0.4,0.7)& (0,0)\\ (0,0)& (0,0)& (0.3,0.6)& (0,0)& (0.3,0.8)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0.6,0.5)& (0,0)& (0.7,0.5)\\ (0.6,0.8)& (0.6,0.7)& (0,0)& (0,0)& (0,0)& (0,0)\end{array}\right].$

$D^{\mathit{out}}\left(\mathcal{D}\right)=\left[\begin{array}{cccccc}(0.3,0.6)& (0,0)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0.7,1.5)& (0,0)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0.9,1.4)& (0,0)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0.6,1.4)& (0,0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (1.3,1.0)& (0,0)\\ (0,0)& (0,0)& (0,0)& (0,0)& (0,0)& (1.2,1.5)\end{array}\right].$

$L\left(\mathcal{D}\right)=\left[\begin{array}{cccccc}(0.3,0.6)& (0,0)& (0,0)& (0,0)& (0,0)& (-0.3,-0.6)\\ (-0.4,-0.7)& (0.7,1.5)& (-0.3,-0.8)& (0,0)& (0,0)& (0,0)\\ (0,0)& (-0.5,-0.7)& (0.9,1.4)& (0,0)& (-0.4,-0.7)& (0,0)\\ (0,0)& (0,0)& (-0.3,-0.6)& (0.6,1.4)& (-0.3,-0.8)& (0,0)\\ (0,0)& (0,0)& (0,0)& (-0.6,-0.5)& (1.3,1.0)& (-0.7,-0.5)\\ (-0.6,-0.8)& (-0.6,-0.7)& (0,0)& (0,0)& (0,0)& (1.2,1.5)\end{array}\right].$

The Laplacian spectrum and the Laplacian energy of a PFDG $\mathcal{D}$, given in Figure 5, are as follows:

$$\begin{array}{c}\mathrm{Laplacian} \mathrm{Spec}({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=\{0,0.2757,0.6371,1.2317+0.3555i,1.2317-0.3555i,1.6237\},\hfill \\ \mathrm{Laplacian} \mathrm{Spec}({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right))=\{0,0.4036,2.1629,1.8081+0.3173i,1.8081-0.3173i,1.2174\}.\hfill \end{array}$$

Therefore, Laplacian Spec$\left(\mathcal{D}\right)=\left\{\right(0,0),(0.2757,0.4036),(0.6371,2.1629),(1.2317+0.3555i,1.8081+0.3173i),(1.2317-0.3555i,1.8081-0.3173i),(1.6237,1.2174\left)\right\}.$

Now,

$$\begin{array}{c}\hfill LE\left({\mu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)\right)=3.1744,LE\left({\nu }_{\overrightarrow{\mathcal{Q}}}\left(z_i{z}_j\right)\right)=4.1582.\end{array}$$

Therefore, $LE\left(\mathcal{D}\right)=(3.1744,4.1582)$.

Furthermore, we have:

$${\displaystyle \sum _{i=1}^6}{r}_i=0,{\displaystyle \sum _{i=1}^6}{s}_i=0.$$

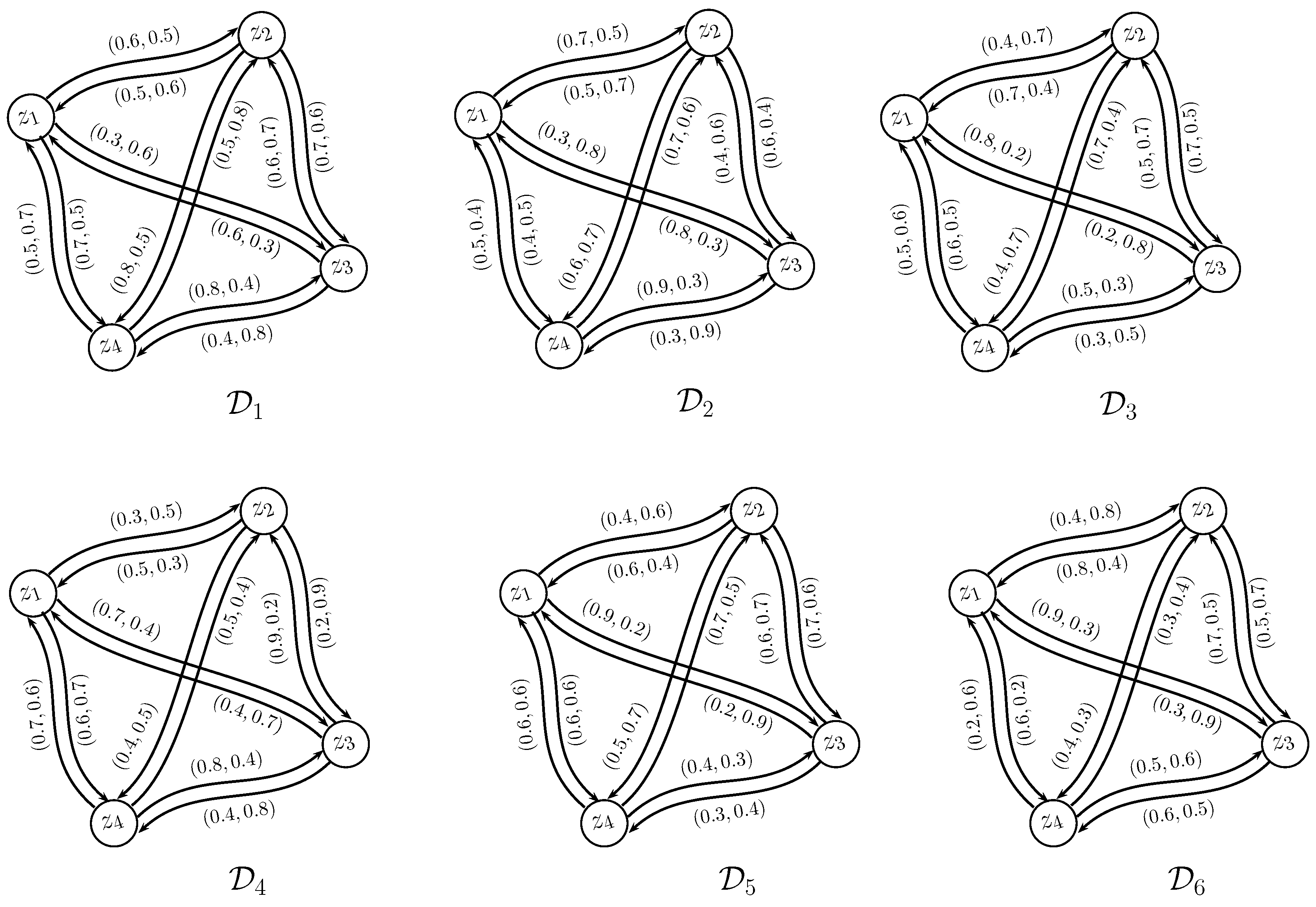
5. Applications of the Energy of PFGs in Decision-Making

In this section, we use two practical examples of the satellite communication system design and the evaluation of the schemes of reservoir operation to illustrate our proposed concepts of the Pythagorean fuzzy graph theory in decision-making.

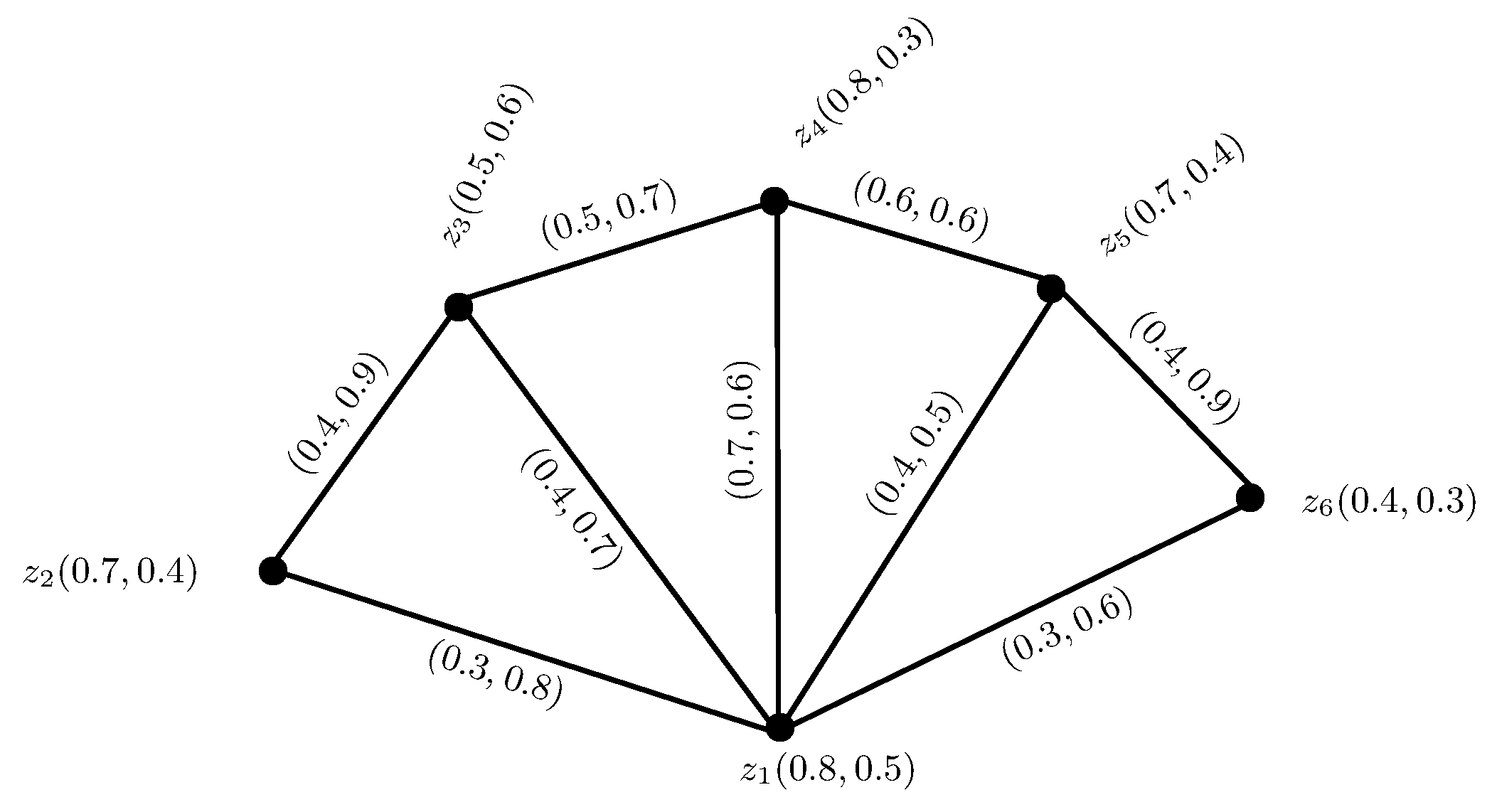
5.1. Designing of a Satellite Communication System

Communication is closely related to social development. In particular, satellite communication [42] has wide coverage area for communication, without geographical restrictions, and is less susceptible to the impact of land disasters. There is a unique advantage of satellite communication in many application areas, such as remote areas, islands, mountains, voyage aircraft and oceangoing vessels. Therefore, satellite communication not only effectively supplements the lack of other means of communication, but also has an irreplaceable role as the primary method of communication in mass media, especially the military. In modern warfare, it is very important to quantify the quality of the communication service. Suppose that a communication joint department in China plans to design a satellite communication system. Thus, a new test methodology for the synthetic communication system needs to be investigated, in order to provide evidence for building satellite Earth stations in the future. According to the expeditions, there are four possible testing venues $z_i(i=1,2,3,4)$ to choose from (Xichang $z_1$, Chengdu $z_2$, Nanjing $z_3$ and Lhasa $z_4$). However, due to resources, funds, and other factors, only the most suitable of these would be selected. A decision-making group composed of six experts $e_k(k=1,2,\dots ,6)$ provides the judgments with six individual Pythagorean fuzzy preference relations (PFPRs) [27] $R_k={(r_{ij}^{\left(k\right)})}_{4\times 4}(k=1,2,\dots ,6)$ as follows:

$R_1=\left[\begin{array}{cccc}(0.5,0.5)& (0.6,0.5)& (0.3,0.6)& (0.7,0.5)\\ (0.5,0.6)& (0.5,0.5)& (0.7,0.6)& (0.8,0.5)\\ (0.6,0.3)& (0.6,0.7)& (0.5,0.5)& (0.4,0.8)\\ (0.5,0.7)& (0.5,0.8)& (0.8,0.4)& (0.5,0.5)\end{array}\right],$$R_2=\left[\begin{array}{cccc}(0.5,0.5)& (0.7,0.5)& (0.3,0.8)& (0.4,0.5)\\ (0.5,0.7)& (0.5,0.5)& (0.6,0.4)& (0.6,0.7)\\ (0.8,0.3)& (0.4,0.6)& (0.5,0.5)& (0.3,0.9)\\ (0.5,0.4)& (0.7,0.6)& (0.9,0.3)& (0.5,0.5)\end{array}\right],$

$R_3=\left[\begin{array}{cccc}(0.5,0.5)& (0.4,0.7)& (0.8,0.2)& (0.6,0.5)\\ (0.7,0.4)& (0.5,0.5)& (0.7,0.5)& (0.4,0.7)\\ (0.2,0.8)& (0.5,0.7)& (0.5,0.5)& (0.3,0.5)\\ (0.5,0.6)& (0.7,0.4)& (0.5,0.3)& (0.5,0.5)\end{array}\right],$$R_4=\left[\begin{array}{cccc}(0.5,0.5)& (0.3,0.5)& (0.7,0.4)& (0.6,0.7)\\ (0.5,0.3)& (0.5,0.5)& (0.2,0.9)& (0.4,0.5)\\ (0.4,0.7)& (0.9,0.2)& (0.5,0.5)& (0.4,0.8)\\ (0.7,0.6)& (0.5,0.4)& (0.8,0.4)& (0.5,0.5)\end{array}\right],$

$R_5=\left[\begin{array}{cccc}(0.5,0.5)& (0.4,0.6)& (0.9,0.2)& (0.6,0.6)\\ (0.6,0.4)& (0.5,0.5)& (0.7,0.6)& (0.5,0.7)\\ (0.2,0.9)& (0.6,0.7)& (0.5,0.5)& (0.3,0.4)\\ (0.6,0.6)& (0.7,0.5)& (0.4,0.3)& (0.5,0.5)\end{array}\right],$$R_6=\left[\begin{array}{cccc}(0.5,0.5)& (0.4,0.8)& (0.9,0.3)& (0.6,0.2)\\ (0.8,0.4)& (0.5,0.5)& (0.5,0.7)& (0.4,0.3)\\ (0.3,0.9)& (0.7,0.5)& (0.5,0.5)& (0.6,0.5)\\ (0.2,0.6)& (0.3,0.4)& (0.5,0.6)& (0.5,0.5)\end{array}\right].$

The PFDGs ${\mathcal{D}}_k$ corresponding to PFPRs given in matrices $R_k(k=1,2,\dots ,6)$ are shown in Figure 6.

Figure 6. Pythagorean fuzzy digraphs.

The energy of each PFDG is calculated as:

$$\begin{array}{c}E\left({\mathcal{D}}_1\right)=(3.5008,3.5008),E\left({\mathcal{D}}_2\right)=(3.3021,3.3021),E\left({\mathcal{D}}_3\right)=(3.0706,3.0706),\hfill \\ E\left({\mathcal{D}}_4\right)=(3.1675,3.1675),E\left({\mathcal{D}}_5\right)=(3.1860,3.1860),E\left({\mathcal{D}}_6\right)=(3.0656,3.0656).\hfill \end{array}$$

Then, the weight of each expert can be calculated as:

$$w_k=({\left(w_{\mu }\right)}_k,{\left(w_{\nu }\right)}_k)=\left(\frac{E\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{E\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,s,$$

$$\begin{array}{c}{w}_1=(0.1815,0.1815),w_2=(0.1712,0.1712),w_3=(0.1592,0.1592),\hfill \\ w_4=(0.1642,0.1642),w_5=(0.1651,0.1651),w_6=(0.1589,0.1589).\hfill \end{array}$$

Therefore, the weight vector of six experts $e_k$ (k = 1, 2, …, 6) is:

$$w={((0.1815,0.1815),(0.1712,0.1712),(0.1592,0.1592),(0.1642,0.1642),(0.1651,0.1651),(0.1589,0.1589))}^T.$$

Compute the averaged Pythagorean fuzzy element (PFE) $p_i^{\left(k\right)}$ of the testing venue $z_i$ over all the other testing venues for the experts $e_k(k=1,2,\dots ,6)$ by the Pythagorean fuzzy averaging (PFA) operator:

$$\begin{array}{c}\hfill p_i^{\left(k\right)}=PFA(p_{i1}^{\left(k\right)},p_{i2}^{\left(k\right)},\dots ,p_{in}^{\left(k\right)})=\left(\sqrt{1-{\left({\prod }_{j=1}^n\left(1-{\mu }_{ij}^2\right)\right)}^{1/n}},{\left({\displaystyle \prod _{j=1}^n}{\nu }_{ij}\right)}^{1/n}\right),i=1,2,3,\dots ,n,\end{array}$$

The aggregation results are listed in Table 1:

Table 1. The aggregation results of the experts $e_k(k=1,2,\dots ,6).$

Experts		The Overall Results of the Experts
$e_1$	$p_1^{\left(1\right)}$	$(0.5595,0.5233)$
	$p_2^{\left(1\right)}$	$(0.6581,0.5477)$
	$p_3^{\left(1\right)}$	$(0.5360,0.5384)$
	$p_4^{\left(1\right)}$	$(0.6130,0.5785)$
$e_2$	$p_1^{\left(2\right)}$	$(0.5145,0.5623)$
	$p_2^{\left(2\right)}$	$(0.5542,0.5595)$
	$p_3^{\left(2\right)}$	$(0.5709,0.5335)$
	$p_4^{\left(2\right)}$	$(0.7189,0.4356)$
$e_3$	$p_1^{\left(3\right)}$	$(0.6187,0.4325)$
	$p_2^{\left(3\right)}$	$(0.6031,0.5144)$
	$p_3^{\left(3\right)}$	$(0.4034,0.6117)$
	$p_4^{\left(3\right)}$	$(0.5647,0.4356)$
$e_4$	$p_1^{\left(4\right)}$	$(0.5595,0.5144)$
	$p_2^{\left(4\right)}$	$(0.4235,0.5097)$
	$p_3^{\left(4\right)}$	$(0.6610,0.4865)$
	$p_4^{\left(4\right)}$	$(0.6581,0.4681)$
$e_5$	$p_1^{\left(5\right)}$	$(0.6884,0.4356)$
	$p_2^{\left(5\right)}$	$(0.5877,0.5384)$
	$p_3^{\left(5\right)}$	$(0.4419,0.5958)$
	$p_4^{\left(5\right)}$	$(0.5715,0.4606)$
$e_6$	$p_1^{\left(6\right)}$	$(0.6884,0.3936)$
	$p_2^{\left(6\right)}$	$(0.5982,0.4527)$
	$p_3^{\left(6\right)}$	$(0.5595,0.5791)$
	$p_4^{\left(6\right)}$	$(0.4034,0.5180)$

Compute a collective PFE $p_i(i=1,2,3,4)$ of the testing venue $z_i$ over all the other testing venues using the Pythagorean fuzzy weighted averaging (PFWA) operator [2].

$$\begin{array}{c}\hfill p_i=\mathrm{PFWA}(p_i^{\left(1\right)},p_i^{\left(2\right)},\dots ,p_i^{\left(s\right)})=\left(\sqrt{1-{\prod }_{k=1}^s{\left(1-\left({\mu }_k^2\right)\right)}^{w_k}},{\displaystyle \prod _{k=1}^s}{\left({\nu }_k\right)}^{w_k}\right).\end{array}$$

$$\mathrm{That}\mathrm{is},p_1=(0.6110,0.4752),p_2=(0.5803,0.5203),p_3=(0.5415,0.5550),p_4=(0.6061,0.4814).$$

Compute the score functions $s\left(p_i\right)={\mu }_i^2-{\nu }_i^2$ [4] of $p_i(i=1,2,3,4)$, and rank all the testing venues $z_i(i=1,2,3,4)$ according to the values of $s\left(p_i\right)(i=1,2,3,4)$.

$$s\left(p_1\right)=0.1475,s\left(p_2\right)=0.0660,s\left(p_3\right)=-0.0148,s\left(p_4\right)=0.1356.$$

Then, $z_1\succ z_4\succ z_2\succ z_3$.

Thus, the best testing venue is $z_1.$

Now, the Laplacian matrices of the PFDGs $L\left({\mathcal{D}}_k\right)=R_k^L(k=1,2,\dots ,6)$ shown in Figure 6 are:

$R_1^L=\left[\begin{array}{cccc}(1.6,1.6)& (-0.6,-0.5)& (-0.3,-0.6)& (-0.7,-0.5)\\ (-0.5,-0.6)& (2.0,1.7)& (-0.7,-0.6)& (-0.8,-0.5)\\ (-0.6,-0.3)& (-0.6,-0.7)& (1.6,1.8)& (-0.4,-0.8)\\ (-0.5,-0.7)& (-0.5,-0.8)& (-0.8,-0.4)& (1.8,1.9)\end{array}\right],$

$R_2^L=\left[\begin{array}{cccc}(1.4,1.8)& (-0.7,-0.5)& (-0.3,-0.8)& (-0.4,-0.5)\\ (-0.5,-0.7)& (1.7,1.8)& (-0.6,-0.4)& (-0.6,-0.7)\\ (-0.8,-0.3)& (-0.4,-0.6)& (1.5,1.8)& (-0.3,-0.9)\\ (-0.5,-0.4)& (-0.7,-0.6)& (-0.9,-0.3)& (2.1,1.3)\end{array}\right],$

$R_3^L=\left[\begin{array}{cccc}(1.8,1.4)& (-0.4,-0.7)& (-0.8,-0.2)& (-0.6,-0.5)\\ (-0.7,-0.4)& (1.8,1.6)& (-0.7,-0.5)& (-0.4,-0.7)\\ (-0.2,-0.8)& (-0.5,-0.7)& (1.0,2.0)& (-0.3,-0.5)\\ (-0.5,-0.6)& (-0.7,-0.4)& (-0.5,-0.3)& (1.7,1.3)\end{array}\right],$

$R_4^L=\left[\begin{array}{cccc}(1.6,1.6)& (-0.3,-0.5)& (-0.7,-0.4)& (-0.6,-0.7)\\ (-0.5,-0.3)& (1.1,1.7)& (-0.2,-0.9)& (-0.4,-0.5)\\ (-0.4,-0.7)& (-0.9,-0.2)& (1.7,1.7)& (-0.4,-0.8)\\ (-0.7,-0.6)& (-0.5,-0.4)& (-0.8,-0.4)& (2.0,1.4)\end{array}\right],$

$R_5^L=\left[\begin{array}{cccc}(1.9,1.4)& (-0.4,-0.6)& (-0.9,-0.2)& (-0.6,-0.6)\\ (-0.6,-0.4)& (1.8,1.7)& (-0.7,-0.6)& (-0.5,-0.7)\\ (-0.2,-0.9)& (-0.6,-0.7)& (1.1,2.0)& (-0.3,-0.4)\\ (-0.6,-0.6)& (-0.7,-0.5)& (-0.4,-0.3)& (1.7,1.4)\end{array}\right],$

$R_6^L=\left[\begin{array}{cccc}(1.9,1.3)& (-0.4,-0.8)& (-0.9,-0.3)& (-0.6,-0.2)\\ (-0.8,-0.4)& (1.7,1.4)& (-0.5,-0.7)& (-0.4,-0.3)\\ (-0.3,-0.9)& (-0.7,-0.5)& (1.6,1.9)& (-0.6,-0.5)\\ (-0.2,-0.6)& (-0.3,-0.4)& (-0.5,-0.6)& (1.0,1.6)\end{array}\right].$

The Laplacian energy of each PFDG is calculated as:

$$\begin{array}{c}LE\left({\mathcal{D}}_1\right)=(3.5000,3.5000), LE\left({\mathcal{D}}_2\right)=(3.3400,3.3400), LE\left({\mathcal{D}}_3\right)=(3.1400,3.1400),\hfill \\ LE\left({\mathcal{D}}_4\right)=(3.2000,3.2000), LE\left({\mathcal{D}}_5\right)=(3.2400,3.2400), LE\left({\mathcal{D}}_6\right)=(3.1302,3.1302).\hfill \end{array}$$

Then, the weight of each expert can be calculated as:

$$w_k=({\left(w_{\mu }\right)}_k,{\left(w_{\nu }\right)}_k)=\left(\frac{LE\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{LE\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,s,$$

$$\begin{array}{c}{w}_1=(0.1790,0.1790),w_2=(0.1708,0.1708),w_3=(0.1606,0.1606),\hfill \\ w_4=(0.1637,0.1637),w_5=(0.1657,0.1657),w_6=(0.1601,0.1601).\hfill \end{array}$$

Based on this, we compute a collective PFE $p_i(i=1,2,3,4)$ of the testing venue $z_i$ over all the other testing venues using the PFWA operator:

$$\begin{array}{c}\hfill p_i=\mathrm{PFWA}(p_i^{\left(1\right)},p_i^{\left(2\right)},\dots ,p_i^{\left(s\right)})\end{array}$$

That is, $p_1=(0.6113,0.4749), p_2=(0.5802,0.5202), p_3=(0.5412,0.5553), p_4=(0.6057,0.4812).$

Compute the score functions $s\left(p_i\right)={\mu }_i^2-{\nu }_i^2$ of $p_i(i=1,2,3,4)$, and rank all the testing venues $z_i(i=1,2,3,4)$ according to the values of $s\left(p_i\right)(i=1,2,3,4)$.

$$s\left(p_1\right)=0.1482, s\left(p_1\right)=0.0660 ,s\left(p_3\right)=-0.0155, s\left(p_4\right)=0.1353.$$

Then, $z_1\succ z_4\succ z_2\succ z_3$.

Thus, the testing venue $z_1$ is the best among the four given testing venues. We present our scheme for this application in the following Algorithm 1.

Algorithm 1 The algorithm for the selection of the most important testing venue.

INPUT: A discrete set of testing venues (alternatives) $Z=\{z_1,z_2,\dots ,z_n\}$, a set of experts $e=\{e_1,e_2,\dots ,e_s\}$ and construction of PFPR $R_k={\left(p_{ij}^{\left(k\right)}\right)}_{n\times n}$ for each expert. OUTPUT: The selection of the optimal testing venue. begin Calculate the energy and Laplacian energy of each PFDG ${\mathcal{D}}_k(k=1,2,\dots ,s).$ Determine the wight vector for experts based on the energy of PFDGs by utilizing $w_k=\left(\frac{E\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{E\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),$ and then, based on the Laplacian energy of PFDGs by utilizing $w_k=\left(\frac{LE\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{LE\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,s$. Aggregate all $p_{ij}^{\left(k\right)}(j=1,2,\dots ,n)$ corresponding to the testing venue $z_i$, and get the PFE $p_i^{\left(k\right)}$ of the testing venue $z_i$ over all the other testing venues for the expert $e_k$ by using the PFA operator. Aggregate all $p_i^{\left(k\right)}(k=1,2,\dots ,s)$ into a collective PFE $p_i$ for the testing venue $z_i$ using the PFWA operator. Compute the score functions $s\left(p_i\right)$ of $p_i(i=1,2,\cdots ,n)$. Rank all the testing venues $z_i(i=1,2,\dots ,n)$ according to $s\left(p_i\right)(i=1,2,\dots ,n)$. Output the optimal testing venue. end

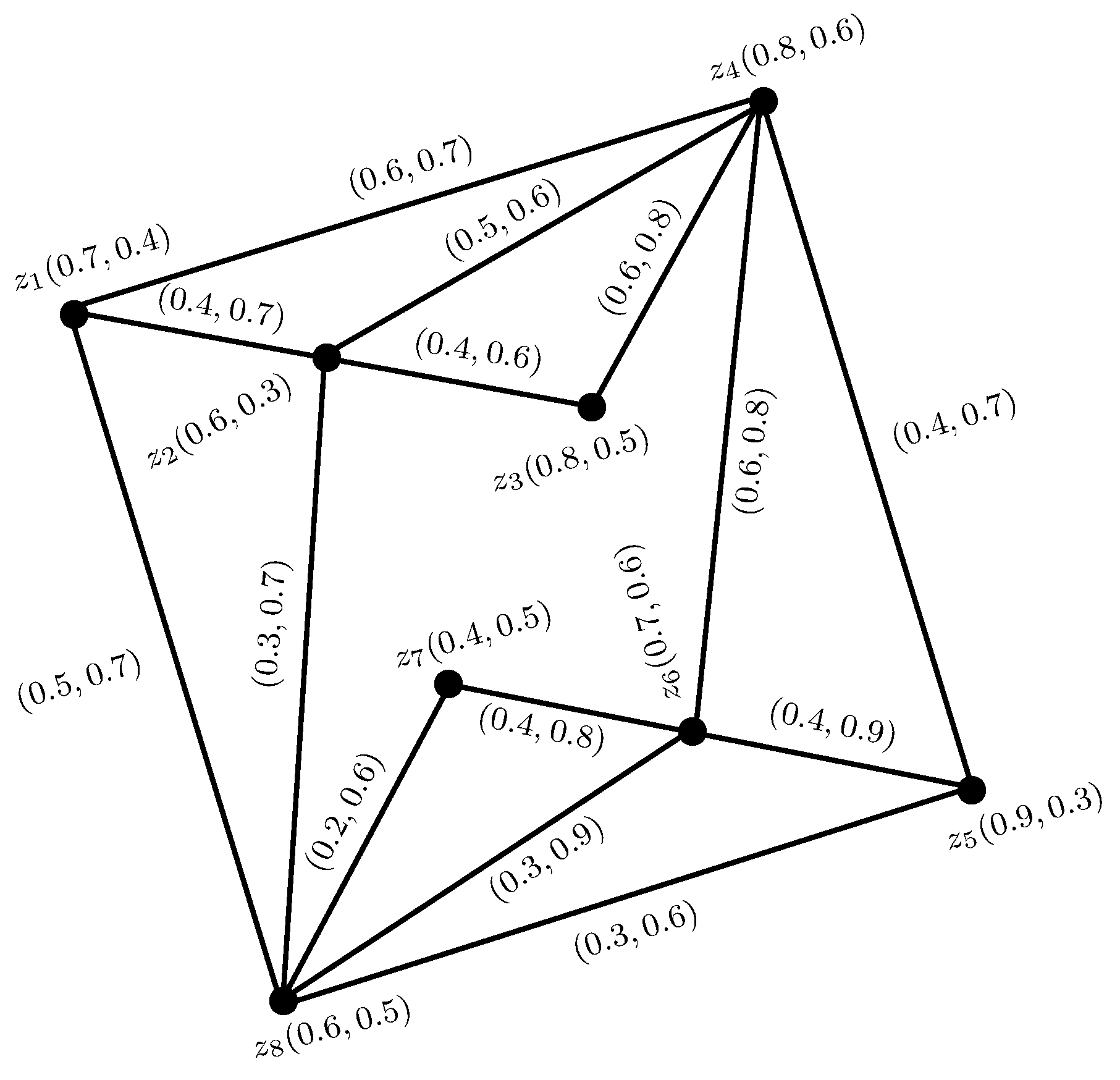
5.2. Evaluation of the Schemes of Reservoir Operation

This section focuses on evaluating the schemes of reservoir operation. It is a water resource system led by Jiudianxia reservoir with a complex condition and multipurpose use along with the Tao River basin and cascaded power stations in the Tao River. The reservoir was designed for many purposes, such as power generation, irrigation, total water supply for agriculture, industry, residents and environment. Due to different requirements for the partition of the amount of water, five reservoir operation schemes $z_1,z_2,z_3$, $z_4$ and $z_5$ are recommended.

z₁:

Maximum plant output, enough supply of water used in the Tao River basin, lower and higher supply for society and the economy;

z₂:

Maximum plant output, enough supply of water used in the Tao River basin, lower and higher supply for society and the economy, lower supply for the ecosystem;

z₃:

Maximum plant output, enough supply of water used in the Tao River basin, lower and higher supply for society and the economy, total supply for the ecosystem and environment, 90% of which is passed down for flushing sands during low water periods;

z₄:

Maximum plant output, enough supply of water used in the Tao River basin, lower and higher supply for society and the economy, total supply for the ecosystem and environment, 50% of which is passed down for flushing sands during low water periods;

z₅:

Maximum plant output, enough supply of water used in the Tao River basin, lower and higher supply for society and the economy, total supply for the ecosystem and environment during level and flood periods.

To select the optimal scheme, the government invites four experts $e_k(k=1,2,3,4)$ to evaluate the five schemes. Based on their experience, the experts compare each pair of schemes and give individual judgments using the following PFPRs $R_k={(r_{ij}^{\left(k\right)})}_{5\times 5}(k=1,2,3,4)$ [43]:

$R_1=\left[\begin{array}{ccccc}(0.5,0.5)& (0.6,0.8)& (0.5,0.7)& (0.7,0.4)& (0.8,0.1)\\ (0.8,0.6)& (0.5,0.5)& (0.5,0.4)& (0.6,0.5)& (0.5,0.3)\\ (0.7,0.5)& (0.4,0.5)& (0.5,0.5)& (0.6,0.7)& (0.7,0.6)\\ (0.4,0.7)& (0.5,0.6)& (0.7,0.6)& (0.5,0.5)& (0.8,0.4)\\ (0.1,0.8)& (0.3,0.5)& (0.6,0.7)& (0.4,0.8)& (0.5,0.5)\end{array}\right],$

$R_2=\left[\begin{array}{ccccc}(0.5,0.5)& (0.7,0.2)& (0.8,0.4)& (0.7,0.6)& (0.7,0.3)\\ (0.2,0.7)& (0.5,0.5)& (0.5,0.7)& (0.8,0.3)& (0.5,0.4)\\ (0.4,0.8)& (0.7,0.5)& (0.5,0.5)& (0.4,0.6)& (0.7,0.6)\\ (0.6,0.7)& (0.3,0.8)& (0.6,0.4)& (0.5,0.5)& (0.5,0.3)\\ (0.3,0.7)& (0.4,0.5)& (0.6,0.7)& (0.3,0.5)& (0.5,0.5)\end{array}\right],$

$R_3=\left[\begin{array}{ccccc}(0.5,0.5)& (0.6,0.7)& (0.8,0.3)& (0.6,0.4)& (0.7,0.2)\\ (0.7,0.6)& (0.5,0.5)& (0.7,0.4)& (0.1,0.8)& (0.5,0.6)\\ (0.3,0.8)& (0.4,0.7)& (0.5,0.5)& (0.5,0.7)& (0.7,0.4)\\ (0.4,0.6)& (0.8,0.1)& (0.7,0.5)& (0.5,0.5)& (0.5,0.3)\\ (0.2,0.7)& (0.6,0.5)& (0.4,0.7)& (0.3,0.5)& (0.5,0.5)\end{array}\right],$

$R_4=\left[\begin{array}{ccccc}(0.5,0.5)& (0.8,0.6)& (0.7,0.1)& (0.8,0.3)& (0.4,0.7)\\ (0.6,0.8)& (0.5,0.5)& (0.5,0.3)& (0.4,0.3)& (0.7,0.6)\\ (0.1,0.7)& (0.3,0.5)& (0.5,0.5)& (0.9,0.2)& (0.5,0.3)\\ (0.3,0.8)& (0.3,0.4)& (0.2,0.9)& (0.5,0.5)& (0.8,0.4)\\ (0.7,0.4)& (0.6,0.7)& (0.3,0.5)& (0.4,0.8)& (0.5,0.5)\end{array}\right].$

The PFDGs ${\mathcal{D}}_k$ corresponding to PFPRs given in matrices $R_k(k=1,2,3,4)$ are shown in Figure 7:

Figure 7. Pythagorean fuzzy digraphs.

The energy of each PFDG is calculated as:

$E\left({\mathcal{D}}_1\right)=(3.3053,3.3053), E\left({\mathcal{D}}_2\right)=(2.9252,2.9252), E\left({\mathcal{D}}_3\right)=(2.8510,2.8510), E\left({\mathcal{D}}_4\right)=(3.0081,3.0081).$

Then, the weight of each expert can be calculated as:

$$w_k=({\left(w_{\mu }\right)}_k,{\left(w_{\nu }\right)}_k)=\left(\frac{E\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^4}E\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{E\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^4}E\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,4,$$

$w_1=(0.2734,0.2734),w_2=(0.2420,0.2420),w_3=(0.2358,0.2358),w_4=(0.2488,0.2488).$

Utilize the aggregation operator to fuse all the individual PFPRs $R_k={(r_{ij}^{\left(k\right)})}_{5\times 5}(k=1,2,3,4)$ into the collective PFPR $R={\left(r_{ij}\right)}_{5\times 5}$. Here, we apply the Pythagorean fuzzy weighted averaging (PFWA) operator [2] to fuse the individual PFPR. Thus, we have:

$$\begin{array}{c}\hfill \mathrm{PFWA}(r_{ij}^{\left(1\right)},r_{ij}^{\left(2\right)},\dots ,r_{ij}^{\left(s\right)})=\left(\sqrt{1-\prod _{k=1}^s{\left(1-{\left({\mu }_{ij}^2\right)}^{\left(k\right)}\right)}^{w_k}},{\displaystyle \prod _{k=1}^s}{\left({\nu }_{ij}^{\left(k\right)}\right)}^{w_k}\right).\end{array}$$

$R=\left[\begin{array}{ccccc}(0.5000,0.5000)& (0.6892,0.5160)& (0.7212,0.3085)& (0.7118,0.4108)& (0.6892,0.2493)\\ (0.6544,0.6690)& (0.5000,0.5000)& (0.5614,0.4264)& (0.5828,0.4347)& (0.5645,0.4500)\\ (0.4712,0.6805)& (0.4905,0.5413)& (0.5000,0.5000)& (0.6895,0.4938)& (0.6623,0.4589)\\ (0.4446,0.6978)& (0.5535,0.3811)& (0.6078,0.5763)& (0.5000,0.5000)& (0.6991,0.3486)\\ (0.4284,0.6317)& (0.4974,0.5437)& (0.5051,0.6438)& (0.3567,0.6391)& (0.5000,0.5000)\end{array}\right].$

Calculate their scores using the score function $s_{ij}={\mu }_{ij}^2-{\nu }_{ij}^2$:

$R=\left[\begin{array}{ccccc}0.0000& 0.2088& 0.4250& 0.3379& 0.4129\\ -0.0194& 0.0000& 0.1334& 0.1507& 0.1161\\ -0.2411& -0.0524& 0.0000& 0.2316& 0.2280\\ -0.2893& 0.1611& 0.0372& 0.0000& 0.3672\\ -0.2155& -0.0481& -0.1593& -0.2812& 0.0000\end{array}\right].$

The net flow of $z_i$ [44], i.e., the net degree of preference of $z_i$ over the other schemes is:

$$\varphi \left(z_i\right)={\displaystyle \sum _{k=1}^s}{w}_k\left({\displaystyle \sum _{j=1j\ne i}^n}(r_{ij}^{\left(k\right)}-r_{ji}^{\left(k\right)})\right),i=1,2,\dots ,n.$$

Therefore, the net flows of the five schemes are:

$$\begin{array}{ccc}\hfill \mathsf{\Phi }& =& {(\varphi \left(z_1\right),\varphi \left(z_2\right),\varphi \left(z_3\right),\varphi \left(z_4\right),\varphi \left(z_5\right))}^T={(2.1499,0.1114,-0.2702,-0.1628,-1.8283)}^T\hfill \end{array}$$

which gives the ranking of $z_1\succ z_2\succ z_4\succ z_3\succ z_5$. Thus, the best scheme is $z_1.$

Now, the Laplacian matrices of the PFDGs $L\left({\mathcal{D}}_k\right)=R_k^L(k=1,2,3,4)$ shown in Figure 7 are:

$R_1^L=\left[\begin{array}{ccccc}(2.6,2.0)& (-0.6,-0.8)& (-0.5,-0.7)& (-0.7,-0.4)& (-0.8,-0.1)\\ (-0.8,-0.6)& (2.4,1.8)& (-0.5,-0.4)& (-0.6,-0.5)& (-0.5,-0.3)\\ (-0.7,-0.5)& (-0.4,-0.5)& (2.4,2.3)& (-0.6,-0.7)& (-0.7,-0.6)\\ (-0.4,-0.7)& (-0.5,-0.6)& (-0.7,-0.6)& (2.4,2.3)& (-0.8,-0.4)\\ (-0.1,-0.8)& (-0.3,-0.5)& (-0.6,-0.7)& (-0.4,-0.8)& (1.4,2.8)\end{array}\right],$

$R_2^L=\left[\begin{array}{ccccc}(2.9,1.5)& (-0.7,-0.2)& (-0.8,-0.4)& (-0.7,-0.6)& (-0.7,-0.3)\\ (-0.2,-0.7)& (2.0,2.1)& (-0.5,-0.7)& (-0.8,-0.3)& (-0.5,-0.4)\\ (-0.4,-0.8)& (-0.7,-0.5)& (2.2,2.5)& (-0.4,-0.6)& (-0.7,-0.6)\\ (-0.6,-0.7)& (-0.3,-0.8)& (-0.6,-0.4)& (2.0,2.2)& (-0.5,-0.3)\\ (-0.3,-0.7)& (-0.4,-0.5)& (-0.6,-0.7)& (-0.3,-0.5)& (1.6,2.4)\end{array}\right],$

$R_3^L=\left[\begin{array}{ccccc}(2.7,1.6)& (-0.6,-0.7)& (-0.8,-0.3)& (-0.6,-0.4)& (-0.7,-0.2)\\ (-0.7,-0.6)& (2.0,2.4)& (-0.7,-0.4)& (-0.1,-0.8)& (-0.5,-0.6)\\ (-0.3,-0.8)& (-0.4,-0.7)& (1.9,2.6)& (-0.5,-0.7)& (-0.7,-0.4)\\ (-0.4,-0.6)& (-0.8,-0.1)& (-0.7,-0.5)& (2.4,1.5)& (-0.5,-0.3)\\ (-0.2,-0.7)& (-0.6,-0.5)& (-0.4,-0.7)& (-0.3,-0.5)& (1.5,2.4)\end{array}\right],$

$R_4^L=\left[\begin{array}{ccccc}(2.7,1.7)& (-0.8,-0.6)& (-0.7,-0.1)& (-0.8,-0.3)& (-0.4,-0.7)\\ (-0.6,-0.8)& (2.2,2.0)& (-0.5,-0.3)& (-0.4,-0.3)& (-0.7,-0.6)\\ (-0.1,-0.7)& (-0.3,-0.5)& (1.8,1.7)& (-0.9,-0.2)& (-0.5,-0.3)\\ (-0.3,-0.8)& (-0.3,-0.4)& (-0.2,-0.9)& (1.6,2.5)& (-0.8,-0.4)\\ (-0.7,-0.4)& (-0.6,-0.7)& (-0.3,-0.5)& (-0.4,-0.8)& (2.0,2.4)\end{array}\right].$

The Laplacian energy of each PFDG is calculated as:

$$\begin{array}{c}LE\left({\mathcal{D}}_1\right)=(4.7399,4.4800),LE\left({\mathcal{D}}_2\right)=(4.2800,4.2800),\hfill \\ LE\left({\mathcal{D}}_3\right)=(4.2000,4.2000),LE\left({\mathcal{D}}_4\right)=(4.1200,4.1200).\hfill \end{array}$$

Then, the weights can be calculated as:

$$w_k=({\left(w_{\mu }\right)}_k,{\left(w_{\nu }\right)}_k)=\left(\frac{LE\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{LE\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,s,$$

$w_1=(0.2734,0.2734),w_2=(0.2468,0.2468),w_3=(0.2422,0.2422),w_4=(0.2376,0.2376).$

Based on this, we utilize the PFWA operator to fuse all the individual PFPRs $R_k={(r_{ij}^{\left(k\right)})}_{5\times 5}(k=1,2,3,4)$ into the collective PFPR $R={\left(r_{ij}\right)}_{5\times 5}$:

$R=\left[\begin{array}{ccccc}(0.5000,0.5000)& (0.6872,0.5138)& (0.7225,0.3127)& (0.7099,0.4129)& (0.6913,0.2463)\\ (0.6542,0.6674)& (0.5000,0.5000)& (0.5629,0.4289)& (0.5845,0.4375)& (0.5618,0.4491)\\ (0.4723,0.6816)& (0.4930,0.5425)& (0.5000,0.5000)& (0.6834,0.5004)& (0.6641,0.4613)\\ (0.4466,0.6961)& (0.5572,0.3790)& (0.6108,0.5719)& (0.5000,0.5000)& (0.6961,0.3475)\\ (0.4218,0.6356)& (0.4964,0.5416)& (0.5068,0.6462)& (0.3556,0.6357)& (0.5000,0.5000)\end{array}\right].$

Calculate their scores using the score function:

$R=\left[\begin{array}{ccccc}0.0000& 0.2082& 0.4242& 0.3335& 0.4173\\ -0.0174& 0.0000& 0.1329& 0.1503& 0.1139\\ -0.2415& -0.0512& 0.0000& 0.2167& 0.2283\\ -0.2851& 0.1668& 0.0460& 0.0000& 0.3638\\ -0.2261& -0.0469& -0.1608& -0.2777& 0.0000\end{array}\right].$

The net flows of the five alternatives are:

$$\begin{array}{ccc}\hfill \mathsf{\Phi }& =& {(\varphi \left(z_1\right),\varphi \left(z_2\right),\varphi \left(z_3\right),\varphi \left(z_4\right),\varphi \left(z_5\right))}^T={(2.1533,0.1028,-0.2900,-0.1313,-1.8348)}^T\hfill \end{array}$$

which gives the ranking of $z_1\succ z_2\succ z_4\succ z_3\succ z_5$. Thus, the best scheme is $z_1.$ We present our proposed method in the following Algorithm 2.

Algorithm 2 The algorithm for the selection of the most important scheme of reservoir operation.

INPUT: A discrete set of schemes (alternatives) $Z=\{z_1,z_2,\dots ,z_n\}$, a set of experts $e=\{e_1,e_2,\dots ,e_s\}$ and construction of PFPR $R_k={(p_{ij}^{\left(k\right)})}_{n\times n}$ for each expert. OUTPUT: The selection of the optimal scheme. begin Calculate the energy and Laplacian energy of each PFDG ${\mathcal{D}}_k(k=1,2,\dots ,s).$ Determine the wight vector for experts based on the energy of PFDGs by utilizing $w_k=\left(\frac{E\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{E\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}E\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),$ and then, based on the Laplacian energy of PFDGs by utilizing $w_k=\left(\frac{LE\left({\left({\mathcal{D}}_{\mu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\mu }\right)}_l\right)},\frac{LE\left({\left({\mathcal{D}}_{\nu }\right)}_k\right)}{{\displaystyle \sum _{l=1}^s}LE\left({\left({\mathcal{D}}_{\nu }\right)}_l\right)}\right),k=1,2,\dots ,s$. Utilize the PFWA operator to fuse all the individual PFPRs $R_k={(r_{ij}^{\left(k\right)})}_{n\times n}(k=1,2,\dots ,s)$ into the collective PFPR $R={\left(r_{ij}\right)}_{n\times n}$. Calculate their scores using the score function $s_{ij}={\mu }_{ij}^2-{\nu }_{ij}^2$. Determine the net degree of preference of scheme $z_i$ over the other schemes by utilizing: $$\varphi \left(z_i\right)={\displaystyle \sum _{k=1}^s}{w}_k\left({\displaystyle \sum _{j=1j\ne i}^n}(r_{ij}^{\left(k\right)}-r_{ji}^{\left(k\right)})\right),i=1,2,\dots ,n.$$ Rank all the schemes $z_i(i=1,2,\dots ,n)$ according to the net flows $\varphi \left(z_i\right)(i=1,2,\dots ,n).$ Output the best scheme. end

6. Conclusions

A Pythagorean fuzzy set model is suitable for modeling problems with uncertainty, indeterminacy and inconsistent information in which human knowledge is necessary and human evaluation needed. Pythagorean fuzzy models give more precision, flexibility and compatibility to the system as compared to the classical, fuzzy and intuitionistic fuzzy models. A PFG can describe the uncertainty of all kinds of networks well. In this paper, we have introduced the concepts of energy and Laplacian energy of graphs in Pythagorean fuzzy circumstances and investigated their interesting properties. We have derived the lower and upper bounds for the energy and Laplacian energy of a PFG. We have also introduced the concept of the energy and Laplacian energy of a PFDG along with its applications in decision making problems. We are planing to extend our research work to: (1) interval-valued Pythagorean fuzzy graphs; (2) simplified interval-valued Pythagorean fuzzy graphs; and (3) hesitant Pythagorean fuzzy graphs.