Prey–Predator Models with Variable Carrying Capacity
Abstract
:1. Introduction
2. Prey–Predator Model with Holling Type I Functional Response
2.1. Model Building
2.2. Mathematical Analysis of the Model
- (i)
- is unstable.
- (ii)
- is locally asymptotically stable if .
- (iii)
- is locally asymptotically stable if .
- (i)
- the eigenvalues of the Jacobian at are r , , and , which implies that is also unstable;
- (ii)
- the eigenvalues of the Jacobian at are , , and , so is stable if ;
- (iii)
- the Jacobian matrix at is given byClearly, is one of the eigenvalues, so the remaining two eigenvalues are the eigenvalues of the reduced matrix:which has the characteristic polynomial:Using Routh–Hurwitz Criteria [10], the local stability is guaranteed if☐
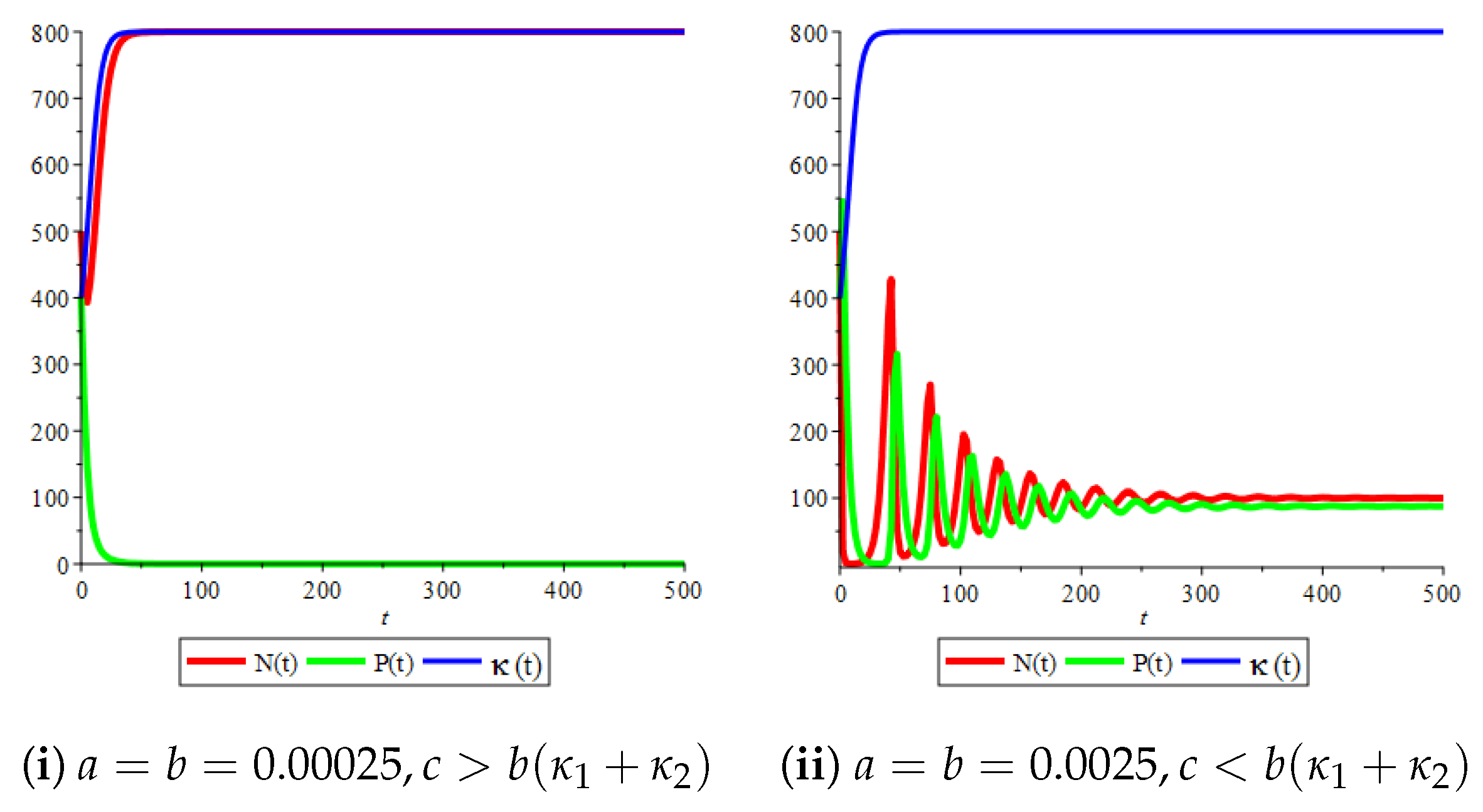
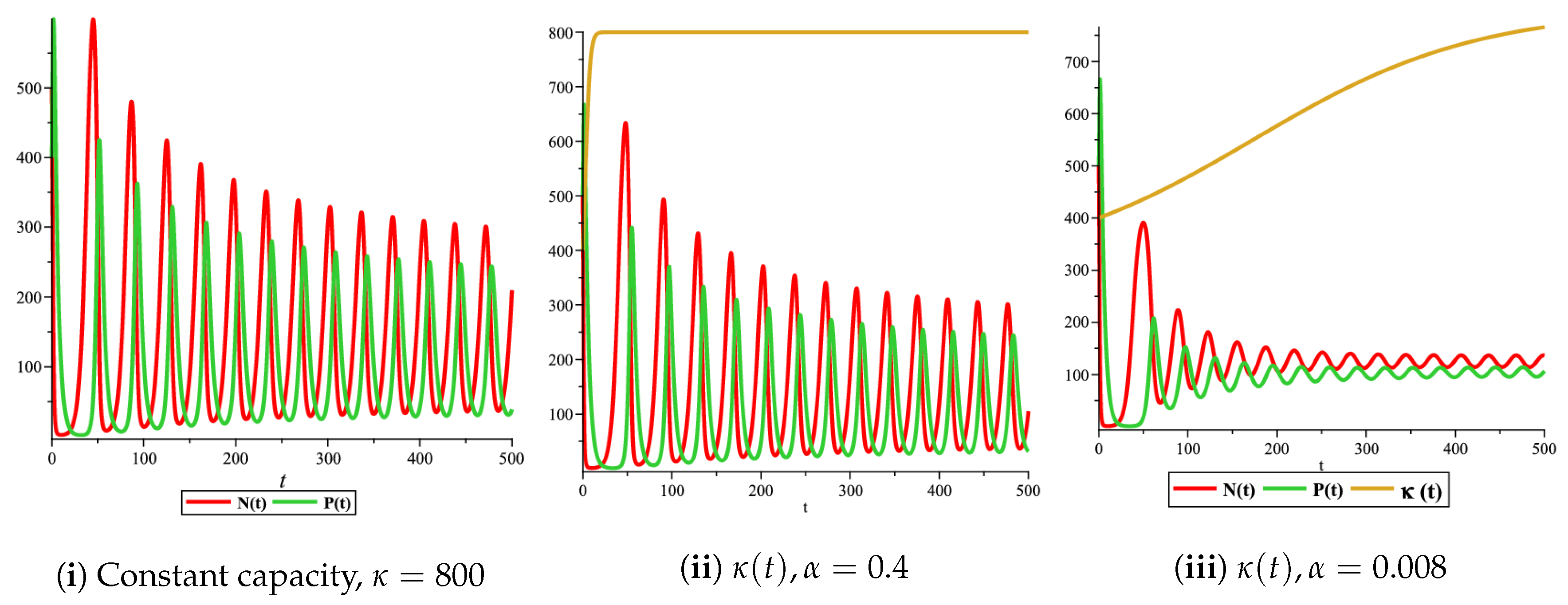
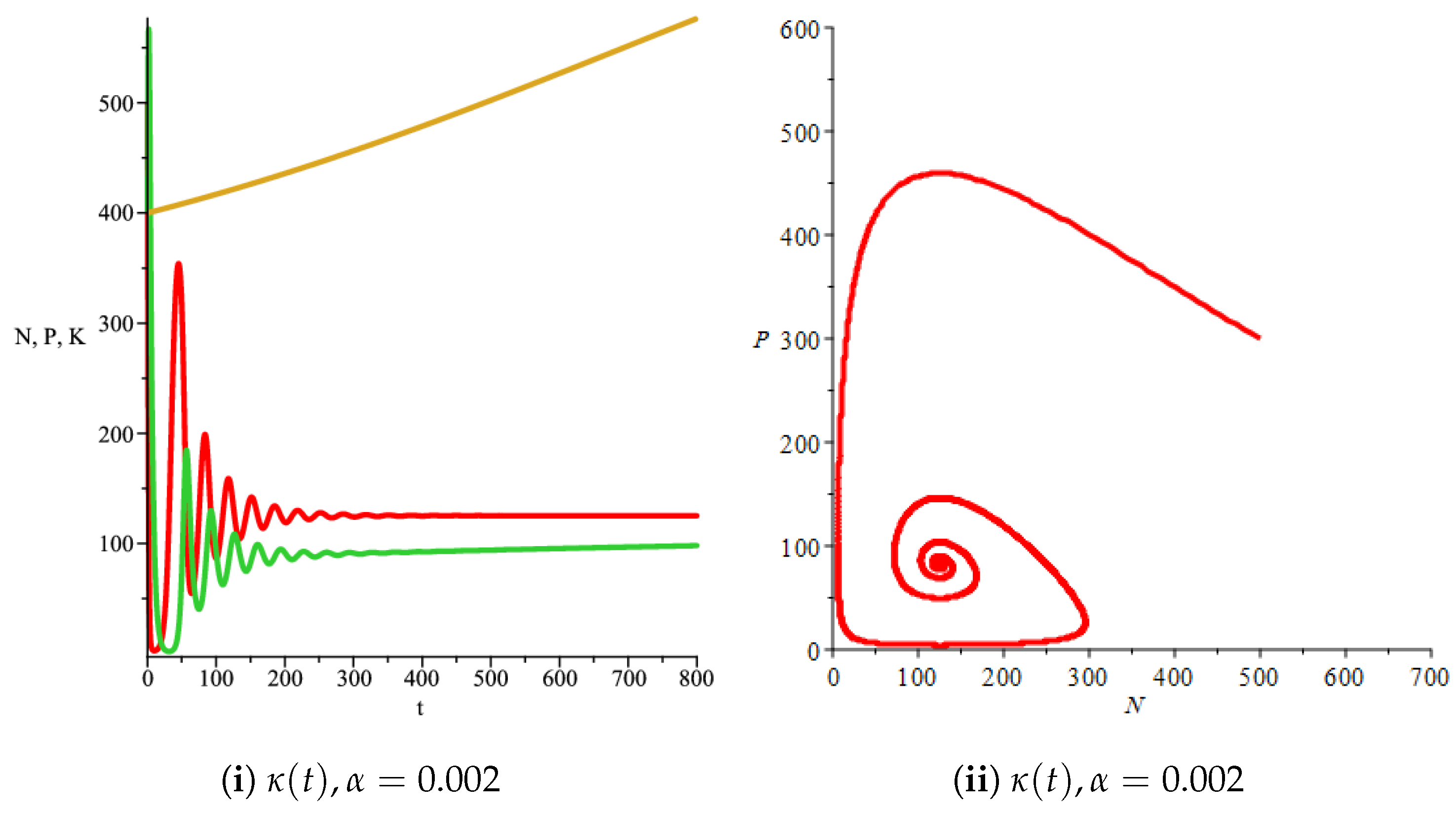
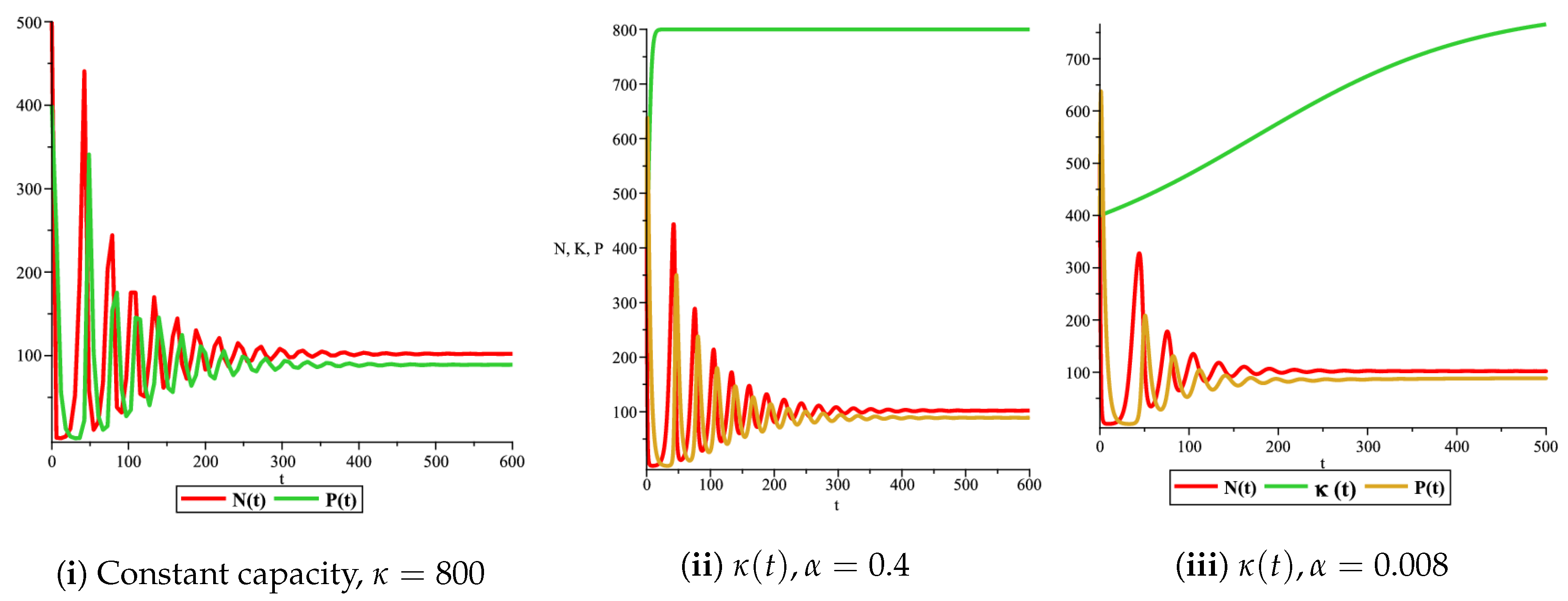
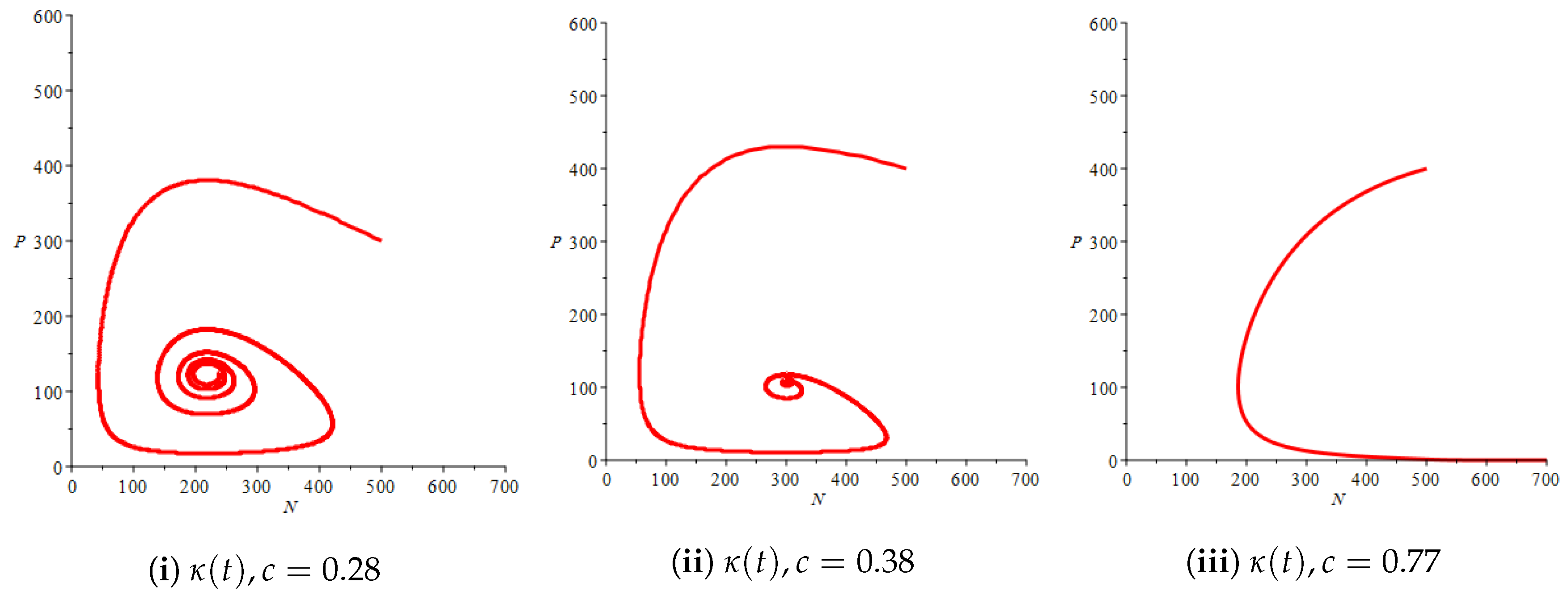
2.3. Numerical Simulation and Discussion
3. Prey–Predator Model with Holling Type II Functional Response
3.1. Model Building
3.2. Mathematical Analysis of the Model
- (i)
- is unstable.
- (ii)
- is locally asymptotically stable if .
- (iii)
- is locally asymptotically stable if .
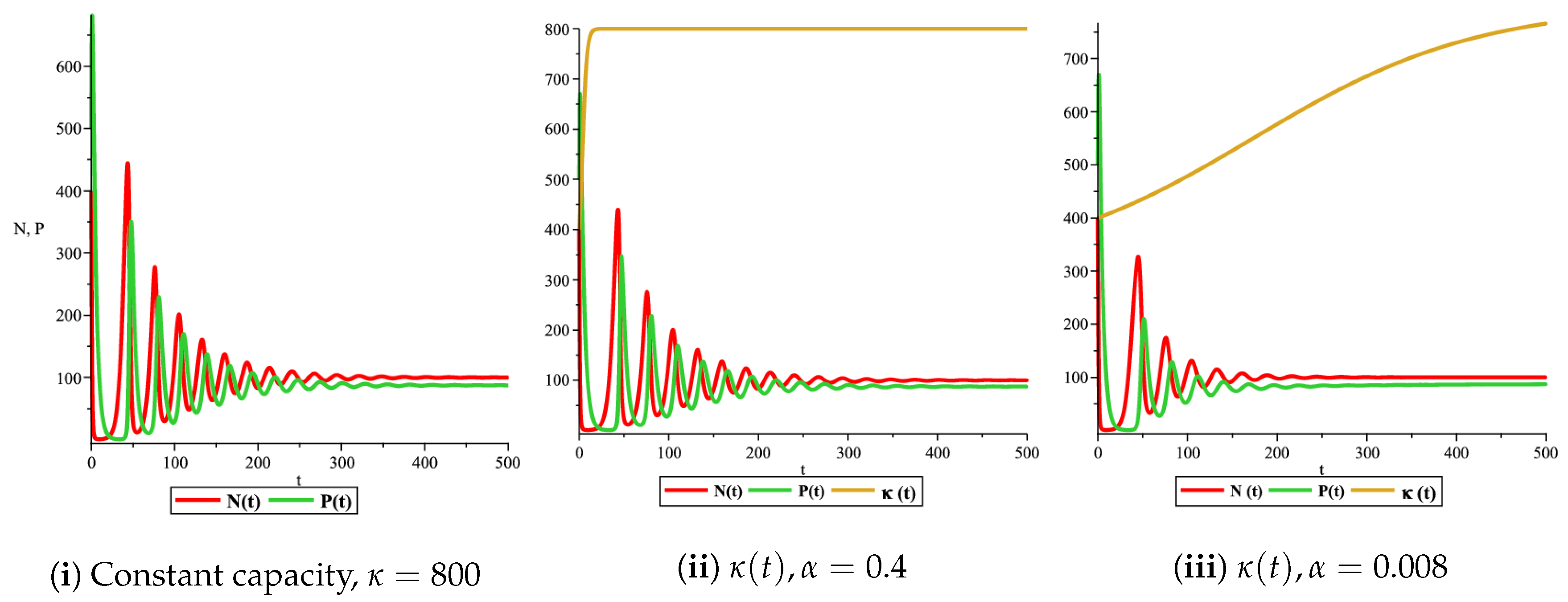
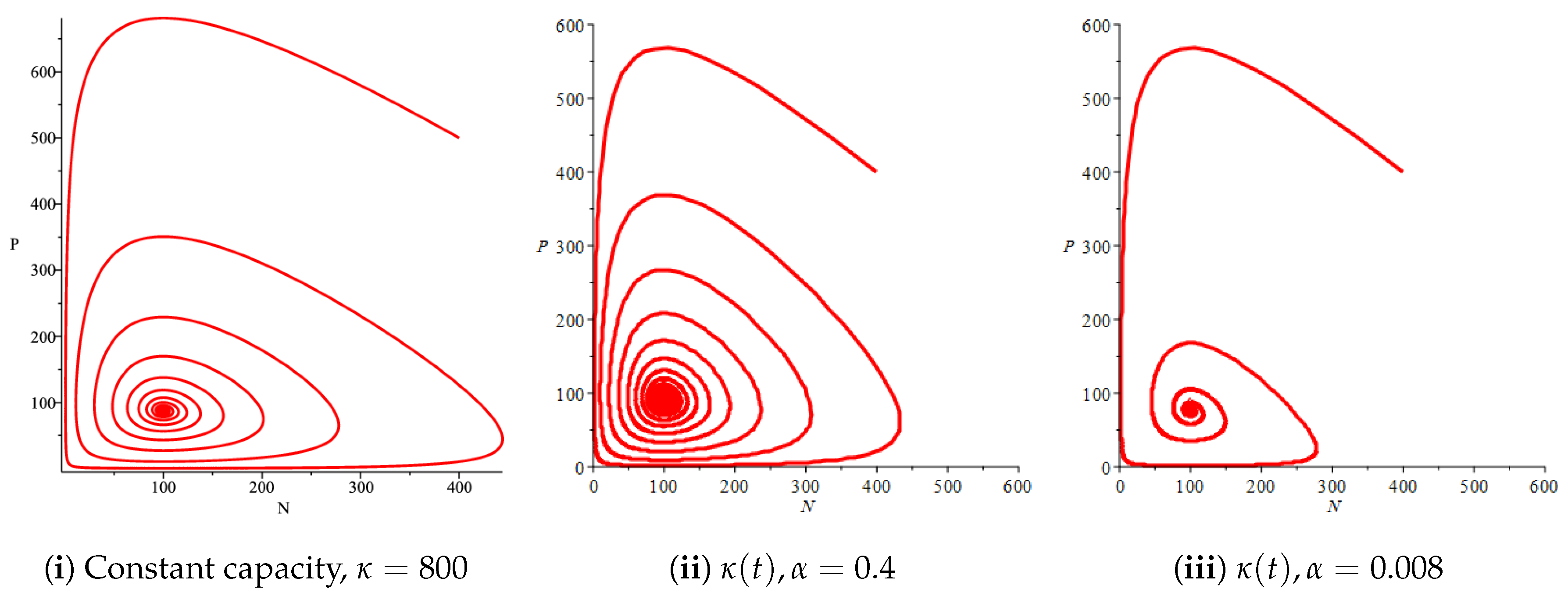
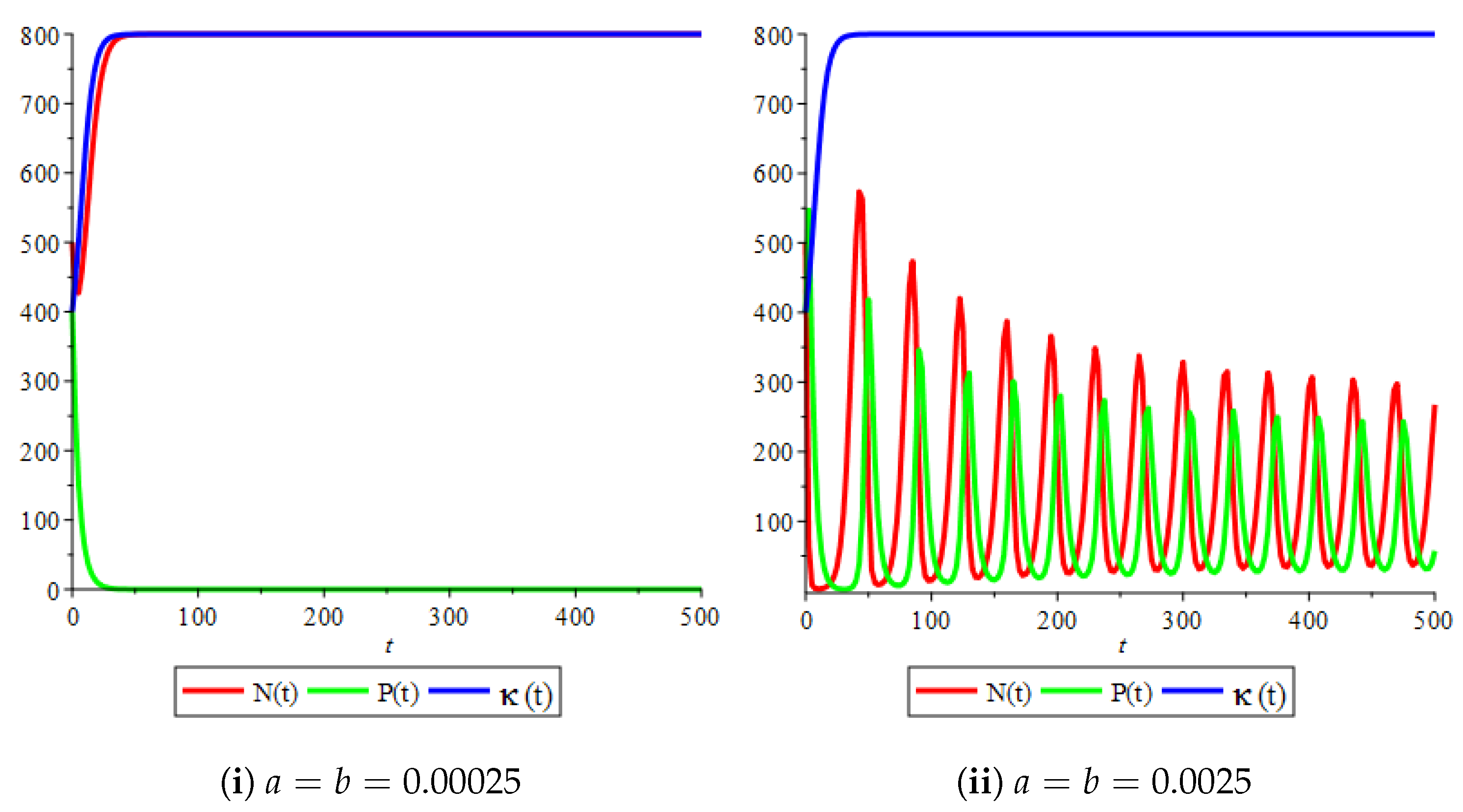
3.3. Numerical Simulation and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Green, J.L.; Hastings, A.; Arzberger, P.; Ayala, F.J.; Cottingham, K.L.; Cuddington, K.; Davis, F.; Dunne, J.A.; Fortin, M.; Gerber, L.; et al. Complexity in Ecology and Conservation: Mathematical, Statistical, and Computational Challenges. BioScience 2005, 55, 501–510. [Google Scholar] [CrossRef]
- Krebs, C.J. Ecology the Experimental Analysis of Distribution and Abundance; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Monte-Luna, D.; Brook, B.W.; Zetina-Rejón, M.J.; Cruz-Escalona, V.H. The carrying capacity of ecosystems. Glob. Ecol. Biogeogr. 2004, 13, 485–495. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.E. How many people can the earth support? Sciences 1995, 35, 18–23. [Google Scholar] [CrossRef]
- Waggoner, P.E. How much land can ten billion people spare for nature? Daedalus 1995, 125, 73–93. [Google Scholar]
- Meerschaert, M.M. Mathematical Modelling; Academic Press: Waltham, MA, USA, 2013. [Google Scholar]
- Ludwig, D.; Hilborn, R.; Walters, C. Uncertainty, resource exploitation, and conservation: Lessons from history. Science 1993, 260, 17. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P. Bi logistic growth. Technol. Forecast. Soc. Chang. 1994, 47, 82–102. [Google Scholar] [CrossRef]
- Shepherd, J.J.; Stojikov, L. The logistic population model with slowly varying carrying capacity. Anziam J. 2007, 47, 492–506. [Google Scholar] [CrossRef]
- Allen, L.S. An Introduction to Mathematical Biology; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Application to Physics, Biology, Chemistry and, Engineering; Perseus Books Publishing: Philadelphia, PA, USA, 2014. [Google Scholar]
- Kuznesov, Y.A. Elements of Applied Bifurcation Theorem; Springer: New York, NY, USA, 1998. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Moqbali, M.K.A.; Al-Salti, N.S.; Elmojtaba, I.M. Prey–Predator Models with Variable Carrying Capacity. Mathematics 2018, 6, 102. https://doi.org/10.3390/math6060102
Al-Moqbali MKA, Al-Salti NS, Elmojtaba IM. Prey–Predator Models with Variable Carrying Capacity. Mathematics. 2018; 6(6):102. https://doi.org/10.3390/math6060102
Chicago/Turabian StyleAl-Moqbali, Mariam K. A., Nasser S. Al-Salti, and Ibrahim M. Elmojtaba. 2018. "Prey–Predator Models with Variable Carrying Capacity" Mathematics 6, no. 6: 102. https://doi.org/10.3390/math6060102
APA StyleAl-Moqbali, M. K. A., Al-Salti, N. S., & Elmojtaba, I. M. (2018). Prey–Predator Models with Variable Carrying Capacity. Mathematics, 6(6), 102. https://doi.org/10.3390/math6060102



