Data Driven Economic Model Predictive Control
Abstract
:1. Introduction
2. Preliminaries
2.1. System Description
2.2. System Identification
2.3. Lyapunov-Based MPC
3. Integrating Lyapunov-Based MPC with Data Driven Models
3.1. Closed-Loop Model Identification
3.2. Control Design and Implementation
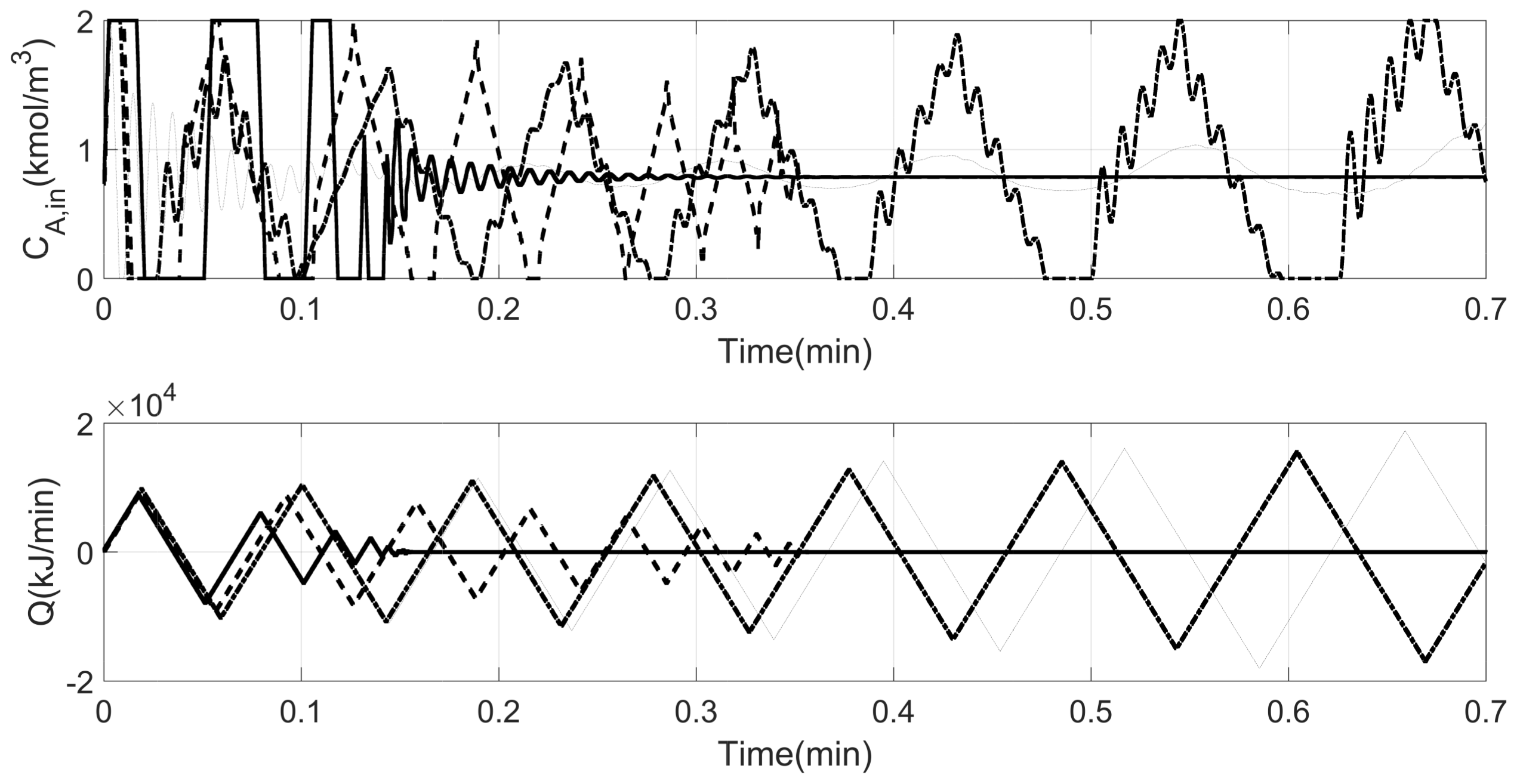
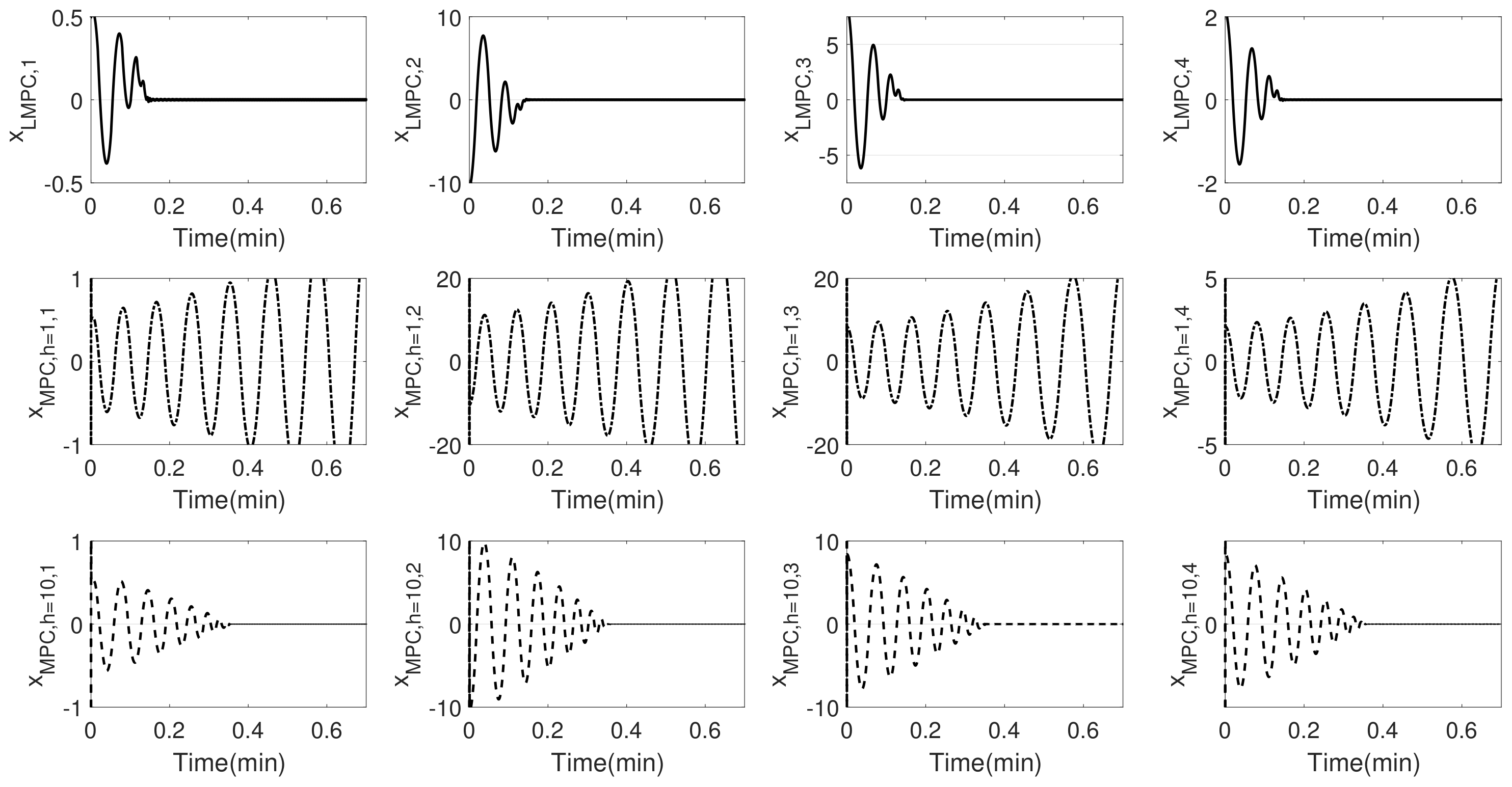
4. Simulation Results
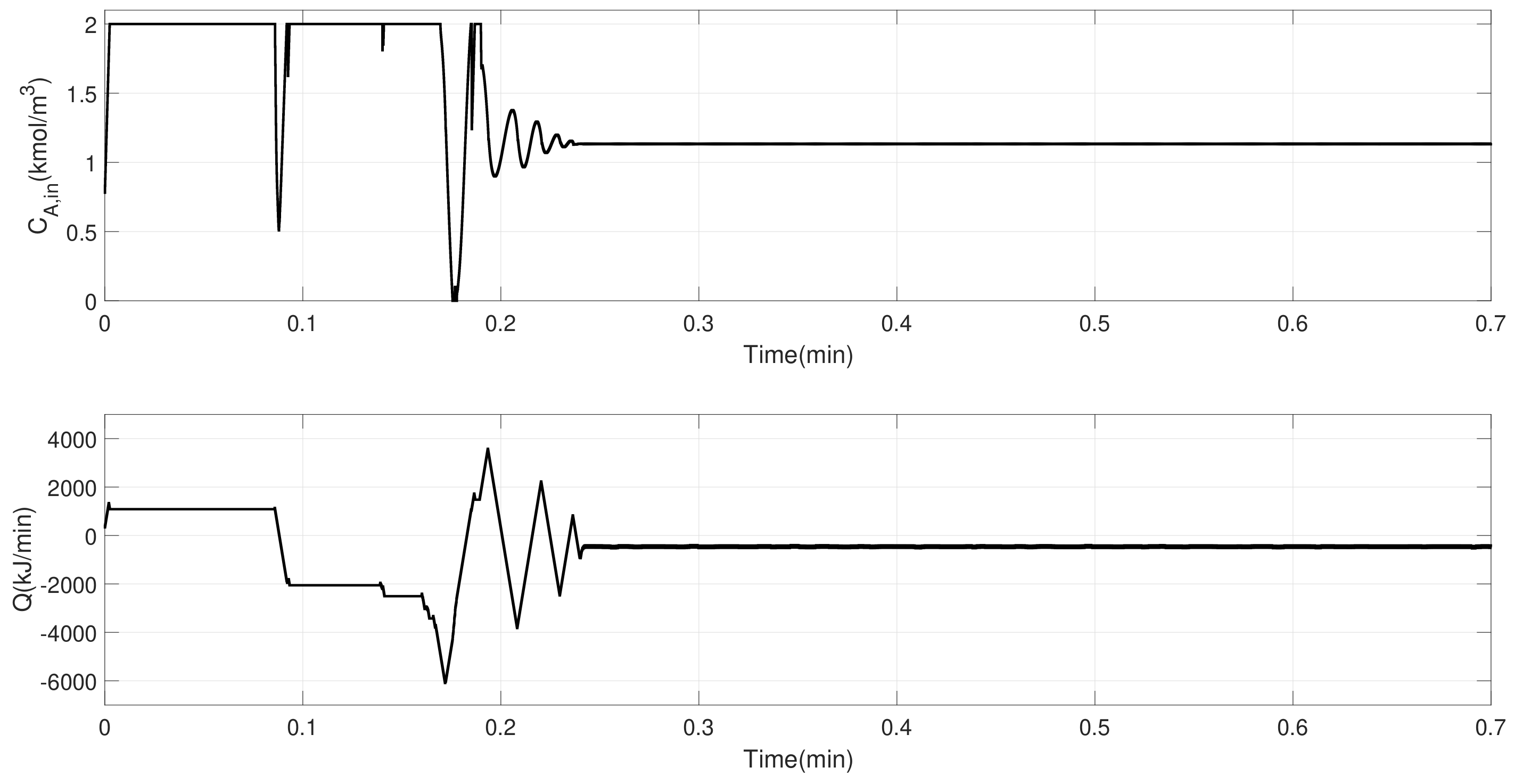
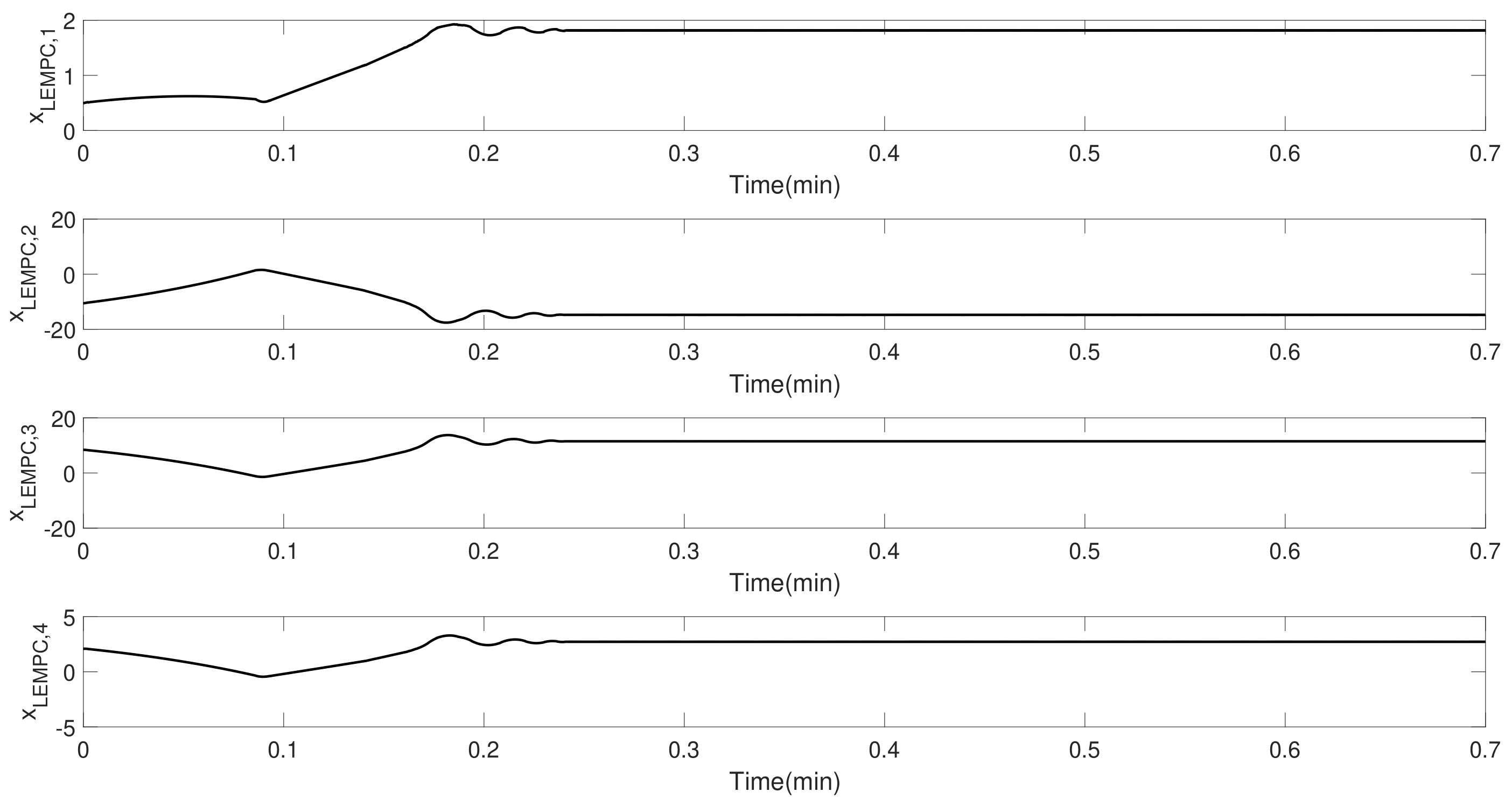
5. Data-Driven EMPC Design and Illustration
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, Wisconsin, 2009. [Google Scholar]
- Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Predictive control of switched nonlinear systems with scheduled mode transitions. IEEE Trans. Autom. Control 2005, 50, 1670–1680. [Google Scholar] [CrossRef]
- Mahmood, M.; Mhaskar, P. Constrained control Lyapunov function based model predictive control design. Int. J. Robust Nonlinear Control 2014, 24, 374–388. [Google Scholar] [CrossRef]
- Angeli, D.; Amrit, R.; Rawlings, J.B. On average performance and stability of economic model predictive control. IEEE Trans. Autom. Control 2012, 57, 1615–1626. [Google Scholar] [CrossRef]
- Bayer, F.A.; Lorenzen, M.; Müller, M.A.; Allgöwer, F. Improving Performance in Robust Economic MPC Using Stochastic Information. IFAC-PapersOnLine 2015, 48, 410–415. [Google Scholar] [CrossRef]
- Liu, S.; Liu, J. Economic model predictive control with extended horizon. Automatica 2016, 73, 180–192. [Google Scholar] [CrossRef]
- Müller, M.A.; Angeli, D.; Allgöwer, F. Economic model predictive control with self-tuning terminal cost. Eur. J. Control 2013, 19, 408–416. [Google Scholar] [CrossRef]
- Golshan, M.; MacGregor, J.F.; Bruwer, M.J.; Mhaskar, P. Latent Variable Model Predictive Control (LV-MPC) for trajectory tracking in batch processes. J. Process Control 2010, 20, 538–550. [Google Scholar] [CrossRef]
- MacGregor, J.; Bruwer, M.; Miletic, I.; Cardin, M.; Liu, Z. Latent variable models and big data in the process industries. IFAC-PapersOnLine 2015, 48, 520–524. [Google Scholar] [CrossRef]
- Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.I. Handling Spatial Heterogeneity in Reservoir Parameters Using Proper Orthogonal Decomposition Based Ensemble Kalman Filter for Model-Based Feedback Control of Hydraulic Fracturing. Ind. Eng. Chem. Res. 2018. [Google Scholar] [CrossRef]
- Narasingam, A.; Kwon, J.S.I. Development of local dynamic mode decomposition with control: Application to model predictive control of hydraulic fracturing. Comput. Chem. Eng. 2017, 106, 501–511. [Google Scholar] [CrossRef]
- Huang, B.; Kadali, R. Dynamic Modeling, Predictive Control and Performance Monitoring: A Data-Driven Subspace Approach; Springer: Berlin/Heidelberg, 2008. [Google Scholar]
- Li, W.; Han, Z.; Shah, S.L. Subspace identification for FDI in systems with non-uniformly sampled multirate data. Automatica 2006, 42, 619–627. [Google Scholar] [CrossRef]
- Hajizadeh, I.; Rashid, M.; Turksoy, K.; Samadi, S.; Feng, J.; Sevil, M.; Hobbs, N.; Lazaro, C.; Maloney, Z.; Littlejohn, E.; et al. Multivariable Recursive Subspace Identification with Application to Artificial Pancreas Systems. IFAC-PapersOnLine 2017, 50, 886–891. [Google Scholar] [CrossRef]
- Shah, S.L.; Patwardhan, R.; Huang, B. Multivariate controller performance analysis: methods, applications and challenges. In AICHE Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1998; Volume 2002, pp. 190–207. [Google Scholar]
- Kheradmandi, M.; Mhaskar, P. Model predictive control with closed-loop re-identification. Comput. Chem. Eng. 2017, 109, 249–260. [Google Scholar] [CrossRef]
- Alanqar, A.; Ellis, M.; Christofides, P.D. Economic model predictive control of nonlinear process systems using empirical models. AIChE J. 2015, 61, 816–830. [Google Scholar] [CrossRef]
- Huang, B.; Ding, S.X.; Qin, S.J. Closed-loop subspace identification: An orthogonal projection approach. J. Process Control 2005, 15, 53–66. [Google Scholar] [CrossRef]
- Qin, S.J. An overview of subspace identification. Comput. Chem. Eng. 2006, 30, 1502–1513. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.J. A new subspace identification approach based on principal component analysis. J. Process Control 2002, 12, 841–855. [Google Scholar] [CrossRef]
- Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Stabilization of nonlinear systems with state and control constraints using Lyapunov-based predictive control. Syst. Control Lett. 2006, 55, 650–659. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Qin, S.J.; Ljung, L. Closed-loop subspace identification with innovation estimation. IFAC Proc. Vol. 2003, 36, 861–866. [Google Scholar] [CrossRef]
- Pannocchia, G.; Rawlings, J.B. Disturbance models for offset-free model-predictive control. AIChE J. 2003, 49, 426–437. [Google Scholar] [CrossRef]
- Ljung, L. System identification. In Signal Analysis and Prediction; Springer: Boston, MA, USA, 1998. [Google Scholar]
- Forssell, U.; Ljung, L. Closed-loop identification revisited. Automatica 1999, 35, 1215–1241. [Google Scholar] [CrossRef]
- Wallace, M.; Pon Kumar, S.S.; Mhaskar, P. Offset-free model predictive control with explicit performance specification. Ind. Eng. Chem. Res. 2016, 55, 995–1003. [Google Scholar] [CrossRef]
- Alanqar, A.; Durand, H.; Christofides, P.D. Fault-Tolerant Economic Model Predictive Control Using Error-Triggered Online Model Identification. Ind. Eng. Chem. Res. 2017, 56, 5652–5667. [Google Scholar] [CrossRef]
- Mahmood, M.; Mhaskar, P. Enhanced Stability Regions for Model Predictive Control of Nonlinear Process Systems. AIChE J. 2008, 54, 1487–1498. [Google Scholar] [CrossRef]


| Variable | Description | Unit | Value |
|---|---|---|---|
| Nominal Value of Concentration | |||
| Nominal Value of Reactor Temperature | K | 395 | |
| F | Flow Rate | ||
| V | Volume of the Reactor | ||
| Nominal Inlet Concentration | |||
| Pre-Exponential Constant | − | ||
| E | Activation Energy | ||
| R | Ideal Gas Constant | ||
| Inlet Temperature | K | ||
| Enthalpy of the Reaction | |||
| Fluid Density | |||
| Heat Capacity |
| Variable | Value |
|---|---|
| min | |
| 0 | |
| 5 | |
| 1 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kheradmandi, M.; Mhaskar, P. Data Driven Economic Model Predictive Control. Mathematics 2018, 6, 51. https://doi.org/10.3390/math6040051
Kheradmandi M, Mhaskar P. Data Driven Economic Model Predictive Control. Mathematics. 2018; 6(4):51. https://doi.org/10.3390/math6040051
Chicago/Turabian StyleKheradmandi, Masoud, and Prashant Mhaskar. 2018. "Data Driven Economic Model Predictive Control" Mathematics 6, no. 4: 51. https://doi.org/10.3390/math6040051
APA StyleKheradmandi, M., & Mhaskar, P. (2018). Data Driven Economic Model Predictive Control. Mathematics, 6(4), 51. https://doi.org/10.3390/math6040051






