Abstract
In this paper, we study a class of fractional nonlinear second order Volterra integro-differential type of singularly perturbed problems with fractional order. We divide the problem into two subproblems. The first subproblems is the reduced problem when The second subproblems is fractional Volterra integro-differential problem. We use the finite difference method to solve the first problem and the reproducing kernel method to solve the second problem. In addition, we use the pade’ approximation. The results show that the proposed analytical method can achieve excellent results in predicting the solutions of such problems. Theoretical results are presented. Numerical results are presented to show the efficiency of the proposed method.
1. Introduction
Volterra integral equations are considered as a type of integral equations. In 1913, Volterra published the first book that talked about Volterra integral equations. In 1884, Volterra began working on integral equations, but his important study was in 1896. However, the name Volterra integral equation was first called by Lalesco in 1908. Volterra integral equations have many applications in science and engineering such as elasticity, semi-conductors, scattering theory, seismology, heat conduction, metallurgy, fluid flow, chemical reactions, population dynamics, and spread of epidemics [1].
Volterra integral equations have growlingly been recognized as useful tools for problems in science and engineering. In [2], they proposed and examined a spectral Jacobi-collocation approximation for fractional order integro-differntial equations. Ray et al. [3], used the Legendre wavelet method to find the solutions for a system of nonlinear Volterra integro-differntial equations. In [4], they used Lagurre polynomials and the collocation method to solve the pantograph-type Volterra integro-differntial equations under some initial conditions. Yang et al. [5], discussed the blow-up of Volterra integro-differntial equations with a dissipative linear term to show the differences of the solutions. In [6], they solved a non-linear system of higher order Volterra integro-differntial equations using the Single Term Walsh Series (STWS) method. Also in [7], they solved the fractional Fredholem-Volterra integro-differntial equations by the fractional-order functions based on the Bernoulli polynomials. We also indicate the interested reader to [8,9,10,11,12,13,14,15,16] for more research works on Volterra integro-differntial equations.
In 1904, A German physicist called Ludwig Prandtl was revolutionized fluid dynamics. He noted that the influence of friction is experienced only very near an object moving through a fluid. In [16], he presented the idea of the boundary layer and its significance for drag and streamlining. In his paper, Ludwig Prandtl assumed that the impact of friction was to cause the fluid instantly adjacent to the surface to stick to the surface. This boundary-layer notion had been the basis stone for the new fluid dynamics. Schlichting was one of the most famous books on boundary layer theory [17]. The scientific justification of boundary layer theory gave us more general hypothesis to determine asymptotic expansions of the solutions to the complete equations of the motion. Singular perturbation problem was the result of reduced the problem which was then solved by the method of matched asymptotic expansions. In 1946, Friedrichs and Wasow were the first time used the expression “singular perturbation” [18].
The differential equations of the singularly perturbed problem indicated the study of a group of differential equations including an asymptotically small parameter. The singularly perturbed problem is very important to both applied and pure mathematicians, physicists and engineers because of the fact that the solutions exhibit some interesting behavior. For example, the boundary layer, interior layer, and resonance phenomena [19].
There are a lot of applications of the singularly perturbed problem such as the nonlinear problems of plates and shells by means of the singular perturbation method [20]. Petar discussed typical applications of singular perturbation techniques to control problems in the last fifteen years [21]. Kokotovic et al., showed results on singular perturbations surveyed as a tool for model order reduction and separation of time scales in control system design [22], Ghorbel and Spong, reviewed results of integral manifolds of singularly perturbed non-linear differential equations and outlined the basic elements of the integral manifold method in the context of control system design [23]. Fridman, studied the control problem for an affine nonlinear singularly perturbed system [24]. Fridman, studied the infinite horizon nonlinear quadratic optimal control problem for a singularly perturbed system [25]. Several other techniques to solve such problems are presented in [26,27,28,29,30,31].
In this paper, we consider the following class of fractional nonlinear second order Volterra integro-differntial type of singularly perturbed problems of the form
subject to
where is a small positive parameter, and are constants, and and are smooth functions. The derivative which we use in this paper is in the Caputo sense. We organize our paper as follows. In Section 2, we present some preliminaries and the reproducing kernel (RKM) method which we use in this paper. In Section 3, we present some analytical results. In Section 4, we present the proposed method. Some numerical results are presented in Section 5. We end this paper by conclusions which presented in Section 6.
2. Reproducing Kernel Method
In this section, we present some preliminaries and RKM which we use in this paper.
Definition 1.
Let and be a positive real number. Then, the Riemann-Liouville fractional integral of order α is given by
where Γ is the Euler gamma function.
Some of its properties are given as follows:
- where a and b are constants.
- If is continuous on , then for positive real numbers and
Definition 2.
Let and x be a positive real number. Then, the Caputo derivative of order α is given by
Some of its properties are given as follows:
- where is a real number grater than
- where c is constant,
- where a and b are constants,
- For and is a positive real number,
For more details, see [32,33].
Definition 3.
Let E be a nonempty abstract set. A function is a reproducing kernel of the Hilbert space H if and only if
- for all
- for all and
The second condition is called the reproducing property and a Hilbert space which possesses a reproducing kernel is called a reproducing kernel Hilbert space.
Consider the second order nonlinear fractional equation of the form
subject to
where and are constants. First, we study the linear case when To homogenize the initial condition, we assume Thus, Equations (3) and (4) can be rewritten as
subject to
In order to solve the linear Equations (5) and (6), we construct the kernel Hilbert spaces and in which every function satisfies the initial condition (6). Let
The inner product in is defined as
and the norm is given by
where
Theorem 1.
The space is a reproducing kernel Hilbert space, i.e.; there exists and its second partial derivative with respect to y exists such that for any and each fixed we have
In this case, is given by
Proof.
Using the integration by parts, one can get
Since is a reproducing kernel of
which implies that
and
Since the characteristic equation of is and its characteristic value is with 2 multiplicity roots, we write as
Since we have
Using Conditions (8)–(11), we get the following system of equations
which implies that
Next, we study the space Let
The inner product in is defined as
and the norm is given by
where ☐
Theorem 2.
The space is a reproducing kernel Hilbert space, i.e.; there exists which has its six partial derivative with respect to y such that for any and each fixed we have
In this case, is given by
where
Proof.
Using integration by parts, one can get
Since and
and
Thus,
Since is a reproducing kernel of
which implies that
where is the dirac-delta function and
Since the characteristic equation of is and its characteristic value is with 6 multiplicity roots, we write as
Since we have
On the other hand, integrating from to with respect to y and letting to get
Using the Conditions 13 and 15–20, we get the following system of equations
We solved the last system using Mathematica to get
Now, we present how to solve Equations (5) and (6). Let
for where is dense on It is clear that is bounded linear operator. Let
where and is the adjoint operator of Using Gram-Schmidt orthonormalization to generate orthonormal set of functions where
and are coefficients of Gram-Schmidt orthonormalization. In the next theorem, we show the existence of the solution of Equations (5) and (6). ☐
Theorem 3.
If is dense on , then
Proof.
First, we want to prove that is complete system of and It is clear that for Simple calculations imply that
For each fixed , let
Then
Since is dense on Since exists, Thus, is the complete system of
In the next theorem, we show the uniformly convergence of the to for ☐
Proof.
First, we prove the theorem for For any
Thus,
From Theorem (4), one can see that converges uniformly to Thus,
which implies that converges uniformly to
Second, we prove the uniformly convergence for Since is bounded function on
Thus, for any
Hence,
which implies that
Therefore, converges uniformly to for Now, we discuss how to solve Equations (3) and (4). Let and are the linear and nonlinear parts of Problem (3), respectively. We construct the homotopy as follows:
where is an embedding parameter. If we get a linear equation
which implies that . If , we turn out to be Problem (3). Following the Homotopy Perturbation method [34], we expand the solution in term of the Homotopy parameter as
Substitute Equation (25) into Equation (24) and equating the coefficients of the identical powers of to get the following system
To solve the above equations, we use the RKM which described above and we obtain
where
3. Analytical Results
In this section, we present the maximum principle, the stability theorem, and the uniqueness theorem. Firstly, Equations (1) and (2) is transformed into an equivalent problem as follows:
The following conditions are needed in order to guarantee that Equations (1) and (2) do not have the turning-point problem
for all where and are positive constants and
Lemma 1.
[35] Let attains its minimum at . Then, and for
Theorem 5.
Proof.
Assume that the conclusion is false, then for some Then, has a local minimum at for some Simple calculations and using Lemma (1) imply that
This is a contradiction. Therefore, in ☐
In the next theorem, the stability result is presented.
Theorem 6.
(stability result). Consider Equations (1) and (2) with conditions and . If is a smooth function, then
where
Proof.
Following [36], let
and
Then,
for all Also,
and
From Theorem (5), we can see that for all Therefore,
☐
Theorem 7.
Proof.
Let Then,
Using Theorem (5), it follows that and for all which imply that for all ☐
4. Solution Method
Consider the following of class of nonlinear second order fractional nonlinear Volterra integro-differential type of singularly perturbed problems of the form
subject to
where is a small positive parameter, and are constant, and and are smooth functions.To solve Equations (1) and (2), we use the following steps.
Step 1: A reduced subproblem is obtained by setting in Equation (1) to get
On most of the interval, the solution of Equation (34) behaves like the solution of Equations (1) and (2). However, there is small interval around in which the solution of problem (1) and (2) does not agree with the solution of problem (1) and (2). To handle this situation, the boundary layer correction subproblem is introduced in step 2.
Step 2: Choose to get
Let Then, and
Thus,
Hence, Equation (1) becomes
or
Setting in Equation (36) implies that
Since the solution of the reduced problem in step 1 does not satisfy the initial condition at then the solution of the above equation should satisfy it. This means, its solution has the form Substitute
in Equation (38) to get the boundary layer correction equation
The solution of Equation (1) will be expressed in the form as
and the initial condition must be satisfied by expression (40). When the condition will be
or
The solution of Equations (1) and (2) can be produced using the RKM as described in the previous section. More details can be found in [36,37,38,39].
5. Numerical Results
In this section, we present two of our examples to show the efficiency of the proposed method.
Example 1: Consider the following problem
subject to
When we get
We discretized the interval by Let for Using the backward finite difference method to approximate and the trapezoidal quadrature to approximate the integral , we get
Thus, we get the following system
where
Using Mathematica, one can see that the solution of the above system for is given in Figure 1. Using the change of variable we get
subject to
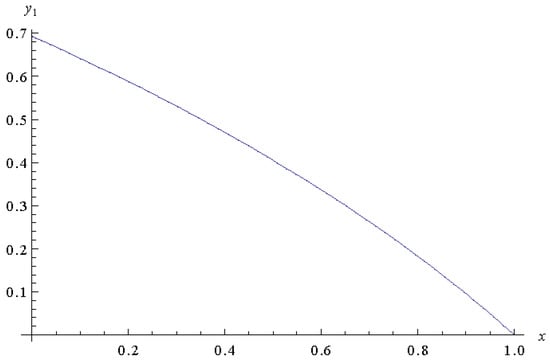
Figure 1.
The approximate solution .
Using the RKM, we get
Using the Pade’ approximation of order , we have In Figure 2, Figure 3 and Figure 4, we plot the approximate solution for and respectively. Let
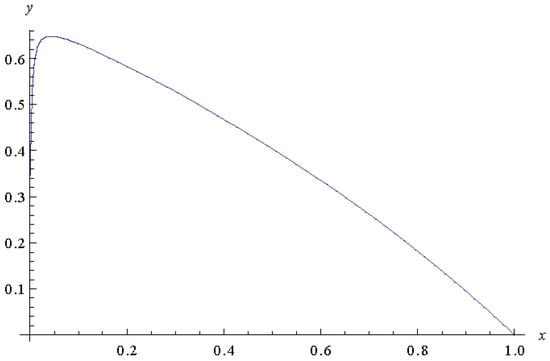
Figure 2.
The approximate solution y for .
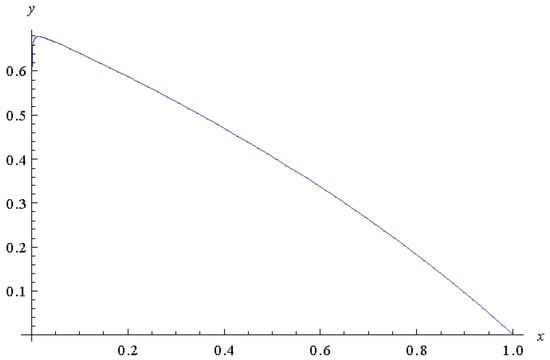
Figure 3.
The approximate solution y for .
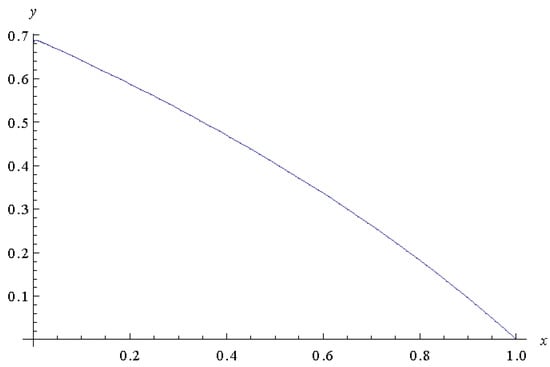
Figure 4.
The approximate solution y for .

Table 1.
The error for = 0.0001, 0.00001, and 0.000001.

Table 2.
Computational time.
Example 2: Consider the following problem
subject to
where
When we get
We discretized the interval by Let for Using the backward finite difference method to approximate and the trapezoidal quadrature to approximate the integral , we get
Using Mathematica, one can see that the solution of the above system for is given in Figure 5. Using the change of variable we get
subject to
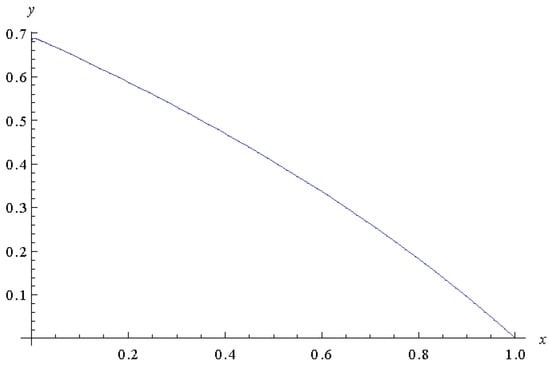
Figure 5.
The approximate solution .
Using the RKM, we get
Using the Pade’ approximation of order , we have In Table 3, we present the error for for and In Table 4, we present the computational time when and

Table 3.
The error for = 0.0001, 0.00001, and 0.000001.

Table 4.
Computational time.
Thus,
In Figure 6, Figure 7 and Figure 8, we plot the approximate solution for =0.001, 0.0001, and 0.00001, respectively.
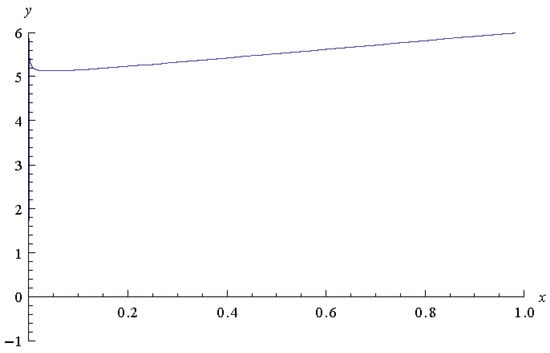
Figure 6.
Approximate solution for .
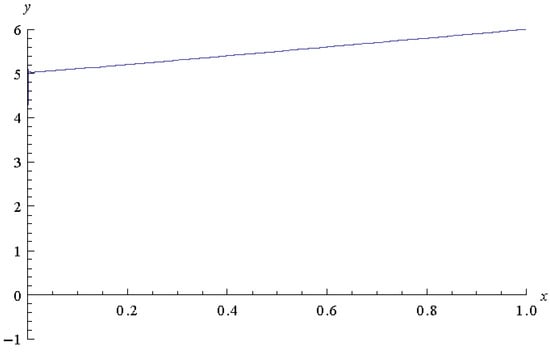
Figure 7.
Approximate solution for .
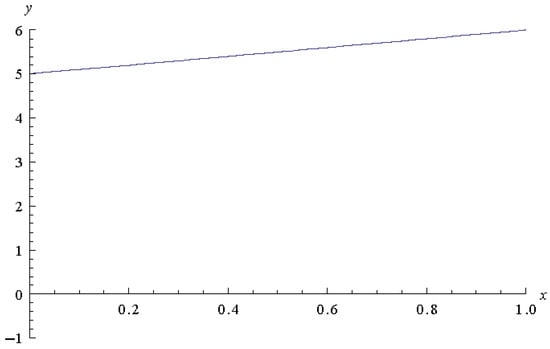
Figure 8.
Approximate solution for .
6. Conclusions
In this paper, we study a class of fractional nonlinear second order Volterra integro-differential type of singularly perturbed problems with fractional order. We divide the problem into two subproblems. The first subproblem is the reduced problem when The second subproblem is the second order fractional Volterra integro-differential problem. We use the finite difference method to solve the first subproblem and the reproducing kernel method to solve the second subproblem. The results show that the proposed analytical method can achieve excellent results in predicting the solutions of such problems. Theoretical results are presented. Numerical results are presented to show the efficiency of the proposed method. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the efficiency of the proposed method.
Acknowledgments
The authors would like to thank the reviewers for the valuable comments.
Author Contributions
All authors have equal contributionss in all parts of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsalyuk, Z.B. Volterra integral equations. J. Sov. Math. 1979, 12, 715–758. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Huang, Y. Spectral-collocation method for fractional Fredholm integro-differntial equations. J. Korean Math. Soc. 2014, 51, 203–224. [Google Scholar] [CrossRef]
- Sahu, P.K.; Ray, S.S. Legendre wavelets operational method for the numerical solutions of nonlinear Volterra integro-differntial equations system. Appl. Math. Comput. 2015, 256, 715–723. [Google Scholar]
- Yüzbaşı, Ş. Laguerre approach for solving pantograph-type Volterra integro-differntial equations. Appl. Math. Comput. 2014, 232, 1183–1199. [Google Scholar]
- Yang, Z.; Tang, T.; Zhang, J. Blowup of Volterra Integro-differntial Equations and Applications to Semi-Linear Volterra Diffusion Equations. Numer. Math. Theory Methods Appl. 2017, 10, 737–759. [Google Scholar] [CrossRef]
- Sekar, R.C.G.; Murugesan, K. Numerical Solutions of Non-Linear System of Higher Order Volterra Integro-differntial Equations using Generalized STWS Technique. In Differential Equations and Dynamical Systems; Oxford University Press: Oxford, UK, 2017; pp. 1–13. [Google Scholar]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Fractional-order Bernoulli functions and their applications in solving fractional Fredholem—Volterra integro-differntial equations. Appl. Numer. Math. 2017, 122, 66–81. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, J. Spectral collocation methods for Volterra-integro differential equations with noncompact kernels. J. Comput. Appl. Math. 2013, 244, 115–124. [Google Scholar] [CrossRef]
- Öztürk, Y.; Gülsu, M. An Operational Matrix Method for Solving a Class of Nonlinear Volterra Integro-differntial Equations by Operational Matrix Method. Int. J. Appl. Comput. Math. 2017, 3, 1–16. [Google Scholar] [CrossRef]
- Alvandi, A.; Paripour, M. Reproducing kernel method with Taylor expansion for linear Volterra integro-differntial equations. Commun. Numer. Anal. 2017, 2017, 40–49. [Google Scholar] [CrossRef]
- Tunç, C. New stability and boundedness results to Volterra integro-differntial equations with delay. J. Egypt. Math. Soc. 2016, 24, 210–213. [Google Scholar] [CrossRef]
- Ma, X.; Huang, C. Spectral collocation method for linear fractional integro-differntial equations. Appl. Math. Model. 2014, 38, 1434–1448. [Google Scholar] [CrossRef]
- Berenguer, M.I.; Garralda-Guillem, A.I.; Galán, M.R. An approximation method for solving systems of Volterra integro-differntial equations. Appl. Numer. Math. 2013, 67, 126–135. [Google Scholar] [CrossRef]
- Lovitt, W.V. Linear Integral Equations; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Song, Y.; Kim, H. The solution of Volterra integral equation of the second kind by using the Elzaki transform. Appl. Math. Sci. 2014, 8, 525–530. [Google Scholar] [CrossRef]
- Prandtle, L. Uber flussigkeits-bewegung bei kleiner reibung verhandlungen. In Proceedings of the III International Math Congress, Tuebner, Leipzig, 5–7 December 1905; pp. 484–491. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory; Mcgraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Friedrichs, K.O.; Wasow, W. Singular perturbations of nonlinear oscillations. Duke Math. J. 1946, 13, 367–381. [Google Scholar] [CrossRef]
- Abrahamsson, L.R. A prior estimates for solutions of singular perturbations with a turning point. Stud. Appl. Math. 1977, 56, 51–69. [Google Scholar] [CrossRef]
- Chou, H. Some applications of the singular perturbation method to the bending problems of thin plates and shells. Appl. Math. Mech. 1948, 5, 1449–1457. [Google Scholar]
- Kokotović, P.V. Applications of singular perturbation techniques to control problems. SIAM Rev. 1984, 26, 501–550. [Google Scholar] [CrossRef]
- Kokotovic, P.V.; O’malley, R.E.; Sannuti, P. Singular perturbations and order reduction in control theory—An overview. Automatic 1976, 12, 123–132. [Google Scholar] [CrossRef]
- Ghorbel, F.; Spong, M.W. Integral manifolds of singularly perturbed systems with application to rigid-link flexible-joint multibody systems. Int. J. Non-Linear Mech. 2000, 35, 133–155. [Google Scholar] [CrossRef]
- Fridman, E. State-feedback H∞ control of nonlinear singularly perturbed systems. Int. J. Robust Nonlinear Control 2001, 11, 1115–1125. [Google Scholar] [CrossRef]
- Fridman, E. Exact slow—Fast decomposition of the nonlinear singularly perturbed optimal control problem. Syst. Control Lett. 2000, 40, 121–131. [Google Scholar] [CrossRef]
- Archibasov, A.A.; Korobeinikov, A.; Sobolev, V.A. Passage to the limit in a singularly perturbed partial integro-differential system. Differ. Equ. 2016, 52, 1115–1122. [Google Scholar] [CrossRef]
- Archibasov, A.A.; Korobeinikov, A.; Sobolev, V.A. Asymptotic expansions of solutions in a singularly perturbed model of virus evolution. Comput. Math. Math. Phys. 2015, 55, 240–250. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Archibasov, A.; Sobolev, V. Order reduction for an rna virus evolution model. Math. Biosci. Eng. 2015, 12, 1007–1016. [Google Scholar] [CrossRef] [PubMed]
- Nefedov, N.N.; Nikitin, A.G. Method of differential inequalities for step-like contrast structures in singularly perturbed integro-differential equations in the spatially two-dimensional case. Diff. Equ. 2006, 42, 739. [Google Scholar] [CrossRef]
- Nefedov, N.N.; Nikitin, A.G. Boundary and internal layers in the reaction-diffusion problem with a nonlocal inhibitor. Comput. Math. Math. Phys. 2011, 51, 1011. [Google Scholar] [CrossRef]
- Omel’chenko, O.E.; Nefedov, N.N. Boundary-layer solutions to quasilinear integro-differential equations of the second order. Comput. Math. Math. Phys. 2002, 42, 470–482. [Google Scholar]
- Kashkari, B.; Syam, M. Fractional-order Legendre operational matrix of fractional integration for solving the Riccati equation with fractional order. Appl. Math. Comput. 2016, 290, 281–291. [Google Scholar] [CrossRef]
- Syam, M.; Siyyam, H.; Al-Subaihi, I. Tau-Path Following method for Solving the Riccati Equation with Fractional Order. J. Comput. Methods Phys. 2014, 2014, 207916. [Google Scholar] [CrossRef]
- Ariel, P.D.; Syam, M.I.; Al-Mdallal, Q.M. The extended homotopy perturbation method for the boundary layer flow due to a stretching sheet with partial slip. Int. J. Comput. Math. 2013, 90, 1990–2002. [Google Scholar] [CrossRef]
- Al-Refai, M. On the Fractional Derivatives at Extreme Points. Electron. J. Qual. Theory Differ. Equ. 2012, 55, 1–5. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Syam, M. An efficient method for solving non-linear singularly perturbed two points boundary-value problems of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2299–2308. [Google Scholar] [CrossRef]
- Syam, M.; Attili, B. Numerical solution of singularly perturbed fifth order two point boundary value problem. Appl. Math. Comput. 2005, 170, 1085–1094. [Google Scholar] [CrossRef]
- Kashkaria, B.; Syam, M. Evolutionary computational intelligence in solving a class of nonlinear Volterra—Fredholm integro-differntial equations. J. Comput.l Appl. Math. 2017, 311, 314–323. [Google Scholar] [CrossRef]
- Nefedov, N.N.; Nikitin, A.G. The asymptotic method of differential inequalities for singularly perturbed integro-differential equations. Differ. Equ. 2000, 36, 1544–1550. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).