Asynchronous Iterations of Parareal Algorithm for Option Pricing Models
Abstract
:1. Introduction
2. Problem Formulation
2.1. Overview
2.2. Derivation of the Black-Scholes Equation
2.3. Transformation into the Heat Equation
2.4. Black-Scholes Pricing Formula
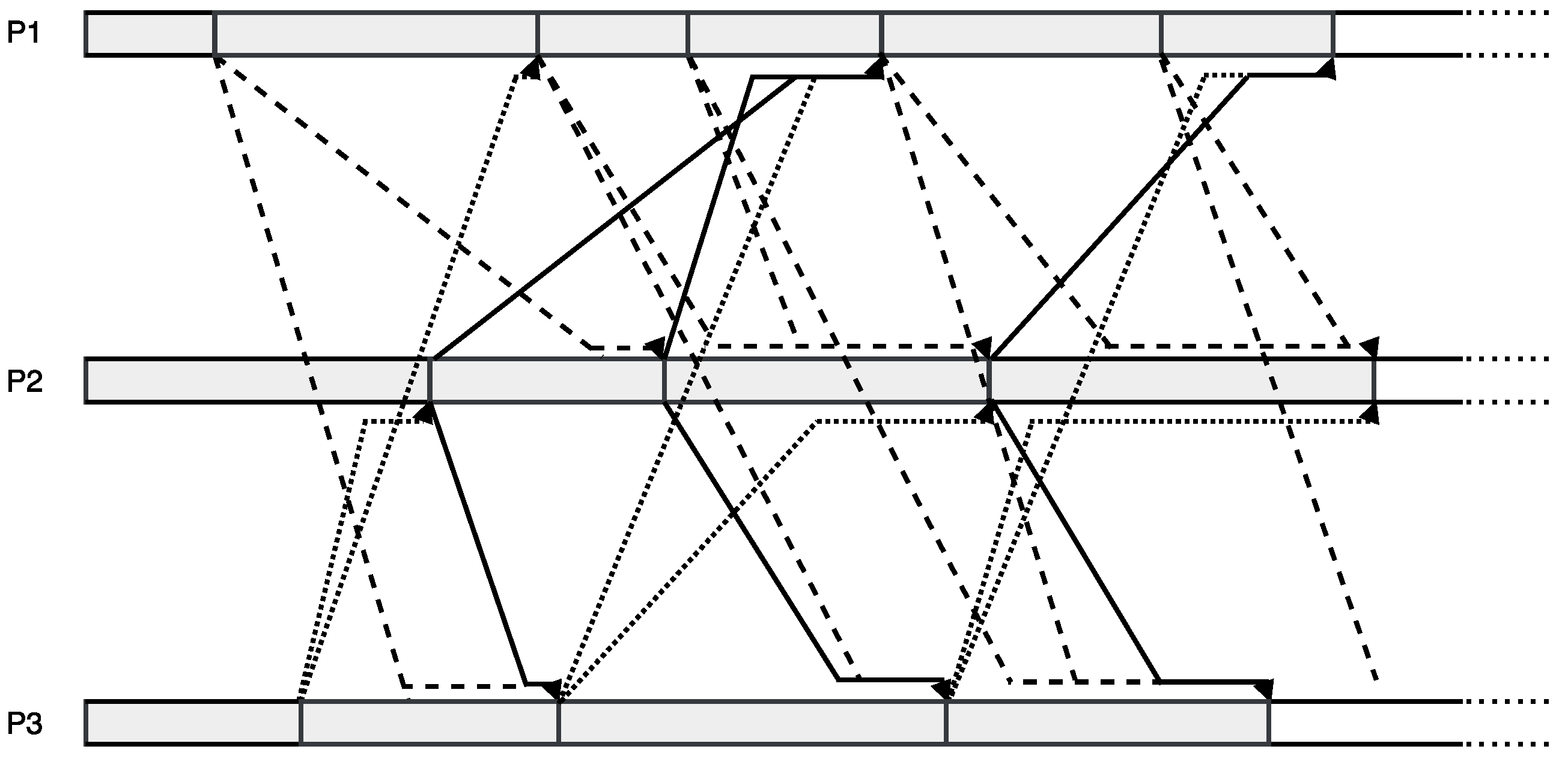
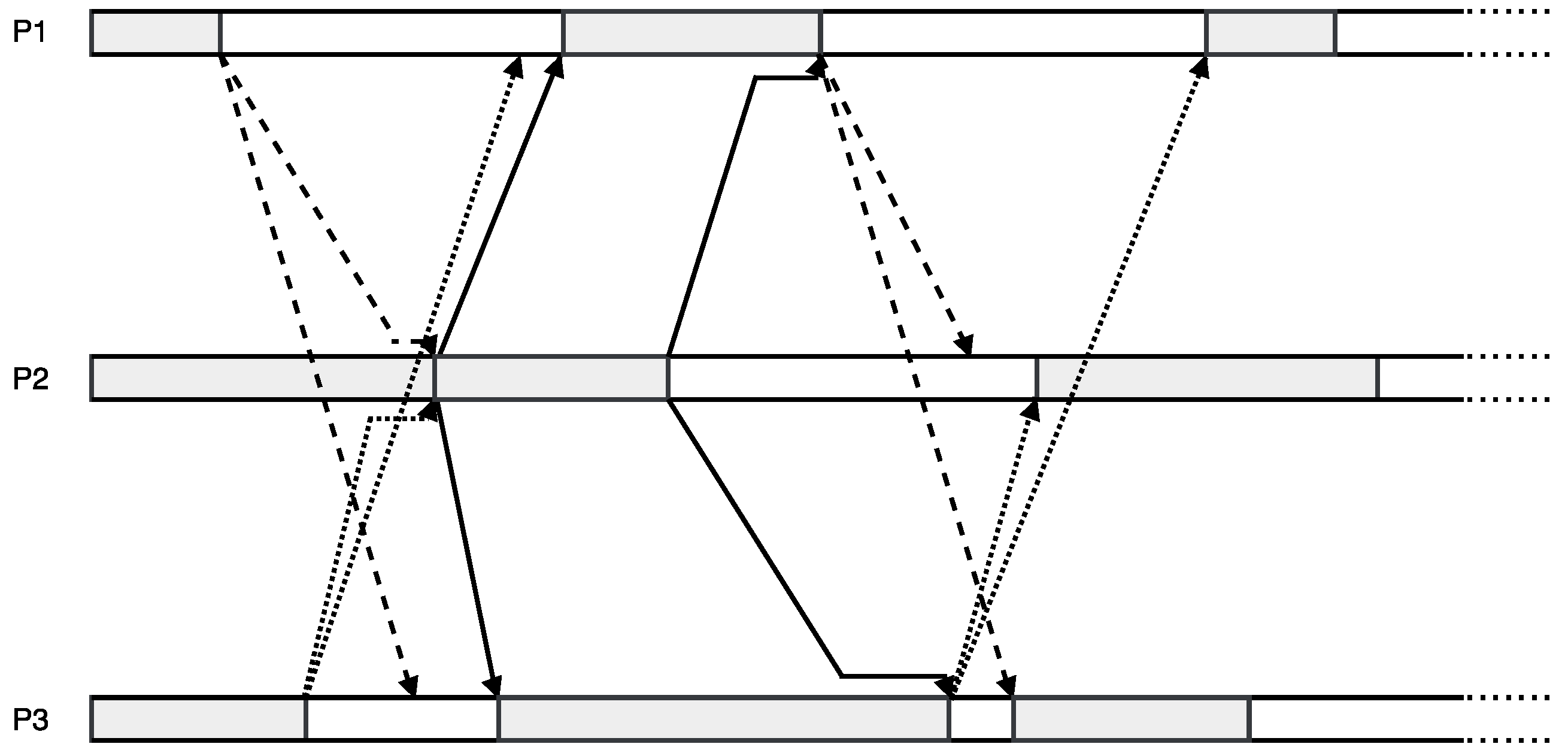
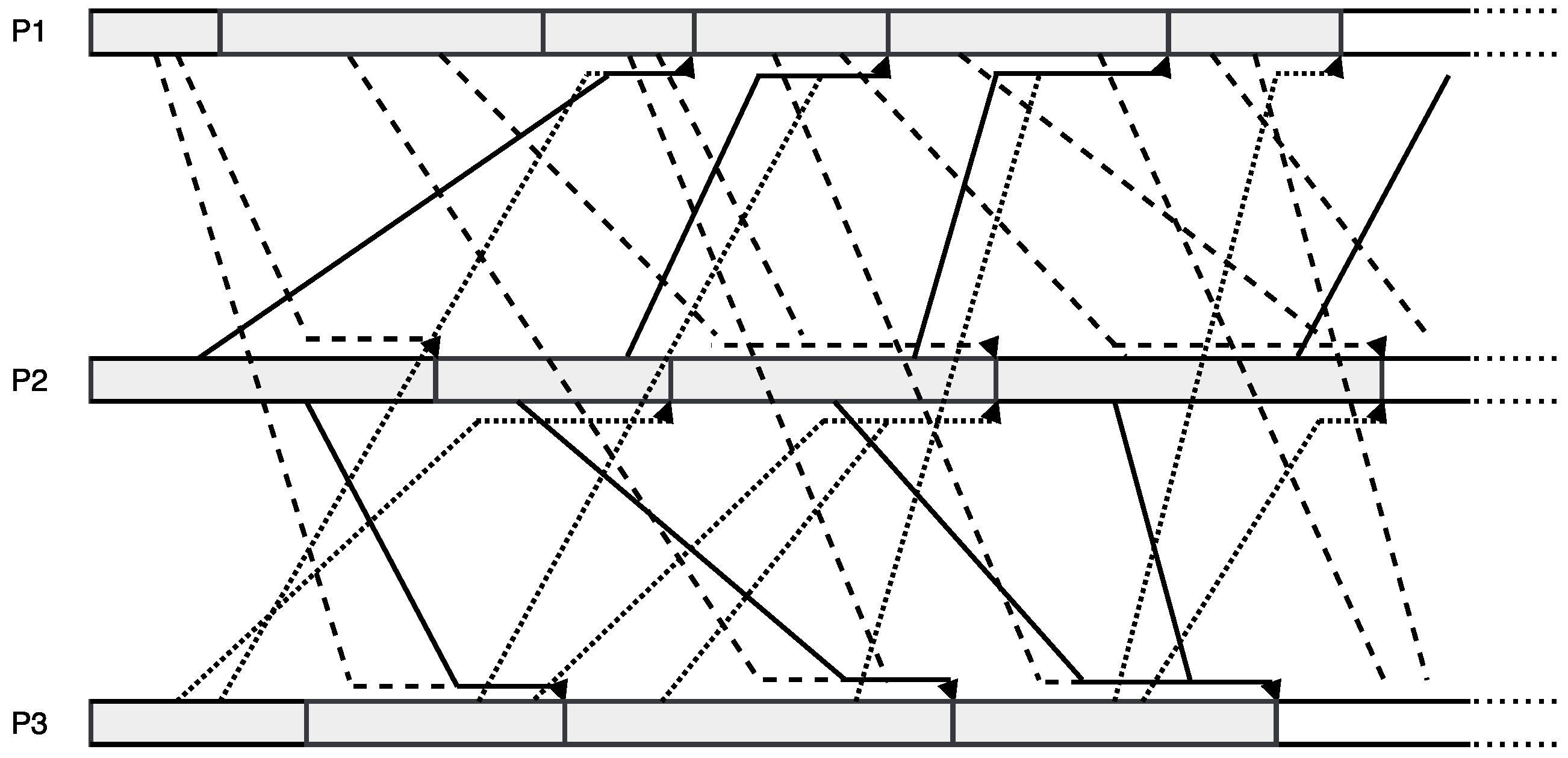
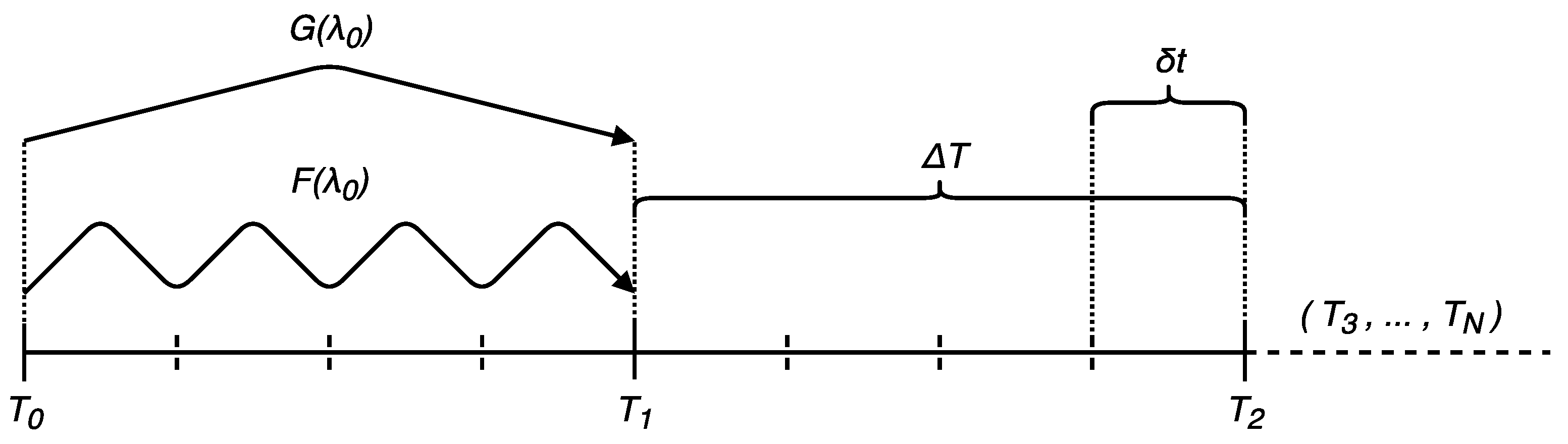
3. Asynchronous Parareal Algorithm
3.1. Asynchronous Iteration
| Algorithm 1 Asynchronous iterations with asynchronous communication. |
|
| Algorithm 2 Asynchronous two-stage iterations with flexible communication. |
|
3.2. Classical Parareal Algorithm
| Algorithm 3 Classical parareal algorithm. |
|
3.3. Asynchronous Parareal Algorithm
| Algorithm 4 Asynchronous parareal algorithm. |
|
4. Implementation
4.1. Asynchronous Communication Library
4.2. Preprocessing
- /* template <typename T, typename U> */
- // T: float, double, ...
- // U: int, long, ...
- U numb_sneighb = 1;
- U numb_rneighb = 1;
- U* sneighb_rank = new U[1]; // outgoing links.
- U* rneighb_rank = new U[1]; // incoming links.
- /* template <typename T, typename U> */
- U* sbuf_size = new U[1];
- U* rbuf_size = new U[1];
- sbuf_size[0] = numb_sub_domain;
- rbuf_size[0] = numb_sub_domain;
- T** send_buf = new T*[1]; // buffers for sending data.
- T** recv_buf = new T*[1]; // buffers for receiving data.
- send_buf[0] = new T[sbuf_size[0]];
- recv_buf[0] = new T[rbuf_size[0]];
- /* template <typename T, typename U> */
- T* res_vec_buf = new T[1]; // local residual vector.
- U res_vec_size = 1;
- T res_vec_norm; // norm of the global residual vector.
- float norm_type = 2; // 2 for Euclidean norm, < 1 for maximum norm.
- /* template <typename T, typename U> */
- T* sol_vec_buf; // local solution vector.
- U sol_vec_size = numb_sub_domain;
- int lconv_flag; // local convergence indicator.
- // -- initializes MPI
- MPI_Init(&argc, &argv);
- JACKComm comm;
- comm.Init(numb_sneighb, numb_rneighb, sneighb_rank, rneighb_rank, MPI_COMM_WORLD);
- comm.Init(sbuf_size, rbuf_size, send_buf, recv_buf);
- comm.Init(res_vec_size, res_vec_buf, &res_vec_norm, norm_type);
- if (async_flag) {
- comm.ConfigAsync(sol_vec_size, &sol_vec_buf, &lconv_flag, &recv_buf);
- comm.SwitchAsync();
- }
4.3. Implementation of Parareal Algorithms
- /* template <typename T, typename U> */
- PDESolver<T,U> coarse_pde;
- PDESolver<T,U> fine_pde;
- Vector<T,U> coarse_vec_U; // coarse results.
- Vector<T,U> fine_vec_U; // fine results.
- Vector<T,U> vec_U; // solution vector.
- Vector<T,U> vec_U0; // initial vector.
- /* template <typename T, typename U> */
- for (U i = 0; i < rank; i++) {
- coarse_pde.Integrate();
- vec_U0 = coarse_vec_U;
- }
- coarse_pde.Integrate();
- vec_U = coarse_vec_U;
- numb_iter = 0;
- while (res_norm >= res_thresh && numb_iter < m_rank) {
- fine_pde.Integrate();
- comm.Recv();
- coarse_vec_U_prev = coarse_vec_U;
- coarse_pde.Integrate();
- vec_U_prev = vec_U;
- vec_U = coarse_vec_U + fine_vec_U - coarse_vec_U_prev;
- comm.Send();
- // -- |Un+1<k+1> - Un+1<k>|
- vec_local_res = vec_U - vec_U_prev;
- (*res_vec_buf) = vec_local_res.NormL2();
- comm.UpdateResidual();
- numb_iter++;
- }
- fine_pde.Integrate();
- vec_U = fine_vec_U;
- comm.Send();
- // -- wait for global termination
- (*res_vec_buf) = 0.0;
- while (res_vec_norm >= res_thresh) {
- comm.UpdateResidual();
- numb_iter++;
- }
- }
- res_norm = res_thresh;
- numb_iter = 0;
- while (res_norm >= res_thresh) {
- fine_pde.Integrate();
- comm.Recv();
- coarse_vec_U_prev = coarse_vec_U;
- coarse_pde.Integrate();
- vec_U_prev = vec_U;
- vec_U = coarse_vec_U + fine_vec_U - coarse_vec_U_prev;
- comm.Send();
- // -- |Un+1<k+1> - Un+1<k>|
- vec_local_res = vec_U - vec_U_prev;
- (*res_vec_buf) = vec_local_res.NormL2();
- lconv_flag = ((*res_vec_buf) < res_thresh);
- comm.UpdateResidual();
- numb_iter++;
- }
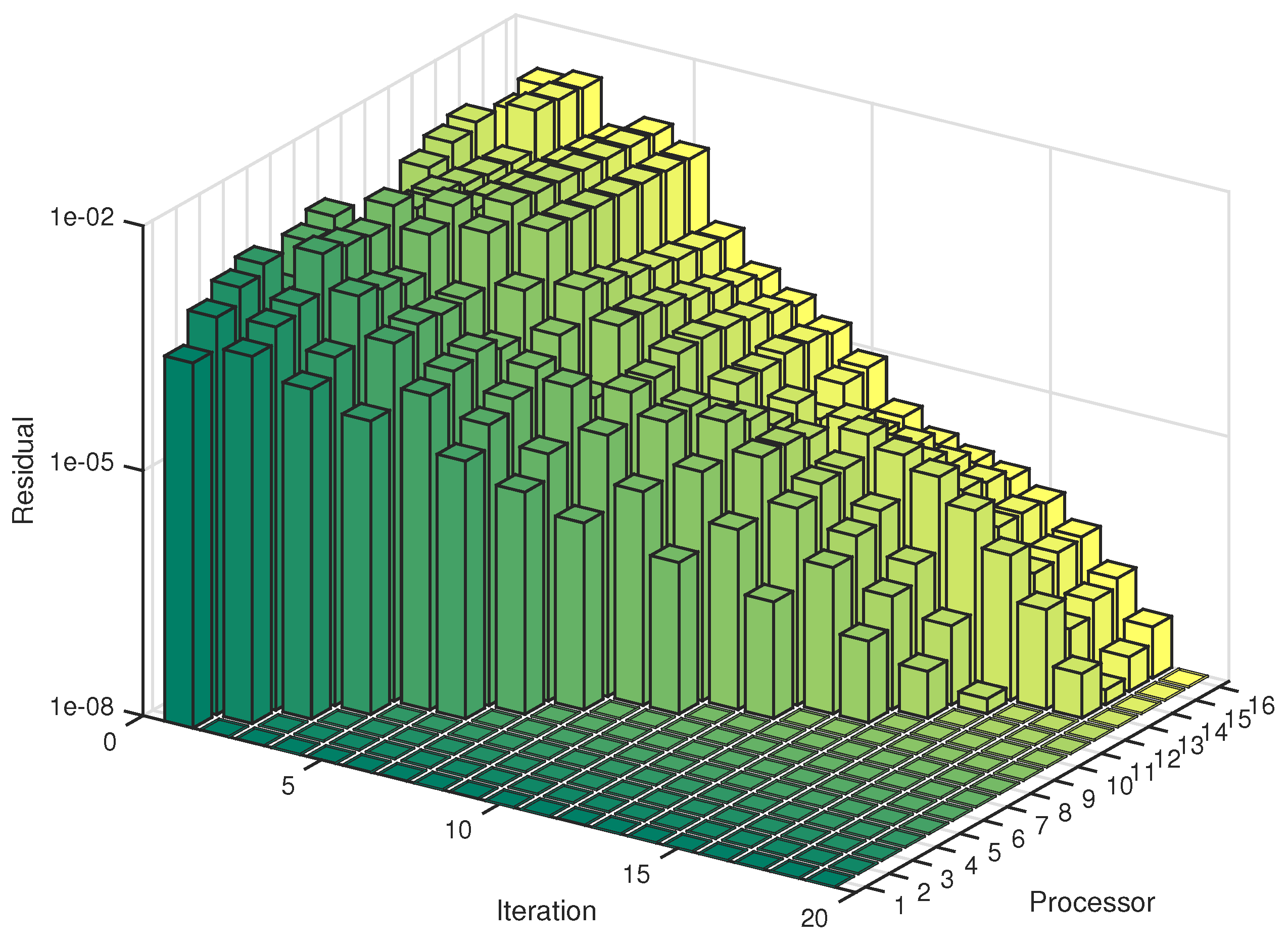
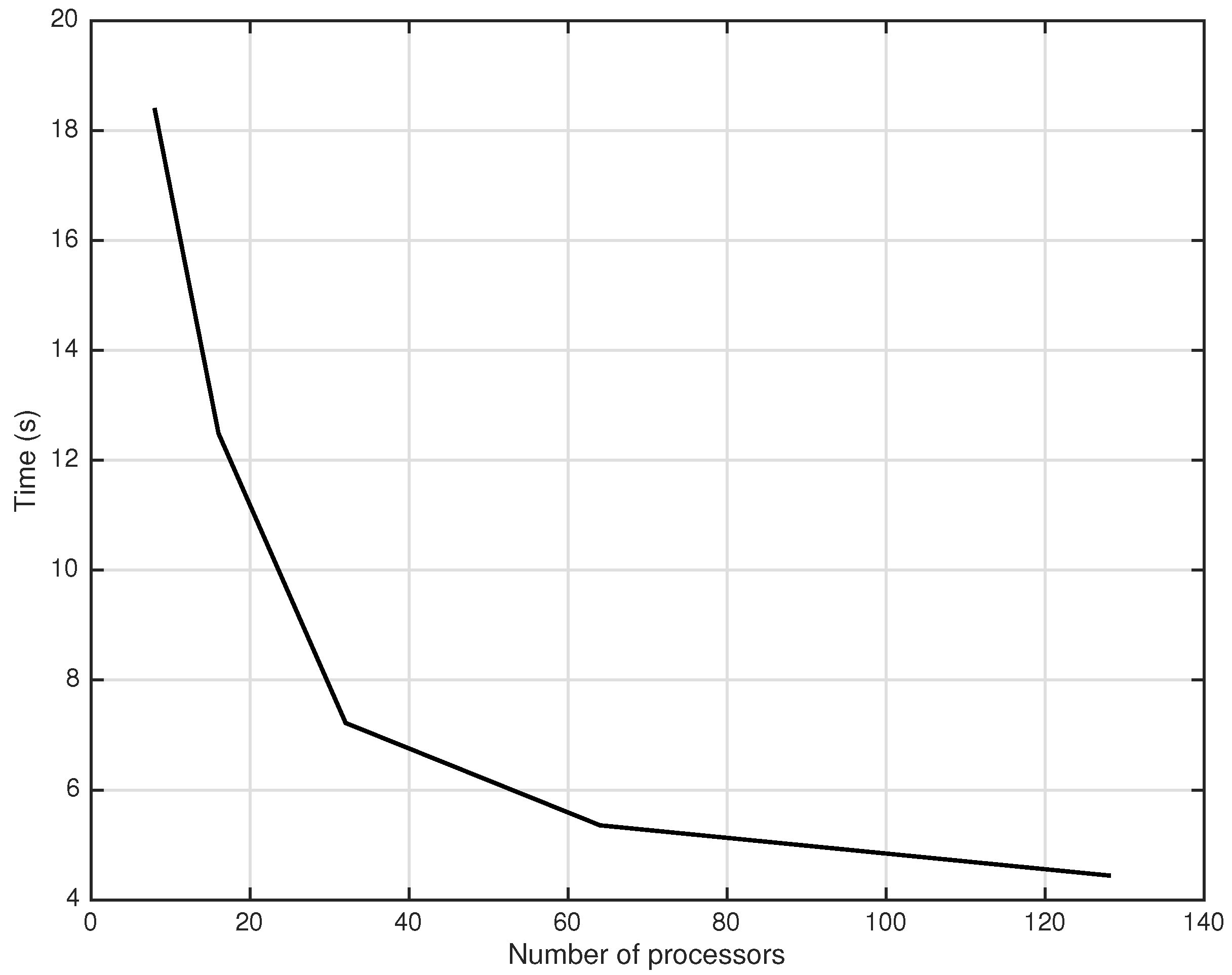
5. Numerical Experiments
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Chartier, P.; Philippe, B. A Parallel Shooting Technique for Solving Dissipative ODE’s. Computing 1993, 51, 209–236. [Google Scholar] [CrossRef]
- Deuflhard, P. Newton Methods for Nonlinear Problems: Affine Invariance and Adaptive Algorithms; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 35. [Google Scholar]
- Horton, G.; Stefan, V. A Space-Time Multigrid Method for Parabolic Partial Differential Equations. SIAM J. Sci. Comput. 1995, 16, 848–864. [Google Scholar] [CrossRef]
- Leimkuhler, B. Timestep Acceleration of Waveform Relaxation. SIAM J. Numer. Anal. 1998, 35, 31–50. [Google Scholar] [CrossRef]
- Gander, M.J.; Zhao, H. Overlapping Schwarz Waveform Relaxation for the Heat Equation in N Dimensions. BIT Numer. Math. 2002, 42, 779–795. [Google Scholar] [CrossRef]
- Gander, M.J.; Halpern, L.; Nataf, F. Optimal Schwarz Waveform Relaxation for the One Dimensional Wave Equation. SIAM J. Numer. Anal. 2003, 41, 1643–1681. [Google Scholar] [CrossRef]
- Lions, J.L.; Maday, Y.; Turinici, G. Résolution d’EDP par Un Schéma en Temps “Pararéel”. Comptes Rendus de l’Académie des Sciences-Série I-Mathématique 2001, 332, 661–668. [Google Scholar] [CrossRef]
- Farhat, C.; Chandesris, M. Time-Decomposed Parallel Time-Integrators: Theory and Feasibility Studies for Fluid, Structure, and Fluid–Structure Applications. Int. J. Numer. Methods Eng. 2003, 58, 1397–1434. [Google Scholar] [CrossRef]
- Chazan, D.; Miranker, W. Chaotic Relaxation. Linear Algebra Appl. 1969, 2, 199–222. [Google Scholar] [CrossRef]
- Miellou, J.C. Algorithmes de Relaxation Chaotique à Retards. ESAIM Math. Model. Numer. Anal. 1975, 9, 55–82. [Google Scholar] [CrossRef]
- Baudet, G.M. Asynchronous Iterative Methods for Multiprocessors. J. ACM 1978, 25, 226–244. [Google Scholar] [CrossRef]
- El Tarazi, M.N. Some Convergence Results for Asynchronous Algorithms. Numer. Math. 1982, 39, 325–340. [Google Scholar] [CrossRef]
- Miellou, J.C.; Spitéri, P. Un Critère de Convergence pour des Méthodes Générales de Point Fixe. ESAIM Math. Model. Numer. Anal. 1985, 19, 645–669. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Distributed Asynchronous Computation of Fixed Points. Math. Program. 1983, 27, 107–120. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Tsitsiklis, J.N. Parallel and Distributed Computation: Numerical Methods; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Magoulès, F.; Venet, C. Asynchronous Iterative Sub-structuring Methods. Math. Comput. Simul. 2018, 145, 34–49. [Google Scholar] [CrossRef]
- Magoulès, F.; Szyld, D.B.; Venet, C. Asynchronous Optimized Schwarz Methods with and without Overlap. Numer. Math. 2017, 137, 199–227. [Google Scholar] [CrossRef]
- El Baz, D.; Spitéri, P.; Miellou, J.C.; Gazen, D. Asynchronous Iterative Algorithms with Flexible Communication for Nonlinear Network Flow Problems. J. Parallel Distrib. Comput. 1996, 38, 1–15. [Google Scholar] [CrossRef]
- Miellou, J.C.; El Baz, D.; Spitéri, P. A New Class of Asynchronous Iterative Algorithms with Order Intervals. AMS Math. Comput. 1998, 67, 237–255. [Google Scholar] [CrossRef]
- Frommer, A.; Szyld, D.B. Asynchronous Iterations with Flexible Communication for Linear Systems. Calculateurs Parallèles 1998, 10, 91–103. [Google Scholar]
- Frommer, A.; Szyld, D.B. On Asynchronous Iterations. J. Comput. Appl. Math. 2000, 123, 201–216. [Google Scholar] [CrossRef]
- El Baz, D.; Frommer, A.; Spiteri, P. Asynchronous Iterations with Flexible Communication: Contracting Operators. J. Comput. Appl. Math. 2005, 176, 91–103. [Google Scholar] [CrossRef]
- Frommer, A.; Szyld, D.B. Asynchronous Two-Stage Iterative Methods. Numer. Math. 1994, 69, 141–153. [Google Scholar] [CrossRef]
- Bahi, J.M.; Contassot-Vivier, S.; Couturier, R. Parallel Iterative Algorithms: From Sequential to Grid Computing, 1st ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of Rational Option Pricing. Bell J. Econ. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Merton, R.C. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. J. Financ. 1974, 29, 449–470. [Google Scholar]
- Cox, J.C.; Ross, S.A. The Valuation of Options for Alternative Stochastic Processes. J. Financ. Econ. 1976, 3, 145–166. [Google Scholar] [CrossRef]
- Harrison, J.M.; Kreps, D.M. Martingales and Arbitrage in Multiperiod Securities Markets. J. Econ. Theory 1979, 20, 381–408. [Google Scholar] [CrossRef]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option Pricing: A Simplified Approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The Pricing of Options on Assets with Stochastic Volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Duan, J.C. The GARCH Option Pricing Model. Math. Financ. 1995, 5, 13–32. [Google Scholar] [CrossRef]
- Itô, K. On Stochastic Differential Equations; American Mathematical Society: Providence, RI, USA, 1951. [Google Scholar]
- Bahi, J.M.; Domas, S.; Mazouzi, K. Jace: A Java Environment for Distributed Asynchronous Iterative Computations. In Proceedings of the 12th Euromicro Conference on Parallel, Distributed and Network-Based Processing, Coruna, Spain, 11–13 February 2004; pp. 350–357. [Google Scholar]
- Bahi, J.M.; Couturier, R.; Vuillemin, P. JaceV: A Programming and Execution Environment for Asynchronous Iterative Computations on Volatile Nodes. In Proceedings of the 2006 International Conference on High Performance Computing for Computational Science, Rio de Janeiro, Brazil, 10–12 July 2006; pp. 79–92. [Google Scholar]
- Bahi, J.M.; Couturier, R.; Vuillemin, P. JaceP2P: An Environment for Asynchronous Computations on Peer-to-Peer Networks. In Proceedings of the 2006 IEEE International Conference on Cluster Computing, Barcelona, Spain, 25–28 September 2006; pp. 1–10. [Google Scholar]
- Charr, J.C.; Couturier, R.; Laiymani, D. JACEP2P-V2: A Fully Decentralized and Fault Tolerant Environment for Executing Parallel Iterative Asynchronous Applications on Volatile Distributed Architectures. In Proceedings of the 2009 International Conference on Advances in Grid and Pervasive Computing, Geneva, Switzerland, 4–8 May 2009; pp. 446–458. [Google Scholar]
- Couturier, R.; Domas, S. CRAC: A Grid Environment to Solve Scientific Applications with Asynchronous Iterative Algorithms. In Proceedings of the 2007 IEEE International Parallel and Distributed Processing Symposium, Rome, Italy, 26–30 March 2007; pp. 1–8. [Google Scholar]
- Magoulès, F.; Gbikpi-Benissan, G. JACK: An Asynchronous Communication Kernel Library for Iterative Algorithms. J. Supercomput. 2017, 73, 3468–3487. [Google Scholar] [CrossRef]
- Magoulès, F.; Gbikpi-Benissan, G. JACK2: An MPI-based Communication Library with Non-blocking Synchronization for Asynchronous Iterations. Adv. Eng. Softw. 2018, in press. [Google Scholar]
- Magoulès, F.; Cheik Ahamed, A.K. Alinea: An Advanced Linear Algebra Library for Massively Parallel Computations on Graphics Processing Units. Int. J. High Perform. Comput. Appl. 2015, 29, 284–310. [Google Scholar] [CrossRef]
- Cheik Ahamed, A.K.; Magoulès, F. Fast Sparse Matrix-Vector Multiplication on Graphics Processing Unit for Finite Element Analysis. In Proceedings of the 14th IEEE International Confernence on High Performance Computing and Communications, Liverpool, UK, 25–27 June 2012. [Google Scholar]
- Magoulès, F.; Cheik Ahamed, A.K.; Putanowicz, R. Fast Iterative Solvers for Large Compressed-Sparse Row Linear Systems on Graphics Processing Unit. Pollack Periodica 2015, 10, 3–18. [Google Scholar] [CrossRef]
- Cheik Ahamed, A.K.; Magoulès, F. Iterative Methods for Sparse Linear Systems on Graphics Processing Unit. In Proceedings of the 14th IEEE International Confernence on High Performance Computing and Communications, Liverpool, UK, 25–27 June 2012. [Google Scholar]
- Magoulès, F.; Cheik Ahamed, A.K.; Putanowicz, R. Auto-Tuned Krylov Methods on Cluster of Graphics Processing Unit. Int. J. Comput. Math. 2015, 92, 1222–1250. [Google Scholar] [CrossRef]
- Magoulès, F.; Cheik Ahamed, A.K.; Suzuki, A. Green Computing on Graphics Processing Units. Concurr. Comput. Pract. Exp. 2016, 28, 4305–4325. [Google Scholar] [CrossRef]
- Magoulès, F.; Cheik Ahamed, A.K.; Putanowicz, R. Optimized Schwarz Method without Overlap for the Gravitational Potential Equation on Cluster of Graphics Processing Unit. Int. J. Comput. Math. 2016, 93, 955–980. [Google Scholar] [CrossRef]
| Time(s) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.05 | 1.6297 | 1.6237 | 0.0060 | 0.0037 | 33 | 43 | 37 | 0.600 |
| 0.20 | 8.3064 | 8.3022 | 0.0042 | 0.0005 | 34 | 47 | 39 | 2.453 |
| 0.35 | 13.9586 | 13.9541 | 0.0045 | 0.0003 | 33 | 43 | 37 | 4.039 |
| 0.50 | 18.7968 | 18.7918 | 0.0050 | 0.0003 | 34 | 47 | 40 | 6.123 |
| 0.65 | 22.9713 | 22.9659 | 0.0054 | 0.0002 | 34 | 45 | 39 | 7.769 |
| 0.80 | 26.5845 | 26.5796 | 0.0049 | 0.0002 | 38 | 47 | 42 | 10.337 |
| 0.95 | 29.7150 | 29.7125 | 0.0025 | 0.0001 | 35 | 45 | 39 | 11.459 |
| N | Synchronous | Asynchronous | ||||||
|---|---|---|---|---|---|---|---|---|
| Iter. | Time(s) | Speedup | Time(s) | Speedup | ||||
| 16 | 11 | 0.620 | 1.28 | 22 | 30 | 26 | 0.490 | 1.62 |
| 32 | 11 | 0.781 | 2.11 | 30 | 47 | 40 | 0.677 | 2.43 |
| 64 | 11 | 0.971 | 3.41 | 44 | 77 | 60 | 0.947 | 3.50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magoulès, F.; Gbikpi-Benissan, G.; Zou, Q. Asynchronous Iterations of Parareal Algorithm for Option Pricing Models. Mathematics 2018, 6, 45. https://doi.org/10.3390/math6040045
Magoulès F, Gbikpi-Benissan G, Zou Q. Asynchronous Iterations of Parareal Algorithm for Option Pricing Models. Mathematics. 2018; 6(4):45. https://doi.org/10.3390/math6040045
Chicago/Turabian StyleMagoulès, Frédéric, Guillaume Gbikpi-Benissan, and Qinmeng Zou. 2018. "Asynchronous Iterations of Parareal Algorithm for Option Pricing Models" Mathematics 6, no. 4: 45. https://doi.org/10.3390/math6040045
APA StyleMagoulès, F., Gbikpi-Benissan, G., & Zou, Q. (2018). Asynchronous Iterations of Parareal Algorithm for Option Pricing Models. Mathematics, 6(4), 45. https://doi.org/10.3390/math6040045




