Serret-Frenet Frame and Curvatures of Bézier Curves
Abstract
:1. Introduction
2. Preliminaries
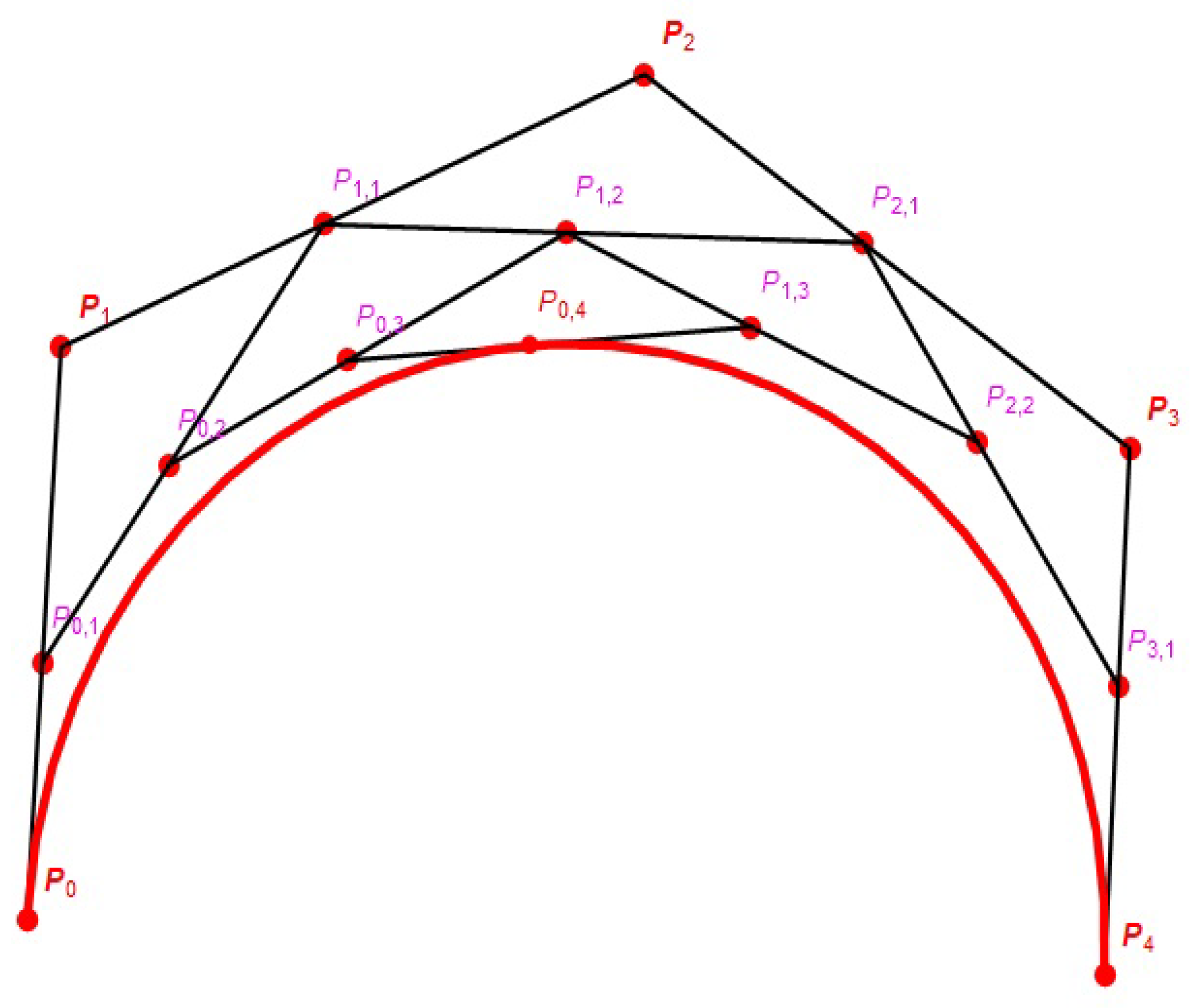
2.1. Some Concepts for Bézier Curve
2.2. The Theory of Curves in and
3. Serret-Frenet Elements of Bézier Curve in
Serret-Frenet Elements of Bézier Curve of Degree n in
4. Serret-Frenet Elements of Bézier Curve in
5. Serret-Frenet Elements of Bézier Curve with the Algorithm in and
5.1. Serret-Frenet Elements of Bézier Curve of Degree n with the Algorithm in
5.2. Serret-Frenet Elements of Bézier Curve of Degree n with the Algorithm in
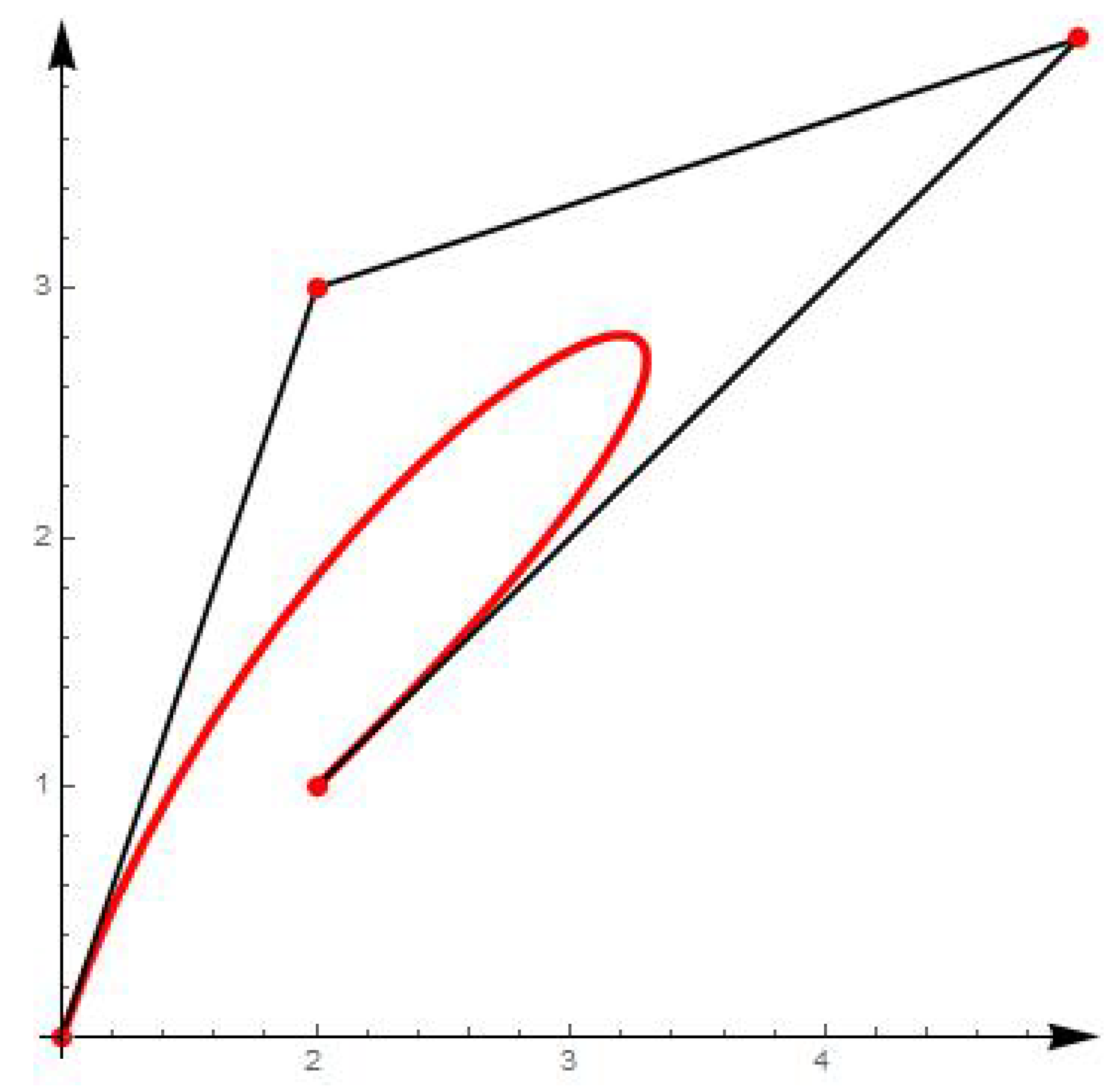
6. Examples in and
- The Serret-Frenet frame and curvature for are
- The Serret-Frenet frame and curvature for are
- The Serret-Frenet frame and curvature for are
- By taking in Theorem 5, we obtain Serret-Frenet elements for cubic Bézier curve as follows:
- By taking in Theorem 3, we obtain Serret-Frenet elements for cubic Bézier curve as follows:
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anand, V.B. Computer Graphics and Geometric Modeling for Engineers, 1st ed.; John Wiley and Sons Inc.: New York, NY, USA, 1992. [Google Scholar]
- Iglesias, A.; Gálvez, A.; Loucera, C. Two Simulated Annealing Optimization Schemas for Rational Bézier Curve Fitting in the Presence of Noise. Math. Prob. Eng. 2016, 2016, 8241275. [Google Scholar] [CrossRef]
- Forrest, A.R. Curves and Surfaces for Computer-Aided Design. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1968. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design a Practical Guide, 4th ed.; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Ghomanjani, F.; Farahi, M.H.; Kılıçman, A.; Kamyad, A.V.; Pariz, N. Bézier Curves Based Numerical Solutions of Delay Systems with Inverse Time. Math. Prob. Eng. 2014. [Google Scholar] [CrossRef]
- Hu, G.; Cao, H.; Zhang, S. Approximate Multidegree Reduction of λ-Bézier Curves. Math. Prob. Eng. 2016. [Google Scholar] [CrossRef]
- Hu, G.; Ji, X.; Qin, X.; Zhang, S. Shape Modification for λ-Bézier Curves Based on Constrained Optimization of Position and Tangent Vector. Math. Prob. Eng. 2015, 12, 735629. [Google Scholar] [CrossRef]
- Misro, M.Y.; Ramli, A.; Ali, J.M. Quintic Trigonometric Bézier Curve with Two Shape Parameters. Sains Malays. 2017, 46, 825–831. [Google Scholar]
- Farin, G.; Sapidis, N. Curvature and the fairness of Curves and Surfaces. IEEE Comput. Gr. Appl. 1989, 9, 52–57. [Google Scholar] [CrossRef]
- Frey, W.H.; Field, D.A. Designing Bézier Conic Segments with Monotone Curvature. Comput. Aided Geom. Des. 2000, 17, 457–483. [Google Scholar] [CrossRef]
- Goldman, R. Curvature Formulas for Implicit Curves and Surfaces. Comput. Aided Geom. Des. 2005, 22, 632–658. [Google Scholar] [CrossRef]
- Farin, G.; Hoschek, J.; Kim, M.S. Handbook of Computer Aided Geometric Design; Elsevier Science: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Marsh, D. Applied Geometry for Computer Graphics and CAD, 2nd ed.; Springer: London, UK; Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kusak Samanci, H.; Celik, S.; Incesu, M. The Bishop Frame of Bézier Curves. Life Sci. J. 2015, 12, 175–180. [Google Scholar]
- Gray, A.; Abbena, E.; Salamon, S. Modern Differential Geometry of Curves and Surfaces with Mathematica; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erkan, E.; Yüce, S. Serret-Frenet Frame and Curvatures of Bézier Curves. Mathematics 2018, 6, 321. https://doi.org/10.3390/math6120321
Erkan E, Yüce S. Serret-Frenet Frame and Curvatures of Bézier Curves. Mathematics. 2018; 6(12):321. https://doi.org/10.3390/math6120321
Chicago/Turabian StyleErkan, Esra, and Salim Yüce. 2018. "Serret-Frenet Frame and Curvatures of Bézier Curves" Mathematics 6, no. 12: 321. https://doi.org/10.3390/math6120321
APA StyleErkan, E., & Yüce, S. (2018). Serret-Frenet Frame and Curvatures of Bézier Curves. Mathematics, 6(12), 321. https://doi.org/10.3390/math6120321




