1. Introduction
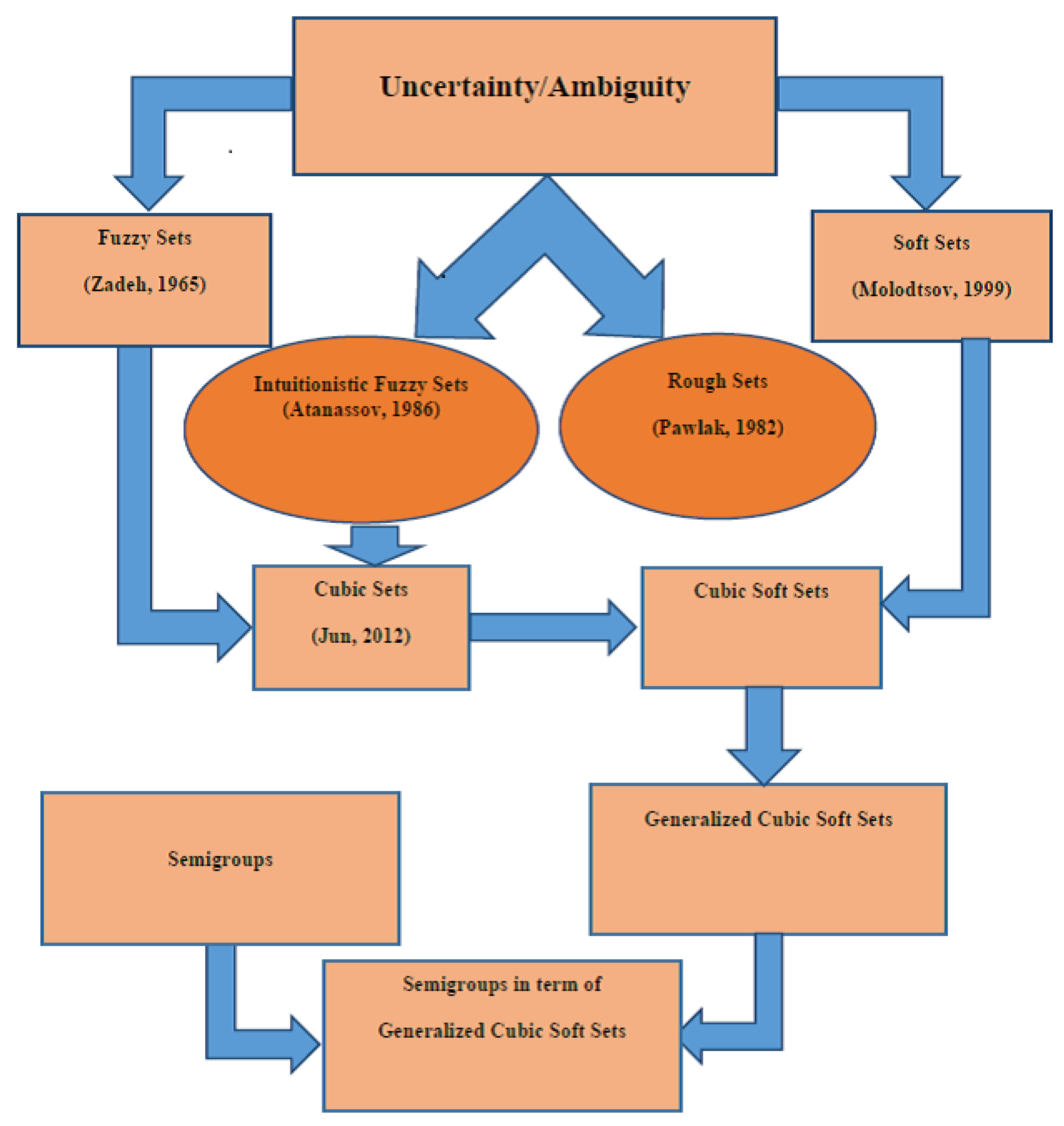
To handle uncertainty in many real world problems the existing methods are not sufficient. To reduce these uncertainties, a few sorts of speculations were presented like hypothesis of fuzzy sets [
1], intuitionistic fuzzy sets [
2] and rough sets [
3]. These sets have some limitations so Molodtsov [
4] initiated the new approach namely soft sets which is a new theory and has the ability to capture the uncertainty in a better way. After this many researchers used the idea of soft sets in many directions, such as Maji et al. [
5], Maji et al. [
6], Aktas and Cagman [
7], and Jun et al. [
8,
9]. Maji et al. [
10] initiated the study of fuzzy soft sets. After this many researcher used fuzzy soft sets such as, Roy et al. [
11], Yang [
12] and Kharal et al. [
13]. Zhou et al. developed the idea of intutionistic fuzzy soft sets which extend the idea of fuzzy soft sets [
14].
Another general version of fuzzy sets and intutionistic fuzzy sets was presented by Jun et al. [
15] namely the cubic sets. After that jun et al. [
16,
17,
18,
19] applied cubic sets in different directions such as in BCK/BCI-algebras. Since then cubic sets were actively being used in many areas such as Akram et al. [
20], in KU-subalgebras, Aslam et al. [
21], in
-semihypergroups, Gulistan et al. [
22], in weak left almost semihypergroups, Gulistan et al. [
23], in regular LA-semihypergroups, Khan et al. [
24], in LA-semihypergroups, Ma et al. [
25], in H
-LA-semihypergroups, Yaqoob et al. [
26], on cubic KU-ideals of KU-algebras, Yaqoob et al. [
27], in cubic hyperideals in LA-semihypergroups. Khan et al. [
28] presented the idea of the generalized version of Jun’s cubic sets in semigroups and several others like, Abughazalah and Yaqoob [
29], Rashid et al. [
30].
Recently, Yin and Zhan [
31] introduced more general forms of
-fuzzy filters and define
-fuzzy filters and gave some interesting results in terms of these notions. See also [
32,
33,
34].
On the other hand semigroups are the very useful associative algebraic structures which has many application in different directions. A very particular class of semigroups namely right weakly regular semigroups was discussed by Feng et al. [
35] and Khan et al. in [
36]. A valuable application of the group of symmetries can be see in network fibres by Mallat [
37] in 2016.
Since we see that the idea of fuzzy soft sets and intutionistic fuzzy soft sets generalize the concept of soft sets so its natural to blend generalized cubic sets presented by Khan et al. in [
28] with Molodtsov’s [
4] soft sets and apply on the right weakly regular semigroups studied by Feng et al. [
35] and Khan et al. [
36]. Thus we initiate the study of special types of cubic soft ideals in semigroups with some interesting properties. We discuss some lattice structures formed by generalized cubic soft ideals of semigroups. We also provide an application of the current proposal and conclusion is given at the end.
3. Cubic Soft Sets
In this section, we introduce the concepts of cubic soft sets, cubic soft ideals and some basic operations on cubic sets.
Definition 3. A pair is called a cubic soft set over S, where and is a mapping given by where denotes the set of all cubic sets of S and E be a set of parameters.
In general, for every is a cubic set in S and it is called cubic value set of parameter
Definition 4. A cubic soft set is contained in other cubic soft set if and for every
Equivalently if and , for all
Definition 5. Let and be two cubic soft sets over S. Then where for all that isfor all Definition 6. Let and be two cubic soft sets over S. Then where for all that isfor all Definition 7. Let and be two cubic soft sets over S. Then where and for all
and
Definition 8. Let and be two cubic soft sets over S. Then where and for all
and
Definition 9. Let and be two cubic soft sets over S. Then where and for all
and
4. Generalized Cubic Soft Ideals of Semigroups
This section is dedicated to the concept of -cubic soft subsemigroup, -cubic soft ideals and their basic properties. Note that and
Definition 10. Let and such that and Then by cubic point we mean whereFor any cubic set and for a cubic point with the condition that such that we have - (i)
if and
- (ii)
if and
- (iii)
if or
Definition 11. A cubic soft set of S is called an -cubic soft subsemigroup of if is an -cubic subsemigroup of
Equivalently;
A cubic soft set of S is called an -cubic soft subsemigroup of ifEquivalently; A cubic soft set of S is called an -cubic soft subsemigroup of ifimplies thatwhere and such that , and such that Example 1. Let and the binary operation “·” be defined on S as follows:Then is a semigroup. Let and Let be the set of parameters. For each parameter is an -cubic subsemigroup of where is a mapping given by Then for each parameter we defineandHence is an -cubic soft subsemigroup of Definition 12. A cubic soft set of S is called an -cubic soft left ideal of if is an -cubic left ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft left ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft left ideal of if and implies that where and such that , and such that
Definition 13. A cubic soft set of S is called an -cubic soft right ideal of if is an -cubic right ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft right ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft right ideal of if and implies that where such that and such that
Definition 14. A cubic soft set of S is called an -cubic soft ideal of if is an -cubic ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft ideal of if and implies that and , where such that , and such that
Definition 15. A cubic soft set of S is called an -cubic soft bi ideal of if is an -cubic bi ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft bi ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft bi ideal of if is an -cubic soft subsemigroup of S, and implies that , where such that , and such that
Definition 16. A cubic soft set of S is called an -cubic soft generalized bi ideal of if is an -cubic generalized bi ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft generalized bi ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft generalized bi ideal of if and implies that , where such that , and such that
Definition 17. A cubic soft set of S is called an -cubic soft interior ideal of if is an -cubic interior ideal of
Equivalently;
A cubic soft set of S is called an -cubic soft interior ideal of ifEquivalently; A cubic soft set of S is called an -cubic soft interior ideal of if is an -cubic soft subsemigroup of S, and implies that , where such that , and such that
Definition 18. Let and be two cubic soft sets over S. We say that is an -cubic soft subset of and write if
for each
Theorem 4. Let and be two -cubic soft subsemigroups of Then
- (i)
is an -cubic soft subsemigroup of S.
- (ii)
is an -cubic soft subsemigroup of S.
- (iii)
is an -cubic soft subsemigroup of
- (iv)
is an -cubic soft subsemigroup of
- (v)
is an -cubic soft subsemigroup of
Proof. Let and be two -cubic soft subsemigroups of S. Let where and for all We consider the following cases.
Case 1: If
then
and
Case 2: Similar to case 1.
Case 3: Let
and consider
On the other hand consider
Hence
is an
-cubic soft subsemigroup of
S.
Let and be two -cubic soft subsemigroup of Let We consider the following cases.
Case 1: If
then
and
Case 2: Similar to case 1.
Case 3: Let
and consider
On the other hand consider
Let
and
be two
-cubic soft subsemigroup of
S and let
where
and
for all
that is
for all
Since
and
are
-cubic subsemigroup of
so by part (i)
is an
-cubic subsemigroup of
S for all
Hence
is an
-cubic soft subsemigroup of
Let
and
be two
-cubic soft subsemigroup of
S and let
where
for all
that is
for all
Since
and
are
-cubic subsemigroup of
so by part (ii)
is an
-cubic subsemigroup of
S for all
Hence
is an
-cubic soft subsemigroup of
Let and be two -cubic soft subsemigroup of and let where and for all We consider the following cases.
Case 1: If
then
and
Case 2: Similar to case one.
Case 3: Let
and consider
and
Hence
is an
-cubic soft subsemigroup of
□
Theorem 5. Let and be two -cubic soft (resp., left, right, bi, interior, generalized bi) ideals of then
- (i)
is an -cubic soft (resp., left, right, bi, interior, generalized bi) ideal of S.
- (ii)
is an -cubic (resp., left, right, bi, interior, generalized bi) ideal of S.
- (iii)
is an -cubic (resp., left, right, bi, interior, generalized bi) ideal of
- (iv)
is an -cubic (resp., left, right, bi, interior, generalized bi) ideal of
- (v)
is an -cubic (resp., left, right, bi, interior, generalized bi) ideal of
Proof. It follows from the proof of Theorem 4. □
Theorem 6. Let be a-cubic soft set of Then is an -cubic soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S if and only ifis soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of Proof. Let
be an
-cubic soft subsemigroup of
S. Let
,
such that
and let
This implies
Now by hypothesis
This implies that
On the other hand again using the hypothesis
This implies that
Thus we get
which implies that
Hence
is a soft subsemigroup of
Conversely let
is a soft subsemigroup of
Suppose there exist
,
with
such that
and
This implies that
which is contradiction. So
and
Hence
is an
-cubic soft subsemigroup of
S. □
Lemma 1. Let then A is a subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S if and only if cubic characteristic function of is an -cubic soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S, where such that , and such that
Proof. Straightforward.
where set of all cubic soft ideals of S is denoted by □
Theorem 7. forms the lattice structure, where is the set of all cubic soft ideals of
Proof. It is obvious that is an ordered relation. Let , then by Theorem 5 It is clear that is the least upper bound and is the greatest lower bound of any two arbitrary elements of Hence the set of becomes a lattice. □
Theorem 8. Let S be a semigroup with identity e such that and Then forms the lattice structure.
Proof. It is obvious that is an ordered relation. Let , then by Theorem 5 It is clear that is the greatest lower bound of any two arbitrary elements of Now we will show that is the least upper bound of any two arbitrary elements of For this let and
Case1: If
then
Case2: If
then
Case3: If
then
and
and so
Similarly
Let
be any other element of
such that
then
Hence least upper bound of
,
is
Hence the
forms the lattice structure. □
Remark 1. In the case when the semigroup S is regular Theorems 7 and 8 concide with each other.