Characterizations of Right Weakly Regular Semigroups in Terms of Generalized Cubic Soft Sets

Abstract

Cubic sets are the very useful generalization of fuzzy sets where one is allowed to extend the output through a subinterval of $[0,1]$ and a number from $[0,1]$. Generalized cubic sets generalized the cubic sets with the help of cubic point. On the other hand Soft sets were proved to be very effective tool for handling imprecision. Semigroups are the associative structures have many applications in the theory of Automata. In this paper we blend the idea of cubic sets, generalized cubic sets and semigroups with the soft sets in order to develop a generalized approach namely generalized cubic soft sets in semigroups. As the ideal theory play a fundamental role in algebraic structures through this we can make a quotient structures. So we apply the idea of neutrosophic cubic soft sets in a very particular class of semigroups namely weakly regular semigroups and characterize it through different types of ideals. By using generalized cubic soft sets we define different types of generalized cubic soft ideals in semigroups through three different ways. We discuss a relationship between the generalized cubic soft ideals and characteristic functions and cubic level sets after providing some basic operations. We discuss two different lattice structures in semigroups and show that in the case when a semigroup is regular both structures coincides with each other. We characterize right weakly regular semigroups using different types of generalized cubic soft ideals. In this characterization we use some classical results as without them we cannot prove the inter relationship between a weakly regular semigroups and generalized cubic soft ideals. This generalization leads us to a new research direction in algebraic structures and in decision making theory.

1. Introduction

To handle uncertainty in many real world problems the existing methods are not sufficient. To reduce these uncertainties, a few sorts of speculations were presented like hypothesis of fuzzy sets [1], intuitionistic fuzzy sets [2] and rough sets [3]. These sets have some limitations so Molodtsov [4] initiated the new approach namely soft sets which is a new theory and has the ability to capture the uncertainty in a better way. After this many researchers used the idea of soft sets in many directions, such as Maji et al. [5], Maji et al. [6], Aktas and Cagman [7], and Jun et al. [8,9]. Maji et al. [10] initiated the study of fuzzy soft sets. After this many researcher used fuzzy soft sets such as, Roy et al. [11], Yang [12] and Kharal et al. [13]. Zhou et al. developed the idea of intutionistic fuzzy soft sets which extend the idea of fuzzy soft sets [14].

Another general version of fuzzy sets and intutionistic fuzzy sets was presented by Jun et al. [15] namely the cubic sets. After that jun et al. [16,17,18,19] applied cubic sets in different directions such as in BCK/BCI-algebras. Since then cubic sets were actively being used in many areas such as Akram et al. [20], in KU-subalgebras, Aslam et al. [21], in $\Gamma$-semihypergroups, Gulistan et al. [22], in weak left almost semihypergroups, Gulistan et al. [23], in regular LA-semihypergroups, Khan et al. [24], in LA-semihypergroups, Ma et al. [25], in H${}_v$-LA-semihypergroups, Yaqoob et al. [26], on cubic KU-ideals of KU-algebras, Yaqoob et al. [27], in cubic hyperideals in LA-semihypergroups. Khan et al. [28] presented the idea of the generalized version of Jun’s cubic sets in semigroups and several others like, Abughazalah and Yaqoob [29], Rashid et al. [30].

Recently, Yin and Zhan [31] introduced more general forms of $(\in ,\in \vee q)$-fuzzy filters and define $({\in }_{\gamma },{\in }_{\gamma }\vee q_{\delta })$-fuzzy filters and gave some interesting results in terms of these notions. See also [32,33,34].

On the other hand semigroups are the very useful associative algebraic structures which has many application in different directions. A very particular class of semigroups namely right weakly regular semigroups was discussed by Feng et al. [35] and Khan et al. in [36]. A valuable application of the group of symmetries can be see in network fibres by Mallat [37] in 2016.

Since we see that the idea of fuzzy soft sets and intutionistic fuzzy soft sets generalize the concept of soft sets so its natural to blend generalized cubic sets presented by Khan et al. in [28] with Molodtsov’s [4] soft sets and apply on the right weakly regular semigroups studied by Feng et al. [35] and Khan et al. [36]. Thus we initiate the study of special types of cubic soft ideals in semigroups with some interesting properties. We discuss some lattice structures formed by generalized cubic soft ideals of semigroups. We also provide an application of the current proposal and conclusion is given at the end.

2. Preliminaries

A semigroup S is called a right weakly regular if for every $a\in S$ there exist $x,y\in S$ such that $a=axay.$ To begin with the main section, we first give the following characterization results of right weakly regular semigroups by the properties of their ideals from the paper [35,36].

Theorem 1.

[35,36] For the semigroup S the following are equivalent;

(i)

S is right weakly regular.

(ii)

$R\cap I\subseteq RI$, where R is right ideal and I is interior ideal of S.

Theorem 2.

[35,36] For the semigroup S the following are equivalent;

(i)

S is right weakly regular.

(ii)

$B\cap I\subseteq BI$, where B is bi-ideal and I is interior ideal of S.

Theorem 3.

[35,36] For a semigroup S the following are equivalent;

(i)

S is right weakly regular.

(ii)

$R\cap B\cap I\subseteq RBI$ for every right ideal $R,$ bi-ideal B and interior ideal I of a semigroup S.

Definition 1.

[4,5] Let U be an initial universe, E be the sets of parameters, $P(U)$ be the power set of U and $A\subseteq E$, then the soft set$F_A$ over U is the function defined by, $F_A:E\to$ $P(U)$ such that $F_A(x)=\varphi$ if $x\notin A,$ where ϕ denote the empty set. Here $F_A$ is called approximate function. A soft set over U can be represented by the ordered pairs

$$F_A=\left\{\left(x,F_A(x)\right);x\in E,F_A(x)\in P(U)\right\}.$$

It shows that a soft set is a parameterized family of subsets of the set U.

Definition 2.

Jun et al. [15], Cubic set on a non-empty set X is an object of the form:

$$C=\{⟨x,{\tilde{\mu }}_C(x),{\nu }_C(x)⟩:x\in X\},$$

which is briefly denoted by $C=⟨{\tilde{\mu }}_C,{\nu }_C⟩,$ with the functions ${\tilde{\mu }}_C:X⟶D[0,1]$ and ${\nu }_C:X\to [0,1]$.

More detail about the soft sets, cubic sets and semigroups can be seen in [4,5,15,35,36].

3. Cubic Soft Sets

In this section, we introduce the concepts of cubic soft sets, cubic soft ideals and some basic operations on cubic sets.

Definition 3.

A pair $⟨C^S,A⟩$ is called a cubic soft set over S, where $A\subseteq E$ and $C^S$ is a mapping given by $C^S:A⟶C(S),$ where $C(S)$ denotes the set of all cubic sets of S and E be a set of parameters.

In general, for every $ϵ\in A,$ $C^S\left[ϵ\right]=⟨{\tilde{\mu }}_{C^S\left[ϵ\right]},{\nu }_{C^S\left[ϵ\right]}⟩$ is a cubic set in S and it is called cubic value set of parameter $ϵ.$

Definition 4.

A cubic soft set $⟨C_1^S,A⟩$ is contained in other cubic soft set $⟨C_2^S,B⟩$ if $A\subseteq B$ and for every $ϵ\in A,$ $C_1^S\left[ϵ\right]\subseteq C_2^S\left[ϵ\right].$

Equivalently $⟨C_1^S,A⟩⊑⟨C_2^S,B⟩$ if $A\subseteq B$ and ${\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)⪯{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)$, ${\nu }_{C_1^S\left[ϵ\right]}(x)\ge {\nu }_{C_2^S\left[ϵ\right]}(x)$ for all $x\in S.$

Definition 5.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. Then $⟨C_1^S,A⟩\wedge ⟨C_2^S,B⟩=⟨C_3^S,$ $A\times B⟩,$ where $C_3^S[ϵ,\kappa ]=C_1^S[ϵ]\sqcap C_2^S[\kappa ]$ for all $(ϵ,\kappa )\in A\times B,$ that is

$$C_3^S[ϵ,\kappa ]=⟨rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[\kappa \right]}(x)),max({\nu }_{C_1^S\left[ϵ\right]},{\nu }_{C_2^S\left[\kappa \right]})⟩$$

for all $(ϵ,\kappa )\in A\times B,$ $x\in S.$

Definition 6.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. Then $⟨C_1^S,A⟩\vee ⟨C_2^S,B⟩=⟨C_3^S,$ $A\times B⟩,$ where $C_3^S[ϵ,\kappa ]=C_1^S[ϵ]\cup C_2^S[\kappa ]$ for all $(ϵ,\kappa )\in A\times B,$ that is

$$C_3^S[ϵ,\kappa ]=⟨rmax({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[\kappa \right]}(x)),min({\nu }_{C_1^S\left[ϵ\right]},{\nu }_{C_2^S\left[\kappa \right]})⟩$$

for all $(ϵ,\kappa )\in A\times B,$ $x\in S.$

Definition 7.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. Then $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩=⟨C_3^S,$ $C⟩,$ where $C=A\cup B$ and for all $ϵ\in A,$ $x\in S,$

${\tilde{\mu }}_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x))\mathit{if}ϵ\in A\cap B,\end{array}\right.$

and

${\nu }_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\nu }_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\nu }_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ max({\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(x))\mathit{if}ϵ\in A\cap B.\end{array}\right.$

Definition 8.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. Then $⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩=⟨C_3^S,$ $C⟩,$ where $C=A\cup B$ and for all $ϵ\in A,$ $x\in S,$

${\tilde{\mu }}_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ rmax({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x))\mathit{if}ϵ\in A\cap B,\end{array}\right.$

and

${\nu }_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\nu }_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\nu }_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ min({\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(x))\mathit{if}ϵ\in A\cap B.\end{array}\right.$

Definition 9.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. Then $⟨C_1^S,A⟩\circ ⟨C_2^S,B⟩=⟨C_3^S,$ $C⟩,$ where $C=A\cup B$ and for all $ϵ\in C,$ $x\in S,$

${\tilde{\mu }}_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ {\displaystyle \underset{x=ab}{\bigvee }}rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(a),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(b))\mathit{if}ϵ\in A\cap B,\end{array}\right.$

and ${\nu }_{C_3^S\left[ϵ\right]}(x)=\left\{\begin{array}{c}{\nu }_{C_1^S\left[ϵ\right]}(x)\mathit{if}ϵ\in A-B\\ {\nu }_{C_2^S\left[ϵ\right]}(x)\mathit{if}ϵ\in B-A\\ {\displaystyle \underset{x=ab}{\bigwedge }}max({\nu }_{C_1^S\left[ϵ\right]}(a),{\nu }_{C_2^S\left[ϵ\right]}(b))\mathit{if}ϵ\in A\cap B.\end{array}\right.$

4. Generalized Cubic Soft Ideals of Semigroups

This section is dedicated to the concept of $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup, $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft ideals and their basic properties. Note that $\left({\tilde{\gamma }}_1,{\gamma }_2\right)=\Gamma$ and $\left({\tilde{\delta }}_1,{\delta }_2\right)=\Delta .$

Definition 10.

Let $\tilde{\alpha }\in D(0,1]$ and $\beta \in [0,1)$ such that $\tilde{0}\prec \tilde{\alpha }$ and $\beta <1.$ Then by cubic point $\left(\mathrm{CP}\right)$ we mean $x_{\left(\tilde{\alpha },\beta \right)}\left(y\right)=⟨x_{\tilde{\alpha }}\left(y\right),x_{\beta }\left(y\right)⟩$ where

$$x_{\tilde{\alpha }}\left(y\right)=\left\{\begin{array}{c}\tilde{\alpha },\mathit{if}x=y\\ \tilde{0}\mathit{otherwise}\end{array}\right.\mathit{and}{x}_{\beta }\left(y\right)=\left\{\begin{array}{c}0,\mathit{if}x=y\\ 1\mathit{otherwise}\end{array}\right..$$

For any cubic set $C=\left({\tilde{\mu }}_C,{\lambda }_C\right)$ and for a cubic point $x_{\left(\tilde{\alpha },\beta \right)},$ with the condition that $\left[\alpha ,\beta \right]+\left[\alpha ,\beta \right]=\left[2\alpha ,2\beta \right]$ such that $2\beta \le 1,$ we have

(i)

$x_{\left(\tilde{\alpha },\beta \right)}{\in }_{\Gamma }C$ if ${\tilde{\mu }}_C(x)⪰\tilde{\alpha }\succ {\tilde{\gamma }}_1$ and ${\lambda }_C\left(x\right)\le \beta <{\gamma }_2.$

(ii)

$x_{\left(\tilde{\alpha },\beta \right)}{q}_{\Delta }C$ if ${\tilde{\mu }}_C(x)+\tilde{\alpha }\succ 2{\tilde{\delta }}_1$ and ${\lambda }_C\left(x\right)+\beta <2{\delta }_2.$

(iii)

$x_{\left(\tilde{\alpha },\beta \right)}{\in }_{\Gamma }\vee q_{\Delta }C$ if $x_{\left(\tilde{\alpha },\beta \right)}{\in }_{\Gamma }C$ or $x_{\left(\tilde{\alpha },\beta \right)}{q}_{\Delta }C.$

Definition 11.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S,$ if

$$rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right),{\tilde{\delta }}_1\}$$

$$\mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}\le max\left\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(y\right),{\delta }_2\right\}.$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S,$ if

$$x_{\left(\widetilde{t_1},s_1\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right]\mathit{and}{y}_{\left(\widetilde{t_2},s_2\right)}{\in }_{\left(\widetilde{{\gamma }_2},{\gamma }_2\right)}{C}^S\left[ϵ\right]$$

implies that

$${\left(xy\right)}_{⟨min\left\{\widetilde{t_1},\widetilde{t_2}\right\},max\left\{s_1,s_2\right\}⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\delta }{C}^S\left[ϵ\right],$$

where ${\tilde{\delta }}_1$ and ${\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,{\gamma }_2\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_2.$

Example 1.

Let $S=\{1,2,3\}$ and the binary operation “·” be defined on S as follows:

$$\begin{array}{|cccc|}\hline \hfill ·& 1& 2\hfill & 3\\ \hfill 1& 1& 1\hfill & 1\\ \hfill 2& 1& 1\hfill & 1\\ \hfill 3& 1& 2\hfill & 1\\ \hline\end{array}$$

Then $(S,·)$ is a semigroup. Let ${\tilde{\gamma }}_1=\left[0.1,0.18\right]\prec {\tilde{\delta }}_1=\left[0.19,0.2\right]$ and ${\delta }_2=0.3<{\gamma }_2=0.4.$ Let $A=\{ϵ,\kappa \}$ be the set of parameters. For each parameter $ϵ\in A,$ $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of $S,$ where $C^S\left[ϵ\right]$ is a mapping given by $C^S\left[ϵ\right]:A⟶C(S).$ Then for each parameter we define

$$C^S\left[ϵ\right]=\{⟨1,\left[0.2,0.3\right],0.1⟩,⟨2,\left[0.3,0.4\right],0.2⟩,⟨3,\left[0.4,0.5\right],0.3⟩\}$$

and

$$C^S\left[\kappa \right]=\{⟨1,\left[0.21,0.32\right],0.12⟩,⟨2,\left[0.32,0.41\right],0.21⟩,⟨3,\left[0.41,0.55\right],0.32⟩\}.$$

Hence $⟨C^S,A⟩$ is an $({\in }_{\left(\left[0.1,0.18\right],0.4\right)},{\in }_{\left(\left[0.1,0.18\right],0.4\right)}\vee q_{\left(\left[0.19,0.2\right],0.3\right)})$-cubic soft subsemigroup of $S.$

Definition 12.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft left ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic left ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft left ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}& ⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right),{\tilde{\delta }}_1\}\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}& \le max\{{\nu }_{C^S\left[ϵ\right]}\left(y\right),{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft left ideal of $S,$ if $x_{\left(\tilde{t},s\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ and $y\in S$ implies that ${\left(yx\right)}_{⟨\tilde{t},s⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\delta }{C}^S\left[ϵ\right],$ where ${\tilde{\delta }}_1$ and ${\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,{\gamma }_1\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 13.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic right ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}& ⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\delta }}_1\}\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}& \le max\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal of $S,$ if $x_{\left(\tilde{t},s\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ and $y\in S$ implies that ${\left(xy\right)}_{⟨\tilde{t},s⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\delta }{C}^S\left[ϵ\right],$ where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$ and ${\delta }_2,{\gamma }_1\in$ $\left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 14.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}& ⪰rmin\{rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right)\},{\tilde{\delta }}_1\},\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}& \le max\{min\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(y\right)\},{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft ideal of $S,$ if $x_{\left(\tilde{t},s\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ and $y\in S$ implies that ${\left(xy\right)}_{⟨\tilde{t},s⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\Delta }{C}^S\left[ϵ\right]$ and ${\left(yx\right)}_{⟨\tilde{t},s⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\delta }{C}^S\left[ϵ\right]$, where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,$ ${\gamma }_1\in$ $\left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 15.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft bi ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic bi ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft bi ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}& ⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right),{\tilde{\delta }}_1\}\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}& \le max\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(y\right),{\delta }_2\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xyz\right),{\tilde{\gamma }}_1\}& ⪰rmin\{rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(z\right)\},{\tilde{\delta }}_1\},\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xyz\right),{\gamma }_2\}& \le max\{min\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(z\right)\},{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft bi ideal of $S,$ if $(1)$ $⟨C^S,A⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S, $(2)x_{\left(\widetilde{t_1},s_1\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ $z_{\left(\widetilde{t_2},s_2\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right]$ and $y\in S$ implies that ${\left(xyz\right)}_{⟨rmin\{{\tilde{t}}_1,{\tilde{t}}_2\},max\{s_1,s_2\}⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\Delta }{C}^S\left[ϵ\right]$, where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,{\gamma }_1\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 16.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic generalized bi ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xyz\right),{\tilde{\gamma }}_1\}& ⪰rmin\{rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(z\right)\},{\tilde{\delta }}_1\},\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xyz\right),{\gamma }_2\}& \le max\{min\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(z\right)\},{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi ideal of $S,$ if $x_{\left(\widetilde{t_1},s_1\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ $z_{\left(\widetilde{t_2},s_2\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right]$ and $y\in S$ implies that ${\left(xyz\right)}_{⟨rmin\{{\tilde{t}}_1,{\tilde{t}}_2\},max\{s_1,s_2\}⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\Delta }{C}^S\left[ϵ\right]$, where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,$ ${\gamma }_1\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 17.

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal of $S,$ if $C^S\left[ϵ\right]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic interior ideal of $S.$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal of $S,$ if

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xy\right),{\tilde{\gamma }}_1\}& ⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(x\right),{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right),{\tilde{\delta }}_1\}\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xy\right),{\gamma }_2\}& \le max\{{\nu }_{C^S\left[ϵ\right]}\left(x\right),{\nu }_{C^S\left[ϵ\right]}\left(y\right),{\delta }_2\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(xyz\right),{\tilde{\gamma }}_1\}& ⪰rmin\{rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}\left(y\right)\},{\tilde{\delta }}_1\},\hfill \\ \hfill \mathit{and}min\{{\nu }_{C^S\left[ϵ\right]}\left(xyz\right),{\gamma }_2\}& \le max\{min\{{\nu }_{C^S\left[ϵ\right]}\left(y\right)\},{\delta }_2\}.\hfill \end{array}$$

Equivalently;

A cubic soft set $⟨C^S,A⟩$ of S is called an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal of $S,$ if $(1)$ $⟨C^S,A⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S, $(2)$ $y_{\left(\tilde{t},s\right)}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}{C}^S\left[ϵ\right],$ and $x,z\in S$ implies that ${\left(xyz\right)}_{⟨t,s⟩}{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\Delta }{C}^S\left[ϵ\right]$, where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,$ ${\gamma }_1\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_1.$

Definition 18.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two cubic soft sets over S. We say that $⟨C_1^S,A⟩$ is an $(\left({\tilde{\gamma }}_1,{\gamma }_1\right),({\tilde{\delta }}_1,{\delta }_2))$-cubic soft subset of $⟨C_2^S,B⟩$ and write $⟨C_1^S,A⟩⊑{\vee }_{\left(\Gamma ,\Delta \right)}⟨C_2^S,B⟩$ if $(i)A\subseteq B.$

$(ii)$ for each $ϵ\in A,$ $C_1^S[ϵ]\subseteq {\vee }_{\left(\Gamma ,\Delta \right)}{C}_2^S[ϵ].$

Theorem 4.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroups of $S.$ Then

(i)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S.

(ii)

$⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S.

(iii)

$⟨C_1^S,A⟩\wedge ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$

(iv)

$⟨C_1^S,A⟩\vee ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$

(v)

$⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$

Proof. 

$\left(i\right)$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroups of S. Let $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩=⟨C_3^S,C⟩,$ where $C=A\cup B$ and for all $ϵ\in C,$ $x,y\in S.$ We consider the following cases.

Case 1: If $ϵ\in A-B,$ then

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\}\hfill \\ & =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\hfill \\ & ⪰rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & =rmin\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}}(x),\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}}(y),{\tilde{\delta }}_1\}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(xy),{\gamma }_2\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2]\hfill \\ & \le min\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(y),{\delta }_2\}.\hfill \end{array}$$

Case 2: Similar to case 1.

Case 3: Let $ϵA\cap B$ and consider

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy)\},{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{rmin\{\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\},\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\}\}\hfill \\ & =rmax\{\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}rmin\{rmax\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\}\}\hfill \\ & ⪰\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}rmin\{rmin\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & =\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x),{\tilde{\delta }}_1\}\}rmin\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & =rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(x),\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}.\hfill \end{array}$$

On the other hand consider

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(xy),{\gamma }_2\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\nu }_{C_2^S\left[ϵ\right]}(xy)\},{\gamma }_2\}\hfill \\ & =min\{min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2\},min\{{\nu }_{C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\}\hfill \\ & \le min\{max\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\},max\{{\nu }_{C_2^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(y),{\delta }_2\}\}\hfill \\ & =max\{{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]\sqcap C_2^S\left[ϵ\right]}(y),{\delta }_2\}.\hfill \end{array}$$

Hence $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S.

$\left(ii\right)$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$ Let $⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩=⟨C_3^S,C⟩.$ We consider the following cases.

Case 1: If $ϵ\in A-B,$ then

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & ⪰rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\hfill \\ & =rmin\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}}(x),\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}}(y),{\tilde{\delta }}_1\}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(xy),{\gamma }_2\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & \le min\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(x),{\nu }_{{}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}}(y),{\delta }_2\}.\hfill \end{array}$$

Case 2: Similar to case 1.

Case 3: Let $ϵA\cap B$ and consider

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy)\},{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{rmax\{\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\},\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\}\}\hfill \\ & =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}rmax\{rmax\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\}\hfill \\ & ⪰\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}rmax\{rmin\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & =\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x),{\tilde{\delta }}_1\}\}rmax\{rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & =rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(x),\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}.\hfill \end{array}$$

On the other hand consider

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(xy),{\gamma }_2\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{max\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\nu }_{C_2^S\left[ϵ\right]}(xy)\},{\gamma }_2\}\hfill \\ & =max\{min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2\},min\{{\nu }_{C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\}\hfill \\ & \le max\{max\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\},max\{{\nu }_{C_2^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(y),{\delta }_2\}\}\hfill \\ & =max\{{\nu }_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]\bigsqcup C_2^S\left[ϵ\right]}(y),{\delta }_2\}.\hfill \end{array}$$

$\left(iii\right)$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S and let $⟨C_1^S,A⟩\wedge ⟨C_2^S,B⟩=⟨C_3^S,C⟩,$ where $C=A\times B$ and $C_3^S[\left(ϵ,\kappa \right)]=C_1^S[ϵ]\sqcap C_2^S[\kappa ]$ for all $(ϵ,\kappa )\in A\times B,$ that is

$$C_3^S[\left(ϵ,\kappa \right)]=⟨rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)),max({\nu }_{C_1^S\left[ϵ\right]},{\nu }_{C_2^S\left[ϵ\right]})⟩$$

for all $(ϵ,\kappa )\in A\times B,$ $x\in S.$ Since $C_1^S[ϵ]$ and $C_2^S[\kappa ]$ are $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of $S,$ so by part (i) $C_3^S[\left(ϵ,\kappa \right)]=C_1^S[ϵ]\sqcap C_2^S[\kappa ]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of S for all $(ϵ,\kappa )\in A\times B.$ Hence $⟨C_1^S,A⟩\wedge ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$

$\left(iv\right)$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S and let $⟨C_1^S,A⟩\vee ⟨C_2^S,B⟩=⟨C_3^S,A\times B⟩,$ where $C_3^S[ϵ,\kappa ]=C_1^S[ϵ]\bigsqcup C_2^S[\kappa ]$ for all $(ϵ,\kappa )\in A\times B,$ that is

$$C_3^S[ϵ,\kappa ]=⟨rmax({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)),min({\nu }_{C_1^S\left[ϵ\right]},{\nu }_{C_2^S\left[ϵ\right]})⟩$$

for all $(ϵ,\kappa )\in A\times B,$ $x\in S.$ Since $C_1^S[ϵ]$ and $C_2^S[\kappa ]$ are $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of $S,$ so by part (ii) $C_3^S[\left(ϵ,\kappa \right)]=C_1^S[ϵ]\bigsqcup C_2^S[\kappa ]$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of S for all $(ϵ,\kappa )\in A\times B.$ Hence $⟨C_1^S,A⟩\vee ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$

$\left(v\right)$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S,$ and let $⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩=⟨C_3^S,C⟩,$ where $C=A\cup B$ and for all $ϵ\in C,$ $x,y\in S.$ We consider the following cases.

Case 1: If $ϵ\in A-B,$ then

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1]\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & ⪰rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\hfill \\ & =rmin\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(x),\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(y),{\tilde{\delta }}_1\}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(xy),{\gamma }_2\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2]\hfill \\ & \le min\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(y),{\delta }_2\}.\hfill \end{array}$$

Case 2: Similar to case one.

Case 3: Let $ϵA\cap B$ and consider

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C_3^S\left[ϵ\right]}(ab),{\tilde{\gamma }}_1]\}& =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(ab),{\tilde{\gamma }}_1]\}\hfill \\ & ={\displaystyle \underset{ab=xyxy}{\bigvee }}rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}{\displaystyle \underset{ab=xyxy}{\bigvee }}rmax\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\hfill \\ & ⪰rmin\{{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_1^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}{\displaystyle \underset{ab=xyxy}{\bigvee }}rmin\{{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & ={\displaystyle \underset{ab=xyxy}{\bigvee }}rmin\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(xy),{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\circ C_2^S\left[ϵ\right]}}(xy),{\tilde{\delta }}_1\}\}\hfill \\ & =rmin\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(a),{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(b),{\tilde{\delta }}_1\}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill min\{{\nu }_{C_3^S\left[ϵ\right]}(ab),{\gamma }_2]\}& =min\{{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(ab),{\gamma }_2]\}\hfill \\ & ={\displaystyle \underset{ab=xyxy}{\bigwedge }}min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\nu }_{C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & =min\{{\nu }_{C_1^S\left[ϵ\right]}(xy),{\gamma }_2\}{\displaystyle \underset{ab=xyxy}{\bigwedge }}min\{{\nu }_{C_2^S\left[ϵ\right]}(xy),{\gamma }_2\}\hfill \\ & \le max\{{\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_1^S\left[ϵ\right]}(y),{\delta }_2\}{\displaystyle \underset{ab=xyxy}{\bigwedge }}max\{{\nu }_{C_2^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(y),{\delta }_2\}\hfill \\ & ={\displaystyle \underset{ab=xyxy}{\bigwedge }}max\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(xy),{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(xy),{\tilde{\delta }}_1\}\}\hfill \\ & =max\{{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(a),{\tilde{\mu }}_{{}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}}(b),{\tilde{\delta }}_1\}\}.\hfill \end{array}$$

Hence $⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of $S.$ □

Theorem 5.

Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be two $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft (resp., left, right, bi, interior, generalized bi) ideals of $S,$ then

(i)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft (resp., left, right, bi, interior, generalized bi) ideal of S.

(ii)

$⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic (resp., left, right, bi, interior, generalized bi) ideal of S.

(iii)

$⟨C_1^S,A⟩\wedge ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic (resp., left, right, bi, interior, generalized bi) ideal of $S.$

(iv)

$⟨C_1^S,A⟩\vee ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic (resp., left, right, bi, interior, generalized bi) ideal of $S.$

(v)

$⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic (resp., left, right, bi, interior, generalized bi) ideal of $S.$

Proof. 

It follows from the proof of Theorem 4. □

Theorem 6.

Let $⟨C^S,A⟩$ be a-cubic soft set of $S.$ Then $⟨C^S,A⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S if and only if

$${⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)}=\{{\tilde{\mu }}_{C^S[ϵ]}\left(x\right)⪰{\tilde{t}}_1\succ \tilde{0},{\nu }_{{}_{C^S[ϵ]}}\left(x\right)\le t_2<1\}$$

is soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of $S.$

Proof. 

Let $⟨C^S,A⟩$ be an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S. Let ${\tilde{t}}_1,{\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D[0,1]$, $t_2,{\delta }_2,{\gamma }_2\in [0,1]$ such that ${\tilde{\gamma }}_1\prec {\tilde{t}}_1\prec {\tilde{\delta }}_1,$ ${\gamma }_2<t_2<{\delta }_2,$ $ϵ\in A$ and let $x,y\in {⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)}.$ This implies

$$\begin{array}{cc}\hfill \{{\tilde{\mu }}_{C^S[ϵ]}\left(x\right)& ⪰{\tilde{t}}_1\succ \tilde{0},{\nu }_{{}_{C^S[ϵ]}}\left(x\right)\le t_2<1\}\hfill \\ \hfill \mathrm{and}\{{\tilde{\mu }}_{C^S[ϵ]}\left(y\right)& ⪰{\tilde{t}}_1\succ \tilde{0},{\nu }_{{}_{C^S[ϵ]}}\left(y\right)\le t_2<1\}.\hfill \end{array}$$

Now by hypothesis

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}& ⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(x),\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}\hfill \\ & ⪰rmin\{{\tilde{t}}_1,{\tilde{t}}_1,{\tilde{\delta }}_1\}⪰{\tilde{t}}_1.\hfill \end{array}$$

This implies that ${\tilde{\mu }}_{C^S\left[ϵ\right]}(xy)⪰{\tilde{t}}_1.$ On the other hand again using the hypothesis

$$\begin{array}{cc}\hfill min\{{\nu }_{C^S\left[ϵ\right]}(xy),{\gamma }_2\}& \le max\{{\nu }_{C^S\left[ϵ\right]}(x),{\nu }_{C^S\left[ϵ\right]}(y),{\delta }_2\}\hfill \\ & \le max\{t_2,t_2,{\delta }_2\}\le t_2.\hfill \end{array}$$

This implies that ${\nu }_{C^S\left[ϵ\right]}(xy)\le t_2.$ Thus we get

$$\{{\tilde{\mu }}_{C^S[ϵ]}\left(xy\right)⪰{\tilde{t}}_1\succ \tilde{0},{\nu }_{{}_{C^S[ϵ]}}\left(xy\right)\le t_2<1\},$$

which implies that $xy\in {⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)}.$ Hence ${⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)}$ is a soft subsemigroup of $S.$ Conversely let ${⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)}$ is a soft subsemigroup of $S.$ Suppose there exist ${\tilde{t}}_1,{\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D[0,1]$, $t_2,{\delta }_2,{\gamma }_2\in [0,1]$ with

$${\tilde{\delta }}_1\prec {\tilde{t}}_1\prec {\tilde{\gamma }}_1,{\delta }_2<t_2<{\gamma }_2$$

such that

$$rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}\prec {\tilde{t}}_1⪯rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(x),\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}$$

and

$$min\{{\nu }_{C^S\left[ϵ\right]}(xy),{\gamma }_2\}>t_2\ge max\{{\nu }_{C^S\left[ϵ\right]}(x),{\nu }_{C^S\left[ϵ\right]}(y),{\delta }_2\}.$$

This implies that $xy\notin {⟨C^S,A⟩}^{\left({\tilde{t}}_1,t_2\right)},$ which is contradiction. So

$$rmax\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(xy),{\tilde{\gamma }}_1\}⪰rmin\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(x),\{{\tilde{\mu }}_{C^S\left[ϵ\right]}(y),{\tilde{\delta }}_1\}\}$$

and

$$min\{{\nu }_{C^S\left[ϵ\right]}(xy),{\gamma }_2\}\le max\{{\nu }_{C^S\left[ϵ\right]}(x),{\nu }_{C^S\left[ϵ\right]}(y),{\delta }_2\}.$$

Hence $⟨C^S,A⟩$ is an $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft subsemigroup of S. □

Lemma 1.

Let $\varnothing \ne A\subseteq S,$ then A is a subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S if and only if cubic characteristic function ${\chi }_{\Gamma }^{\delta }A=⟨{\tilde{\mu }}_{{\chi }_{\Gamma }^{\Delta }A},{\nu }_{{\chi }_{\Gamma }^{\Delta }A}⟩$ of $A=⟨{\tilde{\mu }}_A,{\nu }_A⟩$ is an $({\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)},{\in }_{\left({\tilde{\gamma }}_1,{\gamma }_1\right)}\vee q_{\Delta })$-cubic soft subsemigroup (resp., left, right, bi, interior, generalized bi) ideal of S, where ${\tilde{\delta }}_1,{\tilde{\gamma }}_1\in D(0,1]$ such that ${\tilde{\gamma }}_1<{\tilde{\delta }}_1$, and ${\delta }_2,{\gamma }_2\in \left[0,1\right]$ such that ${\delta }_2<{\gamma }_2.$

Proof. 

Straightforward.

where set of all cubic soft ideals of S is denoted by $C(\Xi ,A).$ □

Theorem 7.

$(C(\Xi ,A),\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)},\bigsqcup ,\sqcap )$ forms the lattice structure, where $C(\Xi ,A)$ is the set of all cubic soft ideals of $S.$

Proof. 

It is obvious that $\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}$ is an ordered relation. Let $⟨C_1^S,A⟩$, $⟨C_2^S,B⟩\in C(\Xi ,A),$ then by Theorem 5$⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩,$ $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\in C(\Xi ,A).$ It is clear that $⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩$ is the least upper bound and $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩$ is the greatest lower bound of any two arbitrary elements $⟨C_1^S,A⟩,$ $⟨C_2^S,B⟩$ of $C(\Xi ,A).$ Hence the set $C(\Xi ,A)$ of $S,$ becomes a lattice. □

Theorem 8.

Let S be a semigroup with identity e such that ${\tilde{\mu }}_{C_1^S\left[ϵ\right]}(e)=\tilde{1}$ and ${\tilde{\mu }}_{C_2^S\left[ϵ\right]}(e)=0.$ Then $(C(\Xi ,A),\subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}},\ast ,\sqcap )$ forms the lattice structure.

Proof. 

It is obvious that $\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}$ is an ordered relation. Let $⟨C_1^S,A⟩$, $⟨C_2^S,B⟩\in C(\Xi ,A),$ then by Theorem 5$⟨C_1^S,A⟩\bigsqcup ⟨C_2^S,B⟩,$ $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\in C(\Xi ,A).$ It is clear that $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩$ is the greatest lower bound of any two arbitrary elements $⟨C_1^S,A⟩,$ $⟨C_2^S,B⟩$ of $C(\Xi ,A).$ Now we will show that $⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ is the least upper bound of any two arbitrary elements $⟨C_1^S,A⟩,$ $⟨C_2^S,B⟩$ of $C(\Xi ,A).$ For this let $\zeta \in A$ and $x\in S.$

Case1: If $\zeta \in A-B,$ then

$${\tilde{\mu }}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)={\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)\mathit{and}{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)={\nu }_{C_1^S\left[ϵ\right]}(x).$$

Case2: If $\zeta \in B-A,$ then

$${\tilde{\mu }}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)={\tilde{\mu }}_{C_2^S\left[ϵ\right]}(x)\mathit{and}{\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)={\nu }_{C_2^S\left[ϵ\right]}(x).$$

Case3: If $\zeta \in A\cap B,$ then

$$\begin{array}{cc}\hfill {\tilde{\mu }}_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)& ={\displaystyle \underset{x=ab}{\bigvee }}rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(a),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(b))\hfill \\ & ⪰rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(e))={\tilde{\mu }}_{C_1^S\left[ϵ\right]}(x)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\nu }_{C_1^S\left[ϵ\right]\ast C_2^S\left[ϵ\right]}(x)& ={\displaystyle \underset{x=ab}{\bigwedge }}max({\nu }_{C_1^S\left[ϵ\right]}(a),{\nu }_{C_2^S\left[ϵ\right]}(b))\hfill \\ & ⪰rmin({\nu }_{C_1^S\left[ϵ\right]}(x),{\nu }_{C_2^S\left[ϵ\right]}(e))={\nu }_{C_1^S\left[ϵ\right]}(x),\hfill \end{array}$$

and so

$$⟨C_1^S,A⟩\subseteq ⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩.$$

Similarly

$$⟨C_2^S,B⟩\subseteq ⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩.$$

Let $⟨C_3^S,C⟩$ be any other element of $C(\Xi ,A)$ such that

$$⟨C_1^S,A⟩\subseteq ⟨C_3^S,C⟩\mathit{and}⟨C_2^S,B⟩\subseteq ⟨C_3^S,C⟩,$$

then

$$⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩\subseteq ⟨C_3^S,C⟩\ast ⟨C_3^S,C⟩\subseteq ⟨C_3^S,C⟩.$$

Hence least upper bound of $⟨C_1^S,A⟩$, $⟨C_2^S,B⟩$ is $⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩.$ Hence the $(C(\Xi ,A),\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)},\ast ,\sqcap )$ forms the lattice structure. □

Remark 1.

In the case when the semigroup S is regular Theorems 7 and 8 concide with each other.

5. Characterizations of Right Weakly Regular Semigroups in Terms of Generalized Cubic Soft Ideals

Based on the useful results obtained above taken from the paper [36], we now characterize right weakly regular semigroups by the properties of their $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft ideals, $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft (generalized) bi-ideals and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideals.

Theorem 9.

For a semigroup S the following conditions are equivalent.

(i)

S is right weakly regular.

(ii)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_2^S,B⟩$ of S.

Proof. 

$\left(i\right)\Rightarrow \left(ii\right):$ Let $⟨C_1^S,A⟩$ and $⟨C_2^S,B⟩$ be $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic interior ideal of S. Here we discuss three different cases.

Case 1: $\kappa \in A\setminus B$. Then${\tilde{\mu }}_{C_1^S(\kappa )}\left(a\right)={\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}\left(a\right)$ and ${\nu }_{C_1^S(\kappa )}\left(a\right)={\nu }_{(C_1^S\circ C_2^S)(\kappa )}\left(a\right)$.

Case 2: $\kappa \in B\setminus A$. Then ${\tilde{\mu }}_{C_2^S(\kappa )}\left(a\right)={\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}\left(a\right)$ and ${\nu }_{C_2^S(\kappa )}\left(a\right)={\nu }_{(C_1^S\circ C_2^S)(\kappa )}\left(a\right)$.

Case 3: $\kappa \in A\cap B$. Then

$${\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}=rmin\{{\tilde{\mu }}_{C_1^S(\kappa )},{\tilde{\mu }}_{C_2^S(\kappa )}\},{\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}=max\{{\nu }_{C_1^S(\kappa )},{\nu }_{C_2^S(\kappa )}\}$$

and

$$\begin{array}{cc}\hfill {\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}& ={\tilde{\mu }}_{C_1^S(\kappa )}\circ {\tilde{\mu }}_{C_2^S(\kappa )}={\displaystyle \underset{x=ab}{\bigvee }}rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(a),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(b)),\hfill \\ \hfill {\nu }_{(C_1^S\circ C_2^S)(\kappa )}& ={\nu }_{C_1^S(\kappa )}\circ {\tilde{\mu }}_{C_2^S(\kappa )}={\displaystyle \underset{x=ab}{\bigwedge }}max({\nu }_{C_1^S\left[ϵ\right]}(a),{\nu }_{C_2^S\left[ϵ\right]}(b)).\hfill \end{array}$$

Now we show that ${\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}{⪯}_{(\Gamma ,\Delta )}{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}$ and ${\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}{\ge }_{(\Gamma ,\Delta )}{\nu }_{(C_1^S\circ C_2^S)(\kappa )}$. Since S is right weakly regular, then for each $a\in S$ there exist $x,y\in S$ such that $a=axay=axaxayy$, so we have

$$\begin{array}{cc}\hfill rmax\left\{{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}(a),{\tilde{\gamma }}_1\right\}& =rmax\{{\displaystyle \underset{a=rp}{\bigvee }}rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(r\right),{\tilde{\mu }}_{C_2^S(\kappa )}(p)\right\},{\tilde{\gamma }}_1\}\hfill \\ & =rmax\{\underset{a=(ax)(axayy)}{{\displaystyle \bigvee }}rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\mu }}_{C_2^S(\kappa )}(axayy)\right\},{\tilde{\gamma }}_1\}\hfill \\ & ⪰rmax\{rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\mu }}_{C_2^S(\kappa )}(axayy)\right\},{\tilde{\gamma }}_1\}\hfill \\ & =rmax\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\gamma }}_1\right\}\sqcap \{rmax\left\{{\tilde{\mu }}_{C_2^S(\kappa )}(axayy),{\tilde{\gamma }}_1\right\}\}\hfill \\ & ⪰rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(a\right),{\tilde{\delta }}_1\right\}\sqcap \{rmin\left\{{\tilde{\mu }}_{C_2^S(\kappa )}(a),{\tilde{\delta }}_1\right\}\}\hfill \\ & =rmin\left\{{\tilde{\mu }}_{(C_1^S\sqcap C_2^S)(\kappa )}(a),{\tilde{\delta }}_1\right\},\hfill \end{array}$$

so ${\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}{⪯}_{(\Gamma ,\Delta )}{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )}.$ On the other hand

$$\begin{array}{cc}\hfill min\{{\nu }_{{}_{(C_1^S\circ C_2^S)(\kappa )}}(a),{\gamma }_2\}& =min\{{\displaystyle \underset{a=rp}{\bigwedge }}max\{{\nu }_{C_1^S(\kappa )}(r),{\nu }_{C_2^S(\kappa )}(p)\},{\gamma }_2\}\hfill \\ & =min\{{\displaystyle \underset{a=(ax)(axayy)}{\bigwedge }}max\{{\nu }_{C_1^S(\kappa )}(ax),{\nu }_{C_2^S(\kappa )}(axayy)\},{\gamma }_2\}\hfill \\ & \le min\{\{max\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\},max\{{\nu }_{C_2^S\left[ϵ\right]}(axayy),{\gamma }_2\}\}\hfill \\ & =max\{min\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\},\{min\{{\nu }_{C_2^S\left[ϵ\right]}(axayy)\},{\gamma }_2\}\}\hfill \\ & \le max\{max\{{\nu }_{C_1^S\left[ϵ\right]}(a),{\delta }_2\},max\{{\nu }_{C_2^S\left[ϵ\right]}(a),{\delta }_2\}\}\hfill \\ & =max\{{\nu }_{(C_1^S\sqcap C_2^S)(\kappa )}(a),{\delta }_2\},\hfill \end{array}$$

hence ${\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa ))}{\ge }_{(\Gamma ,\Delta )}{\nu }_{(C_1^S\circ C_2^S)(\kappa )}.$ Thus $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_2^S,B⟩$ of S.

$(ii)\Rightarrow (i)$ Let $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_2^S,B⟩$ of S. Assume that $C_1^S$ and $C_2^S$ are right and interior ideals of $S,$ then by Lemma 1, ${\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩$ and ${\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩$ are $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal of S. So by hypothesis we have

$${\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}{\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\ast {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩.$$

Hence

$$\begin{array}{cc}\hfill {\chi }_{\Gamma }^{\Delta }⟨C_1^S\sqcap C_2^S,C⟩& {=}_{{}_{(\Gamma ,\Delta )}}{\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\hfill \\ & \subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}{\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\ast {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\hfill \\ & {=}_{{}_{(\Gamma ,\Delta )}}⟨C_1^S\circ C_2^S,C⟩.\hfill \end{array}$$

Thus $C_1^S\sqcap C_2^S\subseteq C_1^S\circ C_2^S.$ Hence S is right weakly regular by Theorem 1. □

Theorem 10.

For a semigroup S the following conditions are equivalent.

(i)

S is right weakly regular.

(ii)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft bi ideal $⟨C_1^S,A⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_2^S,B⟩$ of S.

Proof. 

Straightforward. □

Theorem 11.

For a semigroup S, the following conditions are equivalent.

(i)

S is right weakly regular.

(ii)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\sqcap ⟨C_3^S,C⟩\subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩\ast ⟨C_3^S,C⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩,$ $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft bi-ideal $⟨C_2^S,B⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_3^S,C⟩$ of S.

(iii)

$⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\sqcap ⟨C_3^S,C⟩\subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩\ast ⟨C_3^S,C⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩,$ $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi-ideal $⟨C_2^S,B⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_3^S,C⟩$ of S.

Proof. 

$(i)\Rightarrow (iii):$ Let $⟨C_1^S,A⟩,$ $⟨C_2^S,B⟩$ and $⟨C_3^S,C⟩$ be any $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic right ideal, $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic generalized bi-ideal and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic interior ideal of S. Here we discuss different cases.

Case 1: $\kappa \in A\setminus B\cap C$. Then${\tilde{\mu }}_{C_1^S(\kappa )}\left(a\right)={\tilde{\mu }}_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$ and ${\nu }_{C_1^S(\kappa )}\left(a\right)={\nu }_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$.

Case 2: $\kappa \in B\setminus A\cap C$. Then ${\tilde{\mu }}_{C_2^S(\kappa )}\left(a\right)={\tilde{\mu }}_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$ and ${\nu }_{C_2^S(\kappa )}\left(a\right)={\nu }_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$.

Case 3: $\kappa \in C\setminus A\cap B$. Then ${\tilde{\mu }}_{C_3^S(\kappa )}\left(a\right)={\tilde{\mu }}_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$ and ${\nu }_{C_3^S(\kappa )}\left(a\right)={\nu }_{(C_1^S\circ C_2^S\circ C_3^S)(\kappa )}\left(a\right)$.

Case 4: $\kappa \in A\cap B\cap C$. Then

$$\begin{array}{cc}\hfill {\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}& =rmin\{{\tilde{\mu }}_{C_1^S(\kappa )},{\tilde{\mu }}_{C_2^S(\kappa )},{\tilde{\mu }}_{C_3^S(\kappa )}\},\hfill \\ \hfill {\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}& =max\{{\nu }_{C_1^S(\kappa )},{\nu }_{C_2^S(\kappa )},{\nu }_{C_3^S(\kappa )}\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}& =({\tilde{\mu }}_{C_1^S(\kappa )}\circ {\tilde{\mu }}_{C_2^S(\kappa )})\circ {\tilde{\mu }}_{C_2^S(\kappa )}={\displaystyle \underset{x=ab}{\bigvee }}rmin({\tilde{\mu }}_{C_1^S\left[ϵ\right]}(a),{\tilde{\mu }}_{C_2^S\left[ϵ\right]}(b))\circ {\tilde{\mu }}_{C_2^S(\kappa )},\hfill \\ \hfill {\nu }_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}& =({\nu }_{C_1^S(\kappa )}\circ {\nu }_{C_2^S(\kappa )})\circ {\nu }_{C_3^S(\kappa )}={\displaystyle \underset{x=ab}{\bigwedge }}max({\nu }_{C_1^S\left[ϵ\right]}(a),{\nu }_{C_2^S\left[ϵ\right]}(b))\circ {\nu }_{C_3^S(\kappa )}.\hfill \end{array}$$

Now we show that

$${\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}{⪯}_{(\Gamma ,\Delta )}{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}$$

and

$${\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}{\ge }_{(\Gamma ,\Delta )}{\nu }_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}.$$

Since S is right weakly regular therefore for each $a\in S$ there exists $x,y\in S$ such that

$$a=axay=(axay)(xay)=(ax)(ay)(xay)=(ax)(axayy)(xay)=(ax)(axa)(yyxay).$$

So we have

$$\begin{array}{cc}\hfill rmax\{{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}(a),{\tilde{\gamma }}_1\}& =rmax\{{\displaystyle \underset{a=rp}{\bigvee }}rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(r\right),{\tilde{\mu }}_{C_2^S(\kappa )\circ C_3^S(\kappa )}(p)\right\},{\tilde{\gamma }}_1\}\hfill \\ & ⪰rmax\{rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\mu }}_{C_2^S(\kappa )\circ C_3^S(\kappa )}((axa)(yyxay))\right\},{\tilde{\gamma }}_1\}\hfill \\ & =rmax\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\gamma }}_1\right\}\sqcap \{rmax\left\{{\tilde{\mu }}_{C_2^S(\kappa )\circ C_3^S(\kappa )}((axa)(yyxay)),{\tilde{\gamma }}_1\right\}\}\hfill \\ & =rmax\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\gamma }}_1\right\}\sqcap \{rmax\{{\displaystyle \underset{(axa)(yyxay)=bc}{\bigvee }}rmin\{{\tilde{\mu }}_{C_2^S(\kappa )}(b),{\tilde{\mu }}_{C_3^S(\kappa )}(c)\},{\tilde{\gamma }}_1\}\}\hfill \\ & =rmax\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\gamma }}_1\right\}\hfill \\ & \sqcap \{rmax\{{\displaystyle \underset{(axa)(yyxay)=bc}{\bigvee }}rmin\{{\tilde{\mu }}_{C_2^S(\kappa )}(axa),{\tilde{\mu }}_{C_3^S(\kappa )}(yyxay)\},{\tilde{\gamma }}_1\}\}\hfill \\ & ⪰rmax\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(ax\right),{\tilde{\gamma }}_1\right\}\sqcap rmax\left\{{\tilde{\mu }}_{C_2^S(\kappa )}\left(axa\right),{\tilde{\gamma }}_1\right\}\sqcap rmax\left\{{\tilde{\mu }}_{C_3^S(\kappa )}\left(yyxay\right),{\tilde{\gamma }}_1\right\}\hfill \\ & ⪰rmin\left\{{\tilde{\mu }}_{C_1^S(\kappa )}\left(a\right),{\tilde{\delta }}_1\right\}\sqcap \{rmin\left\{{\tilde{\mu }}_{C_2^S(\kappa )}(a),{\tilde{\delta }}_1\right\}\}\sqcap \{rmin\left\{{\tilde{\mu }}_{C_3^S(\kappa )}(a),{\tilde{\delta }}_1\right\}\}\hfill \\ & =rmin\left\{{\tilde{\mu }}_{{}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}}(a),{\tilde{\delta }}_1\right\},\hfill \end{array}$$

so ${\tilde{\mu }}_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}{⪯}_{(\Gamma ,\delta )}{\tilde{\mu }}_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}.$ On the other hand consider

$$\begin{array}{cc}\hfill min\{{\nu }_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}(a),{\gamma }_2\}& =min\{{\displaystyle \underset{a=rp}{\bigwedge }}max\{{\nu }_{C_1^S(\kappa )}(r),{\nu }_{C_2^S(\kappa )\circ C_3^S(\kappa )}(p)\},{\gamma }_2\}\hfill \\ & =min\{{\displaystyle \underset{a=(ax)(axa)(yyxay)}{\bigwedge }}max\{{\nu }_{C_1^S(\kappa )}(ax),{\nu }_{{}_{C_2^S(\kappa )\circ C_3^S(\kappa )}}((axa)(yyxay))\},{\gamma }_2\}\hfill \\ & \le min\{\{max\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\},max\{{\nu }_{C_2^S(\kappa )\circ C_3^S(\kappa )}((axa)(yyxay)),{\gamma }_2\}\}\hfill \\ & =max\left(\left(min\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\}\right),\left(\{max\{{\nu }_{C_2^S(\kappa )\circ C_3^S(\kappa )}((axa)(yyxay)),{\gamma }_2\}\}\right)\right)\hfill \\ & =max\left(\begin{array}{c}\left(min\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\}\right),\\ \left(\{max\{{\displaystyle \underset{(axa)(yyxay)=bc}{\bigwedge }}max\{{\nu }_{C_2^S(\kappa )}(b),{\nu }_{C_3^S(\kappa )}(c)\},{\gamma }_2\}\}\right)\end{array}\right)\hfill \\ & \le max\left(\left(min\{{\nu }_{C_1^S\left[ϵ\right]}(ax),{\gamma }_2\}\right),\left(min\{{\nu }_{C_1^S\left[ϵ\right]}(axx),{\gamma }_2\}\right),\left(min\{{\nu }_{C_1^S\left[ϵ\right]}(yyxay),{\gamma }_2\}\right)\right)\hfill \\ & \le max\left(\left(max\{{\nu }_{C_1^S\left[ϵ\right]}(a),{\delta }_2\}\right),\left(max\{{\nu }_{C_1^S\left[ϵ\right]}(a),{\delta }_2\}\right),\left(max\{{\nu }_{C_1^S\left[ϵ\right]}(a),{\delta }_2\}\right)\right)\hfill \\ & =max\{{\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}(a),{\delta }_2\}.\hfill \end{array}$$

Thus ${\nu }_{(C_1^S(\kappa )\sqcap C_2^S(\kappa )\sqcap C_3^S(\kappa ))}{\ge }_{(\Gamma ,\delta )}{\nu }_{(C_1^S\circ C_2^S)(\kappa )\circ C_3^S(\kappa )}.$ Hence $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\sqcap ⟨C_3^S,C⟩\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩\ast ⟨C_3^S,C⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩,$ $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi-ideal $⟨C_2^S,B⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_3^S,C⟩$ of S.

$(iii)\Rightarrow (ii)$ is obvious.

$(ii)\Rightarrow (i)$ Let $⟨C_1^S,A⟩\sqcap ⟨C_2^S,B⟩\sqcap ⟨C_3^S,C⟩\subseteq {\vee }_{q\left(\Gamma ,\Delta \right)}⟨C_1^S,A⟩\ast ⟨C_2^S,B⟩\ast ⟨C_3^S,C⟩$ for all $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal $⟨C_1^S,A⟩,$ $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized bi-ideal $⟨C_2^S,B⟩$ and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal $⟨C_3^S,C⟩$ of S. Assume that $C_1^S$, $C_2^S,$ and $C_3^S$ are right, generalized bi and interior ideals of S respectively, then by Lemma 1, ${\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩$, ${\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩$ and ${\chi }_{\Gamma }^{\Delta }⟨C_3^S,C⟩$ are $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft right ideal and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft generalized ideal and $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic soft interior ideal of S. So by hypothesis we have

$$\begin{array}{c}\left({\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\right)\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_3^S,C⟩\hfill \\ \subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}\left({\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\ast {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\right)\ast {\chi }_{\Gamma }^{\Delta }⟨C_3^S,C⟩.\hfill \end{array}$$

Hence

$$\begin{array}{cc}\hfill {\chi }_{\Gamma }^{\Delta }⟨C_1^S\sqcap C_2^S\sqcap C_3^S,D⟩& {=}_{{}_{(\Gamma ,\Delta )}}\left({\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\right)\sqcap {\chi }_{\Gamma }^{\Delta }⟨C_3^S,C⟩\hfill \\ & \subseteq {\vee }_{{}_{q\left(\Gamma ,\Delta \right)}}\left({\chi }_{\Gamma }^{\Delta }⟨C_1^S,A⟩\ast {\chi }_{\Gamma }^{\Delta }⟨C_2^S,B⟩\right)\ast {\chi }_{\Gamma }^{\Delta }⟨C_3^S,C⟩.\hfill \\ & {=}_{{}_{(\Gamma ,\Delta )}}⟨C_1^S\circ C_2^S\circ C_3^S,D⟩.\hfill \end{array}$$

Thus

$$C_1^S\sqcap C_2^S\sqcap C_3^S\subseteq C_1^S\circ C_2^S\circ C_3^S.$$

Hence S is right weakly regular by Theorem 3. □

6. Application

In the following we provide some applications of generalized cubic soft sets.

As for as the applications of generalized cubic soft sets are concern, one can find its applications in the following directions:

• In algebra where one can use generalized cubic soft sets in different directions, as we used in the right weakly regular semigroups.
• In decision making theory where one can have more reliable decision as compared to the previously defined version of fuzzy sets.
• In practical applications by using algebraic structures and decision making theory with the use of generalized cubic soft sets.

We provide an application of generalized cubic soft sets as mention in the point 3.

To compare two generalized cubic soft sets values we define score function as follows:

Definition 19.

Let $⟨C^S,A⟩=\{({\tilde{\mu }}_{C^S\left[ϵ\right]},{\nu }_{C^S\left[ϵ\right]})|ϵ\in A\}$ be a cubic soft of S, we define score function as

$$S\left(C^S,A\right)=\frac{{\mu }_{C^S\left[ϵ\right]}^{-}+{\mu }_{C^S\left[ϵ\right]}^{+}-{\nu }_{C^S\left[ϵ\right]}}{3}$$

where$S\in \left[-1,1\right]$.

Example 2.

Consider a group of colleges consisting of three college namely $S=\{u,v,w\}.$ Let $\ast :S\times S\to S$ a binary operation on S with the following Cayley table,

$$\begin{array}{|cccc|}\hline \ast & u& v& w\\ u& u& u& u\\ v& v& v& v\\ w& w& w& w\\ \hline\end{array}$$

$Surely,$(S, ∗) is a weakly regular semigroup. Define a generalized cubic soft set$⟨C^S,A⟩=\{({\tilde{\mu }}_{C^S\left[ϵ\right]},{\nu }_{C^S\left[ϵ\right]})|ϵ\in A\}$in S by the following table

$$\begin{array}{|ccc|}\hline S& {\tilde{\mu }}_{C^S\left[ϵ\right]}& {\nu }_{C^S\left[ϵ\right]}\\ u& \left[0.3,0.6\right]& 0.4\\ v& \left[0.2,0.4\right]& 0.6\\ w& \left[0.7,0.9\right]& 0.2\\ \hline\end{array}$$

based on the parameters given in the set A like student strength. Further ${\tilde{\mu }}_{C^S\left[ϵ\right]}$ denotes the membership of a college (u, v, w) for future and ${\nu }_{C^S\left[ϵ\right]}$ denotes membership of a college (u, v, w) in the present time in the group S based on the parameters student strength. The panel imposes some extra conditions on the colleges as;

$$\begin{array}{cc}\hfill ({\tilde{\gamma }}_1& =\left[0.2,0.3\right]<{\tilde{\delta }}_1=\left[0.4,0.5\right]),\mathit{for}\mathit{the}\mathit{future}\mathit{time},\hfill \\ \hfill ({\gamma }_2& =0.5>{\delta }_2=0.4),\mathit{for}\mathit{the}\mathit{present}\mathit{time}.\hfill \end{array}$$

It is obvious that $⟨C^S,A⟩=\{({\tilde{\mu }}_{C^S\left[ϵ\right]},{\nu }_{C^S\left[ϵ\right]})|ϵ\in A\}$ is a $({\in }_{\Gamma },{\in }_{\Gamma }\vee q_{\Delta })$-cubic subsemigroup of S. Now in order to find that which college plays a dominant role in the group, we use the score function given in Definition 19, and we get

$$S\left(u\right)=0.166,S\left(v\right)=0\mathit{and}S\left(w\right)=0.466.$$

Thus according to score function, we have w > u > v.

This means that the college w is the best of all in a certain district under the parameters students’ strength. We may consider other parameters like teaching faculty, available facilities, labs and libraries etc. Finally we conclude that the college w should be considered as a cluster college for all the other colleges under consideration. The main advantage of the cluster college is that it can handle many problems at the district level like teacher’s transfer etc. The cluster college will provide every kind of information and recommendations to the higher authorities of the province under his domain. Favoritism is the main disadvantage of the cluster system, which cannot be overcome through our presented model. A neutral penal of experts may help such a deficiency.

7. Conclusions

In this paper we introduced the concept of generalized cubic soft sets which is the most general approach and characterize the right weakly regular semigroups in terms of generalized cubic soft ideals. This paper generalizes the idea of Feng et al. [35] and Khan et al. [36]. Since semigroups has the applications in the theory of automata so the technique of generalized cubic soft sets will be very beneficial. To help better understanding of our work Interdependence of various concepts is shown in Figure 1.

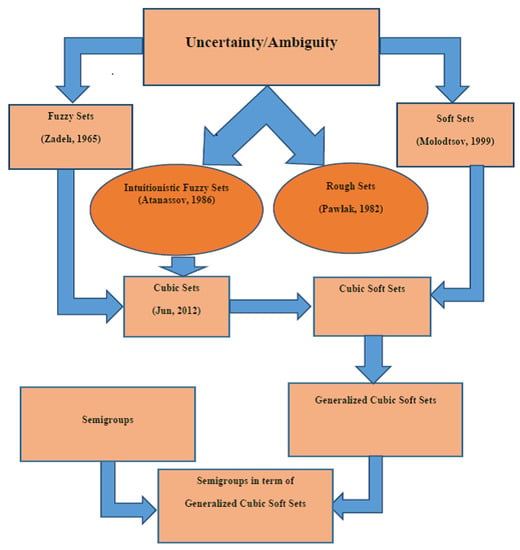
Figure 1. Interdependence of concepts.

In future we are aiming to use generalized cubic soft sets in decision making theory, automata theory and in signal processing. We found a very valuable application of the group of symmetries in [37], where author shows that "network fibres combine invariances along groups of symmetries and distributed pattern representations, which could be sufficiently stable to explain transfer learning of deep networks". In future we are aiming to find applications of generalized cubic soft sets with semigroups by extending the idea presented by Mallat [37] in 2016.