Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation
Abstract
1. Introduction
Problem Statement and the Aim of This Work
2. Methods
3. Results
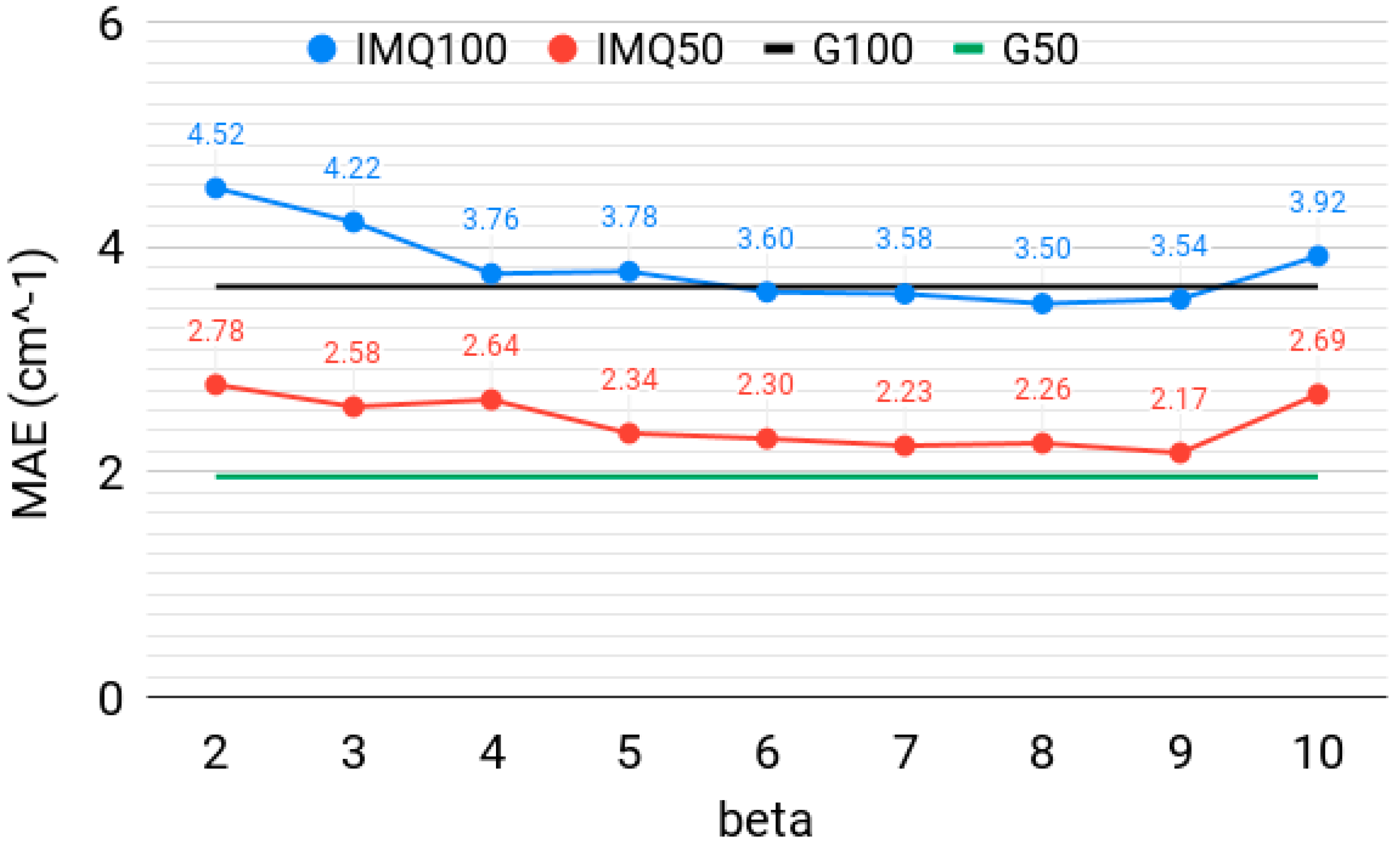
3.1. Effect of the IMQ Exponent
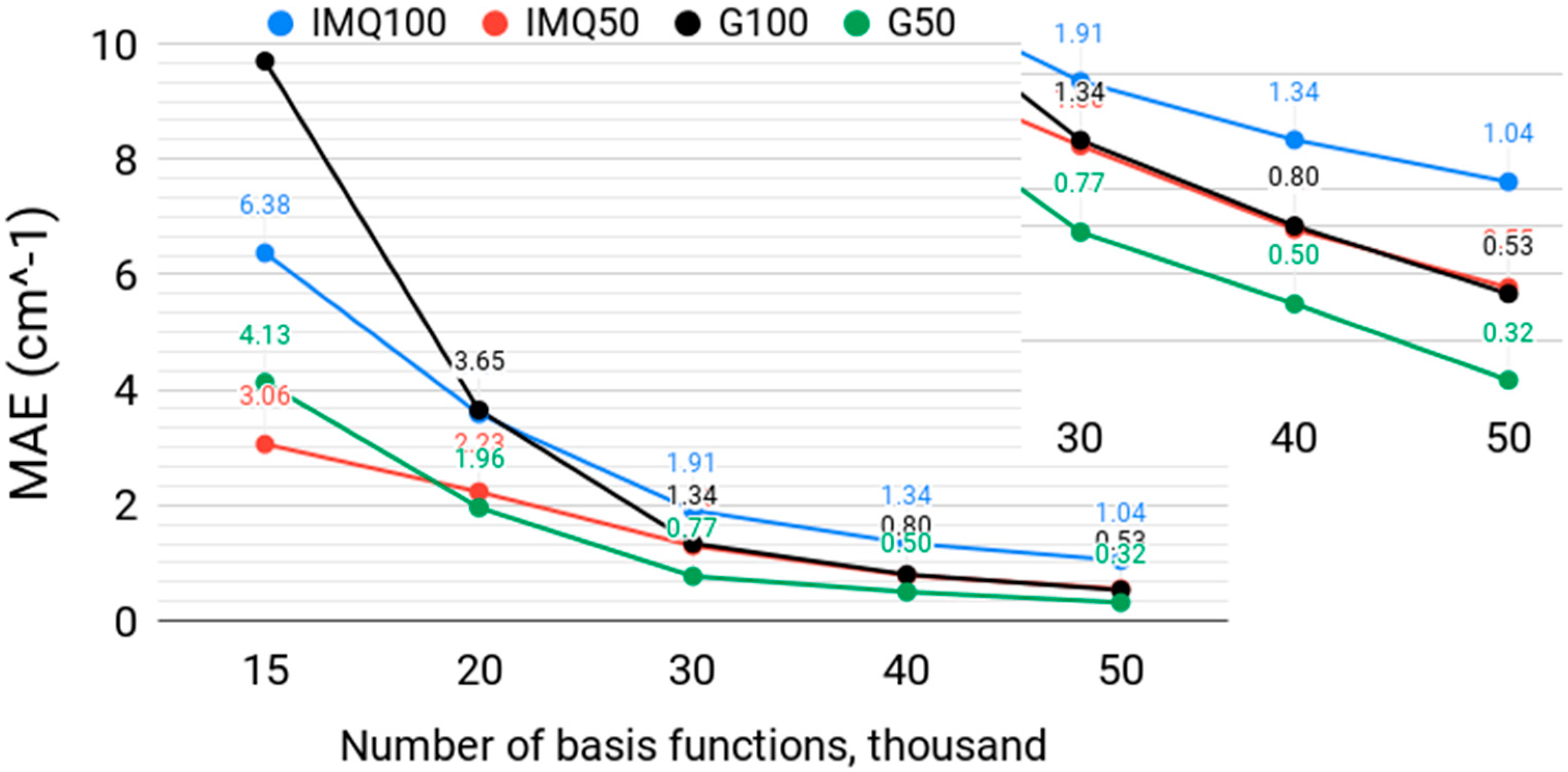
3.2. Effect of the Basis Size
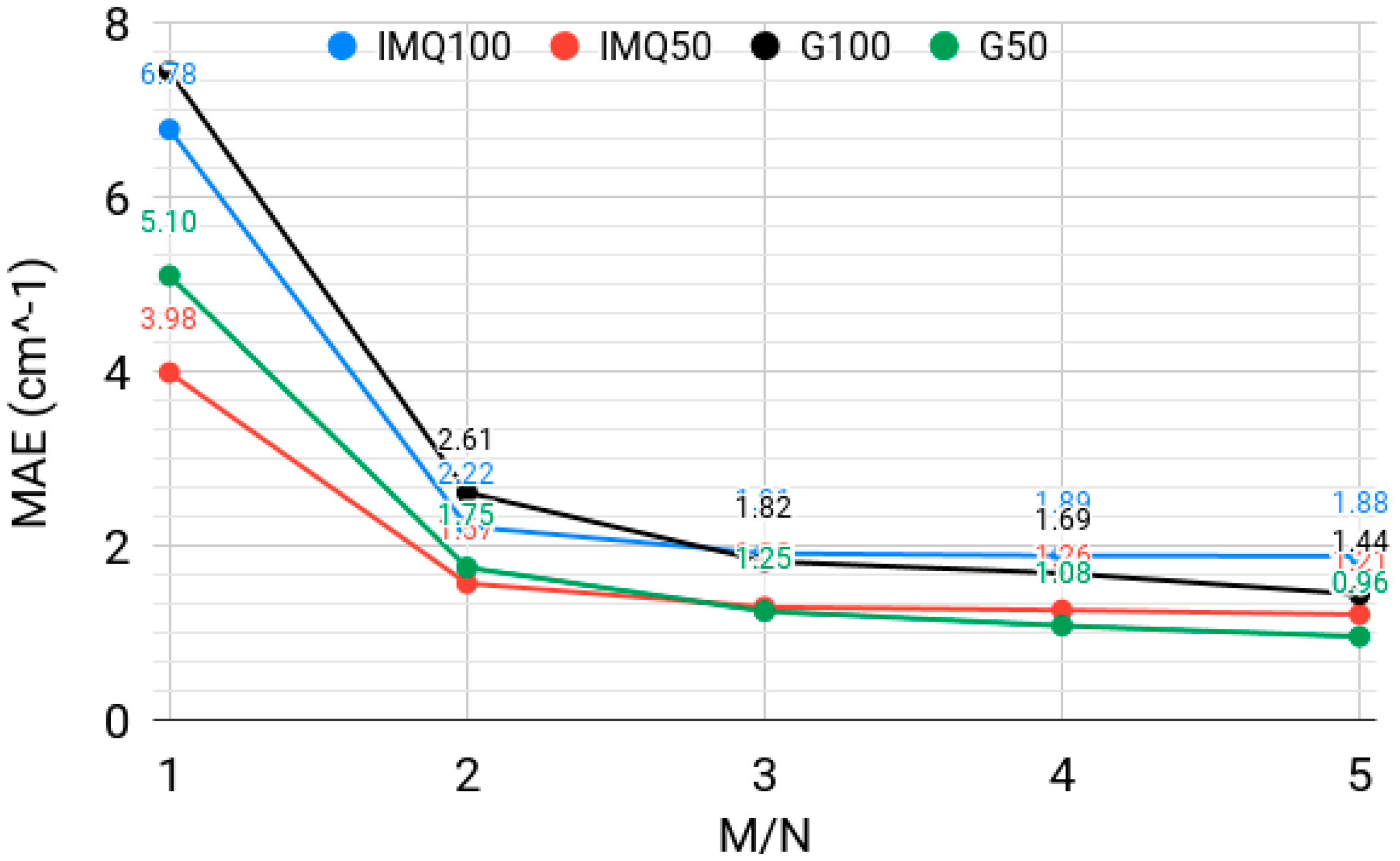
3.3. Effect of the Rectangularity of the Collocation Equation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, J.-T.; Zhou, Z.-Y.; Broadwell, I.; Sun, S.-G. In-situ infrared spectroscopic studies of electrochemical energy conversion and storage. Acc. Chem. Res. 2012, 45, 485–494. [Google Scholar] [CrossRef] [PubMed]
- Cederbaum, L.S.; Hirst, D.M. Potential Energy Surfaces; Taylor + Francis: London, UK; Philadelphia, PA, USA, 1985. [Google Scholar]
- Braams, B.J.; Bowman, J.M. Permutationally invariant potential energy surfaces in high dimensionality. Int. Rev. Phys. Chem. 2009, 28, 577–606. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2015, 115, 1012–1020. [Google Scholar] [CrossRef]
- Peyerimhoff, S.; Murrell, J.N.; Carter, S.; Farantos, S.C.; Huxley, P.; Varandas, A.J.C. Molecular potential energy functions, Verlag John Wiley & Sons, Chichester, New York, Brisbane, Toronto, Singapore 1984. 197 Seiten, Preis: £ 19.95. Ber. Bunsenges. Phys. Chem. 1985, 89, 1122. [Google Scholar] [CrossRef]
- Hollebeek, T.; Ho, T.S.; Rabitz, H. Constructing multidimensional molecular potential energy surfaces from ab initio data. Annu. Rev. Phys. Chem. 1999, 50, 537–570. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.A. Molecular potential-energy surfaces for chemical reaction dynamics. Theor. Chem. Acc. Theory Comput. Model. (Theor. Chim. Acta) 2002, 108, 313–324. [Google Scholar] [CrossRef]
- Handley, C.M.; Popelier, P.L.A. Potential energy surfaces fitted by artificial neural networks. J. Phys. Chem. A 2010, 114, 3371–3383. [Google Scholar] [CrossRef] [PubMed]
- Handy, N.C. The derivation of vibration-rotation kinetic energy operators, in internal coordinates. Mol. Phys. 1987, 61, 207–223. [Google Scholar] [CrossRef]
- Roy, T.K.; Gerber, R.B. Vibrational self-consistent field calculations for spectroscopy of biological molecules: New algorithmic developments and applications. Phys. Chem. Chem. Phys. 2013, 15, 9468–9492. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Laverdure, L.; Mosey, N. Computing the anharmonic vibrational spectrum of UF6 in 15 dimensions with an optimized basis set and rectangular collocation. J. Phys. Chem. A 2015, 119, 9557–9567. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.; Carrington, T.; Manzhos, S. Anharmonic vibrations of the carboxyl group in acetic acid on TiO2: Implications for adsorption mode assignment in dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2013, 15, 10028–10034. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.; Manzhos, S.; Carrington, T.; Yamashita, K. Parameterized bases for calculating vibrational spectra directly from ab initio data using rectangular collocation. J. Chem. Theory Comput. 2012, 8, 2053–2061. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Carrington, T.; Meyer, H.-D. Variational quantum approaches for computing vibrational energies of polyatomic molecules. Mol. Phys. 2008, 106, 2145–2182. [Google Scholar] [CrossRef]
- Schleyer, P.V.R. Encyclopedia of Computational Chemistry; John Wiley Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Manzhos, S.; Wang, X.; Dawes, R.; Carrington, T. A nested molecule-independent neural network approach for high-quality potential fits. J. Phys. Chem. A 2006, 110, 5295–5304. [Google Scholar] [CrossRef] [PubMed]
- Castro, E.; Avila, G.; Manzhos, S.; Agarwal, J.; Schaefer, H.F.; Carrington, T. Applying a smolyak collocation method to Cl2CO. Mol. Phys. 2017, 115, 1775–1785. [Google Scholar] [CrossRef]
- Majumder, M.; Hegger, S.E.; Dawes, R.; Manzhos, S.; Wang, X.-G.; Tucker, C.; Li, J.; Guo, H. Explicitly correlated MRCI-F12 potential energy surfaces for methane fit with several permutation invariant schemes and full-dimensional vibrational calculations. Mol. Phys. 2015, 113, 1823–1833. [Google Scholar] [CrossRef]
- Manzhos, S.; Chan, M.; Carrington, T. Communication: Favorable dimensionality scaling of rectangular collocation with adaptable basis functions up to 7 dimensions. J. Chem. Phys. 2013, 139, 051101. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Yamashita, K. Calculating anharmonic vibrational frequencies of molecules adsorbed on surfaces directly from ab initio energies with a molecule-independent method: H2O on Pt(111). Surf. Sci. 2011, 605, 616–622. [Google Scholar] [CrossRef]
- Christiansen, O. Vibrational structure theory: New vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties. Phys. Chem. Chem. Phys. 2007, 9, 2942. [Google Scholar] [CrossRef] [PubMed]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Yamashita, K. Nonspectral methods for solving the schrödinger equation for electronic and vibrational problems. J. Phys. Chem. Lett. 2011, 2, 2193–2199. [Google Scholar] [CrossRef]
- Yang, W.; Peet, A.C. The collocation method for bound solutions of the Schrödinger equation. Chem. Phys. Lett. 1988, 153, 98–104. [Google Scholar] [CrossRef]
- Peet, A.C.; Yang, W. The collocation method for calculating vibrational bound states of molecular systems—With application to Ar–HCl. J. Chem. Phys. 1989, 90, 1746–1751. [Google Scholar] [CrossRef]
- Yang, W.; Peet, A.C. A method for calculating vibrational bound states: Iterative solution of the collocation equations constructed from localized basis sets. J. Chem. Phys. 1990, 92, 522–526. [Google Scholar] [CrossRef]
- Manzhos, S.; Yamashita, K.; Carrington, T. On the advantages of a rectangular matrix collocation equation for computing vibrational spectra from small basis sets. Chem. Phys. Lett. 2011, 511, 434–439. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. Using rectangular collocation with finite difference derivatives to solve electronic Schrödinger equation. J. Chem. Phys. 2018. accepted. [Google Scholar]
- Boutry, G.; Elad, M.; Golub, G.H.; Milanfar, P. The generalized eigenvalue problem for nonsquare pencils using a minimal perturbation approach. SIAM J. Matrix Anal. Appl. 2005, 27, 582–601. [Google Scholar] [CrossRef]
- Manzhos, S.; Wang, X.; Carrington, T. A multimode-like scheme for selecting the centers of Gaussian basis functions when computing vibrational spectra. Chem. Phys. 2018, 509, 139–144. [Google Scholar] [CrossRef]
- Chan, M.; Yamashita, K.; Carrington, T.; Manzhos, S. Towards accurate spectroscopic identification of species at catalytic surfaces: Anharmonic vibrations of formate on AuPt. MRS Proc. 2012, 1484, imrc12-1484-7a-0016. [Google Scholar] [CrossRef]
- Manzhos, S.; Yamashita, K.; Carrington, T. Using a neural network based method to solve the vibrational Schrödinger equation for H2O. Chem. Phys. Lett. 2009, 474, 217–221. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. Using an internal coordinate gaussian basis and a space-fixed cartesian coordinate kinetic energy operator to compute a vibrational spectrum with rectangular collocation. J. Chem. Phys. 2016, 145, 224110. [Google Scholar] [CrossRef] [PubMed]
- Kamath, A.; Vargas-Hernández, R.A.; Krems, R.V.; Carrington, T.; Manzhos, S. Neural networks vs Gaussian process regression for representing potential energy surfaces: A comparative study of fit quality and vibrational spectrum accuracy. J. Chem. Phys. 2018, 148, 241702. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.-G.; Ho, T.-S.; Rabitz, H. The collocation method based on a generalized inverse multiquadric basis for bound-state problems. Comput. Phys. Commun. 1998, 113, 168–179. [Google Scholar] [CrossRef]
- Carter, S.; Handy, N.C.; Demaison, J. The rotational levels of the ground vibrational state of formaldehyde. Mol. Phys. 1997, 90, 729–738. [Google Scholar] [CrossRef]
- Sobol, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. An improved neural network method for solving the Schrödinger equation. Can. J. Chem. 2009, 87, 864–871. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamath, A.; Manzhos, S. Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation. Mathematics 2018, 6, 253. https://doi.org/10.3390/math6110253
Kamath A, Manzhos S. Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation. Mathematics. 2018; 6(11):253. https://doi.org/10.3390/math6110253
Chicago/Turabian StyleKamath, Aditya, and Sergei Manzhos. 2018. "Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation" Mathematics 6, no. 11: 253. https://doi.org/10.3390/math6110253
APA StyleKamath, A., & Manzhos, S. (2018). Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation. Mathematics, 6(11), 253. https://doi.org/10.3390/math6110253





