Abstract
We explore the use of inverse multiquadratic (IMQ) functions as basis functions when solving the vibrational Schrödinger equation with the rectangular collocation method. The quality of the vibrational spectrum of formaldehyde (in six dimensions) is compared to that obtained using Gaussian basis functions when using different numbers of width-optimized IMQ functions. The effects of the ratio of the number of collocation points to the number of basis functions and of the choice of the IMQ exponent are studied. We show that the IMQ basis can be used with parameters where the IMQ function is not integrable. We find that the quality of the spectrum with IMQ basis functions is somewhat lower that that with a Gaussian basis when the basis size is large, and for a range of IMQ exponents. The IMQ functions are; however, advantageous when a small number of functions is used or with a small number of collocation points (e.g., when using square collocation).
1. Introduction
Computational vibrational spectroscopy is important in the studies of vibrational phenomena in space, atmosphere, and in materials and at interfaces. It is necessary for the assignment of molecular species, including reactants, products, and intermediates, and for the assignment of reaction pathways in many applications [1]. The Born–Oppenheimer approximation is a good approximation to compute the vibrational spectrum in most applications, in which case the vibrational dynamics is described by the Schrödinger equation (SE) for nuclei:
where r denotes coordinates spanning the configuration space, is the potential energy surface (PES), is the kinetic energy operator (KEO), and is the wavefunction. The values of the PES can be computed ab initio or sampled from an analytic function (which itself could be fitted to ab initio data or to empirical data) [2,3,4,5,6,7,8]. The KEO has a simple form in space-fixed Cartesian coordinates rSF:
where is the number of atoms, their masses, and is the Laplacian operator in Cartesian coordinates of the ith atom: (we use atomic units). As space-fixed Cartesian coordinates are redundant for free molecules, typically, the KEO is expressed in internal coordinates, in which it is much more complex [9]. Approximations are often used to simplify the expression for the KEO [10,11,12,13], which are a source of error.
The eigenvalues E are vibrational levels, and differences between them simulate observed spectra. Intensities of transitions are important for comparison with experimental spectra; however, the spectrum (of eigenvalues) itself is already useful for species assignment, and its calculation for polyatomic molecules is nontrivial. Equation (1) can be relatively easily solved for a general PES for three- and four-atomic molecules, and the calculation becomes progressively more complex and CPU- and memory-costly for larger molecules. The commonly used method to solve Equation (1) for a general potential is the variational approach [14,15], in which one expands the wavefunction in a basis:
where N is the basis size. Insertion of Equation (3) into the SE Equation (1), multiplication on the left by basis functions , and integration over all configuration space leads to a matrix equation for the vector of coefficients (c):
where H the Hamiltonian and B the overlap matrix. Already with four atoms (a six dimensional configuration space), it is not unusual to use hundreds of thousands of basis functions (N), and the necessity to compute the integrals often requires PES values at millions of locations [16]. This, practically, requires availability of the PES as a continuous function. Such functions are not trivial to construct with high accuracy, even for a four-atomic system, and become difficult to construct for larger systems [3,16,17,18]. For isolated molecules, it is relatively easy to compute a sufficient amount of high-quality ab initio data to which can be fitted. For vibrations at interfaces and in materials, the cost of ab initio calculations is much higher, and for the vast majority of molecule-surface or aggregate-state systems of practical importance, there are no, and there will never be, ab initio based PES functions, even though vibrational problems with a sufficiently small number of coupled degrees of freedom can be identified in such systems [12,19,20].
These difficulties, in particular, are responsible for the fact that harmonic spectra are still widely used in computational materials science. This is unfortunate, as in many applications anharmonicity is important. For example, the catalytic activity of surfaces is precisely due to their ability to weaken intramolecular bonds in adsorbed molecules, leading to more significant anharmonicity compared to free molecules. Popular methods, which simplify the solution of Equation (1) while allowing for anharmonicity and coupling, also have not found much use in materials modeling [21]. For example, the vibrational self-consistent field approach (VSCF) [10] still requires the availability of the PES, as it relies on integrals. The vibrational perturbation theory (VPT2) approach, implemented in many ab initio codes [22], assumes a simple polynomial form of the PES, which still requires many high-quality ab initio data points around the equilibrium, and fails for degenerate levels. Clearly, a direct solution of Equation (1) for a general is preferred.
A collocation approach is an alternative way to convert the SE (both the vibrational SE, Equation (1) [13,17,23,24,25,26,27], and the electronic SE [28]) into a matrix form. In it, one uses the expansion of Equation (3), but only aims to satisfy the SE at a set of collocation points ():
Although square collocation (M = N) was the type of collocation originally proposed for vibrational problems [24,25,26], in general, M > N. Equation (5) can be solved using approaches developed for rectangular matrices [29] or by squaring it and using common eigensolvers:
There is no requirement that Equation (3) reproduce the wavefunction in all space (although with a sufficiently dense set , covering all regions of space where the wavefunction is not negligible, this will be the case). The collocation points can be distributed in any desired way and do not have to form a quadrature grid (note that even though Equation (6) has the form of a quadrature, the sums need not be equal to any integrals) [30]. This potentially allows computing the spectrum from a smaller number of values, which could be directly computed ab initio. The rectangular collocation (which is solved in the least squares sense) can also be used to tune the basis, so that good accuracy can be achieved with small N [13,27]. Note that M can be smaller if the basis is better. The rectangular collocation approach has been applied to computations of anharmonic spectra of polyatomic molecules, including those on surfaces directly from ab initio samples of [11,12,19,20,31].
The KEO can, in principle, be applied to the basis functions analytically [11,12,32]; however, the complexity of KEO expressions in given internal coordinates () can be avoided when applying the KEO numerically (using finite differences with an appropriate stencil to achieve the desired accuracy) in space-fixed Cartesian coordinates () [30,33,34]:
See Reference [33] for details. In this way, it is easy to use the exact KEO with any coordinates in which the SE is solved and with any basis functions.
Problem Statement and the Aim of This Work
Rectangular collocation can be used with any basis functions. The functions need not be integrable or even continuous, except at the collocation points. For example, Slater type functions (useful in full-potential electronic structure calculations) are easy to use with collocation, even though they are not with the variational approach (which is why Gaussian-like functions are usually preferred in that application) [28]. Localized or delocalized functions can be used. For localized basis functions, only Gaussian functions have been used with rectangular collocation for the vibrational SE [20,30,33,34]. Gaussian functions are general and form a sufficiently small basis set (especially if their parameters are fitted) for the calculation to be doable on a personal computer for low-dimensional problems, such as triatomic molecules, and for a small number of states [13,20,27]. For larger molecules and large numbers of states, either other types of basis functions need to be used, such as parameterized harmonic functions, which allow for a small basis set size, as was tested in up to 15 dimensions [11,12,13,19,31], or a much larger Gaussian basis would be needed. For example, a sub-cm−1 accuracy has been achieved for the vibrational spectrum of formaldehyde (a six-dimensional SE), with about 40,000 basis functions and with more than 100,000 collocation points [30,33,34]. While this kind of calculation is, in principle, doable on a modern workstation with a couple hundred GB of RAM, it is somewhat costly.
It is; therefore, useful to study other types of localized basis functions, which might be advantageous in terms of accuracy, or the required number of basis functions and collocation points to reach a given accuracy. In this work, we explore the generalized inverse multiquadratic (IMQ) function
as the basis function in the rectangular collocation method when solving the vibrational Schrödinger equation. The parameter c controls the width of the function, and the exponent parameter β the degree of locality. It is usually assumed that β must satisfy β > d, the dimensionality of the space. This requirement is; however, made to insure integrability (of and ), and may not be necessary with collocation. The generalized IMQ function was previously used by Rabitz’s group to solve bound-state Schrödinger equations for modelling one- and two-dimensional problems (Morse oscillator and 2D Henon-Heiles potential) with the square (N = M) collocation method [35]. Hu et al. [35] concluded, based on those model problems, that the IMQ basis functions are advantageous for highly anharmonic problems and highly excited states. They also noted a slower rate of growth of the associated condition numbers compared to Gaussians, which bodes well for building a more complete basis.
The aim of this work is to explore the utility of the generalized IMQ basis function when solving a vibrational SE for a real molecule with the rectangular collocation method. We compare the performance of an IMQ basis to that of a Gaussian basis on the example of the spectrum of formaldehyde (i.e., solving a six-dimensional SE), for which results, with Gaussian bases of different sizes, are available, and for which comparisons with the variational approach using DVR (discrete variable representation) have been made in References [30,33,34]. Specifically, we explore the effect of different choices of β, including those which do not satisfy the integrability condition. We also explore the behavior of spectrum quality with the number of basis function and collocation points.
2. Methods
Equations (5) and (6) were solved using the IMQ basis functions. Calculations with Gaussian basis function
are performed for comparison as in References [30,34]. The vibrational SE of formaldehyde, H2CO, was solved for the lowest 100 levels in six bond coordinates, including the CO bond length, the two CH bond lengths, the two HCO angles, and the dihedral angle between the two HCO planes. The six coordinates, in this order, form the vector r =rint. The KEO was applied in space-fixed Cartesian coordinates (Equation (2)) using Equation (7), with a five-point finite difference stencil with all . See Reference [33] for details. The values of at the collocation points were sampled from the analytic PES of Reference [36]. The collocation points were chosen within specific ranges of the six coordinates, from a pseudo-random six-dimensional Sobol sequence [37], and accepted into the collocation point set if
where rand is a (uniformly distributed) random number in [0, 1]. We used Vmax = 17,000 cm−1 and Δ = 500 cm−1. The coordinate ranges were rmin = (1.03, 0.84, 0.84, 83, 83, 105), rmax = (1.50, 1.69, 1.69, 162, 162, 255), where bond lengths were in Å and angles in degrees. The point selection was; therefore, similar to that used in References [30,34] and thus allowed for comparison with results obtained with the Gaussian basis in those works.
The quality of the spectrum was evaluated as the MAE (mean absolute error), for the 50 and 100 lowest vibrational levels, versus a reference spectrum computed in Reference [30] on the same PES with a highly accurate variational scheme. For each combination of the numbers of basis functions (N), collocation points (M), and the IMQ exponent (β), the basis width parameter (c) was optimized. To account for different ranges and types of internal coordinates, the following version of the IMQ function was used:
This allows for the use of a single parameter c for basis width optimization in a similar way to that which was done for Gaussian width parameters in References [30,34]. The Gaussian widths of Equation (9) were optimized in the same way. The optimal width typically corresponded to condition numbers of the overlap matrix STS on the order of 1010.
3. Results
3.1. Effect of the IMQ Exponent
Figure 1 shows the MAE of the lowest 50 and 100 vibrational levels obtained with the width-optimized IMQ basis, using N = 20,000 basis functions and M = 80,000 collocation points, for different exponents (β). The horizontal lines are MAE, obtained with a width-optimized Gaussian basis with the same N and M. Two conclusions can be made from this Figure: (i) The Gaussian basis generally outperforms the IMQ basis for the low-energy levels; however, for several β values, the spectrum quality is practically the same as with the Gaussian basis. The IMQ basis slightly outperforms the Gaussian basis for the higher-energy levels, corroborating the conclusion Hu et al. achieved based on model systems. The specific choice of β seems to be non-critical, as long as the width (c) is optimized. The best quality IMQ bases do satisfy the condition β > d = 6. (ii) The spectrum quality only marginally deteriorates for β = 4–6, which do not satisfy the integrability condition β > d. This highlights the fact that nowhere in the collocation Equations (5) and (6) is it required that integrals over all space be finite. The use of non-integrable functions might be beneficial in some applications and remains little explored. Collocation is a way to harness any advantages associated with such functions.
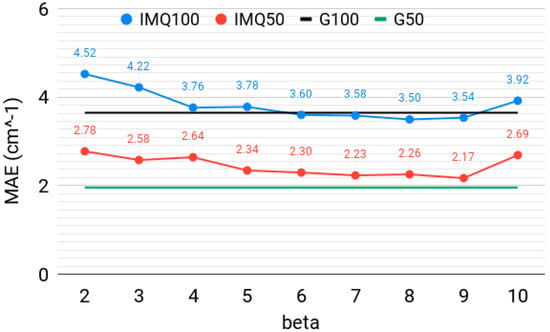
Figure 1.
The mean absolute error (MAE), in cm−1, over the lowest 50 and 100 vibrational levels of H2CO, computed with the inverse multiquadratic (IMQ50, IMQ100) basis with different β (beta) parameters. The horizontal lines at 2 and 3.7 cm−1 are corresponding values obtained with a Gaussian basis (G50, G100, respectively), as in Reference [30]. N = 20,000 basis functions and M = 80,000 collocation points were used.
3.2. Effect of the Basis Size
Next, we tested the performance of the IMQ basis with the basis size at a fixed M:N ratio of 3. Figure 2 shows the MAE of the lowest 50 and 100 vibrational levels obtained with the width-optimized IMQ functions, with β = 7 and with width-optimized Gaussian basis functions. For the lowest 50 level, the Gaussian basis outperforms, although only modestly, the IMQ basis, except at the lowest number of basis functions (N = 15,000), where the IMQ basis is better. N = 15,000 is; however, too small to achieve spectroscopically relevant accuracy on the order of 1 cm−1 or better. A similar result is observed with 100 levels, where IMQ outperforms for N = 15,000 and N = 20,000, but underperforms the Gaussian basis for larger basis sizes. For spectroscopically accurate calculations, the Gaussian basis is clearly preferred for both low-lying and highly excited states. The IMQ basis needs about a third more basis functions than the Gaussian basis to achieve a similar accuracy in this regime.
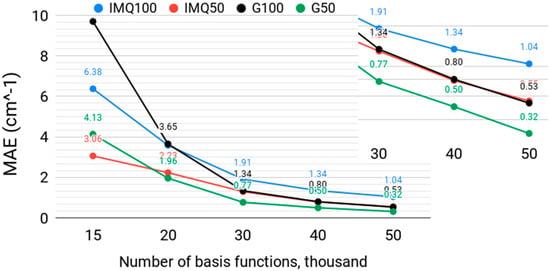
Figure 2.
The mean absolute error (MAE), in cm−1, over the lowest 50 and 100 vibrational levels of H2CO, computed with a width-optimized inverse multiquadratic (IMQ50, IMQ100) basis with β = 7 and a width-optimized multiquadratic Gaussian (G50, G100) basis, for different numbers of basis functions N and M = 3N collocation points. The insert shows part of the graph at the logarithmic scale.
3.3. Effect of the Rectangularity of the Collocation Equation
The IMQ basis functions were previously tested with the quadratic collocation (M = N) [35]. Here, we show that it is advantageous to use rectangular collocation (i.e., M > N). Figure 3 shows the behavior of the spectrum errors over the lowest 50 and 100 vibrational levels, computed with a width-optimized inverse multiquadratic basis with β = 7 and a width-optimized Gaussian basis, for N = 30,000 basis functions and for different ratios of the number of collocation points to the number of basis functions M:N. There is a clear advantage of using M > N, which allows for a several-fold increase in level accuracy versus square collocation. This is a practically important advantage from the point of view of computational cost, which is dominated by N; we have previously shown [33] that, when using Equation (6) to solve the rectangular collocation matrix equation, one only needs to store and manipulate matrices of size N × N for M > N as long as M:N is integer.
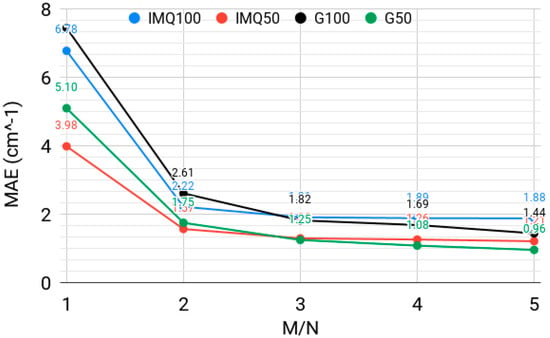
Figure 3.
The mean absolute error (MAE), in cm−1, over the lowest 50 and 100 vibrational levels of H2CO, computed with a width-optimized inverse multiquadratic (IMQ50, IMQ100) basis with β = 7 and a width-optimized multiquadratic Gaussian (G50, G100) basis, for N = 30,000 basis functions and different ratios of the number of collocation points to the number of basis functions M:N.
There are diminishing returns to the increase of the M:N ratio; here, M = 3N appears to be an optimal choice. We note that the effect of rectangularity is problem- and computational setup-dependent (e.g., see Reference [30], where a more or less pronounced effect of increasing the M:N ratio can be observed depending on collocation point and basis function placement, when using Gaussian basis functions). Figure 3 here shows that the behavior with respect to the degree of rectangularity of the collocation equation is qualitatively similar for IMQ and Gaussian bases. Specifically for the case M = N (i.e., that of square collocation), the IMQ basis slightly outperforms the Gaussian basis, corroborating the conclusion of Reference [35]. The square collocation is not, however, able to provide spectroscopic accuracy with N = 30,000, whereas rectangular collocation does allow achieving level errors on the order of 1 cm−1.
4. Conclusions
We have explored the use of inverse multiquadratic functions as basis functions in the rectangular collocation method to solve the vibrational Schrödinger equation. We computed the vibrational spectrum of formaldehyde (in d = six dimensions), which allowed us to compare the behavior of the solution with respect to various calculation parameters (the IMQ exponent parameter (β), basis size (N), and collocation point set size (M)) to that previously observed with the Gaussian basis.
For the lowest basis set size we used (15,000 functions), the IMQ basis outperformed the Gaussian basis. However, to achieve the “spectroscopic accuracy” on the order of 1 cm−1 on the lowest 50 or 100 levels, more than N = 30,000 functions are needed and M > N is needed; for these values of N, the accuracy obtained with the IMQ basis is somewhat lower than that with the Gaussian basis.
The behavior with respect to the ratio of the numbers of the collocation points (M) and basis functions (N) is qualitatively similar to that observed with a Gaussian basis, both showing a significant improvement of errors for M > N up to about M = 3N. This highlights the advantage of the rectangular over the square collocation, notably in the CPU cost, which is dominated by N rather than M. When N = M (i.e., when using square collocation), the IMQ basis outperformed the Gaussian basis, although in that regime the spectrum errors were much larger than 1 cm−1.
Perhaps the most important conclusion of this work is that, with collocation, one can use basis functions that are not even integrable. In this case, this was shown when using IMQ functions with the exponent β ≤ d. There is only a slight increase of error until β became much smaller than d, although the best accuracy is obtained when β > d. This is an important advantage over quadrature based variational methods, as basis functions can be chosen to satisfy requirements that make integrals more difficult to compute (an example being the cusp condition in electronic structure). It would be useful to study other non-integrable functions, as they might result in a more compact, yet sufficiently complete, basis at the collocation points. For example, one could use a neural network representation of the wavefunction with sigmoid neurons that are non-integrable, as opposed to radial neurons which are [38]. This is possible because, with collocation, one does not compute integrals (the sum in Equation (6) need not converge any quadrature). This also should allow any singularities to be dealt with rather easily by not including them in the collocation point set; recent results [28] show promise in this direction that should be further explored.
Author Contributions
Conceptualization, methodology and writing, S.M.; calculations and editing, A.K.
Funding
The authors thank the NUS Strategic India Initiative by the National University of Singapore.
Acknowledgments
S.M. thanks Tucker Carrington for discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.-T.; Zhou, Z.-Y.; Broadwell, I.; Sun, S.-G. In-situ infrared spectroscopic studies of electrochemical energy conversion and storage. Acc. Chem. Res. 2012, 45, 485–494. [Google Scholar] [CrossRef] [PubMed]
- Cederbaum, L.S.; Hirst, D.M. Potential Energy Surfaces; Taylor + Francis: London, UK; Philadelphia, PA, USA, 1985. [Google Scholar]
- Braams, B.J.; Bowman, J.M. Permutationally invariant potential energy surfaces in high dimensionality. Int. Rev. Phys. Chem. 2009, 28, 577–606. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2015, 115, 1012–1020. [Google Scholar] [CrossRef]
- Peyerimhoff, S.; Murrell, J.N.; Carter, S.; Farantos, S.C.; Huxley, P.; Varandas, A.J.C. Molecular potential energy functions, Verlag John Wiley & Sons, Chichester, New York, Brisbane, Toronto, Singapore 1984. 197 Seiten, Preis: £ 19.95. Ber. Bunsenges. Phys. Chem. 1985, 89, 1122. [Google Scholar] [CrossRef]
- Hollebeek, T.; Ho, T.S.; Rabitz, H. Constructing multidimensional molecular potential energy surfaces from ab initio data. Annu. Rev. Phys. Chem. 1999, 50, 537–570. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.A. Molecular potential-energy surfaces for chemical reaction dynamics. Theor. Chem. Acc. Theory Comput. Model. (Theor. Chim. Acta) 2002, 108, 313–324. [Google Scholar] [CrossRef]
- Handley, C.M.; Popelier, P.L.A. Potential energy surfaces fitted by artificial neural networks. J. Phys. Chem. A 2010, 114, 3371–3383. [Google Scholar] [CrossRef] [PubMed]
- Handy, N.C. The derivation of vibration-rotation kinetic energy operators, in internal coordinates. Mol. Phys. 1987, 61, 207–223. [Google Scholar] [CrossRef]
- Roy, T.K.; Gerber, R.B. Vibrational self-consistent field calculations for spectroscopy of biological molecules: New algorithmic developments and applications. Phys. Chem. Chem. Phys. 2013, 15, 9468–9492. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Laverdure, L.; Mosey, N. Computing the anharmonic vibrational spectrum of UF6 in 15 dimensions with an optimized basis set and rectangular collocation. J. Phys. Chem. A 2015, 119, 9557–9567. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.; Carrington, T.; Manzhos, S. Anharmonic vibrations of the carboxyl group in acetic acid on TiO2: Implications for adsorption mode assignment in dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2013, 15, 10028–10034. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.; Manzhos, S.; Carrington, T.; Yamashita, K. Parameterized bases for calculating vibrational spectra directly from ab initio data using rectangular collocation. J. Chem. Theory Comput. 2012, 8, 2053–2061. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Carrington, T.; Meyer, H.-D. Variational quantum approaches for computing vibrational energies of polyatomic molecules. Mol. Phys. 2008, 106, 2145–2182. [Google Scholar] [CrossRef]
- Schleyer, P.V.R. Encyclopedia of Computational Chemistry; John Wiley Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Manzhos, S.; Wang, X.; Dawes, R.; Carrington, T. A nested molecule-independent neural network approach for high-quality potential fits. J. Phys. Chem. A 2006, 110, 5295–5304. [Google Scholar] [CrossRef] [PubMed]
- Castro, E.; Avila, G.; Manzhos, S.; Agarwal, J.; Schaefer, H.F.; Carrington, T. Applying a smolyak collocation method to Cl2CO. Mol. Phys. 2017, 115, 1775–1785. [Google Scholar] [CrossRef]
- Majumder, M.; Hegger, S.E.; Dawes, R.; Manzhos, S.; Wang, X.-G.; Tucker, C.; Li, J.; Guo, H. Explicitly correlated MRCI-F12 potential energy surfaces for methane fit with several permutation invariant schemes and full-dimensional vibrational calculations. Mol. Phys. 2015, 113, 1823–1833. [Google Scholar] [CrossRef]
- Manzhos, S.; Chan, M.; Carrington, T. Communication: Favorable dimensionality scaling of rectangular collocation with adaptable basis functions up to 7 dimensions. J. Chem. Phys. 2013, 139, 051101. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Yamashita, K. Calculating anharmonic vibrational frequencies of molecules adsorbed on surfaces directly from ab initio energies with a molecule-independent method: H2O on Pt(111). Surf. Sci. 2011, 605, 616–622. [Google Scholar] [CrossRef]
- Christiansen, O. Vibrational structure theory: New vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties. Phys. Chem. Chem. Phys. 2007, 9, 2942. [Google Scholar] [CrossRef] [PubMed]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.; Yamashita, K. Nonspectral methods for solving the schrödinger equation for electronic and vibrational problems. J. Phys. Chem. Lett. 2011, 2, 2193–2199. [Google Scholar] [CrossRef]
- Yang, W.; Peet, A.C. The collocation method for bound solutions of the Schrödinger equation. Chem. Phys. Lett. 1988, 153, 98–104. [Google Scholar] [CrossRef]
- Peet, A.C.; Yang, W. The collocation method for calculating vibrational bound states of molecular systems—With application to Ar–HCl. J. Chem. Phys. 1989, 90, 1746–1751. [Google Scholar] [CrossRef]
- Yang, W.; Peet, A.C. A method for calculating vibrational bound states: Iterative solution of the collocation equations constructed from localized basis sets. J. Chem. Phys. 1990, 92, 522–526. [Google Scholar] [CrossRef]
- Manzhos, S.; Yamashita, K.; Carrington, T. On the advantages of a rectangular matrix collocation equation for computing vibrational spectra from small basis sets. Chem. Phys. Lett. 2011, 511, 434–439. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. Using rectangular collocation with finite difference derivatives to solve electronic Schrödinger equation. J. Chem. Phys. 2018. accepted. [Google Scholar]
- Boutry, G.; Elad, M.; Golub, G.H.; Milanfar, P. The generalized eigenvalue problem for nonsquare pencils using a minimal perturbation approach. SIAM J. Matrix Anal. Appl. 2005, 27, 582–601. [Google Scholar] [CrossRef]
- Manzhos, S.; Wang, X.; Carrington, T. A multimode-like scheme for selecting the centers of Gaussian basis functions when computing vibrational spectra. Chem. Phys. 2018, 509, 139–144. [Google Scholar] [CrossRef]
- Chan, M.; Yamashita, K.; Carrington, T.; Manzhos, S. Towards accurate spectroscopic identification of species at catalytic surfaces: Anharmonic vibrations of formate on AuPt. MRS Proc. 2012, 1484, imrc12-1484-7a-0016. [Google Scholar] [CrossRef]
- Manzhos, S.; Yamashita, K.; Carrington, T. Using a neural network based method to solve the vibrational Schrödinger equation for H2O. Chem. Phys. Lett. 2009, 474, 217–221. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. Using an internal coordinate gaussian basis and a space-fixed cartesian coordinate kinetic energy operator to compute a vibrational spectrum with rectangular collocation. J. Chem. Phys. 2016, 145, 224110. [Google Scholar] [CrossRef] [PubMed]
- Kamath, A.; Vargas-Hernández, R.A.; Krems, R.V.; Carrington, T.; Manzhos, S. Neural networks vs Gaussian process regression for representing potential energy surfaces: A comparative study of fit quality and vibrational spectrum accuracy. J. Chem. Phys. 2018, 148, 241702. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.-G.; Ho, T.-S.; Rabitz, H. The collocation method based on a generalized inverse multiquadric basis for bound-state problems. Comput. Phys. Commun. 1998, 113, 168–179. [Google Scholar] [CrossRef]
- Carter, S.; Handy, N.C.; Demaison, J. The rotational levels of the ground vibrational state of formaldehyde. Mol. Phys. 1997, 90, 729–738. [Google Scholar] [CrossRef]
- Sobol, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T. An improved neural network method for solving the Schrödinger equation. Can. J. Chem. 2009, 87, 864–871. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).