Geometric Construction of Some Lehmer Means

Abstract

The main aim of this paper is to contribute to the recently initiated research concerning geometric constructions of means, where the variables are appearing as line segments. The present study shows that all Lehmer means of two variables for integer power k and for $k=\frac{m}{2}$, where m is an integer, can be geometrically constructed, that Lehmer means for power $k=0,1$ and 2 can be geometrically constructed for any number of variables and that Lehmer means for power $k=1/2$ and $-1$ can be geometrically constructed, where the number of variables is $n=2^m$ and m is a positive integer.

1. Introduction

Means and averages have been used at least since human beings began to make easy calculations. Babylonian wedge-shaped scriptures in clay, between 3000 and 4000 years old, show how their mathematicians devised procedures to determine square roots by recursive use of means; see [1,2,3].

The classic Greek scientists (around 500 B.C.) studied the Babylonian texts and further developed the understanding of the Pythagorean means, i.e., the arithmetic, the geometric and the harmonic means of two variables, and used them in their study of mathematics and music. They did not have the arsenal of symbols that are available to modern mathematicians for expressing the different means, but had to resort to the Greek language to describe the functional relation between the variables and the mean. They named the variables “the first number” (the small variable) and “the third number” (the large variable) and called the mean “the second number” and defined the mean through proportions between the two variables and the sought after mean. The Lehmer mean of two variables with power two, the contra-harmonic mean, could then be described as: the difference between “the second number” and the “the first number” is to the difference between “the third number” and “the second number” as “the third number” is to “the first number”. By varying these relations, the Pythagoreans defined a number of different means, 10 in all, that all have the property that the size of the mean is between the two variables; see [2].

After these early discoveries, means and their inequalities attracted great attention in mathematical research; see, e.g., the book [4] by P.S. Bullen, D. S. Mitrinovic and P. M. Vasic from 1988 and also the book [5] by C. Niculescu and L.E. Persson from 2018, where also the close connection to convexity was investigated. See also [6,7,8,9]. We will now continue by putting the most elementary situation presented before into this more general frame.

Today, we would require the following of a mean, m, as a function of two positive variables $a\le b,$ $m=M(a,b),$ $(a,b)\in \mathbb{R}:$

M1	Internality:	$a\le m\le b$
M2	Symmetry:	$M(a,b)=M(b,a)$
M3	Homogeneity:	$M(ka,kb)=kM(a,b)$
M4	Isotonicity:	if $a_1>a_2$ and $b_1>b_2,$ then $M(a_1,b_1)>M(a_2,b_2)$
M5	Equality:	if $a=b,$ then $M(a,b)=a$

Note that M5 is a special case of M1, so in principle, only the four requirements M1–M4 are necessary. There are 10 means listed that were defined by the Pythagoreans. We also consider the quadratic mean and one permutation that was missed by the Greeks; see [2]. In Table 1, we have listed these twelve means and related them to the modern conditions M1–M5 of means (Y for yes and N for no).

Table 1. The basic classic (Babylonian/Hellenistic) means defined by proportions between the variables and the mean.

Mean	Proportions	Modern Definition	M1	M2	M3	M4	M5
1. Arithmetic	$\frac{m-a}{b-m}=1$	$m=\frac{a+b}{2}$	Y	Y	Y	Y	Y
2. Geometric	$\frac{m-a}{b-m}=\frac{a}{m}=\frac{m}{b}$	$m=\sqrt{ab}$	Y	Y	Y	Y	Y
3. Harmonic	$\frac{m-a}{b-m}=\frac{a}{b}$	$m=\frac{2ab}{a+b}$	Y	Y	Y	Y	Y
4. Contraharmonic	$\frac{m-a}{b-m}=\frac{b}{a}$	$m=\frac{a^2+b^2}{a+b}$	Y	Y	Y	Y	Y
5. Quadratic	$\frac{m-a}{b-m}=\frac{b+m}{m+a}$	$m=\sqrt{\frac{a^2+b^2}{2}}$	Y	Y	Y	Y	Y
6.	$\frac{m-a}{b-m}=\frac{m}{a}$	$m=\frac{b-a}{2}+\sqrt{{\left(\frac{b-a}{2}\right)}^2+a^2}$	Y	N	Y	N	Y
7.	$\frac{m-a}{b-m}=\frac{b}{m}$	$m=-\frac{b-a}{2}+\sqrt{{\left(\frac{b-a}{2}\right)}^2+a^2}$	Y	N	Y	N	Y
8.	$\frac{b-a}{m-a}=\frac{b}{a}$	$m=b-\frac{{(b-a)}^2}{b}$	Y	N	Y	Y	Y
9.	$\frac{b-a}{b-m}=\frac{b}{a}$	$m=a+\frac{{(b-a)}^2}{b}$	Y	N	Y	N	Y
10.	$\frac{b-a}{m-a}=\frac{m}{a}$	$m=\frac{a}{2}+\frac{1}{2}\sqrt{4ab-3a^2}$	Y	N	Y	Y	Y
11.	$\frac{b-a}{b-m}=\frac{m}{a}$	$m=max\left\{b-a,a\right\}$	Y	N	Y	N	Y
12.	$\frac{b-a}{b-m}=\frac{b}{m}$	$m=\frac{b^2}{2b-a}$	Y	N	Y	Y	Y

The approach of the classic Greeks to mathematics often started in geometry. For example, Euclid proved his famous theorem of the greatest common divisor geometrically. This was also the case for their study of means. They defined the variables expressed as lengths of line segments and devised methods for geometric construction of the different means. An example is shown in Figure 1, where a and $b,$ $b\le a,$ are the variables, $A=\frac{a+b}{2}$ is the arithmetic mean, $G=\sqrt{ab}$ is the geometric mean, $H=\frac{2ab}{a+b}$ is the harmonic mean, $Q=\sqrt{\frac{1}{2}(a^2+b^2)}$ is the quadratic mean and $C=\frac{a^2+b^2}{a+b}$ is the contraharmonic mean. It is easy to verify the correctness of the constructions. The geometry verifies the basic inequalities: $b\le H\le G\le A\le Q\le C\le a.$

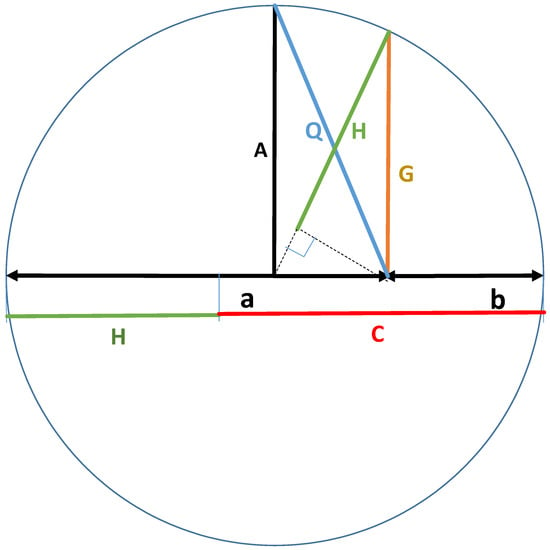
Figure 1. Classic Greek construction of Pythagorean means.

It is relatively easy to construct the rest of the basic classical means of two variables, Mean Nos. 6–12 in Table 1.

The introduction of mathematical symbols in the 16th Century led to remarkable progress in the use and manipulation of such symbols. An example is the search for integer variables resulting in integer power means; see [10,11,12,13,14]. In particular, the importance of the use of power means for calculating effective conductivities in laminates was pointed out in [12,13]. This avenue is still pursued by many mathematicians today, almost to the point where the possibilities and elegance of geometric construction are being neglected or have been relegated to recreational mathematics. However, recently, the classic Greek idea of the geometric construction of means has attracted renewed interest; see [15,16,17,18,19,20,21,22,23], but now based on the modern expressions for means; see [4,7]. Moreover, in [24] (see also [25,26]), we raised the question of doing such Greek-type geometric constructions also for more general means and variables. In particular, the novelty of [24,25] was to demonstrate the geometric construction of:

$$P_2^{2^k}(a,b)={\left(\frac{a^{2^k}+b^{2^k}}{2}\right)}^{\frac{1}{2^k}}$$

for all integer values of the power k and of:

$$P_n^{2^k}(a_1,\dots ,a_n)={\left(\frac{1}{n}(a_1^{2^k}+\dots +a_n^{2^k})\right)}^{\frac{1}{2^k}},$$

where the number of variables is $n=2^m.$ Here, m is a positive integer. The purpose of the present paper is to contribute to this process by showing that the tools developed in [24,25] can be further refined and can be used also in the geometric construction of a number of Lehmer means.

A general two-parameter scale of means is the Gini means of n variables $a_1,\dots ,a_n$ with equal weights, defined by:

$$\begin{array}{ccc}\hfill G_n^{r,s}(a_1,\dots ,a_n)& =& {\left(\frac{a_1^r+\dots +a_n^r}{a_1^s+\dots +a_n^s}\right)}^{\frac{1}{r-s}}\mathrm{for}(r,s)\in \mathbb{R}\mathrm{and}r\ne s,\hfill \\ \hfill G_n^{r,s}(a_1,\dots ,a_n)& =& {\left(a_1{a}_2\dots a_n\right)}^{\frac{1}{n}}\mathrm{for}r=s.\hfill \end{array}$$

Two subsets of Gini means are the power means and the Lehmer means given by setting $(r,s)=(k,0)$ and $(r,s)=(k,k\pm 1),$ respectively, with the power $k\in \mathbb{R}.$

The scale of power means is then defined by:

$$\begin{array}{ccc}\hfill P_n^k(a_1,\dots ,a_n)& =& {\left(\frac{a_1^k+\dots +a_n^k}{n}\right)}^{\frac{1}{k}},\mathrm{for}k\ne 0,\hfill \\ \hfill P_n^0(a_1,\dots ,a_n)& =& {(a_1{a}_2\dots a_n)}^{\frac{1}{n}}\mathrm{for}k=0,\hfill \end{array}$$

and the Lehmer means by:

$$L_n^k(a_1,\dots ,a_n)=\frac{a_1^k+\dots +a_n^k}{a_1^{k-1}+\dots +a_n^{k-1}}.$$

Power means and Lehmer means are consistent with the five requirements for means listed above. In addition, they both adhere to two further conditions:

M6	Power size:	$P_n^k(a_1,\dots ,a_n)>P_n^l(a_1,\dots ,a_n)$ when $k>l.$
M7	Infinite power:	${\displaystyle \underset{k\to +\infty }{lim}}{P}_n^k(a_1,\dots ,a_n)=max\left\{a_1,\dots ,a_n\right\}$ and ${\displaystyle \underset{l\to -\infty }{lim}}{P}_n^l(a_1,\dots ,a_n)=min\left\{a_1,\dots ,a_n\right\}.$

This corresponds to these scales of means having the interesting property that they are nondecreasing in k from the smallest possible mean ($min\left\{a_1,a_2,\dots ,a_n\right\}$) to the greatest possible mean ($max\left\{a_1,a_2,\dots ,a_n\right\}$) in the modern definitions. The Lehmer mean was introduced by D. H. Lehmer in 1971; see [27]. He discovered three fundamental connections between power means and Lehmer means that will be used later in this paper:

$$1.P_2^1(L_2^k(a,b),L_2^{2-k}(a,b))=P_2^1(a,b)\mathrm{or}A(L_2^k(a,b),L_2^{2-k}(a,b))=A(a,b).$$

$$2.P_2^0(L_2^k(a,b),L_2^{1-k}(a,b))=P_2^0(a,b)\mathrm{or}G(L_2^k(a,b),L_2^{1-k}(a,b))=G(a,b).$$

$$3.P_2^{-1}(L_2^k(a,b),L_2^{-k}(a,b))=P_2^{-1}(a,b)\mathrm{or}H(L_2^k(a,b),L_2^{-k}(a,b))=H(a,b).$$

In addition, we have that:

$$A=P_n^1(a_1,\dots ,a_n)=L_n^1(a_1,\dots ,a_n),$$

$$H=P_n^{-1}(a_1,\dots ,a_n)=L_n^0(a_1,\dots ,a_n),$$

$$G=P_2^0(a,b)=L_2^{\frac{1}{2}}(a,b),$$

and:

$$C=L_2^2(a,b)=2P_2^1-P_2^{-1}(a,b).$$

The crossed ladders diagram shows a number of properties, which assist in the construction of means. The Pythagorean and a number of other power means of two variables a and b can be constructed in this diagram; see [16] (cf. also [24,25,26]).

This paper is organized as follows: In Section 2, a number of Lehmer means of two variables are constructed using the properties of the crossed ladders diagram. Section 3 is reserved for presenting some further results and remarks that we judge are of particular interest for further research in this direction. Especially, we show that it is possible to construct Lehmer means with power $k=0,1$ and 2 for any number of variables. Moreover, it is shown that all Lehmer means of two variables for integer power k and for $k=\frac{m}{2}$, where m is an integer, can be constructed by the use of the formulas discovered by Lehmer mentioned above and by using the symmetric crossed ladders diagram. Finally, we show that the Lehmer means for $k=1/2$ and $k=-1,$ where the number of the variables are $n=2^m$ (m is a positive integer), can be geometrically constructed.

2. Geometric Constructions of Some Lehmer Mean of Two Variables

The following Lehmer means will be constructed by the use of the crossed ladders properties:

$$L_2^3=\frac{a^3+b^3}{a^2+b^2}=\frac{(a+b)(a^2-ab+b^2)}{a^2+b^2},$$

$$L_2^2=\frac{a^2+b^2}{a^1+b^1}=\frac{a^2+b^2}{a+b},$$

$$L_2^{\frac{3}{2}}=\frac{a^{\frac{3}{2}}+b^{\frac{3}{2}}}{a^{\frac{1}{2}}+b^{\frac{1}{2}}}=a-\sqrt{ab}+b,$$

$$L_2^1=\frac{a^1+b^1}{a^0+b^0}=\frac{a+b}{2},$$

$$L_2^{\frac{1}{2}}=\frac{a^{\frac{1}{2}}+b^{\frac{1}{2}}}{a^{-\frac{1}{2}}+b^{-\frac{1}{2}}}=\sqrt{ab},$$

$$L_2^0=\frac{a^0+b^0}{a^{-1}+b^{-1}}=\frac{2ab}{a+b},$$

$$L_2^{-\frac{1}{2}}=\frac{a^{-\frac{1}{2}}+b^{-\frac{1}{2}}}{a^{-\frac{3}{2}}+b^{-\frac{3}{2}}}=\frac{ab}{a-\sqrt{ab}+b},$$

$$L_2^{-1}=\frac{a^{-1}+b^{-1}}{a^{-2}+b^{-2}}=\frac{ab(a+b)}{a^2+b^2},$$

$$L_2^{-\frac{3}{2}}=\frac{a^{-\frac{3}{2}}+b^{-\frac{3}{2}}}{a^{-\frac{5}{2}}+b^{-\frac{5}{2}}}=\frac{ab\left(a-\sqrt{ab}+b\right)}{a^2+ab+b^2-(a+b)\sqrt{ab}},$$

$$L_2^{-2}=\frac{a^{-2}+b^{-2}}{a^{-3}+b^{-3}}=\frac{ab(a^2+b^2)}{(a+b)(a^2-ab+b^2)}$$

and:

$$L_2^{-3}=\frac{a^{-3}+b^{-3}}{a^{-4}+b^{-4}}=\frac{ab(a^3+b^3)}{a^4+b^4}.$$

2.1. Geometric Construction of $L_2^{-\frac{1}{2}},L_2^0,L_2^{\frac{1}{2}},L_2^1,L_2^{\frac{3}{2}}$ and $L_2^2$

Since $L_2^1=\frac{a+b}{2},$ $L_2^{\frac{1}{2}}=\sqrt{ab}$ and $L_2^0=\frac{2ab}{a+b}$ are identical to $A,G$ and H for power means, they may be constructed using the methods shown in [25]; see Figure 2 and Figure 3. The arithmetic mean $A(a,b)=\frac{a+b}{2}$ corresponds to the vertical distance between the “floor” and the “roof” at the midpoint between the walls in the basic crossed ladders structure. By use of similar triangles in Figure 2, it has been shown that the harmonic mean is equal to the vertical line between the floor and the roof through the intersection of the diagonals:

$$H(a,b)=IJ=2c=\frac{2ab}{a+b}.$$

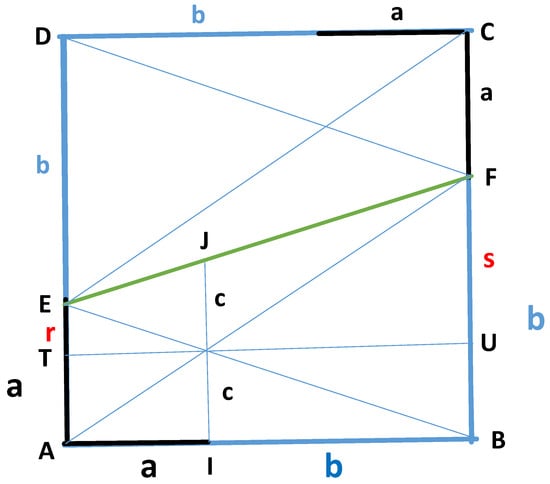
Figure 2. The symmetric crossed ladders diagram.

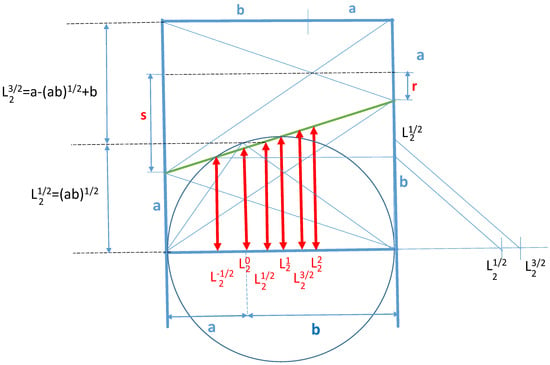
Figure 3. Geometric constructions of $L_2^{-\frac{1}{2}},L_2^0,L_2^{\frac{1}{2}},L_2^1,L_2^{\frac{3}{2}}$ and $L_2^2$.

From similar triangles, it also follows that the geometric mean of $r=GE=a-c$ and $s=HF=b-c$ is equal to $c,$ i.e.,

$$G(r,s)=c=\sqrt{rs}.$$

From the latter formula, the geometric mean of a and b can be constructed by lowering the “floor” in the crossed ladders diagram in Figure 2 downwards until the diagonals of the enlarged crossed ladders intersect at the existing “floor”, $AB$. Then, r and s in the enlarged crossed ladders diagram will be equal to a and $b.$ The vertical distance from the intersection of the new diagonals in the existing “floor” and the “roof” is then the geometric mean of a and $b.$ The above formulas and constructions were demonstrated by Høibakk et al. [24,26].

In Figure 3, we have chosen to determine $L_2^{\frac{1}{2}}=\sqrt{ab}$ as the height in a right-angle triangle. The hypotenuse is $h=a+b$, and the height is the vertical distance from the point where a and b meet in the periphery of a circle with radius $r=\frac{a+b}{2}$ over the hypotenuse.

$L_2^{\frac{3}{2}}$ can, as shown in Figure 3, directly be constructed from:

$$L_2^{\frac{3}{2}}=a-\sqrt{ab}+b.$$

$L_2^{-\frac{1}{2}}$ can be constructed from:

$$\frac{L_2^{-\frac{1}{2}}}{L_2^{\frac{1}{2}}}=\frac{\frac{ab}{a-\sqrt{ab}+b}}{\sqrt{ab}}=\frac{\sqrt{ab}}{a-\sqrt{ab}+b}=\frac{L_2^{\frac{1}{2}}}{L_2^{\frac{3}{2}}}$$

using similar triangles.

From Figure 2, it follows that:

$$r=a-c=a-\frac{ab}{a+b}=\frac{a^2}{a+b}$$

(1)

and:

$$s=b-c=b-\frac{ab}{a+b}=\frac{b^2}{a+b},$$

(2)

resulting in the construction of:

$$L_2^2=r+s=\frac{a^2+b^2}{a+b}.$$

Hence, the geometric constructions of $L_2^{-\frac{1}{2}},L_2^0,L_2^{\frac{1}{2}},L_2^1,L_2^{\frac{3}{2}}$ and $L_2^2$ can be illustrated as in Figure 3.

2.2. Construction of $L_2^{-3},L_2^{-2},L_2^{-\frac{3}{2}},L_2^{-1}$ and $L_2^3$

From (1) and (2), one can deduce that:

$$\frac{r}{s}=\frac{\frac{a^2}{a+b}}{\frac{b^2}{a+b}}=\frac{a^2}{b^2}.$$

(3)

This relation can be used to construct the remaining five means $P_L^{-3},P_L^{-2},P_L^{-\frac{3}{2}},P_L^{-1}$ and $P_L^3$. From the list of the Lehmer means above, one can easily derive that:

$$\frac{L_2^{-1}}{2L_2^1}=\frac{\frac{ab(a+b)}{a^2+b^2}}{2\frac{a+b}{2}}=\frac{ab}{a^2+b^2},$$

(4)

$$\frac{L_2^{-2}}{L_2^2}=\frac{\frac{ab(a^2+b^2)}{(a+b)(a^2-ab+b^2)}}{\frac{a^2+b^2}{a+b}}=\frac{ab}{a^2-ab+b^2},$$

(5)

$$\frac{L_2^{-\frac{3}{2}}}{L_2^{\frac{3}{2}}}=\frac{\frac{ab\left(a-\sqrt{ab}+b\right)}{a^2+ab+b^2-(a+b)\sqrt{ab}}}{a-\sqrt{ab}+b}=\frac{ab}{a^2+ab+b^2-(a+b)\sqrt{ab}},$$

(6)

and:

$$\frac{L_2^3}{L_2^{-1}}=\frac{\frac{(a+b)(a^2-ab+b^2)}{a^2+b^2}}{\frac{ab(a+b)}{a^2+b^2}}=\frac{a^2-ab+b^2}{ab}.$$

(7)

These relations can be used to construct $L_2^{-2},L_2^{-\frac{3}{2}},L_2^{-1}$ and $L_2^3$ by application of (3). If one constructs crossed ladders diagrams where the new variables are $a_1=\sqrt{ab},$ $b_1=\sqrt{a^2+b^2},$ $a_2=\sqrt{ab},$ $b_2=\sqrt{a^2-ab+b^2},$ $a_3=\sqrt{ab},$ $b_3=\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}},$ $a_4=\sqrt{a^2-ab+b^2}$ and $b_4=\sqrt{ab}$, respectively, the line segments $r_i$ and $s_i$ in those crossed ladders diagrams can be determined by:

$$(r_i,s_i)=(\frac{a_i^2}{a_i+b_i},\frac{b_i^2}{a_i+b_i}).$$

Then, the relations $\frac{r_i}{s_i}$ will be:

$$\mathrm{From}(4):\frac{r_1}{s_1}=\frac{a_1^2}{b_1^2}=\frac{ab}{a^2+b^2}=\frac{L_2^{-1}}{2L_2^1},$$

$$\mathrm{From}(5):\frac{r_2}{s_2}=\frac{a_2^2}{b_2^2}=\frac{ab}{a^2-ab+b^2}=\frac{L_2^{-2}}{L_2^2},$$

$$\mathrm{From}(6):\frac{r_3}{s_3}=\frac{a_3^2}{b_3^2}=\frac{ab}{a^2+ab+b^2-(a+b)\sqrt{ab}}=\frac{L_2^{-\frac{3}{2}}}{L_2^{\frac{3}{2}}},$$

and:

$$\mathrm{From}(7):\frac{r_4}{s_4}=\frac{a_4^2}{b_4^2}=\frac{a^2-ab+b^2}{ab}=\frac{L_2^3}{L_2^{-1}}.$$

The geometric construction of $L_2^{-2},L_2^{-\frac{3}{2}},L_2^{-1}$ and $L_2^3$ can then be performed in a new crossed ladders diagram using similar triangles.

Figure 3 shows the construction of $\sqrt{ab}$ and of $a-\sqrt{ab}+b.$ The geometric constructions of:

$$\sqrt{a^2+b^2},\sqrt{a^2\pm ab+b^2},$$

$$\sqrt{(a+b)\sqrt{ab}}$$

and:

$$\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}$$

are shown in Figure 4.

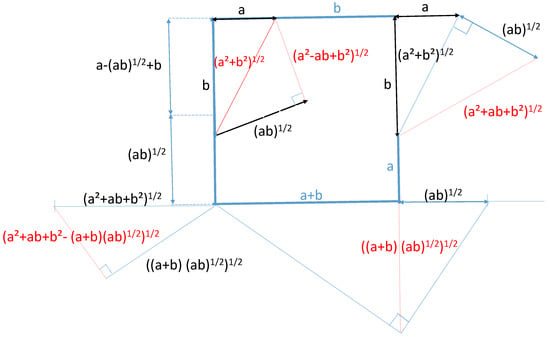
Figure 4. Geometric constructions of $\sqrt{a^2+b^2}$, $\sqrt{a^2\pm ab+b^2},$ $\sqrt{(a+b)\sqrt{ab}}$ and $\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}$.

Moreover, the constructions of:

$$r_1=\frac{ab}{\sqrt{ab}+\sqrt{a^2+b^2}},\mathrm{and}{s}_1=\frac{a^2+b^2}{\sqrt{ab}+\sqrt{a^2+b^2}}$$

are illustrated in Figure 5, while the geometric constructions of:

$$r_2=\frac{ab}{\sqrt{ab}+\sqrt{a^2-ab+b^2}},$$

$$s_2=\frac{a^2-ab+b^2}{\sqrt{ab}+\sqrt{a^2-ab+b^2}},$$

$$r_3=\frac{ab}{\sqrt{ab}+\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}},$$

$$s_3=\frac{a^2+ab+b^2-(a+b)\sqrt{ab}}{\sqrt{ab}+\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}},$$

$$r_4=\frac{a^2-ab+b^2}{\sqrt{ab}+\sqrt{a^2-ab+b^2}}$$

and:

$$s_4=\frac{ab}{\sqrt{ab}+\sqrt{a^2-ab+b^2}}$$

are illustrated in Figure 6 and Figure 7.

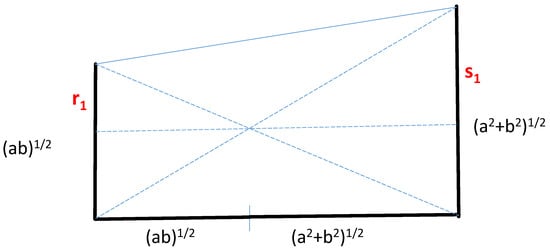
Figure 5. Geometric constructions of $r_1=\frac{ab}{\sqrt{ab}+\sqrt{a^2+b^2}}$ and $s_1=\frac{a^2+b^2}{\sqrt{ab}+\sqrt{a^2+b^2}}$.

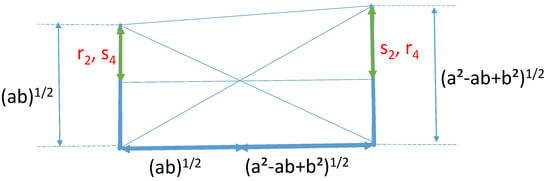
Figure 6. Geometric constructions of $r_2=s_4=\frac{ab}{\sqrt{ab}+\sqrt{a^2-ab+b^2}}$ and $s_2=r_4=\frac{a^2-ab+b^2}{\sqrt{ab}+\sqrt{a^2-ab+b^2}}$.

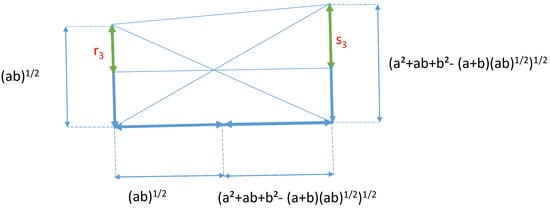
Figure 7. Geometric constructions of $r_3=\frac{ab}{\sqrt{ab}+\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}}$ and $s_3=\frac{a^2+ab+b^2-(a+b)\sqrt{ab}}{\sqrt{ab}+\sqrt{a^2+ab+b^2-(a+b)\sqrt{ab}}}$.

The last mean, $L_2^{-3},$ can be constructed by using the equality:

$$\frac{L_2^3}{L_2^{-3}}=\frac{\frac{(a+b)(a^2-ab+b^2)}{a^2+b^2}}{\frac{ab(a^3+b^3)}{a^4+b^4}}=\frac{a^4+b^4}{ab(a^2+b^2)}.$$

(8)

In fact, by using $a_5=r=\frac{a^2}{a+b}$ and $b_5=s=\frac{b^2}{a+b}$ from (1) and (2) as the variables in a new crossed ladders diagram, we can construct:

$$r_5=\frac{{\left(\frac{a^2}{a+b}\right)}^2}{\frac{a^2}{a+b}+\frac{b^2}{a+b}}=\frac{a^4}{(a+b)(a^2+b^2)}$$

and:

$$s_5=\frac{{\left(\frac{b^2}{a+b}\right)}^2}{\frac{a^2}{a+b}+\frac{b^2}{a+b}}=\frac{b^4}{(a+b)(a^2+b^2)}.$$

Adding these values, we get that:

$$r_5+s_5=\frac{a^4+b^4}{(a+b)(a^2+b^2)}.$$

Inserting this value in (8), we find that:

$$\frac{L_2^3}{L_2^{-3}}=\frac{(r_5+s_5)(a+b)}{ab}.$$

(9)

The construction of $G(a,b)=\sqrt{ab}$ has been shown above, and one can use the same method to construct $G_1\left((r_5+s_5),(a+b)\right)=\sqrt{(r_5+s_5)(a+b)}.$ From these values, one can, by using a new crossed ladders diagram where the variables are $a_6=\sqrt{(r_5+s_5)(a+b)}$ and $b_6=\sqrt{ab}$, construct:

$$r_6=\frac{a_6^2}{a_6+b_6}=\frac{(r_5+s_5)(a+b)}{\sqrt{(r_5+s_5)(a+b)}+\sqrt{ab}}$$

and:

$$s_6=\frac{b_6^2}{a_6+b_6}=\frac{ab}{\sqrt{(r_5+s_5)(a+b)}+\sqrt{ab}}.$$

Inserting these relations in (9), we can deduce that:

$$\frac{L_2^3}{L_2^{-3}}=\frac{r_6}{s_6},$$

(10)

and $L_2^{-3}$ can be constructed using similar triangles.

The constructions of $r_5,$ $s_5,$ $G_1=\sqrt{(r_5+s_5)(a+b)},$ $r_6$ and $s_6$ are illustrated in Figure 8, Figure 9 and Figure 10.

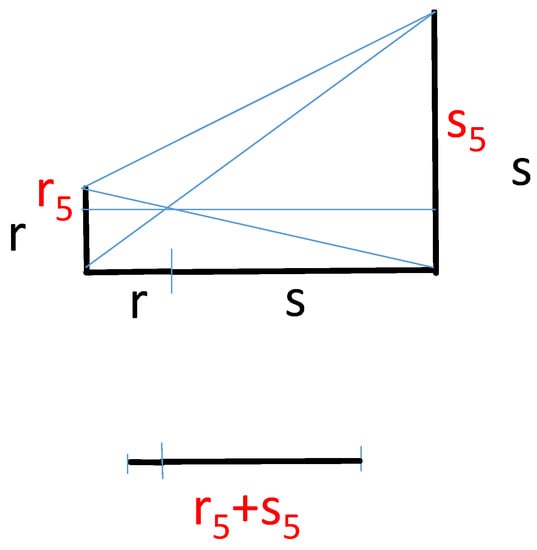
Figure 8. Geometric constructions of $r_5=\frac{a^4}{(a+b)(a^2+b^2)}$, $s_5=\frac{b^4}{(a+b)(a^2+b^2)}$ and $(r_5+s_5)$ from $r=\frac{a^2}{a+b}$ and $s=\frac{b^2}{a+b}$.

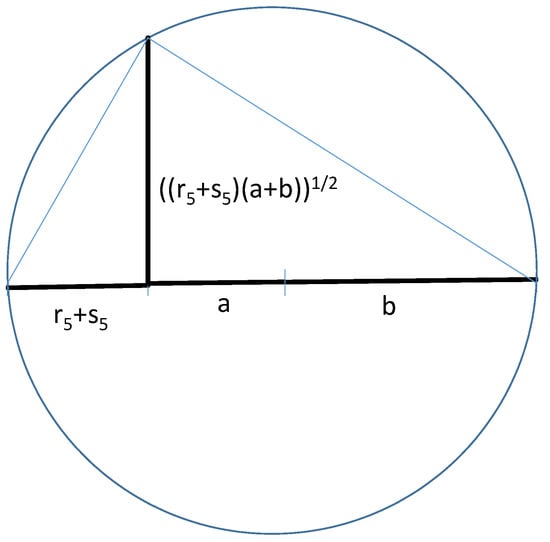
Figure 9. Geometric construction of $\sqrt{(r_5+r_6)(a+b)}$.

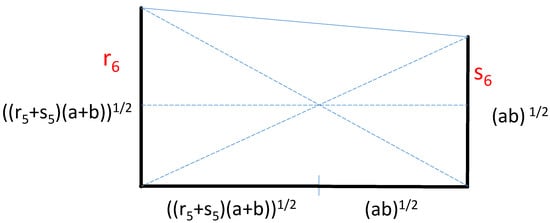
Figure 10. Geometric constructions of $r_6=\frac{(r_5+s_5)(a+b)}{\sqrt{(r_5+s_5)(a+b)}+\sqrt{ab}}$ and $s_6=\frac{ab}{\sqrt{(r_5+s_5)(a+b)}+\sqrt{ab}}$.

Finally, the wanted geometric constructions of $L_2^{-3},L_2^{-2},L_2^{-\frac{3}{2}},L_2^{-1}$ and $L_2^3$ are illustrated in Figure 11.

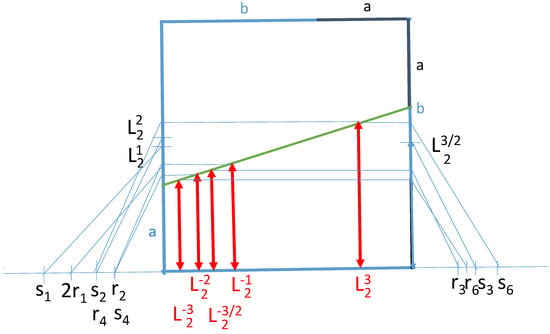
Figure 11. Geometric constructions of $L_2^{-3},L_2^{-2},L_2^{-\frac{3}{2}},L_2^{-1}$ and $L_2^3$.

3. Further Results and Remarks

3.1. On the Geometric Construction of Lehmer Means for Any Number of Variables

3.1.1. Power $k=1$ and $k=0$

$L_n^1(a_1,\dots ,a_n)$ and $L_n^0(a_1,\dots ,a_n)$ are identical to $P_n^1(a_1,\dots ,a_n)$ and $P_n^{-1}(a_1,\dots ,a_n),$ respectively, for power means for all numbers of variables. In [24], the construction of $P_n^1(a_1,\dots ,a_n)$ and $P_n^{-1}(a_1,\dots ,a_n)$ has been demonstrated for all numbers of variables.

3.1.2. Power $k=2$

The Lehmer mean of power two for n variables is:

$$L_n^2=\frac{a_1^2+\dots +a_n^2}{a_1+\dots +a_n}$$

By using (1), we can construct $L_n^2$ for any number of variables. To do this, we construct a crossed ladders diagram with:

$$a=\sqrt{a_1^2+\dots +a_n^2}$$

and $b=(a_1+\dots +a_n)-\sqrt{a_1^2+\dots +a_n^2},$ or

$$b=(a_1+\dots +a_n)-a.$$

We then have:

$$r=\frac{a^2}{a+b}=\frac{{\left(\sqrt{a_1^2+\dots +a_n^2}\right)}^2}{\sqrt{a_1^2+\dots +a_n^2}+(a_1+\dots +a_n)-\sqrt{a_1^2+\dots +a_n^2}}=\frac{a_1^2+\dots +a_n^2}{a_1+\dots +a}=L_n^2.$$

In Figure 12, we have demonstrated this for three variables, $a_1,a_2$ and $a_3.$

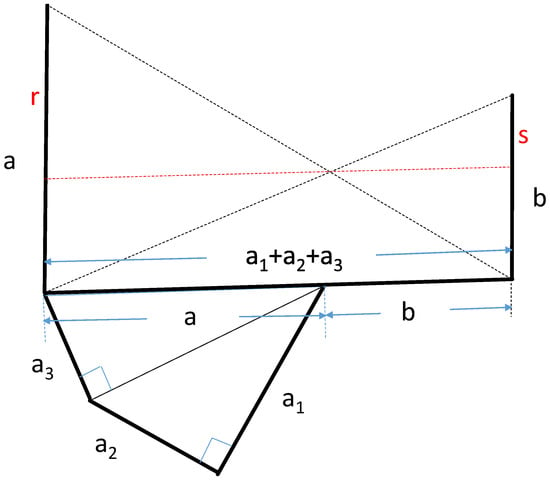
Figure 12. Geometric construction of $r=L_3^2(a_{1,}{a}_2,a_3)$.

3.2. Geometric Construction of All Lehmer Means of Two Variables with Integer Power k and $k=\frac{m}{2}$, Where m Is an Integer

In the Introduction, three identities discovered by D. H. Lehmer were presented:

$$1.A(L_2^k(a,b),L_2^{2-k}(a,b))=A(a,b).$$

$$2.G(L_2^k(a,b),L_2^{1-k}(a,b))=G(a,b).$$

$$3.H(L_2^k(a,b),L_2^{-k}(a,b))=H(a,b).$$

If these identities are rewritten to concern only the Lehmer mean, they will read:

$$L_2^k+L_2^{2-k}=a+b,$$

(11)

$$L_2^k{L}_2^{1-k}=ab,$$

(12)

and:

$$\frac{2L_2^k{L}_2^{-k}}{L_2^k+L_2^{-k}}=\frac{2ab}{a+b},$$

respectively. The latter formula can be rewritten as:

$$\frac{L_2^{-k}}{L_2^k}=\frac{ab}{(a+b)L_2^k-ab}.$$

(13)

Assuming that $L_2^k$ is known, one can, by using the methods shown in this paper, determine $L_2^{-k},$ $L_2^{1-k}$ and $L_2^{2-k}.$

From the identities (11), (12) and (13), the following infinite sequences can be established:

$$\begin{array}{c}{L}_2^1+L_2^1=a+b,L_2^1{L}_2^0=ab\mathrm{and}\frac{L_2^{-1}}{L_2^1}=\frac{ab}{(a+b)L_2^1-ab};\\ L_2^2+L_2^0=a+b,L_2^2{L}_2^{-1}=ab\mathrm{and}\frac{L_2^{-2}}{L_2^2}=\frac{ab}{(a+b)L_2^2-ab};\\ L_2^3+L_2^{-1}=a+b,L_2^3{L}_2^{-2}=ab\mathrm{and}\frac{L_2^{-3}}{L_2^3}=\frac{ab}{(a+b)L_2^3-ab};\\ L_2^4+L_2^{-2}=a+b,L_2^4{L}_2^{-3}=ab\mathrm{and}\frac{L_2^{-4}}{L_2^4}=\frac{ab}{(a+b)L_2^4-ab}.\\ ⋮\end{array}$$

and, correspondingly,

$$\begin{array}{c}{L}_2^{\frac{1}{2}}+L_2^{\frac{3}{2}}=a+b,L_2^{\frac{1}{2}}{L}_2^{\frac{1}{2}}=ab\mathrm{and}\frac{L_2^{-\frac{1}{2}}}{L_2^{\frac{1}{2}}}=\frac{ab}{(a+b)L_2^{\frac{1}{2}}-ab};\\ L_2^{\frac{3}{2}}+L_2^{\frac{1}{2}}=a+b,L_2^{\frac{3}{2}}{L}_2^{-\frac{1}{2}}=ab\mathrm{and}\frac{L_2^{-\frac{3}{2}}}{L_2^{\frac{3}{2}}}=\frac{ab}{(a+b)L_2^{\frac{3}{2}}-ab};\\ L_2^{\frac{5}{2}}+L_2^{-\frac{1}{2}}=a+b,L_2^{\frac{5}{2}}{L}_2^{-\frac{3}{2}}=ab\mathrm{and}\frac{L_2^{-\frac{5}{2}}}{L_2^{\frac{5}{2}}}=\frac{ab}{(a+b)L_2^{\frac{5}{2}}-ab};\\ L_2^{\frac{7}{2}}+L_2^{-\frac{3}{2}}=a+b,L_2^{\frac{7}{2}}{L}_2^{-\frac{5}{2}}=ab\mathrm{and}\frac{L_2^{-\frac{7}{2}}}{L_2^{\frac{7}{2}}}=\frac{ab}{(a+b)L_2^{\frac{7}{2}}-ab}.\\ ⋮\end{array}$$

Starting with the construction of $L_2^1$ and $L_2^{\frac{1}{2}}$ of two variables and by sequential use of the methods demonstrated earlier in this paper, it is easy to see that all Lehmer means of two variables with integer power k and with $k=\frac{m}{2},$ where m is an integer, can geometrically be constructed.

3.3. Final Remarks

Remark 1.

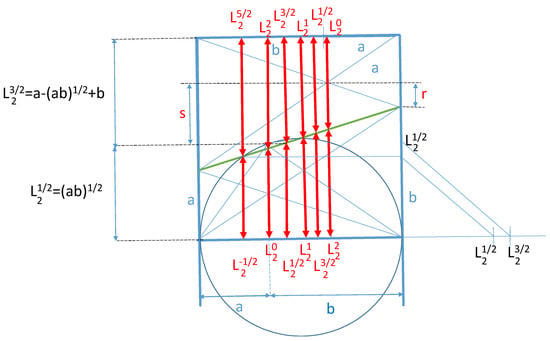
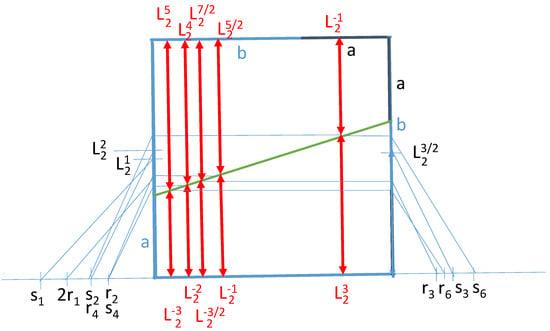
The symmetric crossed ladders diagram represents a practical tool for the geometric construction of these means. Figure 3 and Figure 11 are reprinted in Figure 13 and Figure 14, respectively, where the corresponding Lehmer mean that follows from (11) is constructed in the upper part of the symmetric crossed ladders diagram, using the fact that $L_2^k+L_2^{2-k}=a+b.$

Figure 13. Lehmer means constructed in the bisymmetric crossed ladders diagram.

Figure 14. Lehmer means constructed in the bisymmetric crossed ladders diagram.

Remark 2.

The Lehmer means for $k=\frac{1}{2}$ and $k=-1$ can be constructed, where the number of variables $n=2^m$ (m is a positive integer). To show this, we first need to prove a lemma.

Lemma 3.

Let $n=2,3,4,\dots$ It holds that:

$$L_n^k(a_1,\dots ,a_n){\left(P_n^k(a_1,\dots ,a_n)\right)}^{-k}={\left(P_n^{k-1}(a_1,\dots ,a_n)\right)}^{1-k},$$

(14)

or:

$$L_n^k(a_1,\dots ,a_n)=\frac{{\left(P_n^{k-1}(a_1,\dots ,a_n)\right)}^{1-k}}{{\left(P_n^k(a_1,\dots ,a_n)\right)}^{-k}}.$$

Proof. 

We have that:

$$L_n^k(a_1,\dots ,a_n)=\frac{a_1^k+\dots +a_n^k}{a_1^{k-1}+\dots +a_n^{k-1}},$$

$$P_n^k(a_1,\dots ,a_n)={\left(\frac{1}{n}(a_1^k,\dots ,a_n^k)\right)}^{\frac{1}{k}},$$

and:

$$P_n^{k-1}(a_1,\dots ,a_n)={\left(\frac{1}{n}(a_1^{k-1},\dots ,a_n^{k-1})\right)}^{\frac{1}{k-1}}.$$

Therefore,

$$\begin{array}{ccc}\hfill \frac{{\left(P_n^{k-1}(a_1,\dots ,a_n)\right)}^{1-k}}{{\left(P_n^k(a_1,\dots ,a_n)\right)}^{-k}}& =& \frac{{\left({\left(\frac{1}{n}(a_1^{k-1},\dots ,a_n^{k-1})\right)}^{\frac{1}{k-1}}\right)}^{1-k}}{{\left({\left(\frac{1}{n}(a_1^k,\dots ,a_n^k)\right)}^{\frac{1}{k}}\right)}^{-k}}=\hfill \\ & =& \frac{\frac{1}{n}(a_1^k,\dots ,a_n^k)}{\frac{1}{n}(a_1^{k-1},\dots ,a_n^{k-1})}=\frac{a_1^k,\dots ,a_n^k}{a_1^{k-1},\dots ,a_n^{k-1}}=L_n^k(a_1,\dots ,a_n).\hfill \end{array}$$

The proof is complete. □

$\mathbf{k}=-\mathbf{1}$

Using (14), we find that:

$$L_n^{-1}(a_1,\dots ,a_n)P_n^{-1}(a_1,\dots ,a_n)={\left(P_n^{-2}(a_1,\dots ,a_n)\right)}^2,$$

or

$$\frac{L_n^{-1}(a_1,\dots ,a_n)}{P_n^{-2}(a_1,\dots ,a_n)}=\frac{P_n^{-2}(a_1,\dots ,a_n)}{P_n^{-1}(a_1,\dots ,a_n)}.$$

(15)

In [24], the authors showed that $P_n^{-1}(a_1,\dots ,a_n)$ can be constructed for any number of variables and that $P_n^{-2}(a_1,\dots ,a_n)$ can be constructed where the number of variables $n=2^m.$ For constructing $P_n^{-1}(a_1,\dots ,a_n)$ and $P_n^{-2}(a_1,\dots ,a_n)$, we can then use (15) to construct $L_n^{-1}(a_1,\dots ,a_n),$ where the number of variables $n=2^m.$

$\mathbf{k}=\frac{1}{2}$

From (14), it follows that:

$$L_n^{\frac{1}{2}}(a_1,\dots ,a_n){\left(P_n^{\frac{1}{2}}(a_1,\dots ,a_n)\right)}^{-\frac{1}{2}}={\left(P_n^{-\frac{1}{2}}(a_1,\dots ,a_n)\right)}^{\frac{1}{2}},$$

giving:

$$L_n^{\frac{1}{2}}(a_1,\dots ,a_n)={\left(P_n^{\frac{1}{2}}(a_1,\dots ,a_n)\right)}^{\frac{1}{2}}{\left(P_n^{-\frac{1}{2}}(a_1,\dots ,a_n)\right)}^{\frac{1}{2}},$$

or:

$${\left(L_n^{\frac{1}{2}}(a_1,\dots ,a_n)\right)}^2=P_n^{\frac{1}{2}}(a_1,\dots ,a_n)P_n^{-\frac{1}{2}}(a_1,\dots ,a_n).$$

(16)

In [24], the authors also showed that $P_n^{\frac{1}{2}}(a_1,\dots ,a_n)$ and $P_n^{-\frac{1}{2}}(a_1,\dots ,a_n)$ can be constructed, where the number of variables $n=2^m.$ This means that constructing $P_n^{\frac{1}{2}}(a_1,\dots ,a_n)$ and $P_n^{-\frac{1}{2}}(a_1,\dots ,a_n)$, we can then, using (16), construct $L_n^{\frac{1}{2}}(a_1,\dots ,a_n),$ where the number of variables $n=2^m.$