A New Operational Matrix of Fractional Derivatives to Solve Systems of Fractional Differential Equations via Legendre Wavelets

Abstract

This paper introduces a new numerical approach to solving a system of fractional differential equations (FDEs) using the Legendre wavelet operational matrix method (LWOMM). We first formulated the operational matrix of fractional derivatives in some special conditions using some notable characteristics of Legendre wavelets and shifted Legendre polynomials. Then, the system of fractional differential equations was transformed into a system of algebraic equations by using these operational matrices. At the end of this paper, several examples are presented to illustrate the effectivity and correctness of the proposed approach. Comparing the methodology with several recognized methods demonstrates that the advantages of the Legendre wavelet operational matrix method are its accuracy and the understandability of the calculations.

1. Introduction

Differential and integral operators are the basis of mathematical models, and they are also used as a means of understanding the working principles of natural and artificial systems. Therefore, differential and integral equations are of great importance both theoretically and practically. Such equations have a wide range of applications, including in the physical sciences (such as in physics and engineering) as well as in social science. Systems of differential equations, as differential equations, are often used in issues such as theories of elasticity, dynamics, fluid mechanics, oscillation, and quantum dynamics.

Interest in differential and integral operators has led to the exploration of fractional differential and integral operators by examining these issues further in depth. Owing to a question, the origin of fractional calculus arose in a message from Leibniz to L’Hôpital in 1695. Fractional calculus has received attention in recent years due to its ability to simplify numerous physical, engineering, and economics phenomena such as the fluid dynamic traffic model, damping laws, continuum and statistical mechanics, diffusion processes, solid mechanics, control theory, colored noise, viscoelasticity, electrochemistry, and electromagnetism, among others.

Because a variety of solutions of fractional differential equations (FDEs) cannot be found analytically, numerical and approximate methods are needed. There are a lot of techniques that have been studied by many researchers in solving FDEs and the system of such equations numerically. Some of these techniques are the Adomian decomposition method presented by Song and Wang [1], the collocation method, the improved operational matrix method [2,3,4], the perturbation iteration method introduced by Şenol and Dolapçı [5], the computational matrix method illustrated by Khader et al. [6], the differential transform method demonstrated by Ertürk and Momani [7], the variational iteration method, the Laplace transform method given by Gupta et al. [8], and the fractional complex transform method studied by Ghazanfari and Ghazanfari [9], among others. Kilbas et al. [10] inclusively examined fractional differential and fractional integro-differential equations. In addition, numerical solutions of FDEs and the system of such equations have been presented using the Legendre polynomial operational matrix method [11], Bernstein operational matrix method [12], Genocchi operational matrix method [13], Jacobi operational matrix method [14], Chebyshev wavelet operational matrix method [15], polynomial least squares method (PLSM) [16], Legendre wavelet-like operational matrix method (LWPT) [17], and the Genocchi wavelet-like operational matrix method [18].

This paper focuses on the numerical analysis of a system of fractional order differential equations using the Legendre wavelet operational matrix method. The most important advantage of the proposed method is that it presents an understandable procedure to reduce FDEs and the system of such equations to a system of algebraic equations. First, we begin by presenting some basic definitions and fundamental relations in Section 2 and Section 3, respectively. Then, in Section 4, the operational matrix of the fractional derivate is natively formulated to linear and nonlinear systems of fractional differential equations. Section 5 presents five illustrative examples that were tested with the introduced method. Finally, the last section includes the conclusions.

2. Basic Definitions

The Liouville_Caputo fractional_order derivative, shifted Legendre polynomials, and Legendre wavelets are defined below [19,20].

Definition 1.

The Liouville_Caputo fractional derivative of $u$ is defined as [19]

$$D^{\alpha }u\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{u^{\left(n\right)}\left(\xi \right)}{{\left(t-\xi \right)}^{\alpha +1-n}}d\xi ,n-1<\alpha \le n,n\in \mathrm{N}}.$$

(1)

Some characteristics of the Liouville_Caputo fractional derivative are as follows:

$$D^{\alpha }C=0,$$

(2)

where $C$ is a constant. In addition, there is

$$D^{\alpha }{t}^{\beta }=\{\begin{array}{cc}0,& \beta \in {\mathrm{N}}_{0}and\beta <\lceil \alpha \rceil \\ \frac{\mathsf{\Gamma }\left(\beta +1\right)}{\mathsf{\Gamma }\left(\beta +1-\alpha \right)}{x}^{\beta -\alpha },& \beta \in {\mathrm{N}}_{0}and\beta \ge \lceil \alpha \rceil or\beta \notin \mathrm{N}and\beta >\lfloor \alpha \rfloor \end{array},$$

(3)

in which $\lfloor \alpha \rfloor$ and $\lceil \alpha \rceil$ respectively imply that the largest integer is less than or equal to $\alpha$, and the smallest integer is greater than or equal to $\alpha$.

The Liouville_Caputo fractional order derivative is a linear operation of the integer order derivative

$$D^{\alpha }\left(\eta u\left(t\right)+\zeta v\left(t\right)\right)=\eta D^{\alpha }u\left(t\right)+\zeta D^{\alpha }v\left(t\right),$$

(4)

where $\eta$ and $\zeta$ are constant.

Definition 2.

Let $a$ and $b$ respectively be the parameters of dilation and translation of a single function called the mother wavelet. If $a$ and $b$ change continuously, then we obtain the following family of continuous wavelets [21,22]:

$${\psi }_{ab}\left(t\right)={\left|a\right|}^{-1/2}\psi \left(\frac{t-b}{a}\right),a,b\in R,a\ne 0.$$

(5)

Definition 3.

Let $P_m\left(t\right)$ imply the shifted Legendre polynomials of order $m$. Then $P_m\left(t\right)$ can be formulated as [21]

$$P_m\left(t\right)={\displaystyle \sum _{k=0}^m{\left(-1\right)}^{m+k}\frac{\left(m+k\right)!}{\left(m-k\right)!}\frac{t^k}{{\left(k!\right)}^2}},$$

(6)

and the orthogonality condition is

$${\displaystyle \underset{0}{\overset{1}{\int }}{P}_m\left(t\right)}{P}_n\left(t\right)dt=\{\begin{array}{cc}\frac{1}{2m+1},& form=n\\ 0,& form\ne n\end{array}.$$

(7)

Definition 4.

Let $n$ and $k$ be any positive integer, $m$ be the order of shifted Legendre polynomials, and $t$ be the normalized time. Then the Legendre wavelets ${\psi }_{nm}\left(t\right)=\psi \left(k,n,m,t\right)$ are defined on the interval $\left[0,1\right]$ by [21,22].

$${\psi }_{nm}\left(t\right)=\{\begin{array}{cc}{2}^{\frac{k+1}{2}}\sqrt{m+\frac{1}{2}}{P}_m\left(2^{k}t-n\right),& \frac{n}{2^k}\le t\le \frac{n+1}{2^k}\\ 0,& otherwise\end{array},$$

(8)

where $m=0,1,\dots ,M;n=0,1,\dots ,(2^k-1)$. The coefficient $\sqrt{\frac{m+1}{2}}$ is for orthonormality.

Definition 5.

Let $u\left(t\right)$ and $v\left(t\right)$ be functions defined over $\left[0,1\right]$ and then expanded in the terms of the Legendre wavelet as [21,22]

$$u\left(t\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{c}_{nm}}}{\psi }_{nm}\left(t\right),$$

(9)

where $c_{nm}=\left(u\left(t\right),{\psi }_{nm}\left(t\right)\right)$, in which $\left(.,.\right)$ implies the inner product. If the infinite series in Equation (9) is truncated, then it can be expressed as

$$u\left(t\right)\cong {\displaystyle \sum _{n=0}^{2^k-1}{\displaystyle \sum _{m=0}^M{c}_{nm}{\psi }_{nm}\left(t\right)}}=C^T\psi \left(t\right),$$

(10)

where $C$ and $\psi \left(t\right)$ are matrices, as presented by

$$\begin{array}{l}C={\left[c_{0,0},c_{0,1},\dots ,c_{0,M},\dots ,c_{2,M},\dots ,c_{2^k-1,0},c_{2^k-1,1},\dots ,c_{2^k-1,M}\right]}^T\\ \psi ={\left[{\psi }_{0,0},{\psi }_{0,1},\dots ,{\psi }_{0,M},\dots ,{\psi }_{2,M},\dots ,{\psi }_{2^k-1,0},{\psi }_{2^k-1,1},\dots ,{\psi }_{2^k-1,M}\right]}^T\end{array}.$$

(11)

3. Fundamental Relations

Saadatmandi and Dehghan [11] derived the operational matrix of a fractional derivative by using shifted Legendre polynomials. In this section, we show how we derived the Legendre wavelet operational matrix of fractional derivatives in some special conditions by drawing from Saadatmandi and Dehghan [11]. Additionally, the theorem and corollary related to the Legendre wavelet operational matrix of derivatives illustrated by Mohammadi [21] are cited here as follows.

Theorem 1.

Let $\psi \left(t\right)$ be the Legendre wavelet vector introduced in Equation (8). Then $\psi \left(t\right)$ is expressed as [21,22]

$$\frac{d\psi \left(t\right)}{dt}=D\psi \left(t\right),$$

(12)

where $D$ is the $2^k\left(M+1\right)$ operational matrix of the derivative, which can be stated as

$$D=\left[\begin{array}{cccc}U& O& \cdots & O\\ O& U& \cdots & O\\ ⋮& ⋮& \ddots & ⋮\\ O& O& \cdots & U\end{array}\right],$$

(13)

where $U$ is an $\left(M+1\right)\left(M+1\right)$ matrix and its $\left(r,s\right)\mathrm{th}$ element is written as

$$U_{r,s}=\{\begin{array}{cc}{2}^{k+1}\sqrt{\left(2r-1\right)\left(2s-1\right)},& r=2,\dots ,\left(M+1\right),s=1,\dots ,r-1\mathit{and}(r+s)\mathit{odd}\\ 0,& \mathit{otherwise}\end{array}.$$

(14)

Corollary 1.

Using Equation (12), the operational matrix for the $n\mathrm{th}$ derivative can be stated as [21]

$$\frac{d^n\psi \left(t\right)}{d{t}^n}=D^n\psi \left(t\right),$$

(15)

where $D^n$ is the $n\mathrm{th}$ power of matrix$D$.

Lemma 1.

Let $\psi \left(t\right)$ be the Legendre wavelets vector introduced in Equation (8). Assuming that $k=0$, then

$$D^{\alpha }{\psi }_r\left(t\right)=0,r=0,1,\dots ,\lceil \alpha \rceil -1,\alpha >0.$$

(16)

Proof. 

The desired result can be obtained by using Equations (2) and (4) in Equation (8). □

Theorem 2.

Let $\psi \left(t\right)$ be the Legendre wavelets vector introduced in Equation (8). Supposing that $k=0$ and $\alpha >0$, then

$$D^{\alpha }\psi \left(t\right)\cong D^{\left(\alpha \right)}\psi \left(t\right),$$

(17)

where $D^{\left(\alpha \right)}$ is the $(M+1)x(M+1)$ operational matrix of the fractional derivative of the order $\alpha >0,N-1<\alpha \le N$ in the Liouville_Caputo sense and can be stated as

$$D^{\left(\alpha \right)}=\left(\begin{array}{cccc}0& 0& \cdots & 0\\ ⋮& ⋮& \cdots & ⋮\\ 0& 0& \cdots & 0\\ {\displaystyle \sum _{h=\lceil \alpha \rceil }^{\lceil \alpha \rceil }{\xi }_{\lceil \alpha \rceil ,0,h}}& {\displaystyle \sum _{h=\lceil \alpha \rceil }^{\lceil \alpha \rceil }{\xi }_{\lceil \alpha \rceil ,1,h}}& \cdots & {\displaystyle \sum _{h=\lceil \alpha \rceil }^{\lceil \alpha \rceil }{\xi }_{\lceil \alpha \rceil ,m,h}}\\ ⋮& ⋮& \cdots & ⋮\\ {\displaystyle \sum _{h=\lceil \alpha \rceil }^r{\xi }_{\mathrm{r},0,h}}& {\displaystyle \sum _{h=\lceil \alpha \rceil }^r{\xi }_{\mathrm{r},1,h}}& \cdots & {\displaystyle \sum _{h=\lceil \alpha \rceil }^r{\xi }_{\mathrm{r},\mathrm{m},h}}\\ ⋮& ⋮& \cdots & ⋮\\ {\displaystyle \sum _{h=\lceil \alpha \rceil }^m{\xi }_{\mathrm{m},0,h}}& {\displaystyle \sum _{h=\lceil \alpha \rceil }^m{\xi }_{\mathrm{m},1,h}}& \cdots & {\displaystyle \sum _{h=\lceil \alpha \rceil }^m{\xi }_{\mathrm{m},\mathrm{m},h}}\end{array}\right),$$

(18)

where ${\xi }_{r,s,h}$ is written as

$${\xi }_{r,s,h}=\sqrt{2r+1}\sqrt{2s+1}{\displaystyle \sum _{l=0}^s\frac{{(-1)}^{r+s+h+l}(r+h)!(s+l)!}{(r-h)!h!\mathsf{\Gamma }(h-\alpha +1)(s-l)!{(l!)}^2(h+l-\alpha +1)}}.$$

(19)

Consider in $D^{\left(\alpha \right)}$ that the first $\lceil \alpha \rceil$ rows are all zero.

Proof. 

Presume that ${\psi }_r(t)$ is the $r\mathrm{th}$ element of the vector $\psi \left(t\right)$ introduced in Equation (11), where $r=nM+(m+1),m=0,1,\dots ,M,n=0,1,\dots ,(2^k-1)$. Then ${\psi }_r\left(t\right)$ can be stated as

$${\psi }_r(t)=2^{\frac{k+1}{2}}\sqrt{r+\frac{1}{2}}{P}_r(2^{k}t-n){\chi }_{\left[\frac{n}{2^k},\frac{n+1}{2^k}\right]}.$$

(20)

Accepting that $k=0$, and by using the shifted Legendre polynomial, we obtain

$${\psi }_r(t)=\sqrt{2}\sqrt{r+\frac{1}{2}}{\displaystyle \sum _{h=0}^r\frac{{\left(-1\right)}^{r+h}(r+h)!}{(r-h)!{(h!)}^2}}{t}^h{\chi }_{\left[0,1\right]}.$$

(21)

If we use Equations (3), (4), and (21), then we have

$$\begin{array}{cc}\hfill D^{\left(\alpha \right)}{\psi }_r\left(t\right)& =\sqrt{2}\sqrt{r+\frac{1}{2}}{\displaystyle \sum _{h=0}^r\frac{{\left(-1\right)}^{r+h}(r+h)!}{(r-h)!{(h!)}^2}}{D}^{\alpha }(t^h){\chi }_{\left[0,1\right]}\hfill \\ & =\sqrt{2r+1}{\displaystyle \sum _{h=\lceil \alpha \rceil }^r\frac{{\left(-1\right)}^{r+h}(r+h)!}{(r-h)!(h!)\mathsf{\Gamma }\left(h-\alpha +1\right)}{t}^{h-\alpha }}{\chi }_{\left[0,1\right]},\hspace{1em}r=\lceil \alpha \rceil ,\dots ,m.\hfill \end{array}$$

(22)

Approximating $t^{h-\alpha }$ by $(m+1)$ terms of the Legendre wavelets, then we obtain

$$t^{h-\alpha }\cong {\displaystyle \sum _s^m{b}_{h,s}{\psi }_s\left(t\right)},$$

(23)

where

$$\begin{array}{cc}\hfill b_{h,s}={\displaystyle \underset{0}{\overset{1}{\int }}{t}^{h-\alpha }{\psi }_s\left(t\right)dt}& =\sqrt{2}\sqrt{s+\frac{1}{2}}{\displaystyle \sum _{l=0}^s\frac{{(-1)}^{s+l}(s+l)!}{\left(s-l\right)!{(l!)}^2}}{\displaystyle \underset{0}{\overset{1}{\int }}{t}^{h+l-\alpha }dt}\hfill \\ & =\sqrt{2s+1}{\displaystyle \sum _{l=0}^s\frac{{(-1)}^{s+l}(s+l)!}{\left(s-l\right)!{(l!)}^2(h+l-\alpha +1)}}\hfill \end{array}.$$

(24)

Utilizing Equations (22) and (24), we get

$$\begin{array}{cc}\hfill D^{\alpha }{\psi }_r\left(t\right)& \cong \sqrt{2r+1}{\displaystyle \sum _{h=\lceil \alpha \rceil }^r{\displaystyle \sum _{s=0}^m\frac{{\left(-1\right)}^{r+h}(r+h)!}{(r-h)!(h!)\mathsf{\Gamma }\left(h-\alpha +1\right)}}{b}_{h,s}{\psi }_s\left(t\right)}{\chi }_{\left[0,1\right]}\hfill \\ & ={\displaystyle \sum _{s=0}^m\left({\displaystyle \sum _{h=\lceil \alpha \rceil }^r{\xi }_{r,s,h}}\right)}{\psi }_s(t){\chi }_{\left[0,1\right]},\hspace{1em}r=\lceil \alpha \rceil ,\dots ,m\hfill \end{array},$$

(25)

in which ${\xi }_{r,s,h}$ is presented in Equation (19). In addition, if we use Lemma 1, then we can write

$$D^{\alpha }{\psi }_r(t)=0,\hspace{1em}r=0,1,\dots ,\lceil \alpha \rceil -1,\hspace{1em}\alpha >0.$$

(26)

Combining Equations (25) and (27), the result can be obtained. □

4. Solving Systems of Fractional Order Differential Equations

In this section, the Legendre wavelet operational matrix method was implemented to obtain the numerical solution of the system of fractional order differential equations. Consider a system of fractional differential equations as follows:

$$\begin{array}{c}{D}^{{\eta }_1}{u}_1(t)=U_1(t,u_1,u_2,\dots ,u_m),\\ D^{{\eta }_2}{u}_2(t)=U_2(t,u_1,u_2,\dots ,u_m),\\ ⋮\\ D^{{\eta }_n}{u}_m(t)=U_m(t,u_1,u_2,\dots ,u_m),\end{array}$$

(27)

where $U_i$ is a linear/nonlinear function of $t,u_1,u_2,\dots ,u_m,$ $D^{{\eta }_i}$ is the derivative of $u_i$ with the order of ${\eta }_i$ in the Liouville–Caputo sense and $N-1\le {\eta }_i<N$, and they are subjected to the initial conditions

$$\begin{array}{ccccc}{u}_1\left(t_0\right)=u_{10},& \frac{d{u}_1}{dt}\left(t_0\right)=u_{11},& \frac{d^2{u}_1}{d{t}^2}\left(t_0\right)=u_{12},& \dots ,& \frac{d^{n-1}{u}_1}{d{t}^{n-1}}\left(t_0\right)=u_{1(n-1)}\\ u_2\left(t_0\right)=u_{20},& \frac{d{u}_2}{dt}\left(t_0\right)=u_{21},& \frac{d^2{u}_2}{d{t}^2}\left(t_0\right)=u_{22},& \dots ,& \frac{d^{n-1}{u}_2}{d{t}^{n-1}}\left(t_0\right)=u_{2(n-1)}\\ ⋮& ⋮& ⋮& & ⋮\\ u_m\left(t_0\right)=u_{m0},& \frac{d{u}_m}{dt}\left(t_0\right)=u_{m1},& \frac{d^2{u}_m}{d{t}^2}\left(t_0\right)=u_{m2},& \dots ,& \frac{d^{n-1}{u}_m}{d{t}^{n-1}}\left(t_0\right)=u_{m(n-1)}\end{array}.$$

(28)

First of all, approximating $u_1(t),u_2\left(t\right),\dots ,u_m\left(t\right)$ and $D^{{\eta }_1}{u}_1\left(t\right),D^{{\eta }_2}{u}_2\left(t\right),\dots ,D^{{\eta }_n}{u}_m\left(t\right)$, we obtain

$$\begin{array}{c}{u}_1\left(t\right)\approx {\displaystyle \sum _{n=0}^{2^k-1}{\displaystyle \sum _{m=0}^M{c}_1{}_{n,m}}{\psi }_{n,m}}=C_1{}^T\psi \left(t\right)\\ u_2\left(t\right)\approx {\displaystyle \sum _{n=0}^{2^k-1}{\displaystyle \sum _{m=0}^M{c}_2{}_{n,m}}{\psi }_{n,m}}=C_2{}^T\psi \left(t\right)\\ ⋮\\ u_m\left(t\right)\approx {\displaystyle \sum _{n=0}^{2^k-1}{\displaystyle \sum _{m=0}^M{c}_n{}_{n,m}}{\psi }_{n,m}}=C_m{}^T\psi \left(t\right)\end{array},$$

(29)

where $C_i,i=1,2,\dots ,m$ is an unknown vector and $\psi \left(t\right)$ is the vector introduced in Equation (8). If we utilize Equation (17), then we have

$$\begin{array}{c}{D}^{{\eta }_1}{u}_1\left(t\right)\approx C_1{}^T{D}^{({\eta }_1)}\psi \left(t\right)\\ D^{{\eta }_2}{u}_2\left(t\right)\approx C_2{}^T{D}^{({\eta }_2)}\psi \left(t\right)\\ ⋮\\ D^{{\eta }_n}{u}_m\left(t\right)\approx C_m{}^T{D}^{({\eta }_n)}\psi \left(t\right)\end{array}.$$

(30)

Substituting Equations (29) and (30) into Equation (27), we obtain

$$\begin{array}{c}{R}_1(t)=C_1{}^T{D}^{\left({\eta }_1\right)}\psi \left(t\right)-U_1(t,C_1{}^T\psi \left(t\right),C_2{}^T\psi \left(t\right),\dots ,C_m{}^T\psi \left(t\right))\\ R_2(t)=C_2{}^T{D}^{\left({\eta }_2\right)}\psi \left(t\right)-U_2(t,C_1{}^T\psi \left(t\right),C_2{}^T\psi \left(t\right),\dots ,C_m{}^T\psi \left(t\right))\\ ⋮\\ R_m(t)=C_m{}^T{D}^{\left({\eta }_n\right)}\psi \left(t\right)-U_m(t,C_1{}^T\psi \left(t\right),C_2{}^T\psi \left(t\right),\dots ,C_m{}^T\psi \left(t\right))\end{array}$$

(31)

If $U_i$ is a linear function of $t,u_1,u_2,\dots ,u_m,$ then we produce $2^k\left(M+1\right)-mn$ linear equations by implementing

$${\displaystyle \underset{0}{\overset{1}{\int }}{\psi }_j\left(t\right)}{R}_i\left(t\right)dt=0,j=1,\dots ,2^k\left(M+1\right)-mn,i=1,2,\dots ,m.$$

(32)

Also, by substituting the initial conditions in Equation (28) into Equation (30), then we obtain

$$\begin{array}{cccc}{u}_1\left(t_0\right)\approx C_1{}^T\psi \left(t_0\right)=u_{10},& \frac{d{u}_1}{dt}\left(t_0\right)\approx C_1{}^{T}D\psi \left(t_0\right)=u_{11},& \dots ,& \frac{d^{n-1}{u}_1}{d{t}^{n-1}}\left(t_0\right)\approx C_1{}^T{D}^{n-1}\psi \left(t_0\right)=u_{1(n-1)}\\ u_2\left(t_0\right)\approx C_2{}^T\psi \left(t_0\right)=u_{20},& \frac{d{u}_2}{dt}\left(t_0\right)\approx C_2{}^{T}D\psi \left(t_0\right)=u_{21},& \dots ,& \frac{d^{n-1}{u}_2}{d{t}^{n-1}}\left(t_0\right)\approx C_2{}^T{D}^{n-1}\psi \left(t_0\right)=u_{2(n-1)}\\ ⋮\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮& ⋮\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮& & ⋮\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ u_m\left(t_0\right)\approx C_m{}^T\psi \left(t_0\right)=u_{m0},& \frac{d{u}_m}{dt}\left(t_0\right)\approx C_m{}^{T}D\psi \left(t_0\right)=u_{m1},& \dots ,& \frac{d^{n-1}{u}_m}{d{t}^{n-1}}\left(t_0\right)\approx C_m{}^T{D}^{n-1}\psi \left(t_0\right)=u_{m(n-1)}\end{array}.$$

(33)

A $2^k\left(M+1\right)$ set of linear equations is generated by combining Equations (32) and (33). The solution of these linear equations can be obtained for unknown coefficients of the vector $C$. Consequently, $u_1\left(t\right),u_2\left(t\right),\dots ,u_m\left(t\right)$, introduced in Equation (27), can be computed.

If $U_i$ is a nonlinear function of $t,u_1,u_2,\dots ,u_m,$ then we first compute $R_1(t),R_2(t),\dots ,R_m(t)$ at $2^k(M+1)-mn$ points and, for a better result, use the first $2^k(M+1)-mn$ roots of shifted Legendre $P_{2^k(M+1)}\left(t\right)$. Then these equations, collectively with Equation (33), produce $2^k\left(M+1\right)$ nonlinear equations. The solution of these nonlinear equations can be obtained by employing Newton’s iterative method. Consequently, $u_1\left(t\right),u_2\left(t\right),\dots ,u_m\left(t\right)$, introduced in Equation (27), can be computed.

5. Illustrative Examples

In this section, to show the applicability and powerfulness of the introduced method, we present the solutions to five linear and nonlinear systems of fractional order differential equations.

Example 1.

We first considered the following linear system of fractional differential equations [7,8]:

$$\begin{array}{l}{D}^{\alpha }u\left(t\right)=u(t)+v(t)\\ D^{\alpha }v(t)=-u(t)+v(t)\end{array},$$

subject to

$$u\left(0\right)=0,\hspace{1em}v(0)=1.$$

The exact solution of this system when $\alpha =1$ is known to be

$$u\left(t\right)=e^t\sin t,\hspace{1em}v\left(t\right)=e^t\cos t.$$

This example was examined for $M=2$, $k=0$, and $\alpha =0.9,0.7,0.5$. When the obtained results were matched against the exact solution when $\alpha =1$, as demonstrated in Figure 1, we can clearly observe that when $\alpha$ approached 1, our results approached the exact solution. We also solved this problem by using Legendre polynomial operational matrix method (LPOMM), and we compared the results with the LWOMM. The numerical computations for u(t) and v(t) when $\alpha =0.9$ are revealed in Table 1 and Table 2.

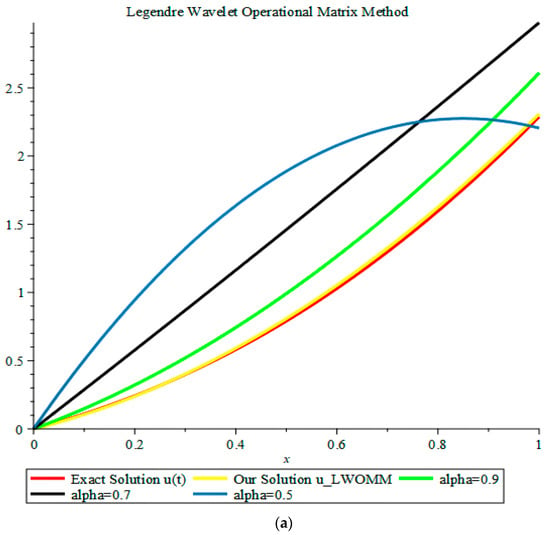
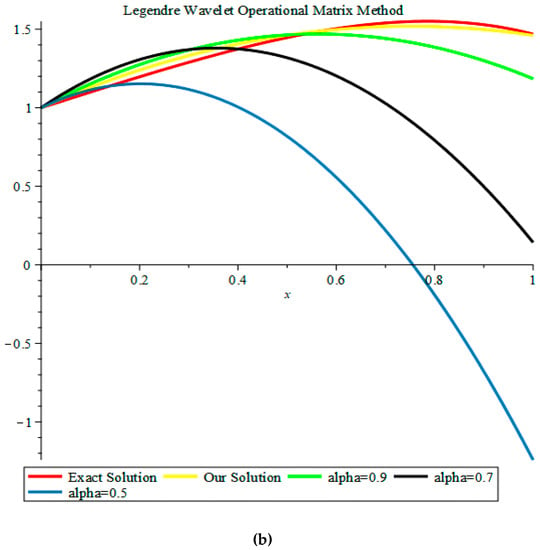
Figure 1. Comparison of our solutions and the exact solution when $\alpha =0.9,0.7,0.5$ in Example 1: (a) Our solution u(t); and (b) Our solution v(t).

Table 1. Numerical solutions of u(t) when $\alpha =0.9$ attained by the introduced method and the LPOMM for Example 1.

$\mathit{t}$	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{u}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	0.3 × ${10}^{-9}$	0.0000000000	0.3 × ${10}^{-9}$
0.1	0.1483784330	0.1483784325	0.12 × ${10}^{-9}$
0.2	0.3217645283	0.3217645277	0.633 × ${10}^{-9}$
0.3	0.5201582862	0.5201582855	0.65 × ${10}^{-9}$
0.4	0.7435597067	0.7435597059	0.83 × ${10}^{-9}$
0.5	0.9919687898	0.9919687890	0.8 × ${10}^{-9}$
0.6	1.265385536	1.265385535	0.53 × ${10}^{-9}$
0.7	1.563809944	1.563809943	0.95 × ${10}^{-9}$
0.8	1.887242014	1.887242014	0.733 × ${10}^{-9}$
0.9	2.235681748	2.235681748	0.62 × ${10}^{-9}$
1.0	2.609129144	2.609129144	0.3 × ${10}^{-9}$

Table 2. Numerical solutions of v(t) when $\alpha =0.9$ attained by the introduced method and the LPOMM for Example 1.

$\mathit{t}$	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{v}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	1.000000000	1.000000000	0.2 × ${10}^{-9}$
0.1	1.152270899	1.152270900	−0.5 × ${10}^{-9}$
0.2	1.274801858	1.274801858	0.599 × ${10}^{-9}$
0.3	1.367592877	1.367592878	−0.67 × ${10}^{-9}$
0.4	1.430643956	1.430643957	−0.13 × ${10}^{-8}$
0.5	1.463955094	1.463955094	−0.1 × ${10}^{-8}$
0.6	1.467526291	1.467526293	−0.13 × ${10}^{-8}$
0.7	1.441357549	1.441357551	−0.171 × ${10}^{-8}$
0.8	1.385448866	1.385448868	−0.1461 × ${10}^{-8}$
0.9	1.299800244	1.299800245	−0.15 × ${10}^{-8}$
1.0	1.184411680	1.184411682	−0.18 × ${10}^{-8}$

Example 2.

We considered the following nonlinear system of fractional differential equations [13]:

$$\begin{array}{l}{D}^{\frac{3}{2}}u\left(t\right)=-8u\left(t\right)+v^2(t)-4t^6+4t^3+\frac{8t^{\frac{3}{2}}}{\sqrt{\pi }}-1\\ D^{\frac{1}{2}}v\left(t\right)=t^{2}Du\left(t\right)+v(t)-3t^4-2t^3+\frac{32t^{\frac{5}{2}}}{5\sqrt{\pi }}-1\end{array}$$

$$u(0)=0,\hspace{1em}v(0)=1,\hspace{1em}u(1)=1,\hspace{1em}v(1)=3,\hspace{1em}{u}^{\prime }(0)=0,\hspace{1em}{u}^{\prime }(1)=3.$$

The exact solution of this system is known to be

$$u\left(t\right)=t^3,\hspace{1em}v\left(t\right)=2t^3+1$$

Using the parameters $M=3$ and $k=0$, we applied both the proposed method and the LPOMM to solve this problem and show that our approach is more efficient and useful. Our numerical results supported the idea that our solution approaches the exact solution more than the approximate solution LPOMM. Comparisons of the approximate and exact solutions are presented in Table 3 and Table 4.

Table 3. The numerical results attained by using the introduced method in comparison to the approximate solution LPOMM and the exact solution u(t) in Example 2.

$\mathit{t}$	Exact Solution	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{u}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$
0.0	0.000	−0.12 × ${10}^{-9}$	0.000000000000
0.1	0.001	0.01000000005	0.001000000000
0.2	0.008	0.02000000016	0.008000000000
0.3	0.027	0.03750000021	0.027000000000
0.4	0.064	0.07000000020	0.064000000000
0.5	0.125	0.12500000001	0.125000000000
0.6	0.216	0.21000000000	0.216000000000
0.7	0.343	0.33249999998	0.343000000000
0.8	0.512	0.49999999996	0.512000000000
0.9	0.729	0.71999999993	0.729000000000
1.0	1.000	0.99999999989	1.000000000000

Table 4. The numerical results attained by using the introduced method in comparison with the approximate solution LPOMM and exact solution v(t) in Example 2.

$\mathit{t}$	Exact Solution	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{v}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$
0.0	1.000	1.000000000	0.9999999998
0.1	1.002	1.034841367	1.165803114
0.2	1.016	1.057587628	1.283854751
0.3	1.054	1.086537668	1.374911456
0.4	1.128	1.139990370	1.459729770
0.5	1.250	1.236244618	1.559066242
0.6	1.432	1.393599296	1.693677414
0.7	1.686	1.630353290	1.884319831
0.8	2.024	1.964805482	2.151750038
0.9	2.458	2.415254758	2.516724579
1.0	3.000	3.000000000	3.000000000

Example 3.

We considered the following nonlinear system of fractional differential equations with the initial conditions [8]

$$\begin{array}{l}{D}^{\alpha }u\left(t\right)=\frac{u(t)}{2}\\ D^{\alpha }v(t)=u^2(t)+v(t)\end{array},$$

$$u(0)=1,\hspace{1em}v(0)=0.$$

The exact solution of this system when $\alpha =1$ is known to be

$$u\left(t\right)=e^{\left(\frac{t}{2}\right)},\hspace{1em}v\left(t\right)=t{e}^t.$$

The parameters $M=2,k=0$, and $\alpha =0.5,0.7,0.9$ were utilized. A comparison of our results and the exact solution when $\alpha =1$ is displayed in Figure 2. The figures support that when $\alpha$ approximated 1, our results approximated the exact solution. We also solved this problem by using the LPOMM, and compared the results to the LWOMM. Finally, we present the numerical computations for u(t) and v(t) when $\alpha =0.9$ in Table 5 and Table 6.

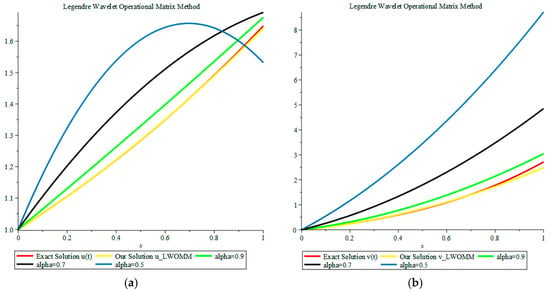
Figure 2. Comparison of our solutions to the exact solution when $\alpha =0.9,0.7,0.5$ for Example 3: (a) Our solution u(t); and (b) Our solution v(t).

Table 5. Our solutions u(t) when $\alpha =0.9$ attained by the presented method and the LPOMM for Example 3.

$\mathit{t}$	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{u}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	1.000000000	1.000000000	−0.37 × ${10}^{-10}$
0.1	1.064816320	1.064816320	−0.132 × ${10}^{-9}$
0.2	1.130248588	1.130248589	−0.1375 × ${10}^{-9}$
0.3	1.196296807	1.196296807	0.44 × ${10}^{-10}$
0.4	1.262960974	1.262960975	−0.808 × ${10}^{-9}$
0.5	1.330241090	1.330241091	−0.532 × ${10}^{-9}$
0.6	1.398137156	1.398137156	−0.168 × ${10}^{-9}$
0.7	1.466649171	1.466649171	−0.756 × ${10}^{-9}$
0.8	1.535777134	1.535777134	−0.1375 × ${10}^{-9}$
0.9	1.605521046	1.605521046	0.468 × ${10}^{-9}$
1.0	1.675880908	1.675880908	0.163 × ${10}^{-9}$

Table 6. Our solutions v(t) when $\alpha =0.9$ attained by the presented method and the LPOMM for Example 3.

$\mathit{t}$	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{v}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	−0.1 × ${10}^{-9}$	0.0000000000	−0.1 × ${10}^{-9}$
0.1	0.1381762603	0.1381762609	−0.7 × ${10}^{-9}$
0.2	0.3133603361	0.3133603363	−0.2 × ${10}^{-9}$
0.3	0.5255522259	0.5255522263	−0.37 × ${10}^{-9}$
0.4	0.7747519304	0.7747519309	−0.5 × ${10}^{-9}$
0.5	1.060959450	1.060959450	−0.5 × ${10}^{-9}$
0.6	1.384174783	1.384174784	−0.8 × ${10}^{-9}$
0.7	1.744397932	1.744397932	−0.47 × ${10}^{-9}$
0.8	2.141628894	2.141628895	−0.7 × ${10}^{-9}$
0.9	2.575867672	2.575867672	0.3 × ${10}^{-9}$
1.0	3.047114264	3.047114264	−0.1 × ${10}^{-9}$

Example 4.

We considered the following nonlinear system of FDEs with initial conditions [13]

$$\begin{array}{l}{D}^{\alpha }u\left(t\right)=-1002u(t)+1000v^2(t)\\ D^{\alpha }v(t)=u(t)-v(t)-v^2(t)\end{array}$$

$$u(0)=1,\hspace{1em}v(0)=1$$

The exact solution of this system when $\alpha =1$ is known to be

$$u\left(t\right)=e^{-2t},\hspace{1em}v\left(t\right)=e^{-t}$$

This example was analyzed for $M=3$, $k=0$, and $\alpha =0.9,0.7,0.5$. When the obtained results were matched against the exact solution when $\alpha =1$, as demonstrated in Figure 3, we can clearly observe that when $\alpha$ approached 1, our results approached the exact solution. We also solved this problem by using the LPOMM, and compared the results with the LWOMM. The numerical computations for u(t) and v(t) when $\alpha =0.99$ are also revealed in Table 7 and Table 8.

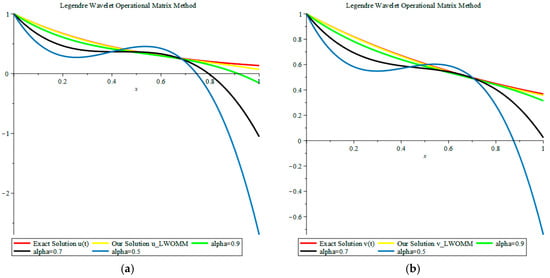
Figure 3. Comparison of our solutions to the exact solution when $\alpha =0.9,0.7,0.5$ for Example 4: (a) Our solution u(t); and (b) Our solution v(t).

Table 7. Numerical solutions of u(t) when $\alpha =0.99$ for Example 4.

$\mathit{t}$	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{u}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	1.000000000	1.000000000	−0.4 × ${10}^{-10}$
0.1	0.8144351529	0.8144351528	−0.21 × ${10}^{-10}$
0.2	0.6639425233	0.6639425233	−0.15 × ${10}^{-9}$
0.3	0.5429947229	0.5429947230	−0.34 × ${10}^{-9}$
0.4	0.4460643636	0.4460643636	−0.42 × ${10}^{-9}$
0.5	0.3676240568	0.3676240568	0
0.6	0.3021464142	0.3021464147	−0.68 × ${10}^{-9}$
0.7	0.2441040487	0.2441040481	−0.24 × ${10}^{-9}$
0.8	0.1879695699	0.1879695690	0.53 × ${10}^{-9}$
0.9	0.1282155920	0.1282155905	0.461 × ${10}^{-9}$
1.0	0.0593147248	0.0593147222	0.144 × ${10}^{-8}$

Table 8. Numerical solutions of v(t) when $\alpha =0.99$ for Example 4.

$\mathit{t}$	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{v}}_{\mathit{L}\mathit{P}\mathit{O}\mathit{M}\mathit{M}}$	Absolute Error
0.0	1.000000000	0.9999999999	0.79 × ${10}^{-10}$
0.1	0.9025601837	0.9025601837	0.1498 × ${10}^{-9}$
0.2	0.8152646487	0.8152646488	−0.119 × ${10}^{-9}$
0.3	0.7371116577	0.7371116578	−0.8 × ${10}^{-10}$
0.4	0.6670994737	0.6670994739	−0.11 × ${10}^{-9}$
0.5	0.6042263597	0.6042263600	−0.24 × ${10}^{-9}$
0.6	0.5474905785	0.5474905788	−0.19 × ${10}^{-9}$
0.7	0.4958903932	0.4958903935	−0.26 × ${10}^{-9}$
0.8	0.4484240664	0.4484240670	−0.443 × ${10}^{-9}$
0.9	0.4040898614	0.4040898620	−0.5898 × ${10}^{-9}$
1.0	0.3618860408	0.3618860417	−0.719 × ${10}^{-9}$

Example 5.

We considered the following fractional order Brusselator system [16,17]:

$$\begin{array}{l}{D}^{\alpha }u\left(t\right)=-2u(t)+u^2(t)v(t)\\ D^{\alpha }v(t)=u(t)-u^2(t)v(t)\end{array}$$

$$u(0)=1,\hspace{1em}v(0)=1.$$

The approximate solutions of this system when $\alpha =1$ and $\alpha =0.98$ were presented by Chang and Isah using the LWPT [17] and by Bota and Caruntu using the PLSM [16]. These solutions when $\alpha =98$ are given by

$$\begin{array}{l}{u}_{LWPT}(t)=1-1.0791t+0.2711t^2-0.0638t^3,\hspace{1em}{v}_{LWPT}(t)=1+0.0151t+0.4185t^2-0.2624t^3\\ u_{PLSM}(t)=1-1.08655t+0.311138t^2+0.0243682t^3,\hspace{1em}{v}_{PLSM}(t)=1+0.0349127t+0.333424t^2-0.184414t^3\end{array}.$$

The parameters $M=2$, $k=0$, and $\alpha =0.98$ were used. A comparison of our results to the approximate solutions introduced by Bota and Caruntu [16] and Chang and Isah [17] when $\alpha =0.98$ is displayed in Figure 4. Finally, we also present the numerical computations for u(t) and v(t) when $\alpha =0.98$ in Table 9 and Table 10.

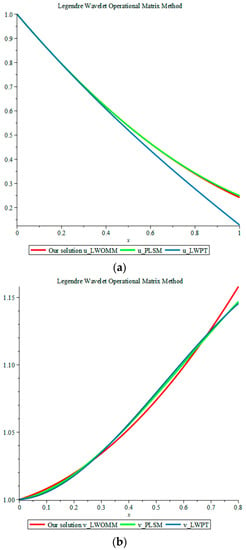
Figure 4. Comparison of our solutions to the approximate solution LWPT and the approximate solution PLSM when $\alpha =0.98$ for Example 5: (a) Our solution u(t); and (b) Our solution v(t).

Table 9. Numerical solutions of u(t) when $\alpha =0.98$ obtained by the introduced method, the LWPT, and the PLSM for Example 5.

$\mathit{t}$	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{u}}_{\mathit{L}\mathit{W}\mathit{P}\mathit{T}}$	${\mathit{u}}_{\mathit{P}\mathit{L}\mathit{S}\mathit{M}}$
0.0	1.000000000	1.0000000	1.0000000000
0.1	0.8942024826	0.8947372	0.8944807482
0.2	0.7950696916	0.7945136	0.7953304656
0.3	0.7026016268	0.6989464	0.7026953614
0.4	0.6167982883	0.6076528	0.6167216448
0.5	0.5376596761	0.5202500	0.5375555250
0.6	0.4651857902	0.4363552	0.4653432112
0.7	0.3993766306	0.3555856	0.4002309126
0.8	0.3402321973	0.2775584	0.3423648384
0.9	0.2877524902	0.2018908	0.2918911978
1.0	0.2419375095	0.1282000	0.2489562000

Table 10. Numerical solutions of v(t) when $\alpha =0.98$ obtained by the introduced method, the LWPT, and the PLSM for Example 5.

$\mathit{t}$	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{O}\mathit{M}\mathit{M}}$	${\mathit{v}}_{\mathit{L}\mathit{W}\mathit{P}\mathit{T}}$	${\mathit{v}}_{\mathit{P}\mathit{L}\mathit{S}\mathit{M}}$
0.0	1.000000000	1.0000000	1.000000000
0.1	1.008069307	1.0054326	1.006641096
0.2	1.019479961	1.0176608	1.018844188
0.3	1.034231959	1.0351102	1.035502792
0.4	1.052325304	1.0562064	1.055510424
0.5	1.073759995	1.0793750	1.077760600
0.6	1.098536032	1.1030416	1.101146836
0.7	1.126653415	1.1256318	1.124562648
0.8	1.158112143	1.1455712	1.146901552
0.9	1.192912217	1.1612854	1.167057064
1.0	1.231053638	1.1712000	1.183922700

6. Conclusions

In this paper, a system of fractional_order differential equations was examined by drawing from a new operational matrix of the fractional derivative in some special conditions. We also systematized a very operational algorithm in order to attain the solution of the linear and nonlinear systems of fractional differential equations in Maple. All numerical results and graphical presentations generated by Maple affirmed that the Legendre wavelet operational matrix method is very effective and applicable. As the next step, the method introduced in this paper can be applied to fractional partial differential equations and the system of such equations, fractional integral equations and the system of such equations, and fractional integro-differential equations. These equations are at least as important as fractional differential equations and they are very significant in science, engineering, and technology.