Stochastic Comparisons and Dynamic Information of Random Lifetimes in a Replacement Model
Abstract
1. Introduction
2. The Stochastic Model
3. Stochastic Comparisons
3.1. Definitions and Main Comparisons
- (a)
- usual stochastic order () if or, equivalently, if ;
- (b)
- hazard rate order () if increases in or, equivalently, if for all , where and are respectively the hazard rates of X and Y, or equivalently if ;
- (c)
- likelihood ratio order () if for all , with or, equivalently, increases in t over the union of supports of X and Y;
- (d)
- reversed hazard rate order () if increases in or, equivalently, if for all , where and are respectively the reversed hazard rates of X and Y.
- (i)
- ⇒ ;
- (ii)
- ⇒ ;
- (iii)
- ⇒ ;
- (iv)
- ⇔ .
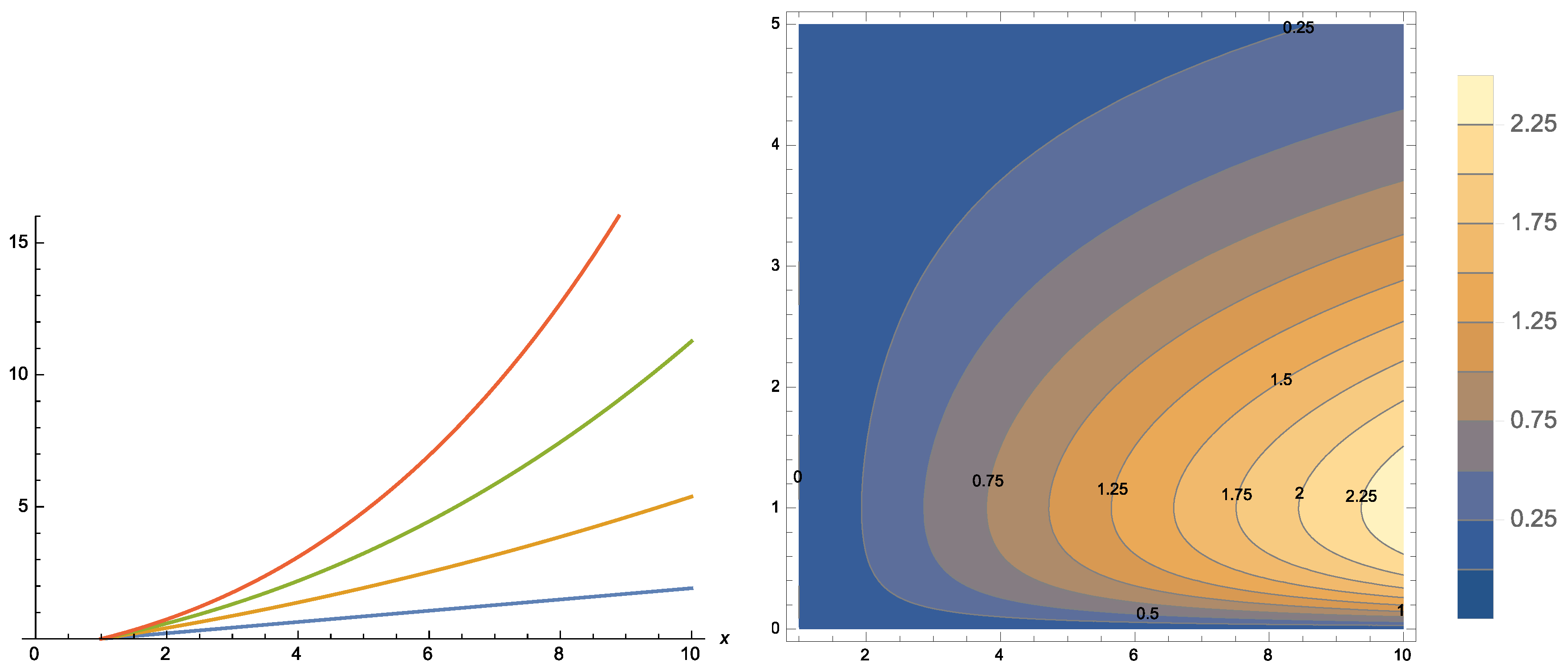
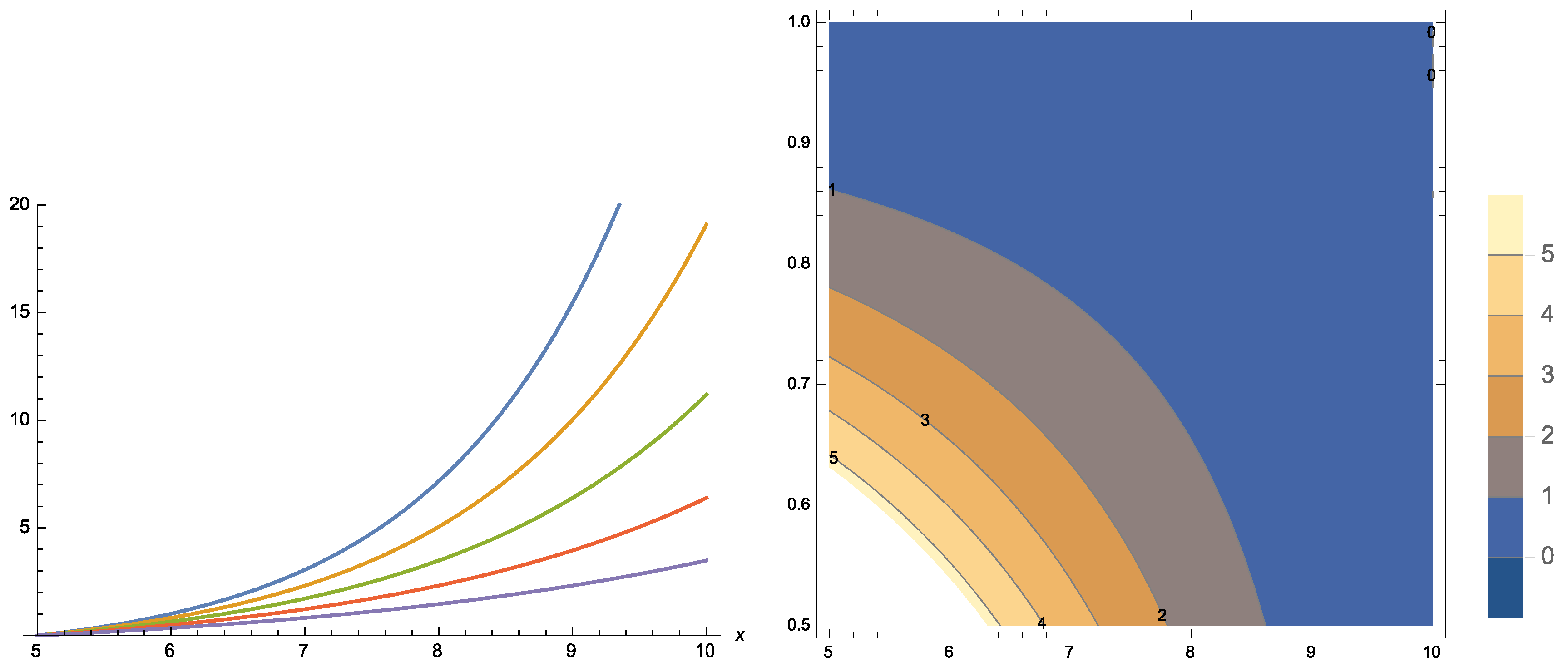
3.2. Scale Family of Distributions
3.3. Further Results
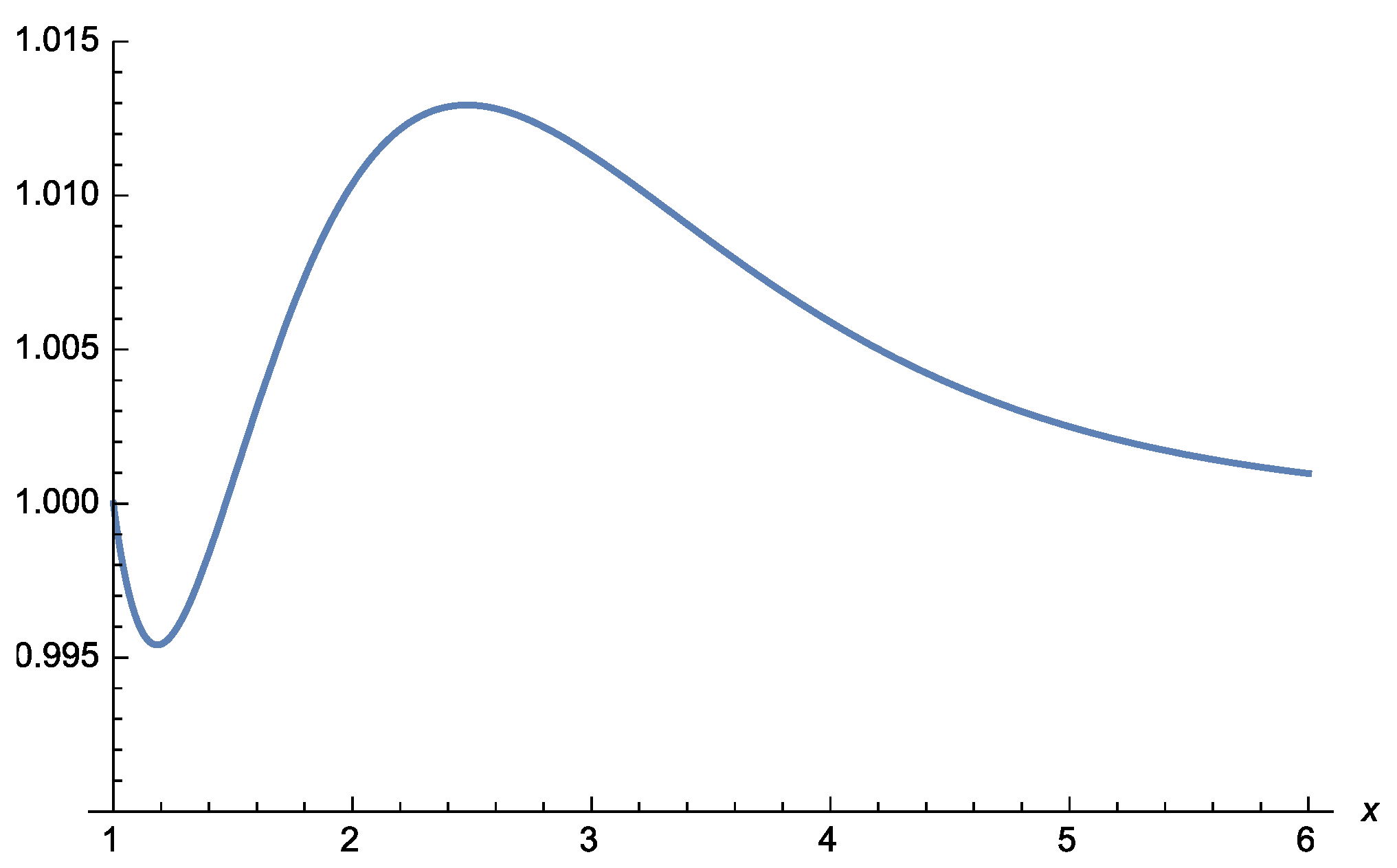
4. Relative Ratio of Improvement
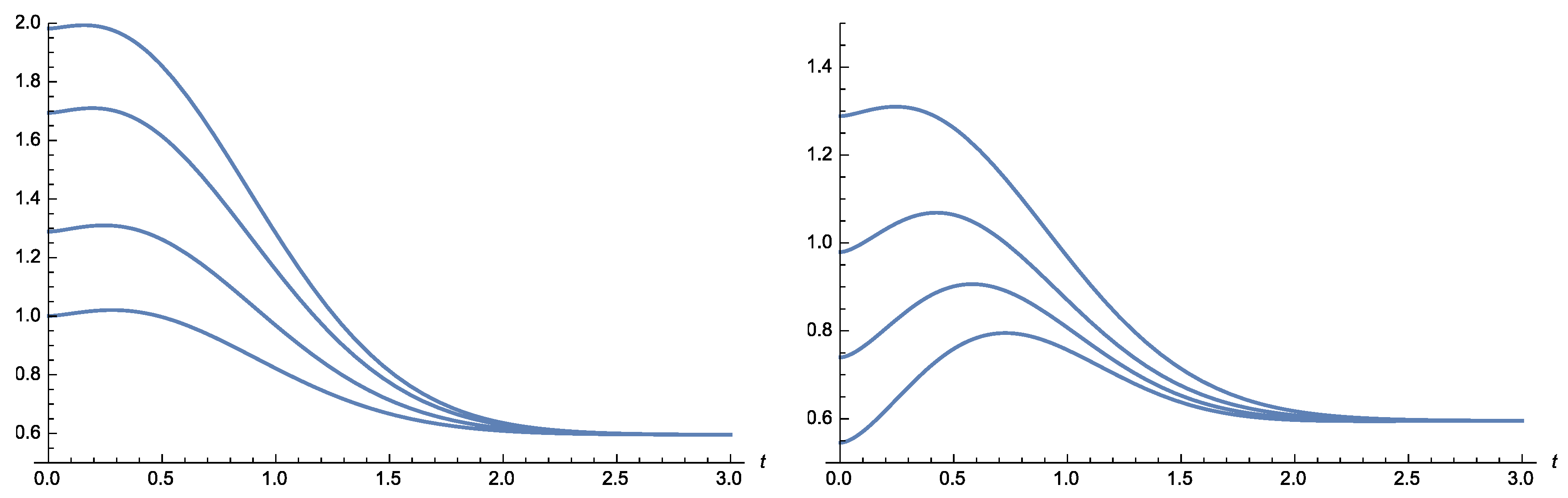
5. Results on Dynamic Differential Entropies
- (i)
- Let . If X is IURL and Y is DURL, then is DURL.
- (ii)
- Let . If X is DURL and Y is IURL, then is IURL.
- (iii)
- If for all , and for all , then is IURL.
- (i)
- Under the given assumptions, we have that the right-hand-side of (24) is nonnegative and decreasing, so that is decreasing.
- (ii)
- (iii)
- By expressing the derivative of in an alternative form, we obtainHence, thanks to the given hypothesis, the right-hand-side of the above identity is nonnegative.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krakowski, M. The relevation transform and a generalization of the gamma distribution function. Rev. Fr. Autom. Inform. Rech. Opér. 1973, 7, 107–120. [Google Scholar] [CrossRef]
- Baxter, L.A. Reliability applications of the relevation transform. J. Appl. Probab. 1982, 29, 323–329. [Google Scholar] [CrossRef]
- Belzunce, F.; Martínez-Riquelme, C.; Ruiz, J.M. Allocation of a relevation in redundancy problems. Appl. Stoch. Model Bus. Ind. 2081. online first. [Google Scholar] [CrossRef]
- Chukova, S.; Dimitrov, B.; Dion, J.P. On relevation transforms that characterize probability distributions. J. Appl. Math. Stoch. Anal. 1993, 6, 345–357. [Google Scholar] [CrossRef]
- Shanthikumar, J.G.; Baxter, L.A. Closure properties of the relevation transform. Nav. Res. Logist. Q. 1985, 32, 185–189. [Google Scholar] [CrossRef]
- Sordo, M.A.; Psarrakos, G. Stochastic comparisons of interfailure times under a relevation replacement policy. J. Appl. Probab. 2017, 54, 134–145. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Toomaj, A. Extension of the past lifetime and its connection to the cumulative entropy. J. Appl. Probab. 2015, 52, 1156–1174. [Google Scholar] [CrossRef]
- Barlow, R.; Proschan, F. Mathematical Theory of Reliability; Classics in Applied Mathematics (Book 17); With Contributions by Larry C. Hunter; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Block, H.W.; Savits, T.H.; Singh, H. The reversed hazard rate function. Probab. Eng. Inf. Sci. 1998, 12, 69–90. [Google Scholar] [CrossRef]
- Santacroce, M.; Siri, P.; Trivellato, B. New results on mixture and exponential models by Orlicz spaces. Bernoulli 2016, 22, 1431–1447. [Google Scholar] [CrossRef]
- Cicalese, F.; Gargano, L.; Vaccaro, U. Bounds on the entropy of a function of a random variable and their applications. IEEE Trans. Inf. Theory 2018, 64, 2220–2230. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Springer Series in Statistics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Belzunce, F.; Martínez-Riquelme, C.; Mulero, J. An Introduction to Stochastic Orders; Elsevier/Academic Press: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditional Specification of Statistical Models; Springer: New York, NY, USA, 1999. [Google Scholar]
- Escobar, L.A.; Meeker, W.Q. A review of accelerated test models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Martinucci, B.; Mulero, J. A quantile-based probabilistic mean value theorem. Probab. Eng. Inf. Sci. 2016, 30, 261–280. [Google Scholar] [CrossRef]
- Di Crescenzo, A. A probabilistic analogue of the mean value theorem and its applications to reliability theory. J. Appl. Probab. 1999, 39, 706–719. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Martinucci, B.; Zacks, S. Compound Poisson process with a Poisson subordinator. J. Appl. Probab. 2015, 52, 360–374. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life tables (with Discussion). J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar]
- Nanda, A.K.; Das, S. Dynamic proportional hazard rate and reversed hazard rate models. J. Stat. Plan. Inference 2011, 141, 2108–2119. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Navarro, J.; Balakrishnan, N. Parametric inference from system lifetime data under a proportional hazard rate model. Metrika 2012, 75, 367–388. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Muliere, P.; Parmigiani, G.; Polson, N.G. A note on the residual entropy function. Probab. Eng. Inf. Sci. 1993, 7, 413–420. [Google Scholar] [CrossRef]
- Ebrahimi, N. How to measure uncertainty in the residual life time distribution. Sankhyā Ser. A 1996, 58, 48–56. [Google Scholar]
- Ebrahimi, N.; Pellerey, F. New partial ordering of survival functions based on the notion of uncertainty. J. Appl. Probab. 1995, 32, 202–211. [Google Scholar] [CrossRef]
- Asadi, M.; Ebrahimi, N. Residual entropy and its characterizations in terms of hazard function and mean residual life function. Stat. Probab. Lett. 2000, 49, 263–269. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Kirmani, S.N.U.A.; Soofi, E.S. Multivariate dynamic information. J. Multivar. Anal. 2007, 98, 328–349. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. Entropy-based measure of uncertainty in past lifetime distributions. J. Appl. Probab. 2002, 39, 434–440. [Google Scholar] [CrossRef]
- Nanda, A.K.; Paul, P. Some properties of past entropy and their applications. Metrika 2006, 64, 47–61. [Google Scholar] [CrossRef]
- Kundu, C.; Nanda, A.K.; Maiti, S.S. Some distributional results through past entropy. J. Stat. Plan. Inference 2010, 140, 1280–1291. [Google Scholar] [CrossRef]
- Sachlas, A.; Papaioannou, T. Residual and past entropy in actuarial science and survival models. Methodol. Comput. Appl. Probab. 2014, 16, 79–99. [Google Scholar] [CrossRef]
- Kundu, A.; Nanda, A.K. On study of dynamic survival and cumulative past entropies. Commun. Stat. Theory Methods 2016, 45, 104–122. [Google Scholar] [CrossRef]
- Ahmadi, J.; Di Crescenzo, A.; Longobardi, M. On dynamic mutual information for bivariate lifetimes. Adv. Appl. Probab. 2015, 47, 1157–1174. [Google Scholar] [CrossRef]
- Bowden, R.J. Information, measure shifts and distribution metrics. Statistics 2012, 46, 249–262. [Google Scholar] [CrossRef]
- Lillo, R.E.; Nanda, A.K.; Shaked, M. Some shifted stochastic orders. In Recent Advances in Reliability Theory; Statistics for Industry and Technology; Birkhäuser: Boston, MA, USA, 2000; pp. 85–103. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Crescenzo, A.; Di Gironimo, P. Stochastic Comparisons and Dynamic Information of Random Lifetimes in a Replacement Model. Mathematics 2018, 6, 204. https://doi.org/10.3390/math6100204
Di Crescenzo A, Di Gironimo P. Stochastic Comparisons and Dynamic Information of Random Lifetimes in a Replacement Model. Mathematics. 2018; 6(10):204. https://doi.org/10.3390/math6100204
Chicago/Turabian StyleDi Crescenzo, Antonio, and Patrizia Di Gironimo. 2018. "Stochastic Comparisons and Dynamic Information of Random Lifetimes in a Replacement Model" Mathematics 6, no. 10: 204. https://doi.org/10.3390/math6100204
APA StyleDi Crescenzo, A., & Di Gironimo, P. (2018). Stochastic Comparisons and Dynamic Information of Random Lifetimes in a Replacement Model. Mathematics, 6(10), 204. https://doi.org/10.3390/math6100204





