Abstract
In this study, a hybrid method based on coupling discrete wavelet transforms (DWTs) and artificial neural network (ANN) for yield spread forecasting is proposed. The discrete wavelet transform (DWT) using five different wavelet families is applied to decompose the five different yield spreads constructed at shorter end, longer end, and policy relevant area of the yield curve to eliminate noise from them. The wavelet coefficients are then used as inputs into Levenberg-Marquardt (LM) ANN models to forecast the predictive power of each of these spreads for output growth. We find that the yield spreads constructed at the shorter end and policy relevant areas of the yield curve have a better predictive power to forecast the output growth, whereas the yield spreads, which are constructed at the longer end of the yield curve do not seem to have predictive information for output growth. These results provide the robustness to the earlier results.
1. Introduction
Forecasting the behaviour of macro and financial variables is of utmost importance to the financial and macroeconomic policy makers. In economics and financial literature, there are number of variables that have useful property of predicting the behaviour of other macro and financial variables. One such variable, defined as the difference between the long term and short term risk free rates, is the yield spread. The yield spreads have an important property of predicting the economic activity in any economy. This property in turn hinges on the several theoretical underpinnings. One possible theoretical plausibility is that the short-term interest rates are instruments of monetary policy and long-term interest rates reflect market’s expectations on future economic conditions. The difference between short and longer-term interest rates may therefore contain useful predictive information about future economic activity in any economy. Further, yield spreads have an edge over simple interest rates because they contain information from both the short and long-term interest rates. Yield spread as a predictor of economic activity, inflation, and stock prices has become a stylized fact in economic and financial lexicon. Yet, more importantly, information about a country’s future economic activity is important to consumers, investors, and policymakers due to number of reasons. Business firms, for example, can use these predictions in deciding the supply capacity to meet the future demand. Government agencies and policy makers can use it for making forecasts of budgetary surpluses and deficits. Also, central banks can use it in deciding the stance of the current monetary policy.
Numerous studies have been devoted to study the usefulness of yield spread as a leading indicator of several macroeconomic variables. Stock and Watson [1] is the first study to include the yield spreads in their newly constructed index of leading economic indicators and find that the yield spread has a property of lead, indicating the economic activity. Estrella and Hardouvelis [2] found that the increase in slope of yield spread is followed by an increase in economic activity.
Estrella and Mishkin [3], find that the term spread shows the significant leading indicator property of yield spread for economic activity in four major European countries (France, Germany, Italy, and the UK). Bonser-Neal and Morley [4], for the broader set of 11 developed countries find that the yield spread is a predictor of future economic activity. Adel et al. [5], after modelling regressor endogeneity in the datasets confirm the earlier results. Bordo and Haubrich [6] test the predictive information in the level and slope of yield curve and find that both the level and slope of yield curve has information about economic activity. All of these results have also found support in studies, like as Stock and Watson [7], and Tabak and Feitosa [8,9].
Some studies either find scant or no evidence of predictive information in the yield spreads (see [10,11]). Researchers attribute this lack of evidence to the several generic and country specific factors. Among the reasons, noteworthy are heavy financial regulation by governments and asymmetric nature monetary policy [12], failing to take into account the structural breaks in relationships [13], and the time varying term premium that have also been found to diminish the predictive power of yield spreads [14].
Studies on the leading indicator property of yield spreads have mostly focussed on the developed countries and ignored the developing and emerging ones. Partly, this can be attributed to the lateral entry of these countries in the market determined interest rate regimes. In India, for example, a yield curve began to emerge only in the mid-nineties and hence it became relevant to test if yield spread possesses the leading indicator property. Kanagasabapathy and Goyal [15] is the first study that shows that the yield spread possess the leading indicator property. Bhaduri and Saraogi [16] find the ability of yield spreads to time the stock markets. More recently, Dar et al. [17] have shown that the ability of yield spread to predict economic activity is more pronounced at the longer time horizons. Empirically the question therefore is still unsettled and deserves further verification.
In this study, we employ a hybrid wavelet neural network (WNN) approach to test the ability of the yield spreads to predict economic growth in India. We improve over earlier studies by combining two relatively newer approaches based on wavelet transforms and neural networks. The proposed hybrid WNN model combines the capability of wavelets and neural networks to capture non-stationary nonlinear attributes that are embedded in financial time series. To the best of our knowledge, this paper is the first attempt in utilizing the WNN based algorithm for forecasting the yield spreads. We use discrete wavelet transform (DWT) to decompose each yield spread and output into component series that carried most of the information. The summed sub-series components obtained by addition of the dominant discrete wavelet components were selected as the inputs of the artificial neural network (ANN) model to predict the future output growth. We find that there is a significant evidence of the leading indicator property of the yield spreads, which are constructed at the shorter end and policy relevant areas of the yield curve; however, spreads that are constructed at the longer end of the yield curve do not have predictive information for output growth. Our model comes with extra benefits that are briefly discussed in Section 2 and Section 4.
The rest of the paper is organized as follows. Theoretical underpinnings of the leading indicator property of the yield spread for economic activity are discussed in Section 2. Second, motivation and a brief description of wavelet transformation, choice of wavelet families, ANN’s, development of hybrid WNN models, and performance parameters are given in Section 3. Section 3 describes details of data used in the study. In Section 4, the results of different wavelet based ANN models are discussed, and finally, the conclusions of the study are presented.
2. Theoretical Underpinnings of the Relationship between Yield Spread and Future Economic Activity
The earlier literature on the use of yield curve as a leading indicator is mostly empirical and focuses on documenting the correlations between lagged yield spread and economic activity. Nevertheless, good theoretical explanations do exist for explaining the leading indicator property of the yield curve. The expectations theory forms as a fundamental building block for various explanations that explains the usefulness of term spread in predicting economic growth. In fact, the theoretical argument underlying the use of yield curve as an indicator for market expectations of real growth is based on the combination of fisher equation and expectation hypothesis.
The expectation hypothesis of term structure states that the yield to maturity of a bond with periods to maturity can be considered as a sum of series of expected one period yields and a risk premium so that
where, is the conditional expectation operator, is the yield to maturity of a bond with n periods maturity, and represents the premium on period bond until it matures.
Using fisher decomposition, Equation (1) can be written as
where, and represents the average real interest rate over periods to and the average expected inflation rate over the periods to , respectively.
Under the expectations hypothesis theory of term structure, the risk premium is assumed to be constant over time. The slope of the yield curves between maturities and can be decomposed into change in real rate and in expected inflation making use of Equation (2). Consider Equation (2) for long term interest rate of maturity ‘’ and a short term interest in maturity ‘’. Subtracting the latter from the former, we obtain
Equation (3) gives the decomposition of nominal yield spread defined as a difference of n and m maturities, into real interest rate spread, expected inflation difference and term premium differential. Thus, the real yield spread forms a component of nominal yield spread. If real activity is related to changing real interest rate and if term premium is constant then Equations (2) and (3) imply that the term spread should contain information about future economic activity through consumption and investment.
Analysts, therefore, look to the yield spread as a potential source of information about future economic conditions. Several hypotheses argue that the information in the yield curve is forward-looking and therefore should have predictive power for real growth [18]. In fact, predicting real economic activity in essence needs the presence of market determined yield curve and its reflection of the expectations about inflation/future movements in short term rates, or to state alternatively, regulation of financial markets should be limited. Further, the financial markets should be integrated and fairly liquid and information efficient.
Different theoretical underpinnings have been proposed to link between the term spread and output growth [19,20]. In fact, the multiple number of channels through which the leading indicator property operates makes it rather cumbersome to suggest one simple reason that defines the predictive power of yield spread. Nevertheless, it also suggests that if one channel is not at work, then other channels may work. This adds the robustness to the relationship between yield spread and economic activity. Depending upon the channel at work, theoretically the term spread may be related to future real output in several channels.
A first channel operates through the effect of current monetary policy on both the slope of the yield curve or term spread and real activity. Monetary tightening by the central bank drives up the short term rates, while long term rates rise by less or relatively sticky, leading to the flattening (or inversion in some cases) of the yield curve. Restrictive monetary policy also dampens economic activity with a lag. This produces a lagged relation of term spread for economic activity. In other words, yield spread acts as a leading indicator of economic activity.
Expectations about the future monetary policy changes in the presence of nominal rigidities are the second channel through which relation between term spread and economic activity operates. For example, the expectation of future tight monetary policy (future shift of the Levenberg-–Marquardt (LM) curve) would mean higher future short term rates, thus higher current long term rates (through expectation hypothesis), and ultimately, an increase in the slope of the yield curve. The expected upward shift in the future LM curve implies current investment saving (IS) curve to shift Left (due to higher long term current rate) and a fall in current and future output.
Real demand shocks represent the third channel. An expected economic upswing represented by a future outward shift in the IS curve raises expected future short-term rates (increased income leads to increased money demand). This expectation turns into higher current long term rates. This leads to an increase in current spread as a response to the expected economic upswing.
Based on the theories of inter temporal consumption, it is possible to derive the relationship between the term spread and economic activity, Harvey [21], for example, posits that during the periods of high income individuals prefer stable consumption rather than high consumption and lower consumption during the falling income. Thus, if consumers expect a slow down or recession two years ahead in future, they will purchase two year bonds and sell shorter term financial instruments to obtain income for slow down (recession) years.
3. Motivation and Methodology
Classic time series models, such as Auto-regressive integrated moving average (ARIMA), generalized autoregressive conditionally heteroscedastic (GARCH) volatility, and the smooth transition autoregressive model (STAR) are widely used for financial time series forecasting. However, they are basically linear models assuming that data are stationary, and have a limited ability to capture non-stationarities and non-linearities in time series data. ANNs represent a recent approach to time series forecasting. There has been an increasing interest in using ANN’s to model and forecast time series over the last decade. For example, Tkacz [22] successfully forecasted the Gross domestic product (GDP) of the Canadian economy using ANN’s and when compared the obtained results with the results of the ARIMA model. Moshiri and Cameron [23] applied neural networks to forecast inflation, and showed that ANN’s had better forecasting results than that of linear models. ANNs offer an effective approach for handling large amounts of dynamic, non-linear, and noisy data, especially when the underlying physical relationships are not fully understood. This makes them well suited to time series modelling problems of a data-driven nature.
In spite of suitable flexibility of ANN in modelling financial time series, sometimes there is a shortage when signal fluctuations are highly non-stationary and operates at different time scales. For example, central banks have different objectives in the short and long run and they operate at different time scales separately (see Aguiar-Conraria et al. [24]). This operation of central banks at different time scales also leads to heterogeneous frequency contents in the yield spreads. Essentially, the actual time series of both yield spread and output growth are generated by the combination of different frequencies or time scales. Therefore, when the relationship between output and yield spread is modelled in time domain framework; it leads to time or frequency aggregation bias, with true relationships remaining veiled under frequencies or time scales. In such a situation, ANNs cannot handle non-stationary data without input data pre-processing. Therefore, an additional research is needed to investigate methods that are better able to handle non-stationary data effectively. An example of such a method is wavelet analysis, which is still in its infancy and many properties of these models are not explored yet in economic and finance literature. There is a scant but significant research that is available for finding the predictive power of term spread for economic activity using wavelet approach, for example Zagaglia [25] used this methodology to find the predictive power of term spread for the USA and his results report a heterogeneous relation across time scales. Recent results in this direction can be found in Tabak and Feitosa [8,9] and Dar and Shah [26]. Therefore, in order to increase the result accuracy and better estimation of yield spread peaks, which is the most and important part in forecast modelling, we develop a hybrid WNN model to test the leading indicator property of yield spreads for India.
3.1. Wavelet Transforms
The wavelet transform is a powerful mathematical tool that provides a time-frequency representation of an analysed signal. Wavelet analysis that is developed during the last three decades, appears to be a more effective tool than the Fourier transform in studying non-stationary time series. The main advantage of wavelet transforms are their ability to simultaneously obtain information on the time, location, and frequency of a signal, while the Fourier transform will only provide the frequency information of a signal. The transform has been formalized into a rigorous mathematical framework and has found applications in diverse fields, such as harmonic analysis, signal and image processing, differential and integral equations, sampling theory, turbulence, geophysics, statistics, medicine, and economics and finance.
Mathematically, a wavelet can be described as a real-valued function that satisfies the conditions:
The first condition means that must be an oscillatory function with zero mean and the second condition ensures that the wavelet function has unit energy. More precisely, wavelets are defined as
where and represents the dilation and translation parameters, respectively. Small values of represent high frequency components of the signal while large values of represent low frequency components of the signal.
The Continuous wavelet transform (CWT) at a time for a time series is defined as follows:
The inverse wavelet transform can be defined so that can be reconstructed by means of the formula
where is the admissibility condition given by
where represents the Fourier transform of the function For practical applications, the economist does not have at his or her disposal a continuous-time signal process, but rather a discrete-time signal. A discretization of Equation (4) based on the trapezoidal rule maybe is the simplest discretization of the CWT. This transform produces coefficients from a data set of length ; hence, redundant information is locked up within the coefficients, which may or may not be a desirable property (See Debnath & Shah [27]).
To overcome this redundancy, the parameters and are restricted to discrete values as so that we have the following family of discrete wavelets:
where and are integers that control the wavelet dilation and translation, respectively; is a specified fined dilation step greater than 1; and is the location parameter and must be greater than zero. The most common and simplest choice for parameters are and . Therefore, the dyadic wavelet family can be written in more compact notation as:
One of the most useful methods to construct discrete wavelets is through the concept of multiresolution analysis (MRA), as introduced by Stephane Mallat [28]. This is a remarkable idea that deals with a general formalism for the construction of an orthogonal basis of wavelets. Indeed, MRA is central to all of the constructions of wavelet basis. Mathematically, an MRA is an increasing family of closed subspaces of satisfying the properties (i); (ii) is dense in and (iii) if and only if ; and, (iv) there is a function called the scaling function, such that form an orthonormal basis for . The function asserted in (iv) is often called the father wavelet. In view of the translation invariant property (iv), it possible to generate a set of functions in such that forms an orthonormal basis for .
Let be the complementary subspaces of in These subspaces inherit the scaling property of , namely if and only if By virtue of this property, one can find a function , such that constitutes an orthonormal basis for , and thus, will form an orthonormal basis for the subspaces Since, s are dense in therefore, it follows that the family will represent an orthonormal basis for . It is called an orthonormal wavelet basis with mother wavelet .
Once we have constructed our mother and father wavelets, then we can represent a given signal as a series of mother and father wavelets as
where is the number of multiresolution components or scales and ranges from 1 to the number of coefficients in the specified components. The coefficients ; in (10) are the wavelet transform coefficients, and can be approximated by the following relations:
The coefficients , are known as the smooth coefficients, and represent the underlying smooth behaviour of the time series at the coarse scale , while , known as the detailed coefficients, describes the coarse scale deviations from the smooth behaviour and provides progressively finer scale deviations from the smooth behaviour. The actual derivation of the smooth and detailed coefficients may be done via the so-called discrete wavelet transform (DWT), which can be computed in several alternative ways. The intuitively most appealing procedure is the pyramid algorithm, suggested in Mallat [26,29] (and fully explained in Percival and Walden [30]). In this context, the Daubechies family of wavelets is very useful because the mother wavelets in this family have compact support. Therefore, with these wavelets, the size of and decreases rapidly as increases for the DWT of most signals. These coefficients are fully equivalent to the information that is contained in the original series and the time series can be perfectly reconstructed from its DWT coefficients. Thus, the wavelet representation in (10) can also be expressed as
where and , are called the smooth and detail signals, respectively. The sequential set of terms (, in Equation (12) represents a set of orthogonal signal components that represent the signal at resolutions 1 to . Each provides the orthogonal increment to the representation of the function at the scale For more details about wavelet transforms and their applications, we refer to the monograph Debnath and Shah [30].
3.2. Choice of Wavelet Families
The choice of the mother wavelet depends on the data to be analyzed. That is, the wavelet should be well adapted to the events to be analyzed (Percival and Walden [30]). Different wavelet functions are characterized by their distinctive features, such as region of support, number of vanishing moments, and the degree of symmetry. The present study, for the first time, compares the effects of 16 selected wavelet functions on the performance of hybrid Wavelet-ANN model. These wavelet functions are from the five most frequently used wavelet families. These five families are, namely, Haar, Daubechies, Coiflets, Symlets, and Meyer. More details on these wavelet families can be found in many standard text books, such as Debnath and Shah [27], and Gençay, Selçuk and Whitcher [31].
3.3. Artificial Neural Networks
An ANN can be defined as a system or mathematical model consisting of many nonlinear artificial neurons running in parallel, which can be generated, as one or multiple layered. The key element of this paradigm is the novel structure of the information processing system. In other words, we can say that ANN models are ‘black box’ models with particular properties, which are greatly suited to dynamic nonlinear system modelling. The main advantage of this approach over traditional methods is that it does not require the complex nature of the underlying process under consideration to be explicitly described in mathematical form.
Many different ANN models have been proposed since 1980s. Perhaps the most influential models are the Multi-layer perceptron (MLP) networks, Radial basis neural networks, Recurrent or dynamical neural networks, Hopfied networks, Elman neural networks, and Kohonen’s self organizing networks. However, the MLP networks have been widely used for financial forecasting due to their ability to correctly classify and predict the dependent variable. The MLP network consists of a number of neurons arranged in different layers. Typically, it consists of an input layer, a hidden layer, and an output layer. A layer usually contains a group of neurons, each of which has the same pattern of connections to the neurons in other layers. Each layer has a different role in overall operation of the network. Each neuron is connected to the neuron in next layer through connections called weights, as shown in Figure 1. Therefore, each neuron in an MLP network is connected with neurons in subsequent layers, and each neuron sums its inputs and later produces its output using a mathematical function, known as the neuron transfer function or an activation function. Commonly used activation functions are sigmoidal function, Gaussian function, or the cubic polynomial. MLPs can be trained using many different learning algorithms. In this study, MLPs were trained using the LM algorithm because it is fast, accurate, and reliable. In addition, previous studies have also indicated that the LM is a very good algorithm to develop an ANN model for financial forecasting in terms of statistical significance, as well as processing flexibility [32]. The LM algorithm is a modification of the classic Newton algorithm for finding an optimum solution to a minimization problem. Furthermore, in order to improve the generalization of the model, the stop training algorithm (STA) approach (Bishop [33]) is used. The use of STA reduced the training time four times, and it provided better and more reliable generalization performance than the use of LM algorithm alone. To implement STA in practice, the available data was split into three parts: training set, validating set, and a testing set. For the theoretical and mathematical treatment of ANN’s, the reader is referred to the monographs Bishop [33] and Haykin [34].
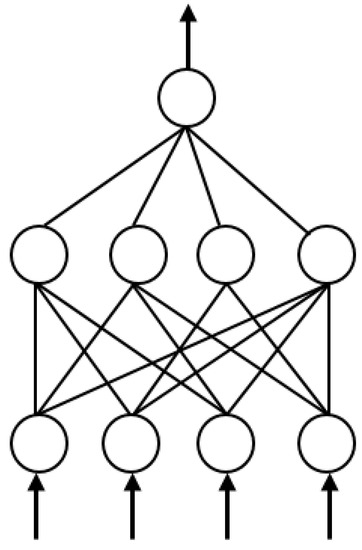
Figure 1.
A typical Multi-layer perceptron (MLP) networks neural network.
3.4. Hybrid Wavelet Neural Network Model
WNNs are recently developed neural network models. WNN models combine the strengths of wavelet transforms and neural networks to achieve strong nonlinear approximation ability, and thus have been successfully applied to forecasting, modelling, and function approximations [35,36,37,38,39,40]. The architecture of the WNN model is usually composed of four parts: DWT, reconstruction of wavelet coefficients, AAN prediction, and reconstruction of data series. The schematic diagram of the developed model is shown in Figure 2. Our approach for creating the proposed hybrid WNN model suggests that the wavelet and the neural network processing portions be performed separately: the financial time series is firstly decomposed into sub-series with different scales using DWT, so that unclear temporal structures can be exposed for further and easier evaluation of the signal. For this purpose, the time series is transformed using the DWT, with some recognized wavelet families, namely, Haar wavelet, Daubechies wavelets, Coiflets, and discrete Meyer wavelet. After the decomposition process, all of the obtained sub-series were used as inputs to the ANN model because each sub-series component plays a different role in the original time series and the behaviour of each sub-series is distinct. This phase is the most significant and effective part of the ANN estimation performance. The selection of the dominant DW’s becomes effective on the output data and has a highly positive effect on the model’s performance. Therefore, the key point in the hybrid wavelet-ANN model is the wavelet decomposition of the time series and the utilization of the DW’s as inputs of the ANN model.
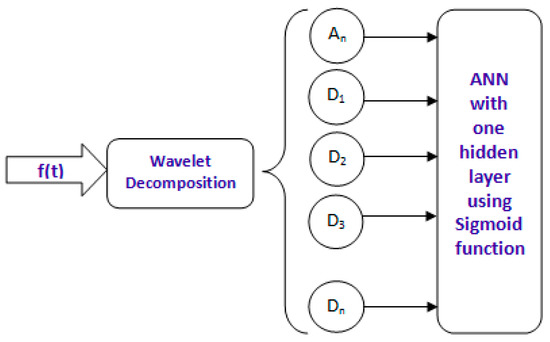
Figure 2.
Schematic diagram of the hybrid wavelet neural network (WNN) approach model.
The modelling steps of the proposed method are described as follows:
Use DWT to decompose original time series into a set of wavelet coefficients, and then separately reconstruct these coefficient series into a set of time sub-series that is equal to the length of original time series.
- (1)
- Establish the hybrid WNN model for these sub-series, and make the short term prediction for each sub-series.
- (2)
- Calculate the sum of forecasting results of all the sub-series to obtain the final forecasting for original time series.
The performance of developed model can be evaluated using several statistical tests that describe the errors that are associated with the model. In order to provide an indication of goodness of fit between the observed and forecasted, the root mean squared error (RMSE) is used in this research. The RMSE is used to measure forecast accuracy, which produces a positive value by squaring the errors. The RMSE evaluates the variance of errors independently of the sample size, and is given by:
where is the number of data points used, and are the actual and predicted value at time respectively. The RMSE increases from zero for perfect forecasts through large positive values as the discrepancies between the forecasts and observations become increasingly large. Obviously small value for RMSE indicates high efficiency of the model.
4. Data, Results and Discussion
In this empirical work, monthly data for the period from October 1996 to April 2011 has been used to test the predictability of yield spreads. The span of the dataset is same as Dar et al., [17] to facilitate the comparisons. This dataset contains 175 observations and monthly growth rate of Index of Industrial Production (IIP) is used as a proxy for economic growth. Spreads are constructed at the various ends of the yield curve. These spreads are the differences between (i) one year Government of India (GoI) bonds and 91-days Treasury bills (Sp 1, 3); (ii) five year GoI bonds minus 91-days Treasury bills (Sp 5, 3); (iii) ten year GoI bonds minus 91-days Treasury bills (Sp 10, 3); (iv) ten year GoI bonds minus five year GoI bonds (Sp 10, 5); and, (v) ten year GoI bonds minus eight year GoI bonds (Sp 10, 8). We then start by decomposing the yield spread and output growth into different frequency components using the methodology of wavelets. For this purpose, we employ five different kinds of wavelet families, namely, Haar wavelet, Daubechies wavelets ( Symlets (, Coiflets (, and discrete Meyer wavelet.
On the data set seven decomposition were possible. Nevertheless, the number of feasible wavelet coefficients gets small for higher levels with more decomposition; we preferred to carry out the wavelet analysis with so that four wavelet coefficients and one scaling coefficient respective were produced (Since components represent the non-stationary component of the time series, in our regression analysis they were not tested for predictive power. Lagged values are used for decomposition and rest 10% of the data has been used for testing as the lagged values rid the data of unwanted biases. Moreover, lagged correlations have been used in our study, which can be calculated for any column V by (; in correl. Similarly, for lag 1, we have (; and so on). Plots of these different period oscillations and their time dynamics are shown in Figure A1, Figure A2 and Figure A3 and Table A1 in the Appendix. The detail levels and represent the very short run dynamics of a signal or time series, detail level and roughly correspond to the frequency dynamics of time series within 8–16 months and 16–32 months, respectively (see Table A2).
The hybrid WNN models are developed with the input being average of time lags, i.e., lag 1, lag 2, lag 3, and lag 4 decomposed at level The level four decomposition comprising of one approximation A4 and four details D4, D3, D2, D1. For the hybrid WNN model, the ANN network that were developed consisted of an input layer, a hidden layer and one out layer containing the output growth. Therefore, in this research, the structure of the hybrid WNN model contains five neurons in the input layer including four details and one approximation. The model was trained in a process called supervised learning. In supervised learning, the input and output are repeatedly fed into the neural network. With each presentation of input data, the model output is matched with the given target output and an error is calculated. This error is back propagated through the network to adjust the weights with the goal of minimizing the error and achieving simulation closer and closer to the desired target output. The LM algorithm is used in the current study to train the network because of its simplicity. It is an iterative algorithm that locates the minimum function value, which is expressed as sum of squares of nonlinear functions. The number of neurons in the hidden layer is determined by error and trail procedure. The model is trained up to maximum of 1000 epochs reached.
After the training was completed, the ANN was applied to the testing data. The tangent sigmoid function was employed for the neurons of the hidden and output layers to process their respective inputs for the hybrid WNN model. The sample values were distributed randomly and it is observed that the lowest RMSE value is obtained when the sample is divided for 65% in the training set, 10% in validation set, and 25% in testing set, where as for other sample combinations, we get large RMSE values. The performance of the 16 selected wavelet functions is accessed by calculating the percentage increase or decrease in the RMSE values of the hybrid WNN is shown in Table 1 and depicted graphically in Figure 3. It is evident from the Table 1 and Figure 3 that the yield spreads Sp (10, 3) constructed at the policy relevant areas of the yield curve has outstanding predictive power for information about output growth, while those constructed at longer end shows very weak predictive power because central bank has little influence on either interest rates of yield spread constructed at the longer end of the yield curve. Therefore, information content for future output growth that one can expect to extract from the spreads constructed at the longer end of the yield curve will be either absent or lower than other spreads. Moreover, the model results show the high merit of Duabechies wavelet (Db4) in comparison with the others wavelets; that is, Haar wavelet, Symlets , Coiflets (, and discrete Meyer wavelet. Furthermore, if we compare the RMS values of wavelet decomposition method, as given in Table A1, with the corresponding WNN model, the numerical experiments confirm that the proposed WNN model is superior to the casual wavelet method and is highly accurate.

Table 1.
Root mean squared error (RMSE) values of the hybrid WNN.
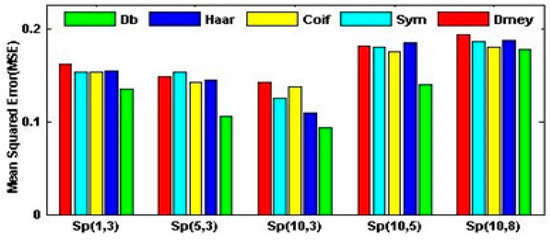
Figure 3.
Relative performance of the hybrid WNN model with different wavelets.
5. Conclusions
In this research, a new method based on coupling DWTs and ANNs for yield spread forecasting applications was proposed to help consumers, investors, and policy makers in a more effective and sustainable manner. The proposed hybrid model combines the capability of wavelets and neural networks to capture non-stationary nonlinear attributes embedded in financial time series. Using the DWT, each of the yield spread was decomposed into component series that carried most of the information, because DWT allowed for most of the noisy data to be removed from the yield spreads. Then, the summed sub-series components obtained by addition of the dominant discrete wavelet components were selected as the inputs of the ANN model to predict the future output growth. Our results based on WNN approach show that yield spreads, which are constructed at the short end and policy relevant areas of the yield curve have information about output growth. We also find that the yields spread that are constructed at long ends of the yield curve lack of predictive power within time domain framework. Overall, it can be seen that the predictive power of yield spreads when performed by using wavelet-neural network models, show the same results as in Dar et al., 2014 [17].
Author Contributions
Firdous Ahmad Shah and Lokenath Debnath performed the research and wrote the paper.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
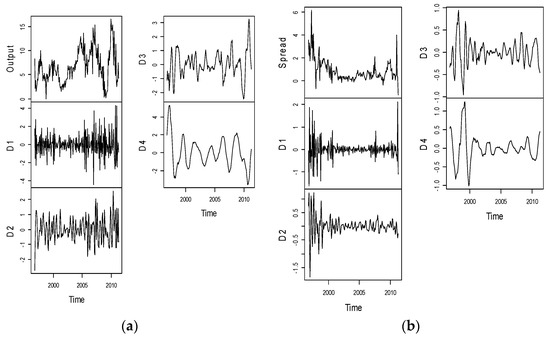
Figure A1.
Plot of Output growth, yield spread constructed at the shorter end of yield curve and their corresponding wavelet decompositions. (a) Output Growth; (b) Sp (1, 3).
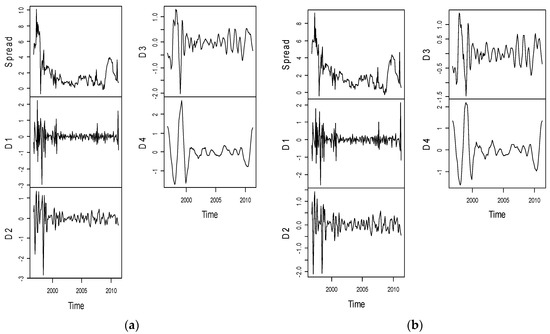
Figure A2.
Plot of yield spreads constructed at the policy relevant area of yield curve and their corresponding wavelet decompositions. (a) Sp (5, 3); (b) Sp (10, 3).
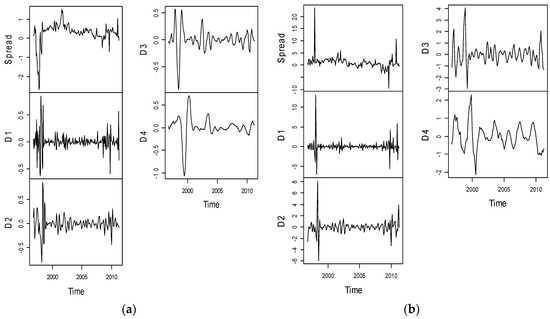
Figure A3.
Plot of yield spreads constructed at the longer end of yield curve and their corresponding wavelet decompositions. (a) Sp (10, 5); (b) Sp (10, 8).

Table A1.
RMSE values of the wavelet decomposition.
Table A1.
RMSE values of the wavelet decomposition.
| Wavelet Family | Decomposition Level | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Haar Wavelet | 0.6774 | 0.8435 | 1.0023 | 1.2541 | 1.7372 | 1.804 | 1.9319 |
| Db2 | 0.6187 | 0.7156 | 0.8818 | 1.3016 | 1.5234 | 1.557 | 1.7482 |
| Db3 | 0.5742 | 0.6979 | 0.8744 | 1.016 | 1.6045 | 1.6404 | 1.8196 |
| Db4 | 0.5608 | 0.748 | 0.8285 | 1.2503 | 1.5977 | 1.7154 | 2.0864 |
| Db5 | 0.575 | 0.7182 | 0.8763 | 1.1831 | 1.5148 | 1.6667 | 2.2136 |
| Db6 | 0.5956 | 0.6985 | 0.8013 | 1.0149 | 1.5921 | 1.631 | 1.9039 |
| Db7 | 0.6074 | 0.7468 | 0.8755 | 1.2356 | 1.5967 | 1.6676 | 1.7276 |
| Sym2 | 0.6187 | 0.7156 | 0.8818 | 1.3016 | 1.5234 | 1.557 | 1.7482 |
| Sym3 | 0.5742 | 0.6979 | 0.8744 | 1.016 | 1.6045 | 1.6404 | 1.8196 |
| Sym4 | 0.6024 | 0.7451 | 0.8618 | 1.0137 | 1.5928 | 1.6594 | 1.7888 |
| Coif1 | 0.5953 | 0.777 | 0.9053 | 1.0553 | 1.5396 | 1.5842 | 1.6634 |
| Coif2 | 0.5912 | 0.7574 | 0.8141 | 1.1058 | 1.6033 | 1.6507 | 1.747 |
| Coif3 | 0.5897 | 0.754 | 0.8757 | 1.2489 | 1.595 | 1.6818 | 1.7783 |
| Coif4 | 0.5889 | 0.7527 | 0.7973 | 1.1763 | 1.5713 | 1.6942 | 1.8072 |
| Coif5 | 0.5886 | 0.7526 | 0.8708 | 1.014 | 1.5551 | 1.6996 | 1.8232 |
| Discrete Meyer | 0.5898 | 0.7518 | 0.8596 | 1.0263 | 1.5882 | 1.6507 | 1.8824 |

Table A2.
Time interpretation of different frequencies.
Table A2.
Time interpretation of different frequencies.
| Time-Scale Level | Time-Frequency |
|---|---|
| D1 | 2–4 months |
| D2 | 4–8 months |
| D3 | 8–16 months |
| D4 | 16–32 months |
| A4 | More than 32 months |
References
- Stock, J.H.; Watson, M.W. New indexes of coincident and leading economic indicators. NBER Macroecon. Annu. 1989, 41, 351–409. [Google Scholar] [CrossRef]
- Estrella, W.; Hardouvelis, G. The term structure as predictor of real activity. J. Finance 1991, 46, 555–576. [Google Scholar] [CrossRef]
- Estrella, W.; Mishkin, F. The predictive power of the term structure of interest rates in Europe and the United States. Eur. Econ. Rev. 1997, 41, 1375–1401. [Google Scholar] [CrossRef]
- Bonser-Neal, C.; Morley, T.R. Does the yield spread predict real economic activity? A multi-country analysis. Econ. Rev. Fed. Reserve Bank Kans. City 1997, 82, 37–53. [Google Scholar]
- Adel, S.; Martin, C.; Heather, J.R.; Jose, A.M. The reaction of stock markets to crashes and events: A comparison study between emerging and mature markets using wavelet transforms. Physica A 2006, 368, 511–521. [Google Scholar]
- Bordo, M.D.; Haubrich, J.G. Forecasting with the yield curve, level, slope, and output. Econ. Lett. 2008, 99, 48–50. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. Forecasting output and inflation: The role of asset prices. J. Econ. Lit. 2003, 41, 788–829. [Google Scholar] [CrossRef]
- Tabak, B.M.; Feitosa, M.A. An analysis of the yield spread as a predictor of inflation in Brazil: Evidence from a wavelets approach. Expert Syst. Appl. 2009, 36, 7129–7134. [Google Scholar] [CrossRef]
- Tabak, B.M.; Feitosa, M.A. Forecasting industrial production in Brazil: Evidence from a wavelets approach. Expert Syst. Appl. 2010, 37, 6345–6351. [Google Scholar] [CrossRef]
- Kim, A.; Limpaphayom, P. The effect of economic regimes on the relation between term structure and real activity in Japan. J. Econ. Bus. 1997, 9, 379–392. [Google Scholar] [CrossRef]
- Jardet, C. Why did the term structure of interest rates lose its predictive power? Econ. Model. 2004, 219, 509–524. [Google Scholar] [CrossRef]
- Tkacz, G. Inflation changes, yield spreads, and threshold effects. Int. Rev. Econ. Finance 2004, 13, 187–199. [Google Scholar] [CrossRef]
- Nakaota, H. The term structure of interest rates in Japan: The predictability of economic activity. Jpn. World Econ. 2005, 17, 311–326. [Google Scholar] [CrossRef]
- Rosenberg, J.V.; Maurer, S. Signal or noise? Implications of the term premium for recession forecasting. Fed. Reserve Bank N. Y. Econ. Policy Rev. 2008, 14, 1–11. [Google Scholar]
- Kanagasabapathy, K.; Goyal, R. Yield Spread as a Leading Indicator of Real Economic Activity: An Empirical Exercise on the Indian Economy. 2002. Available online: https://www.imf.org/en/Publications/WP/Issues/2016/12/30/Yield-Spread-as-a-Leading-Indicator-of-Real-Economic-Activity-An-Empirical-Exercise-on-the-15819 (accessed on 28 September 2017).
- Bhaduri, S.; Saraogi, R. The predictive power of the yield spread in timing the stock market. Emerg. Mark. Rev. 2010, 11, 261–272. [Google Scholar] [CrossRef]
- Dar, A.B.; Samantaraya, A.; Shah, F.A. The predictive power of yield spread: Evidence. Empir. Econ. 2014, 46, 887–901. [Google Scholar] [CrossRef]
- Vieira, F.; Fernandes, M.; Chague, F. Forecasting the Brazilian curve using forward-looking variables. Int. J. Forecast. 2017, 33, 121–131. [Google Scholar] [CrossRef]
- Ang, A.; Piazzesi, M.; Wei, M. What does the yield curve tell us about GDP growth? J. Econ. 2006, 131, 359–403. [Google Scholar] [CrossRef]
- Wheelock, D.; Wohar, M.E. Can the term spread predict output growth and recessions? A survey of the literature. Fed. Reserve Bank St. Louis Rev. 2009, 419, 1–22. [Google Scholar]
- Harvey, C.R. The real term structure and consumption growth. J. Financ. Econ. 1988, 22, 305–333. [Google Scholar] [CrossRef]
- Tkacz, G. Neural network forecasting of Canadian GDP growth. Int. J. Forecast. 2001, 17, 57–69. [Google Scholar] [CrossRef]
- Moshiri, S.; Cameron, N. Econometrics versus ANN models in forecasting inflation. J. Forecast. 2000, 19, 201–217. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Azevedo, N.; Soares, M.J. Using wavelets to decompose the time-frequency effects of monetary policy. Physica A 2008, 387, 2863–2878. [Google Scholar] [CrossRef]
- Zagaglia, P. Does the Yield Spread Predict the Output Gap in the US? Working Paper; Stockholm University: Stockholm, Sweden, 2006. [Google Scholar]
- Dar, A.B.; Shah, F.A. In search of leading indicator property of yield spread for India: An approach based on quantile and wavelet regression. Econ. Res. Int. 2015, 2015, 308567. [Google Scholar] [CrossRef]
- Debnath, L.; Shah, F.A. Wavelet Transforms and Their Applications; Birkhauser: New York, NY, USA, 2015. [Google Scholar]
- Mallat, S.G. Multiresolution approximations and wavelet orthonormal bases of . Tran. Am. Math. Soc. 1986, 315, 69–87. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Perciva, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gençay, R.; Selçuk, F.; Whitcher, B. An Introduction to Wavelets and Other Filtering Methods in Finance and Economics; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Zhang, G.; Patuw, B.E.; Hu, M. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Bishop, M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Minu, K.K.; Lineesh, M.C.; Jess, J.C. Wavelet neural networks for nonlinear time series analysis. Appl. Math. Sci. 2010, 4, 2485–2595. [Google Scholar]
- Murtagh, F.; Starck, J.L.; Renaud, O. On neuro-wavelet modelling. Decis. Support Syst. 2004, 37, 475–484. [Google Scholar] [CrossRef]
- Renaud, O.; Stark, J.L.; Murtagh, F. Prediction based on a multiscale decomposition. Int. J. Wavelets Multiresolut. Inf. Process. 2003, 1, 217–232. [Google Scholar] [CrossRef]
- Ortega, L.; Khashanah, K. A neuro-wavelet model for short-term forecasting of high frequency time series of stock returns. J. Forecast. 2014, 33, 134–146. [Google Scholar] [CrossRef]
- Pir, M.Y.; Shah, F.A.; Asgar, M. Using wavelet neural network to forecast IIP growth with yield spreads. IPASJ Int. J. Comput. Sci. 2014, 2, 31–36. [Google Scholar]
- Zhang, Q.H.; Benveniste, A. Wavelet networks. IEEE Trans. Neural Netw. 1992, 3, 889–898. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).