Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis
Abstract
:1. Introduction
1.1. Diagnosis of Amoebiasis
1.2. Immunity and Vaccine
2. Related Work
- The infection spreads by means of direct contact between the susceptible with the infectious or carrier in a homogeneously-mixed population. (redDirect contact happens when susceptible people ingest cysts of Entamoeba histolytica contained in water or food infected by human feces).
- The period of the Amoebiasis investigation is relatively extended over a short time scale to maintain an equal balancing birth and natural death rates , and hence, the size of the population under study remains constant during the said period.
- The rate at which susceptible members are infected is proportional to the force of infection , which is a function of transmission and the fraction of the infectious and the carriers i.e., .
- Susceptible (S): This is the class of individuals who are not yet infected, but can become infected once they are in contact with contaminated food or drink.
- Exposed (E): The class of individuals who are already infected, but not yet able to diffuse cysts in the environment.
- Infectious (I): This class encompasses the individuals infected in the acute stage of the disease, shedding a much greater number of cysts and trophozoites in a mixture of mild stools of blood and mucus.
- Carrier (C): This is the class of people who are asymptomatic to the disease although shedding cysts occasionally.
- Removal (R): This is a class of individuals who recovered from Amoebiasis.
3. Stability Analysis of the Model
3.1. Threshold Parameters of the Model
3.1.1. The Disease-Free Equilibrium State of Amoebiasis
3.1.2. The Basic Reproduction Number
3.1.3. Endemic Equilibrium State
3.2. Stability Analysis of the Steady States and Sensitivity Analysis
3.2.1. The Stability of the Disease-Free Equilibrium
- Given , it follows that . Hence, . This proves Condition (26).
- We need to show that if , then . Given,but,we obtain:Develop the right side of the inequality by applying the distributive law and the second term to yield the following:Hence, we obtain
3.2.2. Stability of the Endemic Equilibrium
3.3. Sensitivity Analysis
4. Numerical Solution and Simulation
- Abd-Alla et al. have found that antibody reaction to Entamoeba histolyticalasts for a mean duration period of 17 days [39]; we suggest the range for to be between 17 and 30 days.
- The per capita birth rate and natural death rate are assumed to balance each other in most developing countries (or for a study of short duration in developed countries). Therefore, it is necessary to consider to be an approximation (in years) starting from 45 to 50 years [26].
- The estimated duration in the carrier state, , is identified as the mean period of existence of the host’s IgA and IgG antibodies. These antibodies may last for several months [15] and even remain discernible up to three years [2]. Therefore, a mean period varying between two and three years sounds reasonable.
4.1. Numerical Results
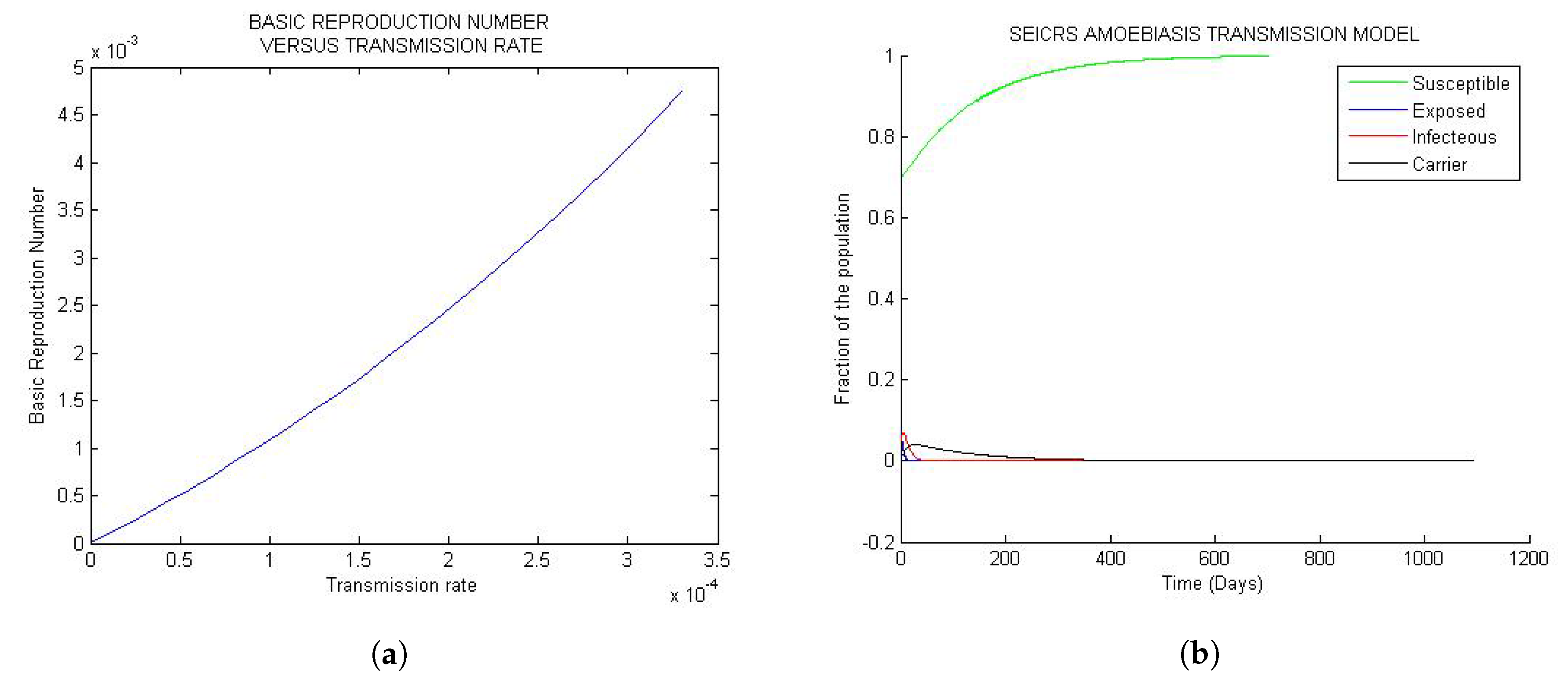
4.1.1. Case 1:
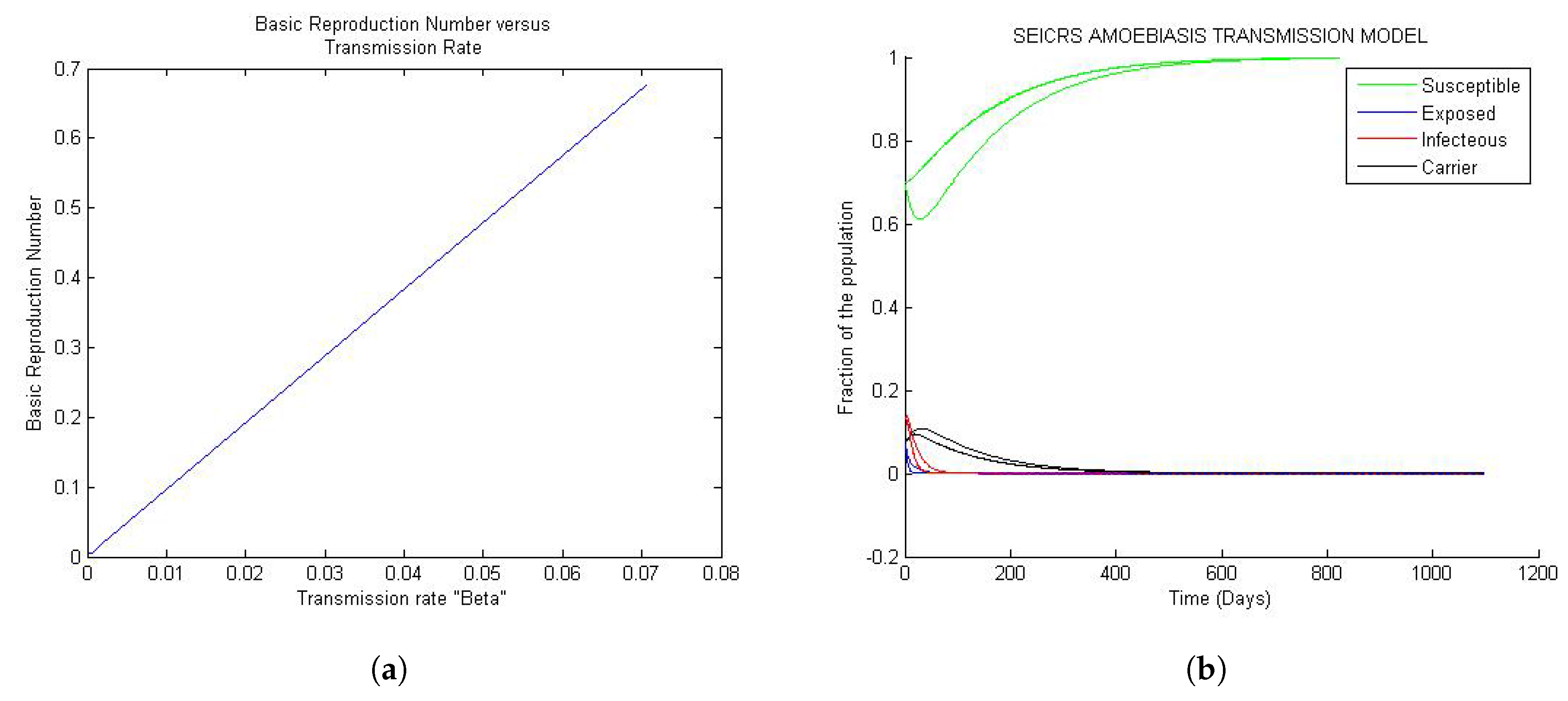
4.1.2. Case 2: Values of
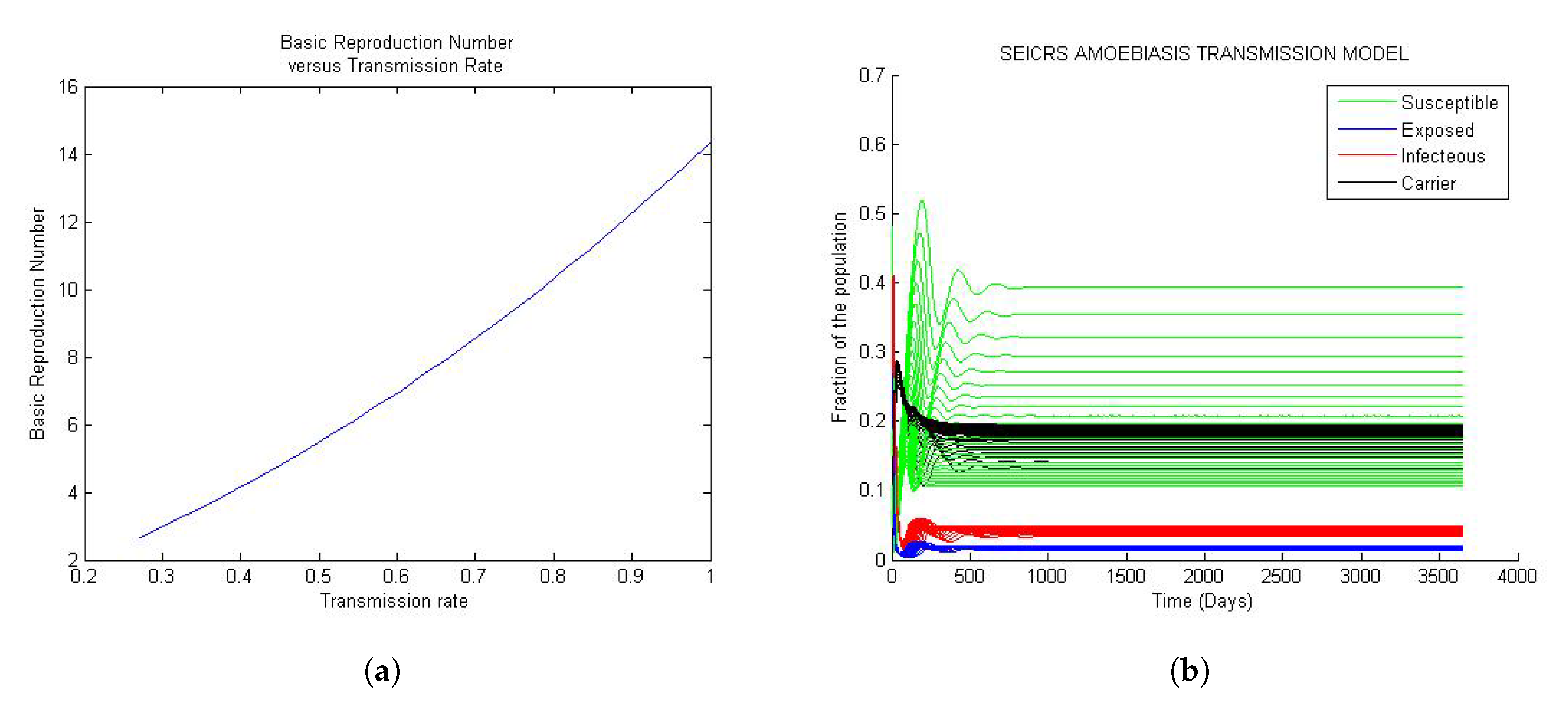
4.1.3. Case 3: Values of
4.2. Stability of the Steady States
4.3. Sensitivity of the Basic Reproduction Number
5. Discussion and Concluding Remarks
- The basic reproduction number is found to be remarkably sensitive to the parameters described above. Consequently, hygienic measures destabilize and decrease the direct transmission rate, as well as the transmission factor. In turn, the combined effects have a considerable contribution toward “cutting off” the basic reproduction number. This action leads to the eradication of Amoebiasis.
- The clinical measure causes the depletion rate of acute infectious state to spike. Eventually, this class/state will cease to exist due to hygienic measures as explained earlier. However, there may still be a portion of the population of carriers of cysts that can trigger Amoebiasis in future.
- Using SEIRS epidemic model the duration of the course of Amoebiasis is made to run over a short time, i.e., the mean time an individual stays in the infectious state is reduced to . The mean duration of the carrier state, , notwithstanding its significance toward sensitivity of , is ignored.
- The SEIRS epidemic model is incapable of predicting the evolution in the carrier state, thereby ignoring a truly relevant aspect in the study of the dynamics of amoebic invasion. The model fails to accommodate the fact that the carrier state is the causative step for the development of the amoebic invasion.
- By comparison of the values of the basic reproduction number for both SEIRS epidemic model and SEICRS epidemic model given by Equation (17), it is observed that SEIRS epidemic model predicts retardant onset of Amoebiasis compared to the prediction made by SEICRS epidemic model. However, the two models will approximately have equal basic reproduction numbers for small values of ϵ and ρ.
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Algorithm to Generate Figure 1, Figure 2 and Figure 3
Appendix A.2. Algorithm to Generate Figure 4
Appendix A.3. Algorithm of Sub-Function “diffamoeba()”
References
- Hotez, P.J.; Molyneux, D.H.; Fenwick, A.; Kumaresan, J.; Sachs, S.E.; Sachs, J.D.; Savioli, L. Control of neglected tropical diseases. N. Engl. J. Med. 2007, 357, 1018–1027. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, W.; Abd-Alla, M.; Ravdin, J.I. Prevalence and Incidence of Entamoeba histolytica Infection in South Africa and Egypt. Arch. Med. Res. 2006, 37, 265–268. [Google Scholar] [CrossRef] [PubMed]
- Walsh, J.A. Problems in Recognition and Diagnosis of Amebiasis: Estimation of the Global Magnitude of Morbidity and Mortality. Rev. Infect. Dis. 1986, 8, 228–238. [Google Scholar] [CrossRef] [PubMed]
- Prevalence and Incidence of amoebiasis. Available online: http://www.rightdiagnosis.com/a/amebiasis/prevalence.htm (accessed on 20 July 2017).
- Hertz, R.; Lulu, S.B.; Shahi, P.; Trebicz, W.; Benhar, M.; Ankri, S. Proteomic Identification of S-Nitrosylated Proteins in Parasite Entamoeba histolytica by Resin-Assisted Capture: Insights into the Regulation of the Gal/GalNAC Lectin by Nitric Oxide. PLoS ONE 2014, 9, e91518. [Google Scholar] [CrossRef] [PubMed]
- Thibeaux, R.; Weber, C.; Hon, C.C.; Dillie, M.A.; Avé, P.; Coppée, J.-Y.; Labruyère, E.; Guillén, N. Identification of the Virulence Landscape Essential for Entamoeba histolytica Invasion of the Human Colon. PLoS Pathog. 2013, 9, e1003824. [Google Scholar] [CrossRef] [PubMed]
- Haque, R.; Ali, I.K.M.; Petri, W.A., Jr. Prevalence and immune response of Entamoeba histolytica infection in preschool children in Bangladesh. Am. J. Trop. Med. Hyg. 1999, 60, 1031–1034. [Google Scholar] [CrossRef] [PubMed]
- Jackson, T.F.; Gathira, V.; Simjee, A.E. Seroepidemiological Study of antibody responses to the zymodemes of Entamoeba histolytica. Lancet 1985, 325, 716–719. [Google Scholar] [CrossRef]
- Xeménez, C.; Moran, P.; Rajas, L.; Valadez, A.; Gomez, A. Reassessment of the epidemiology of amebiasis: State of the arth. Infect. Genet. Evol. 2009, 9, 1023–1032. [Google Scholar] [CrossRef] [PubMed]
- Petri, W.A., Jr.; Singh, U. Diagnosis and Management of Amebiasis. Clin. Infect. Dis. 1999, 29, 1117–1125. [Google Scholar] [CrossRef] [PubMed]
- Samie, A.; ElBakri, A.; AbuOdeh, R. Amoebiasis in the Tropics: Epidemiology and Pathogenesis. In Current Topics in Tropical Medicine; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Dhawan, V.K.; Cleveland, K.O.; Cantey, J.R. Amoebiasis. Available online: http://emedicine.medscape.com/article/212029-overview (accessed on 20 February 2017).
- Caballero-Salcedo, A.; Viveros-Rogel, M.; Salvatierra, B.; Tapia-Conyer, R.; Sepulveda-Amor, J.; Gutierrez, G.; Ortiz-Ortiz, L. Seroepidemiology of amebiasis in Mexico. Am. J. Trop. Med. Hyg. 1994, 50, 412–419. [Google Scholar] [CrossRef] [PubMed]
- Lawson, L.L.O.; Bailey, J.W.; Beeching, N.J.; Gurgel, R.G.; Cuevas, L.E. The stool examination reports amoeba cysts: Should you treat in the face of over diagnosis and lack of specificity of light microscopy? Trop. Doctor 2004, 34, 28–30. [Google Scholar] [CrossRef] [PubMed]
- Tanyuksel, M.; Petri, W.A., Jr. Laboratory Diagnosis of Amebiasis. Clin. Microbiol. Rev. 2003, 16, 713–729. [Google Scholar] [CrossRef] [PubMed]
- Stanley, S.L., Jr. Protective Immunity to Amebiasis: New Insights and New Challenges. J. Infect. Dis. 2001, 184, 504–606. [Google Scholar] [CrossRef] [PubMed]
- Hategekimana, F.; Saha, S.; Chaturvedi, A. Amoebiasis Transmission and Life cycle: A continuous state description by virtue of existence and uniqueness. Glob. J. Pure Appl. Math. 2016, 12, 375–390. [Google Scholar]
- Wang, Y.; Jin, Z.; Yang, Z.; Zhang, Z.-K.; Zhou, T.; Sun, G.-Q. Global analysis of an SIS model with an infective vector on complex network. Nonlinear Anal. Real World Appl. 2012, 13, 543–557. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Population biology of infectious disease I. Nature 1979, 180, 316–367. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Gao, L.Q.; Hethcote, H.W. Disease transmission models with density-dependent demographics. J. Math. Biol. 1992, 30, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Clumax, M. Speciality Consultation Service. Available online: http://www.medall.in/health-information/disease/infectious-disease/amoebiasis/ (accessed on 16 June 2017).
- Logemann, H.; Ryan, E.P. Ordinary Differential Equation, Analysis, Qualitative Theory and Control; Springer: London, UK, 2014. [Google Scholar]
- Wiggis, S. Texts In Applied Mathematics: Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer Science and Business Media: New York, NY, UA, 2003; Volume 2. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous population. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Pejna, R. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NY, USA, 2008. [Google Scholar]
- Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Otieno, G.; Koske, J.K.; Mutiso, J.M. Cost Effectiveness Analysis of Optimal Malaria Control Strategies in Kenya. Mathematics 2016, 4, 14. [Google Scholar] [CrossRef]
- Coddington, A.E.; Levinson, N. Theory of Ordinary Differential Equations; Tata McGraw-Hill: New Dheli, India, 2010. [Google Scholar]
- Perko, L. Differential Equation and Dynamical Systems, 3rd ed.; Springer-Verlag: New York, NY, USA, 2014. [Google Scholar]
- Murray, J.D. Mathematical Biology: I. An Introduction, 3rd ed.; Springer: London, UK, 2002. [Google Scholar]
- Trawicki, M.B. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef]
- Kamgang, J.C.; Sallet, G. Computation of threshold conditions for epidemiological models and global stability of the disease-free equilibrium (DFE). Math. Biosci. 2008, 213, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Xiaolin, F.; Wang, L.; Teng, Z. Global dynamics for class of discrete SEIRS epidemic models with general nonlinear incidence. Adv. Differ. Eq. 2016, 2016, 123. [Google Scholar]
- Cooke, K.L.; van den Driessche, P. Analysis of an SEIRS epidemic model with two delays. J. Math. Biol. 1996, 35, 240–260. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A. Global analysis of an SEIRS epidemic model with new modulated saturated incidence. Commun. Math. Biol. Neurosci. 2014, 2014, 1–11. [Google Scholar]
- Nkamba, L.N.; Ntaganda, J.M.; Abboubakar, H.; Kamgang, J.C.; Lorenzo, C. Global stability of a SVEIR epidemic model: Application to poliomyelitis transmission dynamics. Open J. Model. Simul. 2017, 5, 98–112. [Google Scholar] [CrossRef]
- Chitnis, N.; Cushing, J.; Hyman, J. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math. 2006, 67, 24–45. [Google Scholar] [CrossRef]
- Abd-Alla, M.D.; Jackson, T.F.; Rogers, T.; Reddy, S.; Ravdin, J.I. Mucosal immunity to asymptomatic Entamoeba histolytica and Entamoeba dispar infection is associated with a peak intestinal anti-lectin immunoglobulin A antibody response. Infect. Immun. 2006, 74, 3897–3903. [Google Scholar] [CrossRef] [PubMed]
- Amebiasis: Overview, Causes and Symptoms. Available online: http://www.healthline.com/health/amebiasis (accessed on 23 June 2017).

| Symbol | Description | Unit |
|---|---|---|
| Force of infection | ||
| Direct transmission rate | ||
| Transmission reducing factor | Dimensionless | |
| Average latency period | ||
| Average infectious period of acute infectiousness. | ||
| Average temporary immune period | ||
| Average infectious period of carrier | ||
| Population’s crude birth (per capita death) rate | ||
| Probability of an infectious to becomes carrier | Dimensionless |
| Parameter | Unit | Range | Baseline | Sensitivity Index of |
|---|---|---|---|---|
| (time) | 0.6 | 1 | ||
| Dimensionless | 0.084 | 0.8905 | ||
| Dimensionless | 0.95 | 0.8905 | ||
| (time) | 6.8493 | −0.8307 | ||
| (time) | 0.1 | −0.1089 | ||
| (time) | 0.0714 | 0.0134 | ||
| (time) | −0.8283 | |||
| (time) | 0.0588 | — |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hategekimana, F.; Saha, S.; Chaturvedi, A. Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis. Mathematics 2017, 5, 58. https://doi.org/10.3390/math5040058
Hategekimana F, Saha S, Chaturvedi A. Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis. Mathematics. 2017; 5(4):58. https://doi.org/10.3390/math5040058
Chicago/Turabian StyleHategekimana, Fidele, Snehanshu Saha, and Anita Chaturvedi. 2017. "Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis" Mathematics 5, no. 4: 58. https://doi.org/10.3390/math5040058
APA StyleHategekimana, F., Saha, S., & Chaturvedi, A. (2017). Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis. Mathematics, 5(4), 58. https://doi.org/10.3390/math5040058





