On the Duality of Regular and Local Functions

Abstract

In this paper, we relate Poisson’s summation formula to Heisenberg’s uncertainty principle. They both express Fourier dualities within the space of tempered distributions and these dualities are also inverse of each other. While Poisson’s summation formula expresses a duality between discretization and periodization, Heisenberg’s uncertainty principle expresses a duality between regularization and localization. We define regularization and localization on generalized functions and show that the Fourier transform of regular functions are local functions and, vice versa, the Fourier transform of local functions are regular functions.

1. Introduction

Regularization is a popular trick in applied mathematics; see [1] for example. It is the technique “to approximate functions by more differentiable ones” [2]. Moreover, its terminology coincides with the terminology used in generalized function spaces. They contain two kinds of functions: “regular functions” and “generalized functions”. While regular functions are functions in the ordinary functions sense which are smooth (infinitely differentiable) in the ordinary functions sense, all other functions become smooth (infinitely differentiable) in the “generalized functions sense” [3]. In this way, all functions are smooth. Localization, in contrast to that, is another popular technique. It allows, for example, to integrate functions which could not be integrated otherwise, if we think of “locally integrable” functions or if we think of the Short-Time Fourier Transform (STFT), capable of analyzing infinitely extended signals.

Although regularization (Figure 1) and localization (Figure 2) appear to be quite different, a connection between these operations is no surprise. It is rather ubiquitous in the literature. However, the theorem below (Figure 3) appears in a wider sense. It even holds within the space of tempered distributions and is directly related to Heisenberg’s uncertainty principle. It is moreover the inverse of an already known discretization–periodization duality (Poisson’s Summation Formula). While discretization and periodization map functions from smoothness towards discreteness in both time and frequency domain, the operations investigated in this study, regularization and localization, map functions from discreteness towards smoothness in both time and frequency domain (Figure 4 and Figure 5). In this way, we have a full range of tools (discretization, periodization, regularization, localization) in order to describe any transition from smoothness towards discreteness and also back from discreteness towards smoothness in a mathematically rigorous and formally correct way.

Figure 1. A regularization of generalized function f yields regular function ${\cap }_{\mathsf{\phi }}f$.

Figure 2. A localization of generalized function f yields local function ${\sqcap }_{\mathsf{\phi }}f$.

Figure 3. The regularization–localization theorem.

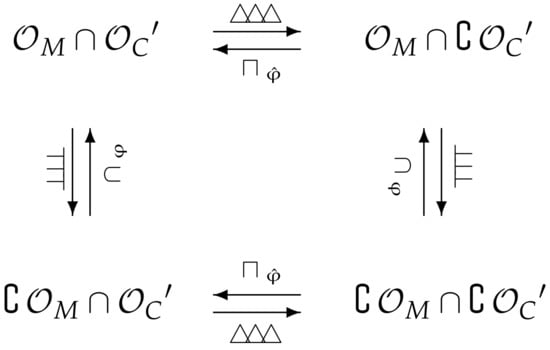
Figure 4. Four subspaces in ${\mathcal{S}}^{\prime }$, linked via operations $\perp \perp \perp ,▵▵▵,{\cap }_{\mathsf{\phi }},{\sqcap }_{\widehat{\mathsf{\phi }}}$.

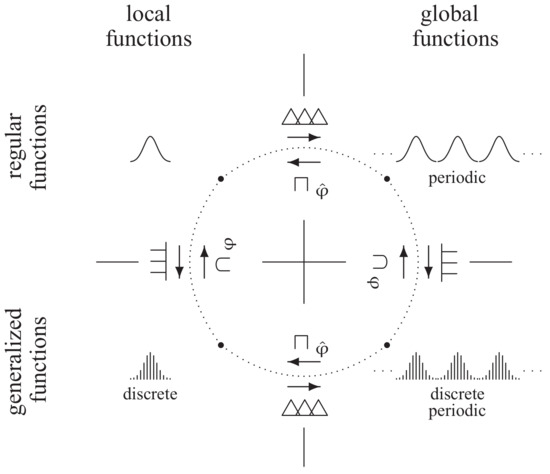
Figure 5. The same diagram as above, drawn in another fashion.

This paper is organized as follows. Section 2 describes the overall motivation for this study and Section 3 explains the rough proof idea. Section 4 provides an introduction to the notations used and previous results. Section 5 presents a justification for Section 6 where regularization and localization within the space of tempered distributions are defined. Section 7 provides symbolic calculation rules based on these definitions, needed to prove the theorem in Section 8. Section 9 connects these results to results in a previous study and Section 10, finally, concludes this study and provides an outlook.

2. Motivation

In contrast to more practical applications of regularizations and localizations, the actual intention of this study is to provide universally valid calculation rules for regularizations and localizations together with the scope of their validity within a preferably most general setting. In this way, regularizations can be expressed in terms of localizations and, vice versa, localizations can be expressed in terms of regularizations, i.e., poorly converging formulas can be replaced by better converging ones. Another important application of our rules is knowing the scope of their validity. Knowing not only a formula but also its validity scope is especially important in applied mathematics. It is simply not very reasonable to implement a formula that will never converge.

2.1. Generalized Functions

The setting of generalized functions, also called distributions, is today a most modern, very general setting in Fourier analysis [3,4,5,6,7,8,9,10,11]. It meets the requirements of Fourier analysis in both theory and practice. It allows, for example, to Fourier transform functions which are not even Lebesgue integrable, such as the Dirac impulse $\delta$ or even constants such as the function that is constantly 1.

In this study, we prove simple symbolic calculation rules within ${\mathcal{S}}^{\prime }$, the space of tempered distributions, for handling both, regularizations and localizations, and their interactions. The space of tempered distributions ${\mathcal{S}}^{\prime }$ is known to be an ideal setting in Fourier analysis, mainly due to three facts. First, the Fourier transform is understood in a much wider sense than usually (on Lebesgue square-integrable functions); secondly, the Fourier transform is still an automorphism in ${\mathcal{S}}^{\prime }$ (as on Lebesgue square-integrable functions), i.e., the Fourier transform of any element in ${\mathcal{S}}^{\prime }$ is again an element in ${\mathcal{S}}^{\prime }$; thirdly, all functions are smooth, i.e., all functions can be derived infinitely often. Smoothness is especially required to treat Fourier series (and the Fourier transform as their limit). They consist of complex exponentials which are functions that can be derived infinitely often. Furthermore, recall that Lebesgue square-integrable functions (and their Fourier transforms accordingly) must decrease to zero as their arguments increase, otherwise they would not be Lebesgue integrable. This very strong restriction has, in fact, never been accepted by those who are working with Fourier transforms practically. It actually led to the acceptance of ${\mathcal{S}}^{\prime }$ as a standard space in Fourier analysis throughout many scientific communities; beside mathematics and engineering, also in physics, especially in quantum mechanics [12,13,14,15]. In ${\mathcal{S}}^{\prime }$, in contrast to traditional approaches, we may even allow functions to grow up to the order of polynomials as their arguments increase and they can still be sampled and/or Fourier transformed.

2.2. Symbolic Calculation

The overall goal in this and in our previous study [16] is to compile a number of rules including their validity scope and therewith to fill a toolbox that will enable us to symbolically calculate with operations of discretization (sampling), periodization (replicating), regularization (smoothing) and localization (windowing). Performing such calculations on a symbolic level has several advantages. We are now able to rigorously prove higher-level theorems in ${\mathcal{S}}^{\prime }$; we may replace more complicated formulas by simpler ones (or by better converging ones) prior to implementing them in software and, lastly, we may even implement these rules in symbolic calculation environments such as in Wolfram Mathematica [17] or in Python SymPy [18] in order to exclude human errors in formula derivations.

Some applications of our rules [19] are, for example, extending the scope of validity of Poisson’s Summation Formula to a validity on tempered distributions [16], proving that four differently defined Fourier transforms (more precisely, the Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT) and the Integral Fourier Transform for periodic functions) coincide in the distributional sense [20,21,22] or deriving a digital radar image from the continuous case (the landscape being imaged) via operations of localization (windowing), discretization (sampling), convolution (defocusing) and deconvolution (focusing) [23].

3. Idea

The proof technique in generalized function spaces may appear a bit unusual to those who are practically oriented. For any equality $f=g$ in generalized function spaces $X^{\prime }$ where $f,\mathcal{g}\in X^{\prime }$, it must be shown that both, f and g, yield the same result if applied to arbitrarily chosen test functions $\mathsf{\phi }\in X$ taken from their test function space X. A very short introduction to this technique is given in the section Distribution Theory in our previous paper [16].

However, the argumentation in this paper is much simpler. We do not need to prove any results on test functions because it has already been done by other authors [24,25,26,27]. Instead, we simply argue with subspaces of ${\mathcal{S}}^{\prime }$. We implicitly use the fact that functions in subspaces in ${\mathcal{S}}^{\prime }$ inherit all function properties from the spaces where they are embedded. This idea is one of the fundamental tricks in distribution theory. A full range of distribution space embeddings can be found in [24], p. 170. However, only a few of these spaces are needed here (see section Notation and Figure 4 in [16]). We need the space of slowly growing regular functions ${\mathcal{O}}_M\subset {\mathcal{S}}^{\prime }$ (where “regular” means smooth functions in the ordinary functions sense), the space of rapidly decreasing generalized functions ${{\mathcal{O}}_C}^{\prime }\subset {\mathcal{S}}^{\prime }$ (where “generalized” means that they are smooth but not necessarily “regular”) and the Schwartz space $\mathcal{S}\subset {\mathcal{S}}^{\prime }$ which is the space of regular, rapidly decreasing functions, i.e., functions in ${\mathcal{O}}_M\cap {{\mathcal{O}}_C}^{\prime }=\mathcal{S}$ are “regular” and “local” (rapidly decreasing). They inherit “regular” from ${\mathcal{O}}_M$ and “local” from ${{\mathcal{O}}_C}^{\prime }$. Another important fact is that $\mathcal{S}$ contains the space $\mathcal{D}\subset \mathcal{S}$ which is the space of compactly supported smooth functions. So, in the special case of having some $\mathsf{\phi }\in \mathcal{D}$, the property of $\mathsf{\phi }$ being “local” turns into $\mathsf{\phi }$ being “finite”, i.e., $\mathsf{\phi }$ is zero outside some given interval. Accordingly, $\mathsf{\phi }·f$ for some $f\in {\mathcal{S}}^{\prime }$ will be zero outside the given interval. In this case, we talk about “finitization” as a special form of “localization”. A concatenation of discretization and finitization is of particular importance, especially for turning integrals into finite sums.

Moreover, we make intensive use of the following dualities of the Fourier transform: $\mathcal{F}\left(\mathcal{S}\right)=\mathcal{S}$ and hence $\mathcal{F}\left({\mathcal{S}}^{\prime }\right)={\mathcal{S}}^{\prime }$ as well as $\mathcal{F}\left({\mathcal{O}}_M\right)={{\mathcal{O}}_C}^{\prime }$ and $\mathcal{F}\left({{\mathcal{O}}_C}^{\prime }\right)={\mathcal{O}}_M$. The first duality means that the Fourier transform maintains the function property of being “regular and local”, the second duality means that “tempered” functions (slowly growing functions, i.e., functions that do not grow faster than polynomials) are again “tempered” after Fourier transforming them and the latter duality (Theorem 3, p. 424 in [26]) means that the Fourier transform of slowly growing (“regular”) functions are rapidly decreasing (“local”) functions and, vice versa, the Fourier transform of rapidly decreasing (“local”) functions are slowly growing (“regular”) functions. This simple circumstance resulted in a validity statement for the Poisson Summation Formula in ${\mathcal{S}}^{\prime }$, see Theorem 1 in [16]—the widest comprehension of the Poisson Summation Formula today to the best of this author’s knowledge.

Another issue in generalized function spaces, hence also in ${\mathcal{S}}^{\prime }$, is the fact that arbitrary generalized functions cannot be multiplied with each other. Accordingly, arbitrary generalized functions cannot be convolved with each other. We evade this problem in ${\mathcal{S}}^{\prime }$ by using Laurent Schwartz’ [24] subspace of multiplication operators ${\mathcal{O}}_M$ and his space of convolution operators ${{\mathcal{O}}_C}^{\prime }$ as introduced above. These spaces provide a secure footing for multiplications and convolutions in ${\mathcal{S}}^{\prime }$, see Theorem 3, p. 424 in [26]. Recall that $\mathcal{O}$ stands for Opérateurs (operators), m for Multiplication, c for Convolution, an apostrophe as $X^{\prime }$ indicates spaces of “generalized” functions, no apostrophe as X indicates spaces of “regular” functions. Elements from $X^{\prime }$ can always be applied to elements of X.

4. Preliminaries

Let ${\delta }_{kT}$ be the Dirac impulse shifted by $k\in {\mathbb{Z}}^n$ units of $T\in {\mathbb{R}}_{+}^n=\{t\in {\mathbb{R}}^n:0<t_{\nu }<\infty ,1⩽\nu ⩽n\}$, $kT$ being component-wise multiplication, within the space ${\mathcal{S}}^{\prime }\equiv {\mathcal{S}}^{\prime }\left({\mathbb{R}}^n\right)$ of tempered distributions (generalized functions that do not grow faster than polynomials) and let

$${\mathrm{III}}_T:=\stackrel{}{\sum _{k\in {\mathbb{Z}}^n}}{\delta }_{kT}$$

be the Dirac comb. Then, ${\delta }_{kT}\in {\mathcal{S}}^{\prime }$ and ${\mathrm{III}}_T\in {\mathcal{S}}^{\prime }$ for any $T\in {\mathbb{R}}_{+}^n$ are tempered distributions [8,24,25]. We shortly write $\delta$ instead of ${\delta }_{kT}$ if $k=0$. The Fourier transform $\mathcal{F}$ in ${\mathcal{S}}^{\prime }$ is defined as usual and such that $\mathcal{F}1=\delta$ and $\mathcal{F}\delta =1$ where 1 is the function being constantly one [3,4,5,6,7,9,11,24]. The Dirac comb is moreover known for its excellent discretization (sampling) and periodization (replicating) properties [4,9,11,28]. While multiplication ${\mathrm{III}}_T·f$ in ${\mathcal{S}}^{\prime }$ samples a function $f\in {\mathcal{S}}^{\prime }$, the corresponding convolution product ${\mathrm{III}}_T\ast f$ periodizes f in ${\mathcal{S}}^{\prime }$.

The following two lemmas summarize the demands that must be put on $f\in {\mathcal{S}}^{\prime }$ such that f can be sampled and/or periodized in ${\mathcal{S}}^{\prime }$. Recall that smoothness, i.e., infinite differentiability, is not a demand. It is a given fact for all functions in generalized function spaces. Also recall that ${\mathcal{O}}_M$ is the space of multiplication operators in ${\mathcal{S}}^{\prime }$ and ${{\mathcal{O}}_C}^{\prime }$ is the space of convolution operators in ${\mathcal{S}}^{\prime }$ according to Laurent Schwartz’ theory of distributions [14,16,24,25,26,27,29,30,31].

Lemma 1 (Discretization).

Generalized functions $f\in {\mathcal{S}}^{\prime }$ can be sampled in ${\mathcal{S}}^{\prime }$ if $f\in {\mathcal{O}}_M$.

Proof. 

Any uniform discretization (sampling) in ${\mathcal{S}}^{\prime }$ corresponds to forming the product

$${\mathrm{III}}_T·f\mathrm{in}{\mathcal{S}}^{\prime }$$

where ${\mathrm{III}}_T\in {\mathcal{S}}^{\prime }$ is the Dirac comb. Furthermore, ${\mathrm{III}}_T$ is not a regular function, i.e., ${\mathrm{III}}_T\in {\mathcal{S}}^{\prime }\backslash {\mathcal{O}}_M$. However, for any multiplication product in ${\mathcal{S}}^{\prime }$, it is required that at least one of the two factors is in ${\mathcal{O}}_M$. Otherwise, the existence of this product cannot be secured. Hence, $f\in {\mathcal{O}}_M\subset {\mathcal{S}}^{\prime }$ or another reasonable definition of this multiplication product would be required. Vice versa, if $f\in {\mathcal{O}}_M$ then ${\mathrm{III}}_T·f$ exists due to ${\mathcal{S}}^{\prime }·{\mathcal{O}}_M\subset {\mathcal{S}}^{\prime }$ (Theorem 3, p. 424 in [26]). ☐

One may observe that even ”if and only if” holds in Lemma 1 if the operation · is not redefined (in the sense that at least one of the two factors converges in any sense). An equivalent statement is the following lemma.

Lemma 2 (Periodization).

Generalized functions $f\in {\mathcal{S}}^{\prime }$ can be periodized in ${\mathcal{S}}^{\prime }$ if $f\in {{\mathcal{O}}_C}^{\prime }$.

Proof. 

Any periodization in ${\mathcal{S}}^{\prime }$ corresponds to forming the convolution product

$${\mathrm{III}}_T\ast f\mathrm{in}{\mathcal{S}}^{\prime }$$

where ${\mathrm{III}}_T\in {\mathcal{S}}^{\prime }$ is the Dirac comb. Furthermore, ${\mathrm{III}}_T$ is of no rapid descent, i.e., ${\mathrm{III}}_T\in {\mathcal{S}}^{\prime }\backslash {{\mathcal{O}}_C}^{\prime }$. However, for any convolution product in ${\mathcal{S}}^{\prime }$, it is required that at least one of the two factors is in ${{\mathcal{O}}_C}^{\prime }$. Otherwise, the existence of this product cannot be secured. Hence, $f\in {{\mathcal{O}}_C}^{\prime }\subset {\mathcal{S}}^{\prime }$ or another reasonable definition of this convolution product would be required. Vice versa, if $f\in {{\mathcal{O}}_C}^{\prime }$, then ${\mathrm{III}}_T\ast f$ exists due to ${\mathcal{S}}^{\prime }\ast {{\mathcal{O}}_C}^{\prime }\subset {\mathcal{S}}^{\prime }$ (Theorem 3, p. 424 in [26]). ☐

In a previous study [16], we used these insights in order to define operations of discretization ${\perp \perp \perp }_T$ and periodization ${▵▵▵}_T$ in ${\mathcal{S}}^{\prime }$. While discretization is an operation ${\perp \perp \perp }_T:{\mathcal{O}}_M\to {\mathcal{S}}^{\prime },f\mapsto {\perp \perp \perp }_{T}f:={\mathrm{III}}_T·f$, periodization is an operation ${▵▵▵}_T:{{\mathcal{O}}_C}^{\prime }\to {\mathcal{S}}^{\prime },\mathcal{g}\mapsto {▵▵▵}_T\mathcal{g}:={\mathrm{III}}_T\ast \mathcal{g}$, respectively. Starting from these two definitions, we proved that

$$\begin{array}{cc}\hfill \mathcal{F}\left(\perp \perp \perp f\right)& =▵▵▵\left(\mathcal{F}f\right)\mathrm{and}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\mathcal{F}\left(▵▵▵\mathcal{g}\right)\hfill & =\perp \perp \perp \left(\mathcal{F}\mathcal{g}\right)\hfill \end{array}$$

(2)

hold in ${\mathcal{S}}^{\prime }$, both being expressions of Poisson’s Summation Formula. We shortly write $\perp \perp \perp$ and $▵▵▵$ instead of ${\perp \perp \perp }_T$ and ${▵▵▵}_T$ if $T_{\nu }=1$ for all $1⩽\nu ⩽n$.

Moreover, recall that these rules are a consequence of the Fourier duality

$$\begin{array}{cc}\hfill \mathcal{F}(\alpha ·f)& =\mathcal{F}\alpha \ast \mathcal{F}f\mathrm{and}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathcal{F}(\mathcal{g}\ast f)& =\mathcal{F}\mathcal{g}·\mathcal{F}f\mathrm{in}{\mathcal{S}}^{\prime }\hfill \end{array}$$

(4)

for any $\alpha \in {\mathcal{O}}_M$, $\mathcal{g}\in {{\mathcal{O}}_C}^{\prime }$ and $f\in {\mathcal{S}}^{\prime }$ which is, according to Laurent Schwartz’ theory of generalized functions, the widest possible comprehension of both multiplication and convolution within the space of tempered distributions [24,26,30]. It lies at the very heart of ${\mathcal{S}}^{\prime }$. Many calculation rules in ${\mathcal{S}}^{\prime }$, including Equations (1), (2), (7), (8), (11), (12) and Lemmas 1, 2, 3, 4 rely on it.

5. Feasibilities

The following two lemmas provide justifications for the way we will define regularizations and localizations in ${\mathcal{S}}^{\prime }$ below. They will allow us to invert discretizations and periodizations in ${\mathcal{S}}^{\prime }$.

Lemma 3 (Regularization).

Let $\mathsf{\phi }\in \mathcal{S}$. Then, for any $f\in {\mathcal{S}}^{\prime }$,$\mathsf{\phi }\ast f$ can be sampled.

Proof. 

This is a consequence of the fact that $\mathcal{S}\ast {\mathcal{S}}^{\prime }\subset {\mathcal{O}}_M$ [7,24,26,30] and Lemma 1. ☐

An equivalent statement is the following lemma.

Lemma 4 (Localization).

Let $\mathsf{\phi }\in \mathcal{S}$. Then for any $f\in {\mathcal{S}}^{\prime }$,$\mathsf{\phi }·f$ can be periodized.

Proof. 

It follows from the fact that $\mathcal{S}·{\mathcal{S}}^{\prime }\subset {{\mathcal{O}}_C}^{\prime }$ [24,30], which is the Fourier dual $\mathcal{F}(\mathcal{S}\ast {\mathcal{S}}^{\prime })=\mathcal{F}\left({\mathcal{O}}_M\right)$ of $\mathcal{S}\ast {\mathcal{S}}^{\prime }\subset {\mathcal{O}}_M$, and Lemma 2. ☐

It is interesting to observe that $\mathsf{\phi }\ast$ and $\mathsf{\phi }·$ stretch and compress $f\in {\mathcal{S}}^{\prime }$, respectively. Moreover, this property is independent of the actual choice of $\mathsf{\phi }\in \mathcal{S}$. It can therefore be attributed to the operations of convolution and multiplication themselves.

6. Definitions

“One of the main applications of convolution is the regularization of a distribution” [26] or the regularization of ordinary functions which are not infinitely differentiable in the conventional functions sense. Its actual importance lies in the fact that it is the reversal of discretization.

Regularization (see Figure 1) is usually understood as the approximation of generalized functions via approximate identities [2,5,6,7,26,32,33,34]. In this paper, however, we extend this idea by allowing any $\mathsf{\phi }\in \mathcal{S}$ and also any$f\in {\mathcal{S}}^{\prime }$, i.e., even ordinary functions (either smooth or not smooth) can be regularized. This approach naturally includes the special case of choosing approximate identities without unnecessarily restricting our theorem below.

Lemmas 3 and 4 above justify the following two definitions.

Definition 1 (Regularization).

Let $\mathsf{\phi }\in \mathcal{S}$. Then, for any tempered distribution $f\in {\mathcal{S}}^{\prime }$ we define another tempered distribution by

$${\cap }_{\mathsf{\phi }}f:=\mathsf{\phi }\ast f$$

(5)

which is a regular, slowly growing function in ${\mathcal{O}}_M\subset {\mathcal{S}}^{\prime }$. The operation ${\cap }_{\mathsf{\phi }}$ is called regularization, approximation, interpolation or smoothing of f by means of $\mathsf{\phi }$. It is a linear continuous operation ${\cap }_{\mathsf{\phi }}:{\mathcal{S}}^{\prime }\to {\mathcal{O}}_M,f\mapsto {\cap }_{\mathsf{\phi }}f$. The result of ${\cap }_{\mathsf{\phi }}$ is called regular function of f in ${\mathcal{S}}^{\prime }$.

Regular functions (according to this definition) are functions in the ordinary functions sense which are smooth (infinitely differentiable) in the ordinary functions sense, a function property that is of immense value in many branches of mathematics. Regular functions belong to ${\mathcal{O}}_M$ because $\mathcal{S}\ast {\mathcal{S}}^{\prime }\subset {\mathcal{O}}_M$, see e.g., [7,24,30]. They maintain the ‘tempered’ property, i.e., they do not grow faster than polynomials, which is common to all tempered distributions but add the regularity of $\mathsf{\phi }$ to f. It follows that regularized functions can always be sampled according to Lemma 1.

Regularizations of type (5), where f as a member in some distribution space $X^{\prime }$ is singular (i.e., there is no locally integrable function representing f) and $\mathsf{\phi }$ as a member in its corresponding space of test functions X is used for its regularization, are usually called “singular convolution” [35,36] and with f replaced by a sequence $f_{ϵ}$ converging towards f, they become so-called “discrete singular convolutions (DSCs)”, a standard technique today for the regularization of singular distributions.

Regularizations are treated in many mathematical textbooks [2,11,25,26,27,32] and scientific papers [1,35,36,37,38,39,40,41,42,43]. They are also known in terms of “smooth cutoff functions” [2,8], “regularizers” [1,35,36,38], “distributed approximating functionals (DAFs)” [39,40,41,42,43] and “mollifiers” [29,44,45,46,47,48], a term that goes back (see [29], p. 63) to K.O. Friedrichs [44]. Regularized rect functions (characteristic functions of an interval) are known as “mesa function”, “tapered box” [11] or “tapered characteristic function” and “taper function” [49] or as “$C^{\infty }$ bell” or “smoothed top hat” function in [50]. Mostly, regularizations are required “to obtain regularized interpolating kernels” such as in [38], finally to speed up convergences (e.g. in [51]). They are closely linked to the “regularity theorem for tempered distributions” [13].

Away from the generalized functions literature, we also encounter regularizations in terms of “smoothings”, “interpolations”, “zero-paddings” or “approximations” because they are not only applied to generalized functions, they are also applied to ordinary functions, usually to obtain better “regularity” properties for functions, i.e., better differentiability. Regularity is also a topic discussed in [52], for example. It is closely related to localization (see Figure 2).

Definition 2 (Localization).

Let $\mathsf{\phi }\in \mathcal{S}$. Then, for any tempered distribution $f\in {\mathcal{S}}^{\prime }$, we define another tempered distribution by

$${\sqcap }_{\mathsf{\phi }}f:=\mathsf{\phi }·f$$

(6)

which is a generalized function of rapid descent in ${{\mathcal{O}}_C}^{\prime }\subset {\mathcal{S}}^{\prime }$. The operation ${\sqcap }_{\mathsf{\phi }}$ is called localization or restriction of f by means of $\mathsf{\phi }$. It is a linear continuous operation ${\sqcap }_{\mathsf{\phi }}:{\mathcal{S}}^{\prime }\to {{\mathcal{O}}_C}^{\prime },f\mapsto {\sqcap }_{\mathsf{\phi }}f$. If $\mathsf{\phi }\in \mathcal{D}\subset \mathcal{S}$, it is also called finitization. The result of ${\sqcap }_{\mathsf{\phi }}$ is called local function of f in ${\mathcal{S}}^{\prime }$.

Local functions (according to this definition) belong to ${{\mathcal{O}}_C}^{\prime }$ because ${\mathcal{S}}^{\prime }·\mathcal{S}\subset {{\mathcal{O}}_C}^{\prime }$ [24,26]. They add the ‘rapid descent’ property of Schwartz functions $\mathsf{\phi }\in \mathcal{S}$ to $f\in {\mathcal{S}}^{\prime }$. It follows that localized functions can always be periodized according to Lemma 2.

The term “local” and the treatment of localizations have a long history in mathematics. It culminated, however, in the term “localization operator”. It appears in 1988 for the first time (see [53], p. 133 in [54]) in Daubechies’ article [55] and later in Daubechies’ 1992 standard textbook [52]. Meanwhile, “localizations” occur in many publications [2,52,54,55,56,57,58,59,60,61,62,63], amongst others as “localized trigonometric functions” or “localized sine basis” [52,57,64], as “localized frames” [65], “local trigonometric bases”, as “local representations” [6] or simply in terms of “locally integrable” functions.

7. Calculation Rules

“One of the basic principles in classical Fourier analysis is the impossibility to find a function f that is arbitrarily well localized together with its Fourier transform $\mathcal{F}f$” [66]. This, in particular, can easily be seen if one tries to localize the function that is constantly 1.

Lemma 5 (Localization Balance).

Let $\mathsf{\phi }\in \mathcal{S}$ and let $\widehat{\mathsf{\phi }}:=\mathcal{F}\mathsf{\phi }$. Then

$$\begin{array}{c}\mathcal{F}\left({\cap }_{\mathsf{\phi }}\delta \right)={\sqcap }_{\widehat{\mathsf{\phi }}}1\in {{\mathcal{O}}_C}^{\prime }\mathit{and}\hfill \end{array}$$

(7)

$$\begin{array}{c}\mathcal{F}\left({\sqcap }_{\widehat{\mathsf{\phi }}}1\right)={\cap }_{\mathsf{\phi }}\delta \in {\mathcal{O}}_M\mathit{in}{\mathcal{S}}^{\prime }.\hfill \end{array}$$

(8)

In (8), we see that by localizing 1, we delocalize $\delta$, i.e., 1 and its Fourier transform $\delta$ cannot be both arbitrarily well localized. This phenomenon is known as Heisenberg’s uncertainty principle [6,7,11,66,67,68]. Vice versa, in (7), we see that by regularizing $\delta$ we increasingly deregularize 1. The entity ${\cap }_{\mathsf{\phi }}\delta$ is also known as an “approximate identity” of $\delta$, usually denoted as ${\delta }_{ϵ}$ where $ϵ$ is a parameter describing the proximity to $\delta$ (see e.g., [26] p. 316, p. 401 or [32] p. 5). Convolving any $f\in {\mathcal{S}}^{\prime }$ with ${\delta }_{ϵ}$, it creates an approximate identity $f_{ϵ}$ of f which is a function in the ordinary sense being infinitely differentiable.

Proof. 

According to (4), $\delta \in {{\mathcal{O}}_C}^{\prime }$ can be convolved with $\mathsf{\phi }\in \mathcal{S}\subset {\mathcal{S}}^{\prime }$ and, equivalently, $1\in {\mathcal{O}}_M$ can be multiplied with $\widehat{\mathsf{\phi }}\in \mathcal{S}\subset {\mathcal{S}}^{\prime }$, hence

$$\mathcal{F}\left({\cap }_{\mathsf{\phi }}\delta \right)=\mathcal{F}(\mathsf{\phi }\ast \delta )=\mathcal{F}\mathsf{\phi }·\mathcal{F}\delta =\widehat{\mathsf{\phi }}·1={\sqcap }_{\widehat{\mathsf{\phi }}}1$$

holds in ${\mathcal{S}}^{\prime }$. The second formula is shown in an analogous manner. ☐

It is also interesting to observe that in analogy to the Dirac comb identity [16]

$$▵▵▵\delta \equiv \mathrm{III}\equiv \perp \perp \perp 1$$

the following identity, let’s say a “localization balance”

$${\cap }_{\mathsf{\phi }}\delta \equiv \mathsf{\Omega }\equiv {\sqcap }_{\widehat{\mathsf{\phi }}}1$$

holds a balance in ${\mathcal{S}}^{\prime }$ if $\mathsf{\phi }\equiv \widehat{\mathsf{\phi }}$ is satisfied for $\mathsf{\phi }\in \mathcal{S}$, which obviously is the best achievable compromise in localizing 1 and thereby delocalizing $\delta$. It is true for the Gaussian $\mathsf{\Omega }\left(t\right)\equiv e^{-\pi t^2}$ and herewith expresses Hardy’s uncertainty principle [69]. However, it is also true for the Hyperbolic secant $\mathsf{\Omega }\left(t\right)\equiv 2/(e^t+e^{-t})$, see e.g., [11], and for every fourth Hermite function H, i.e., all H satisfying $\mathcal{F}H\equiv H$. A connection between Gaussians and Hyperbolic Secants is that both belong to a class of “Pólya frequency functions” [70,71]. Gaussians, Hyperbolic Secants and Hermite functions are treated in [72,73] for example. Hermite polynomials are also known for their very important role in distribution theory [13,35,36,43]. Hyperbolic Secants may also replace Gaussians in Gabor systems; see e.g., Janssen and Strohmer [74]. A link between Gaussians and Hyperbolic Secants is also known in soliton physics where the “initial Gaussian beam reshapes to a squared hyperbolic secant profile” [75]. Studying fixpoints $\mathsf{\Omega }$ of the Fourier transform in $\mathcal{S}$ is therefore a worthwhile goal.

Another calculation rule that we need to prove for the theorem below is the following. It holds in analogy to already shown properties of discretizations and periodizations [16].

Lemma 6.

Let $\mathsf{\phi }\in \mathcal{S}$, $\alpha \in {\mathcal{O}}_M$, $\mathcal{g}\in {{\mathcal{O}}_C}^{\prime }$ and $f\in {\mathcal{S}}^{\prime }$. Then, $\alpha ·f$ and $\mathcal{g}\ast f$ exist in ${\mathcal{S}}^{\prime }$ and

$$\begin{array}{cc}\hfill \alpha ·\left({\sqcap }_{\mathsf{\phi }}f\right)={\sqcap }_{\mathsf{\phi }}(& \alpha ·f)=\left({\sqcap }_{\mathsf{\phi }}\alpha \right)·f\in {{\mathcal{O}}_C}^{\prime }\mathit{and}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathcal{g}\ast \left({\cap }_{\mathsf{\phi }}f\right)={\cap }_{\mathsf{\phi }}(\mathcal{g}& \ast f)=\left({\cap }_{\mathsf{\phi }}\mathcal{g}\right)\ast f\in {\mathcal{O}}_M\mathit{in}{\mathcal{S}}^{\prime }.\hfill \end{array}$$

(10)

Proof. 

We may allow that at most one of the operands in $\mathsf{\phi }\ast \mathcal{g}\ast f$ is not an element in ${{\mathcal{O}}_C}^{\prime }$. This is indeed true as $\mathsf{\phi }\in \mathcal{S}\subset {{\mathcal{O}}_C}^{\prime }$, $\mathcal{g}\in {{\mathcal{O}}_C}^{\prime }$ and f is an arbitrary element in ${\mathcal{S}}^{\prime }$. It follows that $\mathsf{\phi }\ast \mathcal{g}\ast f$ exists in ${\mathcal{S}}^{\prime }$ and, hence, operands may be interchanged arbitrarily. Using ${{\mathcal{O}}_C}^{\prime }\ast {\mathcal{S}}^{\prime }\subset {\mathcal{S}}^{\prime }$ twice and (5), we obtain

$$\mathcal{g}\ast \left({\cap }_{\mathsf{\phi }}f\right)=\mathcal{g}\ast (\mathsf{\phi }\ast f)=\mathsf{\phi }\ast \mathcal{g}\ast f={\cap }_{\mathsf{\phi }}(\mathcal{g}\ast f)$$

in ${\mathcal{S}}^{\prime }$. The other half of this equation results from the fact that the roles of f and g can be exchanged due to commutativity. The second formula is then shown in an analogous manner. ☐

8. A Regularization–Localization Duality

The interaction between regularizations and localizations is ubiquitous in the literature today, for example as “regularization” and multiplication with smooth “cutoff functions” in Hörmander [2], as “two components of the approximation procedure” in ${\mathcal{S}}^{\prime }$, see Strichartz [8], or as “approximation by cutting and regularizing” in Trèves [27], p. 302, or as “cutting out” one period of f and applying “(quasi-)interpolation” [63] or in terms of ”zero-padding in the time domain corresponds to interpolation in the frequency domain” [76]. Detailed studies of the interaction of both regularizations and localizations, can be found for example in [49,53,54,77] and in engineering literature, we encounter these interactions in terms of the interplay between “windowing” on one hand and “interpolation” on the other. An equivalent is the so-called “zero-padding” technique (e.g., in [76,78,79,80,81,82,83]) found in engineering textbooks as a way to implement interpolations. It corresponds to the regularization of a discrete function by embedding it into a higher-dimensional space where it is smooth. However, we may summarize this regularization–localization duality in the following way.

Theorem 1 (Regularization vs. Localization).

Let $\mathsf{\phi }\in \mathcal{S}$, $f\in {\mathcal{S}}^{\prime }$ and let $\widehat{\mathsf{\phi }}:=\mathcal{F}\mathsf{\phi }$. Then

$$\begin{array}{c}\mathcal{F}\left({\cap }_{\mathsf{\phi }}f\right)={\sqcap }_{\widehat{\mathsf{\phi }}}\left(\mathcal{F}f\right)\in {{\mathcal{O}}_C}^{\prime }\mathit{and}\hfill \end{array}$$

(11)

$$\begin{array}{c}\mathcal{F}\left({\sqcap }_{\widehat{\mathsf{\phi }}}f\right)={\cap }_{\mathsf{\phi }}\left(\mathcal{F}f\right)\in {\mathcal{O}}_M\mathit{in}{\mathcal{S}}^{\prime }.\hfill \end{array}$$

(12)

So, this duality asserts that regularizing a function means to localize its Fourier transform and, vice versa, localizing a function means to regularize its Fourier transform. It is the one-to-one counterpart of a discretization–periodization duality in ${\mathcal{S}}^{\prime }$, given in (1) and (2).

Proof. 

Formally, according to the calculation rules shown above, the following equalities hold

$$\begin{array}{cc}\mathcal{F}\left({\cap }_{\mathsf{\phi }}f\right)& =\mathcal{F}{\cap }_{\mathsf{\phi }}(\delta \ast f)=\mathcal{F}({\cap }_{\mathsf{\phi }}\delta \ast f)=\mathcal{F}\left({\cap }_{\mathsf{\phi }}\delta \right)·\mathcal{F}f\\ & ={\sqcap }_{\widehat{\mathsf{\phi }}}1·\mathcal{F}f={\sqcap }_{\widehat{\mathsf{\phi }}}(1·\mathcal{F}f)={\sqcap }_{\widehat{\mathsf{\phi }}}\left(\mathcal{F}f\right)\end{array}$$

in ${\mathcal{S}}^{\prime }$. We start using $f=\delta \ast f$ where $\delta \in {{\mathcal{O}}_C}^{\prime }\subset {\mathcal{S}}^{\prime }$ is the identity element with respect to convolution in ${\mathcal{S}}^{\prime }$. Then, we apply Equations (10), (4), (7) and (9), in this order. Finally, with $\mathcal{F}f=\mathcal{g}\in {\mathcal{S}}^{\prime }$, we use $\mathcal{g}=1·\mathcal{g}$ where $1\in {\mathcal{O}}_M\subset {\mathcal{S}}^{\prime }$ is the identity element with respect to multiplication in ${\mathcal{S}}^{\prime }$. The second formula is now shown in an analogous manner. ☐

An immediate consequence of the theorem is that f and its Fourier transform $\mathcal{F}f$ cannot both be arbitrarily well localized, a fact that is known as Heisenberg’s uncertainty principle. Also note that ${\mathcal{F}}_{\mathit{loc}}$, as shown in Figure 3, is the Short-Time Fourier Transform (STFT) with window function $\mathsf{\phi }\in \mathcal{S}$ and it is the Gabor transform if $\mathsf{\phi }$ is a Gaussian. Consequently, the result of Gabor transforms will be smooth, i.e., they cannot be discrete for example. In contrast, its Fourier dual, the Fourier transform of regular functions ${\mathcal{F}}_{\mathit{reg}}$, as shown in Figure 3, corresponds first to regularizing functions before Fourier transforming them. Consequently, the result of such transforms will be local, i.e., they cannot be periodic for example.

Obviously, by looking at these interactions, one may think of discrete functions as the ‘opposite’ of regular functions and, equivalently, one may think of periodic functions as the ‘opposite’ of local functions. This is examined more closely in the next section.

9. Four Subspaces

Let $\complement {\mathcal{O}}_M$ be the complement of regular functions ${\mathcal{O}}_M$ in ${\mathcal{S}}^{\prime }$. It is the space of all ordinary or generalized functions in ${\mathcal{S}}^{\prime }$ which are not infinitely differentiable in the ordinary functions sense. Furthermore, let $\complement {{\mathcal{O}}_C}^{\prime }$ be the complement of local functions ${{\mathcal{O}}_C}^{\prime }$ in ${\mathcal{S}}^{\prime }$. It consists of all ordinary or generalized functions in ${\mathcal{S}}^{\prime }$ which either do not fade to zero as $\left|t\right|$ increases (periodic functions for example) or they fall to zero but too slowly (with polynomial decay rather than with exponential decay).

Then, the following diagram (Figure 4) holds in ${\mathcal{S}}^{\prime }$.

This diagram can also be expressed in a slightly more “human readable” form (Figure 5) by recalling that ${\mathcal{O}}_M$ are “regular functions” and $\complement {\mathcal{O}}_M$ are “generalized functions” (in the sense that they are not “regular”) and ${{\mathcal{O}}_C}^{\prime }$ are “local functions” and $\complement {{\mathcal{O}}_C}^{\prime }$ are “global functions” (in the sense that they are not “local”).

Apparently, the Schwartz space $\mathcal{S}\equiv {\mathcal{O}}_M\cap {{\mathcal{O}}_C}^{\prime }$, the “smooth world”, in some sense, is the ‘opposite’ of $\complement {\mathcal{O}}_M\cap \complement {{\mathcal{O}}_C}^{\prime }$, the “discrete world”. One may also note that no additional information is used yet beside pure operator definitions. There is also no statement yet on the reversibility of our operations $\perp \perp \perp$ and $▵▵▵$ and ${\cap }_{\mathsf{\phi }}$ and ${\sqcap }_{\widehat{\mathsf{\phi }}}$ in ${\mathcal{S}}^{\prime }$. Such inversions will be treated from a more quantitative point of view in a follow-on study.

10. Conclusions and Outlook

It is shown that in analogy to a discretization–periodization duality in ${\mathcal{S}}^{\prime }$, there is also a regularization–localization duality in ${\mathcal{S}}^{\prime }$. Proving these dualities even follows the same pattern. In addition, the two dualities are inverse of each other in the sense that the first one maps towards discreteness and the latter one maps towards smoothness. In total, we derived several calculation rules that are suitable to symbolically calculate with operations of discretization, periodization, regularization and localization in order to describe transitions from smoothness towards discreteness, even finite discreteness, and back from discreteness towards smoothness in a mathematically rigorous and formally correct way. We may replace, for example, discretizations by periodizations or regularizations by localizations whenever it is advantageous to do so. Our rules can, for example, be used to derive higher-level theorems in ${\mathcal{S}}^{\prime }$. They can also be implemented in symbolic calculation environments such as Wolfram Mathematica or Python SymPy and thereby become a very useful toolbox for algorithm design.