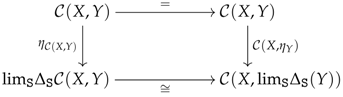
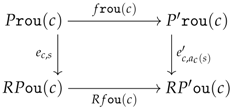
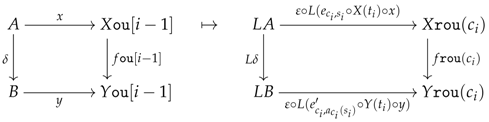
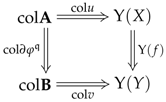
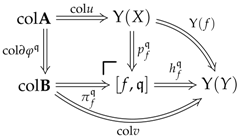
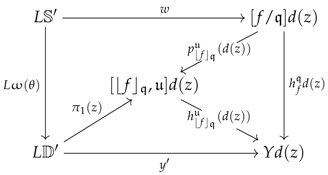
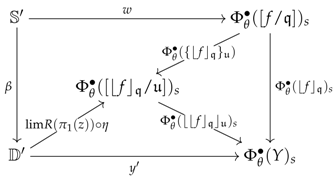
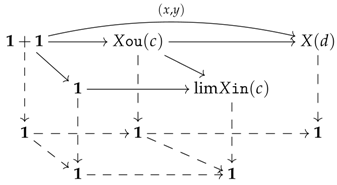
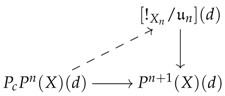
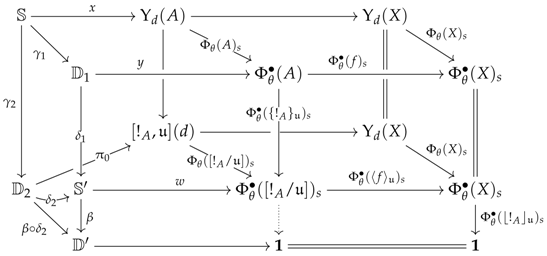
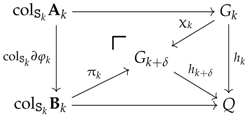
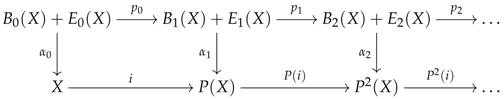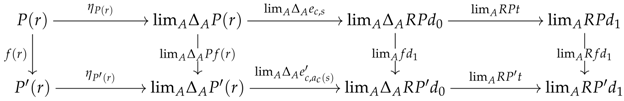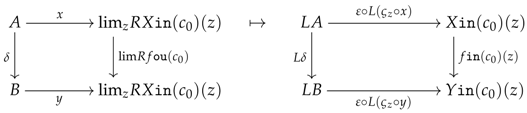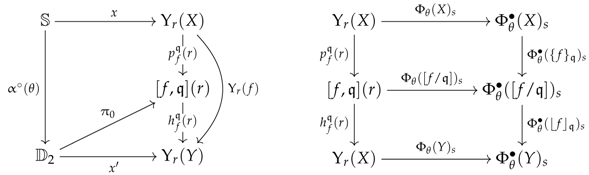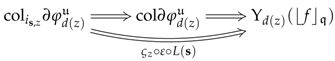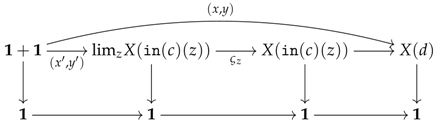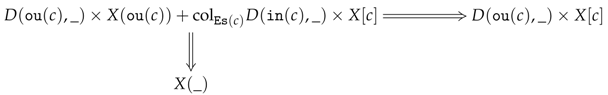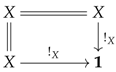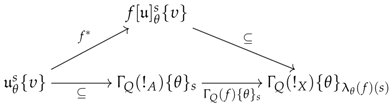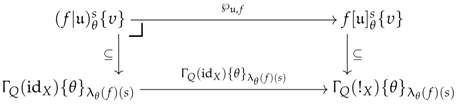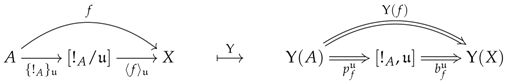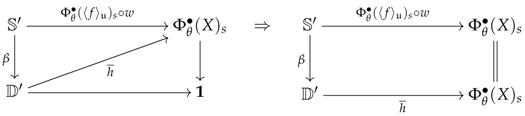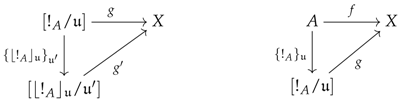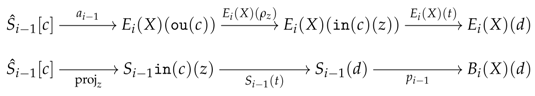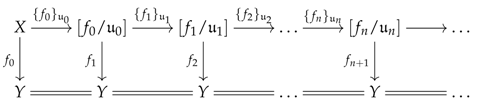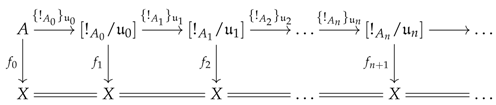6.2. Preconstructors
This section introduces the concept of preconstructor. This notion tries to capture what it takes to specify the data of a localisation. For instance, in Modern Algebra, localising a ring requires one to specify:
- ☆
the underlying set that one wants to act on, which is here the set R;
- ☆
the subset by which one wants to localise the ring;
- ☆
the operation that one wants to inverse, which is here given by the S-indexed family of group morphisms defined by the mappings ;
- ☆
the type of inversion one wants to see happening on the maps .
Regarding this last item, the inversion would, for instance, be expressed in terms of a bijection for the type of localisation used in Classical Algebraic Geometry, but it would be expressed in terms of a quasi-isomorphism in the category of unbounded chain complexes in Derived Algebraic Geometry.
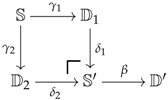
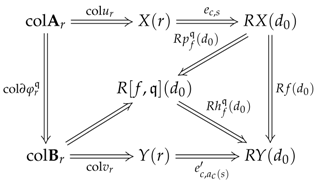
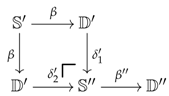
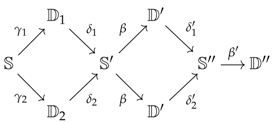
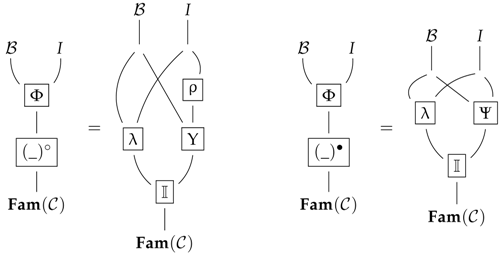
To pass from the earlier description to the formalism of preconstructors, one can try to describe what a preconstructor would be for the previous list of items, so that we could make the following associations (also, see the structure below): the data would specify the object R while the data would give the subset S; the data , and would enumerate the maps with theirs domains R and codomains R (which would be required to be independent of the indices in S); and the data and would specify the type of inversion one wants to see happening. We now give a formal definition.
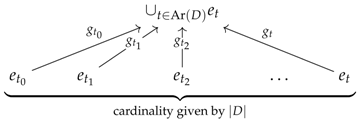
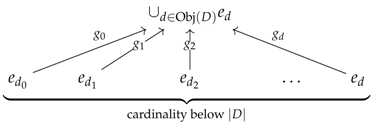
Let and be two categories and D be a small category. A preconstructor of type , let us call it , consists of a discrete category I together with:
- (a)
two functors and , called the regulator and the localisor;
- (b)
three functors as given below, which satisfy the string diagram axioms given underneath them (or the equations given just after);
The previous string diagrams amount to saying that the following equations hold in the functor “category”
for every
;
- (c)
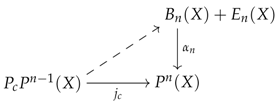
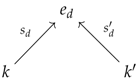
two functors and , called the analysor and the quotientor, such that the image encodes the diskad of a vertebra of stem for every ;
As mentioned in the preamble of
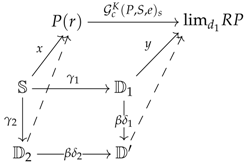
Section 6, a preconstructor contains all the information that is necessary to define the parametrising ‘squares’ on which we will run the small-object-argument algorithm. These so-called parameters will be presented either as families (see Definition 5) or as formal sums (see Definition 6) – both presentations being useful.
Definition 5 (Families)
. For any preconstructor as defined above, the analytic family
of and the quotient family
of are two functors and whose images are determined, for every arrow in and object , by the following mappings (or families) over : Remark 8 (Concept of vertebra)
. The relationship between the analytic family and the quotient family is established in item c) via the concept of vertebra. At this stage, this should suggest to the reader that the notion of vertebra subtly encompass both the idea of quotient—or coherence—via its stem and the idea of cellular structure—or ana-lysis—via its diskad.
Definition 6 (Species)
. For any preconstructor as defined above, the analytic species
of and the quotient species
of are two functors and defined as follows, for every arrow in and object : 6.4. Constructors
This section introduces the concept of constructor. In comparison to the informal introduction of
Section 6.2, a constructor should be seen as a structure giving all the data that we need to describe the localisation of the ring
R by a subset
S in terms of freely-added tuples and relations acting on these.
Specifically, one usually constructs the localisation
by freely adding tuples of the form
, for every
and
, to the set
R. These tuples are often denoted as quotients
. Because
S has not been supposed to be a multiplicative set, one would also need to specify tuples of the form
for every
and
where
. The equivalence relations defined on the pairs
are quite well-known: two pairs
and
are equivalent if there exists
for which the following relation holds:
In the case of the elements of the form , it is less obvious how this should be done. A constructor can help us with this as it contains all the required structure for this type of general description without involving the need of focusing on the encoding.
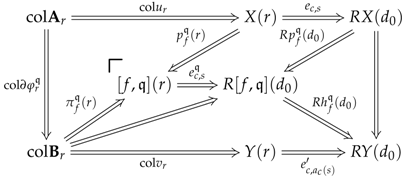
In terms of the notations given below, in the definition of constructor, the data would specify the set of elements that are to be paired with elements in S; the data would specify the set of elements that are to be subject to relations of the form given earlier; the data and , which are used for coherence purposes, would be identities; the data and would specify the types of quotients one would like to see happening: they provide the seeds and the stems of the vertebrae given by the data coming from the preconstructor structure; the maps denoted by would map every element to (for the analytic links) and every pair where to a pair (for the quotient links); and the data j would specify how the set R injects into the localisation . With respect to the definition given below, all of these data would be associated with the canonical ring morphism .
We now give the definition of constructor. Let
and
be two categories and
D be a small category. A
constructor of type consists of a preconstructor
of type
, say
as defined in
Section 6.2, and a mapping
that equips every object
with a pair of sets
together with:
- (1)
two functors and called the analytic and quotient exponents;
- (2)
two functors and called the analytic and quotient indicators;
- (3)
a functor
called the
transitive analysor and, for every
, a function
, called the
analytic link, of the following form:
- (4)
a functor
called the
transitive quotientor and, for every
, a function
, called the
quotient link, of the following form:
- (5)
a functor , called the analytic section, satisfying the equalities , and so that the analytic link is an identity for every ;
For such a constructor, we define, for every object
, an
analytic functor and a
quotient functor whose images
and
are given by the following formulae, respectively:
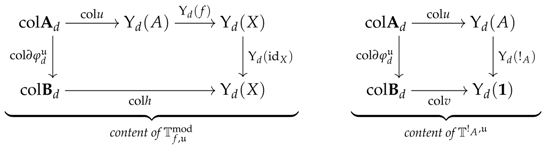
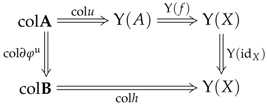
6.5. Constructor of a System of Premodels
Let
be a system of
R-premodels over a small category
D in a category
. The goal of this section is to associate any such system with a constructor of type
. We shall, of course, use the preconstructor structure defined in
Section 6.3. To define the supplementary structure, let us now define the following set (where
denotes the set of objects of the elementary shape of
):
and let us associate every arrow
in
with two sets
and
as follows:
where the set
is defined for every
as the following sum, in which
denotes a tuple of the form
in
and
stands for the products of sets
:
The initial section is taken to be the canonical monomorphism.
Remark 11 (Encoding)
. It will turn out to be convenient to have conventional notations for any element , , or . In this respect, if one denotes:
- -
by any tuple of cones in , for some positive integer n;
- -
by any tuple in , for some tuple of cones as above;
- -
by any tuple of morphisms living in for some object d in D;
the elements of the sets I, , and will be described as tuples of the form: respectively, where , , and, obviously, . Now, if one denotes by , , and any tuple of I, , and as displayed in Remark 11, one defines the mappings , , , , and associated with the constructor structure of as follows:
| Analytic Exponent | | Quotient Exponent |
| on I | | | on I′ |
| otherwise | | | otherwise |
| | | |
| Analytic Indicator | | Quotient Indicator |
| on I | | | on I′ |
| otherwise | | | otherwise |
| | | |
| Transitive Analysor | | Transitive Quotientor |
| on I | | | on I′ |
| otherwise | | | otherwise |
Finally, one produces a constructor of type
by defining the analytic link
as an identity map when
, and, otherwise, as a compositional iteration of the form:
where the triples
, ⋯,
are made out of the obvious components of
and the functor
maps any commutative square as given below, on the left, to the commutative trapezoid given on the right, where
denotes the counit of the adjunction
and the component
is, here, seen as an arrow of the form
with
and
otherwise:
For its part, the quotient link
, which is defined for every
, is given by a first application of the functor
that maps any commutative square as given below, on the left, to the commutative trapezoid given on the right, where
is the universal projection of the adjunction
at
z:
and, in the case where
is not in
, followed by successive iterations of the functor
over the triples
made out of the obvious components of
(see Formula
15). It is easy to check that the initial section
satisfies the axioms of item 5) of
Section 6.4. The constructor associated with
will later be referred to as
.
Remark 12. In the case where the associated maps of our premodels are identities, the functors R and are trivial and the associated sets S are all equal to a fixed one, the set can be set empty for every and so that j can be defined as an identity. In this case, the validity of our results still holds for Examples 28 and 29, but not for Examples 30 and 31, which require to be as above. See Remark 16 and the proof of Theorem 3 for more insight.
Remark 13 (Encoding)
. For every arrow in and object d in D, the image of the analytic functor contains the tuples and the tuples where: is a cone in K; v is a vertebra in ; n is a positive integer; , and are the tuples defined in Remark 11 and used to define the analytic link; t is an arrow in D of the form for the first type of tuple and an arrow otherwise; is an element in and is an arrow in as displayed in Equation (14) for the notation .
Similarly, the image of the quotient functor contains the tuples and the tuples where: is a cone in K; v is a vertebra in ; n is a natural number; , and are the tuples defined in Remark 11 and used to define the quotient link; z is an object of ; t is an arrow in D of the form for the first type of tuple and an arrow otherwise; is an element in and is an arrow in for the notation .
Remark 14 (Encoding)
. It is not hard to see from Remark 13 that any type of tuple in may be written as a tuple of the form where the encoding of the parameter ϑ may vary. Similarly, it follows from Remark 13 that any tuple in may be written as a tuple where the encoding of the parameter ϑ may vary.
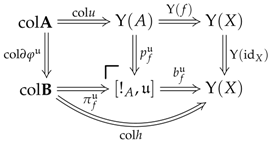
6.7. Quotiented Arrows
Let
denote a constructor of type
as defined in
Section 6.4. This section defines the concept of “quotient” whose essential idea is to restrict the quotient family of
to certain parametrising “squares” only. In this respect, a
-quotient for a morphism
in
consists of a collection of discrete categories, as given below, on the left, as well as a collection of functors as given on the right:
such that the inclusion
holds for every element
. We may associate any such
-quotient
with a functor
defined as follows for every
:
This functor will be called the
species of . In much the same fashion as the quotient species of
was used to define its quotient functor, we use the species of
to define a third functor
given by the following equation:
This functor will be referred to as the quotienting functor of .
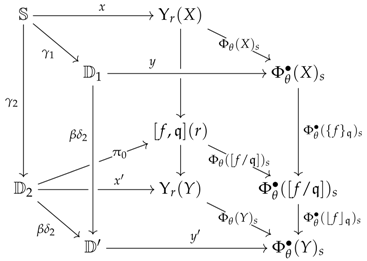
Proposition 12. The inclusions holding for every and induce functions of the form for every , which in turn induce a morphism in .
Proof. By universality of the coproducts. ☐
Convention 10. The natural transformation of Proposition 12 may be composed with the quotient tome of to give a natural transformation . Because this arrow lives in the functor category , it may be factorised into an epimonomorphism followed by a monomorphism as follows (this is an image factorisation): For every object , the image will be thought of as the set , but quotiented by the obvious binary relation. In any case, the elements of and will be denoted as tuples where t is an arrow of the form ; s is an element in ; is an element in and is an element in .
Remark 15 (In preparation for Theorem 3)
. Let be a morphism in as above. For every object , denote by the following sum of sets, which is defined with respect to the structure of f provided by the constructor : The definition of -quotient for implies that any function of the form that maps a pair in to a pair in so that the equality is satisfied lifts to a function mapping any tuple in to the tuple in .
Example 46 (In preparation for Theorem 3)
. In the case of a constructor associated with a system of R-premodels over a small category D in a category , the disjoint sum associated with a morphism in contains two types of tuples, which are of the form and with respect to the same notations given in Remark 13. For every and , if one takes r to be and to be , then it is possible to define a function with the following mapping rules, where stands for , stands for and stands for : Because the following equations hold, it follows from Remark 15 that the function
extends to a function
:
In fact, the function
also restricts to a function
. To see this, take two tuples
and
in
that are equivalent in
, that is to say that have the same image under
(see below, according to Equation (
17)):
It follows that their images via
are also equivalent in
. This comes from the fact that the previous equation gives rise to the following one, after some obvious compositional operations on it (see the definitions for
and
in
Section 6.5):
However, this last equation also amounts to saying that the images of and via are the same, and thus shows that restricts to a function .
Definition 7 (Quotiented arrows)
. From now on, we shall speak of a-quotiented arrow in to refer to any arrow in that is equipped with a -quotient for f.
A -quotiented arrow as defined above will be denoted either as a pair or as a paired arrow . A morphism of -quotiented arrows, denoted as an arrow , will be understood as a morphism in . The category of -quotiented arrows and their morphisms will be denoted by .
6.9. Effectiveness of Quotiented Arrows
The goal of this section is to introduce what logicians could see as a concept of definability. The concept of effectiveness will allow us to designate those arrows that can be equipped with well-defined pushout factorisations in the category associated with a constructor. We prepare the notion of effectiveness by introducing the (almost-trivial) concept of realisability. Let
denote a constructor of type
as defined in
Section 6.4 where
has coproducts. A
-quotiented arrow
in
will be said to be
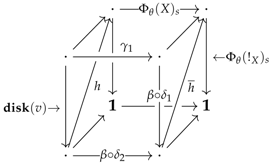
-realised if one may form a componentwise pushout square inside the functorial content of its merolytic tome as shown below:
The functor will then be called the -realisation of while the pair of arrows will be referred to as the -prefactorisation of .
Definition 8 (Effectiveness)
. Let denote a constructor of type as defined in Section 6.4. A -quotiented arrow in will be said to be effective
if it is -realised and its -prefactorisation in lifts to a factorisation of in , as shown in Equation (20), such that the arrow is an identity for every : The leftmost factorisation of Equation (20) will be called the -factorisation of .
Remark 16. Let be a given set and be the constructor of a system of R-premodels over a small category D in a category where every object in is such that S is equal to and e is made of identities only. In this case, the underlying functor is fully faithful and it follows that if has pushouts, then every -quotiented arrow in is effective. This means that the theorem given below becomes trivial, which explains why the set mentioned in Remark 12 may be set empty since it is not really needed anywhere else in the paper except for Theorem 3 (and Theorem 7, which is a copy of it). See Example 48 in the case where is defined as in Section 6.5. Theorem 3. Let be a system of R-premodels over a small category D in a category . If has pushouts and the inclusion is an identity, then every -quotiented arrow in is effective.
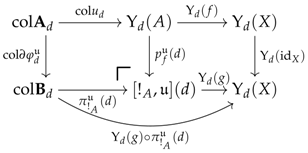
Proof. For convenience, the symbol will be shortened to . Since has pushouts, every -quotiented arrow is -realised by definition. Let be an -quotiented arrow in . We are going to prove that the -realisation of has an R-premodel structure of the form and that this structure lifts the -prefactorisation of in to another one in . In this respect, fix and and denote and by r and , respectively. For simplicity, we will denote by the obvious morphism in whose components are given by the pair of arrows and in .
To prove the statement, we first need to define two functors. The first one is of the form
and is induced by the following mappings, where
stands for
,
stands for
and
stands for
:
Note that the mappings on have already been given in Example 46. The second functor is of the form and maps any arrow to the map , where denotes the unit of the adjunction .
We are now going to show that the following diagram commutes:
On the set
, the calculation on a tuple
goes as follows:
On the set
, the calculation for
goes as follows:
On the set
, the calculation on a tuple
goes as follows:
On the set
, the calculation for
goes as follows:
Now, the equation
tells us that the content of the tome
along
is equal to the content of
after applying the functor
on it. More specifically, the equation means that the respective composites of Equations (
22) and (
23) are equal:
If one denotes by
the unit of the adjunction
, the definition of adjunction implies that the function
is inverse of
. Since the content
appearing in Equation (
22) may be factorised as in Diagram (19) on
, an application of the inverse function of
on the arrow represented by Equations (
22) and (
23) provides the following commutative diagram, where Equation (
22) provides the inside while Equation (
23) provides the outside.
Now, because the top left corner of the previous diagram corresponds to the top left corner of the commutative square defining the
-realisation of
when evaluated at
r, it follows that there exists a natural transformation
making the following diagram commute.
The previous diagram provides a morphism
in the category of
R-premodels
. The universality of
also provides a morphism
in
. These two morphisms obviously define a factorisation of the morphism
in
. Finally, since the second component of the morphism
is the identity on
S, its image via the functor
is an identity for every
(see
Section 6.5). In other words, the arrow
mentioned in Definition 8 is indeed an identity. ☐
Definition 9 (Fibered)
. A system of R-premodels over a small category D in a category will be said to be fibered if the category has pushouts and the -factorisation of any -quotiented arrow (obtained in Theorem 3) lifts to .
Example 47. By Theorem 3, any system of R-premodels where has pushouts and is identified with the category is fibered.
Example 48. In the proof of Theorem 3, note that if the objects and are such that the associated arrows and are identities, then so is . This implies that any system of R-premodels where has pushouts and may be identified with the functor category is fibered (e.g., Examples 34–41)
Example 49. In the proof of Theorem 3, note that if the objects and are such that the images of S and are equal to , then so is the -realisation . This implies that the system of Ω-premodels given in Example 42 is fibered.
Remark 17. A system of R-premodels is not always fibered (e.g., Example 43), which is often due to a too strong restriction of the premodels via the inclusion . However, Theorem 3 shows that if is too strong, we might want to stay in to process most of our calculations. The idea would then be that it is possible to go back to at the very end of a transfinite calculation.
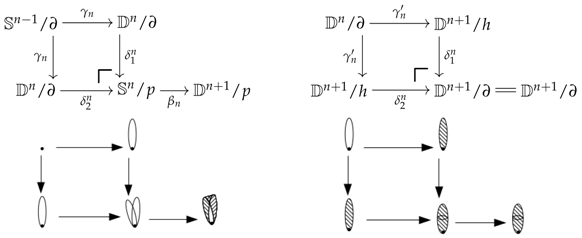
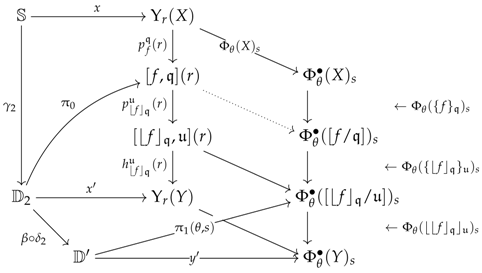
Example 50. This example discusses the form that the -realisation takes when considering categories of models for a limit sketch. Let be a limit sketch seen as a croquis. Consider the system of premodels defined in Example 34 for the category . Recall that the vertebrae associated with any cone were of the following form: It follows from the definition of the transitive analysor and quotientor that, for any
-quotiented arrow
, the
-realisation of
evaluated at an object
is defined over the following types of span:
The contribution of the left span to the construction of the
-realisation
is to add an element to
while the contribution of the right span to the construction of the
-realisation
is to quotient a pair of elements in
. After unravelling the indices that parametrise the two types of span, we may deduce that the colimit
is of the following form, where
and
are the restrictions of
to the vertebrae
and
, respectively:
After further unravelling the parameterisation of the rightmost summand, we may show that the colimit
may be expressed as follows, where
R is a binary relation on
X in
:
Concretely, the set is nothing but the set with respect to the notations of given in Remark 11 while the object is given by for the same notations.
Recall that, according to Remarks 12 and 16, the set
could in fact be given by the set
I itself in the present situation (i.e. premodels for a sketch). In this case, the expression of Equation (
24) turns out to be as follows:
6.10. Rectification of Effective Quotiented Arrows
Let
denote a constructor of type
as defined in
Section 6.9, with the usual notations, and
be an effective
-quotiented arrow in
. Usually, effectiveness does not mean that the quotiented arrow is as we would like it to be. It is in fact necessary to rectify its defaults via a second quotient. The goal of this section is to define the ‘rectification’ of
, which is nothing but a
-quotient
for the arrow
.
To do so, let us define, for every element
and
, the associated functor of the following form:
First, define the discrete category
to be the set
. By definition, an element
may be identified with an element
, which may be sent to the arrow:
via the domain restriction
. The arrow encoded by
may be identified with an element in the image of the analytic tome of
as follows (see Formula (
16) and the assumption of the initial section
):
This therefore defines a function mapping any element to the tuple whose image via the merolytic tome is the arrow encoded by .
This being said, denote by
r the element
and, for every
, denote by
the function
that picks out the element
. From the point of view of these notations, we have showed that the image of the composite
corresponds to the commutative square
. However, this also means that the content of the merolytic tome of
along
is equal to the commutative Square (
25) in
as illustrated below:
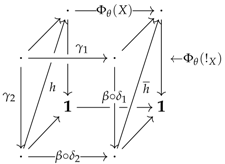
Because the left arrow
(i.e., the content) may be factorised as shown in Diagram (19), it follows that the commutative square encoding
factorises as shown below, on the left:
The diagram displayed above, on the right, is for its part the image of the
-factorisation of
in
via the functor
. The definitions of the diagrams involved in Equation (26) imply that the commutative square
factorises as follows, where the image
is replaced with the diskad of a vertebra
for which
by definition:
Notice that the previous commutative cube provides the following left commutative square:
By using the structure of the vertebra
, we may form a pushout
inside so that we obtain a canonical arrow
making the preceding right diagram commute. It is not hard to deduce from the universality of this pushout that both arrows:
are solutions for a same universal problem over
(Diagram (27) might come in handy to visualise this fact). In particular, this means that the following diagram must commute:
Because
corresponds to the image
, we have defined a functor
mapping a commutative cube
to the subset of
consisting of Diagram (28) only. Thus, the images of
are sets (or singletons) included in
so that the collection of functors given below, denoted by
, defines a
-quotient for the arrow
:
Definition 10 (Rectification)
. The-rectification of the -quotiented arrow is the -quotiented arrow , which will sometimes be denoted by .
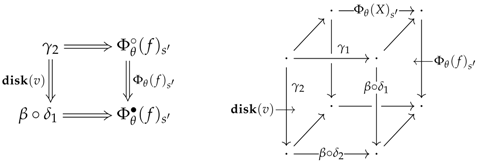
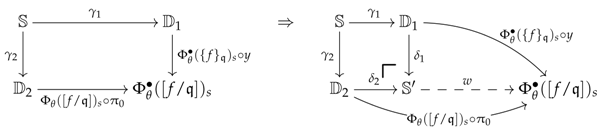
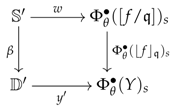
Later on, the diagram obtained in Equation (28), which is entirely determined by the image of the -rectification of above a cube at the parameters and , will be referred to as the obstruction square of for at .
Definition 11 (Ideal)
. A -quotiented arrow will be said to be ideal
if it is effective, its -rectification is effective and for every , and , there exists an arrow factorising the obstruction square of for at as follows: Remark 18 (Structure of narrative of degree 2)
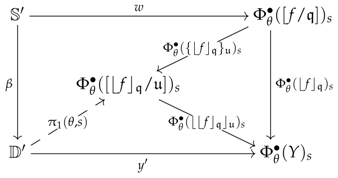
. Consider an ideal -quotiented arrow and a commutative cube in . According to the previous discussion, this cube may be factorised as in Diagram (27). Merging this factorisation of with: (1) the factorisation of the obstruction square of for at on its front face and (2) the -factorisation of the -rectification of on its back face leads to the following factorisation of (where the top front corner has been forgotten and ): This means that the composite arrow given in Equation (
30), whose the leftmost arrow is given by the content of the operadic tome
, admits a lift in
:
This last fact will later imply that we may construct a narrative of degree 2 out of the operadic tome.
Remark 19 (About π
0)
. This section discusses the encoding of the arrow that we have denoted . We shall use the same notations as that introduced at the beginning of the section. Recall that we defined the element , which we used to shift the merolytic tome of and obtain the leftmost diagram of Equation (26). Therefore, we have the following formula if we use the notation of Diagram (19): If we now denote
for some arrow
, the functionality of
and the construction of the merolytic tome of
gives the following Equation:
This formula will later come in handy in the proof of Theorem 9.
Theorem 4. Let be a system of R-premodels over a small category D in a category . If admits pushouts and the inclusion is an identity, then every -quotiented arrow is ideal.
Proof. For convenience, the symbol
will be shortened to
. The present proof uses the construction made in the proof of Theorem 3. In particular, we shall use the notations defined thereof, such as
and
. Let
be an
-quotiented arrow in
. By Theorem 3, it is effective and so is its
-rectification
. There now remains to show the existence of an arrow:
factorising the obstruction square of
for any cube
at any parameter
and
(see Diagram (
29)).
First, recall that, for every
,
and cube
, the obstruction square of
for
at
is given by an arrow in
of the following form:
By using the notations of
Section 6.5 and the adjointness properties of
R and
, the preceding righthand arrow may be turned into the following arrow in
for every
:
Now, observe from the definitions of
Section 6.5 that, for every
and
, we may define an object
in
, which precisely lands in the component
of
. From the notations of
Section 6.5, the arrow given in Equation (
31) may in fact be rewritten as follows (We have the identities
and
):
It therefore follows from Formula (
17) that the arrow given in Equation (
31) may be identified with the image of Tuple (
32) (see below) via the quotient tome
:
In order to avoid overloading the next diagrams, denote by
the functorial mapping
and, for every
, denote by
the function
that picks out Tuple (
32) in
for every
. Now, to resume, the previous discussion showed that the image of the composite
corresponds to the arrow
. However, this is equivalent to saying that the content of the merolytic tome of
along
is equal to the arrow
as illustrated below:
Because the rightmost arrow
may be factorised as shown in Diagram (19), it follows that the commutative square encoded by
factorises as follows:
The idea is now to obtain a factorisation of the form given in Equation (
29) by reconstructing the obstruction square
(from which the previous diagram is derived) without losing the factorisation.
First, note that, by definition of the quotient acting on
(see Convention 10), the collection of arrows
is natural in
since the following tuples have the same images via the functor
for every arrow
in
:
The functoriality of Diagram (19) over
D and the naturality of
in
then implies that the earlier commutative diagram is natural over
. Forming the limit of that diagram over
and then applying the inverse of the function
(which is given by the function
if
denotes the unit of
) provides a factorisation of the original obstruction square
as follows:
This finally shows that the -quotiented arrow is ideal. ☐
Example 51. This example continues the discussion started in Example 50 (we shall use the same notations as those used thereof) in order to describe, in more details, the binary relation acting on (see Formula (24)) in the case where f is taken to be the canonical map . Recall that the quotient was meant to simplify the following expression: Also, recall that, by definition, the binary relations contained in
(see Remark 13 for the encoding of
) are those pairs
that may be related to commutative diagrams as follows:
Precisely: The above diagram says that two elements will be identified if there exist a cone , a morphism and two elements and in such that the identities and hold and the elements and have the same image via the canonical map .
On the other hand, the binary relations contained in
were given as part of our assumptions. However, in the sequel, the idea will be to define
either as the empty binary relation or as we defined the set
in
Section 6.10. In the latter case, in order to make sense of
, we need to suppose that the image
takes the form given below for some functor
and binary relation
:
The quotient
, which will later be shortened as
, is supposed to identify pairs of elements coming from a previous
-quotient
. In this case, the pairs contained in the relation
are those pairs
that are the top parts of commutative diagrams of the form displayed below, where the leftmost commutative square is one of those obstruction squares constructed in
Section 6.10:
Precisely: After unravelling the details of the construction of the corresponding obstruction square, the above diagram says that two elements:
will be identified if there exist a cone
, say encoded by a natural transformation
, an element
, a morphism
and two elements
and
living in
of the form:
such that the following relations hold:
We can clearly see that the role of two binary relations and is to turn the canonical arrow into a surjection and an injection, respectively.
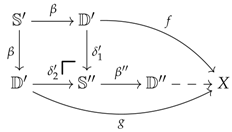
Example 52 (Comparison with Kelly’s construction)
. Let us compare the quotients acting on the pushout object , as described in Examples 51 and 50 (where denotes the canonical arrow ), with those acting on the pushout object of Kelly’s construction [4]. Recall that, for each cone , the latter is given by a well-pointed endofunctor in . More specifically, if we take c to be a cone of the usual the form: in D, then for every functor , the object can be computed in as the pushout object of the following span [4] (diag. (10.1), p. 31), whose components are further detailed below, while the natural transformation is the bottom arrow of the resulting pushout square: For every object , we can decompose the previous span in four parts as follows:
- (1)
The arrow given below, part of the vertical leg, maps every pair
, where
t is an arrow
and
, to the element
in
:
- (2)
The arrow given below, also part of the vertical leg, maps every pair
, where
t is an arrow
in the colimit
and
is a tuple in
, to the element
in
:
- (3)
The arrow given below, part of the horizontal leg, is induced by the canonical arrow
and maps every pair
to the pair
, where
is the tuple
in the limit object
:
- (4)
The arrow given below, also part of the horizontal leg, is induced by the canonical arrow
and maps every pair
, where
t is an arrow
for some object
and
, to the pair
:
It takes a few lines of calculations to see that the pushout
of the previous span evaluated at
d can be described as a quotiented sum of the form:
where:
▹
identifies all pairs
, where
and
, such that there exist
and an arrow
for which the following identities hold:
▹
identifies all pairs
, where
and
, such that there exist
and an arrow
for which the following identities hold:
We can see that the definition of the relation exactly matches that of the relation given in Example 51. On the other hand, we can check that for every relation , as described in Example 51, there is an (obvious) element y for which both relations and are satisfied.
However, a relation of the form cannot be retrieved from the union of the relations and , given in Example 51. It can only be retrieved if one allows a use of these relations up to quotients. Indeed, the reader can check that the identification of the second line, below, cannot be made unless the one given in the fist line has already occured.
| | elt. | Relation | elt. |
| first identify | | | |
| which then allows us to identify | | | |
As mentioned in
Section 1.4, Kelly’s construction is pursued by pushing out all the maps
to give a natural transformation
where
identifies each component
X appearing in the expression of the objects
for every
. We therefore obtain an expression as follows, for very object
:
This expression should be compared with the (similar) expression of the
-realisation
obtained in Example 51, whose sum over
K is, here, quotient-free:
Because the relations contained in
can be written as a zigzag of relations in
, we can construct an obvious arrow from
to
matching all the components
together (here, the symbol ∼ stands for the obvious relation):
In fact, our earlier discussion showed that, if we denote
and
where
and
, then we can continue this process iteratively, by matching the components of the sum over
K, so that we have arrows as follows:
One can check that all these arrows are compatible, in an obvious way, with the arrows
and
. However, one of our previous remarks on the fact that
can only be retrieved from the relations
and
up to quotients shows that if there exists a dashed arrow making the following diagram commute:
then this arrow must factorise through the following canonical arrow (see the reason below):
Indeed, otherwise we could derive a contradiction from every element of the form:
which must be identified with the element
in
via the relation
, but must be left free in the expression of
. The empty case
obviously leads to the same conclusion.
If we now look at Formula (
33), this factorisation means that that all the elements in the component
of
must be identified with elements in the other component
. From the point of view of the relation
at
where
t is taken to be the identity on
, this means that the canonical arrow
must be a surjection.
Finally, observe that, when , the arrow is also an injection because the images of are quotiented by the relations and hence the relation , which precisely characterises its injectiveness (see Example 51). In other words, the canonical arrow is a bijection, which makes the object a model for .