Fractional Fokker-Planck Equation ^†

Abstract

We shall discuss the numerical solution of the Cauchy problem for the fully fractional Fokker-Planck (fFP) equation in connection with Sinc convolution methods. The numerical approximation is based on Caputo and Riesz-Feller fractional derivatives. The use of the transfer function in Laplace and Fourier spaces in connection with Sinc convolutions allow to find exponentially converging computing schemes. Examples using different initial conditions demonstrate the effective computations with a small number of grid points on an infinite spatial domain.

1. Introduction

The Fokker-Planck Equation (FP) is used in models of standard diffusion problems involving external fields:

$${\partial }_{t}u(x,t)=L_{\mathrm{FP}}u(x,t)\mathrm{with}-\infty <x<\infty \mathrm{and}t\ge 0$$

(1)

where the linear FP operator is defined by $L_{\mathrm{FP}}$:

$$L_{\mathrm{FP}}=\frac{\partial }{\partial x}\frac{V^{\prime }(x)}{m\eta }+ϵ\frac{{\partial }^2}{\partial x^2}$$

(2)

with the external potential $V(x)$ [1]. $V^{\prime }$ represents the negative external forces in the system. The parameters m, η and ϵ are the mass, the friction coefficient, and the diffusion constant, respectively. Risken in his book collected and developed a rich variety of solution methods for the FP equation [1]. The basis of the FP equation is a diffusion process re-distributing $u(x,t)$ in space x and time t the quantity may be related e.g., to mass, charge, or probability. From (2) it becomes apparent that the FP equation is a generalization of the diffusion equation. In recent years the integer order diffusion equation was generalized to a fractional diffusion equation in which the differentiations with respect to t and x are replaced by differentiations of non-integer order [2,3,4,5]. The aim of the current paper is to use such fractional generalizations for the FP equation, too.

Let us first examine Risken’s approach. To this end, we first separate the diffusion part from the rest of the equation, as follows:

$${\partial }_{t}u(x,t)-ϵ\frac{{\partial }^{2}u(x,t)}{\partial x^2}=-\frac{\partial }{\partial x}\left(\frac{V^{\prime }(x)}{m\eta }u(x,t)\right)\mathrm{with}-\infty <x<\infty \mathrm{and}t\ge 0$$

(3)

We now assume that the function $u(x,t)$ satisfies natural Dirichlet boundary conditions; i.e., $u(\pm \infty ,t)=0$. The initial condition for the problem is $u(x,t=0)=u^{(0)}(x)$. Without loss of generality, we rescale the temporal coordinate by using the diffusion constant $t\to tϵ$ so that the equation becomes:

$${\partial }_{t}u(x,t)-\frac{{\partial }^{2}u(x,t)}{\partial x^2}=-\frac{\partial }{\partial x}\left(\frac{V^{\prime }(x)}{ϵm\eta }u(x,t)\right)\mathrm{with}-\infty <x<\infty \mathrm{and}t\ge 0$$

(4)

It is well known that for vanishing external forces, the fundamental solution of (4) is given by a Gaussian:

$$G(x,t)={(4\pi t)}^{1/2}exp\left(-\frac{x^2}{4t}\right)$$

(5)

This fundamental solution enables us to transform Equation (4) to the integral equation:

$$\begin{array}{ccc}\hfill u(x,t)& =& v(x,t)+{\int }_0^t{\int }_{\mathbb{R}}G(x-\xi ,t-\tau )\frac{\partial }{\partial \xi }\left(\frac{V^{\prime }(\xi )}{ϵm\eta }u(\xi ,\tau )\right)d\xi d\tau \hfill \\ & =& v(x,t)-{\int }_0^t{\int }_{\mathbb{R}}\frac{\partial }{\partial \xi }(G(x-\xi ,t-\tau ))w(\xi )u(\xi ,\tau )d\xi d\tau \hfill \\ & =& v(x,t)-{\int }_0^t{\int }_{\mathbb{R}}{G}_x(x-\xi ,t-\tau )w(\xi )u(\xi ,\tau )d\xi d\tau \hfill \end{array}$$

(6)

in which $w(x)=V^{\prime }(x)/(ϵm\eta )$ is the scaled external force, and in which the first derivative $G_x$ is given by:

$$G_x(x,t)=-\pi \frac{x}{{(4\pi t)}^{3/2}}exp\left(-\frac{x^2}{4t}\right)$$

(7)

The function $v(x,t)$ related to the initial condition is given by:

$$v(x,t)={\int }_{\mathbb{R}}G(x-\xi ,t)u^{(0)}(\xi )d\xi$$

(8)

The integral equations (IE) (6) and (8) can now be used to derive the solution of the FP equation. These straight forward steps enable us to transform the FP problem into an integral equation, which is suitable for approximate solution by our methods given below in this paper (see also [6,7]). We remark that there already exist a number of other methods for solving the FP equation. We refer to Risken [1] for an overview of such methods, and to [8,9,10,11] for a discussion of more recent developments. Our method of approximate solution has advantages over these other methods, for ease of solution and for exponential convergence.

Our aim in this paper is to generalize the integer order original FP equation to it’s fractional form, the fractional Fokker-Planck (fFP) equation. There exists a large number of papers dealing with such generalizations see e.g., [12,13,14] and references therein. However, constraints were added in each of these papers by way of replacing integer order derivatives by fractional order derivatives. Only the temporal derivative is replaced in some of these publications [13]. Some other papers consider replacing only the second order spacial whereas the other derivatives are kept at integer order, and so on. Thus these other approaches enable solutions which are not the most general possible. We will introduce a fractional representation which uses the full conversion of all integer derivatives to fractional order derivatives in all independent coordinates. Since the FP equation is of order one and two and one in time and spatial coordinates, respectively, we have to consider three different fractional differentiation orders β, α, and μ as follows:

$${}^C{\mathcal{D}}_t^{\beta }u(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }u(x,t)=-{\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(\frac{V^{\prime }(x)}{ϵm\eta }u(x,t)\right)\mathrm{with}-\infty <x<\infty \mathrm{and}t\ge 0$$

(9)

Here $0<\beta \le 1$, $0<\alpha \le 2$, and $0<\mu \le 1$ are constraints for the fractional derivatives consistent with the FP equation. The two skewness parameters ${\theta }_{\alpha }$ and ${\theta }_{\mu }$ satisfy the conditions $\left|{\theta }_{\alpha }\right|=min(\alpha ,2-\alpha )$ and $\left|{\theta }_{\mu }\right|=min(\mu ,1-\mu )$, respectively. The fractional derivatives for temporal and spatial coordinates are defined in terms of Caputo and Riesz-Feller derivatives. For details of these definitions see Appendix A.

We begin by considering the Cauchy problem for the (spatially one-dimensional) space-time fractional FP Equation (9). Note that our approximation method is also applicable to spatially higher dimensional cases and can be generalized to systems of FP equations.

We shall first generate the fundamental solution of the IE via application of Laplace and Fourier transforms to the fractional operators. Assuming, $\Re (s)>{\sigma }_0$, $\kappa \in \mathbb{R}$, the transforms of Laplace and Fourier are defined as:

$$\mathcal{L}(f(t),s)=\tilde{f}(s)={\int }_0^{\infty }f(t)e^{-st}dt$$

(10)

and:

$$\mathcal{F}(g(x),\kappa )=\widehat{g}(\kappa )={\int }_{-\infty }^{\infty }g(x)e^{i\kappa x}dx$$

(11)

Thus the corresponding transform of the fractional derivatives ${}^C{\mathcal{D}}_t^{\beta }f(t)$ and ${\mathcal{D}}_{\theta ;x}^{\alpha }g(x)$ are:

$$\mathcal{L}\left({}^C{\mathcal{D}}_t^{\beta }f(t),s\right)=s^{\beta }\tilde{f}(s)-s^{\beta -1}f(0)$$

(12)

and:

$$\mathcal{F}\left({\mathcal{D}}_{\theta ;x}^{\alpha }g(x),\kappa \right)=-{|\kappa |}^{\alpha }{i}^{\theta \mathrm{sign}(\kappa )}\widehat{g}(\kappa )=-{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa )\theta \pi /2}\widehat{g}(\kappa )$$

(13)

The fundamental solution of the fractional diffusion equation in the Fourier-Laplace domain with the initial condition ${\widehat{u}}_0(\kappa )=1$ thus becomes:

$$\mathcal{F}\left(\mathcal{L}\left({}^C{\mathcal{D}}_t^{\beta }u(x,t),s\right),\kappa \right)-\mathcal{F}\left(\mathcal{L}\left({\mathcal{D}}_{{\theta }_1;x}^{\alpha }u(x,t),s\right),\kappa \right)=0$$

(14)

which delivers the equations:

$$s^{\beta }\widehat{u}(\kappa ,s)-s^{\beta -1}\widehat{u}(0)=-{\left|\kappa \right|}^{\alpha }{e}^{i\mathrm{sign}(\kappa )\theta \pi /2}\widehat{u}(\kappa ,s)$$

(15)

$$\widehat{u}(\kappa ,s)=\frac{s^{\beta -1}\widehat{u}(0)}{s^{\beta }+{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa )\theta \pi /2}}$$

(16)

If we use the initial condition $\widehat{u}(0)=1$ then we finally get:

$$\widehat{u}(\kappa ,s)=\frac{s^{\beta -1}}{s^{\beta }+{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa )\theta \pi /2}}={\widehat{G}}^{\alpha ,\beta }(\kappa ,s)$$

(17)

representing the Laplace-Fourier solution of the Green’s or transfer function for the fractional diffusion equation [15]. In fact the knowledge of the Laplace-Fourier representation of the fractional diffusion equation is sufficient to solve the fractional FP Equation (9) by Sinc convolution approximation.

Next, the Fourier–Laplace of the fFP Equation (9) takes the form:

$$\mathcal{F}\left(\mathcal{L}\left({}^C{\mathcal{D}}_t^{\beta }u(x,t),s\right),\kappa \right)-\mathcal{F}\left(\mathcal{L}\left({\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }u(x,t),s\right),\kappa \right)=-\mathcal{F}\left(\mathcal{L}\left({\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }(w(x)u(x,t)),s\right),\kappa \right)$$

(18)

Applying Leibniz’s rule for fractional derivatives, we write:

$$\begin{array}{ccc}& & \mathcal{F}\left(\mathcal{L}\left({}^C{\mathcal{D}}_t^{\beta }u(x,t),s\right),\kappa \right)-\mathcal{F}\left(\mathcal{L}\left({\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }u(x,t),s\right),\kappa \right)\hfill \\ & =& -\mathcal{F}\left(\mathcal{L}\left(w(x){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }u(x,t)+\mu {\mathrm{w}}^{(1)}(x){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu -1}u(x,t)\mp \dots ,s\right),\kappa \right)\hfill \end{array}$$

(19)

The Green’s function $G^{\alpha ,\beta }(x,t)$ has to satisfy:

$${}^C{\mathcal{D}}_t^{\beta }{G}^{\alpha ,\beta }(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }{G}^{\alpha ,\beta }(x,t)+{\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(w(x)G^{\alpha ,\beta }(x,t)\right)=\delta (t)\delta (x)$$

(20)

with $-\infty <x<\infty$ and $t\ge 0$, which applied to (19) yields:

$${}^C{\mathcal{D}}_t^{\beta }{G}^{\alpha ,\beta }(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }{G}^{\alpha ,\beta }(x,t)+w(x){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(G^{\alpha ,\beta }(x,t)\right)+\mu {\mathrm{w}}^{(1)}(x){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu -1}\left(G^{\alpha ,\beta }(x,t)\right)\mp \dots =\delta (t)\delta (x)$$

(21)

Assuming that $w^{(1)}$ is negligible, relative to w, and since the Green’s function satisfies:

$${}^C{\mathcal{D}}_t^{\beta }{G}^{\alpha ,\beta }(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }{G}^{\alpha ,\beta }(x,t)+w(x){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(G^{\alpha ,\beta }(x,t)\right)\approx \delta (t)\delta (x)$$

(22)

which can be further simplified if we use a Taylor expansion of w around $x=0$:

$${}^C{\mathcal{D}}_t^{\beta }{G}^{\alpha ,\beta }(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }{G}^{\alpha ,\beta }(x,t)+\left(w(0)+w^{(1)}(0)x+\dots \right){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(G^{\alpha ,\beta }(x,t)\right)\approx \delta (t)\delta (x)$$

(23)

The major contribution now is assigned to the constant term $w(0)$ so that:

$${}^C{\mathcal{D}}_t^{\beta }{G}^{\alpha ,\beta }(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }{G}^{\alpha ,\beta }(x,t)+w(0){\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(G^{\alpha ,\beta }(x,t)\right)\approx \delta (t)\delta (x)$$

(24)

Equation (24) delivers when Fourier-Laplace transforms are applied to the determining equation for $G^{\alpha ,\beta }$:

$$s^{\beta }{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)-s^{\beta -1}{\widehat{G}}^{\alpha ,\beta }(0)=-{\left|\kappa \right|}^{\alpha }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\alpha }\pi /2}{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)+w(0){\left|\kappa \right|}^{\mu }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\mu }\pi /2}{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)$$

(25)

Under the assumption that the major contribution is generated by u itself in the Fourier-Laplace space, we approximate $w(0)=1$ which then yields:

$$s^{\beta }{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)-s^{\beta -1}{\widehat{G}}^{\alpha ,\beta }(0)\approx -{\left|\kappa \right|}^{\alpha }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\alpha }\pi /2}{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)+{\left|\kappa \right|}^{\mu }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\mu }\pi /2}{\widehat{G}}^{\alpha ,\beta }(\kappa ,s)$$

(26)

Solving with respect to the Fourier-Laplace variable we get:

$${\widehat{G}}^{\alpha ,\beta }(\kappa ,s)=\frac{s^{\beta -1}{\widehat{G}}^{\alpha ,\beta }(0)}{s^{\beta }+{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\alpha }\pi /2}-{|\kappa |}^{\mu }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\mu }\pi /2}}$$

(27)

and setting ${\widehat{G}}^{\alpha ,\beta }(0)=1$, we finally get:

$${\widehat{G}}^{\alpha ,\beta }(\kappa ,s)=\frac{s^{\beta -1}}{s^{\beta }+{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\alpha }\pi /2}-{|\kappa |}^{\mu }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\mu }\pi /2}}$$

(28)

Here, α as a superscript of $\widehat{G}$ denotes the collection of the parameters $\alpha =\left\{\left(\alpha ,{\theta }_{\alpha }\right),\left(\mu ,{\theta }_{\mu }\right)\right\}$. This transfer/Green function collects the basic information about the fractional FP equation. It will be used in the discrete convolution representation to approximate the fractional IE:

$$u(x,t)=v(x,t)-{\int }_0^t{\int }_{\mathbb{R}}{G}_x^{\alpha ,\beta }(x-\xi ,t-\tau )w(\xi )u(\xi ,\tau )d\xi d\tau$$

(29)

incorporating the initial condition:

$$v(x,t)={\int }_{\mathbb{R}}G(x-\xi ,t)u^{(0)}(\xi )d\xi$$

(30)

with $w(x)=V^{\prime }(x)/(ϵm\eta )$.

Comparing the spectral representation of the fFP equation with the Montrol-Weiss equation used for continuous time random walks (CTRW) [15], we identify the transfer function by means of the expression:

$$\widehat{u}(\kappa ,s)\approx \frac{\Psi (s)}{1-\Phi (\kappa ,s)}$$

(31)

where $\Psi (s)=(1-\psi (s))/s$ and $\Phi (\kappa ,s)=\widehat{W}(\kappa )\psi (s)$ with $\psi (s)=1-s^{\beta }$ representing the asymptotic scaling behavior for $s\to 0$. The separation of Fourier and Laplace variables in ${\widehat{B}}^{\alpha ,\beta }(\kappa ,s)={\widehat{B}}^{\alpha }(\kappa ){\psi }^{1/2}(s)$ and ${\widehat{B}}^{\mu ,\beta }(\kappa ,s)={\widehat{B}}^{\mu }(\kappa ){\psi }^{1/2}(s)$ yields $\Phi (\kappa ,s)=\widehat{W}(\kappa )\psi (s)={\widehat{B}}^{\alpha }(\kappa ){\widehat{B}}^{\mu }(\kappa )\psi (s)$:

$$\widehat{u}(\kappa ,s)\approx \frac{s^{\beta -1}}{s^{\beta }-{\widehat{B}}^{\alpha }(\kappa )+\widehat{w}(\kappa ){\widehat{B}}^{\mu }(\kappa )}$$

(32)

In (32), ${\widehat{B}}^{\gamma }(\kappa )\approx -{|\kappa |}^{\gamma }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\gamma }\pi /2}$ represents the asymptotic scaling law in Fourier space as $\kappa \to 0$, with $\gamma \in \{\alpha ,\mu \}$. If in addition we also assume that $\widehat{w}(k)=\widehat{w}(0)+{\widehat{w}}^{\prime }(0)\kappa +\dots$ as $\kappa \to 0$, we set $\widehat{w}(k)=\widehat{w}(0)=1$ as a proper normalization. Thus the fundamental solution in Fourier-Laplace representation becomes:

$$\widehat{u}(\kappa ,s)\approx \frac{s^{\beta -1}}{s^{\beta }+{|\kappa |}^{\alpha }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\alpha }\pi /2}-{|\kappa |}^{\mu }{e}^{i\mathrm{sign}(\kappa ){\theta }_{\mu }\pi /2}}$$

(33)

corresponding to a CTRW equation of the type:

$$u(x,t)=\delta (x)\Psi (t)+{\int }_0^t\psi (t-\tau )\left[{\int }_{\mathbb{R}}W(x-\xi )u(\xi ,\tau )d\xi \right]d\tau$$

(34)

with the survival function $\Psi (t)={\int }_t^{\infty }\psi (\tau )d\tau$ denoting the probability that at instant t the particle is still sitting in its starting position $x=0$. The transfer function $\widehat{u}(\kappa ,s)$ in (33) will be the key expression in the solution of the fFP equation:

$${}^C{\mathcal{D}}_t^{\beta }u(x,t)-{\mathcal{D}}_{{\theta }_{\alpha };x}^{\alpha }u(x,t)=-{\mathcal{D}}_{{\theta }_{\mu };x}^{\mu }\left(\frac{V^{\prime }(x)}{ϵm\eta }u(x,t)\right)\mathrm{with}-\infty <x<\infty \mathrm{and}t\ge 0$$

(35)

The equivalent IE to (35) is numerically approximated by a successive Neumann iteration. Examples of fractional integral equations are solved for single valued functions in [16,17]. The work in [16] proves that for fractional integral equations the solution exists and converges exponentially under the condition that the functions are analytic. Using the property of separation of variables in convolution representations the results for single valued functions are also valid for multivalued functions [18]. Thus the existence of solutions and convergence of the numerical approximation to the solution is guaranteed (for details see [16,18]). Based on these facts, we shall next introduce Sinc methods to approximate fractional partial differential equations specifically the fFP equation.

2. Methods of Approximation

This section introduced the basic ideas of Sinc methods [19]. We will discuss only the main ideas as a collection of recipes to set up a Sinc approximation. We omit most of the proofs of the different important theorems and lemmas because these proofs are available in literature [6,18,20,21,22]. The following subsections collect information on the basic mathematical functions used in Sinc approximation. We introduce Sinc methods to represent indefinite integrations and convolution integrals. These types of integrals are essential for representing the fractional operators of differentiation and integration [7,18].

2.1. Sinc Basis

To start with we first introduce some definitions and theorems allowing us to specify the space of functions, domains, and arcs for a Sinc approximation.

Definition 1.

Domain and Conditions

Let $\mathcal{D}$ be a simply connected domain in the complex plane and $z\in \mathbb{C}$ having a boundary $\partial \mathcal{D}$. Let a and b denote two distinct points of $\partial \mathcal{D}$ and ϕ denote a conformal map of $\mathcal{D}$ onto ${\mathcal{D}}_d$, where ${\mathcal{D}}_d=\{z\in \mathbb{C}:\left|\mathcal{I}\mathit{m}(z)\right|<d\}$, such that $\varphi (a)=-\infty$ and $\varphi (b)=\infty$. Let $\psi ={\varphi }^{-1}$ denote the inverse conformal map, and let Γ be an arc defined by $\Gamma =\{z\in \mathbb{C}:z=\psi (x),x\in \mathbb{R}\}$. Given ϕ, ψ, and a positive number h, let us set $z_k=\psi (kh)$, $k\in \mathbb{Z}$ to be the Sinc points, let us also define $\rho (z)=e^{\varphi (z)}$.

Note the Sinc points are an optimal choice of approximation points in the sense of Lebesgue measures for Sinc approximations [23].

Definition 2.

Function Space

Let $d\in (0,\pi )$, and let the domains $\mathcal{D}$ and ${\mathcal{D}}_d$ be given as in Definition 1. If $d^{\prime }$ is a number such that $d^{\prime }>d$, and if the function ϕ provides a conformal map of ${\mathcal{D}}^{\prime }$ onto ${\mathcal{D}}_{d^{\prime }}$, then $\mathcal{D}\subset {\mathcal{D}}^{\prime }$. Let α and β denote positive numbers, and let ${\mathit{L}}_{\alpha ,\beta }(\mathcal{D})$ denote the family of functions $u\in \mathit{Hol}(\mathcal{D})$, for which there exists a positive constant $c_1$ such that, for all $z\in \mathcal{D}$:

$$\left|u(z)\right|\le c_1\frac{{\left|\rho (z)\right|}^{\alpha }}{{(1+\left|\rho (z)\right|)}^{\alpha +\beta }}$$

(36)

Now let the positive numbers α and β belong to (0,1], and let ${\mathit{M}}_{\alpha ,\beta }(\mathcal{D})$ denote the family of all functions $g\in \mathit{Hol}(\mathcal{D})$, such that $g(a)$ and $g(b)$ are finite numbers, where $g(a)=li{m}_{z\to a}g(z)$ and $g(b)=li{m}_{z\to b}g(z)$, and such that $u\in {\mathit{L}}_{\alpha ,\beta }(\mathcal{D})$ where:

$$u(z)=g(z)-\frac{g(a)+\rho (z)g(b)}{1+\rho (z)}$$

(37)

The two definitions allow us to formulate the following theorem for Sinc approximations.

Theorem 1.

Sinc Approximation [20]

Let $u\in {\mathit{L}}_{\alpha ,\beta }(\mathcal{D})$ for $\alpha >0$ and $\beta >0$, take M = [β N/α], where [x] denotes the greatest integer in x, and then set $m=M+N+1$. If $u\in {\mathit{M}}_{\alpha ,\beta }(\mathcal{D})$, and if $h={(\pi d/(\beta N))}^{1/2}$ then there exists a positive constant $c_2$ independent of N, such that:

$$\left|u(z)-\sum _{k=-M}^{N}u\left(z_k\right)w_k\right|\le c_2{N}^{1/2}{e}^{-{(\pi d\beta N)}^{1/2}}$$

(38)

with $w_k$ the base function (see (41)).

The proof of this Theorem 1 is given in [20]. Note the choice $h={(\pi d/(\beta N))}^{1/2}$ is close to optimal for an approximation in the space ${\mathit{M}}_{\alpha ,\beta }(\mathcal{D})$ in the sense that the error bound in Theorem 1 cannot be appreciably improved regardless of the basis [20]. It is also optimal in the sense of the Lebesgue measure achieving an optimal value less than Chebyshev approximations [23]. We also note that this behavior is found also in bi-variate approximations based on Poly-Sinc methods [24,25,26].

These definitions and the theorem directly allow the formulation of an algorithm for a Sinc approximation. Let $\mathbb{Z}$ denote the set of all integers. Select positive integers N and $M=[\beta N/\alpha ]$ and set $m=M+N+1$. The step length is determined by $h={(\pi d/(\beta N))}^{1/2}$ where α, β, and d are real parameters. In addition assume there is a conformal map ϕ and its inverse ψ such that we can define Sinc points $z_j=\psi (jh)$, $j\in \mathbb{Z}$ [20]. The following relations define the basis of a Sinc approximation:

$$\mathrm{Sin}\mathrm{c}(z)=\frac{sin(\pi z)}{\pi z}$$

(39)

The shifted Sinc is derived from relation (39) by translating the argument by integer steps of length h and applying the conformal map to the independent variable:

$$S(j,h)\circ \varphi (z)=\mathrm{Sin}\mathrm{c}([\varphi (z)-jh]/h),j=-M,\dots ,N$$

(40)

The discrete shifting allows us to cover the approximation interval $(a,b)$ in a dense way while the conformal map is used to map the interval of approximation from an infinite range of values to a finite one. Using the Sinc basis we are able to represent the basis functions as a piecewise defined function $w_j(z)$ by:

$$w_j=\left\{\begin{array}{cc}& \begin{array}{cc}\frac{1}{1+\rho (z)}-{\sum }_{k=-M+1}^N\frac{1}{1+e^{kh}}S(k,h)\circ \varphi (z)\hfill & j=-M\hfill \\ S(j,h)\circ \varphi (z)\hfill & j=-M+1,\dots ,N-1\hfill \\ \frac{\rho (z)}{1+\rho (z)}-{\sum }_{k=-M}^{N-1}\frac{e^{kh}}{1+e^{kh}}S(k,h)\circ \varphi (z)\hfill & j=N\hfill \end{array}\hfill \end{array}\right.$$

(41)

where $\rho (z)=exp(\varphi (z))$. This form of the Sinc basis is chosen as to satisfy the interpolation at the boundaries. The basis functions defined in (41) suffice for purposes of uniform−norm approximation over $(a,b)$.

This notation allows us to define a row vector $V_m(S)$ of basis functions:

$$V_m(S)=\left(w_{-M},\dots ,w_N\right)$$

(42)

with $w_j$ defined as in (41). For a given vector $V_m(u)=\left(u_{-M},\dots ,u_N\right){}^T$ we now introduce the product as an approximation of the function $u(z)$ by:

$$u(z)\approx V_m(S)V_m(u)=\sum _{k=-M}^N{u}_k{w}_k$$

(43)

Based on this notation, we will introduce in the next few subsections the different integrals we need [18].

2.2. Indefinite Integral

We need for the representation of fractional derivatives indefinite integrals. This subsection describes how indefinite integrals can be defined [20] and how these definitions are related to the definition of definite integrals. For collocating an indefinite integral and for obtaining explicit approximations of the functions $(\mathcal{J}u)(x)$ and $({\mathcal{J}}^{\prime }u)(x)$ defined by:

$$(\mathcal{J}u)(x)={\int }_a^{x}u(t)dt\mathrm{with}x\in (a,b)$$

(44)

$$({\mathcal{J}}^{\prime }u)(x)={\int }_x^{b}u(t)dt\mathrm{with}x\in (a,b)$$

(45)

We use the following basic relations [20]. Let $\mathbb{Z}$ denote the set of all integers, and let $\mathbb{C}$ denote the complex plane. Let $\mathrm{Sin}\mathrm{c}(x)$ be given by (40) and $e_k$ be defined as:

$${\sigma }_k={\int }_0^k\mathrm{Sin}\mathrm{c}(x)dx=\frac{1}{\pi }\mathrm{Si}(\pi k)$$

(46)

with $\mathrm{Si}(x)$ the sine integral. This put us into position to write:

$$e_k=\frac{1}{2}+{\sigma }_k,k\in \mathbb{Z}$$

(47)

If now ϕ denotes a one−to−one transformation of the interval $(a,b)$ onto the real line $\mathbb{R}$, let h denote a fixed positive number, and let the Sinc points be defined on $(a,b)$ by $z_k={\varphi }^{-1}(kh)$, $k\in \mathbb{Z}$, where ${\varphi }^{-1}$ denotes the inverse function of the conformal map ϕ. Let M and N be positive integers, set $m=M+N+1$, and for a given function u defined on $(a,b)$, define a diagonal matrix $D(u)$ by $D(u)=\mathrm{diag}\left[u\left(z_{-M}\right),\dots ,u\left(z_N\right)\right]$. Let $I^{(-1)}$ be a square Töplitz matrix of order m having $e_{i-j}$, as its ${(i,j)}^{\mathrm{th}}$ entry i.e., $i,j=-M,\dots ,N$:

$$\left(I^{(-1)}\right){}_{i,j}=e_{i-j}\mathrm{with}i,j=-M,\dots ,N$$

(48)

Define square matrices $A_m$ and $B_m$ by:

$$A_m=h{I}^{(-1)}D(1/{\varphi }^{\prime })$$

(49)

$$B_m=h{\left\{I^{(-1)}\right\}}^{T}D(1/{\varphi }^{\prime })$$

(50)

where the superscript “T” denotes the transpose. The collocated representation of the indefinite integrals are thus given by:

$${\mathcal{J}}_{m}u=V_m(S)A_m{V}_m(u)=h{V}_m(S)I^{(-1)}D(1/{\varphi }^{\prime })V_m(u)$$

(51)

$${\mathcal{J}}_m^{\prime }u=V_m(S)B_m{V}_m(u)=h{V}_m(S){\left\{I^{(-1)}\right\}}^{T}D(1/{\varphi }^{\prime })V_m(u)$$

(52)

These are collocated representations of the indefinite integrals defined in (44) and (45), respectively [18]. If we compare our results with the target equations for example (35) we observe that we need one additional step to extend the indefinite integrals to convolution integrals.

2.3. Convolution Integrals

Indefinite convolution integrals can also be effectively collocated via Sinc methods [20]. This section discusses the core procedure of this paper, for collocating the convolution integrals and for obtaining explicit approximations of the functions p and q defined by:

$$p(x)={\int }_a^{x}f(x-t)g(t)dt\mathrm{with}x\in (a,b)$$

(53)

$$q(x)={\int }_x^{b}f(t-x)g(t)dt\mathrm{with}x\in (a,b)$$

(54)

where $x\in \Gamma$. In presenting these convolution results, we shall assume that $\Gamma =(a,b)\subseteq \mathbb{R}$, unless otherwise indicated. Note also, that being able to collocate p and q enables us to collocate definite convolutions like ${\int }_a^{b}f(x-t)g(t)dt$.

Before we start to present the collocation of the Equations (53) and (54) we mention that there is a special approach to evaluate the convolution integrals by using a Laplace transform. In fact Lubich [27,28] introduced this way of calculation by the following idea:

$$p(x)={\int }_0^{x}f(x-t)g(t)dt=\frac{1}{2\pi i}{\int }_{\mathcal{C}}{F}_{+}(s){\int }_0^x{e}^{st}g(x-t)dtds$$

(55)

for which the inner integral solves the initial value problem $y^{\prime }=sy+g$ with $g(0)=0$. We assume that the Laplace transform (Stenger-Laplace transform):

$$F_{+}(s)={\int }_{E}f(t)e^{-t/s}dt$$

(56)

with E any subset of $\mathbb{R}$ such that $E\supseteq (0,b-a)$, exists for all $s\in {\Omega }^{+}=\{s\in \mathbb{C}|\Re (s)>0\}$. The eigenvalues of $A_m$ and $B_m$ are all positive which was a 20 year old conjecture by FS. This conjecture was recently solved by Han and Xu [29].

In the notation introduced above we get:

$$p=F_{+}(\mathcal{J})g\approx F_{+}\left({\mathcal{J}}_m\right)g$$

(57)

and:

$$q=F_{+}({\mathcal{J}}^{\prime })g\approx F_{+}\left({\mathcal{J}}_m^{\prime }\right)g$$

(58)

are accurate approximations, provided that the inverse Laplace transform of $F_{+}(1/s)g(1/s)$ again belongs to a space $M_{{\alpha }^{\prime },d^{\prime }}$ for some positive numbers ${\alpha }^{\prime }$ and $d^{\prime }$ [18]. The procedure to calculate the convolution integrals is now as follows. The collocated integral ${\mathcal{J}}_m=V_m(S)A_m{V}_m$ and ${\mathcal{J}}_m^{\prime }=V_m(S)B_m{V}_m$, upon diagonalization of $A_m$ and $B_m$ in the form:

$$A_m=X_m\mathrm{diag}\left[s_{m,-M},\dots ,s_{m,N}\right]X_m^{-1}$$

(59)

$$B_m=Y_m\mathrm{diag}\left[s_{m,-M},\dots ,s_{m,N}\right]Y_m^{-1}$$

(60)

with $\Sigma =\mathrm{diag}\left[s_{-M},\dots ,s_N\right]$ as the eigenvalues arranged in a diagonal matrix for each of the matrices $A_m$ and $B_m$. Note that $A_m$ and $B_m$ have the same vector of eigenvalues. Then the Stenger-Laplace transform (56) delivers the square matrices $F_{+}\left(A_m\right)$ and $F_{+}\left(B_m\right)$ defined via the equations:

$$F_{+}\left(A_m\right)=X_m\mathrm{diag}\left[F_{+}\left(s_{m,-M}\right),\dots ,F_{+}\left(s_{m,N}\right)\right]X_m^{-1}=X_m{F}_{+}(\Sigma )X_m^{-1}$$

(61)

$$F_{+}\left(B_m\right)=Y_m\mathrm{diag}\left[F_{+}\left(s_{m,-M}\right),\dots ,F_{+}\left(s_{m,N}\right)\right]Y_m^{-1}=Y_m{F}_{+}(\Sigma )Y_m^{-1}$$

(62)

We can get the approximation of (57) and (58) by:

$$F_{+}(\mathcal{J})g\approx F_{+}\left({\mathcal{J}}_m\right)g=V_m(S)F_{+}\left(A_m\right)V_m(g)=V_m(S)X_m{F}_{+}(\Sigma )X_m^{-1}{V}_m(g)$$

(63)

$$F_{+}\left({\mathcal{J}}^{*}\right)g\approx F_{+}\left({\mathcal{J}}_m^{*}\right)g=V_m(S)F_{+}\left(B_m\right)V_m(g)=V_m(S)Y_m{F}_{+}(\Sigma )Y_m^{-1}{V}_m(g)$$

(64)

These two formulas deliver a finite approximation of the convolution integrals p and q. The convergence of the method is exponential under the above Laplace transform assumptions—see [20] for a proof of a special case.

2.4. Convolution Integrals in Two Variables

Examining the IE (35) in more detail we realize that we have to extend the one dimensional convolution to a two dimensional one in fact we have to deal with integrals of the type:

$$\begin{array}{ccc}\hfill p(x,t)& =& {\int }_0^t{\int }_{-\infty }^{\infty }f(x-\xi ,t-\tau )g(\xi ,\tau )d\xi d\tau \hfill \\ & =& {\int }_0^t{\int }_{-\infty }^{x}f(x-\xi ,t-\tau )g(\xi ,\tau )d\xi d\tau +{\int }_0^t{\int }_x^{\infty }f(x-\xi ,t-\tau )g(\xi ,\tau )d\xi d\tau \hfill \end{array}$$

(65)

As discussed in the previous section we will use a Laplace representation of the convolution integrals but now in two dimensions. Where the approximation is sought over the region $\left(a_1,b_1\right)\times \left(a_2,b_2\right)$, and with $\left(a_i,b_i\right)\in \mathbb{R},i=1,2$. Note that the method of separation of variables made possible by the one-dimensional convolution approximation, as well as to how easily the final algorithm can be adapted to parallel computation. In order to guarantee some accuracy in the final approximation, we shall simply assume, without going into detail, that the function p belongs to the class ${\mathcal{M}}_{{\alpha }_i,{\beta }_i}$ with respect to each variable $x_j$, for all fixed values of the other variables, each in its respective interval of definition, $j=1,2$.

We shall assume that the mappings ${\varphi }_j$ have been selected properly according to the limits of the intervals. We furthermore assume that positive integers $N_j$ and $M_j$ as well as positive numbers $h_j$$(j=1,2)$ have been selected such that $h_j=\pi /\sqrt{N_j}$. These definitions ensure that we get the same order of accuracy of approximation $ϵ=\mathcal{O}\left(N_1^{1/2}exp\left(-c{N}_1^{1/2}\right)\right.$ in each variable [16,18]. We set $m_j=M_j+N_j+1$, and we define the Sinc points by $z_l^{(j)}={\varphi }_j^{-1}\left(l{h}_j\right)$ for $l=-M_j,\dots ,N_j$; $j=1,2$. Next, we determine matrices $A_j$, $X_j$, $S_j$, and $X_j^{-1}$ such that:

$$A_j=h_j{I}_{m_j}^{(-1)}D\left(1/{\varphi }_j^{\prime }\right)=X_j{S}_j{X}_j^{-1},j=1,2$$

(66)

In (66) $I_{m_j}^{(-1)}$ is defined as in (48), and $S_j$ are diagonal matrices:

$$S_j=\mathrm{diag}\left[s_{-M_j}^{(j)},\dots ,s_{N_j}^{(j)}\right]$$

(67)

Arbitrarily taking $\left.c_j\in \left[2\left(b_j-a_j\right),\infty \right.\right)$, we set:

$$F\left(s^{(1)},x\right)={\int }_0^{c_1}f(t,x)e^{-t/s^{(1)}}dt$$

(68)

$$G\left(s^{(1)},s^{(2)}\right)={\int }_0^{c_2}F\left(s^{(1)},x\right)e^{-x/s^{(2)}}dx$$

(69)

We now illustrate the method of separation of variables. To this end, we first rewrite (65) in the notationally more convenient form:

$$p_1(x,t)={\int }_{a_1}^t{\int }_{a_2}^{x}f(x-\xi ,t-\tau )g(\xi ,\tau )d\xi d\tau$$

(70)

representing the first integral in (65). Discretization with respect to t. We set:

$$g(\xi ,\tau )=\left(g\left(\xi ,z_{-M_1}^{(1)}\right),\dots ,g\left(\xi ,z_{N_1}^{(1)}\right)\right){}^T$$

(71)

and we then define a vector $\mathit{p}(x)$ by:

$$\mathit{p}(x)={\int }_{a_2}^{x}F\left(x-\xi ,A_1\right)\mathit{g}(\xi )d\xi$$

(72)

where $A_1$ and F are defined in (66) and (68) respectively. Using the diagonalization identity $A_1=X_1{S}_1{X}_1^{-1}$ given in (66), it now follows from (72) that:

$$\mathit{p}(x)=X_1{\int }_{a_2}^x\left(\begin{array}{ccc}F\left(x-\xi ,s_{-M_1}^{(1)}\right)& & \\ & \ddots & \\ & & F\left(x-\xi ,s_{N_1}^{(1)}\right)\end{array}\right)X_1^{-1}\mathit{g}(\xi )d\xi$$

(73)

The expression (73) motivates the transformations:

$$\mathit{h}(\xi )=X_1^{-1}\mathit{g}(\xi ),\mathit{q}(x)=X_1^{-1}\mathit{p}(x)$$

(74)

Thus, denoting the components of h and q by $h_i$ and $q_1$ respectively, with $i=-M_1,\dots ,N_1$, Equation (73) reduces to the decoupled set of scalar equations:

$$q_i(x)={\int }_{a_2}^{x}F\left(x-\xi ,s_i^{(1)}\right)h_i(\xi )d\xi$$

(75)

Discretization with respect to x. We now set:

$${\mathit{h}}_i=\left(h_i\left(z_{-M_2}^{(2)}\right),\dots ,h_i\left(z_{N_2}^{(2)}\right)\right){}^T$$

(76)

and we then define a vector $q_i$ by:

$${\mathit{q}}_i(x)={\int }_{a_2}^{x}G\left(A_2,s_i^{(1)}\right){\mathit{h}}_i(\xi )d\xi$$

(77)

where $A_2$ and G are defined in (66) and (69) respectively. Using the diagonalization identity $A_2=X_2{S}_2{X}_2^{-1}$ given in (66), it now follows from (77) that:

$${\mathit{q}}_i(x)=X_2{\int }_{a_2}^x\left(\begin{array}{ccc}G\left(s_{-M_2}^{(2)},s_i^{(1)}\right)& & \\ & \ddots & \\ & & G\left(s_{N_2}^{(2)},s_i^{(1)}\right)\end{array}\right)X_2^{-1}{\mathit{h}}_i(\xi )d\xi$$

(78)

This last expression motivates the transformations:

$${\mathit{k}}_i=X_2^{-1}{\mathit{h}}_i(\xi ),{\mathit{r}}_i=X_2^{-1}{\mathit{q}}_i(\xi )$$

(79)

Denoting the components of ${\mathit{r}}_i$ and ${\mathit{k}}_i$ by $r_{i,j}$ and $k_{i,j}$ respectively, with $i=-M_1,\dots ,N_1$ and $j=-M_2,\dots ,N_2$, Eq. (78) reduces to the decoupled set of scalar equations:

$$r_{i,j}=G\left(s_j^{(2)},s_i^{(1)}\right)k_{i,j}$$

(80)

By assumption, the $k_{i,j}$ are known at this point, and (80) then determines the $r_{i,j}$. The second equation in (79) is then used to determine the vectors ${\mathit{q}}_i$ at the Sinc points $z^{(2)}$. The second transformation of (74) is next used to determine the vector $\mathit{p}(x)$ at the set of Sinc points. We can thus recover the complete array of values $p(x,t)$ at the set of Sinc points $\left(z_i^{(1)},z_j^{(2)}\right)$. The algorithmic procedure is described in more detail in [21].

2.5. Sinc Collocation of fFP

For fractional differential equations there exists a solution in terms of a second kind Volterra integral equation incorporating the initial conditions of the Cauchy problem as given in (29) and (30) in the representation of (34) connected to (33). These relations are equivalent to the fFP Equation (35). The discrete version of Equation (34) follow as a collocation approximation as:

$$u-\lambda F_{+}(\mathcal{J})u=\mathcal{N}\approx V_m(u)-{\lambda }_1{F}_{+}\left(A_m^t,A_m^x\right)V_m(u)-{\lambda }_2{F}_{+}\left(A_m^t,B_m^x\right)V_m(u)=V_m(\mathcal{N})$$

(81)

Here, $\mathcal{N}$ collects the given initial conditions of the problem and ${\lambda }_1=sin((-\alpha +\theta )\pi /2)/(sin(-\alpha \pi )\Gamma (-\alpha )\Gamma (\beta ))$, ${\lambda }_2=sin((-\alpha -\theta )\pi /2)/(sin(-\alpha \pi )\Gamma (-\alpha )\Gamma (\beta ))$ are factors independent of t or x related to the Caputo and Riesz-Feller operators (see Appendix A). The discrete version follows straight forward from (81) to be:

$$\left\{I-{\lambda }_1{F}_{+}\left(A_m^t,A_m^x\right)-{\lambda }_2{F}_{+}\left(A_m^t,B_m^x\right)\right\}{V}_m(u)=V_m(\mathcal{N})$$

(82)

The matrices $F_{+}$ are set up according to the discussion in Section 2.4 using the transfer function (33) in the Laplace transform representation. Solving this linear system with respect to $V_m(u)$ allows us to approximate the solution by:

$$u(t,x)\approx V_m(S)V_m(u)$$

(83)

Note the solution of (82) is generated using a Neumann iteration applying a trash hold level for two consecutive approximations in view of generalizing the linear equation to a nonlinear one [16].

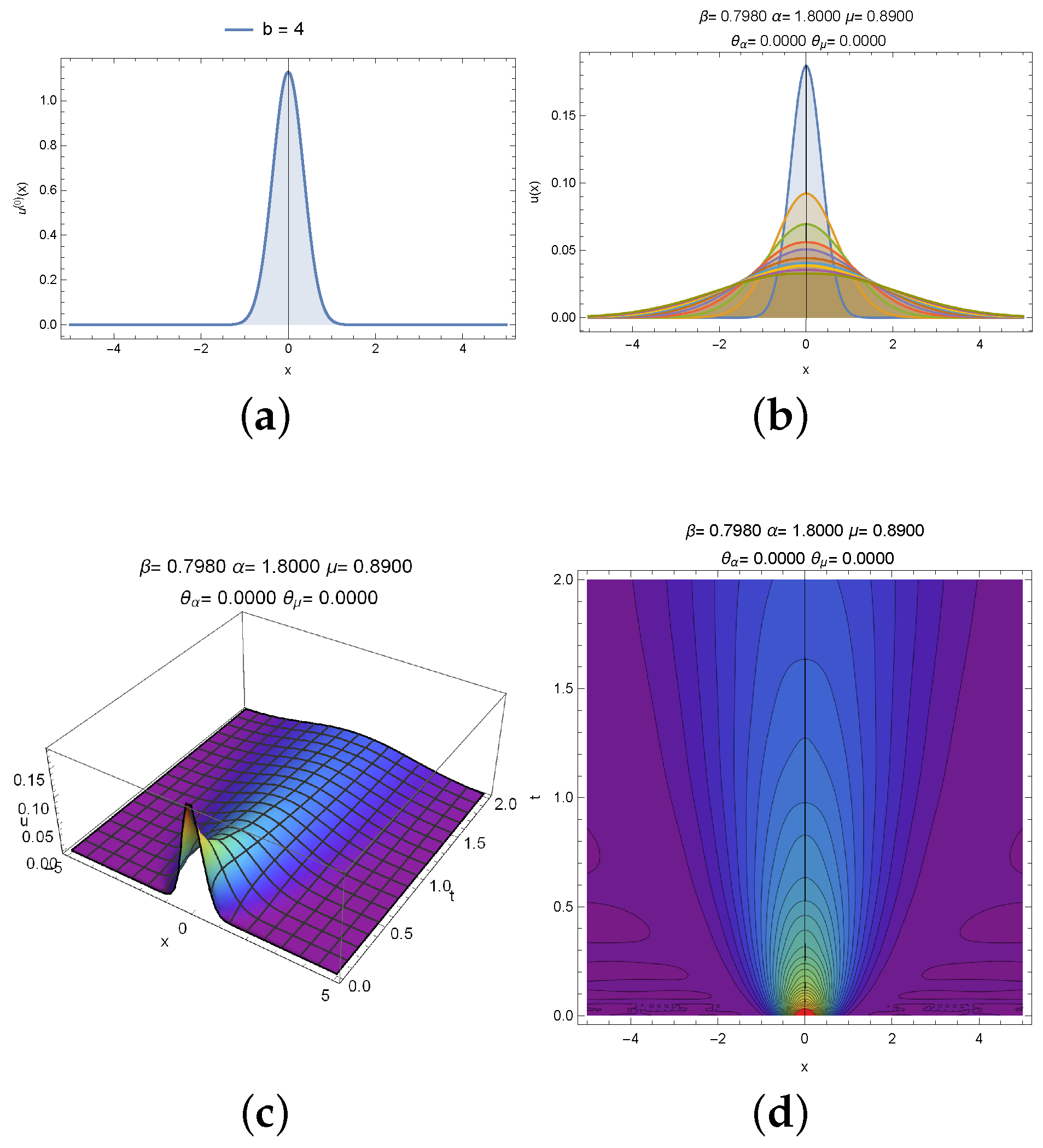
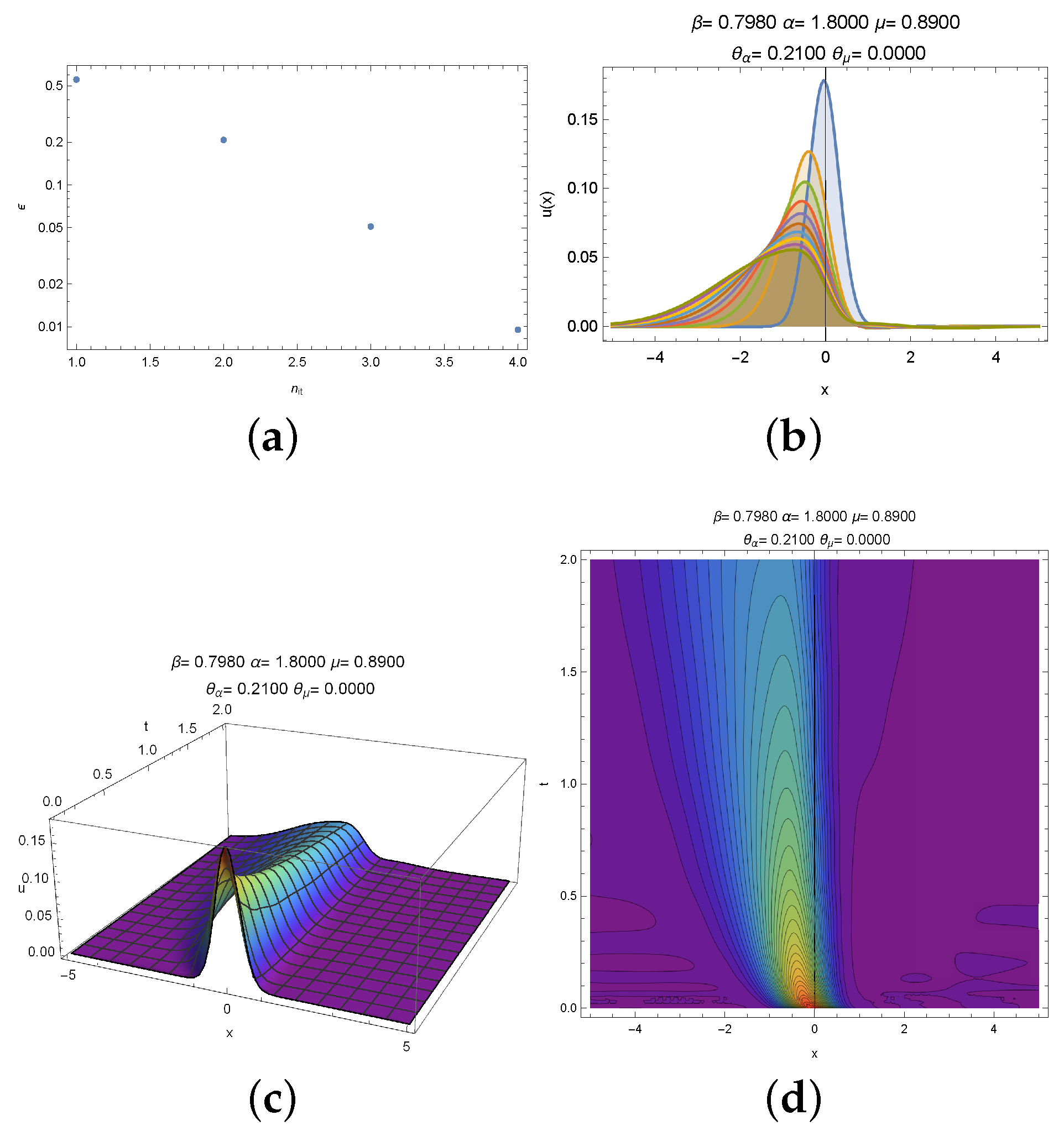
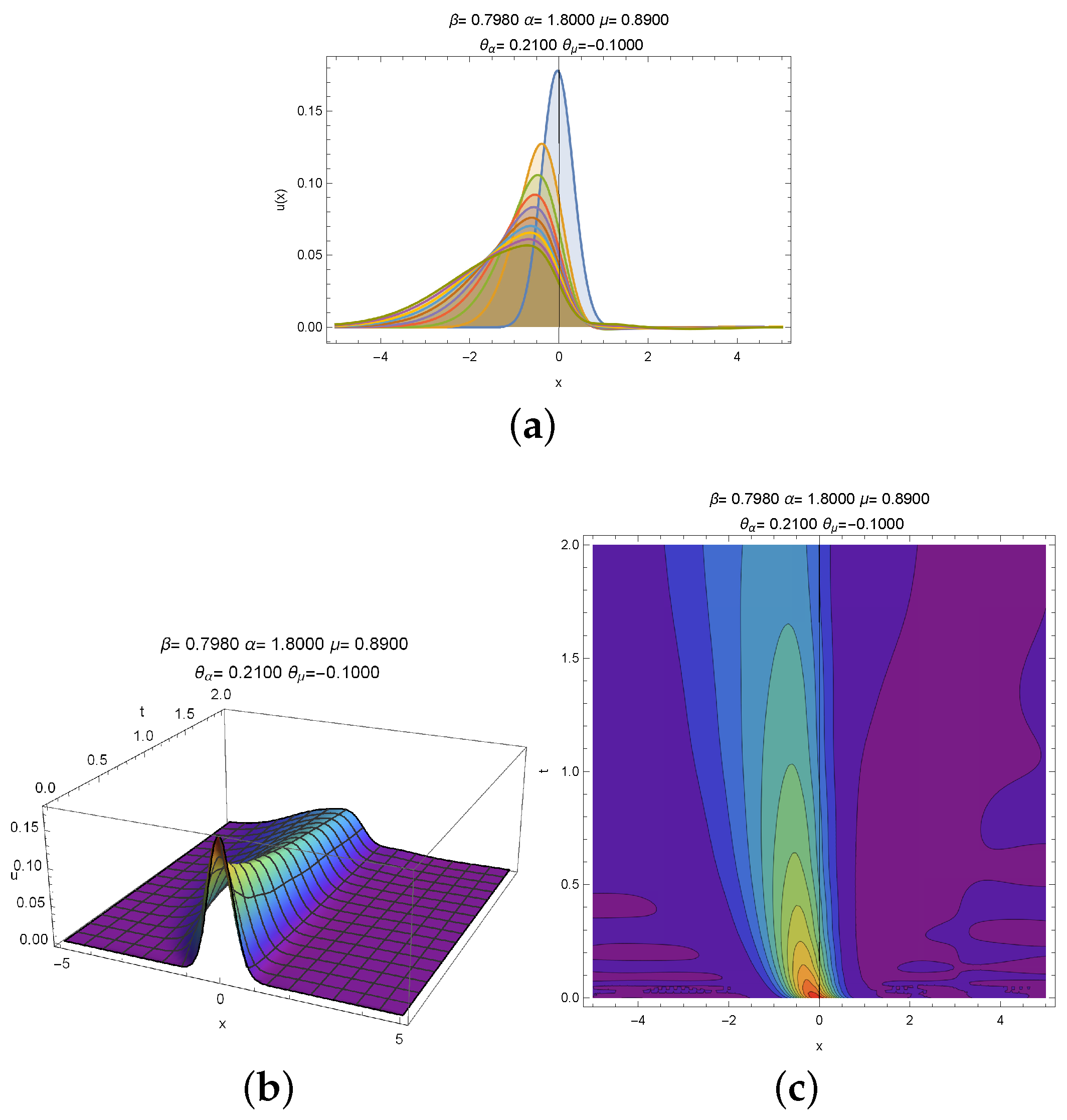
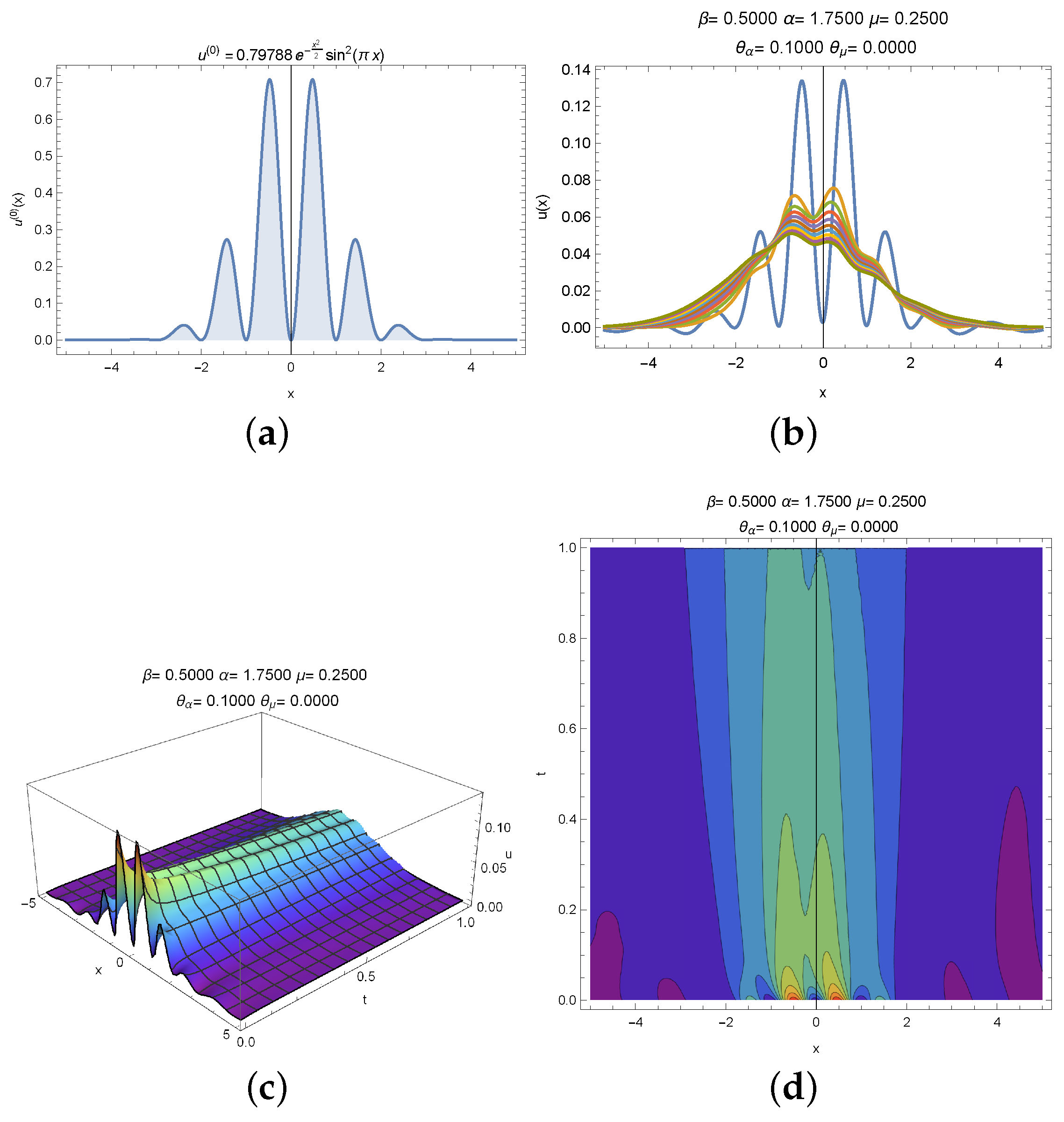
3. Experimental Section

This section collects four examples for the fFP equation using different types of external forces and different values for fractional derivatives. We also demonstrate the influence of the skewness parameters to exemplify the effects on the approximations such as the counter gradient transport [30]. The first three examples use a normalized Gaussian distribution with different amplitudes. Since the Sinc approximation allows an arbitrary initial distribution, we examine in the fourth example the influence of the initial distribution on the solution.

Example 1.

The first example uses a normalized Gaussian as initial distribution. The distribution follows from $u^{(0)}(x)=\sqrt{b}{e}^{-b{x}^2}/\sqrt{\pi }$ with b = 4. The initial state is shown in Figure 1. The approximation on the time domain [0, T] = [0, 2.0] was iteratively generated using a Neumann iteration scheme. The external force $w(x)$ was set to a constant value w(x) =−1. Figure 1 collects the initial distribution, a sequence of temporal steps represented on the spatial domain, and a $(x,t)$ graph of $u(x,t)$. The level lines of this graphs are also shown in a contour plot.

The graphs in Figure 1 demonstrate that the approximations represent the expected dispersive behavior. The initially localized distribution starts to spread with reduced amplitudes for times larger than zero. The dispersion is visible by the broadening of the distribution if we step along the time axis the amplitude $u(x,t)$ is reduced. We also observe that the function is positive; i.e., $u(x,t)\ge 0$.

Example 2.

The second example uses the same fractional parameters β, α, and μ except ${\theta }_{\alpha }=0.21$ and ${\theta }_{\mu }=0$. Figure 2 also includes a graph showing the convergence of the Neumann iteration of the IE (top left). The specified error level ϵ is reached within four iterations. The graphs in Figure 2 show again dispersive behavior of the approximation (broadening of the distribution and reduction of the amplitude). It becomes obvious that the decay of the amplitude is slower than that in Example 1 (see Figure 1). In addition we observe that the decaying maximum in time is shifted to the left in the graphs and the symmetry of the solution is distorted. The finite value of ${\theta }_{\alpha }$ is responsible for this effect. Again the distribution is positive on the whole domain. Figure 2 also shows how the time evolution of the distribution $u(x,t)$ as $3d$ and contour plot. We observe that due to the finite value of ${\theta }_{\alpha }$ the symmetry of the solution is broken and that a steep ramp on the right of the approximation exists. The left side of the solution decays in the spatial direction much more slower than that on the steep ramp. Over all, the dispersion of the solution is present but occurs mainly on the left side of the maximum of the distribution. The maximum location of the distribution follows an asymptotic relation like ∼t${}^{\alpha }$.

Example 3.

The third example uses the same initial condition and fractional parameters as that in Example 2 (see Figure 2) except for ${\theta }_{\mu }=-0.1$. The second skewness parameter is set to a negative value which affects the decay rate and the shifting of the maximum of the distribution. The dispersion rate is also affected by this second skewness parameter (see Figure 3).

In Figure 4 we collect some characteristics of the approximations generated in Example 1,2, and 3. The data shown in Figure 4 represent the location of the maximum $x_0$ of $u(x,t)$, the decay of the maximum value in time, and the change of the width $\Delta \mathrm{x}$ of the maximum on the level $u_{max}(1-e)/e$ corresponding to the 63% value of the maximum. The three graphs summarize the scaling properties of the approximations. The first graph (top row) shows that the maximum location is shifted in time if the skewness parameters are different from zero. The shift of the maximum follows a relation $x_0\sim t^{0.28}$ for ${\theta }_{\alpha }=0.21$ and ${\theta }_{\mu }=-0.1$. As a reference for zero skewness parameters there is no shift of the maximum (top line in Figure 4 top row). The second characteristic of the approximation is the decay of the maximum in time. The decay follows the relation $u_{max}\sim exp\left(-\delta t^{0.1}\right)$. Note the exponent of t is the same for all approximations. The width $\Delta \mathrm{x}$ of the maximum also changes with time according to the dispersion. For vanishing skewness we have a relation $\Delta \mathrm{x}\sim t^{0.67}$ while for the skewness ${\theta }_{\alpha }=0.21$ and ${\theta }_{\mu }=-0.1$ we found the relation $\Delta \mathrm{x}\sim t^{0.21}$. This indicates that the dispersion process is influenced by the skewness parameters.

Example 4.

This example uses an external force $w(x)=-2si{n}^2(2\pi x)$ with an initial condition $u^{(0)}(x)=0.797885e^{-\frac{x^2}{2}}si{n}^2(\pi x)$ where the prefactor is chosen in such a way that the integral on $\mathbb{R}$ is normalized to one. Figure 5 collects the information about the fractional exponents used and displays the behavior of the approximation.

4. Conclusions

Starting from the integer order Fokker-Planck equation and applying the fractional operators to the temporal and spatial coordinates we derived a fully fractional Fokker-Planck equation in temporal and spatial coordinates. The equivalent representation of the Montrol-Weiss equation using the adapted transfer function with three fractional exponents and two skewness parameters provides us with a suitable Volterra integral equation of second type for the numerical approximation. The approximation of the integral equation is using exponentially converging Sinc convolution integrals extended to higher dimensions. The Volterra equation of the second kind is converted in Sinc convolution methods to a linear system of equations which are solved by a Neumann iteration. The convergence of this iteration is absolute and reaches a specified error margin in a reliable fast way. The examples presented demonstrate for a choice of different initial conditions $u^{(0)}(x)$ dispersing approximations. The dispersion is affected by the fractional exponents and the two skewness parameters. Numerical examination of the shift of the maximum and the width of the distribution for different times show that these quantities follow a scaling relation in time. We also observe in these examples so called counter-gradient transport for the function u. Furthermore, a drift of the maximum concentration is observed.