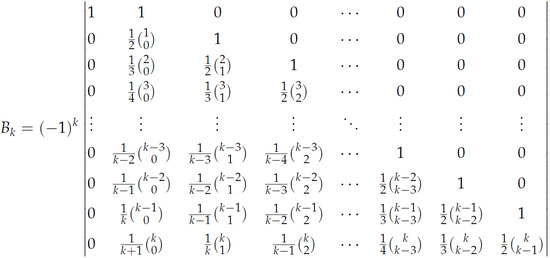Some Determinantal Expressions and Recurrence Relations of the Bernoulli Polynomials
Abstract
:1. Introduction and Main Results
2. Lemmas
3. Proofs of Theorem 1 and Corollary 1
4. Remarks
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Booth, R.; Nguyen, H.D. Bernoulli polynomials and Pascal’s square. Fibonacci Quart 2008, 46, 38–47. [Google Scholar]
- Costabile, F.; Dell’Accio, F.; Gualtieri, M.I. A new approach to Bernoulli polynomials. Rend. Mat. Appl. 2006, 26, 1–12. [Google Scholar]
- Turnbull, H.W. The Theory of Determinants, Matrices, and Invariants, 3rd ed.; Dover Publications: New York, NY, USA, 1960. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers, 2nd ed.; McGraw-Hill Book Co.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1968. [Google Scholar]
- Malenfant, J. Finite, closed-form expressions for the partition function and for Euler, Bernoulli, and Stirling numbers. 2011. Available online: https://arxiv.org/abs/1103.1585 (accessed on 8 March 2011).
- Van Malderen, R. Non-recursive expressions for even-index Bernoulli numbers: A remarkable sequence of determinants. arXiv.org e-Print archive. 2005. Available online: https://arxiv.org/abs/math/0505437 (accessed on 20 May 2005).
- Chen, K.-W. Inversion of generating functions using determinants. J. Integer Seq. 2007, 10. Article 07.10.5. [Google Scholar]
- Chen, H.-W. Bernoulli numbers via determinants. Int. J. Math. Ed. Sci. Technol. 2003, 34, 291–297. [Google Scholar] [CrossRef]
- Qi, F.; Chapman, R.J. Two closed forms for the Bernoulli polynomials. J. Number Theory 2016, 159, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Bourbaki, N. Elementary Theory. In Elements of Mathematics Functions of a Real Variable; Springer: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Cahill, N.D.; D’Errico, J.R.; Narayan, D.A.; Narayan, J.Y. Fibonacci determinants. Coll. Math. J. 2002, 3, 221–225. [Google Scholar] [CrossRef]
- Qi, F.; Zhao, J.-L.; Guo, B.-N. Closed forms for derangement numbers in terms of the Hessenberg determinants. Preprints 2016. [Google Scholar] [CrossRef]
- Temme, N.M. Special Functions: An Introduction to Classical Functions of Mathematical Physics; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Costabile, F.A.; Longo, E. A determinantal approach to Appell polynomials. J. Comput. Appl. Math. 2010, 234, 1528–1542. [Google Scholar] [CrossRef]
- Qi, F.; Guo, B.-N. A determinantal expression and a recurrence relation for the Euler polynomials. Preprints 2016. [Google Scholar] [CrossRef]
- Hu, S.; Kim, M.-S. Two closed forms for the Apostol-Bernoulli polynomials. arXiv.org e-Print archive. 2015. Available online: https://arxiv.org/abs/1509.04190 (accessed on 14 September 2015).
- Qi, F. Derivatives of tangent function and tangent numbers. Appl. Math. Comput. 2015, 268, 844–858. [Google Scholar] [CrossRef]
- Qi, F. Two Nice Determinantal Expressions for the Apostol-Bernoulli Polynomials. Available online: http://dx.doi.org/10.13140/RG.2.2.33797.76004 (accessed on 22 November 2016).
- Qi, F.; Čerňanová, V.; Semenov, Y.S. On Tridiagonal Determinants and the Cauchy Product of Central Delannoy Numbers. Available online: http://dx.doi.org/10.13140/RG.2.1.3772.6967 (accessed on 22 November 2016).
- Qi, F.; Guo, B.-N. Explicit and recursive formulas, integral representations, and properties of the large Schröder numbers. Kragujev. J. Math. 2017, 41, 121–141. [Google Scholar]
- Qi, F.; Guo, B.-N. Expressing the generalized Fibonacci polynomials in terms of a tridiagonal determinant. Matematiche 2016, in press. [Google Scholar]
- Qi, F.; Mahmoud, M.; Shi, X.-T.; Liu, F.-F. Some properties of the Catalan–Qi function related to the Catalan numbers. SpringerPlus 2016. [Google Scholar] [CrossRef] [PubMed]
- Qi, F.; Shi, X.-T.; Guo, B.-N. Two explicit formulas of the Schröder numbers. Integers 2016, 16, A23. [Google Scholar]
- Qi, F.; Shi, X.-T.; Liu, F.-F.; Kruchinin, D.V. Several formulas for special values of the Bell polynomials of the second kind and applications. J. Appl. Anal. Comput. 2017, in press. [Google Scholar] [CrossRef]
- Qi, F.; Wang, J.-L.; Guo, B.-N. A recovery of two determinantal representations for derangement numbers. Cogent Math. 2016. [Google Scholar] [CrossRef]
- Wei, C.-F.; Qi, F. Several closed expressions for the Euler numbers. J. Inequal. Appl. 2015. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, F.; Guo, B.-N. Some Determinantal Expressions and Recurrence Relations of the Bernoulli Polynomials. Mathematics 2016, 4, 65. https://doi.org/10.3390/math4040065
Qi F, Guo B-N. Some Determinantal Expressions and Recurrence Relations of the Bernoulli Polynomials. Mathematics. 2016; 4(4):65. https://doi.org/10.3390/math4040065
Chicago/Turabian StyleQi, Feng, and Bai-Ni Guo. 2016. "Some Determinantal Expressions and Recurrence Relations of the Bernoulli Polynomials" Mathematics 4, no. 4: 65. https://doi.org/10.3390/math4040065
APA StyleQi, F., & Guo, B.-N. (2016). Some Determinantal Expressions and Recurrence Relations of the Bernoulli Polynomials. Mathematics, 4(4), 65. https://doi.org/10.3390/math4040065