Interval Type 2 Fuzzy Set in Fuzzy Shortest Path Problem
Abstract
:1. Introduction
- (i)
- (ii)
- Measurements that activate a type-1 fuzzy logic system may be noisy and therefore uncertain.
- (iii)
- Information, i.e., data varies with time due to the new construction and repair of damaged roads and bridges.
2. Preliminaries
| Algorithm 1 Pseudocode for computing left switch point L and . | |
| 1: | Initialize |
| where
| |
| 2: | do |
| 3: | Set = |
| 4: | Find k (1 ≤k ≤ ) such that ≤ ≤ |
| 5: | for i=1 to N do |
| 6: | if then |
| 7: | = |
| 8: | else |
| 9: | = |
| 10: | end if |
| 11: | end for |
| 12: | Compute |
| 13: | while ( is not equal to ) |
| 14: | = (= ) and L=k |
| 15: | Print the value of and L and terminate |
- ≻ if and only if > .
- ≺ if and only if < .
- ∼ if and only if = .
Path Algebra
- (i)
- ⊕ is associative: ∀ a, b, c ∈ E, a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c
- (ii)
- ∀ a ∈ E, a ⊕ ϵ = ϵ ⊕ a = a.
- (i)
- is a commutative monod with zero element ϵ.
- (ii)
- is a monod with unit element e.
- (iii)
- ⊗ is a right and left distributive with respect to ⊕.
- (iv)
- ϵ is absorbing, i.e., ϵ ⊗ a = a ⊗ ϵ = ϵ ()
- 1.
- is a diod.
- 2.
- The operator ⊕ is idempotent, i.e., ∀ a ∈ L, a ⊕ a = a.
3. Proposed Dijkstra’s Algorithm for IT2FSPP
| Algorithm 2 Pseudocode of the proposed algorithm. | ||
| 1: | rank[s] ← 0 | |
| 2: | dist[s] ← null | ▷ Corresponding IT2FS is empty |
| 3: | add s to Q | |
| 4: | for each vertex i (except the s) in the fuzzy graph do | |
| 5: | rank[i] ← INFINITY | |
| 6: | add i to Q | ▷ Initialize Q with all the nodes of the graph |
| 7: | end for | |
| 8: | ||
| 9: | while (u is not the the destination node d) do | ▷ Shortest path from s to d |
| 10: | remove the node u from Q | |
| 11: | for every node v adjacent to u do | |
| 12: | temp_dist ← dist ⊕ arc_length() | ▷ as described in (6) |
| 13: | temp_rank ← centroid_rank (temp_dist) | |
| 14: | if (temp_rank < rank[v]) then | |
| 15: | dist ← temp_dist | |
| 16: | rank[v] ← temp_rank[v] | |
| 17: | previous[v]←u | |
| 18: | end if | |
| 19: | end for | |
| 20: | vertex in Q with the smallest rank value | |
| 21: | end while | |
| 22: | The IT2FS is an IT2FS and it represents length of the shortest path. | |
| Algorithm 3 Pseudocode of the generalized algorithm for the proposed modification. | ||
| 1: | ← e | |
| 2: | add s to Q | |
| 3: | for each vertex i (except s) in G do | |
| 4: | ← ϵ | ▷ϵ is the highest IT2FS. |
| 5: | add i to Q | |
| 6: | end for | |
| 7: | s | |
| 8: | while (u is not the destination node d) do | |
| 9: | for all v ∈ { ∩ Q} do | ▷ is the set of all nodes connected to u through an arc. |
| 10: | ← (, (, arc_length)) | ▷ Choose a node v for which is minimum. |
| 11: | end for | |
| 12: | previous[v]←u | |
| 13: | Q ← Q \ {u} | |
| 14: | Find u, u ∈ Q such that is minimum among all s, i ∈ Q. | ▷ Using the natural order in the monod |
| 15: | end while | |
| 16: | gives the shortest path length from s to d. | |
4. Numerical Examples
4.1. Example 1
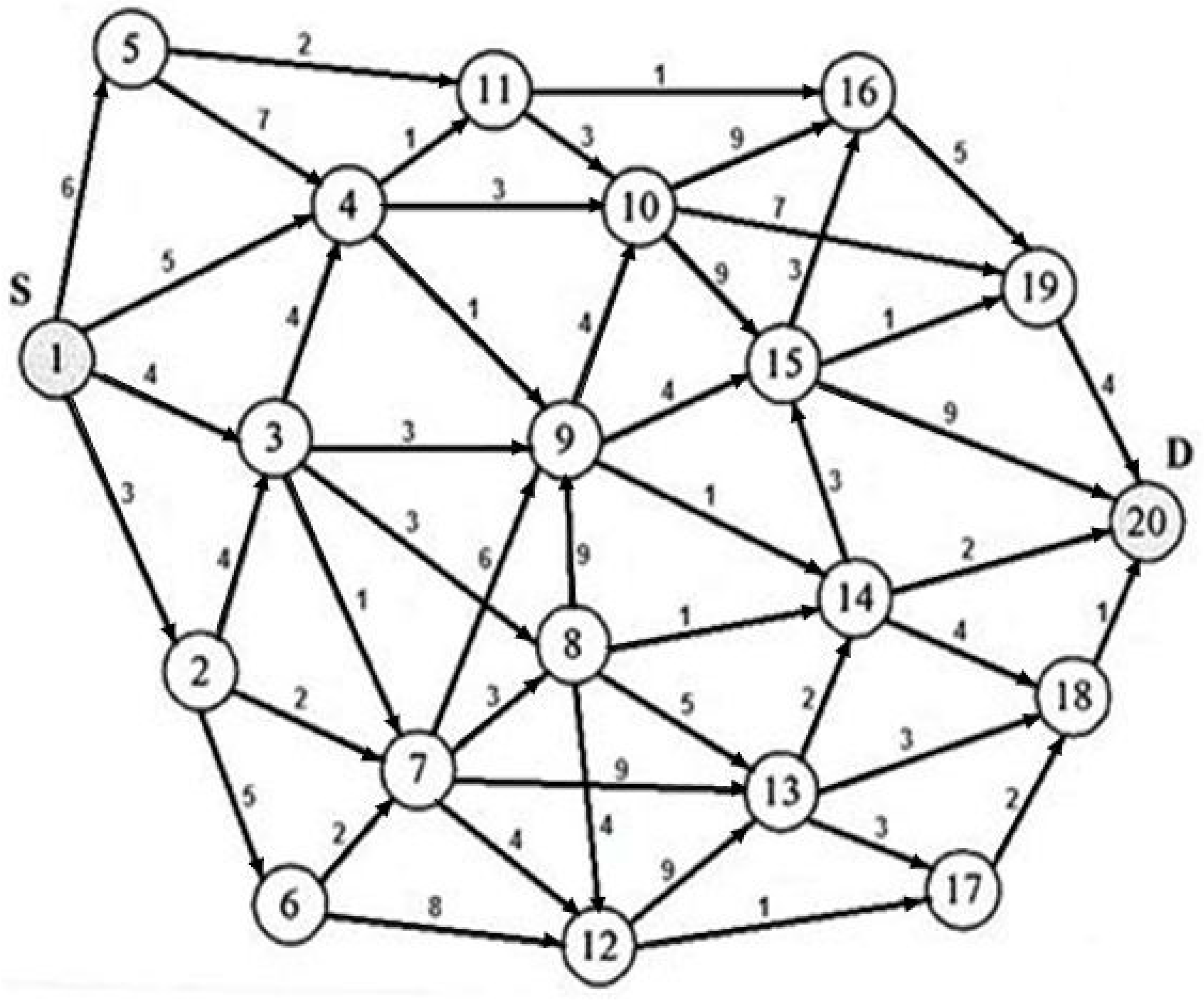
4.2. Example 2
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- (1)
- ∀ a, b, c ∈ p, ( (a, b), c) = ( (, ), ), i.e., operator is associate.Proof: As is the centroid based ranking value of a and ranking value is always a real number. So, ( (a, b), c) = (, , )Thus = (, , )It proves operator is associate.
- (2)
- ∈ p, (a, ϵ) = min(ϵ, a) = a.Proof: =ϵ being the largest IT2FS, = ∞.= aFor the same reason = a.
- (3)
- The centroid based ranking value of IT2FSs are non negative real numbers. So,∀ a,b ∈ p, (a, b) = (, ) = = .It proves that is commutative monod.
- (1)
- ∀ a, b, c ∈ p, ((a,b), c) = (a, b, c) defined in (6).Now, (a, (b,c)) =It proves that operator is associate.
- (2)
- Let . As e = (( 0, 0, 0, 0; 1, 1 ), ( 0, 0, 0, 0; 1, 1)), following the addition operation defined in (6).Similarly, = a.It proves that ∀ a ∈ p, (a e) = (e, a) = a.
- Let .
- As , following the addition operation defined in (6), we can get ∀a ∈ p, (ϵ, a) = (a ,ϵ) = ϵ. It proves that ϵ is absorbing.
- The monod is canonically ordered as the binary relation ≤ on p is antisymmetric relation, i.e., ≤ and ≤ ⇒ = . So, a and b are equal. So, the monod is canonically ordered. A semiring such that is canonically ordered is called a diod. So, L is a diod.
- The operator is idempotent because ∀ a ∈ p, (a, a) = (, ) = a.
References
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Dubois, D.; Parde, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: NewYork, NY, USA, 1980; Volume 144. [Google Scholar]
- Klein, C.M. Fuzzy shortest paths. Fuzzy Sets Syst. 1991, 39, 27–41. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Mahdavi, I.; Mahdavi-Amiri, N.; Tajdin, A. A genetic algorithm for solving fuzzy shortest path problems with mixed fuzzy arc lengths. Math. Comput. Model. 2013, 57, 84–99. [Google Scholar] [CrossRef]
- Chanas, S.; Kamburowski, J. The Fuzzy Shortest Route Problem. In Interval and Fuzzy Mathematics; Proceeding Polish Symposium; Technical University of Poznan: Poznan, Poland, 1983; pp. 35–41. [Google Scholar]
- Blue, M.; Bush, B.; Puckett, J. Unified approach to fuzzy graph problems. Fuzzy Sets Syst. 2002, 125, 355–368. [Google Scholar] [CrossRef]
- Okada, S. Fuzzy shortest path problems incorporating interactivity among paths. Fuzzy Sets Syst. 2004, 142, 335–357. [Google Scholar] [CrossRef]
- Takahashi, M.; Yamakami, A. On Fuzzy Shortest Path Problems with Fuzzy Parameters: An Algorithmic Approach. In Proceedings of the Annual Meeting of the North American Fuzzy Information Processing Society, NAFIPS 2005, Detroit, MI, USA, 26–28 June 2005; pp. 654–657.
- Mahdavi, I.; Nourifar, R.; Heidarzade, A.; Amiri, N.M. A dynamic programming approach for finding shortest chains in a fuzzy network. Appl. Soft Comput. 2009, 9, 503–511. [Google Scholar] [CrossRef]
- Yager, R.R. Paths of least resistance in possibilistic production systems. Fuzzy Sets Syst. 1986, 19, 121–132. [Google Scholar] [CrossRef]
- Lin, K.C.; Chern, M.S. The fuzzy shortest path problem and its most vital arcs. Fuzzy Sets Syst. 1993, 58, 343–353. [Google Scholar] [CrossRef]
- Okada, S.; Soper, T. A shortest path problem on a network with fuzzy arc lengths. Fuzzy Sets Syst. 2000, 109, 129–140. [Google Scholar] [CrossRef]
- Nayeem, S.M.A.; Pal, M. Shortest path problem on a network with imprecise edge weight. Fuzzy Optim. Decis. Mak. 2005, 4, 293–312. [Google Scholar] [CrossRef]
- Moazeni, S. Fuzzy shortest path problem with finite fuzzy quantities. Appl. Math. Comput. 2006, 183, 160–169. [Google Scholar] [CrossRef]
- Hernandes, F.; Lamata, M.T.; Verdegay, J.L.; Yamakami, A. The shortest path problem on networks with fuzzy parameters. Fuzzy Sets Syst. 2007, 158, 1561–1570. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Hansen, P. Bicriterion Path Problems. In Multiple Criteria Decision Making Theory and Application; Springer: Berlin/Heidelberg, Germany, 1980; pp. 109–127. [Google Scholar]
- Sengupta, A.; Pal, T.K. On comparing interval numbers. Eur. J. Operat. Res. 2000, 127, 28–43. [Google Scholar] [CrossRef]
- Min, F.; Xu, J. Semi-greedy heuristics for feature selection with test cost constraints. Granul. Comput. 2016, 1, 199–211. [Google Scholar] [CrossRef]
- Maciel, L.; Ballini, R.; Gomide, F. Evolving granular analytics for interval time series forecasting. Granul. Comput. 2016. [Google Scholar] [CrossRef]
- Song, M.; Wang, Y. A study of granular computing in the agenda of growth of artificial neural networks. Granul. Comput. 2016. [Google Scholar] [CrossRef]
- Liu, H.; Gegov, A.; Cocea, M. Rule-based systems: A granular computing perspective. Granul. Comput. 2016. [Google Scholar] [CrossRef] [Green Version]
- Lingras, P.; Haider, F.; Triff, M. Granular meta-clustering based on hierarchical, network, and temporal connections. Granul. Comput. 2016, 1, 71–92. [Google Scholar] [CrossRef]
- Skowron, A.; Jankowski, A.; Dutta, S. Interactive granular computing. Granul. Comput. 2016, 1, 95–113. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Bridging gaps between several forms of granular computing. Granul. Comput. 2016, 1, 115–126. [Google Scholar] [CrossRef]
- Apolloni, B.; Bassis, S.; Rota, J.; Galliani, G.L.; Gioia, M.; Ferrari, L. A neurofuzzy algorithm for learning from complex granules. Granul. Comput. 2016. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inform. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Dereli, T.; Altun, K. Technology evaluation through the use of interval type-2 fuzzy sets and systems. Comput. Ind. Eng. 2013, 65, 624–633. [Google Scholar] [CrossRef]
- Chen, S.M.; Yang, M.W.; Yang, S.W.; Sheu, T.W.; Liau, C.J. Multicriteria fuzzy decision making based on interval-valued intuitionistic fuzzy sets. Expert Syst. Appl. 2012, 39, 12085–12091. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Qin, Y. Multi-attribute group decision making models under interval type-2 fuzzy environment. Knowl.-Based Syst. 2012, 30, 121–128. [Google Scholar] [CrossRef]
- Chen, T.Y. A linear assignment method for multiple-criteria decision analysis with interval type-2 fuzzy sets. Appl. Soft Comput. 2013, 13, 2735–2748. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.; Liu, F. Interval type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Mendel, J.M. A comparison of three approaches for estimating (synthesizing) an interval type-2 fuzzy set model of a linguistic term for computing with words. Granul. Comput. 2016, 1, 59–69. [Google Scholar] [CrossRef]
- Wilke, G.; Portmann, E. Granular computing as a basis of human–data interaction: A cognitive cities use case. Granul. Comput. 2016, 1, 181–197. [Google Scholar] [CrossRef]
- Loia, V.; D’Aniello, G.; Gaeta, A.; Orciuoli, F. Enforcing situation awareness with granular computing: A systematic overview and new perspectives. Granul. Comput. 2016, 1, 127–143. [Google Scholar] [CrossRef]
- Yao, Y. A triarchic theory of granular computing. Granul. Comput. 2016, 1, 145–157. [Google Scholar] [CrossRef]
- Ciucci, D. Orthopairs and granular computing. Granul. Comput. 2016, 1, 159–170. [Google Scholar] [CrossRef]
- Kreinovich, V. Solving equations (and systems of equations) under uncertainty: How different practical problems lead to different mathematical and computational formulations. Granul. Comput. 2016, 1, 171–179. [Google Scholar] [CrossRef]
- Ciesa, M.; Grigolato, S.; Cavalli, R. Analysis on vehicle and walking speeds of search and rescue ground crews in mountainous areas. J. Outdoor Recreat. Tour. 2014, 5, 48–57. [Google Scholar] [CrossRef]
- Chiou, C.R.; Tsai, W.L.; Leung, Y.F. A GIS-dynamic segmentation approach to planning travel routes on forest trail networks in Central Taiwan. Landsc. Urban Plan. 2010, 97, 221–228. [Google Scholar] [CrossRef]
- Livi, L.; Sadeghian, A. Granular computing, computational intelligence, and the analysis of non-geometric input spaces. Granul. Comput. 2016, 1, 13–20. [Google Scholar] [CrossRef]
- Peters, G.; Weber, R. DCC: A framework for dynamic granular clustering. Granul. Comput. 2016, 1, 1–11. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M. Computing with words for hierarchical decision making applied to evaluating a weapon system. IEEE Trans. Fuzzy Syst. 2010, 18, 441–460. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Wang, J.H.; Hao, J. A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2006, 14, 435–445. [Google Scholar] [CrossRef]
- Herrera, F.; Alonso, S.; Chiclana, F.; Herrera-Viedma, E. Computing with words in decision making: Foundations, trends and prospects. Fuzzy Optim. Decis. Mak. 2009, 8, 337–364. [Google Scholar] [CrossRef]
- Yager, R.R. On the retranslation process in Zadeh’s paradigm of computing with words. IEEE Trans. Syst. Man Cybern. B Cybern. 2004, 34, 1184–1195. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wang, H. Managing multi-granularity linguistic information in qualitative group decision making: An overview. Granul. Comput. 2016, 1, 21–35. [Google Scholar] [CrossRef]
- Antonelli, M.; Ducange, P.; Lazzerini, B.; Marcelloni, F. Multi-objective evolutionary design of granular rule-based classifiers. Granul. Comput. 2016, 1, 37–58. [Google Scholar] [CrossRef]
- Chiao, K.P. Trapezoidal Interval Type-2 Fuzzy Set Extension of Analytic Hierarchy Process. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, Australia, 10-15 June 2012; pp. 1–8.
- Lee, L.W.; Chen, S.M. A New Method for Fuzzy Multiple Attributes Group Decision-Making Based on the Arithmetic Operations of Interval Type-2 Fuzzy Sets. In Proceedings of the 2008 International Conference on Machine Learning and Cybernetics, Kunming, China, 12–15 July 2008; Volume 6, pp. 3084–3089.
- Qin, J.; Liu, X. Frank aggregation operators for triangular interval type-2 fuzzy set and its application in multiple attribute group decision making. J. Appl. Math. 2014, 2014, 923213. [Google Scholar] [CrossRef]
- Anusuya, V.; Sathyaa, R. Shortest path with complement of type-2 fuzzy number. Malaya J. Mat. 2013, 1, 71–76. [Google Scholar]
- Anusuya, V.; Sathyaa, R. Type-2 fuzzy shortest path on similarity measure. Bull. Math. Stat. Res. 2014, 2, 418–422. [Google Scholar]
- Wu, D.; Mendel, J.M. A comparative study of ranking methods, similarity measures and uncertainty measures for interval type-2 fuzzy sets. Inform. Sci. 2009, 179, 1169–1192. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Control. In Fuzzy Set Theory—And Its Applications; Springer: Dordrecht, The Netherlands, 1996; pp. 203–240. [Google Scholar]
- Fortemps, P.; Roubens, M. Ranking and defuzzification methods based on area compensation. Fuzzy Sets Syst. 1996, 82, 319–330. [Google Scholar] [CrossRef]
- Van Leekwijck, W.; Kerre, E.E. Defuzzification: Criteria and classification. Fuzzy Sets Syst. 1999, 108, 159–178. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Centroid of a type-2 fuzzy set. Inform. Sci. 2001, 132, 195–220. [Google Scholar] [CrossRef]
- Morales, O.S.; Devia, J.H.S.; Mendez, J.J.S. Centroid of an interval type-2 fuzzy set: Continuous vs. discrete. Ingeniería 2011, 16, 67–78. [Google Scholar]
- Wu, D.; Mendel, J.M. Uncertainty measures for interval type-2 fuzzy sets. Inform. Sci. 2007, 177, 5378–5393. [Google Scholar] [CrossRef]
- Gondran, M.; Minoux, M. Dioïds and semirings: Links to fuzzy sets and other applications. Fuzzy Sets Syst. 2007, 158, 1273–1294. [Google Scholar] [CrossRef]
- Stawiaski, J. Optimal Path: Theory and Models for Vessel Segmentation. In Proceedings of the International Symposium on Mathematical Morphology and Its Applications to Signal and Image Processing, Verbania-Intra, Italy, 6–8 July 2011; pp. 417–428.
- Mendel, J.M.; Liu, F. Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Trans. Fuzzy Syst. 2007, 15, 309–320. [Google Scholar] [CrossRef]
- Simas, T.; Rocha, L.M. Distance closures on complex networks. Netw. Sci. 2015, 3, 227–268. [Google Scholar] [CrossRef]
- Gondran, M. Algèbre linéaire et Cheminement dans un Graphe. Rech. Opérationnelle 1975, 9, 77–99. [Google Scholar]
- Gondran, M.; Minoux, M. Graphes et Algorithmes, 3rd ed.; Eyrolles: Paris, France, 1995. [Google Scholar]
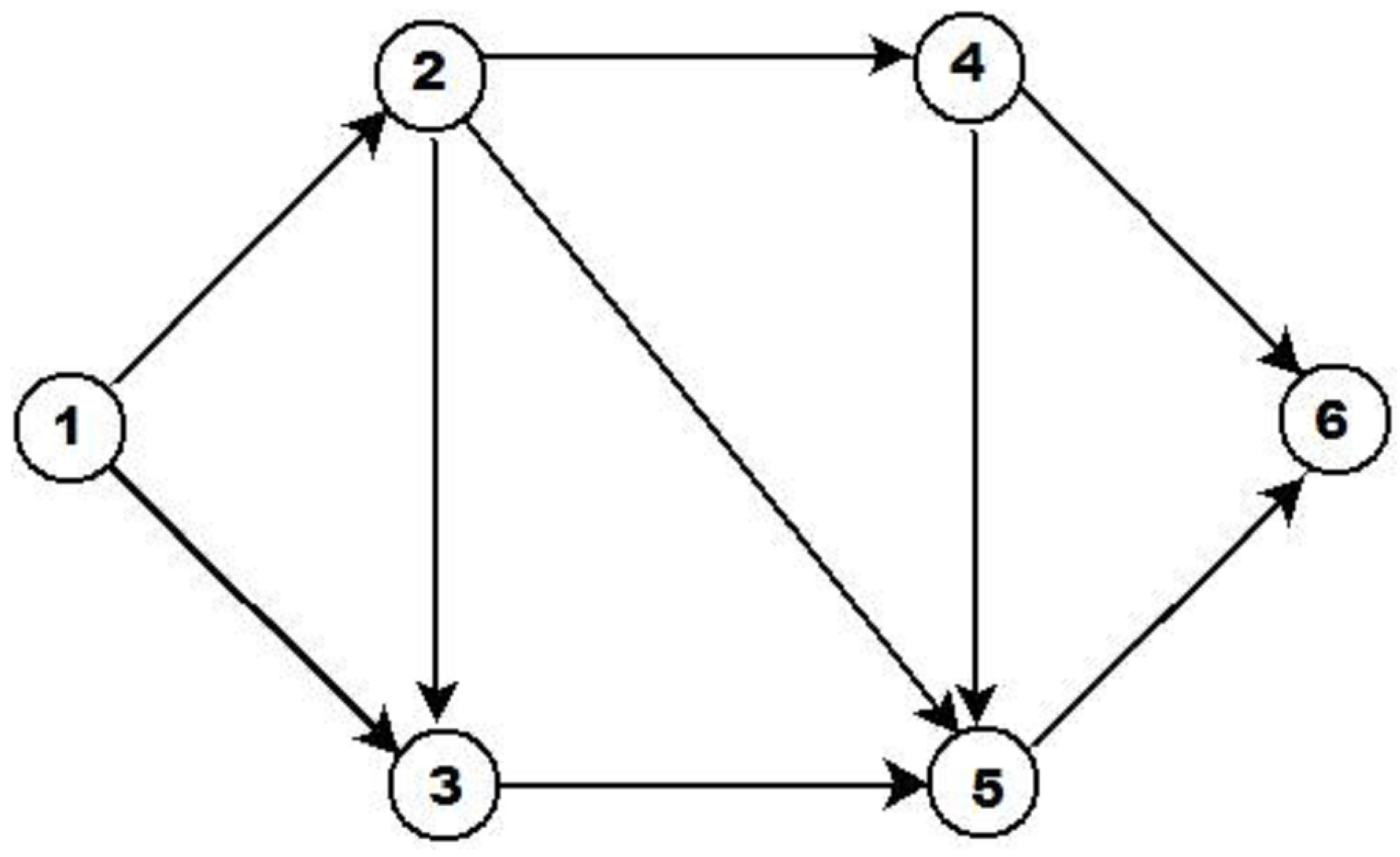
| Arc | IT2FS Representing an Arc |
|---|---|
| 1–2 | (( 5.38, 7.50, 9.00, 9.81; 1, 1 ), ( 8.29, 8.56, 8.56, 9.21; 0.38, 0.38 )) |
| 1–3 | (( 5.98, 7.75, 8.60, 9.52; 1, 1 ), ( 8.03, 8.36, 8.36, 9.17; 0.57, 0.57 )) |
| 2–3 | (( 7.37, 9.41, 10, 10; 1, 1 ), ( 8.72, 9.91, 10, 10; 1, 1 )) |
| 2–4 | (( 7.37, 9.82, 10, 10; 1, 1 ), ( 9.74, 9.98, 10, 10;1, 1 )) |
| 2–5 | (( 7.37, 9.73, 10, 10; 1, 1 ), ( 9.34, 9.95, 10, 10; 1, 1 )) |
| 3–5 | (( 7.37, 9.59, 10, 10; 1, 1 ), ( 8.95, 9.93, 10, 10;1, 1 )) |
| 4–5 | (( 7.37, 9.73, 10, 10; 1, 1 ), ( 9.34, 9.95, 10, 10; 1, 1 )) |
| 4–6 | (( 7.37, 9.82, 10, 10; 1, 1 ), ( 9.37, 9.95, 10, 10; 1, 1 )) |
| 5–6 | (( 8.68, 9.91, 10, 10; 1, 1 ), ( 9.61, 9.97, 10, 10; 1, 1 )) |
| Step | S | Q |
|---|---|---|
| S = | ||
| = 0.0 | ||
| = ∞ | ||
| = ∞ | ||
| 1 | = ∞ | |
| = ∞ | ||
| = ∞ | ||
| Select the node 1 corresponding to the | ||
| lowest value of rank 0 and remove it from Q. | ||
| S = | ||
| = 0.0 | = 7.90 | |
| Adjacent nodes of 1 = {2,3} | = 8.12 | |
| 2 | = 1 | = ∞ |
| = 1 | = ∞ | |
| = ∞ | ||
| Select the node 2 corresponding to the | ||
| lowest value of rank 7.9 and remove it from Q. | ||
| S = | ||
| = 0.0 | = 8.12 | |
| = 7.9 | = 17.21 | |
| 3 | Adjacent nodes of 2 = {3,4,5} | = 17.46 |
| = 1 | = ∞ | |
| = 1 | Select the node 3 corresponding to the | |
| = 2 | lowest value of rank 8.12 and remove it from Q. | |
| = 2 | ||
| S = | ||
| = 0.0 | = 17.21 | |
| = 7.90 | = 17.46 | |
| = 8.12 | = ∞ | |
| 4 | Adjacent node of 3 = {5} | Select the node 4 corresponding to the |
| = 1 | lowest value of rank 17.21 and remove it from Q. | |
| = 1 | ||
| = 2 | ||
| = 2 | ||
| S = | ||
| = 0.0 | = 17.46 | |
| = 7.90 | = 26.49 | |
| = 8.12 | Select the node 5 corresponding to the | |
| = 17.21 | lowest value of rank 17.46 and remove it from Q. | |
| 5 | Adjacent nodes of 4 = {5,6} | |
| = 1 | ||
| = 1 | ||
| = 2 | ||
| = 2 | ||
| = 4 | ||
| S = | ||
| = 0.0 | = 26.49 | |
| = 7.90 | Select the node 6 which is the destination node. | |
| = 8.12 | ||
| = 17.21 | is the length of the | |
| 6 | = 17.46 | shortest path from source node 1 to destination node 6. |
| Adjacent node of 5 = {6} | ||
| = 1 | = 4, = 2, = 1. | |
| = 1 | So, the shortest path from source node 1 to | |
| = 2 | destination node 6 is | |
| = 2 | ||
| = 4 |
| Index | IT2FSs |
|---|---|
| 1 | ((0, 0, 0.14, 1.97; 1, 1) ( 0, 0, 0.05, 0.66; 1, 1)) |
| 2 | ((0, 0, 0.14, 1.97; 1, 1) ( 0, 0, 0.01, 0.63; 1, 1)) |
| 3 | ((0, 0, 0.26, 2.63; 1, 1) ( 0, 0, 0.05, 0.63; 1, 1)) |
| 4 | ((0, 0, 0.36, 2.63; 1, 1) ( 0, 0, 0.05, 0.63; 1, 1)) |
| 5 | ((0, 0, 0.64, 2.47; 1, 1) ( 0, 0, 0.10, 1.16; 1, 1)) |
| 6 | ((0, 0, 0.64, 2.63; 1, 1) ( 0, 0, 0.09, 0.99; 1, 1)) |
| 7 | ((0.59, 1.50, 2.00, 3.41; 1, 1) ( 0.79, 1.68, 1.68, 2.21; 0.74, 0.74)) |
| 8 | ((0.38, 1.50, 2.50, 4.62; 1, 1) ( 1.09, 1.83, 1.83, 2.21; 0.53, 0.53)) |
| 9 | ((0.09, 1.25, 2.50, 4.62; 1, 1) ( 1.67, 1.92, 1.92, 2.21; 0.30, 0.30)) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, A.; Pal, A.; Pal, T. Interval Type 2 Fuzzy Set in Fuzzy Shortest Path Problem. Mathematics 2016, 4, 62. https://doi.org/10.3390/math4040062
Dey A, Pal A, Pal T. Interval Type 2 Fuzzy Set in Fuzzy Shortest Path Problem. Mathematics. 2016; 4(4):62. https://doi.org/10.3390/math4040062
Chicago/Turabian StyleDey, Arindam, Anita Pal, and Tandra Pal. 2016. "Interval Type 2 Fuzzy Set in Fuzzy Shortest Path Problem" Mathematics 4, no. 4: 62. https://doi.org/10.3390/math4040062
APA StyleDey, A., Pal, A., & Pal, T. (2016). Interval Type 2 Fuzzy Set in Fuzzy Shortest Path Problem. Mathematics, 4(4), 62. https://doi.org/10.3390/math4040062





