Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations

Abstract

Fourier spectral methods for solving some linear stochastic space-fractional partial differential equations perturbed by space-time white noises in the one-dimensional case are introduced and analysed. The space-fractional derivative is defined by using the eigenvalues and eigenfunctions of the Laplacian subject to some boundary conditions. We approximate the space-time white noise by using piecewise constant functions and obtain the approximated stochastic space-fractional partial differential equations. The approximated stochastic space-fractional partial differential equations are then solved by using Fourier spectral methods. Error estimates in the $L^2$-norm are obtained, and numerical examples are given.

1. Introduction

In this paper, we will consider a Fourier spectral method for solving the following linear stochastic space fractional partial differential equation:

$$\begin{array}{c}\frac{\partial u(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}u(t,x)=\frac{{\partial }^{2}W(t,x)}{\partial t\partial x},0<t<T,0<x<1\hfill \end{array}$$

(1)

$$\begin{array}{c}u(t,0)=u(t,1)=0,0<t<T\hfill \end{array}$$

(2)

$$\begin{array}{cc}& u(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(3)

where ${(-\Delta )}^{\mathsf{\alpha }}$, $1/2<\mathsf{\alpha }\le 1$, is the fractional Laplacian and $\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}$ is the mixed second order derivative of the Brownian sheet [1]. It is well known that the Laplacian $-\Delta$ has eigenpairs $({\mathsf{\lambda }}_j,e_j)$ with ${\mathsf{\lambda }}_j=j^2{\mathsf{\pi }}^2,e_j=\sqrt{2}sinj\mathsf{\pi }x,j=1,2,3,\cdots$ subject to the homogeneous Dirichlet boundary conditions on $(0,1)$, i.e., $e_j\left(0\right)=e_j\left(1\right)=0$ and:

$$-\Delta e_j={\mathsf{\lambda }}_j{e}_j,j=1,2,3,\cdots .$$

Let $H=L^2(0,1)$ with inner product $(·,·)$ and norm $\parallel ·\parallel$. For any $r\in \mathbb{R}$, we denote:

$$H_0^r:=\left\{v:v=\sum _{j=1}^{\infty }(v,e_j)e_j,\mathrm{where}\sum _{j=1}^{\infty }{\mathsf{\lambda }}_j^r{(v,e_j)}^2<\infty \right\}$$

with norm:

$${\left|v\right|}_r={(\sum _{j=1}^{\infty }{\mathsf{\lambda }}_j^r{(v,e_j)}^2)}^{1/2}$$

Then, for any $v\in H_0^{2\mathsf{\alpha }}(0,1),1/2<\mathsf{\alpha }\le 1$, we have:

$${(-\Delta )}^{\mathsf{\alpha }}v=\sum _{j=1}^{\infty }(v,e_j){\mathsf{\lambda }}_j^{\mathsf{\alpha }}{e}_j$$

(4)

Space-fractional partial differential equations are widely used to model complex phenomena, for example quasi-geostrophic flows, fast rotating fluids, the dynamics of the frontogenesis in meteorology, diffusion in a fractal or disordered medium, pollution problems, mathematical finance and the transport problems; see, e.g., [2,3,4,5,6].

Let us here consider two examples, which apply the fractional Laplacian in the physical models. The first example is the surface quasi-geostrophic (SQG) equation,

$${\partial }_t\mathsf{\theta }+\overrightarrow{u}·\nabla \mathsf{\theta }+\mathsf{\kappa }{(-\Delta )}^{\mathsf{\alpha }}\mathsf{\theta }=0$$

where $\mathsf{\kappa }\ge 0$ and $\mathsf{\alpha }>0$, $\mathsf{\theta }=\mathsf{\theta }(x_1,x_2,t)$ denotes the potential temperature, $\overrightarrow{u}=(u_1,u_2)$ is the velocity field determined by $\mathsf{\theta }$. When $\mathsf{\kappa }>0$, the SQG equation takes into account the dissipation generated by a fractional Laplacian. The SQG equation with $\mathsf{\kappa }>0$ and $\mathsf{\alpha }=1/2$ arises in geophysical studies of strongly-rotating fluids. For the dissipative SQG equation, $\mathsf{\alpha }=1/2$ appears to be a critical index. In the subcritical case when $\mathsf{\alpha }>1/2$, the dissipation is sufficient to control the nonlinearity, and the global regularity is a consequence of a global a priori bound. In the critical case when $\mathsf{\alpha }=1/2$, the global regularity issue is more delicate. There are few theoretical results for the supercritical case $\mathsf{\alpha }<1/2$ in the literature [7].

The second example is about the wave propagation in complex solids, especially viscoelastic materials (for example, polymers) [8]. In this case, the relaxation function has the form $k\left(t\right)=c{t}^{-\nu }$, $0<\nu <1,c\in \mathbb{R}$, instead of the exponential form known in the standard models. This polynomial relaxation is due to the non-uniformity of the material. The far field is then described by a Burgers equation with the leading operator ${(-\Delta )}^{\frac{1+\nu }{2}}$ instead of the Laplacian:

$${\partial }_{t}u=-{(-\Delta )}^{\frac{1+\nu }{2}}u+{\partial }_x\left(u^2\right)$$

This equation also describes the far-field evolution of acoustic waves propagating in a gas-filled tube with a boundary layer.

Frequently, the initial value or the coefficients of the equation are random; therefore, it is natural to consider the stochastic space-fractional partial differential equations. The existence, uniqueness and regularities of the solutions of stochastic space-fractional partial differential equations have been extensively studied; see, for example, [3,4,9,10]. In this work, we will focus on the case $1/2<\mathsf{\alpha }\le 1$, since the existence, uniqueness and regularity of the solution in this case is well understood in the literature; see [11] (Theorem 1.3). However, the numerical methods for solving space-fractional stochastic partial differential equations are quite restricted even for the case $1/2<\mathsf{\alpha }\le 1$. Debbi and Dozzi [11] introduced a discretization of the fractional Laplacian and used it to obtain an approximation scheme for the fractional heat equation perturbed by a multiplicative cylindrical white noise. As far as we know, [11] is the only existing paper in the literature that deals with this kind of numerical approach for such a problem. In this work, we will use the ideas developed in [12] to consider the numerical methods for solving stochastic space-fractional partial differential equations; see also [13,14,15,16]. We first approximate the space-time white noise by using piecewise constant functions and then obtain the approximate solution $\widehat{u}\left(t\right)$ of the exact solution $u\left(t\right)$. Finally, we provide error estimates in the $L^2$-norm for $u\left(t\right)-\widehat{u}\left(t\right)$.

For the deterministic space-fractional partial differential equations, many numerical methods are available in the literature. There are two ways to define the fractional Laplacian. One way of defining ${(-\Delta )}^{\mathsf{\alpha }}v, 1/2<\mathsf{\alpha }\le 1$ is by using the eigenvalues and eigenfunctions of the Laplacian $-\Delta$ subject to the boundary conditions as in (4). Another way of defining ${(-\Delta )}^{\mathsf{\alpha }}v, 1/2<\mathsf{\alpha }\le 1$ is by using the integral for the function $\tilde{v}$, where $\tilde{v}$ is defined on the whole real line $\mathbb{R}$ and is the extension function of v:

$$\tilde{v}\left(x\right)=\left\{\begin{array}{cc}& v\left(x\right),0<x<1\hfill \\ & 0,x\notin (0,1)\hfill \end{array}\right.$$

More precisely, for $\tilde{v}\left(x\right),x\in \mathbb{R}$, we define:

$${(-\Delta )}^{\mathsf{\alpha }}\tilde{v}\left(x\right)=C_{\mathsf{\alpha }}{\int }_{\mathbb{R}-\left\{0\right\}}\frac{2\tilde{v}\left(x\right)+\tilde{v}(x+y)-\tilde{v}(x-y)}{{\left|y\right|}^{1+2\mathsf{\alpha }}}dy,x\in \mathbb{R}$$

where $C_{\mathsf{\alpha }}$ is a positive constant depending on $\mathsf{\alpha }$. We then define [17],

$${(-\Delta )}^{\mathsf{\alpha }}\tilde{v}\left(x\right)={\mathcal{F}}^{-1}\left({\left|\mathsf{\xi }\right|}^{2\mathsf{\alpha }}\left(\mathcal{F}\left(\tilde{v}\right)\right)\left(\mathsf{\xi }\right)\right),x\in \mathbb{R}$$

where $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ denote the Fourier and inverse Fourier transforms, respectively. For $v\left(x\right),x\in (0,1)$, we define the fractional Laplacian by:

$${(-\Delta )}^{\mathsf{\alpha }}v\left(x\right)={(-\Delta )}^{\mathsf{\alpha }}\tilde{v}\left(x\right)$$

It is easy to show that for some suitable functions $w\left(x\right),x\in \mathbb{R}$ [18],

$${(-\Delta )}^{\mathsf{\alpha }}w\left(x\right)={\mathcal{F}}^{-1}\left({\left|\mathsf{\xi }\right|}^{2\mathsf{\alpha }}w\left(\mathsf{\xi }\right)\right)=\frac{1}{2cos\left(\mathsf{\pi }\mathsf{\alpha }\right)}\left({}_{-\infty }^R{D}_x^{2\mathsf{\alpha }}w\left(x\right)+{}_x^R{D}_{\infty }^{2\mathsf{\alpha }}w\left(x\right)\right)$$

where ${}_{-\infty }^R{D}_x^{\mathsf{\beta }}w\left(x\right)$ and ${}_x^R{D}_{\infty }^{\mathsf{\beta }}w\left(x\right),1<\mathsf{\beta }<2$ are called Riemann–Liouville fractional derivatives defined by:

$$\begin{array}{c}{}_{-\infty }^R{D}_x^{\mathsf{\beta }}w\left(x\right)=\frac{1}{\Gamma (2-\mathsf{\beta })}\frac{d^2}{d{x}^2}{\int }_{-\infty }^x{(x-y)}^{1-\mathsf{\beta }}w\left(y\right)dy\hfill \\ {}_x^R{D}_{\infty }^{\mathsf{\beta }}w\left(x\right)=\frac{1}{\Gamma (2-\mathsf{\beta })}\frac{d^2}{d{x}^2}{\int }_x^{\infty }{(y-x)}^{1-\mathsf{\beta }}w\left(y\right)dy\hfill \end{array}$$

Hence, for the function $v\left(x\right)$ defined on the bounded interval $(0,1)$, we have:

$${(-\Delta )}^{\mathsf{\alpha }}v\left(x\right)=\frac{1}{2cos\left(\mathsf{\pi }\mathsf{\alpha }\right)}\left({}_0^R{D}_x^{2\mathsf{\alpha }}v\left(x\right)+{}_x^R{D}_1^{2\mathsf{\alpha }}v\left(x\right)\right),x\in (0,1)$$

(5)

which is also called the Riesz fractional derivative.

We note that Definitions (4) and (5) are not equivalent [17]. For the deterministic space-fractional partial differential equations where the space-fractional derivative is defined by (5), or the Riemann-Liouville space-fractional derivative, or the Caputo space-fractional derivative, many numerical methods are available, for example, finite difference methods [18,19,20,21,22,23,24,25,26,27,28,29,30], finite element methods [14,31,32,33,34,35,36,37,38,39,40] and spectral methods [41,42]. For the deterministic space-fractional partial differential equations where the space-fractional derivative is defined by (4), some numerical methods are also available, for example the matrix transfer method (MTT) [21,22,43] and the Fourier spectral method [44]. In this work, we will use Fourier spectral methods to solve the approximated stochastic space-fractional partial differential equations. The main advantage of this approach is that it gives a full diagonal representation of the fractional operator, being able to achieve spectral convergence regardless of the fractional power in the problem. Let $0=x_0<x_1<x_2<\cdots <x_J=1$ be the space partition of $(0,1)$ and h the space step size. Let $0=t_0<t_1<t_2<\cdots <t_N=T$ be the time partition of $(0,T)$ and k the time step size. To find the approximate solution of (1)–(3), we first approximate the space-time white noise $\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}$ by using a piecewise constant function $\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$ defined by, with $n=1,2,3,...,N,j=1,2,...,J$ [12],

$$\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}:=\frac{{\mathsf{\eta }}_{nj}}{\sqrt{kh}},t_{n-1}\le t\le t_n,x_{j-1}\le x\le x_j$$

(6)

where ${\mathsf{\eta }}_{nj}\in \mathcal{N}(0,1)$ is an independently and identically distributed random variable and:

$${\eta }_{nj}=\frac{1}{\sqrt{kh}}{\int }_{t_{n-1}}^{t_n}{\int }_{x_{j-1}}^{x_j}dW(t,x)$$

Hence:

$$\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}=\frac{1}{kh}{\int }_{t_{n-1}}^{t_n}{\int }_{x_{j-1}}^{x_j}dW(t,x),\mathrm{on}[t_{n-1},t_n]\times [x_{j-1},x_j]$$

(7)

We also note that [12]:

$${\int }_{t_{n-1}}^{t_n}{\int }_{x_{j-1}}^{x_j}d\widehat{W}(t,x)={\int }_{t_{n-1}}^{t_n}{\int }_{x_{j-1}}^{x_j}\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}dxdt$$

The solution $u(t,x)$ of (1)–(3) can then be approximated by $\widehat{u}(t,x)$, which solves the following:

$$\begin{array}{c}\frac{\partial \widehat{u}(t,x)}{\partial t}+{(-\Delta )}^{\alpha }\widehat{u}(t,x)=\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x},0<t<T,0<x<1\hfill \end{array}$$

(8)

$$\begin{array}{c}\widehat{u}(t,0)=\widehat{u}(t,1)=0,0<t<T\hfill \end{array}$$

(9)

$$\begin{array}{c}\widehat{u}(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(10)

Note that $\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$ is a function in $L^2((0,T)\times (0,1))$, and therefore, we can solve (8)–(10) by using any appropriate numerical method for deterministic space-fractional partial differential equations. In Theorem 2, we prove that, if $1/2<\mathsf{\alpha }\le 1$, then:

$$\mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-\widehat{u}(t,x)\right)}^{2}dxdt\le C(k^{1-\frac{1}{2\mathsf{\alpha }}}+h^2{k}^{\frac{2\mathsf{\alpha }-3}{2\mathsf{\alpha }}})$$

(11)

Let us now introduce the Fourier spectral method for solving (8)–(10). Let J be a positive integer, and denote:

$$S_J=\mathrm{span}\{e_1,e_2,\cdots ,e_J\}$$

Define by $P_J:H\to S_J$ the projection from H to $S_J$,

$$P_{J}v:=\sum _{j=1}^J(v,e_j)e_j$$

(12)

The Fourier spectral method for solving (8)–(10) is to find ${\widehat{u}}_J\left(t\right)\in S_J$, such that:

$$\begin{array}{c}\frac{\partial {\widehat{u}}_J(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}{\widehat{u}}_J(t,x)=P_J\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x},0<t<T,0<x<1\hfill \end{array}$$

(13)

$$\begin{array}{c}{\widehat{u}}_J(t,0)={\widehat{u}}_J(t,1)=0,0<t<T\hfill \end{array}$$

(14)

$$\begin{array}{c}{\widehat{u}}_J(0,x)=P_J{u}_0\left(x\right),0<x<1\hfill \end{array}$$

(15)

In Theorem 4, we prove that:

$$\parallel \widehat{u}\left(t\right)-{\widehat{u}}_J\left(t\right)\parallel \le C\parallel u_0-P_J{u}_0\parallel +C\frac{1}{{(J+1)}^{\mathsf{\alpha }}}{\left({\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}ds\right)}^{1/2},\mathrm{for}1/2<\mathsf{\alpha }\le 1$$

(16)

Combining Theorem 2 with Theorem 4, we have:

$$\begin{array}{cc}\hfill \mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-{\widehat{u}}_J(t,x)\right)}^{2}dxdt& \le C(k^{1-\frac{1}{2\mathsf{\alpha }}}+h^2{k}^{\frac{2\mathsf{\alpha }-3}{2\mathsf{\alpha }}})+C{\parallel u_0-P_J{u}_0\parallel }^2\hfill \\ & +C\frac{1}{{(J+1)}^{2\mathsf{\alpha }}}\left(k^{-1-\frac{1}{2\mathsf{\alpha }}}+k^{-1}{h}^{-1}\right)\hfill \end{array}$$

The paper is organized as follows. In Section 2, we consider the approximation of space-time white noise. In Section 3, we consider a Fourier spectral method for deterministic space-fractional partial differential equations, and the error estimates are proven. In Section 4, we provider a numerical example.

2. Approximate White Noise and Regularity

Consider the stochastic space-fractional partial differential equation:

$$\begin{array}{c}\frac{\partial u(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}u(t,x)=f(t,x),0<t<T,0<x<1\hfill \end{array}$$

(17)

$$\begin{array}{c}u(t,0)=u(t,1)=0,0<t<T\hfill \end{array}$$

(18)

$$\begin{array}{c}u(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(19)

where $f(t,x)=\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}$ denotes the mixed second order derivative of the Brownian sheet [12]. There is no strong solution of (17)–(19) since $f(t,x)=\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}\notin L^2((0,T)\times (0,1))$.

The mild solution of (17)–(19) has the following form, for example [9,10],

$$u(t,x)={\int }_0^1{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy+{\int }_0^t{\int }_0^1{G}_{\mathsf{\alpha }}(t-s,x,y)dW(s,y)$$

(20)

where:

$$G_{\mathsf{\alpha }}(t,x,y)=\sum _{j=1}^{\infty }{e}^{-{\mathsf{\lambda }}_j^{\mathsf{\alpha }}t}{e}_j\left(x\right)e_j\left(y\right)$$

and the stochastic integral ${\int }_0^t{\int }_0^1{G}_{\mathsf{\alpha }}(t-s,x,y)dW(s,y)$ is well defined.

We have the following existence and uniqueness theorem, for example [9,10,11],

Theorem 1. 

[11] [Theorem 1.3] Let $1/2<\mathsf{\alpha }\le 1$ and $\mathsf{\beta }>0$. Let $u_0$ be a $H_0^{\mathsf{\beta }}(0,1)$-valued ${\mathcal{F}}_0$-measurable function, such that:

$$\mathbb{E}\parallel u_0{\parallel }_{H_0^{\mathsf{\beta }}(0,1)}^p<\infty$$

for some $p>\frac{4\mathsf{\alpha }}{2\mathsf{\alpha }-1}$. Then, (17)–(19) has a unique mild solution u, such that, for any $0\le \mathsf{\theta }<min\{\frac{2\mathsf{\alpha }-1}{2}-\frac{2\mathsf{\alpha }}{p},\mathsf{\beta }\}$,

$$\mathbb{E}\underset{0\le t\le T}{sup}{\parallel u\left(t\right)\parallel }_{H_0^{\mathsf{\theta }}(0,1)}^p<\infty$$

Our strategy is to approximate the solution $u(t,x)$ of (17)–(19) by $\widehat{u}(t,x)$, which satisfies the following problem:

$$\begin{array}{c}\frac{\partial \widehat{u}(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}(t,x)=\widehat{f}(t,x),0<t<T,0<x<1\hfill \end{array}$$

(21)

$$\begin{array}{c}\widehat{u}(t,0)=\widehat{u}(t,1)=0,0<t<T\hfill \end{array}$$

(22)

$$\begin{array}{c}\widehat{u}(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(23)

Here, $\widehat{f}(t,x)=\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$ is defined by (6). The solution of (21)–(23) has the form of; see, e.g., [12]:

$$\widehat{u}(t,x)={\int }_0^1{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy+{\int }_0^t{\int }_0^1{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)$$

(24)

Theorem 2. 

Let u and $\widehat{u}$ be the solutions of (17)–(19) and (21)–(23), respectively. Assume that $u_0\in H$ and $1/2<\mathsf{\alpha }\le 1$, then:

$$\mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-\widehat{u}(t,x)\right)}^{2}dxdt\le C(k^{1-\frac{1}{2\mathsf{\alpha }}}+h^2{k}^{\frac{2\mathsf{\alpha }-3}{2\mathsf{\alpha }}})$$

(25)

Proof. 

See the Appendix. ☐

Remark 1. 

When $\mathsf{\alpha }=1$, we obtain the same estimates as in [12,14], i.e.,

$$\mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-\widehat{u}(t,x)\right)}^{2}dxdt\le C(k^{\frac{1}{2}}+h^2{k}^{-\frac{1}{2}})$$

Theorem 3. 

Let $\widehat{u}$ be the solution of (21)–(23), then:

$$\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\widehat{u}}_t^2(t,x)dxdt\le C(k^{-\frac{1}{2\mathsf{\alpha }}}+h^{-1}),j\ge 0$$

(26)

and:

$$\mathbb{E}{\int }_0^1|{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}(t,x){|}^{2}dx\le C(k^{-1-\frac{1}{2\mathsf{\alpha }}}+k^{-1}{h}^{-1})$$

(27)

for any $1/2<\mathsf{\alpha }\le 1$.

Proof. 

We only prove (26). The proof of (27) is similar. Note that:

$$\begin{array}{cc}\hfill \widehat{u}(t,x)& ={\int }_0^1{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy+{\int }_0^t{\int }_0^1{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\hfill \\ & ={\int }_0^1{G}_{\alpha }(t,x,y)u_0\left(y\right)dy+{\int }_0^t\left[{\int }_0^1{G}_{\mathsf{\alpha }}(t-s,x,y)\frac{{\partial }^2\widehat{W}(s,y)}{\partial s\partial y}dy\right]ds\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill {\widehat{u}}_t(t,x)& ={\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy+{\int }_0^t\left[{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)\frac{{\partial }^2\widehat{W}(s,y)}{\partial s\partial y}dy\right]ds\hfill \\ & +{\int }_0^1{G}_{\mathsf{\alpha }}(0,x,y)\frac{{\partial }^2\widehat{W}(t,y)}{\partial t\partial y}dy\hfill \end{array}$$

(28)

Since $w(t,x)={\int }_0^1{G}_{\mathsf{\alpha }}(t,x,y)w_0\left(y\right)dy$ is the solution of the following equation:

$$\begin{array}{c}\frac{\partial w(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}w(t,x)=0,0<x<1,0<t<T\hfill \\ w(t,0)=w(t,1)=0,0<t<T\hfill \\ w(0,x)=w_0\left(x\right)\hfill \end{array}$$

we therefore have:

$$w_0\left(x\right)={\int }_0^1{G}_{\mathsf{\alpha }}(0,x,y)w_0\left(y\right)dy$$

Choose $w_0\left(y\right)=\frac{{\partial }^2\widehat{W}(t,y)}{\partial t\partial y}$ for fixed t; then, we have:

$${\int }_0^1{G}_{\mathsf{\alpha }}(0,x,y)\frac{{\partial }^2\widehat{W}(t,y)}{\partial t\partial y}dy=\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$$

Hence, by (28),

$$\begin{array}{cc}\hfill {\widehat{u}}_t(t,x)=& {\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy\hfill \\ & +{\int }_0^t{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)+\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}\hfill \end{array}$$

Using the inequality ${(a+b+c)}^2\le 3(a^2+b^2+c^2),\forall a,b,c\in \mathbb{R}$, we have:

$$\begin{array}{c}\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\widehat{u}}_t^2(t,x)dxdt\hfill \\ \le 3\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_0^t{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ +3\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[\frac{\partial \widehat{W}(t,x)}{\partial t\partial x}\right]}^{2}dxdt+3\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t,x,y)u_0\left(y\right)dy\right]}^{2}dxdt\hfill \\ =3(I+II+III)\hfill \end{array}$$

Now, I, by using ${(a+b)}^2\le 2(a^2+b^2),\forall a,b\in \mathbb{R}$, is written as:

$$\begin{array}{cc}\hfill I& \le 2\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_0^{t_{j-1}}{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & +2\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_{t_{j-1}}^t{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & =2(I_1+I_2)\hfill \end{array}$$

Furthermore $I_1$, with ${\mathsf{\eta }}_{kl}=\mathcal{N}(0,1),k=0,1,2,\cdots ,J-1,l=0,1,2,\cdots ,j-2,j\ge 2$, is expressed as:

$$\begin{array}{cc}\hfill I_1& =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_0^{t_{j-1}}{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}{\left[\sum _{l=0}^{j-2}{\int }_{t_l}^{t_{l+1}}\sum _{k=0}^{J-1}{\int }_{x_k}^{x_{k+1}}\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y){\mathsf{\eta }}_{kl}dyds\right]}^{2}dxdt\hfill \\ & =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}{\left[\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}\left({\int }_{t_l}^{t_{l+1}}{\int }_{x_k}^{x_{k+1}}\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)dyds\right){\eta }_{kl}\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}{\left({\int }_{t_l}^{t_{l+1}}{\int }_{x_k}^{x_{k+1}}\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)dyds\right)}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}{\left({\int }_{t_l}^{t_{l+1}}{\int }_{x_k}^{x_{k+1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}{e}^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-s)}{e}_n\left(x\right)e_n\left(y\right)dyds\right)}^{2}dxdt\hfill \\ & =C{\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}(\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\hfill \\ & e_n\left(x\right)\frac{e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_{l+1})}-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_l)}}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}{)}^{2}dxdt\hfill \end{array}$$

Note that $(e_n,e_m)={\mathsf{\delta }}_{nm},n,m=1,2,\cdots$; we have:

$$\begin{array}{cc}\hfill I_1& =C{\int }_{t_j}^{t_{j+1}}\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2{\left(\frac{e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_{l+1})}-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_l)}}{1}\right)}^{2}dt\hfill \\ & =C{\int }_{t_j}^{t_{j+1}}\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_{l+1})}{\left(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_{l+1}-t_l)}\right)}^{2}dt\hfill \\ & =C\frac{1}{kh}\sum _{l=0}^{j-2}\sum _{k=0}^{J-1}\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2\hfill \\ & \frac{e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_j-t_{l+1})}-e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_{j+1}-t_{l+1})}}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}{\left(1-e^{-{\mathsf{\lambda }}_n^{\alpha }(t_{l+1}-t_l)}\right)}^2\hfill \\ & =C\frac{1}{kh}\sum _{k=0}^{J-1}\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}\sum _{l=0}^{j-2}{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_j-t_{l+1})}\hfill \\ & =C\frac{1}{kh}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }+1}}\left(\sum _{k=0}^{J-1}{(cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k)}^2\right)\sum _{l=0}^{j-2}{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_j-t_{l+1})}\hfill \end{array}$$

Note that, since $|cos\left(n\mathsf{\pi }{x}_{k+1}\right)-cos\left(n\mathsf{\pi }{x}_k\right)|\le {\left(n\mathsf{\pi }h\right)}^2$, then:

$$\sum _{k=0}^{J-1}{(cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k)}^2\le C\sum _{k=0}^{J-1}{\left(n\mathsf{\pi }h\right)}^2=C{\mathsf{\lambda }}_{n}h$$

We have, by (68) and (67):

$$\begin{array}{cc}\hfill I_1& =C\frac{1}{kh}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }+1}}\left({\mathsf{\lambda }}_{n}h\right)\sum _{l=0}^{j-2}{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_j-t_{l+1})}\hfill \\ & =C\frac{1}{kh}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }+1}}\left({\mathsf{\lambda }}_{n}h\right)(k^{-1}{\mathsf{\lambda }}_n^{-\mathsf{\alpha }})\hfill \\ & =C{k}^{-2}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{2\mathsf{\alpha }}}\le C{k}^{-2}{k}^{\frac{4\mathsf{\alpha }-1}{2\mathsf{\alpha }}}=C{k}^{-\frac{1}{2\mathsf{\alpha }}}\hfill \end{array}$$

We remark that $I_1$ can also be estimated by using the following alternative way.

$$\begin{array}{cc}\hfill I_1& =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_0^{t_{j-1}}{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\left[{\int }_0^{t_{j-1}}{\int }_0^1{\left(\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)\right)}^{2}dyds\right]dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1{\int }_0^{t_{j-1}}{\int }_0^1{\left(\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}{e}^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-s)}{e}_n\left(x\right)e_n\left(y\right)\right)}^{2}dydsdxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^{t_{j-1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{2\mathsf{\alpha }}{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-s)}dsdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{2\mathsf{\alpha }}\frac{e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_{j-1})}-e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}t}}{2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}dt\hfill \end{array}$$

Note that $t\ge t_j$, we then have, by using (63),

$$I_1\le C{\int }_{t_j}^{t_{j+1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k}dt=Ck\sum _{n=1}^{\infty }\frac{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}{e^{2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k}}\le C{k}^{-\frac{1}{2\mathsf{\alpha }}}$$

For $I_2$, we have:

$$\begin{array}{cc}\hfill I_2& \le 2\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_{t_{j-1}}^{t_j}{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & +2\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_{t_j}^t{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & =2I_{21}+2I_{22}\hfill \end{array}$$

where $I_{21}$ can be estimated as follows:

$$\begin{array}{cc}\hfill I_{21}& =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}{\left[\sum _{k=0}^{J-1}{\int }_{t_{j-1}}^{t_j}{\int }_{x_k}^{x_{k+1}}\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y){\eta }_{kj}dyds\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{k=0}^{J-1}{\left[{\int }_{t_{j-1}}^{t_j}{\int }_{x_k}^{x_{k+1}}\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)dyds\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{k=0}^{J-1}{\left[{\int }_{t_{j-1}}^{t_j}{\int }_{x_k}^{x_{k+1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}{e}^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-s)}{e}_n\left(x\right)e_n\left(y\right)dyds\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{k=0}^{J-1}[\sum _{n=1}^{\infty }{\lambda }_n^{\mathsf{\alpha }}\frac{e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_j)}-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_{j-1})}}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}\hfill \\ & e_n\left(x\right)\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}{]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}\frac{1}{kh}\sum _{k=0}^{J-1}\left[\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2{e}^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_j)}{\left(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k}\right)}^2\right]dt\hfill \\ & =\frac{1}{kh}\sum _{k=0}^{J-1}\left[\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2\frac{e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_j-t_j)}-e^{-2{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t_{j+1}-t_j)}}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}{\left(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k}\right)}^2\right]\hfill \\ & =\frac{1}{kh}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }+1}}\left(\sum _{k=0}^{J-1}{(cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k)}^2\right)·1\hfill \\ & \le \frac{1}{kh}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }+1}}{\lambda }_{n}h=\frac{1}{k}\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}\le \frac{1}{k}\sum _{n=1}^{\infty }\frac{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}\hfill \end{array}$$

which implies, by (64):

$$I_{21}\le \frac{1}{k}{k}^{1-\frac{1}{2\mathsf{\alpha }}}=k^{-\frac{1}{2\mathsf{\alpha }}}$$

For $I_{22}$, we have:

$$\begin{array}{cc}\hfill I_{22}& =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left[{\int }_{t_j}^t{\int }_0^1\frac{\partial }{\partial t}{G}_{\mathsf{\alpha }}(t-s,x,y)d\widehat{W}(s,y)\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{k=0}^{J-1}{\left[{\int }_{t_j}^t{\int }_{x_k}^{x_{k+1}}\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}{e}^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-s)}{e}_n\left(x\right)e_n\left(y\right)dyds\right]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}{\int }_0^1\frac{1}{kh}\sum _{k=0}^{J-1}[\sum _{n=1}^{\infty }{\mathsf{\lambda }}_n^{\mathsf{\alpha }}\frac{e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t)}-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}(t-t_j)}}{{\mathsf{\lambda }}_n^{\mathsf{\alpha }}}\hfill \\ & e_n\left(x\right)\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}dyds{]}^{2}dxdt\hfill \\ & ={\int }_{t_j}^{t_{j+1}}\frac{1}{kh}\sum _{k=0}^{J-1}\left[\sum _{n=1}^{\infty }{\left(\frac{cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k}{n\mathsf{\pi }}\right)}^2{\left(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k}\right)}^2\right]dt\hfill \\ & =k\frac{1}{kh}\sum _{k=0}^{J-1}\sum _{n=1}^{\infty }{\left(cosn\mathsf{\pi }{x}_{k+1}-cosn\mathsf{\pi }{x}_k\right)}^2\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n}\hfill \end{array}$$

Moreover, applying (66) and taking into account $|cos\left(n\mathsf{\pi }{x}_{k+1}\right)-cosn\mathsf{\pi }{x}_k|\le n\mathsf{\pi }h$, we derive:

$$\begin{array}{cc}\hfill I_{22}& \le \frac{1}{h}\left(\sum _{k=0}^{J-1}{n}^2{\mathsf{\pi }}^2{h}^2\right)\sum _{n=1}^{\infty }\frac{{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2}{{\mathsf{\lambda }}_n}\hfill \\ & \le \sum _{n=1}^{\infty }{(1-e^{-{\mathsf{\lambda }}_n^{\mathsf{\alpha }}k})}^2\le C{k}^{-\frac{1}{2\mathsf{\alpha }}}\hfill \end{array}$$

(29)

For $II$ we have, with ${\mathsf{\eta }}_{kj}=\mathcal{N}(0,1)$,

$$\begin{array}{cc}\hfill II& =\mathbb{E}{\int }_{t_j}^{t_{j+1}}{\int }_0^1{\left(\frac{\partial \widehat{W}(t,x)}{\partial t\partial x}\right)}^{2}dxdt=\mathbb{E}{\int }_{t_j}^{t_{j+1}}\sum _{k=0}^{J-1}{\int }_{x_k}^{x_{k+1}}\frac{1}{kh}{\mathsf{\eta }}_{kj}^{2}dxdt\hfill \\ & =\frac{1}{kh}{\int }_{t_j}^{t_{j+1}}\sum _{k=0}^{J-1}{\int }_{x_k}^{x_{k+1}}dxdt=\frac{1}{kh}k=h^{-1}\hfill \end{array}$$

Similarly, we can estimate $III$. Together, these estimates complete the proof of Theorem 3. ☐

3. Fourier Spectral Method

In this section, we will consider a Fourier spectral method for solving the deterministic space-fractional partial differential equation:

$$\begin{array}{c}\frac{\partial \widehat{u}(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}(t,x)=\widehat{f}(t,x),0<t<T,0<x<1\hfill \end{array}$$

(30)

$$\begin{array}{c}\widehat{u}(t,0)=\widehat{u}(t,1)=0,0<t<T\hfill \end{array}$$

(31)

$$\begin{array}{c}\widehat{u}(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(32)

where $\widehat{f}(t,x)=\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$ is defined by (6) and $\widehat{f}\in L^2((0,T)\times (0,1))$.

Denote $A=-\Delta$ with $\mathcal{D}\left(A\right)=H_0^1(0,1)\cap H^2(0,1)$. For any $s>0$ and $v\in H_0^{2s}(0,1)$, we have $A^{s}v={\sum }_{j=1}^{\infty }{\mathsf{\lambda }}_j^s(v,e_j)e_j$. It is obvious that:

$${\left|v\right|}_r=\parallel A^{r/2}v\parallel ={\left(\sum _{j=1}^{\infty }{\mathsf{\lambda }}_j^r{(v,e_j)}^2\right)}^{1/2},\forall v\in H_0^r(0,1),r>0$$

Further, we denote $E_{\mathsf{\alpha }}\left(t\right)=e^{-t{A}^{\mathsf{\alpha }}},1/2<\mathsf{\alpha }\le 1$. Then, the solution of (30)–(32) can be written as the following operator form:

$$\widehat{u}\left(t\right)=E_{\mathsf{\alpha }}\left(t\right){\widehat{u}}_0+{\int }_0^t{E}_{\mathsf{\alpha }}(t-s)\widehat{f}\left(s\right)ds,{\widehat{u}}_J\left(0\right)=u_0$$

(33)

The spectral method of (30)–(32) consists of finding ${\widehat{u}}_J\left(t\right)\in S_J$, such that:

$$\begin{array}{c}\frac{\partial {\widehat{u}}_J(t,x)}{\partial t}+{(-\Delta )}^{\mathsf{\alpha }}{\widehat{u}}_J(t,x)=P_J\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x},0<t<T,0<x<1\hfill \end{array}$$

(34)

$$\begin{array}{c}{\widehat{u}}_J(t,0)={\widehat{u}}_J(t,1)=0,0<t<T\hfill \end{array}$$

(35)

$$\begin{array}{c}{\widehat{u}}_J(0,x)=P_J{u}_0\left(x\right),0<x<1\hfill \end{array}$$

(36)

where $P_J:H\to S_J$ is defined by (12).

Similarly, the solution of (34)–(36) has the form of:

$${\widehat{u}}_J\left(t\right)=E_{\mathsf{\alpha }}\left(t\right)P_J{\widehat{u}}_0+{\int }_0^t{E}_{\mathsf{\alpha }}(t-s)P_J\widehat{f}\left(s\right)ds,{\widehat{u}}_J\left(0\right)=P_J{u}_0$$

(37)

Theorem 4. 

Assume that $\widehat{u}$ and ${\widehat{u}}_J$ are the solutions of (33) and (37), respectively. Let $0\le r<1/2$, and assume that $u_0\in H_0^r(0,1)$. Then, there exists a positive constant C, such that:

$$|\widehat{u}\left(t\right)-{\widehat{u}}_J{\left(t\right)|}_r\le C{|u_0-P_J{u}_0|}_r+C\frac{1}{{(J+1)}^{\alpha (1-r/\mathsf{\alpha })}}{\left({\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}ds\right)}^{1/2}$$

(38)

In particular, we have, with $r=0$,

$$\parallel \widehat{u}\left(t\right)-{\widehat{u}}_J\left(t\right)\parallel \le C\parallel u_0-P_J{u}_0\parallel +C\frac{1}{{(J+1)}^{\mathsf{\alpha }}}{\left({\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}ds\right)}^{1/2}$$

(39)

To prove Theorem 4, we need the following smoothing property for the solution operator $E_{\alpha }\left(t\right)$.

Lemma 5. 

1.

Let $s>0$. We have:

$$\parallel A^s{E}_{\mathsf{\alpha }}\left(t\right)\parallel \le C{t}^{-\frac{s}{\mathsf{\alpha }}}{e}^{-\mathsf{\delta }t},t>0,with1/2<\mathsf{\alpha }\le 1$$

(40)

for some constants C and $\mathsf{\delta }$ which depend on s and $\mathsf{\alpha }$.

2.

Let $P_J:H\to S_J$ be defined by (12), then:

$$\parallel E_{\mathsf{\alpha }}\left(t\right)(I-P_J)\parallel \le e^{-t{\mathsf{\lambda }}_{J+1}^{\mathsf{\alpha }}}\parallel v\parallel ,t>0,with1/2<\mathsf{\alpha }\le 1$$

(41)

Proof. 

Note that A is a positive definite operator with eigenvalues $0<{\mathsf{\lambda }}_1<{\mathsf{\lambda }}_2<{\mathsf{\lambda }}_3<\cdots$. For any function $g(·)$, we have:

$$\parallel g\left(A\right)\parallel =\underset{\mathsf{\lambda }>{\mathsf{\lambda }}_1>0}{sup}\left|g\left(\mathsf{\lambda }\right)\right|$$

Hence, with $\mathsf{\delta }=\frac{1}{2}{\mathsf{\lambda }}_1^{\mathsf{\alpha }}$,

$$\begin{array}{c}\parallel A^s{E}_{\mathsf{\alpha }}\left(t\right)\parallel =\parallel A^s{E}_{\mathsf{\alpha }}(t/2)E_{\mathsf{\alpha }}(t/2)\parallel \le \parallel A^s{E}_{\mathsf{\alpha }}(t/2)\parallel \parallel E_{\mathsf{\alpha }}(t/2)\parallel \hfill \\ =\underset{\mathsf{\lambda }>{\mathsf{\lambda }}_1}{sup}\left({\mathsf{\lambda }}^s{e}^{-\frac{t}{2}{\mathsf{\lambda }}^{\mathsf{\alpha }}}\right)·\underset{\mathsf{\lambda }>{\mathsf{\lambda }}_1}{sup}\left(e^{-\frac{t}{2}{\mathsf{\lambda }}^{\mathsf{\alpha }}}\right)=\underset{\mathsf{\lambda }>{\mathsf{\lambda }}_1}{sup}\left(\frac{{\left(\frac{t}{2}{\mathsf{\lambda }}^{\mathsf{\alpha }}\right)}^{s/\mathsf{\alpha }}}{e^{\frac{t}{2}{\mathsf{\lambda }}^{\mathsf{\alpha }}}}{\left(\frac{t}{2}\right)}^{-s/\mathsf{\alpha }}\right)e^{-\frac{t}{2}{\mathsf{\lambda }}_1^{\mathsf{\alpha }}}\hfill \\ \le C{(t/2)}^{-s/\mathsf{\alpha }}{e}^{-\mathsf{\delta }t}\le C{t}^{-s/\mathsf{\alpha }}{e}^{-\mathsf{\delta }t}\hfill \end{array}$$

which is (40). To show (41), we note that:

$$\parallel E_{\mathsf{\alpha }}\left(t\right)(I-P_J)v\parallel ={\left(\sum _{j=J+1}^{\infty }{e}^{-2t{\mathsf{\lambda }}_j^{\mathsf{\alpha }}}{(v,e_j)}^2\right)}^{1/2}\le e^{-t{\mathsf{\lambda }}_{N+1}^{\mathsf{\alpha }}}\parallel v\parallel$$

The proof of Lemma 5 is complete. ☐

Proof of Theorem 4. 

Subtracting (37) from (33), we get:

$$\widehat{u}\left(t\right)-{\widehat{u}}_J\left(t\right)=E_{\mathsf{\alpha }}\left(t\right)(u_0-P_J{u}_0)+{\int }_0^t{E}_{\mathsf{\alpha }}(t-s)\left(f\left(s\right)-P_{J}f\left(s\right)\right)ds=I+II$$

(42)

For I, we have, with $0\le r<1/2$,

$$\begin{array}{cc}\hfill {\left|I\right|}_r={\left|E_{\mathsf{\alpha }}\left(t\right)(u_0-P_J{u}_0)\right|}_r& =\parallel A^{\frac{r}{2}}{E}_{\mathsf{\alpha }}\left(t\right)\left(u_0-P_J{u}_0\right)\parallel \hfill \\ & ={\left(\sum _{j=J+1}^{\infty }{e}^{-2t{\mathsf{\lambda }}_j^{\mathsf{\alpha }}}{\mathsf{\lambda }}_j^r{(u_0,e_j)}^2\right)}^{1/2}\le e^{-t{\mathsf{\lambda }}_{J+1}^{\mathsf{\alpha }}}{|u_0-P_J{u}_0|}_r\hfill \end{array}$$

For $II$, by virtue of Lemma 5, for some $\mathsf{\gamma }\in (0,1)$, we get:

$$\begin{array}{cc}\hfill {\left|II\right|}_r& =|{\int }_0^t{E}_{\mathsf{\alpha }}(t-s)\left(\widehat{f}\left(s\right)-P_J\widehat{f}\left(s\right)\right)ds{|}_r=\parallel {\int }_0^t{A}^{\frac{r}{2}}{E}_{\mathsf{\alpha }}(t-s)\left(I-P_J\right)\widehat{f}\left(s\right)ds\parallel \hfill \\ & \parallel {\int }_0^t{A}^{\frac{r}{2}}{E}_{\mathsf{\alpha }}(1-\mathsf{\gamma })(t-s)E\left(\mathsf{\gamma }(t-s)\right)(I-P_J)\widehat{f}\left(s\right)ds\parallel \hfill \\ & \le C{\int }_0^t{(t-s)}^{-\frac{r}{2\mathsf{\alpha }}}{e}^{-{\mathsf{\kappa }}_{\mathsf{\alpha }}(t-s)}\parallel \widehat{f}\left(s\right)\parallel ds\hfill \end{array}$$

where ${\kappa }_{\mathsf{\alpha }}=\mathsf{\delta }(1-\mathsf{\gamma })+{\mathsf{\lambda }}_{J+1}^{\mathsf{\alpha }}\mathsf{\gamma }$.

By the Cauchy-Schwarz inequality:

$${\left|II\right|}_r\le {\left({\int }_0^{\infty }{({(t-s)}^{-\frac{r}{2\mathsf{\alpha }}}{e}^{-\mathsf{\kappa }(t-s)})}^{2}ds\right)}^{1/2}·{\left({\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}ds\right)}^{1/2}$$

Note that $r<\mathsf{\alpha }$ and ${\mathsf{\lambda }}_{J+1}={(J+1)}^2\mathsf{\pi }$ imply:

$${\int }_0^{\infty }\frac{e^{-2{\mathsf{\kappa }}_{\mathsf{\alpha }}s}}{s^{r/\mathsf{\alpha }}}ds\le \frac{{\int }_0^{\infty }{s}^{-r/\mathsf{\alpha }}{e}^{-2s}ds}{{\mathsf{\kappa }}_{\mathsf{\alpha }}^{1-r/\mathsf{\alpha }}}\le C\frac{1}{{\mathsf{\kappa }}_{\mathsf{\alpha }}^{1-r/\mathsf{\alpha }}}\le C\frac{1}{{\left({\mathsf{\lambda }}_{J+1}^{\mathsf{\alpha }}\right)}^{1-r/\mathsf{\alpha }}}\le C\frac{1}{{(J+1)}^{2\mathsf{\alpha }(1-r/\mathsf{\alpha })}}$$

Thus:

$${\left|II\right|}_r\le C\frac{1}{{(J+1)}^{2\mathsf{\alpha }(1-r/\mathsf{\alpha })}}{\left({\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}ds\right)}^{1/2}$$

Together, these estimates complete the proof of Theorem 4. ☐

Combining Theorem 2 with Theorem 4, we obtain:

Theorem 6. 

Let u and ${\widehat{u}}_J$ be the solutions of (17)–(19) and (34)–(36), respectively. Assume that $u_0\in H$. We have:

$$\begin{array}{cc}\hfill \mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-{\widehat{u}}_J(t,x)\right)}^{2}dxdt& \le C(k^{1-\frac{1}{2\mathsf{\alpha }}}+h^2{k}^{\frac{2\mathsf{\alpha }-3}{2\mathsf{\alpha }}})+C{\parallel u_0-P_J{u}_0\parallel }^2\hfill \\ & +C\frac{1}{{(J+1)}^{2\mathsf{\alpha }}}(k^{-1-\frac{1}{2\mathsf{\alpha }}}+k^{-1}{h}^{-1}),for1/2<\mathsf{\alpha }\le 1\hfill \end{array}$$

Proof. 

Note that:

$$\begin{array}{c}\mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-{\widehat{u}}_J(t,x)\right)}^{2}dxdt\hfill \\ \le 2\mathbb{E}{\int }_0^T{\int }_0^1{\left(u(t,x)-\widehat{u}(t,x)\right)}^{2}dxdt+2\mathbb{E}{\int }_0^T{\int }_0^1{\left(\widehat{u}(t,x)-{\widehat{u}}_J(t,x)\right)}^{2}dxdt\hfill \\ =2I+2II\hfill \end{array}$$

For I, due to Theorem 2, we derive:

$$I\le C(k^{1-\frac{1}{2\mathsf{\alpha }}}+h^2{k}^{\frac{2\mathsf{\alpha }-3}{2\mathsf{\alpha }}})$$

For $II$, we have:

$$II=\mathbb{E}{\int }_0^T\parallel \widehat{u}\left(t\right)-{\widehat{u}}_J{\left(t\right)\parallel }^{2}dt\le C\parallel u_0-P_J{u}_0{\parallel }^2+C\frac{1}{{(J+1)}^{2\mathsf{\alpha }}}\mathbb{E}{\int }_0^T{\int }_0^t{\parallel \widehat{f}\left(s\right)\parallel }^{2}dsdt$$

Note that $\widehat{f}\left(s\right)={\widehat{u}}_s\left(s\right)-{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}\left(s\right)$, and hence, by virtue of Theorem 3, we take:

$$\begin{array}{c}\mathbb{E}{\int }_0^T{\int }_0^t\parallel \widehat{f}{\left(s\right)\parallel }^{2}dsdt\le \mathbb{E}{\int }_0^T{\int }_0^t{\parallel {\widehat{u}}_s\left(s\right)-{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}\left(s\right)\parallel }^{2}dsdt\hfill \\ \le C\mathbb{E}{\int }_0^T{\int }_0^T{\int }_0^1\left({\widehat{u}}_s^2(s,x)+{|{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}(s,x)|}^2\right)dxdsdt\hfill \\ \le C\sum _{j=0}^N\left(k^{-\frac{1}{2\mathsf{\alpha }}}+h^{-1}\right)\le C\left(k^{-1-\frac{1}{2\mathsf{\alpha }}}+k^{-1}{h}^{-1}\right)\hfill \end{array}$$

Together, these estimates complete the proof of Theorem 6. ☐

4. Numerical Simulations

In this section, we will present the computational issues for solving the following stochastic space-fractional parabolic partial differential equations by using the spectral method developed in the previous section, with $1/2<\mathsf{\alpha }\le 1$,

$$\begin{array}{c}\frac{\partial u(t,x)}{\partial t}+\mathsf{ϵ}{(-\Delta )}^{\mathsf{\alpha }}u(t,x)=f\left(u(t,x)\right)+\frac{{\partial }^{2}W(t,x)}{\partial t\partial x},0<x<1,0<t\le T\hfill \end{array}$$

(43)

$$\begin{array}{c}u(t,0)=u(t,1)=0,0<t\le T\hfill \end{array}$$

(44)

$$\begin{array}{c}u(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(45)

where ${(-\Delta )}^{\mathsf{\alpha }}$ is the fractional Laplacian defined by using the eigenvalues and eigenfunctions of the Laplacian operator $-\Delta$ subject to some boundary conditions. Here, $f:\mathbb{R}\to \mathbb{R}$ is a smooth function, and $\mathsf{ϵ}>0$ denotes the diffusion coefficient. In our numerical example, we will use the discrete sine transform MATLAB functions dst and idst. We also include the nonlinear term f, although the error estimates in the previous sections are only proven for $f=0$. In our future work, we will consider the error estimates for solving the nonlinear stochastic space-fractional partial differential equations with multiplicative noise by using the spectral method.

Let $x_0<x_1<\cdots <x_J=1$ be a space partition of $[0,1]$ and $\Delta x=h$ be the space step size. Let $0=t_0<t_1<\cdots <t_N=T$ be the time partition of $[0,T]$ and $\Delta t=k$ the time step size. The space-time noise $\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}$ is approximated by using piecewise constant function $\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$, where:

$$\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}=\frac{{\mathsf{\eta }}_{n,j}}{\sqrt{\Delta t\Delta x}},t_{n-1}\le t\le t_n,x_{j-1}\le x\le x_j$$

(46)

For convenience, we will denote $\widehat{G}(t,x)=\frac{{\partial }^2\widehat{W}(t,x)}{\partial t\partial x}$ below.

Equations (43)–(45) can then be approximated by the following, with $1/2<\mathsf{\alpha }\le 1$,

$$\begin{array}{c}\frac{\partial \widehat{u}(t,x)}{\partial t}+\mathsf{ϵ}{(-\Delta )}^{\mathsf{\alpha }}\widehat{u}(t,x)=f\left(\widehat{u}(t,x)\right)+\widehat{G}(t,x),0<x<1,0<t\le T\hfill \end{array}$$

(47)

$$\begin{array}{c}\widehat{u}(t,0)=\widehat{u}(t,1)=0,0<t\le T\hfill \end{array}$$

(48)

$$\begin{array}{c}\widehat{u}(0,x)=u_0\left(x\right),0<x<1\hfill \end{array}$$

(49)

Denote $A=-\frac{{\partial }^2}{\partial x^2}$ with $\mathcal{D}\left(A\right)=H_0^1(0,1)\cap H^2(0,1)$. Then, A has eigenvalues ${\mathsf{\lambda }}_j$ and eigenfunctions $e_j$ where:

$${\mathsf{\lambda }}_j=j^2{\mathsf{\pi }}^2,e_j=sin\left(j\pi x\right),j\in {\mathbb{Z}}^{+}$$

That is:

$$A{e}_j={\mathsf{\lambda }}_j{e}_j,j\in {\mathbb{Z}}^{+}$$

Equations (47)–(49) can further be written as the following abstract form: find $\widehat{u}\left(t\right)\in H_0^1(0,1)\cap H^2(0,1)$, such that:

$$\begin{array}{c}\frac{d\widehat{u}\left(t\right)}{dt}+A\widehat{u}\left(t\right)=f\left(\widehat{u}\left(t\right)\right)+\widehat{G}\left(t\right),0<t\le T\hfill \end{array}$$

(50)

$$\begin{array}{c}\widehat{u}\left(0\right)=u_0\hfill \end{array}$$

(51)

Let $S_{J-1}:=\mathrm{span}\{e_1,e_2,\cdots ,e_{J-1}\}$. The spectral method for solving (47)–(49) is to find $u_{J-1}\left(t\right)\in S_{J-1}$, such that, with $0<t\le T$,

$$\begin{array}{c}\frac{d{\widehat{u}}_{J-1}\left(t\right)}{dt}+A_{J-1}{\widehat{u}}_{J-1}\left(t\right)=P_{J-1}f\left(u_{J-1}\left(t\right)\right)+P_{J-1}\widehat{G}\left(t\right)\hfill \end{array}$$

(52)

$$\begin{array}{c}{\widehat{u}}_{J-1}\left(0\right)=P_{J-1}{u}_0\hfill \end{array}$$

(53)

where $P_{J-1}:H\to S_{J-1}$ is the orthogonal projection operator defined by:

$$P_{J-1}v=\sum _{j=1}^{J-1}{\tilde{v}}_j{e}_j,{\tilde{v}}_j=(v,e_j)$$

where $A_{J-1}=P_{J-1}A:S_{J-1}\to S_{J-1}$ and $(·,·)$ denotes the inner product in $H=L^2(0,1)$. We remark that we use $S_{J-1}$ (not $S_J$), since we will apply the MATLAB functions dst and idst in our numerical algorithms below.

The semi-implicit Euler method for solving (47)–(49) is to find $u_{J-1,n}\approx u_{J-1}\left(t_n\right)$, such that:

$$\begin{array}{c}\frac{{\widehat{u}}_{J-1,n+1}-{\widehat{u}}_{J-1,n}}{\Delta t}+A_{J-1}{\widehat{u}}_{J-1,n+1}=P_{J-1}f\left({\widehat{u}}_{J-1,n}\right)+P_{J-1}\widehat{G}\left(t_n\right)\hfill \end{array}$$

(54)

$$\begin{array}{c}{\widehat{u}}_{J-1,0}=P_{J-1}{u}_0\hfill \end{array}$$

(55)

Let:

$${\widehat{u}}_{J-1,n}=\sum _{j=1}^{J-1}{\tilde{u}}_{j,n}{e}_j\in S_{J-1}$$

(56)

It is easy to see that the Fourier coefficients ${\tilde{u}}_{j,n}$ satisfy, with $j=1,2,\cdots ,J-1$,

$$\begin{array}{c}{\tilde{u}}_{j,n+1}={(1+\Delta t{\lambda }_j)}^{-1}\left({\tilde{u}}_{j,n}+\Delta t{\tilde{f}}_j\left({\widehat{u}}_{J-1,n}\right)+\Delta t{\tilde{G}}_{j,n}\right)\hfill \end{array}$$

(57)

$$\begin{array}{c}{\tilde{u}}_{j,0}=(P_{J-1}{u}_0,e_j)\hfill \end{array}$$

(58)

where:

$$P_{J-1}\widehat{G}\left(t_n\right)=\sum _{j=1}^{J-1}{\tilde{G}}_{j,n}{e}_j\in S_{J-1},P_{J-1}f\left({\widehat{u}}_{J,n}\right)=\sum _{j=1}^{J-1}{\tilde{f}}_j\left({\widehat{u}}_{J,n}\right)e_j$$

Here, ${\tilde{u}}_{j,n},{\tilde{G}}_{j,n},{\tilde{f}}_j\left({\widehat{u}}_{J,n}\right)$ denote the Fourier coefficients of ${\widehat{u}}_{J-1,n},\widehat{G}\left(t_n\right)$ and $f\left({\widehat{u}}_{J-1,n}\right)$, respectively.

We may use the following steps to describe how to solve (47)–(49) numerically by using the spectral method:

Step 1: Given initial value ${\widehat{u}}_0\left(x\right)$ and f, we get the approximation $u_{J-1,0}\left(x\right)=P_{J-1}{u}_0\approx u_0$ and $P_{J-1}f\left({\widehat{u}}_{J-1,0}\right)\approx f\left({\widehat{u}}_0\left(x\right)\right)$.

Step 2: Find the Fourier coefficients ${\tilde{u}}_{j,0}$ and ${\tilde{f}}_j\left({\widehat{u}}_{J-1,0}\right)$ by:

$$\left(\begin{array}{c}{\tilde{u}}_{1,0}\\ {\widehat{u}}_{2,0}\\ ⋮\\ {\widehat{u}}_{J-1,0}\end{array}\right)={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}{u}_0\left(x_1\right)\\ u_0\left(x_2\right)\\ ⋮\\ u_0\left(x_J\right)\end{array}\right)$$

$$\left(\begin{array}{c}{\tilde{f}}_0\left(u_{J,0}\right)\\ {\tilde{f}}_1\left(u_{J,0}\right)\\ ⋮\\ {\tilde{f}}_J\left(u_{J,0}\right)\end{array}\right)={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}f\left(u_0\left(x_1\right)\right)\\ f\left(u_0\left(x_2\right)\right)\\ ⋮\\ f\left(u_0\left(x_J\right)\right)\end{array}\right)$$

and:

$$\left(\begin{array}{c}{\tilde{G}}_{0,0}\\ {\tilde{G}}_{1,0}\\ ⋮\\ {\tilde{G}}_{J-1,0}\end{array}\right)={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}\widehat{G}(t_0,x_1)\\ \widehat{G}(t_0,x_2)\\ ⋮\\ \widehat{G}(t_0,x_{J-1})\end{array}\right)$$

Here, $\left(\begin{array}{c}\widehat{G}(t_0,x_1)\\ \widehat{G}(t_0,x_2)\\ ⋮\\ \widehat{G}(t_0,x_{J-1})\end{array}\right)=\widehat{W}(1,:)$, and $\widehat{W}$ is generated by:

$$\widehat{W}=\frac{1}{\sqrt{\Delta t\Delta x}}*\mathbf{randn}(N,J-1)$$

(59)

Step 3: Find the Fourier coefficients ${\tilde{u}}_{j,1},j=1,2,\cdots ,J$ by:

$$\left(\begin{array}{c}{\tilde{u}}_{1,1}\\ {\tilde{u}}_{2,1}\\ ⋮\\ {\widehat{u}}_{J-1,1}\end{array}\right)=GG./EE$$

where $./$ denotes the element-wise division and:

$$\begin{array}{cc}\hfill GG& ={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}{u}_0\left(x_1\right)\\ u_0\left(x_2\right)\\ ⋮\\ u_0\left(x_J\right)\end{array}\right)+\Delta t{\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}f\left(u_0\left(x_1\right)\right)\\ f\left(u_0\left(x_2\right)\right)\\ ⋮\\ f\left(u_0\left(x_J\right)\right)\end{array}\right)\hfill \\ & +\Delta t{\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}\widehat{G}(t_0,x_1)\\ \widehat{G}(t_0,x_2)\\ ⋮\\ \widehat{G}(t_0,x_{J-1})\end{array}\right)\hfill \end{array}$$

with ${\mathsf{\lambda }}_j=\pi j$,

$$EE=\left(\begin{array}{c}1+\Delta t*{\mathsf{\lambda }}_1^2\\ 1+\Delta t*{\mathsf{\lambda }}_2^2\\ ⋮\\ 1+\Delta t*{\mathsf{\lambda }}_{J-1}^2\end{array}\right)$$

Step 4: Find the Fourier coefficients ${\tilde{u}}_{j,2},j=1,2,\cdots ,J-1$ by:

$${\widehat{u}}_{j,2}={(1+\Delta t{\lambda }_j)}^{-1}\left({\tilde{u}}_{j,1}+\Delta t{\tilde{f}}_j\left({\widehat{u}}_{J-1,1}\right)+\Delta t{\tilde{G}}_{j,1}\right)$$

where:

$$\left(\begin{array}{c}{\tilde{f}}_1\left({\widehat{u}}_{J-1,1}\right)\\ {\tilde{f}}_2\left({\widehat{u}}_{J-1,1}\right)\\ ⋮\\ {\tilde{f}}_{J-1}\left({\widehat{u}}_{J-1,1}\right)\end{array}\right)={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}f\left({\widehat{u}}_{J-1,1}\left(x_1\right)\right)\\ f\left({\widehat{u}}_{J-1,1}\left(x_2\right)\right)\\ ⋮\\ f\left({\widehat{u}}_{J-1,1}\left(x_{J-1}\right)\right)\end{array}\right)$$

and:

$$\left(\begin{array}{c}{\tilde{G}}_{1,1}\\ {\tilde{G}}_{2,1}\\ ⋮\\ {\tilde{G}}_{J-1,1}\end{array}\right)={\left(\sqrt{2}\right)}^{-1}{\left(\frac{J}{2}\right)}^{-1}·\mathbf{dst}\left(\begin{array}{c}\widehat{G}(t_1,x_1)\\ \widehat{G}(t_1,x_2)\\ ⋮\\ \widehat{G}(t_1,x_{J-1})\end{array}\right)$$

Here, $\left(\begin{array}{c}\widehat{G}(t_1,x_1)\\ \widehat{G}(t_1,x_2)\\ ⋮\\ \widehat{G}(t_1,x_{J-1})\end{array}\right)=\widehat{W}(2,:)$, and $\widehat{W}$ is defined in (59).

Step 5: Find ${\widehat{u}}_{J,2}\left(x_k\right),k=1,2,\cdots ,J-1$ by:

$$\left(\begin{array}{c}{\widehat{u}}_{J-1,2}\left(x_1\right)\\ {\widehat{u}}_{J-1,2}\left(x_2\right)\\ ⋮\\ {\widehat{u}}_{J-1,2}\left(x_{J-1}\right)\end{array}\right)=\sqrt{2}\left(\frac{J}{2}\right)·\mathbf{idst}\left(\begin{array}{c}{\tilde{u}}_{1,2}\\ {\tilde{u}}_{2,2}\\ ⋮\\ {\tilde{u}}_{J-1,2}\end{array}\right)$$

Step 6: Repeating Steps 3–5, we obtain all ${\widehat{u}}_{J-1,n}\left(x_k\right),k=1,2,\cdots ,J-1$.

Let us now introduce the MATLAB functions to solve our problem. Let $u_0$ denote the initial value vector, that is $u_0=[u_0\left(x_1\right),u_0\left(x_2\right),\cdots ,u_0\left(x_{J-1}\right)]$. Let u denote the approximate solution vector at time T, that is $u=[u(x_1,T),u(x_2,T),\cdots ,u(x_{J-1},T)]$. We may use the following MATLAB function to get the approximate solution u at T for any function f. Here, we choose $f\left(u\right)=u-u^3$.

Let $x=[x_1,x_2,\cdots ,x_{J-1}],epsilon=1,kappa=1$. We can obtain the approximate solution u at time T at the different $x_k,k=1,2,\cdots ,J-1$ by the following MATLAB function.

        function [u]=spde_oned_Gal(u0,x,T,N,kappa,W1,J, epsilon)
       dt=T/N; Dt=kappa*dt; % kappa for the different time steps
       N=T/Dt;
       lambda= pi*[1:(J-1)]’; M= epsilon*lambda.^2; EE=1./(1+Dt*M);
        for n=1:N
        u0_hat=(sqrt(2)*J/2)^(-1)*dst(u0);
        f_u0 = u0-u0.^3; % f(u) = u-u^3
        f_u0_hat=(sqrt(2)*J/2)^(-1)*dst(f_u0);
        W=W1(kappa*(n-1)+1,:); W=W’; % kappa for the different tim steps
        G_hat=(sqrt(2)*J/2)^(-1)*dst(W);
        u1_hat=(u0_hat + Dt*f_u0_hat + Dt*G_hat).*EE;
        u1=(sqrt(2)*J/2)*idst(u1_hat);
        u0=u1;
       end
       u=u1;
      

where W1 denotes the Brownian sheet generated by:

$$W1=\frac{1}{\sqrt{\Delta t*\Delta x}}*\mathbf{randn}(N,J-1)$$

Example 1. 

Consider, with $0<x<1,0<t\le T$, [12,14],

$$\begin{array}{c}\frac{\partial u(t,x)}{\partial t}+\mathsf{ϵ}{(-\Delta )}^{\mathsf{\alpha }}u(t,x)=f\left(u(t,x)\right)+h(t,x)+\frac{{\partial }^{2}W(t,x)}{\partial t\partial x}\hfill \end{array}$$

(60)

$$\begin{array}{c}u(t,0)=u(t,1)=0\hfill \end{array}$$

(61)

$$\begin{array}{c}u(0,x)=u_0\left(x\right)\hfill \end{array}$$

(62)

where $ϵ=1,f\left(u\right)=-bu,b=0.5$ and $u_0\left(x\right)=10x^2{(1-x)}^2$ and:

$$h(t,x)=10(1+b)x^2{(1-x)}^2{e}^t-10(2-12x+12x^2)e^t$$

Allen, Novosel and Zhang [12] and Du and Zhang [14] provide the numerical approximation of $\mathbb{E}\left(u\right(t,x\left)\right)$ and $\mathbb{E}(u{(t,x)}^2)$ with $\alpha =1$ at time $t=1$ and $x=0.5$ by using the finite element method and the finite difference method. In

Table 1. The approximation of $\mathbb{E}u(1,0.5)$ and $\mathbb{E}{\left(u(1,0.5)\right)}^2$.

$\mathbf{\Delta }\mathit{x}$	$\mathbf{\Delta }\mathit{t}$	$\mathbf{𝔼}\mathit{u}\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{0.5}\mathbf{)}$	$\mathbf{𝔼}{\mathbf{\left(}\mathit{u}\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{0.5}\mathbf{)}\mathbf{\right)}}^{\mathbf{2}}$
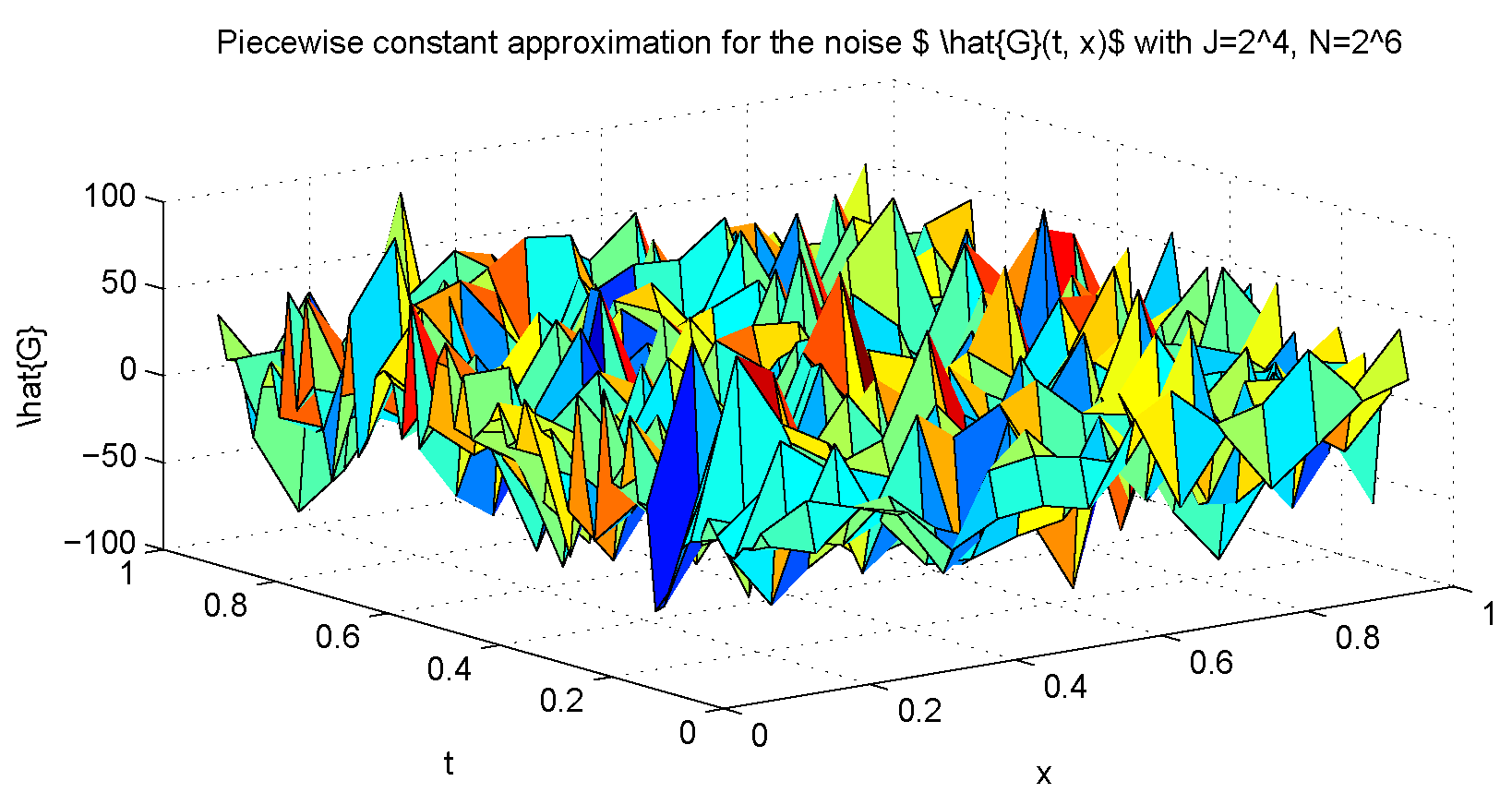
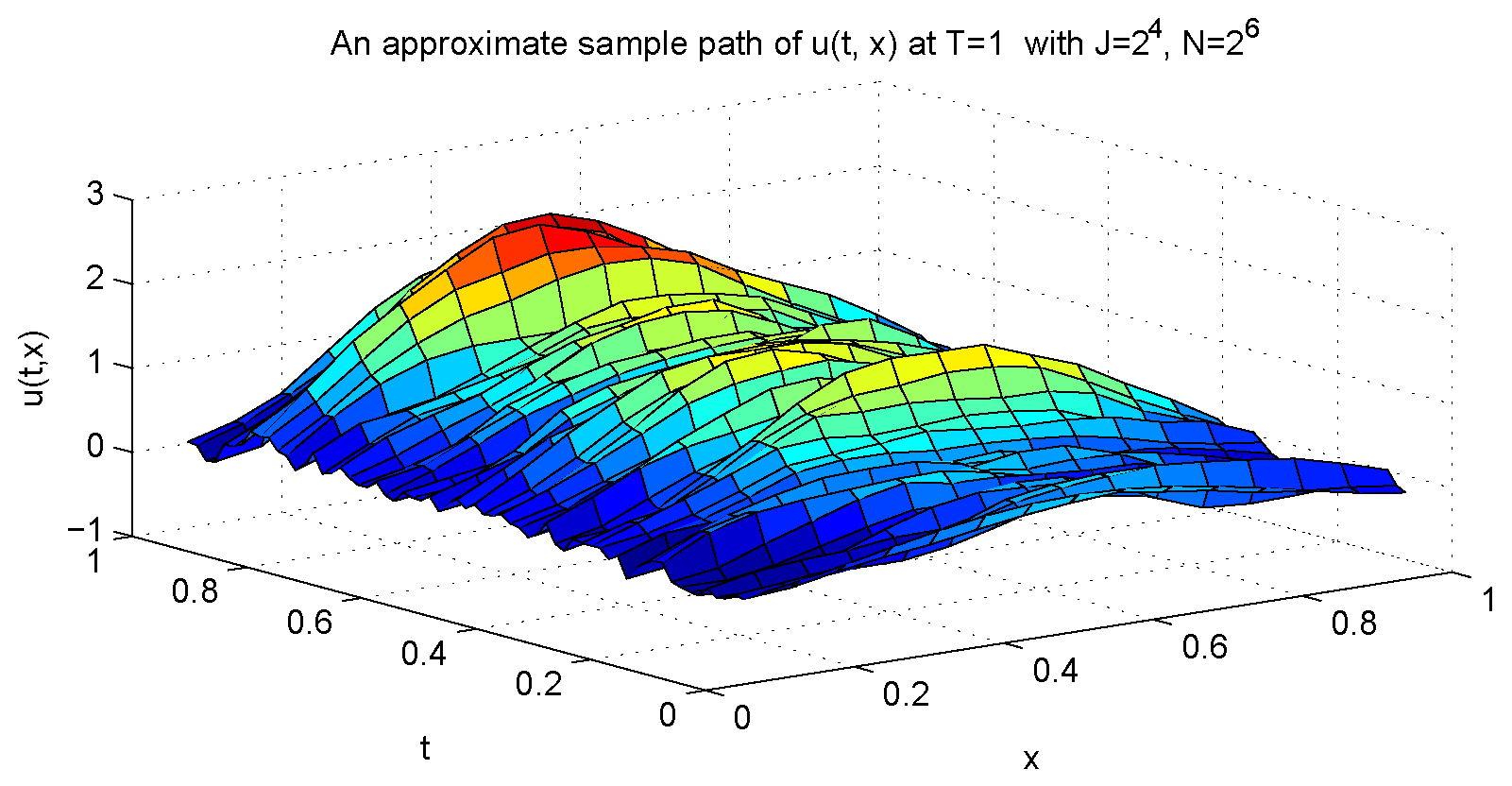
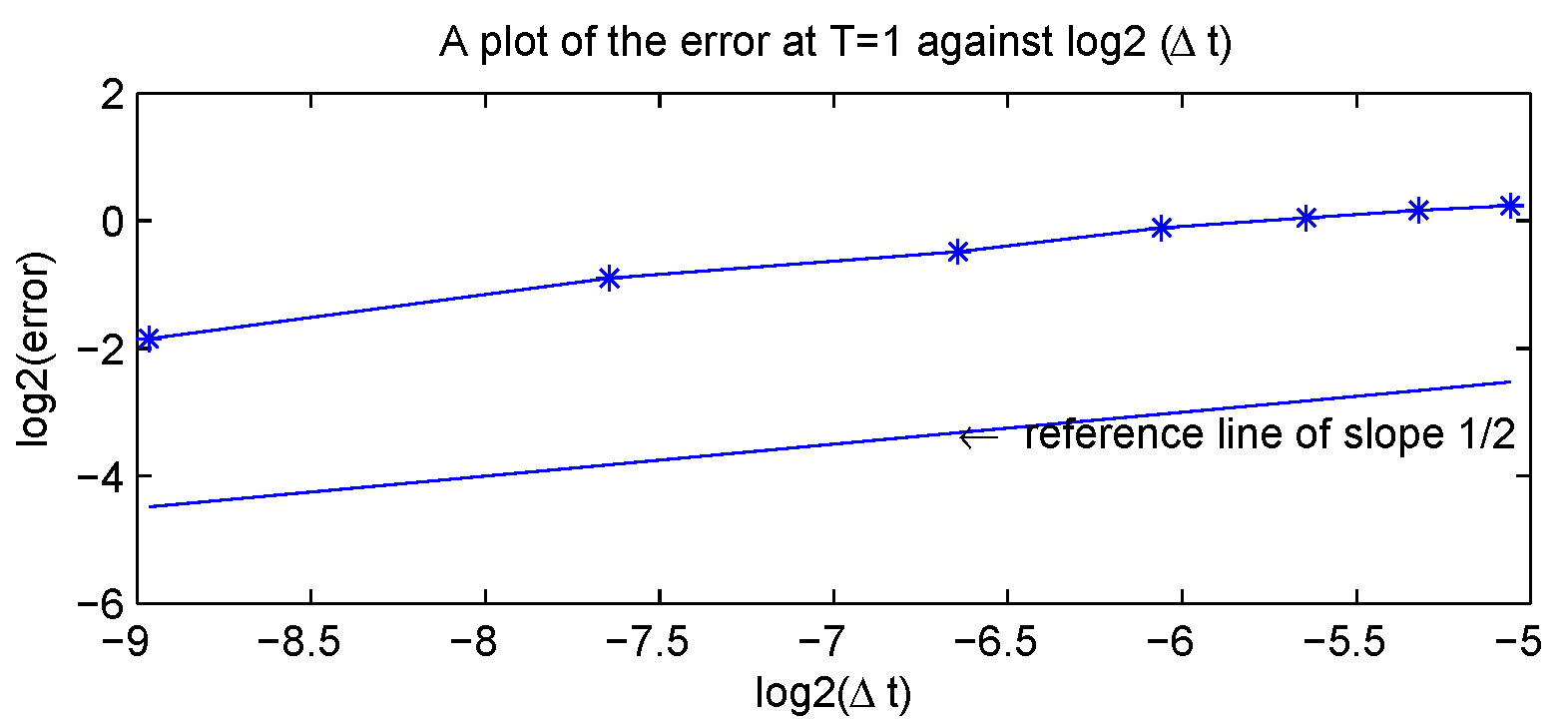
1/4	1/4	1.6108	2.6386
1/4	1/8	1.7003	2.9883
1/4	1/16	1.9051	3.6534
1/4	1/32	1.9051	3.6534
1/8	1/4	1.4838	2.5923
1/8	1/8	1.6574	2.7709
1/8	1/16	1.7323	2.7585
1/8	1/32	1.6676	2.8153
1/16	1/4	1.4681	2.3333
1/16	1/8	1.6097	2.6420
1/16	1/16	1.6110	2.5681
1/16	1/32	1.6133	2.8737
1/32	1/4	1.3605	2.4143
1/32	1/8	1.6099	2.6095
1/32	1/16	1.6839	2.7930
1/32	1/32	1.7061	2.8747

, we obtain similar approximation values as in their papers for different pair $(\Delta t,\Delta x)$ by using the spectral method. In our experiment, for each pair $(\Delta t,\Delta x)$, 1000 runs are performed. In Table 1, $u(1,0.5)$ denotes the approximation of $u(t,x)$ at $t=1$ and $x=0.5$. The computational results converge as $\Delta t$ and $\Delta x$ approach zero.

In Figure 1, we plot a piecewise constant approximation of the noise $\widehat{G}(t,x)$ with $J=2^4$ and $N=2^6$ on $0\le t\le 1$ and $0\le x\le 1$.

In Figure 2, we plot an approximation sample path of $u(t,x)$ with $J=2^4$ and $N=2^6$ on $0\le t\le 1$ and $0\le x\le 1$.

In Figure 3, we consider the convergence rate against the different time steps. Choose the fixed $J=64$; we then consider the different time steps. The reference solution is obtained by using the time step $\Delta tref=T/Nref$ with $Nref={10}^4$. Let $kappa=[20,50,100,150,200,250,300]$; we will consider the approximate solutions with the different time steps $\Delta t_i=\Delta tref*kappa\left(i\right),i=1,2,\cdots ,7$.

In our experiment, for saving the computation time, we will consider the error estimates $\parallel {\widehat{u}}_N\left(t_n\right)-u\left(t_n\right){\parallel }_{L^2(\Omega ,H)}$ at time $t_n$. We hope to observe the same convergence order as in Theorem 6.

To do this, we consider $M=100$ simulations. For each simulation ${\mathsf{\omega }}_m,m=1,2,\cdots ,M$, we compute ${\widehat{u}}_N\left(t_n\right)\approx \widehat{u}\left(t_n\right)$ at time $t_n=1$ by using the different time steps. We then compute the following $L^2$ norm of the error at $t_n=1$ for the simulations ${\mathsf{\omega }}_m,m=1,2,\cdots ,M$,

$$ϵ(\Delta t_i,{\mathsf{\omega }}_m)=\mathsf{ϵ}(\Delta t_i,{\mathsf{\omega }}_m,t_n)={\parallel {\widehat{u}}_N(t_n,{\mathsf{\omega }}_m)-\text{uref}(t_n,{\mathsf{\omega }}_m)\parallel }^2$$

where the reference (or “true ”) solution $\text{uref}(t_n,{\mathsf{\omega }}_m)$ is approximated by the time step $\Delta tref=T/Nref$. We then average $\mathsf{ϵ}(\Delta t_i,{\mathsf{\omega }}_m)$ with respect to ${\mathsf{\omega }}_m$ to obtain the following approximation of $\parallel {\widehat{u}}_N\left(t_n\right){)-\text{uref}\left(t_n\right)\parallel }_{L^2(\Omega ,H^r)}$ with respect to the different time step $\Delta t_i$,

$$S(\Delta t_i)={\left(\frac{1}{M}\sum _{m=1}^M\mathsf{ϵ}(\Delta t_i,{\mathsf{\omega }}_m)\right)}^{1/2}={\left(\frac{1}{M}\sum _{m=1}^M{\parallel \widehat{u}(t_n,{\mathsf{\omega }}_m)-\mathbf{uref}(t_n,{\mathsf{\omega }}_m)\parallel }^2\right)}^{1/2}$$

Since the convergence rate with respect to the time step is $O(\Delta t^{1/2})$, i.e.,

$$S(\Delta t_i)\approx \Delta t_i^{1/2}$$

this implies that:

$$\log \left(S(\Delta t_i)\right)\approx 1/2\log (\Delta t_i),i=1,2,\cdots ,7$$

In Figure 3, we plot the points $\left(\log (\Delta t_i),\log \left(S(\Delta t_i)\right)\right),i=1,2,\cdots ,7$, and we see that the points are parallel to the reference line, which has the slope $1/2$, as we expected in our theoretical results.

In

Table 2. The $L^2$ norm error at $T=1$ against $\Delta t$.

$\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}$	$\mathbf{2}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{3}}$	$\mathbf{5}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{3}}$	$\mathbf{1}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$	$\mathbf{1.5}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$	$\mathbf{2}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$	$\mathbf{2.5}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$	$\mathbf{3}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$
$L^2$-error	0.2775	0.5355	0.7116	0.9249	1.0306	1.1159	1.1742

, we list the error $S(\Delta t_i)$ against the different time steps $\Delta t_i$.

In Figure 4, we plot the $L^2$ error $S(\Delta t)$ against the different J where the $L^2$ errors are approximated by using $M=100$ simulations. We indeed observe the convergence with respect to the different J.

5. Conclusions

In this work, we present a Fourier spectral method for solving space-fractional partial differential equations. The space-time white noise is approximated by using piecewise constant functions. For the linear problem, we obtain the exact error estimates in the $L_2$-norm and find the relations between the convergence order and the fractional power $\mathsf{\alpha },1/2<\mathsf{\alpha }\le 1$. For the nonlinear problem, we introduce the numerical algorithm and the MATLAB code for solving it based on the discrete sine transform and inverse discrete sine transform MATLAB functions dst.m and idst.m. The MATLAB code in this paper can be easily modified to solve other nonlinear stochastic fractional partial differential equations with Dirichlet boundary conditions.