Abstract
Toric posets are in some sense a natural “cyclic” version of finite posets in that they capture the fundamental features of a partial order but without the notion of minimal or maximal elements. They can be thought of combinatorially as equivalence classes of acyclic orientations under the equivalence relation generated by converting sources into sinks, or geometrically as chambers of toric graphic hyperplane arrangements. In this paper, we define toric intervals and toric order-preserving maps, which lead to toric analogues of poset morphisms and order ideals. We develop this theory, discuss some fundamental differences between the toric and ordinary cases, and outline some areas for future research. Additionally, we provide a connection to cyclic reducibility and conjugacy in Coxeter groups.
Keywords:
Coxeter group; cyclic order; cyclic reducibility; morphism; partial order; preposet; order ideal; order-preserving map; toric hyperplane arrangement; toric poset; 06A06, 52C35 MSC:
06A06, 52C35
1. Introduction
A finite poset can be described by at least one directed acyclic graph where the elements are vertices and directed edges encode relations. We say “at least one” because edges implied by transitivity may be present or absent. The operation of converting a source vertex into a sink generates an equivalence relation on finite posets over a fixed graph. Equivalence classes are called toric posets. These objects have arisen in a variety of contexts in the literature, including but not limited to chip-firing games [1], Coxeter groups [2,3,4], graph polynomials [5], lattices [6,7], and quiver representations [8]. These equivalence classes were first formalized as toric posets in [9], where the effort was made to develop a theory of these objects in conjunction with the existing theory of ordinary posets. The name “toric poset” is motivated by a bijection between toric posets over a fixed (undirected) graph and chambers of the toric graphic hyperplane arrangement of that graph. This is an analogue to the well-known bijection between ordinary posets over a fixed graph G and chambers of the graphic hyperplane arrangement of G, first observed by Greene [10] and later extended to signed graphs by Zaslavsky [11].
Combinatorially, a poset over a graph G is determined by an acyclic orientationω of G. We denote the resulting poset by . A toric poset over G is determined by an acyclic orientation, up to the equivalence generated by converting sources into sinks. We denote this by . Though most standard features of posets have elegant geometric interpretations, this viewpoint is usually unnecessary. In contrast, for most features of toric posets, i.e., the toric analogues of standard posets features, the geometric viewpoint is needed to see the natural proper definitions and to prove structure theorems. Once this is done, the definitions and characterizations frequently have simple combinatorial (non-geometric) interpretations.
To motivate our affinity for the geometric approach, consider one of the fundamental hallmarks of an ordinary poset P: its binary relation, . Most of the classic features of posets (chains, transitivity, morphisms, order ideals, etc.) are defined in terms of this relation. Toric posets have no such binary relation, and so this is why we need to go to the geometric setting to define the basic features. Perhaps surprisingly, much of the theory of posets carries over to the toric setting despite the absence of a relation, and current toric poset research strives to understand just how much and what does carry over. As an analogy from a different area of mathematics, topology can be thought of as “analysis without the metric.” A fundamental hallmark of a metric space is its distance function. Many of the classic features of metric spaces, such as open, closed, and compact sets, and continuous functions, are defined using the distance function. However, once one establishes an equivalent characterization of continuity in terms of the inverse image of open sets, many results can be proven in two distinct ways: via epsilon-delta proofs, or topologically. When one moves from metric spaces to topological spaces, one loses the distance function and all of the tools associated with it, so this first approach goes out the window. Remarkably, much of the theory of real analysis carries over from metric spaces to topological spaces. Back to the poset world, one can prove theorems of ordinary posets using either the binary relation or the geometric definitions. However, upon passing to toric posets, the binary relation and all of the tools associated with it are lost, so one is forced to go to the geometric setting. Remarkably, much of the theory of ordinary posets still carries over to toric posets. This analogy is not perfect, because toric posets are not a generalization of ordinary posets like how topological spaces extend metric spaces. However, it should motivate the reliance on geometric methods throughout this paper.
An emerging theme of toric poset structure theorems, from both the original paper [9] and this one, is that characterizations of toric analogues, when they exist, usually have one of two forms. In one, the feature of a toric poset is characterized by it being the analogous feature of the ordinary poset , for all . In the other, the feature of is characterized by it being the analogous feature of for some . Several examples of this are given below. It is not obvious why this should happen or which type of characterization a given toric analogue should have a priori. Most of these are results from this paper, and so this list provides a good overview for what is to come.
The “For All” structure theorems:
- ■
- A set is a toric chain of iff C is a chain of for all . (Proposition 5.3)
- ■
- The edge is in the toric transitive closure of iff is in the transitive closure of for all . (Proposition 5.15)
The “For Some” structure theorems:
- ■
- A partition is a closed toric face partition of iff π is a closed face partition of for some . (Theorem 4.7)
- ■
- A set is a (geometric) toric antichain of iff A is an antichain of for some . (Proposition 5.17)
- ■
- If a set is a toric interval of , then I is an interval of for some . (Proposition 5.14)
- ■
- A set is a toric order ideal of iff J is an order ideal of for some . (Proposition 7.3)
- ■
- Collapsing by a partition is a morphism of toric posets iff collapsing by π is a poset morphism for some . (Corollary 6.2)
- ■
- If an edge is in the Hasse diagram of for some , then it is in the toric Hasse diagram of . (Proposition 5.15)
This paper is organized as follows. In the next section, we formally define posets and preposets and review how to view them geometrically in terms of faces of chambers of graphic hyperplane arrangements. In Section 3, we translate well-known properties of poset morphisms to this geometric setting. In Section 4, we define toric posets and preposets geometrically in terms of faces of chambers of toric hyperplane arrangements, and we study the corresponding “toric face partitions” and the bijection between toric preposets and lower-dimensional faces. In Section 5, we define the notion of a toric interval and review some features of toric posets needed for toric order-preserving maps, or morphisms, which are finally presented in Section 6. In Section 7, we introduce toric order ideals and filters, which are essentially the preimage of one element upon mapping into a two-element toric poset. The toric order ideals and filters of a toric poset turn out to coincide. They form a graded poset , but unlike the ordinary case, this need not be a lattice. In Section 8, we provide a connection of this theory to Coxeter groups, and then we conclude with a summary and discussion of current and future research in Section 9.
2. Posets Geometrically
2.1. Posets and Preposets
A binary relation R on a set V is a subset . A preorder or preposet is a binary relation that is reflexive and transitive. This means that for all , and if , then . We will use the notation instead of , and say that if and . Much of the basics on preposets can be found in [12].
An equivalence relation is a preposet whose binary relation is symmetric. For any preposet P, we can define an equivalence relation on P by saying if and only if and both hold. A partially ordered set, or poset, is a preposet P such that every -class has size 1. We say that a preposet is acyclic if it is also a poset.
Every preorder P over V determines a directed graph over V that contains a directed edge (which we denote by ) if and only if and . Not every directed graph arises from such a preorder, since edge transitivity is required. That is, if and are edges, then must also be an edge if . However, for any directed graph Γ, there is a unique minimal preorder containing the edge set of Γ; is the transitive closure of Γ. The graph is acyclic if and only if P is a poset. The strongly connected components are the -classes, and so the quotient is acyclic and inherits a natural poset structure from P.
If and are preorders on V, then we can define their union as the union of the subsets and of . This need not be a preorder, but its transitive closure will be.
Another way we can create a new preorder from an old one is by an operation called contraction. Given a binary relation , let denote the opposite binary relation, meaning that if and only if . If P and Q are preposets on V, then Q is a contraction of P if there is a binary relation such that . Intuitively, each added edge forces because by construction. Note that in this context, contraction is a different concept than what it often means in graph theory – modding out by a subset of vertices, or “collapsing” a set of vertices into a single vertex.
2.2. Chambers of Hyperplane Arrangements
Every finite poset corresponds to a chamber of at least one graphic hyperplane arrangement. The interested reader is encouraged to consult the excellent texts of Zaslavsky [13] on the combinatorial geometry of arrangements, or of Wachs [14] on poset topology. A brief correspondence between posets and chambers of graphic hyperplane arrangements will be descsribed here.
Let P be a poset over a finite set . This poset can be identified with the following open polyhedral cone in :
The (topological) closure of the cone is .
It is easy to see how the cone c determines the poset : one has if and only if for all x in c. Each such cone c is a connected component of the complement of the graphic hyperplane arrangement for at least one graph . In this case, we say that P is a poset over G (or “on G”; both are used interchangeably). Given distinct vertices of a simple graph G, the hyperplane is the set
The graphic arrangement of G is the set of all hyperplanes in where is in E. Under a slight abuse of notation, at times it is convenient to refer to as the set of points in on the hyperplanes, as opposed to the actual finite set of hyperplanes themselves. It should always be clear from the context which is which.
Each point in the complement determines an acyclic orientation of the edge set E: direct the edge in E as if and only if . Clearly, the fibers of the mapping are the chambers of the hyperplane arrangement . Thus, induces a bijection between the set of acyclic orientations of G and the set of chambers of :
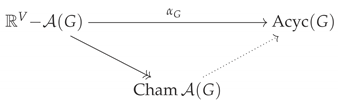

We denote the poset arising from an acyclic orientation by . An open cone may be a chamber in several graphic arrangements, because adding or removing edges implied by transitivity does not change the poset. Geometrically, the hyperplanes corresponding to these edges do not cut c, though they intersect its boundary. Thus, there are, in general, many pairs of a graph G and acyclic orientation ω that lead to the same poset . Fortunately, this ambiguity is not too bad, in that with respect to inclusion of edge sets, there is a unique minimal graph called the Hasse diagram of P and a unique maximal graph , where is transitive closure.
Given two posets on a set V, one says that is an extension of P when implies . Geometrically, is an extension of P if and only if . Moreover, is a linear extension if is a chamber of , where is the complete graph.
2.3. Face Structure of Chambers
Let be a partition of V into nonempty blocks. The set of all such partitions has a natural poset structure: if every block in π is contained in some block in . When this happens, we say that π is finer than , or that is coarser than π.
Intersections of hyperplanes in are called flats, and the set of flats is a lattice, denoted . Flats are partially ordered by reverse inclusion: If , then . Every flat of has the form
for some partition π of V. Note that if and only if ; this should motivate the convention of partially ordering by reverse inclusion.
Given a poset over , a partition π of V defines a preposet on the blocks, where whenever for some and (and taking the transitive closure). This defines a directed graph , formed by collapsing out each block into a single vertex. Depending on the context, we may use or interchangeably. If this preposet is acyclic (i.e., if is a poset, or equivalently, the directed graph is acyclic), then we say that π is compatible with P. In this case, there is a canonical surjective poset morphism . We call such a morphism a quotient, as to distinguish it from inclusions and extensions which are fundamentally different.
Compatibility of partitions with a poset can be characterized by a closure operator on . If is a preposet, then there is a unique minimal coarsening of π such that the contraction is acyclic. This is the partition achieved by merging all pairs of blocks and such that , and we call it the closure of π with respect to P. If P is understood, then we may write this as simply . A partition π is closed (with respect to P) if , which is equivalent to being compatible with P. Geometrically, it means that for any , there is some such that for some and . If π is not closed, then has strictly lower dimension than . In this case, is the unique coarsening that is closed with respect to P and satisfies .
Still assuming that P is a poset over , and π is a partition of V, define
If is a flat of , then is a face of the (topologically) closed polyhedral cone . In the latter case, we say that π is a face partition of P. Since it is almost always clear what P is, we will usually write instead of . If is not a flat of , then the subspace still intersects in at least the line . Though this may intersect in the interior of , it is a face of , for at least one extension of P.
To characterize the facial structure of the cone , it suffices to characterize the closed face partitions. This is well known – it was first described by Geissinger [15], and also done in 1 of Stanley [16] in the characterization of the face structure of the order polytope of a poset, defined by
Our notation is a little different from [16]; for example, we do not adjoin a minimal or maximal element ( or ) to P. Also, our definition of “closed faced partitions” is in terms of rather than , but since , our “closed face partitions” correspond to those of with and as singleton blocks, yielding the faces of that don’t lie in any hyperplane . These correspond to the faces of , and each closed face intersects at least the diagonal . Clearly, if π is a closed face partition of P, then the subposets induced by the individual blocks are connected (that is, their Hasse diagrams are connected). We call such a partition connected, with respect to P.
Theorem 2.1.
([16], Theorem 1.2) Let P be a poset over . A partition π of V is a closed face partition of P if and only if it is connected and compatible with P.
To summarize Theorem 2.1, characterizing the faces of amounts to characterizing which face partitions π are closed. If π is not compatible with P, then it is not closed. On the other hand, if π not connected, then the flat might cut through the interior of (and hence of ); see Example 2.2, or it might lie in a proper face of ; see Example 2.5. In either case, π is not a face partition.
Example 2.2.
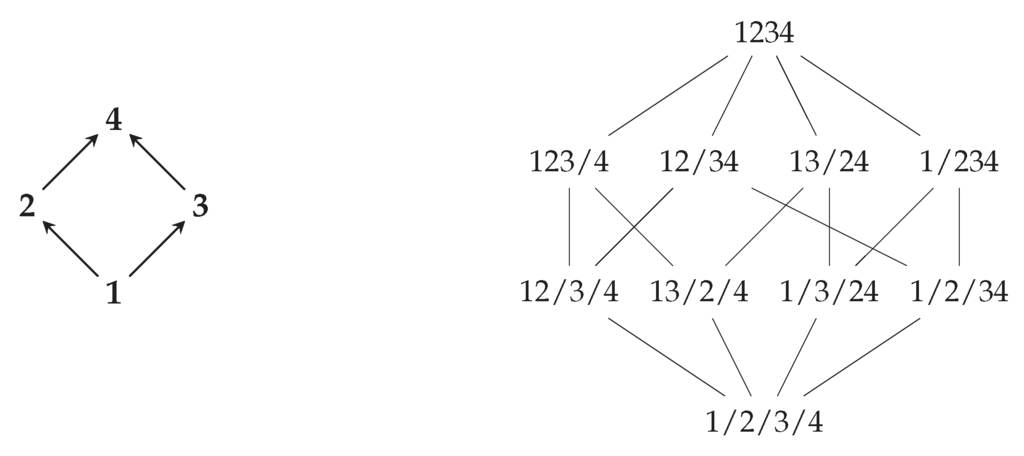
Let P be the poset shown at left in Figure 1; its lattice of closed face partitions is shown at right. In this and in later examples, we denote the blocks of a partition using dividers rather than set braces, e.g., .

Figure 1.
A poset P and its lattice of closed face partitions.
The partition is closed but not connected; it is not a face partition because intersects the interior of . The partition is connected but not closed. Finally, the partition is neither connected nor closed. However, both π and are face partitions because the subspaces and intersect in the line , which is the flat . Therefore, both of these partitions have the same closure: .
If is a closed face partition of P, then is an r-dimensional flat of , and the closed face is an r-dimensional subset of . The interior of with respect to the subspace topology of will be called an open face. So as to avoid confusion between open and closed faces, and open and closed chambers, we will speak of faces as being features of the actual poset, not of the chambers. It should be easy to relate these definitions back to the chambers if one so desires.
Definition 2.3. A set is a closed face of the poset P if for some closed face partition of V. The interior of with respect to the subspace topology of is called an open face of P, and denoted . Let and denote the set of open and closed faces of P, respectively. Finally, define the faces of the graphic arrangement to be the faces of the posets over G:
Faces of co-dimension 1 are called facets.
Remark 2.4.
The dimension of the face is the number of strongly connected components of . As long as G is connected, there is a unique 1-dimensional face of , which is the line and is contained in the closure of every chamber. There are no 0-dimensional faces of . The open n-dimensional faces of are its chambers. Additionally, is a disjoint union of open faces of :
Example 2.5.
Let P be the poset over , where the only covering relation is , and consider the partition , which is closed but not connected with respect to P. Explicitly, and are the following sets:
Since , the intersection is , which is not a face of the polyhedral cone ; rather it is a proper subset of the face
Finally, note that is a face of an extension of P, namely the one formed by adding the covering relation . Therefore, π is not a face partition of P, but it is a face partition of .
If P is a fixed poset over G, then there is a canonical isomorphism between the lattice of closed face partitions and the lattice of faces of P, given by the mapping . Recall that since π is closed, is an acyclic preposet (i.e., poset) of size . This induces an additional preposet over V (i.e., of size ), which is with the additional relations that for all . We will say that this is a preposet over G, because it can be described by an (not necessarily acyclic) orientation of G, where one allows bi-directed edges. These were called Type B fourientations in a recent paper by Backman and Hopkins [17], though we will simply call them “orientations” since we don’t refer to them often, and when we do, it should always be clear from the context that bi-directed edges are allowed. The notation reflects the fact that this orientation can be constructed by starting with some and then making each edge bidirected if both endpoints are contained in the same block of π. Specifically, orients edge as if and as if additionally . Let be the set of all such orientations of G that arise in this manner. That is,
when working with preposets over G, sometimes it is more convenient to quotient out by the strongly connected components and get an acyclic graph . Note that this quotient is the same as for at least one . In particular, will always do. In summary, a preposet over G can be expressed several ways:
- (i)
- as a unique orientation of G, where π is the partition into the strongly connected components;
- (ii)
- as a unique acyclic quotient of an acyclic orientation .
Note that while the orientation and acyclic quotient are both unique to the preposet, the choice of representative ω is not. Regardless of how an element in is written, it induces a canonical partial order on the blocks of π. However, information is lost by writing it this way; in particular, the original graph G cannot necessarily be determined from just .
The mapping in Equation (2) can be extended to all of by adding both edges and if . This induces a bijection between the set of all preposets on G and the set of faces of the graphic hyperplane arrangement:
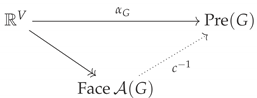

Consequently, for any preposet over G, we can let denote the open face of containing any (equivalently, all) such that .
Moreover, if we restrict to the preposets on exactly r strongly connected components, then the -fibers are the r-dimensional open faces of . If x lies on a face for some poset P and closed face partition , then the preposet has vertex set ; these are the strongly connected components of the orientation .
3. Morphisms of Ordinary Posets
Poset isomorphisms are easy to describe both combinatorially and geometrically. An isomorphism between two finite posets P and on vertex sets V and is a bijection characterized
- combinatorially by the condition that is equivalent to for all ;
- geometrically by the equivalent condition that the induced isomorphism maps to bijectively.
By “induced isomorphism,” we mean that Φ permutes the coordinates of in the same way that ϕ permutes the vertices of V:
Morphisms of ordinary posets are also well understood. The “combinatorial” definition is easiest to modify. If P and are as above, then a morphism, or order-preserving map, is a function such that implies for all . The geometric characterization is trickier because quotients, injections, and extensions are inherently different. These three types of order-preserving maps generate all poset morphisms, up to isomorphism. Below we will review this and give a geometric interpretation of each, which will motivate their toric analogues.
3.1. Quotient
3.1.1. Contracting Partitions
Roughly speaking, a quotient morphism of a poset is described combinatorially by contracting ω by the blocks of a partition while preserving acyclicity. Geometrically, the chamber is orthogonally projected to , where . This is the mapping
By construction, the image of this map is , which is a face of P if π is a face partition. Though the map extends to the closure , it does not do so in a well-defined manner; the image for some x on a hyperplane depends on the choice of P, and each hyperplane intersects at least two (closed) chambers along facets, and intersects the boundary of every chamber (because each hyperplane and each closed chamber contains the line ).
Remark 3.1.
The map simply replaces every coordinate of x by the average of the coordinates from the same π-block. This is a basic fact from statistics about the usual estimator for the mean; see a book on linear models, e.g., Chapter 2 (Estimation) of [18] for details.
Example 3.2.
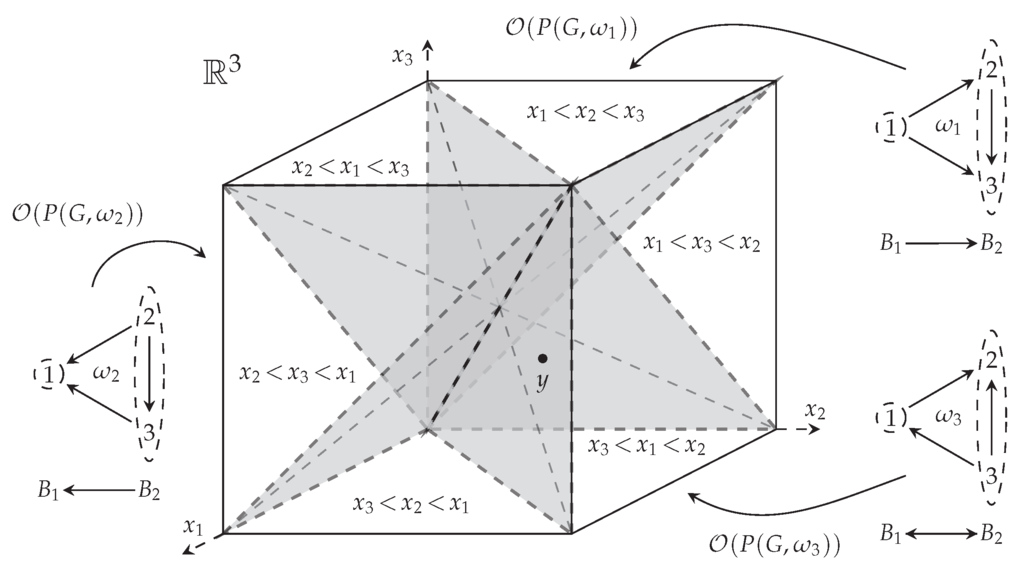
Let , the complete graph on three vertices. There are six acyclic orientations of G, and three of them are shown in Figure 2. The curved arrows point to the chamber of for each , . The intersection of each closed chamber with is the order polytope, .

Figure 2.
The hyperplane arrangement for . Three orientations in are shown, along with the corresponding chambers of , and the preposet that results when contracting by the partition of V. The intersection of each (closed) chamber with is the order polytope of . The point y is supposed to lie on the hyperplane .
Contracting and by the partition yields a poset over ; these are shown directly below the orientations in Figure 2. Therefore, π is closed with respect to and . Geometrically, the flat intersects the closed chambers for in 2-dimensional faces.
In contrast, contracting by π yields a preposet that is not a poset. Therefore, π is not closed with respect to . Indeed, , and the flat intersects the closed chamber in a line. Modding out the preposet by its strongly connected components yields a one-element poset. Geometrically, the chamber projects onto the one-dimensional face .
To see why the map from Equation (7) does not extend to the closure of the chambers in a well-defined manner, consider the point y shown in Figure 2 that lies on the hyperplane , and the same partition, . The orthogonal projection as defined in Equation (7) and extended continuously to the closed chamber maps onto the line . However, if is the other closed chamber containing y (that is, the one for which ), then extended to the closure maps onto a two-dimensional closed face . The point y is projected orthogonally onto the plane , and does not end up on the line .
Despite this, there is a natural way to extend to all of , though not continuously. To do this, we first have to extend the notion of the closure of a partition π with respect to a poset, to a preposet P over G. This is easy, since the original definition did not specifically require P to actually be a poset. Specifically, the closure of π with respect to a preposet P is the unique minimal coarsening of π such that is acyclic. The map can now be extended to all of , as
where is the map from Equation (5) sending a point to the unique open face (i.e., preposet over G) containing it.
Let us return to the case where P is a poset over G, and examine the case when π is not a face partition of P. Indeed, for an arbitrary partition π of V with , the subset need not be a face of P; it could cut through the interior of the chamber. In this case, it is the face of at least one extension of P. Specifically, let be the graph formed by making each block a clique, and let be the graph formed by contracting these cliques into vertices, with loops and multiedges removed. Clearly, is a flat of the graphic arrangement (this choice is not unique, but it is a canonical one that works). Thus, the set , for , is a closed face of , and hence a face of some poset over for which .
Whether or not π is a face partition of a particular poset P over G, the map in Equation (8) projects a chamber onto a flat of , where . From here, we need to project it homeomorphically onto a coordinate subspace of so it is a chamber of a lower-dimensional arrangement. Specifically, for a partition , let be any subset formed by removing all but 1 coordinate from each , and let be the induced projection. Each hyperplane in either gets mapped to a hyperplane in or to all of , and every hyperplane in is the -image of at least one hyperplane in . In other words, -preimage of is . The following ensures that is a homeomorphism, and that the choice of W does not matter. We omit the elementary proof.
Lemma 3.3.
Let be a partition of V, and with . The restriction is a homeomorphism.
Moreover, all such projection maps for a fixed π are topologically conjugate in the following sense: If with and projection map , and σ is the permutation of V that transposes each with , then the following diagram commutes:
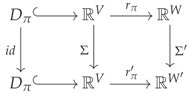

Here, is the map , with Σ and being the induced linear maps as defined in Equation (6).
By convexity, induces a well-defined map making the following diagram commute:
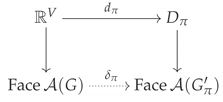

The map is best understood by looking at a related map on closed faces. Let be a closed face of , for some closed face partition . Then the map is defined by
The map is between the corresponding open faces. These faces are then mapped to faces of the arrangement under the projection . [Alternatively, we could simply identity the quotient space with .]
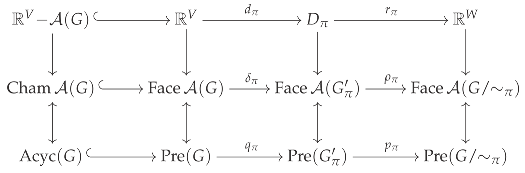
To summarize, the open faces of arise from preposets in , where without loss of generality, the blocks for are the strongly connected components. The contraction of this preposet formed by adding all relations (edges) of the form for yields a preposet over . Then, modding out by the strongly connected components yields an acyclic preposet, i.e., a poset. This two-step process is a composition of maps
Here, , the closure of π with respect to the preposet , which we have been denoting by under a slight abuse of notation.
Putting this all together gives a commutative diagram that illustrates the relationship between the points in , the open faces of the graphic arrangement , and the preposets over G. The left column depicts the acyclic preposets – those that are also posets.

3.1.2. Intervals and Antichains
Poset morphisms that are quotients are characterized geometrically by projecting the chamber onto a flat of for some partition , and then homeomorphically mapping this down to a chamber of a lower-dimensional graphic arrangement . Equivalently, contracting by yields an acyclic preposet . It is well known that contracting a poset by an interval or an antichain yields an acyclic preposet. Verification of this is elementary, but first recall how these are defined.
Definition 3.4.
Let P be a poset over V. An interval of P is a subset , sometimes denoted , such that
An antichain of P is a subset such that any two elements are incomparable.
We will take a moment to understand how contracting an interval or antichain fits in the partition framework described above, which will help us understand the toric analogue. Given a nonempty subset , define the partition of V by
Contracting an interval in a poset P yields the poset . In this case, is a face partition and is a -dimensional face of P. Similarly, collapsing an antichain yields the poset . Note that is a flat of and lies on the boundary of , but the )-dimensional subspace cuts through the interior of . For both of these cases, and , the subspace is trivially a flat of .
3.2. Extension
Given two posets on a set V, one says that is an extension of P when implies . In this case, the identity map is a poset morphism. Geometrically, is an extension of P if and only if one has an inclusion of their open polyhedral cones . Each added relation amounts to intersecting with the half-space .
3.3. Inclusion
The last operation that yields a poset morphism is an injection . This induces a canonical inclusion . Note that implies , but not necessarily vice-versa. Thus, up to isomorphism, an inclusion can be decomposed into the composition , where the first map adds the elements of to P but no extra relations, and then the map is an extension. This gives an inclusion of polyhedral cones:
3.4. Summary
Up to isomorphism, every morphism from a poset can be decomposed into a sequence of three steps:
- (i)
- quotient: Collapsing G by a partition π that preserves acyclicity of ω (projecting to a flat of for some closed partition ).
- (ii)
- inclusion: Adding vertices (adding dimensions).
- (iii)
- extension: Adding relations (intersecting with half-spaces).
In the special case of the morphism being surjective, the inclusion step is eliminated and the entire process can be described geometrically by projecting to a flat and then intersecting with a collection of half-spaces.
4. Toric Posets and Preposets
4.1. Toric Chambers and Posets
Toric posets, introduced in [9], arise from ordinary (finite) posets defined by acyclic orientations under the equivalence relation generated by converting maximal elements into minimal elements, or sources into sinks. Whereas an ordinary poset corresponds to a chamber of a graphic arrangement , a toric poset corresponds to a chamber of a toric graphic arrangement , which is the image of under the quotient map . Elements of are toric hyperplanes
Though a point is a residue class, we will at times want to compare its coordinates, modulo 1. The convenient way to do this is to identify x with its unique representative in , and under this slight abuse of notation we can unambiguously make statements such as .
Definition 4.1.
A connected component c of the complement is called a toric chamber for G, or simply a chamber of . Let denote the set of all chambers of .
A toric poset P is a set c that arises as a toric chamber for at least one graph G. We may write or , depending upon the context.
If we fix a graph and consider the arrangement , then each point in naturally determines a preposet on G via a map . Explicitly, for in , the directed graph is constructed by doing the following for each edge in E:
- ■
- If , then include edge ;
- ■
- If , then include edge .
The mapping is essentially the same as from Equation (5) except done modulo 1, so many of its properties are predictably analogous. For example, the undirected version of is G. The edge is bidirected in if and only if . Therefore, is acyclic if and only if x lies in ; in this case describes a poset. Otherwise it describes a preposet (that is not a poset). Modding out by the strongly connected components yields an acyclic graph that describes a poset.
Definition 4.2.
When two preposets and are such that the directed graphs and differ only by converting a source vertex (equivalence class) into a sink, or vice-versa, we say they differ by a flip. The transitive closure of the flip operation generates an equivalence relation on , denoted by ≡.
In the special case of restricting to preposets that are acyclic, we get and a bijective correspondence between toric posets and chambers of toric graphic arrangements. This is Theorem 1.4 in [9]. A generalization of this to a bijection between toric preposets and faces of the toric graphic arrangement appears later in this section (Proposition 4.11).
Theorem 4.3.
([9], Theorem 1.4) The map induces a bijection between and as follows:
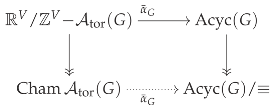
In other words, two points in have if and only if lie in the same toric chamber of .
By Theorem 4.3, every pair of a graph G and determines a toric poset, and we denote this by . Specifically, is the toric poset such that . If the graph G is understood, then we may denote the corresponding toric chamber by .
If is fixed, then the unit cube in is the union of order polytopes , any two of which only intersect in a subset of a flat of :
when G is understood, we will say that the order polytopes and are torically equivalent whenever . Under the natural quotient , each order polytope is mapped into the closed toric chamber . Moreover, by Theorem 4.3, the closed chambers of are unions of q-images of torically equivalent order polytopes.
Corollary 4.4.
Let be a toric poset, and the natural quotient. The closure of the chamber is
4.2. Toric Faces and Preposets
Let be a toric poset over . To define objects like a face of P or its dimension, it helps to first lift c up to a chamber of the affine graphic arrangement which lies in :
where is the natural quotient. The affine chambers are open unbounded convex polyhedral regions in , the universal cover of . The path lifting property guarantees that two points x and y in are in the same toric chamber if and only if they have lifts and that are in the same affine chamber. Moreover, since Corollary 4.4 characterizes the closed toric chamber as a union of torically equivalent order polytopes under a universal covering map, each closed affine chamber is a union of translated copies of torically equivalent order polytopes in .
We usually denote an affine chamber by or . Each hyperplane has a unique preimage containing the origin in called its central preimage; this is the ordinary hyperplane . Thus, the set of central preimages of is precisely the graphic arrangement in . Each closed affine chamber contains at most one order polytope for . Affine chambers whose closures contain precisely one order polytope are central affine chambers.
We will call nonempty sets that arise as intersections of hyperplanes in affine flats and nonempty sets that are intersections of hyperplanes in toric flats. Since the toric flats have a nonempty intersection, they form a lattice that is denoted , and partially ordered by reverse inclusion.
Since a toric flat of is the image of a flat of , it too is determined by a partition π of V, and so it is of the form
Since is a covering map, it is well-founded to declare the dimension of a toric flat in to be the same as the dimension of its central preimage in .
Recall that a partition is compatible with an ordinary poset P if contracting the blocks of π yields a preposet that is acyclic (also a poset). The notion of compatible partitions does not carry over well to toric posets, because compatibility is not preserved by toric equivalence. Figure 2 shows an example of this: the preposets and are acyclic but is not. Despite this, every set , whether or not it is a toric flat of , intersects the closed toric chamber in at least the line . We denote this intersection by
If does not intersect , then we say that π is a toric face partition, since it intersects the closed toric chamber along its boundary. Compare this to the definition of face partitions of an ordinary poset , which are those characterized by being a flat of the graphic arrangement of the transitive closure, or equivalently, by . The transitive closure is formed from G by adding all additional edges such that . Similarly, we can define the toric transitive closure of as the graph G along with the extra edges such that . This was done in [9], and we will return to it in the Section 5.3 when we discuss toric Hasse diagrams.
Now, let be an arbitrary partition. Since flats of are closed under intersections, there is a unique maximal toric subspace (that is, of minimal dimension) for which . The partition is the unique minimal coarsening of π for which , and it is the lattice-join of all such partitions. We call it the closure of π with respect to the toric poset P, denoted , and we define . A partition π is closed with respect to the toric poset P if . Note that the closure is defined for all partitions, not just toric face partitions.
Definition 4.5.
A set is a closed face of the toric poset P if for some closed toric face partition . The interior of with respect to the subspace topology of is called an open face of P, and denoted . Let and denote the set of open and closed faces of P, respectively. Finally, define the faces of the toric graphic arrangement to be the faces of the toric posets over G:
Toric faces of co-dimension 1 are called facets.
The following remark is the toric analogue of Remark 2.4.
Remark 4.6.
Let be a toric poset. The dimension of is simply the maximum dimension of taken over all affine chambers that descend down to . Since closed affine chambers are unions of translations of order polytopes, this is the maximum dimension of taken over all . In other words,
On the level of graphs, this is the maximum number of strongly connected components that can have for some . In particular, a partition π is closed with respect to if and only if is acyclic for some .
As long as G is connected, there is a unique 1-dimensional face of , which is the line and is contained in the closure of every chamber. There are no 0-dimensional faces of . The n-dimensional faces of are its chambers. Additionally, is a disjoint union of open faces of :
As in the case of ordinary posets, there is a canonical bijection between the closed toric face partitions of P and open faces (or closed faces) of P, via . To classify the faces of a toric poset, it suffices to classify the closed toric face partitions.
Theorem 4.7.
Let be a toric poset over . A partition π of V is a closed toric face partition of P if and only if it is connected and compatible with , for some .
The proof of Theorem 4.7 will be done later in this section, after the following lemma, which establishes that is a closure operator [19] on the partition lattice and compares it with .
Lemma 4.8.
Let ω be an acyclic orientation of a graph , and π a partition of V.
- (a)
- If π is closed with respect to , then π is closed with respect to .
- (b)
- Closure is monotone: if , then .
- (c)
- If , then .
- (d)
- .
Proof.
If π is closed with respect to , then the preposet is acyclic. By Remark 4.6, this means that π is closed with respect to , which establishes (a).
Part (b) is obvious. Part (c) follows from taking the closure of each term in the chain of inequalities :
To prove (d), let , which is closed with respect to . By (a), is closed with respect to . Using this, along with (b) applied to , yields
whence the theorem. ☐
Example 4.9.
For an example both of where the converse to Lemma 4.8 (a) fails, and where , consider , and the partition . Using the same notation as in Example 3.2 and Figure 2, we see that , because the intersection of and is one-dimensional. Equivalently, the preposet has one strongly connected component. In contrast, the intersection of with is two-dimensional. Indeed, the preposets and both have two strongly connected components, and . Therefore,
and so π is closed with respect to but not with respect to .
Proof of Theorem 4.7.
Suppose π is a closed toric face partition of , and that has dimension k. Then for some , the hyperplane must intersect the order polytope in a k-dimensional face. Thus, has dimension k for some , and so π is a face partition of . To see why π is closed with respect to , suppose there were a coarsening such that
It suffices to show that . Descending down to the torus, the intersection must have dimension at least k by Equation (17), but no more than k because . Thus, we have equality , which means , whence . Since π is a closed face partition with respect to , it is connected and compatible with by Theorem 2.1.
Conversely, suppose that π is connected and compatible with for some . By Theorem 2.1, π is a closed face partition of . Since π is connected, is a flat of . Therefore, is a toric flat of , and so is a face of the toric poset . Therefore, π is a toric face partition. Closure of π with respect to follows immediately from Lemma 4.8 (a) applied to the fact that π is closed with respect to . ☐
Unlike the ordinary case, where faces of posets are literally faces of a convex polyhedral cone, it is not quite so “geometrically obvious” what subsets can be toric faces. The following example illustrates this.
Example 4.10.
There are only two simple graphs over : The edgeless graph , and the complete graph . For both graphs, the complement is connected. The respective chambers are
and so they represent different toric posets, and . Despite this, these chambers have the same topological closures: . The lattice of flats of contains one element: , and this flat arises from the permutation . The lattice of flats of has two elements: , where , and . Thus, the closed faces of the corresponding toric posets are
The subtlety in Example 4.10 does not arise for ordinary posets, because distinct ordinary posets never have chambers with the same topological closure. In contrast, if and are both forests, then and both have a single toric chamber. This is because the number of chambers is counted by the Tutte polynomial evaluation , which is always 1 for a forest; see [9]. In this case, the closures of both chambers will be all of . A more complicated example involving a toric poset over a graph with three vertices, will appear soon in Example 4.13.
Recall the map from Equation (11) that sends a point x in to a preposet . By Theorem 4.3, when restricted to the points in , this map induces a bijection between toric posets and toric chambers. Toric faces that are open in are chambers in lower-dimensional arrangements that are contractions of , namely by the subspace . Thus, the bijection between toric equivalence classes of (n-element preposets) and toric chambers (n-dimensional faces) extends naturally to a bijection between toric preposets over G and open faces of .
Proposition 4.11.
The map induces a bijection between and as follows:
In other words, given two points in the equivalence holds if and only if lie on the same open face of .
Definition 4.12.
A toric preposet is a set that arises as an open face of a toric poset for at least one graph G.
If x lies on a toric face of P, where (without loss of generality) , then the strongly connected components of the preposet are .
Example 4.13.
Let , as in Example 3.2. The six acyclic orientations of G fall into two toric equivalence classes. The three orientations shown in Figure 2 comprise one class, and so the corresponding toric poset is for any . Equivalently, the closed toric chamber is a union of order polytopes under the natural quotient map:
This should be visually clear from Figure 2. The two chambers in are the three-dimensional faces of P. Each of the three toric hyperplanes in are two-dimensional faces of P, and these (toric preposets) correspond to the following toric equivalence classes of size-2 preposets over :
The toric flat is the unique one-dimensional face of P, and this corresponds to the unique size-1 preposet over ; when , which is trivially in its own toric equivalence class.
5. Toric Intervals and Antichains
Collapsing an interval or antichain of an ordinary poset defines a poset morphism. This remains true in the toric case, as will be shown in Section 6, though the toric analogues of these concepts are trickier to define. Toric antichains were introduced in [9], but toric intervals are new to this paper. First, we need to review some terminology and results about toric total orders, chains, transitivity, and Hasse diagrams. This will also be needed to study toric order ideals and filters in Section 7. Much of the content in Section 5.1, Section 5.2 and Section 5.3 can be found in [9]. Throughout, is a fixed undirected graph with , and coordinates of points in a toric chamber are assumed to be reduced modulo 1, i.e., .
5.1. Toric Total Orders
A toric poset is a total toric order if is a chamber of . If is a total toric order, then is a total order for each , and thus has precisely elements. Since each has exactly one linear extension, total toric orders are indexed by the cyclic equivalence classes of permutations of V:
Recall that if P and are toric posets over G, then is an extension of P if . Moreover, is a total toric extension if is a total toric order. Analogous to how a poset is determined by its linear extensions, a toric poset P is determined by its set of total toric extensions, denoted .
Theorem 5.1.
([9], Proposition 1.7) Any toric poset P is completely determined by its total toric extensions in the following sense:
5.2. Toric Directed Paths, Chains, and Transitivity
A chain in a poset is a totally ordered subset . Equivalently, this means that the elements in C all lie on a common directed path in ω. Transitivity can be characterized in this language: if i and j lie on a common chain, then i and j are comparable in . Geometrically, i and j being comparable means the hyperplane does not cut (i.e., is disjoint from) the chamber .
The toric analogue of a chain is “essentially” a totally cyclically ordered set, but care must be taken in the case when because every size-two subset is trivially totally cyclically ordered. Define a toric directed path in ω, to be a directed path such that the edge is also present. We denote such a path by . Toric directed paths of size 2 are simply edges, and every singleton set is a toric directed path of size 1. A fundamental property of toric directed paths is that up to cyclic shifts, they are invariants of toric-equivalence classes. That is, is a toric directed path of ω if and only if each has a toric directed path , for some cyclic shift in . This is Proposition 4.2 of [9], and it leads to the notion of a toric chain, which is a totally cyclically ordered subset.
Definition 5.2.
Let be a toric poset. A subset is a toric chain of P if there exists a cyclic equivalence class of linear orderings of C with the following property: for every there exists some in for which
In this situation, we will say that .
The following is a reformulation of Proposition 6.3 of [9] using the language of this paper, where notation such as and is new.
Proposition 5.3.
Fix a toric poset , and . The first three of the following four conditions are equivalent, and when , they are also equivalent to the fourth.
- (a)
- C is a toric chain in P, with .
- (b)
- For every , the set C is a chain of , ordered in some cyclic shift of .
- (c)
- For every , the set C occurs as a subsequence of a toric directed path in , in some cyclic shift of the order .
- (d)
- Every total toric extension in has the same restriction .
For ordinary posets, all subsets of chains are chains. The same holds in the toric case.
Proposition 5.4.
Subsets of toric chains are toric chains.
Having the concept of a toric chain leads to the notion of toric transitivity, which is completely analogous to ordinary transitivity when stated geometrically.
Proposition 5.5.
Let be distinct. Then the hyperplane does not cut the chamber if and only if i and j lie on a common toric chain.
5.3. Toric Hasse Diagrams
One of the major drawbacks to studying toric posets combinatorially, as equivalences of acyclic orientations (rather than geometrically, as toric chambers), is that a toric poset P or chamber generally arises in multiple toric graphic arrangements over the same vertex set. That is, one can have for different graphs, leading to ambiguity in labeling a toric poset P with a pair consisting of a graph G and equivalence class in .
Toric transitivity resolves this issue. As with ordinary posets, there is a well-defined notion for toric posets of what it means for an edge to be “implied by transitivity.” The toric Hasse diagram is the graph with all such edges removed. In Section 5.3, we encountered the toric transitive closure, which is the graph with all such edges included. In other words, given any toric poset , there is always a unique minimal pair and maximal pair with the property that the set is in iff
where ⊆ is inclusion of edges. In this case, ω can be taken to be the restriction to G of any orientation in .
Geometrically, the existence of a unique toric Hasse diagram is intuitive; it corresponds to the minimal set of toric hyperplanes that bound the chamber , and the edges implied by transitivity correspond to the additional hyperplanes that do not cut . The technical combinatorial reason for the existence of a unique Hasse diagram (respectively, toric Hasse diagram) follows because the transitive closure (respectively, toric transitive closure) is a convex closure, meaning it satisfies the following anti-exchange condition; also see [20]:
Edges in the Hasse diagram (respectively, toric Hasse diagram) are precisely those whose removal “change” the poset (respectively, toric poset), and the geometric definitions make this precise. Though the ordinary and toric cases are analogous, there are a few subtle differences. For example, consider the following “folk theorem.”
Proposition 5.6.
Let P be a poset over and . Then the following are equivalent:
- (i)
- The edge is in the Hasse diagram, .
- (ii)
- Removing enlarges the chamber .
- (iii)
- is a (closed) facet of P.
- (iv)
- The interval is precisely .
Since toric posets are defined geometrically as subsets of that are chambers of a graphic hyperplane arrangement, the equivalence (i)⇔(ii) is immediate for toric posets. Condition (iii) says that the edges of the Hasse diagram are precisely the size-2 intervals, and Condition (iv) says these are the closed face partitions having two blocks of the form .
Since adding or removing edges implied by toric transitivity does not change the toric poset, it does not change which sets are toric chains. Thus, to characterize the toric chains of , it suffices to characterize the toric chains of . The following is immediate.
Remark 5.7.
Let P be a toric poset. A size-2 subset of V is a toric chain of P if and only if is an edge of . In particular, if C is a maximal toric chain, then is an edge in .
5.4. Toric Intervals
To motivate the definition of a toric interval, it helps to first interpret the classical definition in several different ways.
Definition 5.8.
Let i and j be elements of a poset . The interval is the set I characterized by one of the following equivalent conditions:
- (i)
- ;
- (ii)
- ;
- (iii)
- .
Note that if , then , and if , then .
We will define toric intervals geometrically, motivated by Condition (i), and show how it is equivalent to the toric version of Condition (ii). In contrast, Condition (iii) has a small wrinkle—the property of lying on a directed path from i to j does not depend on the choice of for P. Specifically, if and k lies on an ω-directed path from i to j, then k lies on an -directed path from i to j. This is not the case for toric directed paths in toric posets, as the following example illustrates. As a result, we will formulate and prove a modified version of Condition (iii) for toric intervals.
Example 5.9.
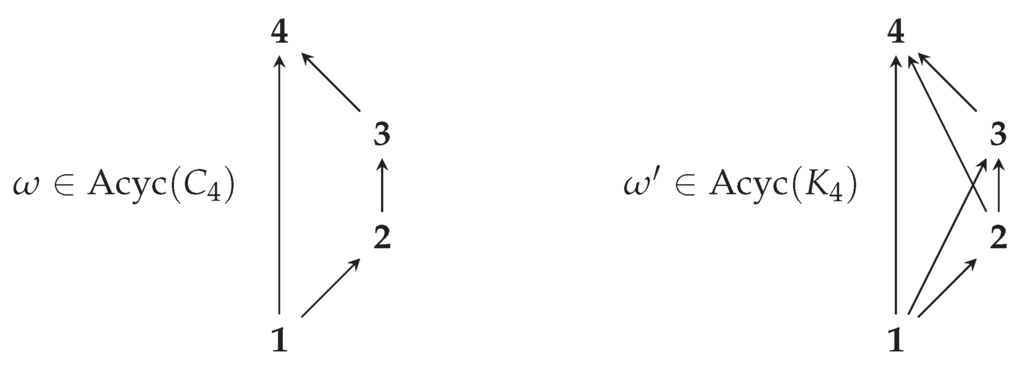
Consider the circular graph , and as shown at left in Figure 3. Let , which is a total toric order. Therefore, the toric transitive closure of is the pair , where is shown in Figure 3 on the right. Therefore, .

Figure 3.
Despite the equality , the set lies on a toric directed path in but not for any representative of .
Now, let and . The set lies on a toric directed path from 1 to 3 in (which also contains 2). However, none of the 4 representatives in contain a toric directed path from 1 to 3.
Another obstacle to formulating the correct toric analogue of an interval is how to characterize which size-2 subsets should be toric intervals. This ambiguity arises from the aforementioned “size-2 chain problem” of all size-2 subsets being totally cyclically ordered. Since ordinary intervals are unions of chains, we will require this to be a feature of toric intervals.
Definition 5.10.
Let i and j be elements of a toric poset . The toric interval is the empty set if do not lie on a common toric chain, and otherwise is the set
If there is no satisfying Equation (19), then . If , then .
Remark 5.11.
If are distinct elements of the toric interval of , then for each x in , exactly one of the following must hold:
By Theorem 5.1, we can rephrase Remark 5.11 as the toric analogue of Definition 5.8 (ii): the toric interval in P is the set of elements between i and j in the cyclic order of any total toric extension of P.
Corollary 5.12.
Suppose is a toric interval of of size . Then
Finally, the toric analogue of Definition 5.8(iii) can be obtained by first passing to the toric transitive closure.
Proposition 5.13.
Fix a toric poset . An element k is in if and only if k lies on a toric directed path in , for some .
Proof.
Throughout, let . Assume that ; the result is trivial otherwise. Suppose k is in , which means that . Take any for which i is a source. By Proposition 5.3, the elements of C occur as a subsequence of a toric directed path in , ordered . Since this is a toric chain, the edges , , and are all implied by toric transitivity. Thus, k lies on a toric directed path in , the unique orientation of whose restriction to G is .
Conversely, suppose that k lies on a toric directed path in , for some . Then C is a toric chain, ordered , hence k is in . ☐
Proposition 5.14.
Let be a toric poset. If a set is a toric interval , then there is some for which the set I is the interval of . The converse need not hold.
Proof.
Without loss of generality, assume that . The statement is trivial if . We need to consider the cases and separately. In both cases, we will show that one can take to be any orientation that has i as a source.
First, suppose , which means that is an edge of G. Take any for which i is a source. Since , there is no other on a directed path from i to j in , as this would form a toric directed path. Therefore, the interval in is simply .
Next, suppose . As before, take any such that i is a source in . Since , the directed edge is present, and so by Proposition 5.13, consists of all that lie on a directed path from i to j. This is precisely the definition of the interval in .
To see how the converse can fail, take G to be the line graph on 3 vertices, and ω to be the orientation . In , the interval is but since 1 and 3 do not lie on a common toric chain, in . ☐
Proposition 5.15.
For any toric poset ,
Proof.
Given the toric Hasse diagram of , the ordinary Hasse diagram of is obtained by removing the edge for each toric directed path in of size at least . This establishes the first inequality in Equation (21).
The second inequality is obvious. Loosely speaking, the final equality holds because edges in the toric transitive closure are precisely the size-2 toric chains, which are precisely the subsets that are size-2 chains in every representative poset. We will prove each containment explicitly. For “⊆”, take an edge of , which is a size-2 toric chain. By Proposition 5.3, is a toric chain of for all , which means that it is an edge of the transitive closure . The “⊇” containment is analogous: suppose is an edge of for each . Then by Proposition 5.3, it is a toric chain of P, and hence an edge of . ☐
5.5. Toric Antichains
An antichain of an ordinary poset P is a subset characterized
- combinatorially by the condition that no pair with are comparable, that is, they lie on no common chain of P, or
- geometrically by the equivalent condition that the -dimensional subspace intersects the open polyhedral cone in .
As shown in [9], these two conditions in the toric setting lead to different notions of toric antichains which are both easy to formulate. Unlike the case of ordinary posets, these two definitions are non-equivalent; leading to two distinct versions of a toric antichains, combinatorial and geometric. The following is the geometric one which we will use in this paper. Its appearance in Proposition 5.17, which is one of the “For Some” structure theorems listed in the Introduction, suggests that it is the more natural toric analogue of the two.
Definition 5.16. Given a toric poset P on V, say that is a geometric toric antichain if intersects the open toric chamber in .
The following characterization of toric antichains was established in [9]. It follows because if intersects the open toric chamber in , then intersects the open chamber upstairs in .
Proposition 5.17.
Let be a toric poset. Then a set is a geometric toric antichain of P if and only if A is an antichain of for some .
6. Morphisms of Toric Posets
Morphisms of ordinary posets have equivalent combinatorial and geometric characterizations. In contrast, while there seems to be no simple or obvious combinatorial description for morphisms of toric posets, the geometric version has a natural toric analogue.
Firstly, it is clear how to define a toric isomorphism between two toric posets P and on vertex sets V and : a bijection such that the induced isomorphism on maps to bijectively. The other types of ordinary poset morphisms have the following toric analogues:
- ■
- quotients that correspond to projecting the toric chamber onto a flat of for some closed toric face partition ;
- ■
- inclusions that correspond to embedding a toric chamber into a higher-dimensional chamber;
- ■
- extensions that add relations (toric hyperplanes).
Since every poset morphism can be expressed as the composition of a quotient, an inclusion, and an extension, it is well-founded to define a toric poset morphism to be the composition of the toric analogues of these maps. In the remainder of this section, we will describe toric morphisms in detail. Most of the difficulties have already been done in Section 3, when interpreting the well-known concept of an ordinary poset morphism geometrically. In contrast, this section is simply an adaptation of this geometric framework from to , though there are some noticeable differences. For example, there is no toric analogue of intersecting a chamber with a half-space, because the torus minus a hyperplane is connected.
6.1. Quotient
In the ordinary poset case, a quotient is performed by contracting by a partition . Each gets collapsed into a single vertex, and the resulting acyclic graph is denoted by , which is an element of . This does not carry over to the toric case, because in general, contracting a partition will make some representatives acyclic and others not. However, the geometric definition has a natural analogue.
Now, let be a toric poset, and π be any partition of V closed with respect to P, i.e., . By construction, is a flat of , and so the subset is a face of . First, we need a map that projects a point x in onto this face, which is relatively open in the subspace topology of . This can be extended to the entire torus, by taking the unique map that makes the following diagram commute, where is the mapping from Equation (9):
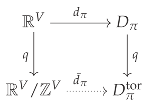
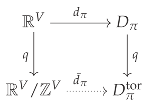
Explicitly, the map takes a point , lifts it to a point in an order polytope in , projects it onto the flat as in Equation (9), and then maps that point down to the toric flat . In light of this, we will say that the map is a projection onto the toric flat .
After projecting a chamber onto a flat of , we need to project it homeomorphically onto a coordinate subspace of so it is a chamber of a lower-dimensional toric arrangement. As in the ordinary case, let be any subset formed by removing all but 1 coordinate from each , and let be the induced projection. The -image of will be the toric arrangement . As before, the following easily verifiable lemma ensures that our choice of does not matter.
Lemma 6.1.
Let be a partition of V, and with . The restriction is a homeomorphism.
Moreover, all such projection maps for a fixed π are topologically conjugate in the following sense: If with , and projection map , and σ is the permutation of V that transposes each with , then the following diagram commutes:
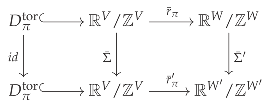 here, is the map , with and being the induced linear maps as defined in Equation (6), but done modulo 1.
here, is the map , with and being the induced linear maps as defined in Equation (6), but done modulo 1.
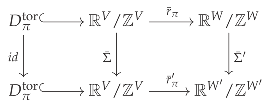
By convexity (in the fundamental affine chambers), two points in the same face of get mapped to the same face in . In other words, induces a well-defined map from to making the following diagram commute:
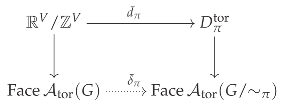

Explicitly, the map is easiest to defined by the analogous map on closed faces:
The open faces of are then mapped to faces of the arrangement under the projection . Combinatorially, the open faces of are toric preposets over G (i.e., in ). These are mapped to toric preposets over via the composition
The following commutative diagram illustrates the relationship between the points in , the faces of the toric graphic arrangement , and the toric preposets over G. The left column depicts the toric preposets over G that are also toric posets.
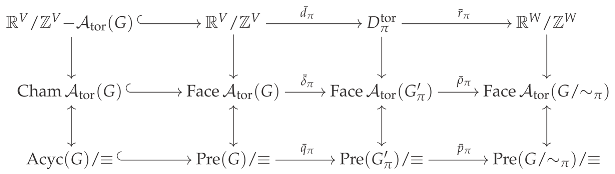

To summarize, toric poset morphisms that are quotients are characterized geometrically by projecting the toric chamber onto a flat of , for some closed toric face partition . Applying Theorem 4.7 gives a combinatorial interpretation of this, which was not a priori obvious.
Corollary 6.2.
Let be a toric poset. Contracting G by a partition yields a morphism to a toric poset over if and only if is acyclic for some orientation . □
The following is now immediate from Propositions 5.14 and 5.17.
Corollary 6.3.
Let P be a toric poset over V. Then contracting a toric interval or a geometric toric antichain defines a toric morphism. □
6.2. Inclusion
Just like for ordinary posets, a toric poset can be included in larger one. Let P be a poset over V and let . The simplest injection adds vertices (dimension) but no edges (extra relations). In this case, the inclusion defines a canonical inclusion . This sends the arrangement in , where , to the same higher-dimensional arrangement:
The toric chamber is sent to the chamber
More generally, an injection can have added relations in either among the vertices in P or those in . Such a map is simply the composition of an inclusion described above and a toric extension, described below.
6.3. Extension
Extensions of ordinary posets were discussed in Section 3.2. A poset is an extension of P (both assumed to be over the same set V) if any of the three equivalent conditions holds:
- ■
- implies ;
- ■
- , where ⊆ is inclusion of edge sets;
- ■
- .
The first of these conditions does not carry over nicely to the toric setting, but the second two do. A toric poset is a toric extension of P if and only one has an inclusion of their open polyhedral cones in , which is equivalent to .
6.4. Summary
Up to isomorphism, every toric poset morphism can be decomposed into a sequence of three steps:
- (i)
- quotient: Collapsing G by a partition π that preserves acyclicity of some (projecting to a flat of for some partition ).
- (ii)
- inclusion: Adding vertices (adding dimensions).
- (iii)
- extension: Adding relations (cutting the chamber with toric hyperplanes).
Note that in the special case of the morphism being surjective, the inclusion step is eliminated and the entire process can be described geometrically by projecting to a toric flat and a then adding toric hyperplanes.
7. Toric Order Ideals and Filters
Let P be a poset over a set V of size at least 2, and suppose is a morphism to a poset over a size-2 subset . This is achieved by projecting onto a flat of such that has at most two blocks, and hence is at most 2-dimensional. A point on has at most two distinct entries. Thus, the partition of V satisfies
- ■
- for all in I;
- ■
- for all in J;
- ■
- for all and .
The set I is called an order ideal or just an ideal of P and J is called a filter.
Ideal/filter pairs are thus characterized by closed partitions π of V such that intersects in at most two dimensions. The set of ideals has a natural poset structure by subset inclusion. Allowing I or J to be empty, this poset has a unique maximal element (corresponding to ) and minimal element (corresponding to ). Moreover, the order ideal poset is a lattice; this is well-known [21]. Similarly, the set of filters is a lattice as well.
Toric order ideals and filters can be defined similarly.
Definition 7.1.
Let P be a toric poset over V, and suppose is a morphism to a toric poset over a size-2 subset . This projects onto a toric flat of for some such that is at most 2-dimensional. For the partition of V, each point on satisfies
- ■
- for all in I;
- ■
- for all in J.
The set I is called a toric order ideal of P.
Remark 7.2.
By symmetry, if I is a toric order ideal, then so is . A toric filter can be defined analogously, and it is clear that these two concepts are identical. Henceforth, we will stick with the term “toric filter” to avoid ambiguity with the well-established but unrelated notion of a toric ideal from commutative algebra and algebraic geometry [22].
By construction, toric filters are characterized by closed toric partitions π of V such that intersects in at most two dimensions – either a two-dimensional face of P or of an extension over .
Proposition 7.3.
Let be a toric poset. The following are equivalent for a subset .
- (i)
- I is a toric filter of ;
- (ii)
- I is an ideal of for some ;
- (iii)
- I is a filter of for some ;
- (iv)
- In at least one total toric extension of , the elements in I appear in consecutive cyclic order.
Proof.
The result is obvious if or , so assume that , and . This forces to be two-dimensional (rather than one-dimensional).
(i)⇒(ii): If I is a toric filter of , then intersects in two-dimensions, and so intersects an order polytope in two-dimensions, for some . Therefore, intersects the chamber in two-dimensions, and hence I is an ideal of .
(ii)⇒(i): Suppose that I is an ideal of for . Then is two-dimensional, and it descends to a two-dimensional face of the toric poset or of some extension (if intersects the interior). Therefore, I is a toric filter of .
(ii)⇔(iii): Immediate by Remark 7.2 upon reversing the roles of I and .
(ii)⇒(iv): If I is a size-k ideal of , then by a well-known property of posets, there is a linear extension of the form , where each . The cyclic equivalence class is a total toric extension of in which the elements of I appear in consecutive cyclic order.
(iv)⇒(ii): Suppose is a toric total extension of . This means that for some ,
The unique preimage of this point in under the quotient map is in the order polytope of some that maps into . Since the coordinates of are totally ordered as in Equation (22), is a linear extension of . Moreover, the coordinates in I form an initial segment of this linear extension, hence I is an ideal of .
(iii)⇔(iv): Immediate by Remark 7.2 upon reversing the roles of I and . ☐
Proposition 7.3 along with a result of Stanley gives a nice characterization of the toric filters in terms of vertices of order polytopes. Every filter I of a poset P has a characteristic function
We identify with the corresponding vector in .
Proposition 7.4.
([16], Corollary 1.3) Let P be a poset. The vertices of the order polytope are the characteristic functions of filters of P.
Given a toric poset, we can define the characteristic function of a toric filter similarly. However, one must be careful because under the canonical quotient to the torus, the vertices of every order polytope get identified to . Therefore, we will still identify with a point in , not .
Corollary 7.5.
Let be a toric poset and . Then is the characteristic function of a toric filter of P if and only if is a vertex of for some .
Let denote the set of toric filters of P. This has a natural poset structure by subset inclusion. Once again, there is a unique maximal element and minimal element .
Proposition 7.6.
With respect to subset inclusion and cardinality rank function, is a graded poset.
Proof.
Let be a toric poset over . It suffices to show that every nonempty toric filter J contains a toric filter of cardinality .
By Proposition 7.3, the set J is an order ideal of for some . Choose any minimal element of , which is a source of . Let be the orientation obtained by flipping v into a sink. The set is an ideal of , and so by Proposition 7.3, it is a toric filter of . ☐
Example 7.7.
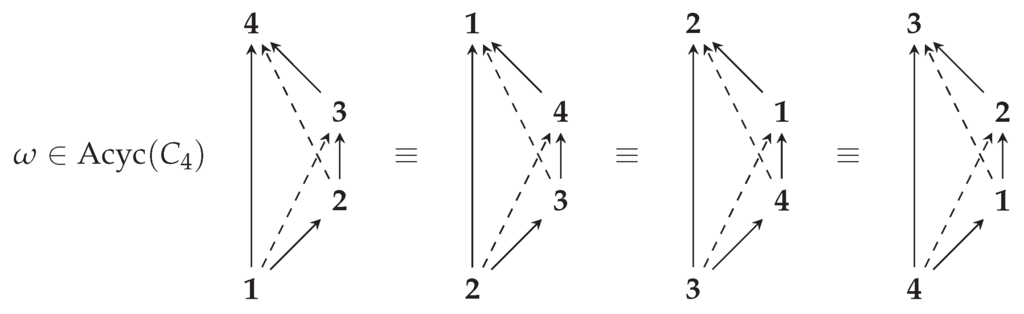
Let , the circle graph on 4 vertices, and let be the orientation shown at left in Figure 4. The Hasse diagram of the poset is a line graph , and the transitive closure is . Since V is a size-4 toric chain, it is totally cyclically ordered in every , and the dashed edges are additionally implied by toric transitivity. Thus,

Figure 4.
The four torically equivalent orientations to , shown at left. The edges implied by toric transitivity are dashed.
The 4 torically equivalent orientations are shown in Figure 4. The only total toric extension of is
and this is shown at right in Figure 5. The toric filters are all subsets of V that appear as an initial segment in one of these four total orders. The poset is shown at left in Figure 5. Note that unlike the ordinary poset case, it is not a lattice.
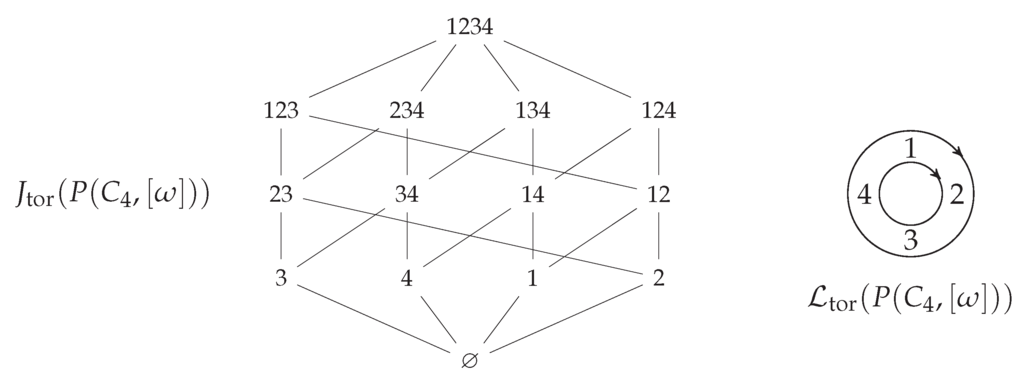
Figure 5.
The toric filters of the toric poset form a poset that is not a lattice. The vertices should be thought of as subsets of ; order does not matter. That is, 134 represents .
Example 7.8.

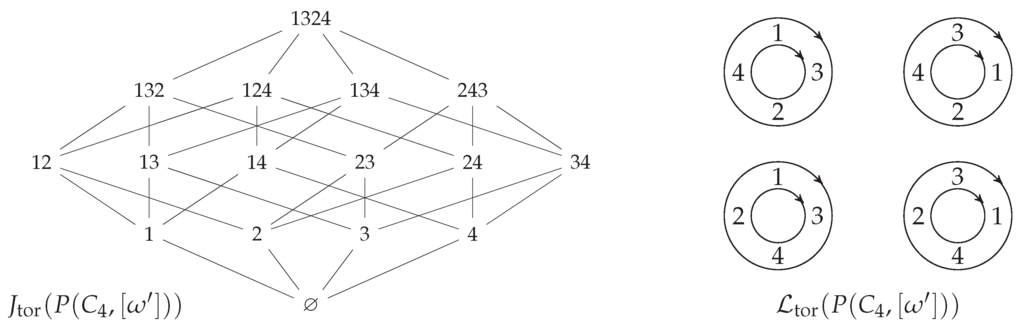
Let , as in Example 7.7, but now let be the orientation shown at left in Figure 6. The only nonempty toric chains are the four vertices (size 1) and the four edges (size 2). Since has no toric chains of size greater than 2, the Hasse diagram and the transitive closure of the toric poset are both . Note that the transitive closure of the (ordinary) poset contains the edge , and so as graphs, . The 6 torically equivalent orientations of are shown in Figure 6. There are four total toric extensions of which are shown on the right in Figure 7, as cyclic words. The toric filters are all subsets of V that appear as a consecutive segment in one of these four total orders. The poset of toric filters is shown at left in Figure 7. In this particular case, the poset of toric filters is a lattice. In fact, it is isomorphic to a Boolean lattice, because every subset of appears consecutively (ignoring relative order) in one of the four cyclic words in Figure 7.

Figure 6.
The six torically equivalent orientations to , shown at left.

Figure 7.
The toric filters of the toric poset form a poset that happens to be a lattice. Each toric filter appears as a consecutive sequence in one of the total toric extensions, shown at right.
8. Application to Coxeter Groups
A Coxeter system is a pair consisting of a Coxeter groupW generated by a finite set of involutions with presentation
where for . The corresponding Coxeter graph Γ has vertex set and edges for each labeled with (label usually omitted if ). A Coxeter element is the product of the generators in some order, and every Coxeter element defines a partial ordering on S via an acyclic orientation : Orient iff precedes in some (equivalently, every) reduced expression for c. Conjugating a Coxeter element by an initial generator (note that ) cyclically shifts it:
and the corresponding acyclic orientation differs by reversing the orientations of all edges incident to , thereby converting it from a source to a sink vertex. In 2009, H. and K. Eriksson showed [2] that two Coxeter elements c and are conjugate if and only if . Thus, there are bijections between the set of Coxeter elements and , as well as between the corresponding conjugacy classes and the toric equivalence classes:
As an example, suppose , the affine Coxeter group of type A, and let (using instead of the usual ), as shown below:


The conjugate Coxeter elements to are thus , , , and . The toric filters of describe which subwords can appear in an initial segment of some reduced expression of one of these conjugate Coxeter elements. The poset of these toric filters was shown in Figure 5 (replace k with ).
Now, consider the element in , as shown below:


The toric equivalence class containing has six orientations, which were shown in Figure 6. Each of these describes a unique conjugate Coxeter element:
These are listed above so that the Coxeter element in the column corresponds to the orientation in Figure 6. The linear extensions of each orientation describe the reduced expressions of the corresponding Coxeter element, which are listed in the same column above.
9. Concluding Remarks
In this paper, we further developed the theory of toric posets by formalizing the notion of toric intervals, morphisms, and order ideals. In some regards, much of the theory is fairly analogous to that of ordinary posets, though there are some noticeable differences. Generally speaking, the one recurring theme was the characterization of the toric analogue of a feature in by the characterization of the ordinary version of that feature in either for some , or for all .
One question that arises immediately is whether there is a toric order complex. While there may exist such an object, there are some difficulties unique to the toric case. For example, a poset is completely determined by its chains, in that if one specifies which subsets of V are the chains of P, and then the toric order of the elements within each chain, the entire poset can be reconstructed. This is not the case for toric posets, as shown in Figure 8. Here, two torically non-equivalent orientations of are given, but the toric posets and have the same sets of toric chains: the 5 vertices and the 5 edges.
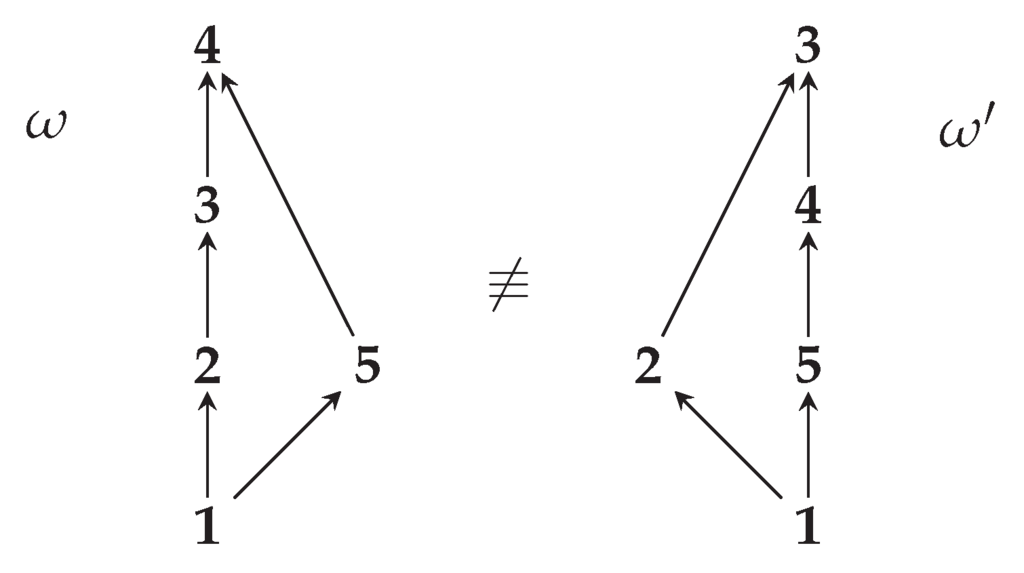
Figure 8.
Two non-torically equivalent orientations in for which and have the same set of toric chains.
The fact that an ordinary poset is determined by its chains just means that once one specifies the total order between every chain of size , then the entire partial order is determined. The problem for toric posets, which we encountered in this paper, is that every size-2 subset is trivially cyclically ordered, whether it lies on a toric chain or not. In other words, a total order can be defined on two elements, but a cyclic order needs three. The analogous statement for toric posets would be that specifying the total cyclic order between every toric chain of size specifies the entire toric order. Such a statement would establish the intuitive idea that knowing all total cyclic orders should determine the toric partial order “modulo the size-2 toric chains.” Current works suggests that there is an analogue of the aforementioned properties for toric posets, but it requires a new generalization of the concept of a chain. The details are too preliminary and complicated to describe here, and it is not clear whether it will lead to a combinatorial object such as a toric order complex. Without this, there might not be a natural way to study toric posets topologically.
Another important feature of ordinary posets that does not seem to have any obvious toric analogue are Möbius functions, and this is vital to much of the theory of ordinary posets. Recall the analogy from the Introduction about how topology is like “analysis without the metric.” Similarly, many of the basic features of ordinary posets have toric analogues, despite the fact that toric posets have no binary relation. However, much of the more advanced theory is likely to fail because one also seems to lose valuable tools such as an order complex and a Möbius function. Even the theory that does carry over has its shortcomings. For example, morphisms have a simple combinatorial characterization using the binary relation: implies . The geometric definition requires a patchwork of quotients, extensions, and inclusions. It would be desirable to have a more “holistic” characterization of toric poset morphisms, though it is not clear that that such a description should exist.
Finally, the connection of toric posets to Coxeter groups is the subject of a paper nearing completion on cyclic reducibility and conjugacy in Coxeter groups. Loosely speaking, reduced expressions can be formalized as labeled posets called heaps. This was formalized by Stembridge [23,24] in the 1990s. The fully commutative (FC) elements are those such that “long braid relations” (e.g., ) do not arise. Equivalently, they have a unique heap. The cyclic version of the FC elements are the cyclically fully commutative CFC elements, introduced by the author and collaborators in [25]. In 2013, T. Marquis showed that two CFC elements are conjugate if and only if their heaps are torically equivalent [26]. These elements were further studied by M. Pétréolle [27]. In our forthcoming paper, we will formalize the notion of a toric heap, which will essentially be a labeled toric poset. This allows us to formalize objects such as cyclic words, cyclic commutativity classes, and develop a theory of cyclic reducibility in Coxeter groups using the toric heap framework.
Conflicts of Interest
The author declares no conflict of interest.
References
- Eriksson, K. Node firing games on graphs. Contemp. Math. 1994, 178, 117–127. [Google Scholar]
- Eriksson, H.; Eriksson, K. Conjugacy of Coxeter Elements. Electron. J. Combin. 2009, 16, 9. [Google Scholar]
- Shi, J.Y. Conjugacy Relation on Coxeter Elements. Adv. Math. 2001, 161, 1–19. [Google Scholar] [CrossRef]
- Speyer, D. Powers of Coxeter Elements in Infinite Groups are Reduced. Proc. Am. Math. Soc. 2009, 137, 1295–1302. [Google Scholar] [CrossRef]
- Chen, B. Orientations, lattice polytopes, and group arrangements I, Chromatic and tension polynomials of graphs. Ann. Comb. 2010, 13, 425–452. [Google Scholar] [CrossRef]
- Ehrenborg, R.; Slone, M. A geometric approach to acyclic orientations. Order 2009, 26, 283–288. [Google Scholar] [CrossRef]
- Propp, J. Lattice structure for orientations of graphs. 1993. Available online: http://arxiv.org/abs/math/0209005 (accessed on 30 May 2016).
- Marsh, R.; Reineke, M.; Zelevinsky, A. Generalized associahedra via quiver representations. Trans. Am. Math. Soc. 2003, 355, 4171–4186. [Google Scholar] [CrossRef]
- Develin, M.; Macauley, M.; Reiner, V. Toric partial orders. Trans. Am. Math. Soc. 2016, 368, 2263–2287. [Google Scholar] [CrossRef]
- Greene, C. Acyclic orientations. In Higher Combinatorics; Aigner, M., Ed.; D. Reidel: Dordrecht, The Netherlands, 1977; pp. 65–68. [Google Scholar]
- Zaslavsky, T. Orientation of signed graphs. Eur. J. Comb. 1991, 12, 361–375. [Google Scholar] [CrossRef]
- Postnikov, A.; Reiner, V.; Williams, L. Faces of generalized permutohedra. Doc. Math. 2008, 13, 207–273. [Google Scholar]
- Zaslavsky, T. Facing up to Arrangements: Face-Count Formulas for Partitions of Space by Hyperplanes: Face-count Formulas for Partitions of Space by Hyperplanes; American Mathematical Society: Providence, RI, USA, 1975; Volume 154. [Google Scholar]
- Wachs, M. Poset topology: Tools and applications. In Geometric Combinatorics, IAS/Park City Mathematics Series; IAS/Park City Mathematics Institute: Salt Lake City, UT, USA, 2007; pp. 497–615. [Google Scholar]
- Geissinger, L. The face structure of a poset polytope. In Proceedings of the Third Caribbean Conference on Combinatorics and Computing, Cave Hill, Barbados, 5–8 January 1981.
- Stanley, R. Two poset polytopes. Discret. Computat. Geom. 1986, 1, 9–23. [Google Scholar] [CrossRef]
- Backman, S.; Hopkins, S. Fourientations and the Tutte polynomial. 2015. Available online: http://arxiv.org/abs/1503.05885 (accessed on 30 May 2016).
- Christensen, R. Plane Answers to Complex Questions: The Theory of Linear Models; Springer: Berlin, Germany, 2011. [Google Scholar]
- Ward, M. The closure operators of a lattice. Ann. Math. 1942, 43, 191–196. [Google Scholar] [CrossRef]
- Edelman, P.H.; Jamison, R.E. The theory of convex geometries. Geom. Dedicata 1985, 19, 247–270. [Google Scholar] [CrossRef]
- Stanley, R. Enumerative Combinatorics; Cambridge University Press: Cambridge, UK, 2001; Volume 2. [Google Scholar]
- Sturmfels, B. Gröbner Bases and Convex Polytopes; American Mathematical Society: Providence, RI, USA, 1996; Volume 8. [Google Scholar]
- Stembridge, J.R. On the fully commutative elements of Coxeter groups. J. Algebraic Comb. 1996, 5, 353–385. [Google Scholar] [CrossRef]
- Stembridge, J.R. The enumeration of fully commutative elements of Coxeter groups. J. Algebraic Comb. 1998, 7, 291–320. [Google Scholar] [CrossRef]
- Boothby, T.; Burkert, J.; Eichwald, M.; Ernst, D.; Green, R.; Macauley, M. On the cyclically fully commuative elements of Coxeter groups. J. Algebraic Combin. 2012, 36, 123–148. [Google Scholar] [CrossRef]
- Marquis, T. Conjugacy classes and straight elements in Coxeter groups. J. Algebra 2014, 407, 68–80. [Google Scholar] [CrossRef]
- Pétréolle, M. Characterization of cyclically fully commutative elements in finite and affine Coxeter groups. 2014. Available online: http://arxiv.org/abs/1403.1130 (accessed on 30 May 2016).
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).