Abstract
The relation between analyticity in mathematics and the concept of a global information field in physics is reviewed. Mathematics is complete in the complex plane only. In the complex plane, a very powerful tool appears—analyticity. According to this property, if an analytic function is known on the countable set of points having an accumulation point, then it is known everywhere. This mysterious property has profound consequences in quantum physics. Analyticity allows one to obtain asymptotic (approximate) results in terms of some singular points in the complex plane which accumulate all necessary data on a given process. As an example, slow atomic collisions are presented, where the cross-sections of inelastic transitions are determined by branch-points of the adiabatic energy surface at a complex internuclear distance. Common aspects of the non-local nature of analyticity and a recently introduced interpretation of classical electrodynamics and quantum physics as theories of a global information field are discussed.
1. Introduction
The scientific approach to the study of inorganic nature was formulated by Galileo Galilei. He discovered the fundamental role of experiment in inorganic nature—physical events are reproduced at any place and any moment under the same external conditions, i.e., they obey the laws of nature. In the most famous experiment, Galileo dropped different balls from the Leaning Tower of Pisa to demonstrate that their time of descent was independent of their mass, and the distance, starting from rest, is proportional to the square of the elapsed time. He found also that a simple pendulum is isochronous, i.e., that its swings always take the same amount of time, independently of the amplitude, and the square of the period varies directly with the length of the pendulum. Galileo discovered also the basic principle of relativity, that the laws of physics are the same in any system that is moving at a constant speed in a straight line, regardless of its speed or direction—hence, there is no absolute motion or absolute rest. Later, Isaac Newton generalized these observations, formulated them in the form of mathematical equations, and physics got a very powerful tool—mathematics. Mathematics is a scientific language that is based on a few axioms with successive identical transformation of them.
Mathematics has its own internal logic for development. For instance, the equation a × a = 2, cannot be resolved in terms of rational numbers. To find its solution we must introduce new abstract constructions—real numbers, which are the converging sequences of rational numbers. They form a new space—the space of the converging sequences, where all arithmetic operations must be redefined again. However, this extension is not enough to make mathematics self-consistent. The equation a × a = −1 leads to the appearance of complex numbers, and mathematics is complete in the complex plane only.
In the complex plane, a very powerful concept appears—analyticity. An analytic function f(z) is an infinitely differentiable function such that the Taylor series at any point z0 converges to f(z). The first global property following from this definition is that the line integral of every analytic function along a loop γ vanishes:
An analytic function depending on a small parameter λ can be calculated approximately using an asymptotic expansion. The asymptotic series for the function f(z, λ) with respect to a small parameter λ has the form:
Originally, the asymptotic term an(z)λn is the estimation of the accuracy in the (n − 1)-st order. At the beginning, the terms an(z)λn decrease with increasing n up to some index n = nmin(λ). After that the terms start to increase and we lose the accuracy. The term an(z)λn can be considered as a correction only if the next term is smaller. Since the larger λ the smaller is nmin(λ), the leading term gives the correct result in the widest interval of λ. Inclusion of higher-order corrections just reduces the interval of validity of the asymptotic expansion.
To estimate the integral
in the limit λ → 0 (where a is some constant, i is imaginary unit, and h(z) is holomorphic function) the method of steepest descent was developed. This method is based on the theorem that the deformation of the contour of integration in the complex z-plane does not change the value of I(λ), if the integrand is an analytic function. Then, the zeroth-order approximation and all power-type corrections are determined by the behaviour of the integrand in the vicinity of the saddle-point zs.p. = i, where the fist derivative of the exponent is equal to zero. In the leading order
Thus, an approximate value of the integral is determined by its value at the point zs.p. = i, which is quite far from the initial contour of integration. This result demonstrates in the most simple way the non-local character of analyticity.
Analyticity is the general case in physics. For instance, the solutions of the Schrödinger equation are analytic functions with respect to all variables analytically entering in the Hamiltonian. In the next section an adiabatic asymptotic expansion is presented to demonstrate the global nature of analyticity in quantum physics. Atomic units are used in Figure 1: ħ= me = e = 1.
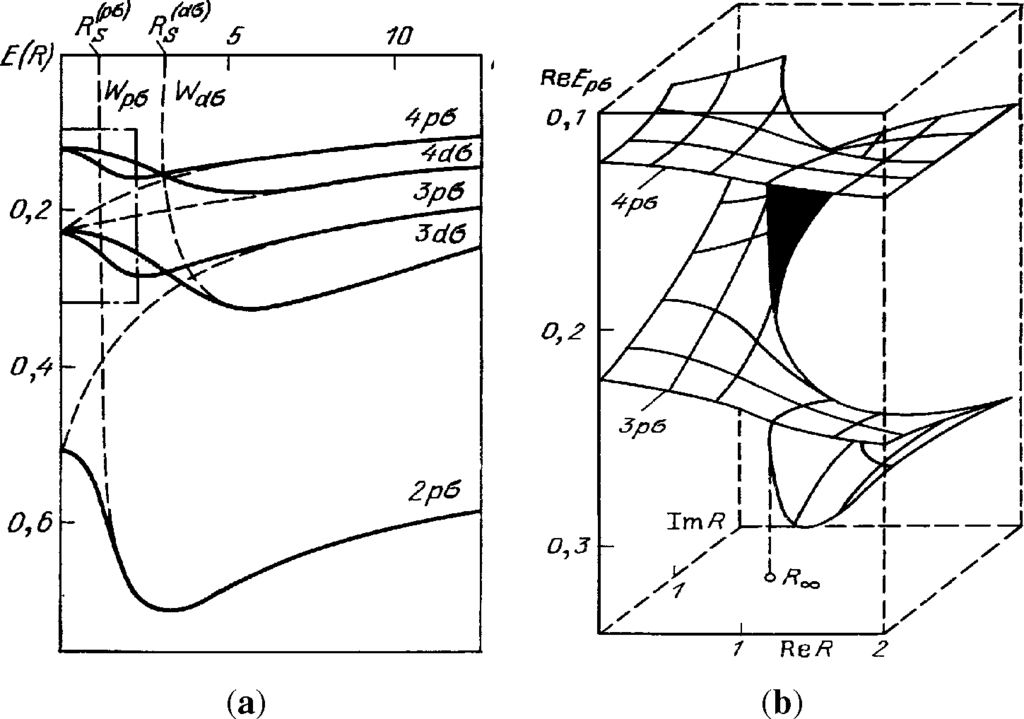
Figure 1.
(a) Adiabatic energy curves at real value of R for the
quasi-molecule. Dashed lines indicate the super-promotion channels Wpσ, Wdσ of inelastic transitions, where p, d, σ are spectroscopic quantum numbers of adiabatic states at R = 0. A rectangular box marked by a chain line represents the front cut of the energy surface in Figure 1b; (b) The surface ReE(R) in the complex R-plane. From [1].
2. Adiabatic Approximation
In quantum physics the adiabatic approximation was formulated by Born and Fock [2] for a Hamiltonian
varying slowly in time. They proved that in the limit λ → 0 the population of eigenstates of the instantaneous Hamiltonian
does not change (τ = λt), i.e., the adiabatic states φi(r, τ) are the correct states of zeroth order in the adiabatic approximation. For the original time-dependent Schrödinger equation these states take the form
In 1932 Stueckelberg [3] obtained the adiabatic asymptote for the probability of an inelastic transition. His derivation is based on analyticity of the Hamiltonian with respect to the adiabatic parameter τ. Analyticity plays a key role in the adiabatic approach. It allows the problem to be reduced to the analysis of some singular points in the complex plane that accumulate all necessary data on a given process. For instance, in atomic collision theory the electronic Hamiltonian depends on time through the internuclear distance R(vt), where v has the meaning of impact velocity. In slow collisions the role of the small parameter λ plays the impact velocity v. The adiabatic energies of the same symmetry Ei(R) are different branches of the single analytic function E(R) connected with each other by complex branch points Rc. This property follows from the implicit function theorem in complex analysis:
where Î is the identity operator. According to the Zwaan method [4], the transition from initial φi(r, R) to final φf(r, R) adiabatic states can be obtained by analytic continuation of the adiabatic wave-function Equation (6) along a contour in the complex R-plane enclosing the branch point Rc, which connects these states. The final result for the probability of inelastic transition reads [3]
Thus, the probability of inelastic transitions is determined by the integral from the real axis to the complex branch point Rc. Of course, during a collision inelastic transitions occur at real values of R. The physical reason for the decisive role of the complex branch points Rc is the following (for details, see review paper [1]). A branch point appears in the complex R-plane near a real value of R, where one of the energy curves Ei(R) crosses the top of the barrier in the effective electron potential. Here, according to the semiclassical approach, the adiabatic eigenstate φi(r, R) dramatically concentrates on the top of barrier involving the neighbouring state φf(r, R) to ensure smooth behaviour of the two-state subspace. As a rule, such reconstruction within the two-state subspace cannot be identified on the plot of the Ei(R) for real internuclear separations R (see Figure 1a). That is why the denotation ‘hidden crossing’ was introduced for this connection. But, they are clearly manifested in the matrix element of non-adiabatic coupling Wif(R) = ⟨i|d/dR|f⟩, which has a maximum at this point producing inelastic transitions. At the point of degeneracy of two eigenvalues Ei(Rc) = Ef(Rc) ≡ Ec, the Hamiltonian reduces not to a diagonal form but rather to the Jordan form. In the vicinity of Rc perturbation theory with respect to small value of (R−Rc) can be used
which gives the energies in the first approximation
Thus, a square-root dependence arises instead of the usual linear dependence of ΔEif(R) on (R−Rc) at real R, i.e., Ei(R) and Ef(R) are different branches of a single (multi-valued) analytic function E(R) (see Figure 1b). The same property is manifested by the adiabatic wave-functions φi(r, R). But the Jordan form has only one eigenvector, and to ensure the orthonormalization condition at branch point Rc, the adiabatic wave-function φi(r, R) must have a singular factor ~(R−Rc)−1/4 leading to an indeterminacy at R = Rc, which is resolved in a different way, so that a zero is obtained for the condition of orthogonality and unity for the normalization condition. As a result, the matrix element of non-adiabatic coupling Wif(R) has a pole of the first order Wif(R) ≈ 1/[4(R−Rc)] and a bell-shaped profile at a real value of R—curve A in Figure 2.
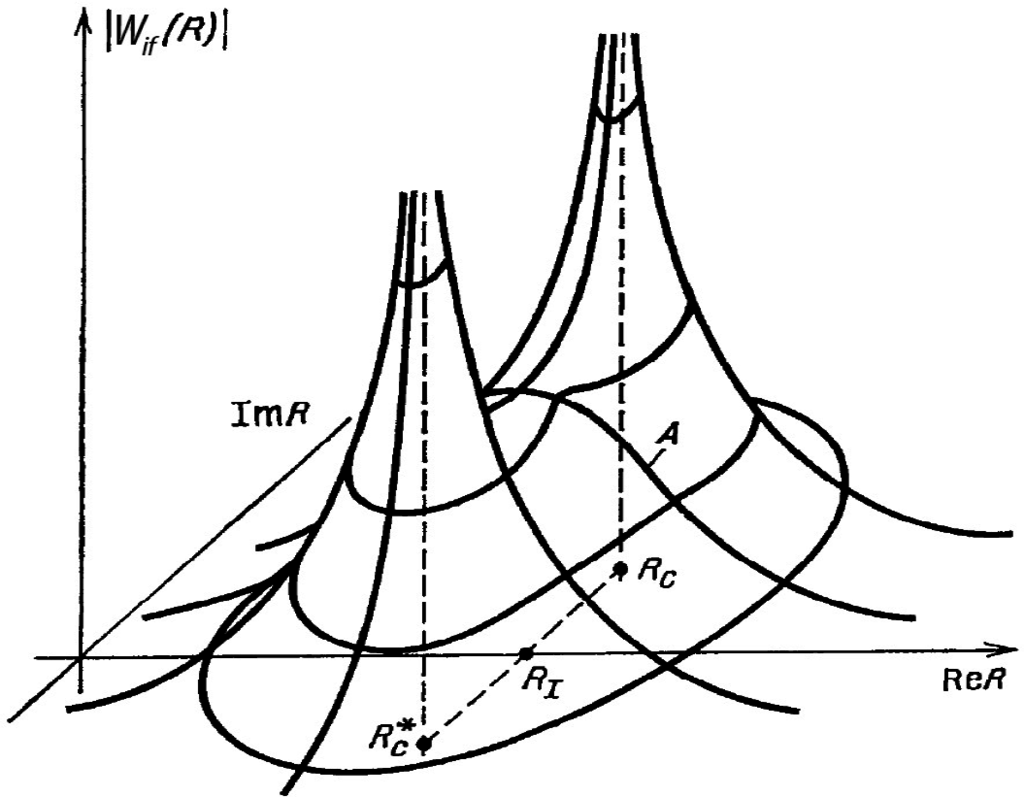
Figure 2.
The matrix element of non-adiabatic coupling Wif(R) in the complex R-plane. Curve A is Wif(R) at real value of R. From [1].
Non-analytic behaviour of the Hamiltonian destroys the exponential smallness of the transition probability Equation (8) at ħ → 0. For instance [5], if the adiabatic energy has a cusp (Ei(R) ~ |R|), inelastic transitions are described by sudden-perturbation theory (which is the opposite asymptote with respect to the adiabatic approximation), so that the transition probability is proportional to v2. However, such non-analytic behaviour appears in a modelling approach; it is introduced by hand in advance. Thus, it has no physical meaning.
Finally, it should be noted that the adiabatic approach, as well as the semiclassical approach is not well defined, since it is based on a guess of the singularity of the zeroth order approximation, when the explicit expression for exact solution is unknown. The validity of such a guess can not be proved, i.e., this approach is beyond standard mathematics.
3. Classical Electrodynamics and Quantum Physics as Theories of a Global Information Field
Recently, the interpretation of quantum physics and classical electrodynamics as global information field theories has been proposed [6–8]. For the first time, physics encounters the existence of the global information field (GIF) in classical electrodynamics. The study of the diffraction of light demonstrates that the distribution of photons on the screen is predicted by the Maxwell equations. The same phenomenon for propagation of electrons through double slits is governed by the Schrödinger equation. In quantum theory GIF dictates also that the stable bound states can exist at some discrete value of energy only. In both cases the GIF is described by the wave-type differential equations—the Maxwell equations in classical electrodynamics and the Schrödinger equation in quantum physics. Standard notations for the solutions of these equations are electromagnetic field {E(r), H(r)} and wave-function Ψ(r), respectively. However, a more adequate name for them is a global information field as stated in [8].
We obtain all physical data from measurement. The nontrivial role of measurement was most clearly realized in quantum physics. What is the relation between classical electrodynamics or quantum theory and measurement? All experimental devices are designed on classical principles, and a single measurement gives a fixed value of the classical (or particle) quantity. After multiple repetition of a measurement we obtain the distribution of the classical quantity, according to the GIF Ψ(r) (or {E(r), H(r)} for photons). The global information field itself is unique. The probabilities arise at a measurement stage in the transfer of the data from the quantum (GIF) to the classical (particle) level.
A direct demonstration of the existence of the GIF is the Einstein-Podolsky-Rosen experiment. Namely, decay of the 2S metastable states of a hydrogen atom is accompanied by emission of two photons having opposite direction of spin. However, the orientation of each spin is uncertain. If the measurement of the direction of the spin of the first photon is performed, the spin of the second photon takes the opposite direction, according to GIF, independently of the distance between photons. The fixation of the spin orientation of the second photon happens immediately and it is an actual changing of state of the second photon without any contact. In the experiment [9] the distance between photons at the moment of measurement was 18.0 km. It was found that the propagation of quantum information at the moment of measurement is at least 104 times faster than the speed of light c.
The concept of a ‘global information field’ makes more transparent such phenomena as the motivation for plants and consciousness/memory of animals. A common basis for plants and animals has been adopted already by druids in the Iron Age. The given interpretation states that the material (classical) world is accompanied by a global information field on all levels. This aspect was not realized up to recent times. Here an analogy with the electromagnetic field could be to draw—nobody suspected its existence before classical electrodynamics appeared.
4. Conclusions
Mathematics is a logical scheme making conclusions by identical transformations from the laws of nature. At first sight, mathematics does not produce new information; it just transforms the laws of nature into a form more transparent for our consciousness. But, mathematics itself contains a mystical concept—analyticity. It has prognostic power—namely, if an analytic function is known on the countable set of points having an accumulation point, then it is known everywhere. Apparently, it has an obscure relation to the global information field in classical electrodynamics and quantum physics. Further cogitation on this connection should serve for a deeper understanding of nature.
Acknowledgments
I am grateful to John Briggs and Tasko Grozdanov for critical reading of the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Solov’ev, E.A. Nonadiabatic transitions in atomic collisions. Sov. Phys. USP 1989, 157, 437–476. [Google Scholar]
- Born, M.; Fock, V.F. Beweis des Adiabatensatzes. Z. Phys. 1928, 51, 165–180. [Google Scholar]
- Stueckelberg, E.C.G. Theorie der unelastischen Stösse zwischen Atomen. Helv. Phys. Acta. 1932, 5, 369–422. [Google Scholar]
- Zwaan, A. Intensitäten im Ca-Funkenspectrum. Arch. Néerl. Sci. Exactes Nat. (Ser. IIIA) 1929, 12, 1–76. [Google Scholar]
- Solov’ev, E.A. Rearrangement and stripping in exactly solvable models taking the motion of nuclei into account. Theor. Math. Phys. 1976, 28, 757–763. [Google Scholar]
- Solov’ev, E.A. On foundation of quantum physics. Phys. At. Nucl. 2009, 72, 853–857. [Google Scholar]
- Solov’ev, E.A. On the foundations of quantum physics. Phys. Essays. 2012, 25, 27–33. [Google Scholar]
- Solov’ev, E.A. Physical and metaphysical aspects of time and consciousness. Cosmology. 2014, 18, 201–211. [Google Scholar]
- Salart, D.; Baas, A.; Branciard, C.; Gisin, N.; Zbinden, H. Testing the speed of ‘spooky action at a distance’. Nature. 2008, 454, 861–864. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).