The Second-Order Shape Derivative of Kohn–Vogelius-Type Cost Functional Using the Boundary Differentiation Approach
Abstract
:1. Introduction
2. Outline of the work
3. Preliminaries
3.1. Properties of the Perturbation of Identity Operator
- , and
- there exists such that , for .
- is a homeomorphism,
- is a diffeomorphism, and in particular, is a diffeomorphism,
- , and .
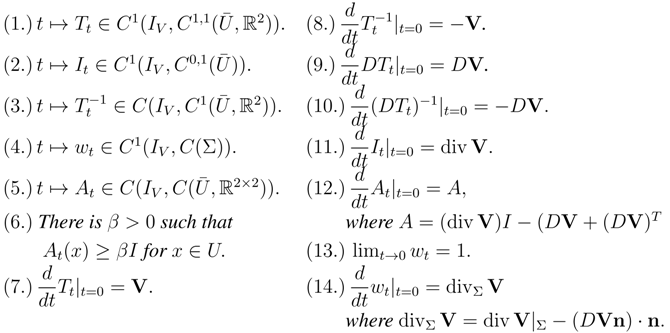
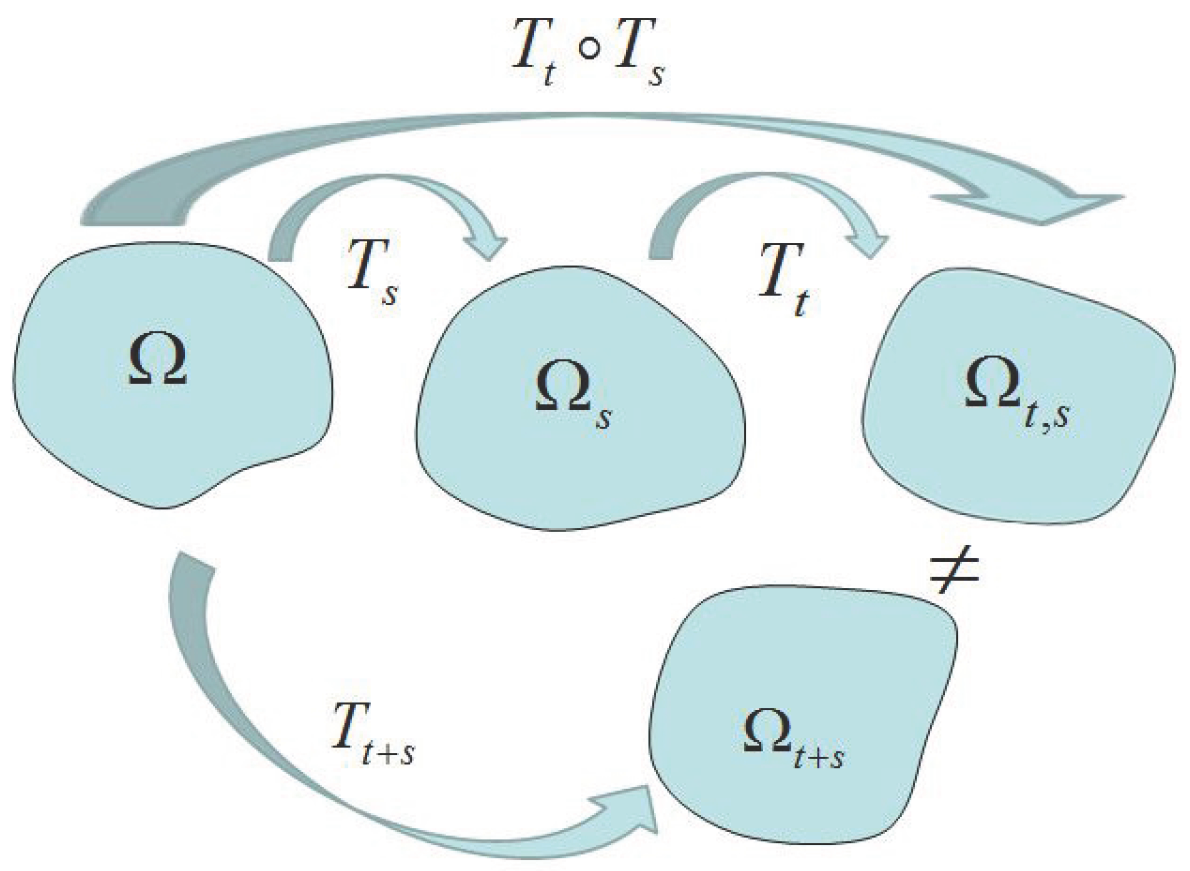
3.2. Concepts in the Method of Mapping
- The tangential gradient of is given by
- The tangential Jacobian matrix of a vector function is given by
- The tangential divergence of a vector function on Γ is given bywhere and are any corresponding extensions of f and into a neighborhood of Γ.
- The first-order Eulerian derivative of a shape functional at the domain Ω in the direction of the deformation field is given byif the limit exists.
- The second-order Eulerian derivative of J at the domain Ω in the direction of the deformation fields and is given byif the limit exists. Here, is defined by Equation (9).
3.3 Anatomy of the Second-Order Shape Derivative
- (i)
- there exists an open neighborhood of 0 inand functions and such that for any ,
- (ii)
- Moreover, the values of the first- and second-order (Fréchet) derivatives of Ψ at in the directions are given by
- (a)
- , and
- (b)
- for , where and .
- (i)
- If and is differentiable at 0 in , then there is a continuous linear map such that for any ,
- (ii)
- If and is twice differentiable at 0 in then there exists a continuous bilinear symmetric map such that for any we have
4. Main Results
4.1 Second-Order Shape Derivative of KV by Boundary Differentiation
4.2 Shape Derivative at the Solution of the Bernoulli Problem
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Tiihonen, T. Shape optimization and trial methods for free boundary problems. RAIRO—Model. Math. Anal. Numer. 1997, 31, 805–825. [Google Scholar]
- Caffarelli, L.A.; Salsa, S. A Geometric Approach to Free Boundary Problems; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Friedman, A. Free boundary problems in science and technology. Not. AMS 2000, 47, 854–861. [Google Scholar]
- Abda, B.; Bouchon, F.; Peichl, G.; Sayeh, M.; Touzani, R. A Dirichlet-Neumann cost functional approach for the Bernoulli problem. J. Eng. Math. 2013, 81, 157–176. [Google Scholar] [CrossRef]
- Crank, J. Free and Moving Boundary Problems; Oxford University Press Inc.: New York, NY, USA, 1984. [Google Scholar]
- Flucher, M.; Rumpf, M. Bernoulli’s free-boundary problem, qualitative theory and numerical approximation. J. Reine Angew. Math. 1997, 486, 165–204. [Google Scholar]
- Toivanen, J.I.; Haslinger, J.; Mäkinen, R.A.E. Shape optimization of systems governed by Bernoulli free boundary problems. Comput. Methods Appl. Mech. Eng. 2008, 197, 3803–3815. [Google Scholar] [CrossRef]
- Eppler, K.; Harbrecht, H. A regularized Newton method in electrical impedance tomography using shape Hessian information. Control Cybern. 2005, 34, 203–225. [Google Scholar]
- Aparicio, N.D.; Pidcock, M.K. On a class of free boundary problems for the Laplace equation in two dimensions. Inverse Probl. 1998, 14, 9–18. [Google Scholar] [CrossRef]
- Beurling, A. On free boundary problems for the Laplace equation. In Proceedings of the Seminars on Analytic Functions; 1957; pp. 248–263. [Google Scholar]
- Cardaliaguet, P.; Tahraoui, R. Some uniqueness results for Bernoulli interior free-boundary problems in convex domains. Electron. J. Diff. Equ. 2002, 2002, 1–16. [Google Scholar]
- Haslinger, J.; Ito, K.; Kozubek, T.; Kunisch, K.; Peichl, G. On the shape derivative for problems of Bernoulli type. Interfaces Free Bound. 2009, 1, 317–330. [Google Scholar] [CrossRef]
- Haslinger, J.; Kozubek, T.; Kunisch, K.; Peichl, G. Shape optimization and fictitious domain approach for solving free-boundary value problems of Bernoulli type. Comput. Optim. Appl. 2003, 26, 231–251. [Google Scholar] [CrossRef]
- Henrot, A.; Shahgholian, H. Convexity of free boundaries with Bernoulli type boundary condition. Nonlinear Anal. Theory Methods Appl. 1997, 28, 815–823. [Google Scholar] [CrossRef]
- Tepper, D.E. A free boundary problem in an annulus. J. Aust. Math. Soc. A 1983, 34, 177–181. [Google Scholar] [CrossRef]
- Kohn, R.; Vogelius, M. Determining conductivity by boundary measurements. Commun. Pure Appl. Math. 1984, 37, 289–298. [Google Scholar] [CrossRef]
- Eppler, K.; Harbrecht, H. On a Kohn-Vogelius like formulation of free boundary problems. Comput. Optim. Appl. 2012, 52, 69–85. [Google Scholar] [CrossRef]
- Bacani, J.B.; Peichl, G. On the first-order shape derivative of the Kohn-Vogelius cost functional of the Bernoulli problem. Abstr. Appl. Anal. 2013, 2013. [Google Scholar] [CrossRef]
- Ito, K.; Kunisch, K.; Peichl, G. Variational approach to shape derivatives for a class of Bernoulli problems. J. Math. Anal. Appl. 2006, 314, 126–149. [Google Scholar] [CrossRef]
- Bacani, J. B.; Peichl, G. Solving the exterior Bernoulli problem using the shape derivative approach. In Mathematics and Computing 2013: Springer Proceedings in Mathematics and Statistics, Vol.91; Mohapatra, R., Giri, D., Saxena, P.K., Srivastava, P.D., Eds.; Springer India: New Delhi, India, 2014; Volume XXV, pp. 251–269. [Google Scholar]
- Bacani, J.B.; Peichl, G. The second-order Eulerian derivative of a shape functional of a free Bernoulli problem. J. Korean Math. Soc. 2014. submitted for publication. [Google Scholar]
- Sokolowski, J.; Zolesio, J.P. Introduction to Shape Optimization; Springer-Verlag: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Eppler, K. Boundary integral representations of second derivatives in shape optimization. Discuss. Math. (Diff. Incl. Control Optim.) 2000, 20, 63–78. [Google Scholar] [CrossRef]
- Delfour, M.C.; Zolesio, J.P. Shapes and Geometries; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Haslinger, J.; Mäkinen, R.A.E. Introduction to Shape Optimization (Theory, Approximation, and Computation); SIAM Advances and Control: Philadelphia, PA, USA, 2003. [Google Scholar]
- Afraites, L.; Dambrine, M.; Kateb, D. On second-order shape optimization methods for electrical impedance tomography. SIAM J. Control Optim. 2008, 47, 1556–1590. [Google Scholar] [CrossRef]
- Henrot, A.; Pierre, M. Variation et Optimisation de Formes; Springer-Verlag: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Murat, F.; Simon, J. Sur le Contrôle par un Domaine Géométrique; Rapport 76015; University Pierre et Marie Curie: Paris, France, 1976. [Google Scholar]
- Novruzi, A.; Pierre, M. Structure of shape derivatives. J. Evol. Equ. 2002, 2, 365–382. [Google Scholar] [CrossRef]
- Simon, J. Differentiation with respect to the domain in boundary value. Numer. Funct. Anal. Optim. 1980, 2, 649–687. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, S. Preconditioning the Poincaré- Steklov operator by using Green’s function. Math. Comput. 1997, 31, 125–138. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacani, J.B.; Peichl, G. The Second-Order Shape Derivative of Kohn–Vogelius-Type Cost Functional Using the Boundary Differentiation Approach. Mathematics 2014, 2, 196-217. https://doi.org/10.3390/math2040196
Bacani JB, Peichl G. The Second-Order Shape Derivative of Kohn–Vogelius-Type Cost Functional Using the Boundary Differentiation Approach. Mathematics. 2014; 2(4):196-217. https://doi.org/10.3390/math2040196
Chicago/Turabian StyleBacani, Jerico B., and Gunther Peichl. 2014. "The Second-Order Shape Derivative of Kohn–Vogelius-Type Cost Functional Using the Boundary Differentiation Approach" Mathematics 2, no. 4: 196-217. https://doi.org/10.3390/math2040196
APA StyleBacani, J. B., & Peichl, G. (2014). The Second-Order Shape Derivative of Kohn–Vogelius-Type Cost Functional Using the Boundary Differentiation Approach. Mathematics, 2(4), 196-217. https://doi.org/10.3390/math2040196



