The Riccati System and a Diffusion-Type Equation
Abstract
:1. Introduction
2. Transformation to the Standard Form
3. Fundamental Solution
4. Symmetries of the Autonomous Diffusion Equation
5. Eigenfunction Expansion and Ermakov-Type System
6. Nonautonomous Burgers Equation
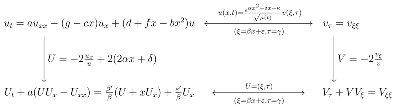
7. Traveling Wave Solutions of Burgers-Type Equation
8. Examples
9. Conclusions
Acknowledgments
Author Contributions
Appendix A
Conflicts of Interest
References
- Suazo, E.; Suslov, S.K.; Vega-Guzmán, J.M. The Riccati equation and a diffusion-type equation. N. Y. J. Math. 2011, 17a, 225–244. [Google Scholar]
- Cordero-Soto, R.; Lopez, R.M.; Suazo, E.; Suslov, S.K. Propagator of a charged particle with a spin in uniform magnetic and perpendicular electric fields. Lett. Math. Phys. 2008, 84, 159–178. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suazo, E.; Suslov, S.K. Models of damped oscillators in quantum mechanics. J. Phys. Math. 2009, 1, S090603:1–S090603:16. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suazo, E.; Suslov, S.K. Quantum integrals of motion for variable quadratic Hamiltonians. Ann. Phys. 2010, 325, 1884–1912. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suslov, S.K. Time reversal for modified oscillators. Theor. Math. Phys. 2010, 162, 286–316. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suslov, S.K. The degenerate parametric oscillator and Ince’s equation. J. Phys. A: Math. Theor. 2011, 44, 015101:1–015101:9. [Google Scholar] [CrossRef]
- Lanfear, N.; López, R.M.; Suslov, S.K. Exact wave functions for generalized harmonic oscillators. 2011, 32, 352–361. [Google Scholar] [CrossRef]
- Lanfear, N.; Suslov, S.K. The time-dependent Schrö dinger equation, Riccati equation and Airy functions. 22 April 2009; arXiv:0903.3608v5 [math-ph]. [Google Scholar]
- Lopez, R.M.; Suslov, S.K. The Cauchy problem for a forced harmonic oscillator. Rev. Mex. Fís. 2009, 55, 195–215. [Google Scholar]
- Meiler, M.; Cordero-Soto, R.; Suslov, S.K. Solution of the Cauchy problem for a time-dependent Schrödinger equation. J. Math. Phys. 2008, 49, 072102:1–072102:27. [Google Scholar] [CrossRef]
- Suazo, E.; Suslov, S.K. Cauchy problem for Schrö dinger equation with variable quadratic Hamiltonians. Suslov, S.K., Ed.; Arizona State University: Tempe, AZ., Under preparation; 2014. [Google Scholar]
- Suslov, S.K. Dynamical invariants for variable quadratic Hamiltonians. Phys. Scr. 2010, 81, 055006:1–055006:11. [Google Scholar] [CrossRef]
- Suslov, S.K. On integrability of nonautonomous nonlinear Schrödinger equations. 18 March 2011; arXiv:1012.3661v2 [math-ph]. [Google Scholar] [CrossRef]
- Gagnon, L.; Winternitz, P. Symmetry classes of variable coefficient nonlinear Schrödinger equations. J. Phys. A: Math. Gen. 1993, 26, 7061–7076. [Google Scholar] [CrossRef]
- Miller, W., Jr. Symmetry and Separation of Variables, Encyclopedia of Mathematics and Its Applications; Addison–Wesley Publishing Company: Reading, MA, USA, 1977; Volume 4. [Google Scholar]
- Rosencrans, S. Perturbation algebra of an elliptic operator. J. Math. Anal. Appl. 1976, 56, 317–329. [Google Scholar] [CrossRef]
- Friedman, A. Partial Differential Equations of Parabolic Type; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Craddock, M. Fundamental solutions, transition densities and the integration of Lie symmetries. J. Differ. Equ. 2009, 207, 2538–2560. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S. Brownian Motion and Stochastic Calculus (Graduate Texts in Mathematics), 2nd ed.; Springer-Verlag: New York, NY, USA, 1991; Volume 113. [Google Scholar]
- Albeverio, S.; Rozanova, O. Suppression of unbounded gradients in an SDE associated with Burgers equation. Trans. Am. Math. Soc. 2010, 138, 241–251. [Google Scholar] [CrossRef]
- Kambarbaeva, G.S. Some explicit formulas for calculation of conditional mathematical expectations of random variables and their applications. Mosc. Univ. Math. Bull. 2010, 65, 186–190. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Merton, R.C. Option pricing when underlying stock returns discontinous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Merton, R.C. The impact on option pricing of specification error in the underlying stock price returns. J. Financ. 1976, 31, 333–350. [Google Scholar] [CrossRef]
- Tao, T. The Black-Scholes equation. Available online: http://terrytao.wordpress.com/2008/07/01/the-black-scholes-equation/ (accessed on 9 May 2014).
- Sengupta, A.N. Pricing Derivatives: The Financial Concepts Underlying the Mathematics of Pricing Derivatives; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Romero, J.M.; González-Gaxiola, O.; Ruíz de Chávez, J. The Black-Scholes Equation and Certain Quantum Hamiltonians. Int. J. Pure Appl. Math. (IJPAM) 2011, 67. 12 January 2011, arXiv:1002.1667v2 [math-ph]. [Google Scholar]
- Raid, W.T. Riccati Differential Equations; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Nikiforov, A.F. Lectures on Equations and Methods of Mathematical Physics; Intellect: Dolgoprudny, Russia, 2009. (In Russian) [Google Scholar]
- Cari nena, J.F.; Marmo, G.; Nasarre, J. The nonlinear superposition principle and the Wei-Norman method. Int. J. Mod. Phys. A 1998, 13, 3601. [Google Scholar] [CrossRef]
- Ray, J.R. Nonlinear superposition law for generalized Ermakov systems. Phys. Lett. A 1980, 78, 4–6. [Google Scholar] [CrossRef]
- Kalnins, E.G.; Miller, W. Lie theory and separation of variables. 5. The equations iUt + Uxx = 0 and iUt + Uxx − c/x2U = 0. J. Math. Phys. 1974, 15, 1728–1737. [Google Scholar] [CrossRef]
- Niederer, U. The maximum kinematical invariance group of the free Schrödinger equation. Helv. Phys. Acta 1972, 45, 802–810. [Google Scholar]
- Niederer, U. The maximum kinematical invariance group of the harmonic oscillator. Helv. Phys. Acta 1973, 46, 191–200. [Google Scholar]
- Vinet, L.; Zhedanov, A. Representations of the Schrödinger group and matrix orthogonal polynomials. J. Phys. A: Math. Theor. 2011, 44, 355201:1–355201:28. [Google Scholar] [CrossRef]
- Krattenthaler, C.; Kryuchkov, S.I.; Mahalov, A.; Suslov, S.K. On the problem of electromagnetic-field quantization. Int. J. Theor. Phys. 2013, 52, 4445–4460. [Google Scholar] [CrossRef]
- Erdélyi, A. Higher Transcendental Functions; Erdélyi, A., Ed.; McGraw–Hill: New York, NY, USA, 1953; Volumes I–III. [Google Scholar]
- Erdélyi, A. Tables of Integral Transforms; Erdélyi, A., Ed.; McGraw–Hill: New York, NY, USA, 1954; Volumes I–II. [Google Scholar]
- Nikiforov, A.F.; Suslov, S.K.; Uvarov, V.B. Classical Orthogonal Polynomials of a Discrete Variable; Springer–Verlag: Berlin, Germany; New York, NY, USA, 1991. [Google Scholar]
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Cole, J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar]
- Hopf, E. Partial differential equation ut + uux = uxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Kadomtsev, B.B.; Karpman, V.I. Nonlinear Waves. Sov. Phys. Uspekhi 1971, 14, 40–60. [Google Scholar] [CrossRef]
- Sachdev, P.L. Nonlinear Diffusive Waves; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley, John & Sons: New York, NY, USA, 1999. [Google Scholar]
- Sakai, J.-I. Nonlinear magnetosonic waves propagating perpendicular to a magnetic neutral sheet. Astrophys. Space Sci. 1973, 23, 285–300. [Google Scholar] [CrossRef]
- Nikiforov, A.F.; Uvarov, V.B. Special Functions of Mathematical Physics; Birkhäuser: Basel, Switzerlands; Boston, MA, USA, 1988. [Google Scholar]
- Kudryashov, N.A. Methods of Nonlinear Mathematical Physics; Intellect: Dolgoprudny, Russia, 2010. (In Russian) [Google Scholar]
- Kudryashov, N.A.; Sinelshchikov, D.I. A note on “New abundant solutions for the Burgers equation”. 8 December 2009; arXiv:0912.1542v1 [nlin.SI]. [Google Scholar]
- Cannon, J.R. The One-Dimensional Heat Equation, Encyclopedia of Mathematics and Its Applications; Addison–Wesley Publishing Company: Reading, MA, USA, 1984; Volume 32. [Google Scholar]
- Jack, J.J.B.; Noble, D.; Tsien, R.W. Electric Current Flow in Excitable Cells; Oxford University Press: Oxford, United Kingdom, 1983. [Google Scholar]
- Herrera-Valdéz, M.; Suslov, S.K. A Graphical approach to a model of neuronal tree with variable diameter. 31 December 2010; arXiv:1101.0296v1 [q-bio.NC]. [Google Scholar] [CrossRef]
- Risken, H. The Fokker–Planck Equation. Methods of Solution and Applications, 2nd ed.; Springer–Verlag: New York, NY, USA, 1989. [Google Scholar]
- Yau, S. Computation of Fokker–Planck equation. Q. Appl. Math. 2004, 62, 643–650. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer-Verlag: New York, NY, USA, 2001. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suazo, E.; Suslov, S.K.; Vega-Guzmán, J.M. The Riccati System and a Diffusion-Type Equation. Mathematics 2014, 2, 96-118. https://doi.org/10.3390/math2020096
Suazo E, Suslov SK, Vega-Guzmán JM. The Riccati System and a Diffusion-Type Equation. Mathematics. 2014; 2(2):96-118. https://doi.org/10.3390/math2020096
Chicago/Turabian StyleSuazo, Erwin, Sergei K. Suslov, and José M. Vega-Guzmán. 2014. "The Riccati System and a Diffusion-Type Equation" Mathematics 2, no. 2: 96-118. https://doi.org/10.3390/math2020096
APA StyleSuazo, E., Suslov, S. K., & Vega-Guzmán, J. M. (2014). The Riccati System and a Diffusion-Type Equation. Mathematics, 2(2), 96-118. https://doi.org/10.3390/math2020096




