The Riccati System and a Diffusion-Type Equation

Abstract

We discuss a method of constructing solutions of the initial value problem for diffusion-type equations in terms of solutions of certain Riccati and Ermakov-type systems. A nonautonomous Burgers-type equation is also considered. Examples include, but are not limited to the Fokker-Planck equation in physics, the Black-Scholes equation and the Hull-White model in finance.

1. Introduction

A goal of this work, complementary to our recent paper [1], is to elaborate on the Cauchy initial value problem for a class of nonautonomous and inhomogeneous diffusion-type equations on $\mathbb{R}.$ A corresponding nonautonomous Burgers-type equation is also analyzed as a by-product. Here, we use explicit transformations to the standard forms and emphasize natural relations with certain Riccati (and Ermakov)-type systems, which seem to be missing in the available literature. Similar methods are applied to the corresponding Schrödinger equation (see, for example, [2,3,4,5,6,7,8,9,10,11,12,13] and references therein). A group theoretical approach to a similar class of partial differential equations is discussed in Refs. [14,15,16].

For an introduction to fundamental solutions for parabolic equations, see chapter one of the book by Friedman [17]. Among numerous applications, we only elaborate here on an important role of fundamental solutions in probability theory [18,19]. Consider an Itô diffusion $X=\left\{X_t:t\ge 0\right\}$ which satisfies the stochastic differential equation

$$d{X}_t=b\left(X_t,t\right)dt+\sigma \left(X_t,t\right)d{W}_t,X_0=x$$

(1)

in which $W=\left\{W_t:t\ge 0\right\}$ is a standard Wiener process. The existence and uniqueness of solutions of Equation (1) depends on the coefficients b and $\sigma .$ (See Ref. [19] for conditions of unique strong solution to Equation (1).) If the Equation (1) has a unique solution, then the expectations

$$u\left(x,t\right)=E_x\left[\varphi \left(X_t\right)\right]=E\left[\varphi \left(X_t\right)|X_0=x\right]$$

(2)

are solutions of the Cauchy problem

$$u_t=\frac{1}{2}{\sigma }^2\left(x,t\right)u_{xx}+b\left(x,t\right)u_x,u\left(x,0\right)=\varphi \left(x\right)$$

(3)

This PDE is known as Kolmogorov forward equation [18,19]. Thus if $p\left(x,y,t\right)$ is the appropriate fundamental solution of Equation (3), then one can compute the given expectations according to

$$E_x\left[\varphi \left(X_t\right)\right]={\int }_{\Omega }p\left(x,y,t\right)\varphi \left(y\right)dy$$

(4)

In this context, the fundamental solution is known as the probability transition density for the process and

$${\int }_{\Omega }p\left(x,y,t\right)dy=1.$$

(5)

See also Refs. [20,21] for applications to stochastic differential equations related to Fokker–Planck and Burgers equations. The Black-Scholes model of financial markets is discussed in [22,23,24,25,26,27] (see also [28] for the one-factor Gaussian Hull-White model and [29] for a connection with quantum mechanics).

The paper is organized as follows: We present the main result and sketch the proof in the next section. In Section 3 and Section 4, a solution of the Cauchy initial value problem and the symmetry group of diffusion equations are revisited from a new perspective. An extension to a Ermarov-type system is discussed in Section 5. Section 6 and Section 7 deal with nonautonomous Burgers-type equations. In the last section, we discuss some examples.

2. Transformation to the Standard Form

We present the following result.

Lemma 1. 

The nonautonomous and inhomogeneous diffusion-type equation

$$\frac{\partial u}{\partial t}=a\left(t\right)\frac{{\partial }^{2}u}{\partial x^2}-\left(g\left(t\right)-c\left(t\right)x\right)\frac{\partial u}{\partial x}+\left(d\left(t\right)+f\left(t\right)x-b\left(t\right)x^2\right)u$$

(6)

where $a,b,c,d,f,g$ are suitable functions of time t only, can be reduced to the standard autonomous form

$$\frac{\partial v}{\partial \tau }=\frac{{\partial }^{2}v}{\partial {\xi }^2}$$

(7)

with the help of the following substitution:

$$\begin{array}{cc}\hfill u\left(x,t\right)& =\frac{1}{\sqrt{\mu \left(t\right)}}{e}^{\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)}v\left(\xi ,\tau \right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \xi & =\beta \left(t\right)x+\epsilon \left(t\right),\tau =\gamma \left(t\right)\hfill \end{array}$$

Here, $\mu ,\alpha ,\beta ,\gamma ,\delta ,\epsilon ,\kappa$ are functions of t that satisfy

$$\frac{{\mu }^{\prime }}{2\mu }+2a\alpha +d=0$$

(9)

and

$$\begin{array}{cc}& \frac{d\alpha }{dt}+b-2c\alpha -4a{\alpha }^2=0\hfill \end{array}$$

(10)

$$\begin{array}{cc}& \frac{d\beta }{dt}-\left(c+4a\alpha \right)\beta =0\hfill \end{array}$$

(11)

$$\begin{array}{cc}& \frac{d\gamma }{dt}-a{\beta }^2=0\hfill \end{array}$$

(12)

$$\begin{array}{cc}& \frac{d\delta }{dt}-\left(c+4a\alpha \right)\delta =f-2\alpha g\hfill \end{array}$$

(13)

$$\begin{array}{cc}& \frac{d\epsilon }{dt}+\left(g-2a\delta \right)\beta =0\hfill \end{array}$$

(14)

$$\begin{array}{cc}& \frac{d\kappa }{dt}+g\delta -a{\delta }^2=0\hfill \end{array}$$

(15)

Proof. 

Let $S=\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)$ and $v=v(\xi ,\tau )$. To reduce Equation (6) into the standard nonautonomous form Equation (7) we need the following derivatives:

$$\begin{array}{cc}& \frac{\partial u}{\partial t}=\frac{e^S}{\sqrt{\mu \left(t\right)}}\left[-\frac{{\mu }^{\prime }\left(t\right)}{2\mu \left(t\right)}v+({\alpha }^{\prime }\left(t\right)x^2+{\delta }^{\prime }\left(t\right)x+{\kappa }^{\prime }\left(t\right))v+({\beta }^{\prime }\left(t\right)x+{\epsilon }^{\prime }\left(t\right))v_{\xi }+{\gamma }^{\prime }\left(t\right)v_{\tau }\right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}& \frac{\partial u}{\partial x}=\frac{e^S}{\sqrt{\mu \left(t\right)}}\left[(2\alpha \left(t\right)x+\delta \left(t\right))v+\beta \left(t\right)v_{\xi }\right]\hfill \end{array}$$

(17)

$$\begin{array}{cc}& \frac{{\partial }^{2}u}{\partial x^2}=\frac{e^S}{\sqrt{\mu \left(t\right)}}\left[{(2\alpha \left(t\right)x+\delta \left(t\right))}^{2}v+2\beta \left(t\right)(2\alpha \left(t\right)x+\delta \left(t\right))v_{\xi }+2\alpha \left(t\right)v+{\beta }^2\left(t\right)v_{\xi \xi }\right]\hfill \end{array}$$

(18)

Direct substitution of Equations (16)–(18) into Equation (6) leads to the desired reduced form (7) subject to Equations (9)–(15). Further details are left to the reader. ☐

Equation (10) is called the Riccati nonlinear differential equation [30,31,32] and we shall refer to the system (10)–(15) as a Riccati-type system.

The substitution (9) reduces the nonlinear Riccati Equation (10) to the second order linear equation

$${\mu }^{″}-\tau \left(t\right){\mu }^{\prime }-4\sigma \left(t\right)\mu =0$$

(19)

where

$$\tau \left(t\right)=\frac{a^{\prime }}{a}+2c-4d,\sigma \left(t\right)=ab+cd-d^2+\frac{d}{2}\left(\frac{a^{\prime }}{a}-\frac{d^{\prime }}{d}\right)$$

(20)

which shall be referred to as a characteristic equation [1].

It is also known [1] that the diffusion-type equation (6) has a particular solution of the form

$$u=\frac{1}{\sqrt{\mu \left(t\right)}}{e}^{\alpha \left(t\right)x^2+\beta \left(t\right)xy+\gamma \left(t\right)y^2+\delta \left(t\right)x+\epsilon \left(t\right)y+\kappa \left(t\right)}$$

(21)

provided that the time dependent functions $\mu ,\alpha ,\beta ,\gamma ,\delta ,\epsilon ,\kappa$ satisfy the Riccati-type system (9)–(15) (our original interpretation of this system).

A group theoretical approach to a similar class of partial differential equations is discussed in [14,15,16].

3. Fundamental Solution

By the superposition principle one can solve (formally) the Cauchy initial value problem for the diffusion-type equation (6) subject to initial data $u\left(x,0\right)=\phi \left(x\right)$ on the entire real line $-\infty <x<\infty$ in an integral form

$$u\left(x,t\right)={\int }_{-\infty }^{\infty }{K}_0\left(x,y,t\right)\phi \left(y\right)dy$$

(22)

with the fundamental solution (heat kernel) [1]:

$$K_0\left(x,y,t\right)=\frac{1}{\sqrt{2\pi {\mu }_0\left(t\right)}}{e}^{{\alpha }_0\left(t\right)x^2+{\beta }_0\left(t\right)xy+{\gamma }_0\left(t\right)y^2+{\delta }_0\left(t\right)x+{\epsilon }_0\left(t\right)y+{\kappa }_0\left(t\right)}$$

(23)

where a particular solution of the Riccati-type system (10)–(15) is given by

$${\alpha }_0\left(t\right)=-\frac{1}{4a\left(t\right)}\frac{{\mu }_0^{\prime }\left(t\right)}{{\mu }_0\left(t\right)}-\frac{d\left(t\right)}{2a\left(t\right)}$$

(24)

$${\beta }_0\left(t\right)=\frac{h\left(t\right)}{{\mu }_0\left(t\right)},h\left(t\right)=exp\left({\int }_0^t\left(c\left(s\right)-2d\left(s\right)\right)ds\right)$$

(25)

$$\begin{array}{cc}\hfill {\gamma }_0\left(t\right)& =\frac{d\left(0\right)}{2a\left(0\right)}-\frac{a\left(t\right)h^2\left(t\right)}{{\mu }_0\left(t\right){\mu }_0^{\prime }\left(t\right)}-4{\int }_0^t\frac{a\left(s\right)\sigma \left(s\right)h^2\left(s\right)}{{\left({\mu }_0^{\prime }\left(s\right)\right)}^2}ds\hfill \end{array}$$

(26)

$$\begin{array}{cc}& =\frac{d\left(0\right)}{2a\left(0\right)}-\frac{1}{2{\mu }_1\left(0\right)}\frac{{\mu }_1\left(t\right)}{{\mu }_0\left(t\right)}\hfill \end{array}$$

(27)

$${\delta }_0\left(t\right)=\frac{h\left(t\right)}{{\mu }_0\left(t\right)}{\int }_0^t\left[\left(f\left(s\right)+\frac{d\left(s\right)}{a\left(s\right)}g\left(s\right)\right){\mu }_0\left(s\right)+\frac{g\left(s\right)}{2a\left(s\right)}{\mu }_0^{\prime }\left(s\right)\right]\frac{ds}{h\left(s\right)}$$

(28)

$$\begin{array}{cc}\hfill {\epsilon }_0\left(t\right)& =-\frac{2a\left(t\right)h\left(t\right)}{{\mu }_0^{\prime }\left(t\right)}{\delta }_0\left(t\right)-8{\int }_0^t\frac{a\left(s\right)\sigma \left(s\right)h\left(s\right)}{{\left({\mu }_0^{\prime }\left(s\right)\right)}^2}\left({\mu }_0\left(s\right){\delta }_0\left(s\right)\right)ds\hfill \\ & +2{\int }_0^t\frac{a\left(s\right)h\left(s\right)}{{\mu }_0^{\prime }\left(s\right)}\left[f\left(s\right)+\frac{d\left(s\right)}{a\left(s\right)}g\left(s\right)\right]ds\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\kappa }_0\left(t\right)& =-\frac{a\left(t\right){\mu }_0\left(t\right)}{{\mu }_0^{\prime }\left(t\right)}{\delta }_0^2\left(t\right)-4{\int }_0^t\frac{a\left(s\right)\sigma \left(s\right)}{{\left({\mu }_0^{\prime }\left(s\right)\right)}^2}{\left({\mu }_0\left(s\right){\delta }_0\left(s\right)\right)}^{2}ds\hfill \\ & +2{\int }_0^t\frac{a\left(s\right)}{{\mu }_0^{\prime }\left(s\right)}\left({\mu }_0\left(s\right){\delta }_0\left(s\right)\right)\left[f\left(s\right)+\frac{d\left(s\right)}{a\left(s\right)}g\left(s\right)\right]ds\hfill \end{array}$$

(30)

with $\delta \left(0\right)=g\left(0\right)/\left(2a\left(0\right)\right),$ $\epsilon \left(0\right)=-\delta \left(0\right),$ $\kappa \left(0\right)=0$. Here, ${\mu }_0$ and ${\mu }_1$ are the so-called standard solutions of the characteristic equation (19) subject to the following initial data

$${\mu }_0\left(0\right)=0,{\mu }_0^{\prime }\left(0\right)=2a\left(0\right)\ne 0{\mu }_1\left(0\right)\ne 0,{\mu }_1^{\prime }\left(0\right)=0$$

(31)

Solution (24)–(30) shall be referred to as a fundamental solution of the Riccati-type system (10)–(15); see Equations (48)–(52) and (60) for the corresponding asymptotics.

Lemma 2. 

The Riccati-type system (9)–(15) has the following (general) solution:

$$\begin{array}{cc}& \mu \left(t\right)=-2\mu \left(0\right){\mu }_0\left(t\right)\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)\hfill \end{array}$$

(32)

$$\begin{array}{cc}& \alpha \left(t\right)={\alpha }_0\left(t\right)-\frac{{\beta }_0^2\left(t\right)}{4\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(33)

$$\begin{array}{cc}& \beta \left(t\right)=-\frac{\beta \left(0\right){\beta }_0\left(t\right)}{2\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(34)

$$\begin{array}{cc}& \gamma \left(t\right)=\gamma \left(0\right)-\frac{{\beta }^2\left(0\right)}{4\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(35)

and

$$\begin{array}{cc}\hfill \delta \left(t\right)& ={\delta }_0\left(t\right)-\frac{{\beta }_0\left(t\right)\left(\delta \left(0\right)+{\epsilon }_0\left(t\right)\right)}{2\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \epsilon \left(t\right)& =\epsilon \left(0\right)-\frac{\beta \left(0\right)\left(\delta \left(0\right)+{\epsilon }_0\left(t\right)\right)}{2\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \kappa \left(t\right)& =\kappa \left(0\right)+{\kappa }_0\left(t\right)-\frac{{\left(\delta \left(0\right)+{\epsilon }_0\left(t\right)\right)}^2}{4\left(\alpha \left(0\right)+{\gamma }_0\left(t\right)\right)}\hfill \end{array}$$

(38)

in terms of the fundamental solution (24)–(30) subject to arbitrary initial data $\mu \left(0\right),$$\alpha \left(0\right),$$\beta \left(0\right)\ne 0,$$\gamma \left(0\right),$$\delta \left(0\right),$$\epsilon \left(0\right),$$\kappa \left(0\right).$

Proof. 

Use Equations (21)–(23), uniqueness of the solution and the elementary integral:

$${\int }_{-\infty }^{\infty }{e}^{-a{y}^2+2by}dy=\sqrt{\frac{\pi }{a}}{e}^{b^2/a},a>0$$

(39)

Computational details are left to the reader. ☐

Remark 1. 

It is worth noting that our transformation (8), combined with the standard heat kernel [33]:

$$K_0\left(\xi ,\eta ,\tau \right)=\frac{1}{\sqrt{4\pi \left(\tau -{\tau }_0\right)}}exp\left[-\frac{{\left(\xi -\eta \right)}^2}{4\left(\tau -{\tau }_0\right)}\right]$$

(40)

for the diffusion equation (7) and (32)–(38), allows one to derive the fundamental solution (23) of the diffusion-type equation (6) from a new perspective.

Our next result is the following:

Lemma 3. 

Solution (32)–(38) implies:

$$\begin{array}{cc}& {\mu }_0=\frac{2\mu }{\mu \left(0\right){\beta }^2\left(0\right)}\left(\gamma -\gamma \left(0\right)\right)\hfill \end{array}$$

(41)

$$\begin{array}{cc}& {\alpha }_0=\alpha -\frac{{\beta }^2}{4\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(42)

$$\begin{array}{cc}& {\beta }_0=\frac{\beta \left(0\right)\beta }{2\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(43)

$$\begin{array}{cc}& {\gamma }_0=-\alpha \left(0\right)-\frac{{\beta }^2\left(0\right)}{4\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(44)

and

$$\begin{array}{cc}\hfill {\delta }_0& =\delta -\frac{\beta \left(\epsilon -\epsilon \left(0\right)\right)}{2\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\epsilon }_0& =-\delta \left(0\right)+\frac{\beta \left(0\right)\left(\epsilon -\epsilon \left(0\right)\right)}{2\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\kappa }_0& =\kappa -\kappa \left(0\right)-\frac{{\left(\epsilon -\epsilon \left(0\right)\right)}^2}{4\left(\gamma -\gamma \left(0\right)\right)}\hfill \end{array}$$

(47)

which gives the following asymptotics

$$\begin{array}{cc}& {\alpha }_0\left(t\right)=-\frac{1}{4a\left(0\right)t}-\frac{c\left(0\right)}{4a\left(0\right)}+\frac{a^{\prime }\left(0\right)}{8a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(48)

$$\begin{array}{cc}& {\beta }_0\left(t\right)=\frac{1}{2a\left(0\right)t}-\frac{a^{\prime }\left(0\right)}{4a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(49)

$$\begin{array}{cc}& {\gamma }_0\left(t\right)=-\frac{1}{4a\left(0\right)t}+\frac{c\left(0\right)}{4a\left(0\right)}+\frac{a^{\prime }\left(0\right)}{8a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(50)

$$\begin{array}{cc}& {\delta }_0\left(t\right)=\frac{g\left(0\right)}{2a\left(0\right)}+\mathcal{O}\left(t\right),{\epsilon }_0\left(t\right)=-\frac{g\left(0\right)}{2a\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(51)

$$\begin{array}{cc}& {\kappa }_0\left(t\right)=\mathcal{O}\left(t\right)\hfill \end{array}$$

(52)

after Taylor expanding Equations (41)–(47) as $t\to 0^{+}.$

Proof. 

For the derivations of the corresponding asymptotics consider first the Taylor expansion of ${\alpha }_0$, ${\beta }_0$ and ${\gamma }_0$ centered at 0 as follow:

$$\begin{array}{ccc}\hfill {\alpha }_0\left(t\right)& =& \alpha \left(t\right)-\frac{{\beta }^2\left(t\right)}{4\left(\gamma \right(t)-\gamma (0\left)\right)}\hfill \end{array}$$

(53)

$$\begin{array}{ccc}& =& \alpha \left(0\right)+{\alpha }^{\prime }\left(0\right)t-\left(\frac{{\beta }^2\left(0\right)+2\beta \left(0\right){\beta }^{\prime }\left(0\right)t}{4{\gamma }^{\prime }\left(0\right)t}\right)\left(1-\frac{{\gamma }^{{}^{″}}\left(0\right)t}{2{\gamma }^{\prime }\left(0\right)}\right)+\mathcal{O}\left(t^2\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& \alpha \left(0\right)+{\alpha }^{\prime }\left(0\right)t-\frac{1+2\left(c\right(0)+4a(0\left)\alpha \right(0\left)\right)}{4a\left(0\right)t}\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{a^{\prime }\left(0\right)+2a\left(0\right)(c\left(0\right)+4a\left(0\right)\alpha \left(0\right))}{8a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& -\frac{1}{4a\left(0\right)t}-\frac{c\left(0\right)}{4a\left(0\right)t}+\frac{a^{\prime }\left(0\right)}{8a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(54)

and similarly

$$\begin{array}{ccc}\hfill {\beta }_0\left(t\right)& =& \frac{\beta \left(0\right)\beta \left(t\right)}{2\left(\gamma \right(t)-\gamma (0\left)\right)}\hfill \\ & =& \beta \left(0\right)\left(\frac{\beta \left(0\right)+{\beta }^{\prime }\left(0\right)t}{2{\gamma }^{\prime }\left(0\right)t}\right)\left(1-\frac{{\gamma }^{{}^{″}}\left(0\right)t}{2{\gamma }^{\prime }\left(0\right)}\right)+\mathcal{O}\left(t^2\right)\hfill \\ & =& \frac{1+\left(c\right(0)+4a(0\left)\alpha \right(0\left)\right)}{2a\left(0\right)t}-\frac{a^{\prime }\left(0\right)+2a\left(0\right)(c\left(0\right)+4a\left(0\right)\alpha \left(0\right))}{4a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \\ & =& \frac{1}{2a\left(0\right)t}-\frac{a^{\prime }\left(0\right)}{4a^2\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(55)

as $t\to$$0^{+}$. In order to obtain the corresponding asypmtotic for ${\gamma }_0\left(t\right)$ we can follow similar procedure as for Equation (54) resulting in

$${\gamma }_0\left(t\right)=-\frac{1}{4a\left(0\right)t}+\frac{c\left(0\right)}{4a\left(0\right)t}+\frac{a^{\prime }\left(0\right)}{8a^2\left(0\right)}+\mathcal{O}\left(t\right)$$

Consider now Equation (45). Then, for the asymptotic of ${\delta }_0\left(t\right)$ we have that:

$$\begin{array}{cc}\hfill {\delta }_0\left(t\right)& =\delta \left(t\right)-\frac{\beta \left(t\right)\left(\epsilon \right(t)-\epsilon (0\left)\right)}{2\left(\gamma \right(t)-\gamma (0\left)\right)}\hfill \\ & =\delta \left(0\right)-\frac{\beta \left(0\right){\epsilon }^{\prime }\left(0\right)}{4{\gamma }^{\prime }\left(0\right)}+\mathcal{O}\left(t^2\right)\hfill \\ & =\frac{g\left(0\right)}{2a\left(0\right)}+\mathcal{O}\left(t\right)\hfill \end{array}$$

(56)

and similarly

$${\epsilon }_0\left(t\right)=-\frac{g\left(0\right)}{2a\left(0\right)}+\mathcal{O}\left(t\right)$$

as $t\to 0^{+}$. Finally, considering the Taylor expansion of ${\kappa }_0\left(t\right)$ and ${\epsilon }_0\left(t\right)$ centered at the zero, the asymptotic for ${\kappa }_0\left(t\right)$ results in

$$\begin{array}{cc}\hfill {\kappa }_0\left(t\right)& =\kappa \left(t\right)-\kappa \left(0\right)-\frac{\left(\epsilon \right(t)-\epsilon (0\left)\right)}{2\left(\gamma \right(t)-\gamma (0\left)\right)}\hfill \\ & =-\frac{{\epsilon }^{\prime }\left(0\right)t}{4{\gamma }^{\prime }\left(0\right)}\left(1-\frac{{\gamma }^{{}^{″}}\left(0\right)t}{2{\gamma }^{\prime }\left(0\right)}\right)+\mathcal{O}\left(t^2\right)\hfill \\ & =\mathcal{O}\left(t\right)\hfill \end{array}$$

(57)

as $t\to 0^{+}$. In the case of ${\mu }_0\left(t\right)$ the corresponding expansion is given by

$$\begin{array}{cc}\hfill {\mu }_0\left(t\right)& =\frac{(2\mu \left(0\right)+{\mu }^{\prime }\left(0\right)t)\left({\gamma }^{\prime }\left(0\right)t\right)}{\mu \left(0\right){\beta }^2\left(0\right)}+\mathcal{O}\left(t^3\right)\hfill \end{array}$$

(58)

$$\begin{array}{cc}& =\frac{2{\gamma }^{\prime }\left(0\right)}{{\beta }^2\left(0\right)}t+\mathcal{O}\left(t^2\right)\hfill \end{array}$$

$$\begin{array}{cc}& =2a\left(0\right)t+\mathcal{O}\left(t^2\right)\hfill \end{array}$$

(59)

☐

Notice that Equations (41)–(47) are inversions of Equations (32)–(38). These formulas allows to establish a required asymptotic of the fundamental solution (23):

$$\begin{array}{cc}\hfill K_0\left(x,y,t\right)& \sim \frac{1}{\sqrt{4\pi a\left(0\right)t}}exp\left[-\frac{{\left(x-y\right)}^2}{4a\left(0\right)t}\right]\hfill \\ & \times exp\left[\frac{a^{\prime }\left(0\right)}{8a^2\left(0\right)}{\left(x-y\right)}^2-\frac{c\left(0\right)}{4a\left(0\right)}\left(x^2-y^2\right)\right]exp\left[\frac{g\left(0\right)}{2a\left(0\right)}\left(x-y\right)\right]\hfill \end{array}$$

(60)

We have corrected a typo in [1] (Here, $f\sim g$ as $t\to 0^{+},$ if ${lim}_{t\to 0^{+}}\left(f/g\right)=$$1.$ The proof is left to the reader.)

By a direct substitution one can verify that the right hand sides of Equations (32)–(38) satisfy the Riccati-type system (9)–(15) and that the asymptotics (48)–(52) result in the continuity with respect to initial data:

$$\underset{t\to 0^{+}}{lim}\mu \left(t\right)=\mu \left(0\right),\underset{t\to 0^{+}}{lim}\alpha \left(t\right)=\alpha \left(0\right),\text{etc.}$$

(61)

The transformation property (32)–(38) allows one to find solution of the initial value problem in terms of the fundamental solution (24)–(30) and may be referred to as a nonlinear superposition principle for the Riccati-type system see also [34,35].

4. Symmetries of the Autonomous Diffusion Equation

In the simplest case $a=1,$$b=c=d=f=g=0$, when $u_t=u_{xx},$ our Lemma 1 provides the following general transformation

$$\begin{array}{ccc}\hfill u\left(x,t\right)& =& \frac{1}{\sqrt{\mu \left(0\right)\left(1-4\alpha \left(0\right)t\right)}}exp\left(\frac{\alpha \left(0\right)x^2+\delta \left(0\right)x+{\delta }^2\left(0\right)t}{1-4\alpha \left(0\right)t}+\kappa \left(0\right)\right)\hfill \\ & & \times v\left(\frac{\beta \left(0\right)x+2\beta \left(0\right)\delta \left(0\right)t}{1-4\alpha \left(0\right)t}+\epsilon \left(0\right),\frac{{\beta }^2\left(0\right)t}{1-4\alpha \left(0\right)t}+\gamma \left(0\right)\right)\hfill \end{array}$$

(62)

with ${\mu }^{\prime }\left(0\right)=-4\alpha \left(0\right)\mu \left(0\right)$ of the diffusion equation into itself (see [15,16,36]). It includes the familiar Galilei transformations:

$$u\left(x,t\right)=exp\left(\frac{V}{2}x+\frac{V^2}{4}t\right)v\left(x+Vt+x_0,t+t_0\right)$$

(63)

when $\alpha \left(0\right)=0,$$\beta \left(0\right)=\mu \left(0\right)=1,$$\kappa \left(0\right)=0$ and $\delta \left(0\right)=V/2;$ supplemented by dilatations:

$$u\left(x,t\right)=v\left(lx,l^{2}t\right)$$

(64)

with $\alpha \left(0\right)=\gamma \left(0\right)=\delta \left(0\right)=\epsilon \left(0\right)=\kappa \left(0\right)=0,$$\mu \left(0\right)=1$ and $\beta \left(0\right)=l;$ and expansions:

$$\begin{array}{ccc}\hfill u\left(x,t\right)& =& \frac{1}{\sqrt{1+mt}}exp\left(-\frac{m{x}^2}{1+mt}\right)v\left(\frac{x}{1+mt},\frac{t}{1+mt}\right)\hfill \\ & & \left(\mu \left(0\right)=1\left(\ne 0\right),{\mu }^{\prime }\left(0\right)=m\right),\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill u\left(x,t\right)& =& \frac{1}{\sqrt{2t}}exp\left(-\frac{x^2}{4t}\right)v\left(\frac{x}{2t},-\frac{1}{4t}\right)\hfill \\ & & \left(\mu \left(0\right)=0,{\mu }^{\prime }\left(0\right)=2\left(\ne 0\right)\right)\hfill \end{array}$$

(66)

with $\beta \left(0\right)=1,$$\delta \left(0\right)=\epsilon \left(0\right)=\kappa \left(0\right)=0$. The symmety group of the corresponding Schrödinger equations is discussed in [14,15,36,37,38,39].

5. Eigenfunction Expansion and Ermakov-Type System

With the help of transformation (8) one can reduce the diffusion equation (6) to another convenient form

$$\frac{\partial v}{\partial \tau }=\frac{{\partial }^{2}v}{\partial {\xi }^2}-c_0{\xi }^{2}v\left(c_0=0,1\right)$$

(67)

when

$$\begin{array}{cc}& \frac{d\alpha }{dt}+b-2c\alpha -4a{\alpha }^2=c_{0}a{\beta }^4\hfill \end{array}$$

(68)

$$\begin{array}{cc}& \frac{d\beta }{dt}-\left(c+4a\alpha \right)\beta =0\hfill \end{array}$$

(69)

$$\begin{array}{cc}& \frac{d\gamma }{dt}-a{\beta }^2=0\hfill \end{array}$$

(70)

$$\begin{array}{cc}& \frac{d\delta }{dt}-\left(c+4a\alpha \right)\delta =f-2\alpha g+2c_{0}a{\beta }^3\epsilon \hfill \end{array}$$

(71)

$$\begin{array}{cc}& \frac{d\epsilon }{dt}+\left(g-2a\delta \right)\beta =0\hfill \end{array}$$

(72)

$$\begin{array}{cc}& \frac{d\kappa }{dt}+g\delta -a{\delta }^2=c_{0}a{\beta }^2{\epsilon }^2\hfill \end{array}$$

(73)

and Equation (9) holds.

It is important to notice that with the substitution (9) Equation (68) can be transformed into a Ermakov type equation of the form

$${\mu }^{″}-\tau \left(t\right){\mu }^{\prime }-4\sigma \left(t\right)\mu =c_0{\left(2a\right)}^2{\beta }^4\mu$$

(74)

where

$$\tau \left(t\right)=\frac{a^{\prime }}{a}+2c-4d,\sigma \left(t\right)=ab+cd-d^2+\frac{d}{2}\left(\frac{a^{\prime }}{a}-\frac{d^{\prime }}{d}\right)$$

(75)

However, in this paper, we work with the module of the solution; because we are considering real solutions, the complex solution has been used in the case of linear and nonlinear Schrödinger equation see [40] for more details.

We present the following result.

Lemma 4. 

The Ermakov-type system with $c_0=1$ has the following solution:

$$\begin{array}{cc}& \mu \left(t\right)={\mu }_0\mu \left(0\right)\sqrt{4{\left({\gamma }_0+\alpha \left(0\right)\right)}^2-{\beta }^4\left(0\right)}\hfill \end{array}$$

(76)

$$\begin{array}{cc}& \alpha \left(t\right)={\alpha }_0-\frac{{\beta }_0^2\left({\gamma }_0+\alpha \left(0\right)\right)}{4{\left({\gamma }_0+\alpha \left(0\right)\right)}^2-{\beta }^4\left(0\right)}\hfill \end{array}$$

(77)

$$\begin{array}{cc}& \beta \left(t\right)=\frac{\beta \left(0\right){\beta }_0}{\sqrt{4{\left({\gamma }_0+\alpha \left(0\right)\right)}^2-{\beta }^4\left(0\right)}}\hfill \end{array}$$

(78)

$$\begin{array}{cc}& \gamma \left(t\right)=\gamma \left(0\right)-\frac{1}{4}ln\left[\frac{({\gamma }_0+\alpha \left(0\right))+\frac{1}{2}{\beta }^2\left(0\right)}{({\gamma }_0+\alpha \left(0\right))-\frac{1}{2}{\beta }^2\left(0\right)}\right]\hfill \end{array}$$

(79)

and

$$\begin{array}{cc}& \delta \left(t\right)={\delta }_0+{\beta }_0\frac{\epsilon \left(0\right){\beta }^3\left(0\right)-2({\gamma }_0+\alpha \left(0\right))({\epsilon }_0+\delta \left(0\right))}{4{({\gamma }_0+\alpha \left(0\right))}^2-{\beta }^4\left(0\right)}\hfill \end{array}$$

(80)

$$\begin{array}{cc}& \epsilon \left(t\right)=\frac{\beta \left(0\right)\left(\delta \left(0\right)+{\epsilon }_0\right)-2\epsilon \left(0\right)\left({\gamma }_0+\alpha \left(0\right)\right)}{\sqrt{4{\left({\gamma }_0+\alpha \left(0\right)\right)}^2-{\beta }^4\left(0\right)}}\hfill \end{array}$$

(81)

$$\begin{array}{cc}& \kappa \left(t\right)={\kappa }_0+\kappa \left(0\right)+\frac{{\beta }^3\left(0\right)\epsilon \left(0\right)({\epsilon }_0+\delta \left(0\right))}{4{({\gamma }_0+\alpha \left(0\right))}^2-{\beta }^4\left(0\right)}\hfill \end{array}$$

(82)

$$\begin{array}{cc}& -\frac{({\gamma }_0+\alpha \left(0\right))\left[{\beta }^2\left(0\right){\epsilon }^2\left(0\right)+{({\epsilon }_0+\delta \left(0\right))}^2\right]}{4{({\gamma }_0+\alpha \left(0\right))}^2-{\beta }^4\left(0\right)}\hfill \end{array}$$

(83)

in terms of the fundamental solution of the Riccati-system (24)–(30) subject to arbitrary initial data $\mu \left(0\right),$$\alpha \left(0\right),$$\beta \left(0\right)\ne 0,$$\gamma \left(0\right),$ $\delta \left(0\right),$$\epsilon \left(0\right),$$\kappa \left(0\right).$

(See Appendix A for a sketch of the proof for this Lemma. The corresponding integral can be found in [41,42].)

Then a particular solution of the diffusion equation (6) has the form

$$u_n\left(x,t\right)=\frac{e^{\alpha x^2+\delta x+\kappa -\left(2n+1\right)\left(\gamma -\gamma \left(0\right)\right)}}{\sqrt{2^{n}n!\mu \sqrt{\pi }}}{e}^{-{\left(\beta x+\epsilon \right)}^2/2}{H}_n\left(\beta x+\epsilon \right)$$

(84)

where $H_n\left(x\right)$ are the Hermite polynomials [43]. The solution of the Ermakov-type system (68)–(73) is provided by our Lemma 4.

The solution of the Cauchy initial value problem can be found in terms of an eigenfunction expansion by the superposition principle, similar to the case of the corresponding Schrödinger equationin [7,12]:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{c}_n{u}_n\left(x,t\right)$$

(85)

with

$$u_n\left(x,0\right)=\frac{e^{\alpha \left(0\right)x^2+\delta \left(0\right)x+\kappa \left(0\right)-\left(2n+1\right)\left(\gamma -\gamma \left(0\right)\right)}}{\sqrt{2^{n}n!\mu \left(0\right)\sqrt{\pi }}}{e}^{-{\left(\beta \left(0\right)x+\epsilon \left(0\right)\right)}^2/2}{H}_n\left(\beta \left(0\right)x+\epsilon \left(0\right)\right)$$

(86)

One can choose $\alpha \left(0\right)=\delta \left(0\right)=\epsilon \left(0\right)=\kappa \left(0\right)=0$ and $\beta \left(0\right)=\mu \left(0\right)=1,$ when the eigenfunctions are orthonormal

$${\int }_{-\infty }^{\infty }{u}_m\left(x,0\right)u_n\left(x,0\right)dx={\delta }_{mn}$$

(87)

in view of the orthogonality property of Hermite polynomials [43]. Then the expansion coefficients are given by

$$c_n={\int }_{-\infty }^{\infty }{u}_n\left(x,0\right)u\left(x,0\right)dx$$

(88)

Equations (85) and (88) provide the solution of the initial value problem.

6. Nonautonomous Burgers Equation

The nonlinear equation

$$\begin{array}{cc}& \frac{\partial v}{\partial t}+a\left(t\right)\left(v\frac{\partial v}{\partial x}-\frac{{\partial }^{2}v}{\partial x^2}\right)-c\left(t\right)\left(x\frac{\partial v}{\partial x}+v\right)+g\left(t\right)\frac{\partial v}{\partial x}\hfill \\ & =2\left(2b\left(t\right)x-f\left(t\right)\right)\hfill \end{array}$$

(89)

when $a=1$ and $b=c=f=g=0,$ is known as Burgers’ equation [44,45,46,47,48,49,50] and we shall refer to Equation (89) as a nonautonomous Burgers-type equation; see also [16,51].

Lemma 5. 

The following identity holds (Occationally is custom to use the shorten notation $v_t=\frac{\partial v}{\partial t},v_{tt}=\frac{{\partial }^{2}v}{\partial t^2}$, etc.)

$$\begin{array}{cc}& v_t+a\left(v{v}_x-v_{xx}\right)+\left(g-cx\right)v_x-cv+2\left(f-2bx\right)\hfill \\ & =-2{\left(\frac{u_t-Qu}{u}\right)}_x\hfill \end{array}$$

(90)

if

$$v=-2\frac{u_x}{u}\left(\text{T}\text{h}\text{e}\mathit{\text{Cole--Hopf}}\mathit{\text{transformation}}\right)$$

(91)

and

$$Qu=a{u}_{xx}-\left(g-cx\right)u_x+\left(d+fx-b{x}^2\right)u$$

(92)

($a,$$b,$$c,$$d,$$f,$g are functions of t only).

Proof. 

From the Cole–Hopf transformation (91):

$$\begin{array}{cc}& v_t=-2\frac{u_{xt}}{u}+2\frac{u_x{u}_t}{u^2}\hfill \end{array}$$

(93)

$$\begin{array}{cc}& v_x=-2\frac{u_{xx}}{u}+\frac{1}{2}{v}^2\hfill \end{array}$$

(94)

$$\begin{array}{cc}& v_{xx}=-2\frac{u_{xxx}}{u}+\frac{3}{2}v{v}_x-\frac{1}{4}{v}^3\hfill \end{array}$$

(95)

and by Equation (92) we know that

$$\begin{array}{cc}& Qu=a{u}_{xx}-(g-cx)u_x+(d+fx-b{x}^2)u\hfill \end{array}$$

(96)

$$\begin{array}{cc}& Q_{x}u=c{u}_x+(f-2bx)u\hfill \end{array}$$

(97)

$$\begin{array}{cc}& Q{u}_x=a{u}_{xxx}-(g-cx)u_{xx}+(d+fx-b{x}^2)u_x\hfill \end{array}$$

(98)

In view of Equations (93)–(98), the RHS of Equation (90) becomes

$$\begin{array}{cc}& -2{\left(\frac{u_t-Qu}{u}\right)}_x=v_t+\frac{2}{u}(Q_{x}u+Q{u}_x)+\frac{v}{u}Qu\hfill \end{array}$$

(99)

$$\begin{array}{cc}& =v_t+c\left(2\frac{u_x}{u}\right)+2(f-2bx)+a\left(2\frac{u_{xxx}}{u}\right)-\left(2\frac{u_{xx}}{u}\right)(g-cx)\hfill \end{array}$$

$$\begin{array}{cc}& +\left(2\frac{u_x}{u}\right)(d+fx-b{x}^2)+v\left[a\left(\frac{u_{xx}}{u}\right)-\frac{u_x}{u}(g-cx)+(d+fx-b{x}^2)\right]\hfill \end{array}$$

$$\begin{array}{cc}& =v_t+a(v{v}_x-v_{xx})+(g-cx)v_x-cv+2(f-2bx)\hfill \end{array}$$

(100)

as desired. Backward procedure complete the proof. Additional details are left to the reader. ☐

The substitution (91) turns the nonlinear Burgers-type equation (89) into the diffusion-type equation (6). Then solution of the corresponding Cauchy initial value problem can be represented as

$$v\left(x,t\right)=-2\frac{\partial }{\partial x}ln\left[{\int }_{-\infty }^{\infty }{K}_0\left(x,y,t\right)exp\left(-\frac{1}{2}{\int }_0^{y}v\left(z,0\right)dz\right)dy\right]$$

(101)

where the heat kernel is given by Equation (23), for suitable initial data $v\left(z,0\right)$ on $\mathbb{R}.$

In a similar fashion, we can associate the diffusion-type equation (6) to another non-autonomous Burgers-type equation.

Lemma 6. 

The nonautonomous diffusion-type equation (6) can be transformed to the nonautonomous and inhomogeneous Burgers-type equation

$$\begin{array}{c}\hfill U_t+a\left(U{U}_x-U_{xx}\right)=\frac{{\beta }^{\prime }}{\beta }\left(U+x{U}_x\right)+\frac{{\epsilon }^{\prime }}{\beta }{U}_x\end{array}$$

(102)

with the aid of the extended Cole-Hopf transformation

$$\begin{array}{c}\hfill U=-2\frac{u_x}{u}+2(2\alpha x+\delta )\end{array}$$

(103)

Proof. 

Let $\tilde{U}=-2\frac{u_x}{u}$. Then we have from Equation (103) that

$$\begin{array}{c}\hfill \tilde{U}=U-2(2\alpha x+\delta )\end{array}$$

(104)

From Lemma 5 we know that

$$\begin{array}{cc}& \widetilde{U_t}+a\left(\tilde{U}{\tilde{U}}_x-{\tilde{U}}_{xx}\right)+\left(g-cx\right){\tilde{U}}_x-c\tilde{U}+2\left(f-2bx\right)=-2{\left(\frac{u_t-Qu}{u}\right)}_x\hfill \end{array}$$

(105)

Substitution of space and time derivatives of Equation (104) into Equation (105) leads to

$$\begin{array}{cc}& U_t+a\left(U{U}_x-U_{xx}\right)-\frac{{\beta }^{\prime }}{\beta }\left(U+x{U}_x\right)-\frac{{\epsilon }^{\prime }}{\beta }{U}_x=-2{\left(\frac{u_t-Qu}{u}\right)}_x\hfill \end{array}$$

(106)

from which we can establish the desired commutative relation. Additional details are left to the reader. ☐

Diagram 1. A diagram summarizing the relations between the non-autonomous and inhomogeneous diffusion-type equation (6), the linear heat equation (7) and the Burgers-type equations (102) and (113).

Following the same strategy, if we consider the transformation

$$U=\beta \left(t\right)V(\xi ,\tau )$$

(107)

with $\xi =\beta \left(t\right)x+\epsilon \left(t\right)$ and $\tau =\gamma \left(t\right)$, the corresponding space and time derivatives will be given by

$$\begin{array}{cc}& U_t={\beta }^{\prime }V+\beta ({\beta }^{\prime }x+{\epsilon }^{\prime })V_{\xi }+\beta {\gamma }^{\prime }{V}_{\tau }\hfill \end{array}$$

(108)

$$\begin{array}{cc}& U_x={\beta }^2{V}_{\xi }\hfill \end{array}$$

(109)

$$\begin{array}{cc}& U_{xx}={\beta }^3{V}_{\xi \xi }\hfill \end{array}$$

(110)

Susbtitution of Equations (107)–(110) into Equation (102) yields

$${\beta }^{\prime }V+\beta ({\beta }^{\prime }x+{\epsilon }^{\prime })V_{\xi }+\beta {\gamma }^{\prime }{V}_{\tau }+a{\beta }^3\left(V{V}_{\xi }-V_{\xi \xi }\right)={\beta }^{\prime }(V+\beta x{V}_{\xi })+{\epsilon }^{\prime }\beta V_{\xi }$$

(111)

simplifying to

$$\beta {\gamma }^{\prime }{V}_{\tau }+a{\beta }^3\left(V{V}_{\xi }-V_{\xi \xi }\right)=0$$

(112)

After dividing by $a{\beta }^3$ and using Equation (12), Equation (112) reduces to the Burgers equation

$$V_t+V{V}_x=V_{xx}$$

(113)

We refer the reader to the existent literature for further details regarding forced Burgers equations. The connections between the inhomogeneous diffusion equation (6), the linear heat equation (7), the Burgers equation (113) and the non-autonomous and inhomogeneous Burgers equation (102) is portrayed in Diagram 1. Equations (89) and (102) may be useful generalizations in a diverse of Physical contexts, and could be used to test certain numerical schemes.

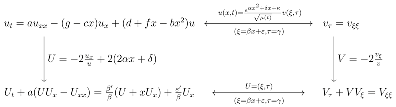
7. Traveling Wave Solutions of Burgers-Type Equation

Looking for solutions of our Equation (89) in the form

$$v=\beta \left(t\right)F\left(\beta \left(t\right)x+\gamma \left(t\right)\right)=\beta F\left(z\right),z=\beta \left(t\right)x+\gamma \left(t\right)$$

(114)

(β and γ are functions of t only), one gets

$$F^{″}=\left(c_0+c_1\right)F^{\prime }+F{F}^{\prime }+2c_{2}z+c_3$$

(115)

provided that

$$\begin{array}{ccc}& & {\beta }^{\prime }=c\beta ,{\gamma }^{\prime }=c_{0}a{\beta }^2\hfill \end{array}$$

(116)

$$\begin{array}{ccc}& & g=c_{1}a\beta ,b=-\frac{1}{2}{c}_{2}a{\beta }^4\hfill \end{array}$$

(117)

$$\begin{array}{ccc}& & f=\frac{1}{2}a{\beta }^3\left(2c_2\gamma +c_3\right)\hfill \end{array}$$

(118)

($c_0,$$c_1,$$c_2,$$c_3$ are constants). Integration of Equation (115) yields

$$F^{\prime }=\left(c_0+c_1\right)F+\frac{1}{2}{F}^2+c_2{z}^2+c_{3}z+c_4$$

(119)

where $c_4$ is a constant of integration. The substitution

$$F=-2\frac{{\mu }^{\prime }}{\mu }$$

(120)

transforms the Riccati equation (119) into a special case of generalized equation of hypergeometric type:

$${\mu }^{″}-\left(c_0+c_1\right){\mu }^{\prime }+\frac{1}{2}\left(c_2{z}^2+c_{3}z+c_4\right)\mu =0$$

(121)

which can be solved in general by methods of [52]. Elementary solutions are discussed, for example, in [53,54].

8. Examples

Now we consider from a united viewpoint several elementary diffusion and Burgers-type equations that are important in applications.

Example 1 For the standard diffusion equation on $\mathbb{R}:$

$$\frac{\partial u}{\partial t}=a\frac{{\partial }^{2}u}{\partial x^2},a=\text{constant}>0$$

(122)

the heat kernel is given by

$$K\left(x,y,t\right)=\frac{1}{\sqrt{4\pi at}}exp\left[-\frac{{\left(x-y\right)}^2}{4at}\right],t>0$$

(123)

(See [33,55] and references therein for a detailed investigation of the classical one-dimensional heat equation.)

Example 2 In a mathematical description of the nerve cell a dendritic branch is typically modeled by using cylindrical cable equation [56]:

$$\tau \frac{\partial u}{\partial t}={\lambda }^2\frac{{\partial }^{2}u}{\partial x^2}+u,\tau =\text{constant}>0$$

(124)

The fundamental solution on $\mathbb{R}$ is given by

$$K_0\left(x,y,t\right)=\frac{\sqrt{\tau }{e}^{t/\tau }}{\sqrt{4\pi {\lambda }^{2}t}}exp\left[-\frac{\tau {\left(x-y\right)}^2}{4{\lambda }^{2}t}\right],t>0$$

(125)

(See also [57] and references therein.)

Example 3 The fundamental solution of the Fokker-Planck equation [58,59]:

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+x\frac{\partial u}{\partial x}+u$$

(126)

on $\mathbb{R}$ is given by [1]:

$$K_0\left(x,y,t\right)=\frac{1}{\sqrt{2\pi \left(1-e^{-2t}\right)}}exp\left[-\frac{{\left(x-e^{-t}y\right)}^2}{2\left(1-e^{-2t}\right)}\right],t>0$$

(127)

Here,

$$\underset{t\to \infty }{lim}{K}_0\left(x,y,t\right)=\frac{e^{-x^2/2}}{\sqrt{2\pi }},y=\text{constant}$$

(128)

The solution of the Cauchy initial value problem for the Fokker-Planck equation on $\mathbb{R}$ can also be given in terms of eigenfunction expansion with the aid of the superposition principle. In the corresponding eigenfunction expansion:

$$u(x,t)=\sum _{n=0}^{\infty }{c}_n{u}_n(x,t)$$

(129)

and after choosing $\delta \left(0\right)=\epsilon \left(0\right)=\kappa \left(0\right)=0$, $\alpha \left(0\right)=-3/8$, $\beta \left(0\right)=1/2$ and $\mu \left(0\right)=1$, the corresponding eigenfunction is given by

$$u_n(x,t)=\frac{e^{-\frac{1}{2}{x}^2+\frac{1}{4}(2n+1)\left(ln\frac{1+e^{-2t}}{2}\right)}}{\sqrt{2^{n}n!\sqrt{\pi }\sqrt{\frac{1}{2}(1+e^{-2t})}}}{H}_n\left(\frac{x{e}^{-t}}{\sqrt{2(1+e^{-2t})}}\right)$$

(130)

and the expansion coefficients are

$$c_n={\int }_{-\infty }^{\infty }\frac{e^{-\frac{1}{2}{x}^2}}{\sqrt{2^{n}n!\sqrt{\pi }}}{H}_n\left(\frac{x}{2}\right)u(x,0)dx$$

Further details are left to the reader.

Example 4 Equation

$$\frac{\partial u}{\partial t}=a\frac{{\partial }^{2}u}{\partial x^2}+\left(g-kx\right)\frac{\partial u}{\partial x},a,k>0,g\ge 0$$

(131)

corresponds to the heat equation with linear drift when $g=0$ [15]. In stochastic differential equations this equation corresponds the Kolmogorov forward equation for the regular Ornstein–Uhlenbech process [18]. The fundamental solution is given by

$$\begin{array}{cc}& K_0\left(x,y,t\right)=\frac{\sqrt{k}{e}^{kt/2}}{\sqrt{4\pi asinh\left(kt\right)}}\hfill \\ & \times exp\left[-\frac{{\left(k\left(x{e}^{-kt/2}-y{e}^{kt/2}\right)+2gsinh\left(kt/2\right)\right)}^2}{4aksinh\left(kt\right)}\right],t>0\hfill \end{array}$$

(132)

(See [1,18] for more details.)

Example 5 The Black-Scholes model provides a mathematical description of financial markets and derivative investment instruments [22,24]. If S is the price of the stock, $V\left(S,t\right)$ is the price of a derivative as a function of time and stock price, r is the annualized risk-free interest rate, continuously compound, σ is the volatility of stock’s returnes; this is the square root of the quadratic variation of the stock’s log price process, the celebrated Black-Scholes equation is given by [22,23,24,25,26,27]:

$$\frac{\partial V}{\partial t}+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^{2}V}{\partial S^2}+rS\frac{\partial V}{\partial S}-rV=0$$

(133)

The substitution $V\left(S,t\right)=v\left(x,\tau \right),$ where $S=e^x$ (due to Euler) and $\tau =T-t$ (the time to maturity), results in the diffusion-type equation

$$v_t=\frac{1}{2}{\sigma }^2{v}_{xx}+\left(r-\frac{1}{2}{\sigma }^2\right)v_x-rv$$

(134)

which can be transformed into the standard heat equation for variable r and σ with the help of Lemma 1.

The corresponding characteristic equation,

$${\mu }^{″}-\left(4r+2\frac{{\sigma }^{\prime }}{\sigma }\right){\mu }^{\prime }+4r\left(r-\frac{r^{\prime }}{2r}+\frac{{\sigma }^{\prime }}{\sigma }\right)\mu =0$$

(135)

can be solved explicitly when σ and r are constants. The standard solutions are given by

$${\mu }_0={\sigma }^2\tau e^{2r\tau },{\mu }_1=\left(1-2r\tau \right)e^{2r\tau }$$

(136)

and the corresponding fundamental solution can be obtain in a closed form [22]:

$$K_0\left(x,y,\tau \right)=\frac{e^{-r\tau }}{\sigma \sqrt{2\pi \tau }}exp\left[-\frac{{\left(x-y+\left(r-{\sigma }^2/2\right)\tau \right)}^2}{2{\sigma }^2\tau }\right],\tau >0$$

(137)

from our Equations (24)–(30). Then, by using initial conditions, V can be computed explicitly in terms of the error function, leading to Black-Scholes formula [22].

It is worth adding, in conclusion, that by our Lemma 1 the following transformation:

$$v\left(x,\tau \right)=\frac{1}{\sqrt{\mu \left(\tau \right)}}{e}^{\alpha \left(\tau \right)x^2+\delta \left(\tau \right)x+\kappa \left(\tau \right)}u\left(\xi ,{\tau }_0\right),\xi =\beta \left(\tau \right)x+\epsilon \left(\tau \right),{\tau }_0=\gamma \left(\tau \right)$$

(138)

results in $u_{{\tau }_0}=u_{\xi \xi },$ where $\mu =\mu \left(0\right)\left(1-2\alpha \left(0\right){\sigma }^2\tau \right)e^{2r\tau }$ and

$$\alpha =\frac{\alpha \left(0\right)}{1-2\alpha \left(0\right){\sigma }^2\tau },\beta =\frac{\beta \left(0\right)}{1-2\alpha \left(0\right){\sigma }^2\tau }$$

(139)

$$\begin{array}{ccc}\hfill \gamma & =& \gamma \left(0\right)+\frac{{\beta }^2\left(0\right){\sigma }^2\tau }{2\left(1-2\alpha \left(0\right){\sigma }^2\tau \right)}\hfill \end{array}$$

(140)

$$\begin{array}{ccc}\hfill \delta & =& \frac{\delta \left(0\right)-2\alpha \left(0\right){\delta }_0{\sigma }^2\tau }{1-2\alpha \left(0\right){\sigma }^2\tau }\hfill \end{array}$$

(141)

$$\begin{array}{ccc}\hfill \epsilon & =& \epsilon \left(0\right)+\frac{\beta \left(0\right)\left(\delta \left(0\right)-{\delta }_0\right){\sigma }^2\tau }{1-2\alpha \left(0\right){\sigma }^2\tau }\hfill \end{array}$$

(142)

$$\begin{array}{ccc}\hfill \kappa & =& \kappa \left(0\right)+{\sigma }^2\tau \frac{{\delta }^2\left(0\right)-2\delta \left(0\right){\delta }_0+2\alpha \left(0\right){\delta }_0^2{\sigma }^2\tau }{2\left(1-2\alpha \left(0\right){\sigma }^2\tau \right)}\hfill \end{array}$$

(143)

with ${\delta }_0=\left({\sigma }^2/2-r\right)/{\sigma }^2.$ The classical subsitution [22],

$$v=u\left(x+\left(r-{\sigma }^2/2\right)\tau ,\left({\sigma }^2/2\right)\tau \right)e^{-r\tau }$$

(144)

occurs when $\alpha \left(0\right)=\gamma \left(0\right)=\delta \left(0\right)=\epsilon \left(0\right)=\kappa \left(0\right)=0$ and $\beta \left(0\right)=\gamma \left(0\right)=1$

Example 6 In the one-factor Gaussian Hull-White model [28], the state of the market, at any instant time, is determined by one factor $x.$ The interest rate $r\left(t\right),$ at time $t,$ is given by

$$r\left(t\right)=r_0\left(t\right)+x\left(t\right)$$

(145)

where $r_0$ is a deterministic function, and x is a stochastically varying factor, which evolution is described by the stochastic differential equation

$$dx\left(t\right)=-\alpha x\left(t\right)dt+\sigma dB\left(t\right)$$

(146)

(α and σ are real positive constants) with respect to the pricing measure $Q_0$ [28]. The expectation value

$$f\left(x,t\right)=E_{Q_0}\left[\left.e^{-{\int }_t^{T}r\left(s\right)ds}F\left(x\left(T\right)\right)\right|x\left(t\right)=x\right]$$

(147)

satisfies the partial differential equation

$$\frac{\partial f}{\partial t}=-\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}f}{\partial x^2}+\alpha x\frac{\partial f}{\partial x}+\left(r_0\left(t\right)+x\right)f$$

(148)

and the terminal condition is

$$f\left(x,T\right)=F\left(x\right)\text{for}\text{all}x\in \mathbb{R}$$

(149)

The following substitution

$$f\left(x,t\right)=e^{-{\int }_t^T{r}_0\left(s\right)ds}g\left(x,\tau \right),\tau =T-t$$

(150)

reduces Equation (148) to an autonomous form

$$g_{\tau }=\frac{1}{2}{\sigma }^2{g}_{xx}-\alpha x{g}_x-xg$$

(151)

The characteristic equation, ${\mu }^{″}+2\alpha {\mu }^{\prime }=0,$ has two standard solutions:

$${\mu }_0=\frac{{\sigma }^2}{2\alpha }\left(1-e^{-2\alpha \tau }\right),{\mu }_1=1$$

(152)

and the corresponding Green function:

$$\begin{array}{ccc}\hfill K_0\left(x,y,\tau \right)& =& \frac{\sqrt{\alpha }}{\sigma \sqrt{\pi \left(e^{2\alpha \tau }-1\right)}}exp\left[\left(\alpha +\frac{{\sigma }^2}{2{\alpha }^2}\right)\tau \right]\hfill \\ & & \times exp\left[-\frac{\alpha {\left(x-y{e}^{\alpha \tau }\right)}^2}{{\sigma }^2\left(e^{2\alpha \tau }-1\right)}-\frac{e^{\alpha \tau }-1}{\alpha \left(e^{\alpha \tau }+1\right)}\left(x+y+\frac{{\sigma }^2}{{\alpha }^2}\right)\right]\hfill \end{array}$$

(153)

for $\tau >0$ can be found by the method of this paper.

Example 7 The viscous Burgers equation [44,45,48,50,54]:

$$\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=a\frac{{\partial }^{2}v}{\partial x^2},a=\text{constant}>0$$

(154)

can be linearized by the Cole–Hopf substitution [46,47]:

$$v=-\frac{2a}{u}\frac{\partial u}{\partial x}$$

(155)

which turns it into the diffusion equation (122). Solution of the initial value problem has the form:

$$v\left(x,t\right)=-\frac{a}{\sqrt{\pi at}}\frac{\partial }{\partial x}ln\left[{\int }_{-\infty }^{\infty }exp\left(-\frac{{\left(x-y\right)}^2}{4at}-\frac{1}{2a}{\int }_0^{y}v\left(z,0\right)dz\right)dy\right]$$

(156)

for $t>0$ and suitable initial data on $\mathbb{R}.$

Example 8 Equation (154) possesses a solution of the form:

$$v=F\left(x+Vt\right),V=\text{constant}$$

(157)

(we follow the original Bateman paper [44] with slightly different notations), if

$$V{F}^{\prime }+F{F}^{\prime }=a{F}^{″}$$

(158)

or

$${\left(F+V\right)}^2\pm A^2=2a{F}^{\prime }$$

(159)

where A is a positive constant. The solution is thus either

$$v+V=Atan\left[\frac{A\left(x+Vt-c\right)}{2a}\right]$$

(160)

or

$$\frac{A-v-V}{A+v+V}=exp\left[\frac{A}{a}\left(x+Vt-c\right)\right]$$

(161)

according as the + or − sign is taken. In the first case there is no definite value of v when a tends to zero, while in the second case the limiting value of v is either $A-V$ or $A+V$ according as $x+Vt$ is less or greater than $c.$ The limiting form of the solution is thus discontinuous [44].

Example 9 According to Ref. [51], the propagation of nonlinear magnetosonic waves is governed by a modified Burgers equation,

$$\frac{\partial \varphi }{\partial \eta }+A\left(\eta \right)\varphi \frac{\partial \varphi }{\partial \xi }-B\left(\eta \right)\frac{{\partial }^2\varphi }{\partial {\xi }^2}+C\left(\eta \right)\varphi =0$$

(162)

where $\varphi \left(\xi ,\eta \right)$ is the amplitude of the wave, $\xi =\int k_{x}dx+k_{y}y-\omega t$ and $\eta =\epsilon x$ is the coordinate streched by a smallness parameter $\epsilon .$

If $B=A{e}^{-{\int }_0^{\eta }C\left(s\right)ds},$ the following substitution

$$\varphi =e^{-{\int }_0^{\eta }C\left(s\right)ds}\psi \left(z,t\right)$$

(163)

with

$$z=\xi ,t={\int }_0^{\eta }B\left(\tau \right)d\tau$$

(164)

transforms the nonautonomous equation (162) into the Burgers equation

$$\frac{\partial \psi }{\partial t}+\psi \frac{\partial \psi }{\partial z}=\frac{{\partial }^2\psi }{\partial z^2}$$

(165)

that is completely integrable.

Example 10 Assuming (formally) $r=r_0+r_{1}V$ in the Black-Scholes equation (133), one gets a nonlinear equation of the form

$$\frac{\partial V}{\partial t}+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^{2}V}{\partial S^2}+r_0\left(S\frac{\partial V}{\partial S}-V\right)+r_{1}V\left(S\frac{\partial V}{\partial S}-V\right)=0$$

(166)

This modification of the Black-Scholes equation can be used for a mathematical description of market collapse. The substitution $V\left(S,t\right)=v\left(x,\tau \right),$ where $S=e^x$ and $\tau =T-t,$ transforms Equation (166) into the generalized Burgers-Huxley equation [53,60].

Further examples can be found in [1,9,15,18,54].

9. Conclusions

In this paper, we have discussed connections of certain nonautonomous and inhomogeneous diffusion-type equations, and the Burgers equation with solutions of the Riccati-type system, which seem to be missing in the available literature in general. Traveling wave solutions of the Burgers-type equations are also discussed. Examples include, but are not limited to, the Fokker-Planck equation in physics, the Black-Scholes equation and the Hull-White model in finance.