Reaction–Diffusion on the Sphere with a Nonlinear Source Term: Symmetry Analysis, Group Classification, and Similarity Solutions

Abstract

We consider the nonlinear reaction–diffusion equation on the unit sphere $u_t={\mathrm{\Delta }}_{{\mathbb{S}}^2}u+f\left(u\right)$, $f_{uu}\ne 0$, and carry out a complete Lie point symmetry analysis. Solving the associated determining system yields a rigidity theorem: for every genuinely nonlinear $f\left(u\right)$, the admitted symmetry algebra is $\mathfrak{so}\left(3\right)\oplus ⟨{\partial }_t⟩$, generated by the rotational Killing fields and time translation. We further show through a group classification that the source families that enlarge symmetries in Euclidean space do not produce any additional point symmetries on ${\mathbb{S}}^2$. From an optimal system of subalgebras, we derive curvature-adapted reductions in which the Laplace–Beltrami operator becomes a Legendre-type operator in intrinsic invariants. For the specific nonlinear source $f\left(u\right)=-e^u-2$, specific reduced ODEs admit a hidden one-parameter symmetry, yielding a first integral and explicit steady states on ${\mathbb{S}}^2$.

1. Introduction and Motivation

Reaction–diffusion equations, and more broadly diffusion-type partial differential equations, form a unifying mathematical framework for transport, spreading, and interaction phenomena across physics, chemistry, biology, and geometry. They model, among other things, heat conduction, mass transfer in reactive media, charge transport in semiconductors, population dynamics, and biological pattern formation. In such systems, diffusion acts to redistribute a scalar quantity u (temperature, concentration, density, etc.), while source or sink terms model production, decay, reaction, or nonlinear feedback. The nonlinear heat equation is a canonical representative of this class: it captures the competition between spatial smoothing induced by diffusion and potentially amplifying, saturating, or destabilizing effects encoded in the nonlinear source term. This interplay between transport and nonlinearity is tightly connected to questions of stability, pattern formation, blow-up, and the long-time structure of solutions.

While diffusion processes are often first studied on flat Euclidean domains, many physically relevant systems evolve on curved geometries [1]. Examples include temperature redistribution on planetary atmospheres, morphogen transport and reaction on evolving biological membranes, chemical activity on spherical nanoparticles, and charge transport on curved interfaces [2]. In all such cases, the underlying space is not ${\mathbb{R}}^n$ but a Riemannian manifold $(M,g)$, meaning a smooth manifold M equipped with a Riemannian metric g. The metric g is a smoothly varying, positive-definite inner product on the tangent space at each point of M. This structure provides the geometric foundation for measuring lengths, angles, areas, and curvature on the manifold, thus modifying the structure of the diffusion operator itself [3].

The systematic analysis of PDE symmetries originates in the work of Sophus Lie, who developed the theory of continuous transformation groups and introduced what is now known as Lie group analysis of differential equations. The central idea is that one can algorithmically determine the continuous symmetries of a differential equation, use them to construct invariant solutions, reduce the number of independent variables, and, in some cases, integrate the resulting reduced equations exactly. This methodology was put into a general and mature form in the works of Ovsiannikov [4], Olver [5], Bluman and Cole [6], Bluman and Kumei [7], and Ibragimov [8,9], with further exposition available in texts such as those by Hydon [10] and Stephani [11].

For the classical linear heat equation

$$u_t=u_{xx},$$

(1)

the admitted Lie point symmetry algebra is extremely large: it includes time and space translations, Galilean boosts, scaling of space and time, solution scaling, and even an infinite-dimensional ideal generated by solutions of the associated linear homogeneous equation. This algebra underlies the construction of similarity solutions, fundamental solutions, and self-similar blow-up/scaling laws.

For nonlinear diffusion equations of the general form

$$u_t={\left(k\left(u\right)u_x\right)}_x+Q\left(u\right),$$

(2)

Lie symmetry classification results reveal precisely which functional forms of the diffusivity $k\left(u\right)$ and source term $Q\left(u\right)$ lead to enlarged symmetry algebras. These classical classification studies show that nonlinearities are not arbitrary if one demands rich symmetry; instead, they must satisfy compatibility conditions that can be solved explicitly [12,13]. Such results are now standard in the Euclidean setting and have become part of the modern methodology for constructing exact solutions and similarity reductions of nonlinear parabolic equations [14].

A major extension of this program is the analysis of diffusion-type equations on curved manifolds. On a Riemannian manifold $(M,g)$, the geometry enters both through the Laplace–Beltrami operator and through the allowed point symmetries of the PDE. The Laplace–Beltrami operator ${\mathrm{\Delta }}_M$ is the natural generalization of the Euclidean Laplacian to a Riemannian manifold $(M,g)$. This operator governs diffusion and wave propagation on curved surfaces. Tsamparlis and Paliathanasis showed that, for the homogeneous heat equation on $(M,g)$,

$$u_t={\mathrm{\Delta }}_{M}u,$$

(3)

the Lie point symmetries are generated by the homothetic algebra of the metric: specifically, Killing and homothetic vector fields of g lift to point symmetries of the PDE [15]. On constant-curvature manifolds such as spheres, this implies that the isometry group—namely, the group of all differentiable transformations of M onto itself that preserve the metric g—plays a direct role in the admitted symmetry algebra and in the associated similarity reductions. This observation connects diffusion on ${\mathbb{S}}^n$ with geometric analysis, spectral theory [16,17], and representation-theoretic approaches to parabolic and Schrödinger-type equations [18], where the isometry or conformal groups act in a structured way on families of solutions.

Despite these advances, there remains a fundamental gap in the curved-geometry theory of nonlinear parabolic equations. In Euclidean space, the group classification of nonlinear diffusion equations with reaction terms is well established [14,19]; on Riemannian manifolds, however, the situation is dramatically less developed. In particular, a complete Lie point symmetry classification for a nonlinear reaction–diffusion equation on the two-sphere ${\mathbb{S}}^2$ with a general nonlinear source term $f\left(u\right)$ does not appear to have been carried out. The presence of curvature-dependent coefficients such as $cotx$ and ${csc}^{2}x$ in the spherical Laplace–Beltrami operator leads to determining equations for the symmetry generators that are qualitatively different from their flat analogs, and this obstructs naive transplantation of Euclidean classification results to the spherical setting.

The present work addresses this gap. We consider the nonlinear reaction–diffusion equation on the unit sphere,

$$u_t=u_{xx}+(cotx)u_x+\left({csc}^{2}x\right)u_{yy}+f\left(u\right),$$

(4)

where $u=u(x,y,t)$ is the dependent variable as a function of colatitude x, longitude y, and time t, and $f\left(u\right)$ is an arbitrary nonlinear reaction term with $f_{uu}\ne 0$. We carry out a full Lie symmetry analysis of Equation (4), solving the associated determining system. Our first result establishes that, for a generic nonlinear source term $f\left(u\right)$, the Lie point symmetries of Equation (4) reduce to the rotational Killing fields of the sphere together with time translation. No additional point symmetries survive for a genuinely nonlinear $f\left(u\right)$. In particular, none of the familiar flat-space symmetries for diffusion-type equations, such as spatial translations, Galilean boosts, scaling of space and time, or rescalings in the dependent variable u, are admitted on ${\mathbb{S}}^2$ for a nonlinear source term. This establishes that curvature enforces a universal minimal symmetry algebra for nonlinear reaction–diffusion on the sphere.

We then carry out a group classification analysis [20] for the source term $f\left(u\right)$. By deriving and solving the functional constraints that arise from the invariance condition, we identify all candidate nonlinearities (polynomial, power-law, exponential, and logarithmic forms among them) that could in principle enlarge the symmetry algebra. Such nonlinearities are known, in the Euclidean setting, to produce extended Lie algebras and to admit similarity reductions of a special type. We show that, on ${\mathbb{S}}^2$, none of them lead to any additional point symmetries once the full geometric determining equations are enforced.

Having established the admitted symmetry algebra, we next construct curvature-adapted reductions using optimal systems of one- and two-dimensional subalgebras. These reductions transform the original $(2+1)$-dimensional equation into either $(1+1)$-dimensional parabolic equations with curvature-induced terms or into stationary ordinary differential equations in a single invariant variable.

Finally, we examine a specific nonlinear source term, $f\left(u\right)=-e^u-2$, for which certain reduced ODEs admit an additional one-parameter Lie symmetry at the ODE level, even though the full PDE does not acquire any new global point symmetry. This hidden symmetry allows us to integrate the reduced ODEs explicitly and construct exact stationary solutions on ${\mathbb{S}}^2$ in closed form. These solutions are expressed using elementary functions such as ${tanh}^{-1}$, ${sech}^2$, and ${sec}^2$, and they represent nontrivial nonlinear steady states shaped jointly by curvature and reaction. To our knowledge, these explicit closed-form steady-state solutions are among the first exact nonlinear equilibrium profiles for a reaction–diffusion equation with a non-polynomial source on the sphere. These results clarify how intrinsic curvature constrains, and in some cases enables, the symmetry-driven analysis of nonlinear parabolic equations. They also provide a geometric foundation for future investigations of anisotropic diffusion, higher-dimensional compact manifolds, and stability of invariant steady states in reaction–diffusion systems on curved surfaces [15,18].

In summary, this work provides a complete classification of point symmetries for nonlinear reaction–diffusion on ${\mathbb{S}}^2$ and illustrates how curvature constrains the symmetry algebra. It also demonstrates how, for special choices of the nonlinearity, one can obtain exact invariant solutions through a combination of symmetry reduction and hidden integrability. These results establish a foundation for further investigations, such as extending the classification to higher-dimensional spheres ${\mathbb{S}}^n$ or to manifolds with varying curvature, and examining how curvature-induced symmetry constraints influence pattern formation in nonlinear diffusion systems.

2. Mathematical Preliminaries and Geometric Setting

A rigorous Lie symmetry analysis of a partial differential equation on a curved manifold requires a clear formulation of the underlying geometry, the associated differential operators, and the transformation properties of dependent and independent variables. This section outlines the geometric structure of the two-dimensional sphere ${\mathbb{S}}^2$, derives the corresponding Laplace–Beltrami operator, and summarizes the fundamental elements of Lie group theory used in the symmetry classification of the nonlinear heat-type Equation (4).

Diffusion on a Riemannian manifold $(M,g)$ is governed by the Laplace–Beltrami operator,

$${\mathrm{\Delta }}_{M}f={\displaystyle \frac{1}{\sqrt{\left|g\right|}}}{\partial }_i\left(\sqrt{\left|g\right|}{g}^{ij}{\partial }_{j}f\right),$$

(5)

which generalizes the Euclidean Laplacian to curved spaces [16,17]. The presence of geometric coefficients in ${\mathrm{\Delta }}_M$ directly influences transport and equilibration and fundamentally alters the admitted symmetry structure of the PDE. For the unit sphere ${\mathbb{S}}^2\subset {\mathbb{R}}^3$ with coordinates $(x,y)$, where x denotes colatitude and y the azimuthal angle, the induced metric

$$d{s}^2=d{x}^2+{sin}^{2}xd{y}^2$$

(6)

has determinant $\left|g\right|={sin}^{2}x$ and inverse tensor $g^{ij}=diag(1,{csc}^{2}x)$. Substituting into the definition above yields the Laplacian operator

$${\mathrm{\Delta }}_{{\mathbb{S}}^2}={\partial }_x^2+cotx{\partial }_x+{csc}^{2}x{\partial }_y^2,$$

(7)

which governs diffusion on the sphere. The geometric coefficients $cotx$ and ${csc}^{2}x$ illustrate curvature effects: they vanish in the flat limit, recovering the Euclidean Laplacian. The isometry group of ${\mathbb{S}}^2$ is $SO\left(3\right)$, generated by three Killing vector fields corresponding to infinitesimal rotations about orthogonal axes [11]. These fields form the core of the symmetry algebra of ${\mathrm{\Delta }}_{{\mathbb{S}}^2}$ and hence of any isotropic diffusion process on the sphere. From the perspective of symmetry, the fact that ${\mathbb{S}}^2$ admits a three-dimensional space of Killing vector fields (infinitesimal rotations) suggests that any rotationally invariant diffusion equation on ${\mathbb{S}}^2$ will inherit those geometric symmetries. A central question is whether these are the only point symmetries or whether one can recover on the sphere some of the richer symmetry structures known in the flat case.

The Lie group method, introduced by Sophus Lie and later developed in modern form by Ovsiannikov [4], Olver [5], Bluman and Kumei [7], and Ibragimov [8], provides a systematic means of identifying continuous transformations that map solutions of a PDE into other solutions.

A one-parameter local Lie group of transformations is a smooth family of transformations, parameterized by a real variable $ϵ$ defined in a neighborhood of zero, acting on the space of variables $(x,y,t,u)$ and satisfying the local group properties. In particular, the family contains the identity transformation at $ϵ=0$ and is locally closed under composition and inversion. Such a local group is completely characterized, up to its domain of definition, by its infinitesimal generator, which is the vector field X obtained by differentiating the transformation with respect to $ϵ$ at $ϵ=0$. The coefficients of X, denoted ${\xi }^x$, ${\xi }^y$, ${\xi }^t$, and ${\eta }^u$, describe the first-order infinitesimal action of the group on each coordinate. A one-parameter local Lie group acts on $(x,y,t,u)$ as

$$x^{*}=x+ϵ\xi ,y^{*}=y+ϵ\theta ,t^{*}=t+ϵ\tau ,u^{*}=u+ϵ\varphi ,$$

(8)

where $ϵ$ is an infinitesimal parameter and $(\xi ,\theta ,\tau ,\varphi )$ are smooth functions defining the group’s infinitesimal generator,

$$X=\xi (x,y,t,u){\displaystyle \frac{\partial }{\partial x}}+\theta (x,y,t,u){\displaystyle \frac{\partial }{\partial y}}+\tau (x,y,t,u){\displaystyle \frac{\partial }{\partial t}}+\varphi (x,y,t,u){\displaystyle \frac{\partial }{\partial u}}.$$

(9)

The generator acts on derivatives of u through its second prolongation $X^{\left[2\right]}$, obtained via total differentiation [5,10].

In coordinates, the second prolongation can be written as

$$X^{\left[2\right]}=X+{\eta }^{\left[x\right]}{\displaystyle \frac{\partial }{\partial u_x}}+{\eta }^{\left[y\right]}{\displaystyle \frac{\partial }{\partial u_y}}+{\eta }^{\left[t\right]}{\displaystyle \frac{\partial }{\partial u_t}}+{\eta }^{\left[xx\right]}{\displaystyle \frac{\partial }{\partial u_{xx}}}+{\eta }^{\left[xy\right]}{\displaystyle \frac{\partial }{\partial u_{xy}}}+{\eta }^{\left[yy\right]}{\displaystyle \frac{\partial }{\partial u_{yy}}}+{\eta }^{\left[xt\right]}{\displaystyle \frac{\partial }{\partial u_{xt}}}+{\eta }^{\left[yt\right]}{\displaystyle \frac{\partial }{\partial u_{yt}}}+{\eta }^{\left[tt\right]}{\displaystyle \frac{\partial }{\partial u_{tt}}}$$

where the coefficients ${\eta }^{\left[i\right]}$ and ${\eta }^{\left[ij\right]}$ are the prolonged infinitesimals associated with the first- and second-order derivatives of u. They are defined by

$${\eta }^{\left[i\right]}=D_i\left(\varphi \right)-u_j{D}_i\left({\xi }^j\right),{\eta }^{\left[ij\right]}=D_j\left({\eta }^{\left[i\right]}\right)-u_{ik}{D}_j\left({\xi }^k\right),$$

(10)

with indices $i,j,k\in \{x,y,t\}$ and summation over repeated indices. Here $D_i$ denotes the total derivative with respect to the variable i.

Explicitly, the total derivative with respect to x is given by

$$D_x={\displaystyle \frac{\partial }{\partial x}}+u_x{\displaystyle \frac{\partial }{\partial u}}+u_{xx}{\displaystyle \frac{\partial }{\partial u_x}}+u_{xy}{\displaystyle \frac{\partial }{\partial u_y}}+u_{xt}{\displaystyle \frac{\partial }{\partial u_t}}+\dots ,$$

(11)

with analogous expressions for $D_y$ and $D_t$. These prolonged infinitesimals determine how the infinitesimal generator X acts on derivatives of u and are required to enforce the invariance condition

$$X^{\left[2\right]}\left(\mathcal{F}\right){|}_{\mathcal{F}=0}=0,$$

(12)

where $\mathcal{F}=0$ denotes the governing partial differential equation.

The invariance condition (12) yields a linear overdetermined system for the infinitesimals $(\xi ,\theta ,\tau ,\varphi )$. Solving this system determines the Lie point symmetries admitted by the equation.

For the nonlinear heat-type Equation (4), dependence on an arbitrary function $f\left(u\right)$ typically restricts the infinitesimals to geometric symmetries of ${\mathbb{S}}^2$ and time translations [13,15].

Once the infinitesimal generators are known, invariant reductions follow by solving the characteristic system

$${\displaystyle \frac{dx}{\xi }}={\displaystyle \frac{dy}{\theta }}={\displaystyle \frac{dt}{\tau }}={\displaystyle \frac{du}{\varphi }},$$

(13)

which defines the similarity variables that reduce the PDE to a lower-dimensional form. On ${\mathbb{S}}^2$, the dominant symmetries correspond to the rotational Killing fields of $SO\left(3\right)$, leading to reductions that represent axisymmetric diffusion, rotating wave modes, or stationary spherical harmonics [20]. These invariant solutions possess direct geometric and physical meaning, describing diffusion patterns constrained by curvature and global symmetry. In Section 5 we derive several such reductions and in Section 6 we obtain closed-form invariant solutions for the special nonlinear source $f\left(u\right)=-e^u-2$.

Remark 1. 

In this paper, we focus on genuinely nonlinear source terms ($f_{uu}\ne 0$). It is worth noting that, in the excluded linear or linearizable cases (for example, $f\left(u\right)=\alpha u+\beta$, including the homogeneous linear case $f\left(u\right)=\alpha u$), the symmetry algebra of the linear heat equation is known to be much larger. In particular, when $f\left(u\right)$ is linear, the superposition principle introduces an infinite-dimensional symmetry associated with arbitrary solutions of the homogeneous linear equation [5]. One also recovers additional point symmetries such as scalings in u.

3. Minimal Symmetry Algebra and Group Classification

This section establishes the minimal Lie point symmetry structure of the nonlinear heat-type equation on the sphere, (4), and then investigates when additional symmetries arise. Using the standard Lie algorithm (second prolongation and invariance condition) [5,7], we derive the full determining system and solve it in the generic case of an arbitrary nonlinear source $f\left(u\right)$. The main outcome (Theorem 1) is that the symmetry algebra is precisely $\mathfrak{so}\left(3\right)\oplus \mathbb{R}$, generated by spatial rotations on ${\mathbb{S}}^2$ and time translation. We then turn to the group classification problem: for special choices of $f\left(u\right)$, the algebra may extend beyond this minimal form. The analysis provides the symmetry foundations for the reductions and exact solutions constructed in the subsequent sections.

Theorem 1. 

Consider the nonlinear evolution Equation (4):

$$u_t=u_{xx}+\left(cotx\right)u_x+\left({csc}^{2}x\right)u_{yy}+f\left(u\right).$$

For a generic function $f\left(u\right)$ such that $f_{uu}\ne 0$, the full Lie point symmetry algebra is four-dimensional and generated by

$$\begin{array}{cc}\hfill L_1& =cosy{\displaystyle \frac{\partial }{\partial x}}-sinycotx{\displaystyle \frac{\partial }{\partial y}}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill L_2& =siny{\displaystyle \frac{\partial }{\partial x}}+cosycotx{\displaystyle \frac{\partial }{\partial y}}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill L_3& ={\displaystyle \frac{\partial }{\partial y}}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill T& ={\displaystyle \frac{\partial }{\partial t}}\hfill \end{array}$$

(17)

The subalgebra $\mathrm{span}\{L_1,L_2,L_3\}$ is isomorphic to $\mathfrak{so}\left(3\right)$ (rotations in $(x,y)$), and T (time translation) commutes with it, so the algebra is $\mathfrak{so}\left(3\right)\oplus \mathbb{R}$.

Proof. 

We begin with the general infinitesimal generator for a Lie point symmetry:

$$X=\xi \left(x,y,t,u\right){\displaystyle \frac{\partial }{\partial x}}+\theta \left(x,y,t,u\right){\displaystyle \frac{\partial }{\partial y}}+\tau \left(x,y,t,u\right){\displaystyle \frac{\partial }{\partial t}}+\varphi \left(x,y,t,u\right){\displaystyle \frac{\partial }{\partial u}}$$

(18)

where $\xi ,\theta ,\tau ,\varphi$ are the infinitesimals to be determined. Let $X^{\left[2\right]}$ denote the second prolongation of X. The invariance condition requires that

$$X^{\left[2\right]}\left(u_t-cotx{u}_x-u_{xx}-{csc}^{2}x{u}_{yy}-f\left(u\right)\right)=0,\mathrm{when}\mathrm{Equation}\left(4\right)\mathrm{holds}.$$

(19)

The second prolongation is given by

$$\begin{array}{c}{X}^{\left[2\right]}=X+{\eta }^{\left[x\right]}{\displaystyle \frac{\partial }{\partial u_x}}+{\eta }^{\left[y\right]}{\displaystyle \frac{\partial }{\partial u_y}}+{\eta }^{\left[t\right]}{\displaystyle \frac{\partial }{\partial u_t}}+{\eta }^{\left[xx\right]}{\displaystyle \frac{\partial }{\partial u_{xx}}}+{\eta }^{\left[yy\right]}{\displaystyle \frac{\partial }{\partial u_{yy}}}+{\eta }^{\left[tt\right]}{\displaystyle \frac{\partial }{\partial u_{tt}}}\hfill \\ +{\eta }^{\left[xy\right]}{\displaystyle \frac{\partial }{\partial u_{xy}}}+{\eta }^{\left[xt\right]}{\displaystyle \frac{\partial }{\partial u_{xt}}}+{\eta }^{\left[yt\right]}{\displaystyle \frac{\partial }{\partial u_{yt}}}.\hfill \end{array}.$$

(20)

Applying $X^{\left[2\right]}$ to Equation (4) and equating coefficients of various derivative terms to zero yields the following system of determining equations:

$$\begin{array}{cc}\hfill e_1& :{\xi }_u=0,\hfill \\ \hfill e_2& :{\theta }_u=0,\hfill \\ \hfill e_3& :{csc}^{2}x{\xi }_y+{\theta }_x=0,\hfill \\ \hfill e_4& :{\tau }_u=0,\hfill \\ \hfill e_5& :{\xi }_x-{\tau }_t=0,\hfill \\ \hfill e_6& :cotx\xi -{\tau }_t+{\theta }_y=0,\hfill \\ \hfill e_7& :{csc}^{2}x{\tau }_y-{\theta }_t=0,\hfill \\ \hfill e_8& :{\tau }_x-{\xi }_t=0,\hfill \\ \hfill e_9& :{\varphi }_{uu}=0,\hfill \\ \hfill e_{10}& :cotx{\tau }_x-{\tau }_{tt}+{\tau }_{xx}+{csc}^{2}x{\tau }_{yy}+2{\varphi }_{tu}=0,\hfill \\ \hfill e_{11}& :cotx{\theta }_x-{\theta }_{tt}+{\theta }_{xx}+{csc}^{2}x{\theta }_{yy}-2{csc}^{2}x{\varphi }_{yu}=0,\hfill \\ \hfill e_{12}& :-cotx{\xi }_x-{\xi }_{tt}+{\xi }_{xx}+{csc}^{2}x\xi +{csc}^{2}x{\xi }_{yy}-2{\varphi }_{xu}=0,\hfill \\ \hfill e_{13}& :f{\varphi }_u-\varphi f_u-{\varphi }_{xx}+{\varphi }_{tt}-2f{\tau }_t-{csc}^{2}x{\varphi }_{yy}-cotx{\varphi }_x=0.\hfill \end{array}$$

We now solve this system systematically using a triangulation procedure based on techniques for obtaining differential Gröbner bases developed by Mansfield [21].

From equations $e_1$, $e_2$, and $e_4$,

$${\xi }_u=0,{\theta }_u=0,{\tau }_u=0,$$

(21)

we immediately obtain that $\xi$, $\theta$, and $\tau$ are independent of u:

$$\xi =\xi (x,y,t),\theta =\theta (x,y,t),\tau =\tau (x,y,t).$$

(22)

From equation $e_9$, ${\varphi }_{uu}=0$, we deduce that $\varphi$ is at most affine in u:

$$\varphi (x,y,t,u)=a(x,y,t)u+b(x,y,t),$$

(23)

with corresponding partial derivatives

$${\varphi }_u=a,{\varphi }_{xu}=a_x,{\varphi }_{yu}=a_y,{\varphi }_{tu}=a_t.$$

(24)

The equations $e_5$, $e_8$, $e_3$, $e_7$, and $e_6$ provide kinematic couplings between the infinitesimals:

$$e_5:{\xi }_x-{\tau }_t=0,e_8:{\tau }_x-{\xi }_t=0,$$

(25)

$$e_3:{csc}^{2}x{\xi }_y+{\theta }_x=0,e_7:{csc}^{2}x{\tau }_y-{\theta }_t=0,$$

(26)

$$e_6:cotx\xi -{\tau }_t+{\theta }_y=0.$$

(27)

We can eliminate $\theta$ in favor of $\xi$ and $\tau$ using

$${\theta }_x=-{csc}^{2}x{\xi }_y,{\theta }_t={csc}^{2}x{\tau }_y,{\theta }_y={\tau }_t-cotx\xi ={\xi }_x-cotx\xi .$$

(28)

Since the determining equations provide expressions for ${\theta }_x$, ${\theta }_y$, and ${\theta }_t$ in terms of $\xi$ and $\tau$, the existence of a smooth function $\theta (x,y,t)$ imposes the corresponding compatibility (integrability) conditions obtained by commuting mixed partial derivatives, namely

$${\partial }_y\left({\theta }_x\right)={\partial }_x\left({\theta }_y\right),\mathrm{and}{\partial }_y\left({\theta }_t\right)={\partial }_t\left({\theta }_y\right).$$

(29)

Applying the first identity ${\partial }_y\left({\theta }_x\right)={\partial }_x\left({\theta }_y\right)$ yields

$$-{csc}^{2}x{\xi }_{yy}={\xi }_{xx}+{csc}^{2}x\xi -cotx{\xi }_x,$$

(30)

which simplifies to

$${\xi }_{xx}+{csc}^{2}x{\xi }_{yy}-cotx{\xi }_x+{csc}^{2}x\xi =0.$$

(31)

Next, applying ${\partial }_y\left({\theta }_t\right)={\partial }_t\left({\theta }_y\right)$ and using $e_5$ (${\tau }_t={\xi }_x$) and $e_8$ (${\xi }_t={\tau }_x$),

$${csc}^{2}x{\tau }_{yy}={\xi }_{xt}-cotx{\xi }_t={\tau }_{tt}-cotx{\tau }_x,$$

(32)

yielding

$$-{\tau }_{tt}+{csc}^{2}x{\tau }_{yy}+cotx{\tau }_x=0.$$

(33)

From $e_5$ and $e_8$ (cross-differentiation), we obtain

$${\xi }_{tt}={\xi }_{xx},{\tau }_{tt}={\tau }_{xx}.$$

(34)

Thus far, $\theta$ can be recovered from $\xi$ and $\tau$ via the three first-order relations above, and $\xi ,\tau$ must satisfy Equations (31)–(34).

Now we substitute the expression for $\varphi$ into equations $e_{10},e_{11},e_{12}$ using Equation (24):

$$\begin{array}{cc}\hfill & e_{10}:cotx{\tau }_x-{\tau }_{tt}+{\tau }_{xx}+{csc}^{2}x{\tau }_{yy}+2a_t=0,\hfill \\ \hfill & e_{11}:cotx{\theta }_x-{\theta }_{tt}+{\theta }_{xx}+{csc}^{2}x{\theta }_{yy}-2{csc}^{2}x{a}_y=0,\hfill \\ \hfill & e_{12}:-cotx{\xi }_x-{\xi }_{tt}+{\xi }_{xx}+{csc}^{2}x\xi +{csc}^{2}x{\xi }_{yy}-2a_x=0.\hfill \end{array}$$

Using Equations (31)–(34), these reduce to

$$a_x=-\frac{1}{2}{\xi }_{tt}=-\frac{1}{2}{\xi }_{xx},a_t=-\frac{1}{2}{\tau }_{xx}=-\frac{1}{2}{\tau }_{tt},a_y=0.$$

(35)

Hence $a=a(x,t)$ only.

Now we analyze equation $e_{13}$ with $\varphi =au+b$ and ${\tau }_t={\xi }_x$:

$$\left[(a_{tt}-a_{xx}-cotx{a}_x)u\right]+\left[b_{tt}-b_{xx}-{csc}^{2}x{b}_{yy}-cotx{b}_x\right]+\left(af-au{f}_u-b{f}_u-2f{\tau }_t\right)=0.$$

(36)

For a generic nonlinear function $f\left(u\right)$, the term $u{f}_u\left(u\right)$ depends explicitly on u while the other terms depend only on $(x,y,t)$. This forces the coefficient of $u{f}_u\left(u\right)$ to vanish, requiring $a\equiv 0$. Then Equation (36) reduces to

$$b_{tt}-b_{xx}-{csc}^{2}x{b}_{yy}-cotx{b}_x-b{f}_u\left(u\right)-2f\left(u\right){\tau }_t=0.$$

(37)

Since f and $f_u$ depend only on u while the remaining terms depend only on $(x,y,t)$, the generic case implies that

$$b\equiv 0,{\tau }_t\equiv 0.$$

(38)

Thus, for an arbitrary nonlinear function $f\left(u\right)$,

$$\varphi \equiv 0,{\tau }_t=0,{\xi }_x=0.$$

(39)

Using $e_8$: ${\tau }_x={\xi }_t$ then gives ${\tau }_x=0$ and ${\xi }_t=0$, and Equation (31) reduces to

$${csc}^{2}x({\xi }_{yy}+\xi )=0⟹{\xi }_{yy}+\xi =0.$$

(40)

Hence,

$$\xi \left(y\right)=Acosy+Bsiny(A,B\in \mathbb{R}).$$

(41)

From $e_7$: ${\theta }_t={csc}^{2}x{\tau }_y$ and $e_3$: ${\theta }_x=-{csc}^{2}x{\xi }_y$ (no t-dependence), we get ${\tau }_y=0$; hence, ${\theta }_t=0$. With ${\tau }_t=0$ and ${\tau }_x=0$, we conclude that $\tau$ is constant: $\tau =c_0$.

We now recover $\theta (x,y)$ from

$${\theta }_x=-{csc}^{2}x{\xi }_y,{\theta }_y={\xi }_x-cotx\xi =-cotx\xi .$$

(42)

Integrating in x,

$$\theta (x,y)=-{\xi }_y\left(y\right)\int {csc}^{2}xdx+h\left(y\right)={\xi }_y\left(y\right)cotx+h\left(y\right).$$

(43)

Differentiating in y and using ${\theta }_y=-cotx\xi \left(y\right)$ with ${\xi }_{yy}=-\xi$ yields $h^{\prime }\left(y\right)=0$, so $h\left(y\right)=c_1$. Writing ${\xi }_y=-Asiny+Bcosy$, we obtain

$$\theta (x,y)=\left(-Asiny+Bcosy\right)cotx+c_1.$$

(44)

Finally, the general solution is given as

$$\begin{array}{cc}\hfill & \xi \left(y\right)=Acosy+Bsiny,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & \theta (x,y)=(-Asiny+Bcosy)cotx+c_1,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & \tau =c_0,\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & \varphi =0\hfill \end{array}$$

(48)

where $A,B,c_0,c_1\in \mathbb{R}$ are arbitrary constants.

Activating one constant at a time, we obtain the basis vector fields:

$$\begin{array}{cc}\hfill & L_1=cosy{\partial }_x-cotxsiny{\partial }_y(A=1,B=0,c_0=0,c_1=0),\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & L_2=siny{\partial }_x+cotxcosy{\partial }_y(A=0,B=1,c_0=0,c_1=0),\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill & L_3={\partial }_y(A=0,B=0,c_0=0,c_1=1),\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & T={\partial }_t(A=0,B=0,c_0=1,c_1=0).\hfill \end{array}$$

(52)

Therefore, the full symmetry algebra for generic $f\left(u\right)$ is the span of $\{L_1,L_2,L_3,T\}$. Here $L_1,L_2,L_3$ satisfy the $\mathfrak{so}\left(3\right)$ commutation relations; T commutes with them. □

Without forcing $a=0$, equation $e_{13}$ leads to admissible forms of f (e.g., linear $f\left(u\right)=\alpha u+\mu$, power laws, exponentials, etc.). For each candidate f, one solves the split from $e_{13}$ to determine $a(x,t)$, $b(x,y,t)$ and possibly relax ${\tau }_t,{\xi }_x$.

Remark 2. 

For arbitrary nonlinear $f\left(u\right)$, the determining equations force $\varphi \equiv 0$, so no scaling or superposition symmetry in u occurs. The spatial generators

$$L_1=cosy{\partial }_x-cotxsiny{\partial }_y,L_2=siny{\partial }_x+cotxcosy{\partial }_y,L_3={\partial }_y$$

form the Killing algebra of the round 2–sphere with metric $d{x}^2+{sin}^{2}xd{y}^2$; hence,

$$[L_1,L_2]=-L_3,[L_3,L_1]=-L_2,[L_3,L_2]=L_1.$$

(53)

Time translations $T={\partial }_t$ commute with all spatial generators. Therefore the full Lie symmetry algebra is

$$\mathfrak{g}=\langle T,L_1,L_2,L_3\rangle \simeq \mathbb{R}\oplus \mathfrak{so}\left(3\right).$$

(54)

The commutator structure of $\mathfrak{g}$ is given in

Table 1. Commutator table for the Lie algebra generated by $\{L_1,L_2,L_3,T\}$.

$[·,·]$	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$	T
$L_1$	0	$-L_3$	$L_2$	0
$L_2$	$L_3$	0	$-L_1$	0
$L_3$	$-L_2$	$L_1$	0	0
T	0	0	0	0

.

4. Classification of Nonlinearities Potentially Admitting Extended Point Symmetries

In the context of nonlinear heat-type equations on curved geometries such as the unit sphere, identifying the precise forms of the nonlinear source term $f\left(u\right)$ that could potentially admit enlarged Lie point symmetry algebras is both mathematically rich and physically insightful. In this section, we rigorously derive the compatibility constraints that govern such symmetry extensions and prove that, despite a wide variety of candidate nonlinearities, the geometry of the sphere enforces severe restrictions that ultimately yield a minimal symmetry algebra.

To determine which nonlinearities $f\left(u\right)$ may yield extended point symmetries beyond the canonical rotational and time-translation invariance on the sphere, we note that the determining system reduces the symmetry condition involving $f\left(u\right)$ to the scalar ODE:

$$(a-2{\tau }_t)f\left(u\right)-(au+b)f^{\prime }\left(u\right)=0.$$

(55)

This equation governs all nonlinearities $f\left(u\right)$ that could, in principle, admit symmetry extensions through nonzero a, b, or ${\tau }_t$.

Starting from the determining equation $e_{13}$, we repeatedly differentiate with respect to u to obtain a hierarchy of linear relations involving $\varphi$, ${\varphi }_u$, and higher derivatives of the source term $f\left(u\right)$. By taking appropriate linear combinations of these relations, the auxiliary quantities $\varphi$ and ${\varphi }_u$ are eliminated, yielding a single compatibility condition that factors into a differential expression depending only on $f\left(u\right)$ multiplied by ${\tau }_t$. If ${\tau }_t=0$, this condition is identically satisfied for arbitrary $f\left(u\right)$. Assuming that ${\tau }_t\ne 0$, the elimination procedure leads to the fifth-order nonlinear differential constraint on $f\left(u\right)$:

$$f_{uu}{f}_{uuu}{f}_{uuuuu}-2f_{uu}{f}_{uuuu}^2+f_{uuu}^2{f}_{uuuu}=0.$$

(56)

The general solution of Equation (56) identifies the following families of nonlinear functions $f\left(u\right)$ as the only possible forms that could yield extended symmetries:

1. Quadratic:	$f\left(u\right)=u^2+\alpha u+\beta$;
2. Cubic:	$f\left(u\right)=u^3+\alpha u^2+\beta u+\gamma$;
3. Exponential:	$f\left(u\right)=A{e}^{ku}+Cu+D$,    $A,k\ne 0$;
4. Power Law:	$f\left(u\right)={(u+\beta )}^m+Cu+D,m\notin \{0,1,2,3\}$;
5. Logarithmic:	$f\left(u\right)=-ln(u+\beta )+Cu+D$;
6. Mixed Logarithmic:	$f\left(u\right)=(u+\beta )ln(u+\beta )-(u+\beta )+Cu+D$.

Each candidate nonlinearity is subsequently tested against the full determining system to rigorously verify whether it produces additional independent symmetry generators beyond the minimal algebra.

Theorem 2. 

Let $f\left(u\right)$ be a nonlinear reaction term in Equation (4). Then no nontrivial solution of the classification Equation (56) produces an enlargement of the point symmetry algebra on the sphere. In particular, for every nonlinear $f\left(u\right)$, the full Lie point symmetry algebra of Equation (4) is

$$\mathfrak{g}=\mathfrak{so}\left(3\right)\oplus \langle {\partial }_t\rangle ,$$

(57)

generated by the spherical rotations and the time translation.

Proof. 

From the determining equations $e_1$–$e_{13}$, we know that

$$\xi =\xi (x,y,t),\theta =\theta (x,y,t),\tau =\tau (x,y,t),\varphi (x,y,t,u)=a(x,y,t)u+b(x,y,t),$$

(58)

i.e., $\xi ,\theta ,\tau$ are independent of u, and $\varphi$ is affine in u.

The kinematic subsystem $e_3,e_5,e_6,e_7,e_8$ expresses $\theta$ in terms of $\xi$ and $\tau$ and enforces the wave-type and spherical compatibility relations

$${\xi }_{tt}={\xi }_{xx},{\tau }_{tt}={\tau }_{xx},$$

(59)

$${csc}^{2}x({\xi }_{yy}+\xi )=cotx{\tau }_t.$$

(60)

In particular, unless ${\tau }_t\equiv 0$, the left-hand side depends on y while the right-hand side depends only on x, so consistency on ${\mathbb{S}}^2$ forces

$${\tau }_t=0,{\xi }_{yy}+\xi =0.$$

(61)

Next, insert $\varphi =au+b$ into $e_{10}$, $e_{11}$, $e_{12}$. Using the relations ${\xi }_{tt}={\xi }_{xx}$ and ${\tau }_{tt}={\tau }_{xx}$, these reduce to

$$a_x=-\frac{1}{2}{\xi }_{xx},a_t=-\frac{1}{2}{\tau }_{tt},a_y=0.$$

(62)

If ${\tau }_t\ne 0$ or $a\ne 0$, then ${\tau }_{tt}$ and ${\xi }_{xx}$ must be constant, so a itself must be constant in $(x,y,t)$. In this case, $a_x=a_t=a_y=0$, and likewise $b_x,b_y,b_t=0$. Consequently ${\varphi }_x,{\varphi }_{xx},{\varphi }_t,{\varphi }_{tt},{\varphi }_y,{\varphi }_{yy}$ all vanish in $e_{13}$, and the f-dependent invariance condition $e_{13}$ simplifies to

$$af\left(u\right)-(au+b)f^{\prime }\left(u\right)-2f\left(u\right){\tau }_t=0.$$

(63)

This scalar ODE in u is the algebraic obstruction for extending the symmetry beyond $\mathfrak{so}\left(3\right)\oplus \langle {\partial }_t\rangle$.

We now analyze Equation (63) for the canonical nonlinearities obtained from the classification Equation (56).

• Case 1: Quadratic nonlinearity. Let $f\left(u\right)=u^2+\alpha u+\beta$; thus, $f^{\prime }\left(u\right)=2u+\alpha$. Substituting into Equation (63) and equating coefficients of $u^2,u^1,u^0$ gives

  $$a=-2{\tau }_t,b=-\alpha {\tau }_t,{\tau }_t({\alpha }^2-4\beta )=0.$$

  (64)

Thus, unless ${\tau }_t=0$, the parameters must satisfy $\beta =\frac{{\alpha }^2}{4}$, i.e., $f\left(u\right)={(u+\frac{\alpha }{2})}^2$ is a perfect square. However, the geometric compatibility condition (60) forces ${\tau }_t=0$ on ${\mathbb{S}}^2$, cf. (61). Hence ${\tau }_t=0$, and therefore $a=0$, $b=0$. No additional symmetry survives.

• Case 2: Cubic nonlinearity. Let $f\left(u\right)=u^3+\alpha u^2+\beta u+\gamma$; thus, $f^{\prime }\left(u\right)=3u^2+2\alpha u+\beta$. Substituting into Equation (63) and comparing powers of u yields

  $$a=-{\tau }_t,b=-\frac{1}{3}\alpha {\tau }_t,$$

  (65)

  together with further linear relations among $(\beta ,\gamma ,{\tau }_t)$. As in the quadratic case, these relations admit ${\tau }_t\ne 0$ only if $a,b$ are constants and ${\tau }_t$ is constant. But then the spherical compatibility again enforces ${\tau }_t=0$; hence, $a=b=0$. Thus even the perfect cube form $f\left(u\right)={(u+{\displaystyle \frac{\alpha }{3}})}^3$ fails to generate an extra point symmetry on ${\mathbb{S}}^2$.
• Case 3: Exponential nonlinearity. Let $f\left(u\right)=A{e}^{ku}+Cu+D$ with $Ak\ne 0$. Then $f^{\prime }\left(u\right)=Ak{e}^{ku}+C$. Inserting into Equation (63) gives a linear combination of the functionally independent terms $u{e}^{ku}$, $e^{ku}$, u, and 1. The $u{e}^{ku}$ component forces $a=0$. The remaining terms then imply that $b=-\frac{2}{k}{\tau }_t$, but the spherical compatibility (61) yields ${\tau }_t=0$, so $b=0$. Thus $a=b={\tau }_t=0$. Hence, no additional symmetry arises.
• Case 4: Power nonlinearity. Let $f\left(u\right)={(u+\beta )}^m+Cu+D$ with $m\notin \{0,1,2,3\}$ and m not reducing to a lower-degree polynomial. Then $f^{\prime }\left(u\right)=m{(u+\beta )}^{m-1}+C$. Substituting into Equation (63) and isolating the distinct powers ${(u+\beta )}^m$ and ${(u+\beta )}^{m-1}$ shows that

  $$a=2{\tau }_t,(au+b)m{(u+\beta )}^{m-1}\equiv 0.$$

  (66)

The only way this can hold for all u with nonlinear ${(u+\beta )}^m$ is $a=0$, $b=0$; hence, ${\tau }_t=0$.

• Case 5: Logarithmic nonlinearity. Let $f\left(u\right)=-ln(u+\beta )+Cu+D$; thus, $f^{\prime }\left(u\right)=-{(u+\beta )}^{-1}+C$. The most singular term ${(u+\beta )}^{-1}$ in Equation (63) forces $b=0$. The mixed $uln(u+\beta )$ and $ln(u+\beta )$ terms then force $a=0$. The remaining linear terms again collapse under ${\tau }_t=0$.
• Case 6: Mixed logarithmic nonlinearity. Let $f\left(u\right)=(u+\beta )ln(u+\beta )-(u+\beta )+Cu+D$; thus, $f^{\prime }\left(u\right)=ln(u+\beta )+C$. The distinct functional dependencies $\{uln(u+\beta ),ln(u+\beta ),u,1\}$ in Equation (63) imply that $a=0$, $b=0$, and then ${\tau }_t=0$.

Therefore, in every admissible nonlinear case produced by Equation (56), consistency with the spherical determining equations enforces

$${\tau }_t=0,a=0,b=0.$$

(67)

With ${\tau }_t=0$ we also have ${\xi }_x=0$ from $e_5$, and the kinematic subsystem then reduces exactly to the Killing algebra of the round 2-sphere together with time translation. These span $\mathfrak{so}\left(3\right)\oplus \langle {\partial }_t\rangle$, and no further generator survives. □

We now examine explicitly how commonly used nonlinearities, particularly power-law and exponential reaction terms, fit within the classification result of Theorem 2. Consider first the power-law family $f\left(u\right)=u^n$ or, more generally, $f\left(u\right)={(u+a)}^n$ with $n\ne 0,1$. In Euclidean space, such nonlinearities are known to generate additional scaling or dilation symmetries for specific values of n. In the present spherical setting, however, substitution of these forms into the invariance condition (55) leads to algebraic constraints that are incompatible with the geometric determining equations unless $a=b={\tau }_t=0$. Consequently, no scaling or amplitude symmetry survives, and the admitted Lie point symmetry algebra remains $\mathfrak{so}\left(3\right)\oplus \langle {\partial }_t\rangle$ for all genuine power-law nonlinearities.

A similar conclusion holds for the exponential nonlinearity $f\left(u\right)=e^u$ (and its affine generalizations $f\left(u\right)=A{e}^{ku}+Cu+D$). Although exponential source terms frequently produce extended symmetry algebras in flat-space diffusion equations, on ${\mathbb{S}}^2$ the curvature-dependent compatibility conditions force the time-scaling parameter ${\tau }_t$ to vanish. As a result, the exponential nonlinearity does not enlarge the point symmetry algebra of the full PDE beyond rotations and time translation.

These results emphasize a fundamental geometric effect: while the classification equation admits power-law and exponential nonlinearities at a formal level, the curvature-induced terms in the determining equations eliminate the corresponding symmetry extensions.

Remark 3. 

The quadratic perfect square and perfect cube nonlinearities, which in flat Cartesian geometries sometimes trigger dilation- or Galilean-type extensions, do not produce additional point symmetries on ${\mathbb{S}}^2$, as the curvature enters through the $cotx$ and ${csc}^{2}x$ terms in the determining equations and forces ${\tau }_t=0$, collapsing any potential amplitude or scaling symmetry in u. Thus the rotational isometries of the sphere and time translation exhaust the Lie point symmetries for all nonlinear $f\left(u\right)$.

5. Symmetry Reductions and Invariant Solutions for the Nonlinear Heat Equation

This section provides a systematic classification of symmetry reductions for Equation (4) based on one- and two-dimensional subalgebras of this symmetry algebra.

The strategy of symmetry reduction is a powerful technique in the analysis of partial differential equations, particularly for extracting exact solutions in cases where direct integration is difficult. For differential equations posed on curved manifolds such as the sphere, symmetry methods remain robust, enabling dimensional reductions that utilize the geometric structure. In this setting, the nonlinear heat equation admits a natural symmetry algebra tied to the rotational invariance of the sphere and time translation.

The reduction strategy involves identifying invariants under each subalgebra, rewriting the dependent variable in terms of those invariants, computing transformed derivatives via the chain rule, and substituting into the original PDE to obtain reduced models.

5.1. Reductions by One-Dimensional Subalgebras

For each one-dimensional subalgebra, we compute the similarity variables and the corresponding reduced PDE.

5.1.1. Rotational Reduction by $L_1=\langle cosy{\partial }_x-cotxsiny{\partial }_y\rangle$

This corresponds to rotational symmetry about a fixed axis. The characteristic equations yield the invariant $\xi =sinxsiny$. With $\tau =t$, we write $u=P(\xi ,\tau )$. The vector field $L_2$ generates a specific spherical rotation; the corresponding invariant $\xi$ represents a coordinate adapted to this symmetry. The advantage is that the reduction leads to a PDE in a single geometrically meaningful invariant, reflecting how certain profiles evolve under rotation-invariant flows. A standard computation for the spherical Laplacian gives

$$u_{xx}+(cotx)u_x+{csc}^{2}x{u}_{yy}=(1-{\xi }^2){\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}-2\xi {\displaystyle \frac{\partial P}{\partial \xi }}.$$

(68)

The reduced PDE becomes

$${\displaystyle \frac{\partial P}{\partial \tau }}=(1-{\xi }^2){\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}-2\xi {\displaystyle \frac{\partial P}{\partial \xi }}+f\left(P\right).$$

(69)

5.1.2. Rotational Reduction by $L_2=\langle siny{\partial }_x+cotxcosy{\partial }_y\rangle$

This is analogous to $L_2$, using the invariant $\xi =sinxcosy$. This reduction corresponds to a different axis of rotation, but it yields the same reduced PDE form, highlighting the geometric equivalence of the symmetry classes under the full rotation group. The reduced PDE is identical in form to Equation (69):

$${\displaystyle \frac{\partial P}{\partial \tau }}=(1-{\xi }^2){\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}-2\xi {\displaystyle \frac{\partial P}{\partial \xi }}+f\left(P\right).$$

(70)

5.1.3. Axially Symmetric Reduction by $L_3=\langle {\partial }_y\rangle$

This symmetry corresponds to solutions invariant under translations in y.

$$\xi =x,\tau =t,u(x,y,t)=P(\xi ,\tau ).$$

(71)

This reduction simplifies the original PDE by suppressing variation in the y direction, yielding a PDE that depends only on the latitudinal variable x and time t. It is particularly useful for studying axisymmetric evolution. Substitution into Equation (4) yields the reduced $(1+1)$-dimensional PDE:

$${\displaystyle \frac{\partial P}{\partial \tau }}={\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}+cot\xi {\displaystyle \frac{\partial P}{\partial \xi }}+f\left(P\right).$$

(72)

5.1.4. Reduction by $\langle T+c{L}_3\rangle =\langle {\partial }_t+c{\partial }_y\rangle$

This symmetry corresponds to a traveling-wave frame in the y-direction. The invariants are

$$\xi =x,\tau =y-ct,u(x,y,t)=P(\xi ,\tau ).$$

(73)

Such traveling-frame reductions are important in pattern propagation and front dynamics, where the PDE is reduced in a co-moving frame. Substituting into Equation (4) gives the following reduced PDE:

$$-c{\displaystyle \frac{\partial P}{\partial \tau }}={\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}+cot\xi {\displaystyle \frac{\partial P}{\partial \xi }}+{csc}^2\xi {\displaystyle \frac{{\partial }^{2}P}{\partial {\tau }^2}}+f\left(P\right).$$

(74)

5.2. Reductions by Two-Dimensional Subalgebras

We now perform double reductions to obtain ODEs. These two-step symmetry reductions collapse the original PDE into ordinary differential equations, enabling exact analysis and construction of special solutions. Such reductions are especially effective when the original equation resists direct integration or numerical analysis methods. Commutativity of generators ensures the second generator is inherited after the first reduction.

5.2.1. Steady Rotated States Reduction by $\langle T,L_1\rangle$

In this reduction, we impose invariance under both time translations ($T={\partial }_t$) and the rotational Killing field $L_1=cosy{\partial }_x-cotxsiny{\partial }_y$.

This symmetry combination captures stationary states that also respect a specific spherical rotation symmetry. The invariants of the system under this two-generator subalgebra reduce the solution space to functions of a single composite variable $\xi =sinxsiny$, encoding the orbits of the symmetry action on the sphere. Thus, the dependent variable reduces to the form $u(x,y,t)=\omega \left(\xi \right)$, with $\xi$ expressing the angular dependence of the invariant surface.

The resulting ODE after substitution becomes

$$(1-{\xi }^2){\displaystyle \frac{d^2\omega }{d{\xi }^2}}-2\xi {\displaystyle \frac{d\omega }{d\xi }}+f\left(\omega \right)=0.$$

(75)

This equation has a structure reminiscent of Legendre-type equations, but with an added nonlinearity $f\left(\omega \right)$. Such reductions are important for classifying axially symmetric stationary solutions.

We observe that the second-order differential operator

$${\mathcal{L}}_{\xi }:=(1-{\xi }^2){\displaystyle \frac{d^2}{d{\xi }^2}}-2\xi {\displaystyle \frac{d}{d\xi }}$$

(76)

appearing in the reduced equations is precisely the classical Legendre operator. In the linear case $f\left(u\right)=0$, the eigenvalue problem

$${\mathcal{L}}_{\xi }\omega +\lambda \omega =0$$

(77)

reduces to the standard Legendre equation, whose solutions are the Legendre polynomials and, more generally, the angular components of spherical harmonics. This reflects the well-known spectral decomposition of the Laplace–Beltrami operator on ${\mathbb{S}}^2$.

In the present nonlinear setting, the same operator emerges naturally from the reduction in the Laplace–Beltrami operator along the orbits of the rotational Killing fields. For this reason, we refer to the reduced equations as Legendre-type equations: they preserve the intrinsic spherical geometry while incorporating a nonlinear reaction term $f\left(\omega \right)$. This structure highlights how curvature enforces a canonical angular operator in all rotationally invariant reductions, independent of the choice of symmetry axis.

5.2.2. Steady Rotated States Reduction by $\langle T,L_2\rangle$

This case mirrors the previous one but uses the second spherical Killing field $L_2=siny{\partial }_x+cotxcosy{\partial }_y$ instead of $L_1$.

The action of $L_2$ defines an orthogonal rotational symmetry to $L_1$, and the corresponding invariant is $\xi =sinxcosy$. Applying both symmetries together yields a steady-state solution of the form $u=\omega \left(\xi \right)$.

Substituting this ansatz into the governing PDE again produces a nonlinear Legendre-type ODE:

$$(1-{\xi }^2){\displaystyle \frac{d^2\omega }{d{\xi }^2}}-2\xi {\displaystyle \frac{d\omega }{d\xi }}+f\left(\omega \right)=0.$$

(78)

While the analytic form is identical to that in Equation (75), the physical and geometric interpretation is distinct due to the different symmetry axis. This highlights the flexibility of symmetry reductions in probing rotationally invariant structures from multiple orientations.

5.2.3. Steady Axisymmetric States Reduction by $\langle T,L_3\rangle$

This case explores the structure of solutions that are both steady-state and invariant under translations in the y-direction. The symmetry algebra generated by the pair $\langle T,L_3\rangle =\langle {\partial }_t,{\partial }_y\rangle$ annihilates both t and y, so any invariant solution must be independent of these two variables.

Hence, the dependent variable $u(x,y,t)$ reduces to a function of a single spatial variable, x, giving the ansatz $u(x,y,t)=\omega \left(x\right)$. This reduction is especially significant because it collapses the original partial differential equation to an ordinary differential equation, thereby greatly simplifying the analysis of equilibrium states on the spherical domain.

Substituting this form into the original PDE yields the following reduced ODE:

$${\displaystyle \frac{d^2\omega }{d{\xi }^2}}+cot\xi {\displaystyle \frac{d\omega }{d\xi }}+f\left(\omega \right)=0.$$

(79)

This equation can be interpreted as a nonlinear diffusion balance equation in the angular coordinate $\xi =x$, reflecting the geometry of the sphere through the appearance of the cotangent term. Solutions to this ODE represent all steady profiles that are homogeneous in the azimuthal y-direction.

5.2.4. Steady Traveling-Wave States Reduction by $\langle T+L_3,L_3\rangle$

This scenario combines a traveling-frame symmetry in the y-direction (generated by $T+L_3={\partial }_t+{\partial }_y$) with pure translation invariance in y (from $L_3={\partial }_y$).

The first reduction, by the generator $T+L_3$, identifies a moving coordinate frame traveling along the azimuthal angle y at unit speed. The corresponding invariants are $\xi =x$ and $\tau =y-t$, and the solution ansatz becomes $u(x,y,t)=P(\xi ,\tau )$. This shifts the PDE into a co-moving reference frame.

Substituting into the PDE leads to

$$-{\displaystyle \frac{\partial P}{\partial \tau }}={\displaystyle \frac{{\partial }^{2}P}{\partial {\xi }^2}}+cot\xi {\displaystyle \frac{\partial P}{\partial \xi }}+{csc}^2\xi {\displaystyle \frac{{\partial }^{2}P}{\partial {\tau }^2}}+f\left(P\right).$$

(80)

In this intermediate equation, the spatial Laplacian includes derivatives in both $\xi$ and $\tau$, reflecting the persistent dependence on the traveling coordinate. However, the second reduction via $L_3$ enforces independence from $\tau$, simplifying the equation further.

By imposing $P_{\tau }=0$, we reduce the system to the same steady-state ODE encountered earlier:

$${\displaystyle \frac{d^2\omega }{d{\xi }^2}}+cot\xi {\displaystyle \frac{d\omega }{d\xi }}+f\left(\omega \right)=0.$$

(81)

Thus, this reduction path offers an alternative interpretation of axisymmetric equilibrium profiles as steady traveling-wave forms when viewed from a moving azimuthal frame.

Remark 4. 

Any pair of generators involving T commute, ensuring that time-translation symmetry is inherited in all sequential reductions involving T. In particular, the relation $[T+c{L}_3,L_3]=0$ guarantees that the generator $L_3$ is inherited in the traveling-frame reduction using $T+c{L}_3$. This commutation property guarantees the compatibility of multiple symmetry reductions and preserves structure throughout the reduction process.

6. Exact Symmetry Reductions and Closed-Form Solutions for a Nonlinear Source Term

In this section, we construct exact solutions of the nonlinear heat equation on the two-sphere

$$u_t=u_{xx}+(cotx)u_x+\left({csc}^{2}x\right)u_{yy}-e^u-2,$$

(82)

This choice lies within the exponential family discussed in Section 4. For a generic $f\left(u\right)$, Equation (4) admits only the minimal Lie algebra $\mathfrak{so}\left(3\right)\oplus \langle {\partial }_t\rangle$, generated by the rotations of the sphere and time translation. However, when $f\left(u\right)$ obeys certain compatibility conditions in the determining equations, the reduced equations obtained from invariant ansatzes admit extra point symmetries. This choice $f\left(u\right)=-e^u-2$ is non-generic in that it is precisely one of the functional forms that allows for nonzero constants for the infinitesimals ${\tau }_t$, a, and b in the original determining system before the geometric constraints are fully imposed. These nonzero constant values for ${\tau }_t$ and the affine components of $\varphi$ ($a,b$) are essential to generating a non-trivial similarity solution.

Although the curvature of ${\mathbb{S}}^2$ ultimately forces ${\tau }_t=a=b=0$ for the full PDE, the specific structure of this exponential nonlinearity, when substituted into the f-dependent invariance condition, coincides with the integrability conditions required for the reduced ODEs to possess an additional hidden one-parameter first-order Lie symmetry. That extra symmetry allows for a second reduction by invariants, which makes the ODE explicitly integrable and produces closed-form solutions. In geometric terms, curvature does not create new global point symmetries of the full PDE but, in special nonlinear cases, it still permits axisymmetric invariant profiles that can be written analytically. We use this extra symmetry to obtain exact nonlinear steady states solutions for a reaction–diffusion equation on the sphere. To our knowledge, these are among the first explicit closed-form nonlinear steady states for a reaction–diffusion equation with a non-polynomial source on ${\mathbb{S}}^2$.

6.1. Rotationally Deformed Reductions Using $\langle T,L_1\rangle$

Referring to Section 5.2.1 and assuming invariance under the subalgebra $\langle T,L_1\rangle$, the dependent variable $u(x,y,t)$ is expressed as a function of a single invariant $\xi =sinxsiny$. Substituting this ansatz into Equation (82) gives the reduced ODE

$$(1-{\xi }^2){\displaystyle \frac{d^2\omega }{d{\xi }^2}}-2\xi {\displaystyle \frac{d\omega }{d\xi }}-e^{\omega }-2=0.$$

(83)

Equation (83) admits the additional Lie point symmetry

$$X=({\xi }^2-1){\displaystyle \frac{\partial }{\partial \xi }}-2\xi {\displaystyle \frac{\partial }{\partial \omega }},$$

(84)

Using the invariants

$$r=e^{\omega }({\xi }^2-1),Y=({\xi }^2-1){\omega }^{\prime }+2\xi ,$$

(85)

the ODE is transformed into the system

$${\displaystyle \frac{dY}{d\xi }}=-{\displaystyle \frac{r}{{\xi }^2-1}},{\displaystyle \frac{dr}{d\xi }}={\displaystyle \frac{rY}{{\xi }^2-1}}.$$

(86)

Eliminating $\xi$ yields

$$YdY=-dr\Rightarrow Y^2=-2r+k,$$

(87)

where k is a constant of integration. Reverting to the original variables,

$${\left(({\xi }^2-1){\omega }^{\prime }+2\xi \right)}^2=-2e^{\omega }({\xi }^2-1)+k.$$

(88)

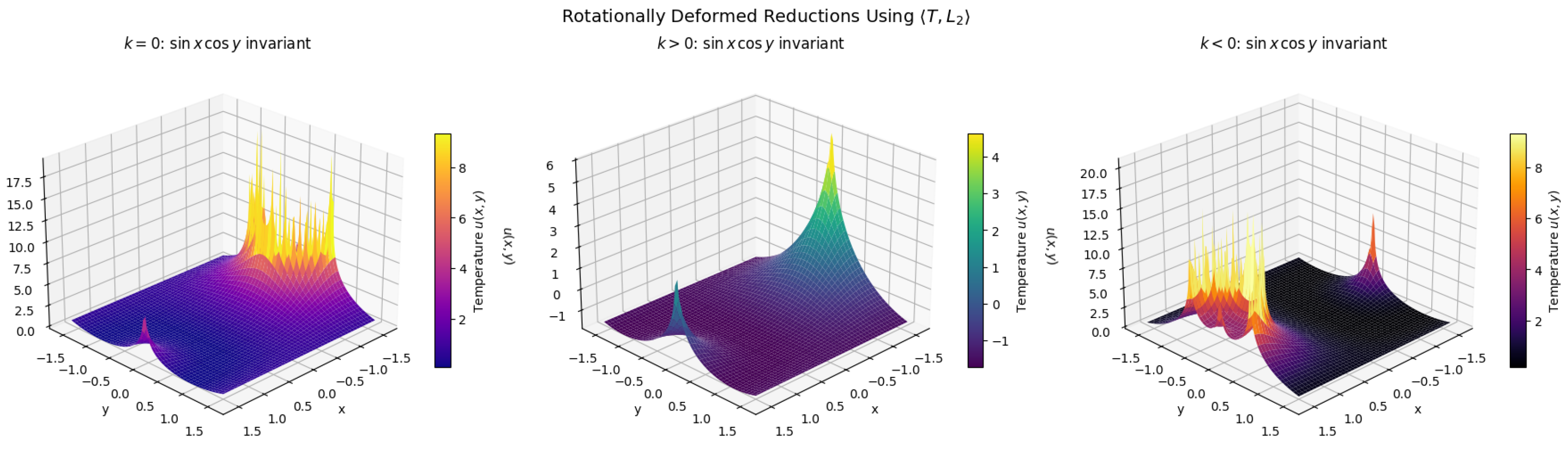
Equation (88) is separable and integrable in three distinct cases: $k=0$, $k>0$, and $k<0$.

• Case 1: $k=0$

  $$u(x,y)=ln\left|{\displaystyle \frac{2}{\left(1-{sin}^{2}x{sin}^{2}y\right){\left({tanh}^{-1}(sinxsiny)+C\right)}^2}}\right|.$$

  (89)
• Case 2: $k>0$

  $$u(x,y)=ln\left|{\displaystyle \frac{k}{2\left(1-{sin}^{2}x{sin}^{2}y\right)}}{sech}^2\left({\displaystyle \frac{\sqrt{k}}{2}}{tanh}^{-1}(sinxsiny)+C\right)\right|.$$

  (90)
• Case 3: $k<0$

  $$u(x,y)=ln\left|{\displaystyle \frac{-k}{2\left(1-{sin}^{2}x{sin}^{2}y\right)}}{sec}^2\left({\displaystyle \frac{\sqrt{-k}}{2}}{tanh}^{-1}(sinxsiny)+C\right)\right|.$$

  (91)

All three solution forms corresponding to this subalgebra are defined on the entire spherical surface with the invariant variable $\xi =sinxsiny$ taking values in $(-1,1)$. Each solution is smooth for $-1<\xi <1$, though singular behavior may occur as $\left|\xi \right|\to 1$, corresponding to specific great circles where the invariant coordinate reaches its limiting value. By construction, these solutions are invariant under the one-parameter Lie rotation generated by $L_1$ combined with the time-translation T for steady states. Geometrically, this invariance implies that the temperature field $u(x,y)$ remains constant along circular orbits of a fixed rotational axis lying in the equatorial plane.

These families represent steady-state dipolar temperature distributions on the unit sphere ${\mathbb{S}}^2$. One lobe of the sphere, where $sinxsiny>0$, corresponds to a warm region, while the opposite lobe, where $sinxsiny<0$, is cooler. The nonlinear source term $-e^u-2$ acts as a distributed heat sink, stronger in hotter regions, which balances diffusion to maintain equilibrium. Figure 1 illustrates these solutions for representative values of k. The parameter C shifts the profile while k controls the contrast between the two lobes.

6.2. Rotationally Deformed Reductions Using $\langle T,L_2\rangle$

Referring to Section 5.2.2 and assuming invariance under the subalgebra $\langle T,L_2\rangle$, the dependent variable $u(x,y,t)$ is expressed as a function of a single invariant $\xi =sinxcosy$. Substituting this ansatz into Equation (82) gives the reduced ODE

$$(1-{\xi }^2){\displaystyle \frac{d^2\omega }{d{\xi }^2}}-2\xi {\displaystyle \frac{d\omega }{d\xi }}-e^{\omega }-2=0.$$

(92)

Equation (92) admits the additional Lie point symmetry

$$X=({\xi }^2-1){\displaystyle \frac{\partial }{\partial \xi }}-2\xi {\displaystyle \frac{\partial }{\partial \omega }},$$

(93)

Using the invariants

$$r=e^{\omega }({\xi }^2-1),Y=({\xi }^2-1){\omega }^{\prime }+2\xi ,$$

(94)

the ODE is transformed into the system

$${\displaystyle \frac{dY}{d\xi }}=-{\displaystyle \frac{r}{{\xi }^2-1}},{\displaystyle \frac{dr}{d\xi }}={\displaystyle \frac{rY}{{\xi }^2-1}}.$$

(95)

Eliminating $\xi$ yields

$$YdY=-dr\Rightarrow Y^2=-2r+k,$$

(96)

where k is a constant of integration. Reverting to the original variables,

$${\left(({\xi }^2-1){\omega }^{\prime }+2\xi \right)}^2=-2e^{\omega }({\xi }^2-1)+k.$$

(97)

Equation (97) is separable and integrable in three distinct cases: $k=0$, $k>0$, and $k<0$.

• Case 1: $k=0$

  $$u(x,y)=ln\left|{\displaystyle \frac{2}{\left(1-{sin}^{2}x{cos}^{2}y\right){\left({tanh}^{-1}(sinxcosy)+C\right)}^2}}\right|.$$

  (98)
• Case 2: $k>0$

  $$u(x,y)=ln\left|{\displaystyle \frac{k}{2\left(1-{sin}^{2}x{cos}^{2}y\right)}}{sech}^2\left({\displaystyle \frac{\sqrt{k}}{2}}{tanh}^{-1}(sinxcosy)+C\right)\right|.$$

  (99)
• Case 3: $k<0$

  $$u(x,y)=ln\left|{\displaystyle \frac{-k}{2\left(1-{sin}^{2}x{cos}^{2}y\right)}}{sec}^2\left({\displaystyle \frac{\sqrt{-k}}{2}}{tanh}^{-1}(sinxcosy)+C\right)\right|.$$

  (100)

These solutions also cover the entire sphere. Invariance under $L_2$, together with T, corresponds to rotation about an axis orthogonal to that associated with $L_1$. Consequently, the temperature is constant along orbits of this perpendicular rotation, producing a pattern identical in form to the $L_1$ case but rotated by ${90}^{\circ }$ on the sphere.

The nonlinear reaction term $-e^u-2$ removes heat preferentially from the hot side, establishing a stable temperature contrast across the sphere. The dividing curve $sinxcosy=0$ serves as a thermal equator separating the two hemispheric zones. The qualitative behavior of the solution mirrors that of the $L_1$ family, though the temperature maximum now aligns with the hot regions at $\left|\xi \right|\to 1$. Figure 2 shows that these invariant solutions correspond to the same parameter choices as in Figure 1 but are rotated about the polar axis in the azimuthal angle y. This shift in the longitudinal position of the hot and cold regions illustrates the spherical symmetry of the problem.

6.3. Axisymmetric Reduction in x Using $\langle T,L_3\rangle$

Referring to Section 5.2.3 and assuming invariance under the subalgebra $\langle T,L_3\rangle$, the dependent variable $u(x,y,t)$ is expressed as a function of a single invariant $\xi =x$. Substituting this ansatz into Equation (82) gives the reduced ODE

$${\omega }^{\prime \prime }+(cot\xi ){\omega }^{\prime }-e^{\omega }-2=0.$$

(101)

Equation (101) admits the additional Lie point symmetry

$$X=sin\xi {\displaystyle \frac{\partial }{\partial \xi }}-2cos\xi {\displaystyle \frac{\partial }{\partial \omega }},$$

(102)

which enables its reduction to quadrature. Using the invariants

$$r=e^{\omega }{sin}^2\xi ,Y=sin\xi {\omega }^{\prime }+2cos\xi ,$$

(103)

the ODE is transformed into the system

$${\displaystyle \frac{dY}{d\xi }}={\displaystyle \frac{r}{sin\xi }},{\displaystyle \frac{dr}{d\xi }}={\displaystyle \frac{rY}{sin\xi }}.$$

(104)

Eliminating $\xi$ yields

$$YdY=dr\Rightarrow Y^2=2r+k,$$

(105)

where k is a constant of integration. Reverting to the original variables,

$${\left(sin\xi {\omega }^{\prime }+2cos\xi \right)}^2=2e^{\omega }{sin}^2\xi +k.$$

(106)

Equation (106) is separable and integrable in three distinct cases: $k=0$, $k>0$, and $k<0$.

Case 1: $k=0$

$$u\left(x\right)=ln\left[{\displaystyle \frac{2{csc}^{2}x}{{\left(ln(cscx+cotx)+C\right)}^2}}\right].$$

(107)

Case 2: $k>0$

$$u\left(x\right)=ln\left|{\displaystyle \frac{k}{2}}{csc}^{2}x{sech}^2\left({\displaystyle \frac{\sqrt{k}}{2}}ln(cscx+cotx)\right)\right|.$$

(108)

Case 3: $k<0$

$$u\left(x\right)=ln\left|{\displaystyle \frac{-k}{2}}{csc}^{2}x{sec}^2\left({\displaystyle \frac{\sqrt{-k}}{2}}ln(cscx+cotx)\right)\right|.$$

(109)

The axisymmetric solutions depend on the colatitude and are independent of the longitude. They remain regular throughout most of their interval, except possibly at the poles, where singular behavior may occur depending on k. Invariance under $L_3$ enforces azimuthal symmetry, meaning that the temperature is constant along each circle of latitude. These configurations are fully symmetric about the polar axis of the sphere.

This family corresponds to zonal or polar heat distributions in which temperature varies only with latitude. Depending on the parameter k, the solutions can represent a hot polar cap that cools gradually toward the equator, a warm equatorial belt with cooler poles, or limiting cases featuring a hot or cold pole modeled by singular behavior. Each configuration represents a static equilibrium in which diffusion and nonlinear heat removal balance exactly. The function $u\left(x\right)$ is generally single-peaked or single-valley, reflecting one dominant temperature extreme along the polar axis. Figure 3 shows typical profiles for these axisymmetric solutions. Notably, because of the spherical geometry, even moderate values of $k>0$ or $k<0$ can cause the profile to concentrate near one pole or the other, illustrating how curvature influences the spread of the pattern.

7. Conclusions

This paper provides a full Lie point symmetry classification for the nonlinear reaction–diffusion equation $u_t={\mathrm{\Delta }}_{{\mathbb{S}}^2}u+f\left(u\right)$ with $f_{uu}\ne 0$. The analysis establishes a symmetry constraint for nonlinear reaction–diffusion equations on the sphere, showing that the symmetry algebra is restricted to rotations and time translation for general nonlinear source terms. Nevertheless, using this minimal algebra, explicit closed-form stationary solutions are obtained for the source $f\left(u\right)=-e^u-2$ by exploiting an additional symmetry that emerges in the lower-dimensional reduced equations. It would be natural to extend the classification to ${\mathbb{S}}^n$ and to compact manifolds of variable curvature, where the homothetic algebra is smaller and the compatibility conditions sharpen, and to determine when PDE-level rigidity coexists with ODE-level integrability after reduction. Another direction is to study spectral and nonlinear stability of the steady states derived here and their transitions under parameter variation, including the effects of anisotropic diffusivities and weak inhomogeneities in the reaction term. Such problems would test the reach of curvature-induced rigidity beyond the constant-curvature setting and further connect symmetry methods with qualitative dynamics on curved surfaces.