Multistage Threshold Segmentation Method Based on Improved Electric Eel Foraging Optimization

Abstract

Multi-threshold segmentation of color images is a critical component of modern image processing. However, as the number of thresholds increases, traditional multi-threshold image segmentation methods face challenges such as low accuracy and slow convergence speed. To optimize threshold selection in color image segmentation, this paper proposes a multi-strategy improved Electric Eel Foraging Optimization (MIEEFO). The proposed algorithm integrates Differential Evolution and Quasi-Opposition-Based Learning strategies into the Electric Eel Foraging Optimization, enhancing its search capability, accelerating convergence, and preventing the population from falling into local optima. To further boost the algorithm’s search performance, a Cauchy mutation strategy is applied to mutate the best individual, improving convergence speed. To evaluate the segmentation performance of the proposed MIEEFO, 15 benchmark functions are used, and comparisons are made with seven other algorithms. Experimental results show that the MIEEFO algorithm outperforms other algorithms in at least 75% of cases and exhibits similar performance in up to 25% of cases. To further explore its application potential, a multi-level Kapur entropy-based MIEEFO threshold segmentation method is proposed and applied to different types of benchmark images and forest fire images. Experimental results indicate that the improved MIEEFO achieves higher segmentation quality and more accurate thresholds, providing a more effective method for color image segmentation.

1. Introduction

With the development of computer computing resources, the field of computer vision has developed rapidly. Image segmentation is not only an important branch of computer vision, but also one of the most difficult problems in image processing [1]. Image segmentation is widely used in automatic driving [2,3], intelligent medicine [4], industrial testing [5] and other fields. Currently, the most widely used image segmentation methods include threshold segmentation [6], edge segmentation [7], region segmentation [8], clustering segmentation [9,10] and deep learning segmentation [11,12]. Threshold segmentation has gained attention due to its simplicity, low computational cost, and ease of implementation. Threshold segmentation has become a research hotspot owing to its advantages of simplicity, small computation and easy solution [13].

Threshold segmentation can be divided into two types, single-threshold segmentation and multi-threshold segmentation [14]. Single-threshold segmentation divides an image into target and background, whereas multi-threshold segmentation segments an image into multiple regions. Because single-threshold segmentation often fails to provide the necessary patterns for the problem at hand, multi-threshold segmentation is generally preferred. However, with the increase in thresholds, the computational complexity of traditional segmentation methods grows exponentially, leading to issues such as low accuracy and slow convergence speed. In order to solve this problem, an increasing number of researchers are introducing swarm intelligence optimization algorithms for image segmentation to enhance accuracy and speed [15]. Common multi-threshold segmentation methods include Otsu’s entropy [16,17], Kapur entropy [18,19], fuzzy entropy [20] and the cross-entropy method [21,22]. The Kapur entropy technique is insensitive to regions and preserves details better, which is why it has been widely applied in multi-level image segmentation.

However, multi-level threshold segmentation techniques rely heavily on threshold combinations and involve a large search space [23]. Therefore, improving the segmentation performance necessitates optimization of the multi-level threshold selection process. Traditional methods often optimize the optimal thresholds by employing operational research techniques or exhaustive enumeration methods. However, as the number of thresholds increases, the computational complexity grows exponentially. To address this issue, researchers have introduced heuristic algorithms, which alleviate the problem of low computational efficiency to a certain extent. Houssein, E. H. et al. [24] proposed an improved chimp optimization algorithm (ICHOA) and applied it to the problem of multi-level threshold image segmentation. Sabha, M. et al. [25] introduced a cooperative simulated meta-heuristic algorithm called CPGH, which combines particle swarm optimization (PSO), gray wolf optimization (GWO), and Harris hawks optimization (HHO)to run in parallel, ultimately applied to coronavirus image segmentation. Hao, S. et al. [26] developed an improved salp swarm algorithm (ILSSA) that integrates chaotic mapping with local escape operators and applied it to dermoscopic skin cancer image segmentation. Chauhan, D. et al. [27] presented a crossover optimization artificial electric field algorithm (AEFA) that uses a Kapur’s entropy function, applied to the Berkeley segmentation dataset. Qian, Y. et al. [28] proposed a continuous foraging ant colony optimization algorithm (SSACO) based on salp foraging (SSACO), and applied it to remote sensing image segmentation. Dhal, K. G. et al. [29] introduced an improved slime mould algorithm (ISMA), employing oppositional learning and differential evolution mutation strategies to enhance the algorithm’s performance, applied to the segmentation of unlabeled white blood cell images. Shi, J. et al. [30] proposed an improved variant of the whale optimization algorithm (GTMWOA) and applied it to lupus nephritis images. Houssein, E. et al. [31] introduced an efficient search rescue optimization algorithm (SAR) based on oppositional learning for segmenting blood cell images and addressing multi-level threshold issues.

SIO is a powerful family of heuristic algorithms that have demonstrated remarkable capabilities in solving computationally intensive and complex problems, where classical algorithms often prove inefficient [32]. In most cases, swarm intelligence algorithms begin by randomly generating a population in the early stages of iteration and utilize specific formulas to explore the search space during the process, ultimately identifying the optimal solution. These operations are inspired by natural phenomena such as natural behaviors, physical rules, social interactions, and evolutionary principles. Representative SIO methods, including Particle Swarm Optimization (PSO) [33], Differential Evolution (DE) [34], Artificial Bee Colony (ABC) [35] and the Whale Optimization Algorithm (WOA) [36], have been successfully applied to various fields such as path planning, power systems and image processing. Although SIO methods differ in form, their core idea remains similar: simulating natural behaviors to construct mathematical models for solving specific problems.

EEFO, a novel SIO algorithm proposed in 2024, simulates the predatory behavior of electric eels [37]. It has been tested using various benchmark functions and engineering problems and compared with standard algorithms such as the Whale Optimization Algorithm (WOA), the Arithmetic Optimization Algorithm (AOA) [38], Harris Hawks Optimization (HHO) [39] and Beluga Whale Optimization (BWO) [40]. Experimental results indicate that EEFO exhibits significant potential. Thus, EEFO holds promise for further research and applications. However, there is still considerable room for improvement when applying EEFO to complex problems such as image segmentation. According to the “No Free Lunch” theorem [41], no algorithm is universally optimal for solving all problems. In other words, every algorithm has its limitations. Nevertheless, its performance can be enhanced by introducing new strategies and adjusting the parameter settings.

In this study, we further develop the EEFO method to enhance its effectiveness in addressing the challenges of color image segmentation.

The main contributions of this study are as follows:

i. This paper proposes an improved Electric Eel Foraging Optimization, which incorporates a differential evolution strategy, a quasi-oppositional learning strategy and the Cauchy mutation strategy, named MIEEFO.

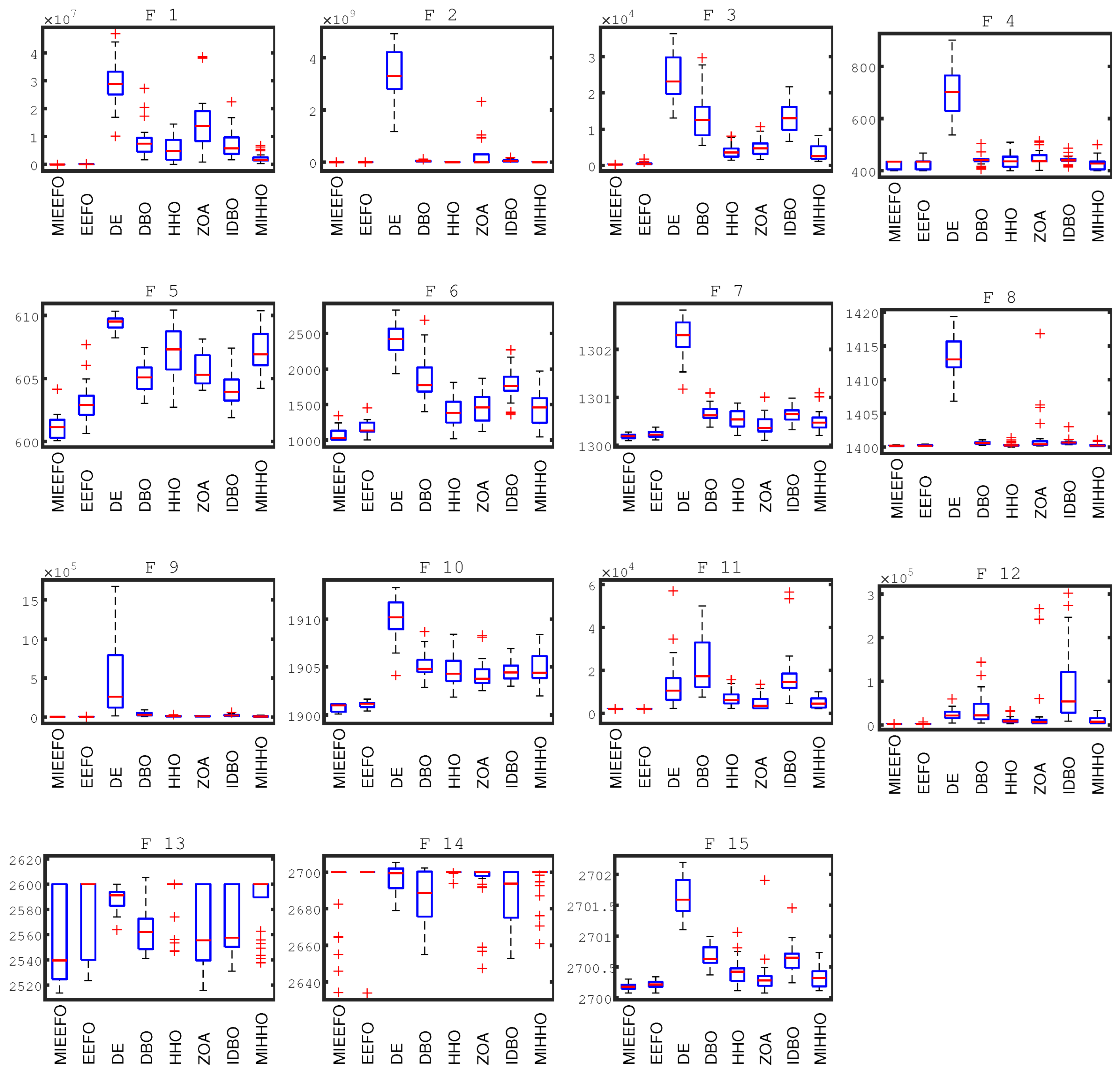
ii. A set of 15 benchmark test functions are used to evaluate the algorithm, and MIEEFO is compared with several state-of-the-art heuristic algorithms. Analysis using different evaluation methods demonstrates that MIEEFO exhibits superior performance.

iii. We introduce an efficient MIEEFO-based color image segmentation technique. Experiments were conducted comparing MIEEFO with other similar algorithms at multiple threshold levels, using Kapur’s entropy as the fitness function. The results show that the segmentation method based on MIEEFO significantly improves the accuracy of image segmentation.

iv. The proposed image segmentation method was applied to forest fire images, providing an effective solution for segmenting forest fire imagery.

The remainder of this paper is organized as follows: Section 2 provides an overview of the EEFO algorithm. Section 3 describes the proposed enhanced MIEEFO algorithm. Section 4 presents the simulation results of MIEEFO for the test functions. Section 5 outlines the image segmentation principles of MIEEFO and provides experimental results of the segmentation method. Finally, Section 6 presents our conclusions and future work.

2. Electric Eel Foraging Optimization

Electric Eel Foraging Optimization (EEFO) [37] was proposed by Weiguo Zhao and Liying Wang et al. in 2024, which simulates the predation behavior of electric eels in nature. The algorithm can be divided into an interacting stage, resting stage, hunting stage and migrating stage. These mechanisms are illustrated in Figure 1.

Figure 1. Physical structure and electricity producing organs of electric eels.

2.1. Interacting Stage

When eels encounter a school of fish, they interact by swimming and agitating each other. The eels then begin to swim in a large electrified circle, catching many small fish in the center of the circle. The following model represents this churn.

$$\left\{\begin{array}{c}\left\{\begin{array}{c}{v}_i(\mathrm{t}+1)=x_j\left(t\right)+C\times \left(\overline{x}\left(t\right)-x_i\left(t\right)\right)p_1>0.5\\ v_i(\mathrm{t}+1)=x_j\left(t\right)+C\times \left(x_r\left(t\right)-x_i\left(t\right)\right)p_1⩽0.5\end{array}\mathrm{fit}\left(x_j\left(t\right)\right)<\mathrm{fit}\left(x_i\left(t\right)\right)\right.\hfill \\ \left\{\begin{array}{c}{v}_i(\mathrm{t}+1)=x_i\left(t\right)+C\times \left(\overline{x}\left(t\right)-x_j\left(t\right)\right)p_2>0.5\\ v_i(\mathrm{t}+1)=x_i\left(t\right)+C\times \left(x_r\left(t\right)-x_j\left(t\right)\right)p_2⩽0.5\end{array}\mathrm{fit}\left(x_j\left(t\right)\right)⩾\mathrm{fit}\left(x_i\left(t\right)\right)\right.\hfill \end{array}\right.$$

(1)

$$\overline{x}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{i=1}^n{x}_i\left(t\right)$$

(2)

$$x_r=\mathrm{lb}+r\times (\mathrm{ub}-\mathrm{lb})$$

(3)

$$B=\left[b_1,b_2,\cdots ,b_k,\cdots ,b_d\right]$$

(4)

$$b\left(k\right)=\left\{\begin{array}{cc}1\hfill & ifk==g\{l\hfill \\ 0\hfill & else\hfill \end{array}\right.$$

(5)

$$l=1,\cdots ,\lceil ({\displaystyle \frac{T_{max}-t}{T_{max}}}\times r_1\times (d-2)+2)\rceil$$

(6)

where $C=n_1\times B$, $p_1,p_2,r,r_1$ are random numbers within (0, 1), g is a random population individual, $fit\left(x\right(i\left)\right)$ is the fitness of the candidate solution of electric eel i, $x_j$ is the position of an electric eel randomly selected from the current population, and lb and ub are the lower and upper boundaries, respectively.

2.2. Resting Stage

Before the electric eel enters the resting phase, it establishes a resting zone. Once the resting zone is determined, the eel is moved to this area. The mathematical model for the resting phase of the eel is shown as follows.

$$\left\{X|X-Z\left(t\right)|\le {\alpha }_0\times |Z\left(t\right)-x_{prey}\left(t\right)|\right\}$$

(7)

$${\alpha }_0=2·({\mathrm{e}-\mathrm{e}}^{{\displaystyle \frac{t}{{\mathrm{T}}_{\max }}}})$$

(8)

$$Z\left(t\right)=\mathrm{lb}+z\left(t\right)\times (\mathrm{ub}-\mathrm{lb})$$

(9)

$$Z\{t={\displaystyle \frac{x_{rand\{n}^{rand\{d}\{t-\mathrm{l}{b}^{rand\{d}}{u{b}^{rand\{d}-l{b}^{rand\{d}}}$$

(10)

$$R_i(t+1)=Z\left(t\right)+\alpha \times |Z\left(t\right)-x_{prey}\left(t\right)|$$

(11)

$$\alpha ={\alpha }_0\times sin\left(2\pi r_2\right)$$

(12)

$$v_i(t+1)=R_i(t+1)+{\eta }_2\times (R_i(t+1)round\left(rand\right)\times x_i\left(t\right))$$

(13)

where $x_{prey}$ is the best position vector so far, ${\alpha }_0$ is the initial scale of the rest area, $x_{rand}$ is a random dimension of individuals randomly selected from the current population, $r_2$ is a random number within (0, 1), and ${\eta }_2$ follows a Gaussian uniform distribution, ${\eta }_2\sim N(0,1)$.

2.3. Hunting Stage

After determining the hunting area, the electric eel will capture prey within that zone. When eels detect prey, they do not simply swarm to hunt it. Instead, they tend to cooperate by swimming in a large circle to surround the prey, and then capture it using organ discharge. The simulation of the hunting phase of an eel is represented by the following equation.

$$\left\{X|X-x_{prey}\left(t\right)|\le {\beta }_0\times |\overline{x}\left(t\right)-x_{prey}\left(t\right)|\right\}$$

(14)

$${\beta }_0=2\times (\mathrm{e}-{\mathrm{e}}^{{\displaystyle \frac{t}{{\mathrm{T}}_{\max }}}}\times sin\left(2\pi r_3\right))$$

(15)

$$H_{prey}(t+1)=x_{prey}\left(t\right)+\beta \times |\overline{x}\left(t\right)-x_{prey}\left(t\right)|$$

(16)

$$v_i(t+1)=H_{prey}(t+1)+\eta \times (H_{prey}(t+1)-round\left(rand\right)\times x_i\left(t\right))$$

(17)

$$\eta ={\mathrm{e}}^{{\displaystyle \frac{r_4(1-t)}{{\mathrm{T}}_{\max }}}}\times cos\left(2\pi r_4\right)$$

(18)

where ${\beta }_0$ is the initialization scale of the hunting region, $r_3$ and $r_4$ are random numbers in (0, 1), and $\eta$ is the crimp factor.

2.4. Migrating Stage

When eels spot prey, they tend to migrate from resting to hunting areas. To model the migration behavior of eels mathematically, the following formula is used:

$$v_i(t+1)=-r_5\times R_i(t+1)+r_6\times H_r(t+1)-L\times (H_r(t+1)-x_i\left(t\right))$$

(19)

$$H_r(t+1)=x_{prey}\left(t\right)+\beta \times |\overline{x}\left(t\right)-x_{prey}\left(t\right)|$$

(20)

$$x_i(t+1)=\left\{\begin{array}{cc}{x}_i\left(t\right)\hfill & fit\left(x_i\left(t\right)\right)\le fit\left(v_i(t+1)\right)\hfill \\ v_i(t+1)\hfill & fit\left(x_i\left(t\right)\right)>fit\left(v_i(t+1)\right)\hfill \end{array}\right.$$

(21)

where $H_r$ represents any position in the hunting area, $r_5$ and $r_6$ are random numbers within (0, 1), $(H_r(t+1)-x_i\left(t\right))$ represents eel movement to the hunting area, and L is the Levy flight function.

In EEFO, the search behavior is determined by the energy factor, which can effectively manage the transition between exploration and utilization, thereby improving the optimization performance of the algorithm, and the energy factor is defined as follows:

$$E\left(t\right)=4\times sin(1-{\displaystyle \frac{t}{{\mathrm{T}}_{\max }}})\times ln{\displaystyle \frac{1}{r_7}}$$

(22)

where $r_7$ is a random number between (0, 1). In addition, Figure 2 shows the flow chart of the EEFO algorithm.

Figure 2. Flow chart of the proposed EEFO method.

3. Improve the Optimization Algorithm

3.1. Differential Evolution Algorithm

Although EEFO has a good search capability, it still faces issues such as a weak search ability and slow convergence speed in certain problems. To further enhance the global search ability and accelerate the convergence speed of the EEFO algorithm, a differential evolution (DE) strategy was introduced to improve its global search capability and speed up convergence. The Differential Evolution Algorithm (DE) primarily consists of three processes: mutation, crossover, and selection [34,42]. The mathematical model is as follows:

$$V_i(t+1)=v_{r1}\left(t\right)+\mathrm{F}·(v_{r2}\left(t\right)-v_{r3}\left(t\right))$$

(23)

where F is the variance factor, a random number within the range $\left[0,1\right]$, and $v_{r1}$, $v_{r2}$, and $v_{r3}$ are three different and unequal individuals. After generating a mutated solution through the mutation operation, the mutated solution undergoes a crossover operation with the original solution to produce a new solution. The two common crossover methods are binomial and exponential crossover. Among these, binomial crossover is more frequently used, defined as follows:

$$U_{i,j}(t+1)=\left\{\begin{array}{cc}{V}_{i,j}(t+1),\hfill & ran{d}_{i,j}\left[0,1\right]\le CR\hfill \\ v_{i,j}\left(t\right),\hfill & otherwise\hfill \end{array}\right.$$

(24)

where $V_{i,j}(t+1)$ is the j dimension of the i individual generated in the previous step, $ran{d}_{i,j}\left[0,1\right]$ is a random number between $\left[0,1\right]$, and CR is the crossover factor, a random number within $\left[0,1\right]$. The new solution is then compared with the original solution, retaining the individual with better fitness. The mathematical model for the selection operation is as follows.

$$v_i(t+1)=\left\{\begin{array}{cc}{U}_i(t+1),\hfill & fit\left(U_i(t+1)\right)\le fit\left(v_i\left(t\right)\right)\hfill \\ v_i\left(t\right),\hfill & fit\left(U_i(t+1)\right)>fit\left(v_i\left(t\right)\right)\hfill \end{array}\right.$$

(25)

3.2. Quasi-Oppositional-Based Learning

In 2005, Tizhoosh proposed Opposition-Based Learning (OBL) [43] as a framework for machine intelligence. OBL extracts complementary candidate solutions from a set of solutions and then generates opposing solutions. Quasi-Opposition-Based Learning (QOBL) [44] is an improved version of OBL. In recent years, QOBL has been widely applied to algorithm improvements to enhance convergence speed and accuracy.

$$x^{qo}=rand\left[\left({\displaystyle \frac{lb+ub}{2}}\right),x^o\right]$$

(26)

In this context, $x^o=lb+ub-v_i\left(t\right)$, with $x^o$ being the opposite individual of the current search individual. The random number uniformly distributed between $\left({\displaystyle \frac{lb+ub}{2}}\right)$ and $x^o$ is represented as $rand\left[\left({\displaystyle \frac{lb+ub}{2}}\right),x^o\right]$.

3.3. Cauchy Variation

EEFO faces the issue of getting trapped in local optima during the iterative process. To address this, the Cauchy mutation strategy is adopted, which combines the best solution with the Cauchy distribution function to form a new solution. Cauchy Mutation (CM) is an optimization operator based on the Cauchy distribution. It uses changes in the original position to perform a local neighborhood search. The Cauchy distribution has a probability density function given by

$$cauchy\left(x\right)={\displaystyle \frac{1}{\pi }}\left[{\displaystyle \frac{\gamma }{{(x-x_0)}^2+{\gamma }^2}}\right]$$

(27)

In this context, $x_0$ is the parameter defining the peak position of the Cauchy distribution, and $\gamma$ is the scale parameter representing half the width at half maximum. This paper employs the standard Cauchy distribution with $x_0=0$ and $\gamma =1$. In this study, the best solution was combined with the Cauchy distribution function to form a new solution. The Cauchy mutation strategy was applied as follows [45]:

$$x_{new}=x_{prey}\times cauchy\left(x\right)$$

(28)

where $x_{new}$ is the introduction of the Cauchy mutation mechanism to the mutated individual. A flow chart and the pseudocode for the EEFO method are provided in Algorithm 1 and Figure 3, respectively.

Algorithm 1. Pseudo-code of MIEEFO
1	Initialize population parameters, N, D, ub, lb, T
2	while t < T do
3	Calculate the value of population fitness Fit(i)
4	Update the location of the optimal population Xi
5	Calculate E using Equation (22)
6	for each eel Xi do
7	if E > 1 then (Exploration)
8	if rand < 0.5 then(Interacting stage)
9	Perform the interacting stage using Equation (1).
10	else(Differential evolution)
11	Differential evolution is performed according to Equation (25).
12	end if
13	else (Exploitation)
14	if rand < 1/3 then (Resting stage)
15	Perform the resting stage using Equation (13).
16	elseif rand > 2/3 then (Migrating stage)
17	Perform the migrating stage using Equation (19).
18	else (Hunting stage)
19	Perform the hunting stage using Equation (17).
20	Simulate the Quasi-Opposition-Based Learning strategy using Equation (26).
22	end if
23	The position of each population is calculated using Equation (21).
24	end for
25	According to Equation (28), the Cauchy variation strategy is used to mutate the optimal individuals of the population
26	t = t + 1;
27	end while

Figure 3. Flow chart of the proposed MIEEFO method.

3.4. Time Complexity

In order to fully understand and evaluate the optimizer, it is crucial to examine computational complexity. The main components of MIEEFO are as follows: N denotes the number of eels, D denotes the variable dimensions of the problem, and T denotes the maximum number of iterations. The total computational complexity of MIEEFO is shown in Equation (29).

$$\begin{array}{cc}\hfill O\left(MIEEFO\right)& =O\left(initialization\right)+O\left(functionevaluation\right)+O\left(interacting\right)\hfill \\ \hfill & +O\left(DE\right)+O\left(inresting\right)+O\left(hunting\right)\hfill \\ \hfill & +O\left(inmigrating\right)+O\left(Cauchymutation\right)+O\left(QOBL\right)\hfill \\ \hfill & =O\left(ND\right)+O\left(2Nlog\left(2N\right)\right)+O(1/4T_{max}ND)+O(1/4T_{max}ND)\hfill \\ \hfill & +O(1/6T_{max}ND)+O(1/6T_{max}ND)+O(1/6T_{max}ND)+O\left(T_{max}\right)\hfill \\ \hfill & =O(T_{max}ND+ND+2Nlog\left(2N\right)+T_{max})\hfill \\ \hfill & \cong O\left(T_{max}ND\right)\hfill \end{array}$$

(29)

4. Experimental Results and Discussion

This section analyzes the algorithm through simulation experiments on the 15 test functions and discusses the results.

4.1. Parameter Settings

Fifteen benchmark test functions were used to evaluate the performance of the MIEEFO algorithm. These test functions were categorized into four types: unimodal, multimodal, hybrid and composite. The mathematical formulas for the test functions are presented in Table 1; “$F{i}^{\ast }$” indicates the global optimum. The parameter settings are detailed in Table 2.

Table 1. Description of the test functions (search range: $\left[-100,100\right]$).

Class	Function	Description	${\mathit{Fi}}^{\ast }$
Unimodal	F1	Rotated High Conditioned Elliptic Function	100
	F2	Rotated Bent Cigar Function	200
	F3	Rotated Discus Function	300
Multimodal	F4	Shifted and Rotated Rosenbrock’s Function	400
	F5	Shifted and Rotated Weierstrass Function	600
	F6	Shifted Schwefel’s Function	1000
	F7	Shifted and Rotated HappyCat Function	1300
	F8	Shifted and Rotated HGBat Function	1400
Hybrid	F9	Hybrid Function 2	1800
	F10	Hybrid Function 3	1900
	F11	Hybrid Function 4	2000
	F12	Hybrid Function 5	2100
Composition	F13	Composition Function 2	2400
	F14	Composition Function 3	2500
	F15	Composition Function 4	2600

Table 2. Algorithm parameter settings.

Algorithm	Parameters
MIEEFO	$\mathrm{fi}=1.5,\mathrm{TR}=0.3$ F = 0.5, ${\mathrm{C}}_{\mathrm{r}}=0.9$
EEFO	$\beta =1.5$
DE	F = 0.5, ${\mathrm{C}}_{\mathrm{r}}=0.9$
DBO	k = 0.1, b = 0.3, $\mathrm{ff}=1$
HHO	$E_0ϵ\left(-1,1\right)$
ZOA	l$ϵ$$\left(1,2\right)$
IDBO	k = 0.1, b = 0.3,$\mathrm{ff}=1$
MIHHO	$\mathrm{fi}=1.5$

MIEEFO was compared with the following seven advanced meta-heuristic methods: EEFO, DE, DBO [46], HHO, ZOA [47], IDBO [48], and MIHHO [49]. To ensure a fair comparison, the population size for each algorithm was set to 30 individuals, with 30 runs and 1000 iterations for each run. The default parameters for using the metaheuristic are listed in Table 2. The experimental platform was set up on a computer with an Intel(R) Core(TM) i7-8750H CPU, 2.2 GHz clock speed and 16 GB of RAM, running the Windows 10 (64-bit) operating system, with Matalab2022b as the software.

4.2. Analysis of Statistical Results

The performance of the algorithms was analyzed using the mean, standard deviation (STD), and the Friedman test. Among these, the average (Avg) is the mean rank obtained by each algorithm across all benchmarks, while the rank is the experimental result calculated through the Friedman test, as shown in Table 3, with the best results highlighted in bold. It can be observed that MIEEFO outperforms other algorithms across all 15 test functions. Additionally, MIEEFO ranks first in the Friedman test. In conclusion, the MIEEFO algorithm demonstrates strong global and local search capabilities.

Table 3. The experimental results of different algorithms on the test functions.

ID		MIEEFO	EEFO	DE	DBO	HHO	ZOA	IDBO	MIHHO
F1	Mean	498.03	3.33 $\times {10}^4$	2.82 $\times {10}^7$	7.99 $\times {10}^6$	8.18 $\times {10}^6$	1.46 $\times {10}^7$	9.62 $\times {10}^6$	2.93 $\times {10}^6$
	Std	437.55	4.80 $\times {10}^4$	9.52 $\times {10}^6$	3.23 $\times {10}^6$	6.03 $\times {10}^6$	9.46 $\times {10}^6$	4.78 $\times {10}^6$	2.48 $\times {10}^6$
F2	Mean	1914.02	2005.42	3.19 × 109	4.80 $\times {10}^7$	3.47 $\times {10}^5$	2.32 × 108	5.10 $\times {10}^7$	2.62 $\times {10}^5$
	Std	2111.58	2200.18	9.45 × 108	2.70 $\times {10}^7$	1.36 $\times {10}^5$	3.57 × 108	2.51 $\times {10}^7$	9.28 $\times {10}^4$
F3	Mean	300.08	520.34	2.28 $\times {10}^4$	1.32 $\times {10}^4$	4101.36	4695.30	12077.08	3920.48
	Std	0.11	277.73	5829.80	6082.42	1832.58	2611.16	3881.98	1820.69
F4	Mean	413.91	418.70	704.47	443.22	436.04	449.91	443.75	432.74
	Std	15.96	16.28	76.71	26.64	16.02	37.69	14.19	24.73
F5	Mean	600.91	602.40	609.51	605.22	607.32	605.90	604.73	606.97
	Std	0.71	1.10	0.80	1.38	1.81	1.62	1.37	1.57
F6	Mean	1105.26	1148.69	2476.30	1926.61	1492.78	1421.38	1777.99	1304.50
	Std	92.38	123.62	159.93	321.87	256.26	187.79	243.82	183.96
F7	Mean	1300.18	1300.23	1302.28	1300.67	1300.52	1300.45	1300.63	1300.58
	Std	0.06	0.09	0.31	0.17	0.16	0.20	0.19	0.25
F8	Mean	1400.22	1400.25	1414.71	1400.71	1400.34	1401.31	1400.60	1400.22
	Std	0.07	0.10	2.83	0.22	0.31	2.74	0.20	0.07
F9	Mean	1804.73	2516.83	4.20 $\times {10}^5$	4.48 $\times {10}^4$	9889.607	8552.73	2.71 $\times {10}^4$	1.05 $\times {10}^4$
	Std	2.53	2344.31	4.23 $\times {10}^5$	4.71 $\times {10}^4$	4150.397	3926.93	2.58 $\times {10}^4$	7929.32
F10	Mean	1900.77	1901.07	1910.21	1905.05	1904.45	1906.01	1904.848	1905.10
	Std	0.37	0.48	2.27	0.94	1.24	7.46	0.99	1.61
F11	Mean	2001.94	2004.49	1.17 $\times {10}^4$	2.12 $\times {10}^4$	6142.06	5650.58	15657.61	4365.96
	Std	1.26	3.37	5909.704	1.50 $\times {10}^4$	3090.36	2220.30	8158.86	1861.18
F12	Mean	2109.19	2233.66	2.43 $\times {10}^4$	5.70 $\times {10}^4$	9984.14	6.70 $\times {10}^4$	4.28 $\times {10}^4$	1.32 $\times {10}^4$
	Std	11.92	167.04	2.00 $\times {10}^4$	5.43 $\times {10}^4$	7232.61	1.03 $\times {10}^5$	4.00 $\times {10}^4$	1.05 $\times {10}^4$
F13	Mean	2550.66	2563.34	2585.91	2569.80	2594.19	2563.05	2570.75	2583.15
	Std	31.48	32.66	10.04	18.63	13.80	30.87	20.97	25.62
F14	Mean	2689.46	2696.11	2696.15	2692.71	2699.65	2694.86	2689.60	2697.14
	Std	16.24	12.72	8.43	12.45	1.91	12.63	14.59	10.57
F15	Mean	2700.16	2700.18	2701.78	2700.59	2700.36	2700.36	2700.61	2700.38
	Std	0.05	0.05	0.38	0.10	0.17	0.38	0.12	0.15
Friedman	Avg	1.7522	2.5067	7.2289	5.6222	4.6567	4.5133	5.4722	4.2478
	Rank	1	2	8	7	5	4	6	3

4.3. Convergence Curve Analysis of MIEEFO Algorithm

This section presents the convergence curves of the proposed MIEEFO algorithm compared with other competing algorithms on the 15 test functions, as shown in Figure 4. MIEEFO achieves superior experimental results on functions F1 to F10 and F12 to F15, demonstrating its strong local search capability and ability to avoid becoming trapped in local optima. For the F11 function, MIEEFO produces results similar to those of the competing algorithms but with faster convergence. This indicates that MIEEFO has robust global search capabilities, which significantly accelerates the convergence speed of the algorithm.

Figure 4. Convergence diagram of MIEEFO algorithm in test function.

4.4. Box Diagram Analysis

In this subsection, box plots are used to compare MIEEFO with the other algorithms. The upper and lower bounds of the box plots represent the maximum and minimum data values, respectively. The upper quartile corresponds to the 75th percentile of the ordered data, whereas the lower quartile corresponds to the 25th percentile. The median represents the 50th percentile of ordered values. Box plots allow us to visualize outliers, the spread of the distribution, and the symmetry of the data. As shown in Figure 5, it is evident that MIEEFO exhibits very narrow boxes, consistently maintaining the lowest points across most test functions. Compared to algorithms such as EEFO, MIEEFO achieves lower values in the box plots, while demonstrating better optimization performance than DE, DBO, and ZOA. Overall, MIEEFO demonstrates strong optimization capabilities.

Figure 5. Function box diagram test.

4.5. Statistical Analysis

To validate the stability of the MIEEFO algorithm, the Wilcoxon test was employed. Table 4 presents the Wilcoxon test results for 30 runs across 15 test functions, where the p-value indicates the significance of differences between results. A threshold of 0.05 was set for the p-value: If the p-value is below 0.05, MIEEFO outperforms the compared algorithm. If the p-value equals 0.05, the performance is similar. If the p-value is above 0.05, the compared algorithm outperforms MIEEFO. The results indicate that MIEEFO outperforms other algorithms on at least 12 test functions, while the performance is comparable on the remaining functions. Overall, MIEEFO exhibits superior performance and stability.

Table 4. Wilcoxon test results.

Function	EEFO	DE	DBO	HHO	ZOA	IDBO	MIHHO
F1	5.87 $\times {10}^{-10}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F2	5.00 $\times {10}^{-2}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.02 $\times {10}^{-9}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F3	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F4	2.11 $\times {10}^{-4}$	1.51 $\times {10}^{-11}$	2.37 $\times {10}^{-6}$	3.87 $\times {10}^{-6}$	4.42 $\times {10}^{-7}$	8.47 $\times {10}^{-10}$	3.18 $\times {10}^{-5}$
F5	1.66 $\times {10}^{-6}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F6	5.00 $\times {10}^{-2}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.42 $\times {10}^{-8}$	1.11 $\times {10}^{-9}$	1.51 $\times {10}^{-11}$	2.59 $\times {10}^{-7}$
F7	5.00 $\times {10}^{-2}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	2.37 $\times {10}^{-6}$	1.51 $\times {10}^{-11}$	9.28 $\times {10}^{-10}$
F8	6.51 $\times {10}^{-4}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	5.00 $\times {10}^{-2}$	2.73 $\times {10}^{-9}$	1.51 $\times {10}^{-11}$	3.81 $\times {10}^{-3}$
F9	2.49 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F10	1.14 $\times {10}^{-5}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F11	3.37 $\times {10}^{-6}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F12	3.52 $\times {10}^{-7}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$
F13	1.53 $\times {10}^{-2}$	3.93 $\times {10}^{-3}$	3.60 $\times {10}^{-3}$	1.31 $\times {10}^{-7}$	1.72 $\times {10}^{-3}$	1.77 $\times {10}^{-2}$	1.26 $\times {10}^{-3}$
F14	2.08 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$
F15	2.63 $\times {10}^{-5}$	1.51 $\times {10}^{-11}$	1.51 $\times {10}^{-11}$	1.84 $\times {10}^{-11}$	1.30 $\times {10}^{-5}$	1.51 $\times {10}^{-11}$	2.09 $\times {10}^{-9}$
+/=/−	12/3/0	13/1/0	14/1/0	13/2/0	14/1/0	14/1/0	14/1/0

5. MIEEFO Is Used for Image Segmentation

In this section, the MIEEFO algorithm is compared with six other algorithms—EEFO, LHHO, NHHGWO [50], HSMAWOA [51] and HVSFLA [52]—on the Multithreshold Image Segmentation (MTLIS) task. The experiments were conducted on images 37073, 42049, 94079, 118035, 189011 and 385028. The segmentation was performed at four threshold levels (4, 6, 8, and 12), where 4 and 6 represent low threshold levels, and 8 and 12 represent high threshold levels. To further ensure the fairness of the experiment, we conducted tests using the same parameters. The population size was set to 30, the number of iterations to 500, and the image resolution to 1980 × 1080. The experiment was conducted on a computer with an Intel(R) Core(TM) i7-8750H CPU, a clock speed of 2.2 GHz and 16GB RAM, running the Windows 10 (64-bit) operating system, and using MATLAB 2022b as the software platform. The experimental results are evaluated using PSNR, FSIM and SSIM as performance metrics.

5.1. Kapur Entropy

In this subsection, for a given image with a gray level of G, ranging from 0 to $G-1$, and a total of N pixels, the i-th intensity level has a frequency of $f\left(i\right)$.

$$N=f\left(0\right)+f\left(1\right)+f\left(2\right)+\cdots +f(G-1)$$

(30)

The probability of the intensity class is given by Equation (31).

$$P_i={\displaystyle \frac{f_i}{N}}$$

(31)

Assume that M has the following thresholds: $t{h}_1,t{h}_2,\cdots ,t{h}_M$, at $1\le M\le G-1$. Using the threshold value, a given image is divided into segments of M + 1, and given the following symbols: $Class\left(0\right)=0,\cdots ,t{h}_1-1$, $Class\left(1\right)=t{h}_1,t{h}_1+1,\cdots ,t{h}_2-1$ and $Class\left(M\right)=t{h}_M,t{h}_M+1,\cdots ,G-1$. MIEEFO uses Equation (32) as the objective function, and the optimal solution of $t{h}_1,t{h}_2,\cdots ,t{h}_M$ in MIEEFO is the optimal threshold.

$$F(t{h}_1,t{h}_2,\cdots ,t{h}_M)=E_0+E_1+\cdots +E_M$$

(32)

$$\begin{array}{c}\hfill E_0=-\sum _{i=0}^{i=t{h}_1-1}{\displaystyle \frac{P_i}{\omega }}ln{\displaystyle \frac{P_i}{{\omega }_0}},{\omega }_0=\sum _{i=0}^{i=t{h}_1-1}{P}_i\\ \hfill E_1=-\sum _{i=t{h}_1}^{i=t{h}_2-1}{\displaystyle \frac{P_i}{{\omega }_1}}ln{\displaystyle \frac{P_i}{{\omega }_1}},{\omega }_1=\sum _{i=t{h}_1}^{i=t{h}_2-1}{P}_i\\ \hfill E_M=-\sum _{i=t{h}_M}^{i=G-1}{\displaystyle \frac{P_i}{{\omega }_M}}ln{\displaystyle \frac{P_i}{{\omega }_M}},{\omega }_M=\sum _{i=t{h}_M}^{i=G-1}{P}_i\\ \hfill H_{kapur}=argmax\left\{F(t{h}_1,t{h}_2,\cdots ,t{h}_M)\right\}\end{array}$$

(33)

5.2. Performance Specifications

In order to effectively evaluate the quality of the image segmentation results, PSNR, SSIM and FSIM are used as evaluation indexes. Figure 6 present the original image and corresponding histograms for each color channel.

Figure 6. The original image and corresponding histograms for each color channel (red, green, blue).

The Peak Signal-to-Noise Ratio (PSNR) has been one of the most commonly used objective metrics for evaluating image quality in recent years. It primarily measures the error between corresponding pixel values of two images. Mathematically, PSNR is defined as follows:

$$PSNR=20·{log}_{10}\left[{\displaystyle \frac{255}{\sqrt{\frac{{\sum }_{i=0}^{M-1}{\sum }_{j=0}^{N-1}{(I_{ij}-Se{g}_{ij})}^2}{M\times N}}}}\right]$$

(34)

where $I_{ij}$ and $Se{g}_{ij}$ represent the pixel values of the original image and the distorted image at position and $M\times N$ is the total number of pixels in the image.

PSNR is expressed in decibels (dB), and higher PSNR values generally indicate better image quality.

The Structural Similarity Index (SSIM) is a metric used to measure the similarity between two images, typically before and after compression or processing.

The SSIM formula is expressed as follows:

$$SSIM={\displaystyle \frac{(2{\mu }_I{\mu }_{Seg}+c_1)(2{\sigma }_{I,Seg}+c_2)}{({\mu }_I^2+{\mu }_{Seg}^2+c_1)({\sigma }_I^2+{\sigma }_{Seg}^2+c_2)}}$$

(35)

where ${\mu }_I$ and ${\mu }_{Seg}$ are the mean intensities of images I and Seg, respectively. ${\sigma }_I^2$ and ${\sigma }_{Seg}^2$ are the variances of images I and Seg. ${\sigma }_{I,Seg}$ is the covariance between I and Seg; $c_1$ and $c_2$ are small constants used to stabilize the division, preventing instability when the denominator is close to zero.

The SSIM value ranges from 0 to 1. A higher SSIM value indicates smaller differences between the two images, reflecting better segmentation quality and effectiveness. Conversely, a lower SSIM indicates greater dissimilarity, often implying poorer segmentation quality.

The FSIM metric focuses on perceptually relevant features. A higher FSIM value indicates a higher similarity between two images, presenting better image quality or segmentation accuracy.

The FSIM formula is typically expressed as follows:

$$FSIM={\displaystyle \frac{{\sum }_{Iϵ\Omega }{S}_L\left(x\right)P{C}_m\left(x\right)}{{\sum }_{Iϵ\Omega }P{C}_m\left(x\right)}}$$

(36)

where $S_L\left(x\right)$ is the local similarity measure computed for the pixel X and $P{C}_m\left(x\right)$ is the importance weight assigned to pixel X, where $P{C}_m\left(x\right)=max(P{C}_1\left(x\right),P{C}_2\left(x\right))$. $\Omega$ represents the set of all pixels in the image.

$$S_L\left(x\right)={\left[S_{PC}\left(x\right)\right]}^{\alpha }.{\left[S_G\left(x\right)\right]}^{\beta }$$

(37)

$$S_{PC}\left(x\right)={\displaystyle \frac{2P{C}_1\left(x\right)\times P{C}_2+T_1}{P{C}_1^2\left(x\right)+P{C}_1^2\left(x\right)+T_1}}$$

(38)

$$S_G\left(x\right)={\displaystyle \frac{2G_1\left(x\right)\times G_2\left(x\right)+T_2}{G_1^2\left(x\right)+G_1^2\left(x\right)+T_2}}$$

(39)

where $S_{PC}\left(X\right)$ represents the feature similarity of the image, and $S_G\left(X\right)$ represents the gradient similarity of the image. $G_1\left(X\right)$ and $G_2\left(X\right)$ denote the gradient magnitudes of the reference image and the enhanced image at pixel X, respectively. The parameters $\alpha$ and $\beta$ are generally taken as 1.

The FSIM metric focuses on perceptually relevant features, making it more aligned with human visual perception compared to general pixel-wise metrics. A higher FSIM value (close to 1) indicates higher similarity between the two images, suggesting better image quality or segmentation accuracy.

5.3. Image Segmentation Results

This article compares Kapur entropy multithreshold image segmentation algorithms based on EEFO, LHHO, NHHGWO, HSMAWOA, and HVSFLA. Meanwhile, Figure 7, Figure 8 and Figure 9 present bar charts of PSNR, SSIM and FSIM results across multiple thresholds, providing a clearer display of the evaluation results. Figure 10 and Figure 11 show the segmentation results of different algorithms with thresholds of 4 and 12. From Figure 10 and Figure 11, it can be seen that as the threshold increases, the images become clearer, indicating that a higher threshold can effectively capture more information. Table 5, Table 6 and Table 7 provide the numerical evaluation results for the PSNR, SSIM and FSIM in the image segmentation task. The data show that MIEEFO generally outperforms other algorithms. Additionally, as the threshold gradually increased, the PSNR, FSIM and SSIM values of the segmented images also increased. Experimental results demonstrate that MIEEFO has a significant advantage in experiments based on Kapur entropy threshold segmentation.

Figure 7. Four threshold level values for PSNR evaluation.

Figure 8. Four threshold level values for SSIM evaluation.

Figure 9. Four threshold level values for FSIM evaluation.

Figure 10. Results of image segmentation with a threshold of 4.

Figure 11. Results of image segmentation with a threshold of 12.

Table 5. PSNR values for each method.

Image	Dim	MIEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image1	4	21.5237	21.5054	21.5237	21.4534	21.5237	20.4470
	6	22.8780	22.0905	22.1423	22.7002	22.8193	22.5626
	8	24.5226	24.0488	24.1771	24.1563	24.1377	24.0919
	12	26.5225	26.4710	26.1978	25.9245	26.2178	26.3472
Image2	4	20.9224	20.9224	20.8910	20.7794	20.8910	20.9200
	6	22.5912	22.5403	22.3680	22.4673	22.5658	22.5770
	8	24.5105	24.4915	24.4611	24.4146	24.3607	24.4154
	12	28.3130	28.2247	28.2297	28.0077	28.1418	27.9479
Image3	4	18.2743	18.2743	18.2743	18.3577	18.2743	18.2925
	6	21.3361	21.1643	21.3307	21.3040	21.3307	21.3275
	8	23.5397	23.5081	23.4820	23.4462	23.4394	23.5385
	12	27.7488	27.6157	27.6634	27.2064	27.6788	27.6355
Image4	4	19.6593	19.6389	19.6570	19.5204	19.6572	19.6572
	6	23.0897	23.0446	23.0780	22.8569	23.0874	22.9759
	8	24.0519	23.9469	24.0481	23.7149	23.8600	24.0359
	12	27.7628	27.4562	27.5392	27.3174	27.7527	27.3130
Image5	4	19.6606	19.6606	19.6606	19.6338	19.6606	19.6464
	6	21.4753	21.4685	21.4217	19.6338	21.4512	21.4498
	8	24.0748	23.9375	24.0340	23.6882	23.9239	23.9936
	12	27.5855	27.5280	27.5441	27.4261	27.5139	27.5788
Image6	4	18.5560	18.5560	18.5560	18.5437	18.5560	18.5541
	6	21.2951	21.2905	21.2947	21.2376	21.2947	21.2807
	8	23.6303	23.6025	23.6025	23.3302	23.6252	23.5916
	12	27.1381	27.0896	27.0419	26.9596	27.0698	27.1381

Table 6. SSIM values for each method.

Image	Dim	MIEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image1	4	0.6673	0.6614	0.6618	0.6618	0.6618	0.6268
	6	0.7246	0.7173	0.7176	0.7246	0.7177	0.7075
	8	0.7823	0.7734	0.7720	0.7760	0.7819	0.7814
	12	0.8391	0.8391	0.8372	0.8255	0.8319	0.8350
Image2	4	0.8607	0.8607	0.8594	0.8606	0.8594	0.8564
	6	0.8920	0.8872	0.8857	0.8865	0.8860	0.8874
	8	0.9175	0.9163	0.9143	0.9159	0.9127	0.9162
	12	0.9378	0.9320	0.9334	0.9355	0.9355	0.9358
Image3	4	0.6888	0.6869	0.6869	0.6887	0.6869	0.6869
	6	0.8025	0.8021	0.8023	0.8022	0.8022	0.8016
	8	0.8610	0.8601	0.8587	0.8554	0.8586	0.8586
	12	0.9324	0.9309	0.9309	0.9167	0.9278	0.9323
Image4	4	0.8843	0.8840	0.8842	0.8840	0.8843	0.8840
	6	0.9148	0.9147	0.9144	0.9145	0.9148	0.9147
	8	0.9241	0.9231	0.9223	0.9203	0.9231	0.9238
	12	0.9280	0.9267	0.9260	0.9220	0.9279	0.9274
Image5	4	0.5407	0.5407	0.5407	0.5395	0.5407	0.5407
	6	0.5956	0.5865	0.5859	0.6246	0.5869	0.5869
	8	0.6739	0.6730	0.6732	0.6731	0.6682	0.6716
	12	0.8015	0.7933	0.7921	0.8096	0.7901	0.7883
Image6	4	0.6854	0.6854	0.6854	0.6796	0.6854	0.6555
	6	0.7574	0.7573	0.7570	0.7568	0.7570	0.7562
	8	0.8207	0.8196	0.8196	0.8109	0.8196	0.8199
	12	0.8989	0.8981	0.8880	0.8933	0.8974	0.8799

Table 7. FSIM values for each method.

Image	Dim	MIEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image1	4	0.7945	0.7944	0.7945	0.7930	0.7945	0.7700
	6	0.8304	0.8146	0.8074	0.8146	0.8226	0.8244
	8	0.8592	0.8589	0.8579	0.8577	0.8591	0.8546
	12	0.9089	0.9078	0.9053	0.9083	0.9066	0.9053
Image2	4	0.8536	0.8533	0.8525	0.8533	0.8525	0.8533
	6	0.8748	0.8748	0.8703	0.8731	0.8747	0.8748
	8	0.8916	0.8915	0.8910	0.8916	0.8896	0.8915
	12	0.9212	0.9181	0.9198	0.9170	0.9190	0.9208
Image3	4	0.7933	0.7926	0.7926	0.7924	0.7926	0.7926
	6	0.8706	0.8702	0.8705	0.8669	0.8703	0.8703
	8	0.9109	0.9083	0.9079	0.9098	0.9081	0.9084
	12	0.9586	0.9572	0.9578	0.9555	0.9536	0.9577
Image4	4	0.8777	0.8777	0.8776	0.8775	0.8777	0.8774
	6	0.9034	0.9033	0.9033	0.9031	0.9025	0.9024
	8	0.9159	0.9157	0.9152	0.9150	0.9156	0.9141
	12	0.9342	0.9335	0.9383	0.9336	0.9341	0.9310
Image5	4	0.7219	0.7219	0.7219	0.7207	0.7219	0.7120
	6	0.7709	0.7703	0.7702	0.7556	0.7610	0.7608
	8	0.8046	0.8039	0.8029	0.8002	0.8021	0.8032
	12	0.8793	0.8770	0.8792	0.8782	0.8771	0.8745
Image6	4	0.8121	0.8120	0.8120	0.8119	0.8120	0.8121
	6	0.8678	0.8676	0.8675	0.8627	0.8675	0.8742
	8	0.9046	0.9044	0.9040	0.9021	0.9040	0.9040
	12	0.9438	0.9435	0.9435	0.9416	0.9433	0.9435

5.4. Forest Fire Image Segmentation

In forest ecosystems, wildfires are characterized by their sudden onset and uncontrollabled nature. Once they exceed human control, they can cause severe damage to human lives and property, as well as significant harm to the ecological environment, and ultimately evolve into forest fires. An image-segmentation-based forest fire detection technique was proposed to minimize the damage caused by forest fires. The goal of forest fire image segmentation is to separate the fire-affected areas from the forest images for subsequent fire identification [53]. To verify the effectiveness of this algorithm in practical engineering applications, MIEEFO is used to segment forest fire images. Images captured using digital cameras were used as experimental samples. Figure 12 shows two forest fire images. All algorithms were tested under the same experimental conditions to ensure objectivity and fairness of the experiment. The algorithm parameters were set as described in the previous section. To verify the effectiveness of the algorithm in different dimensions, the number of thresholds used in the experiment was set to 2, 4, 8, 10 and 12. The image segmentation results of the multilevel thresholding algorithm based on MIEEFO for the different dimensions are shown in Figure 13. There is no obvious contrast or distinction between the fire-affected areas and background, which limits the optimization ability of the algorithm.

Figure 12. Forest fire image.

Figure 13. Result of MIEEFO-based multilevel thresholding segmentation algorithm.

The segmentation results show that the MIEEFO-based algorithm is proficient in identifying fire regions on forest surfaces. In the image segmentation experiments, MIEEFO was compared to EEFO, LHHO, NHHGWO, HSMAWOA and HVSFLA, and the experimental results were evaluated using three metrics: FSIM, SSIM and PSNR. The data for the performance of each algorithm in the segmentation experiments are shown in Table 8, Table 9 and Table 10. The experimental results indicate that MIEEFO achieved the best SSIM, FSIM and PSNR values, demonstrating superior performance. Therefore, MIEEFO provided stable results and excellent performance across different threshold levels. The MIEEFO-based segmentation algorithm demonstrates ideal segmentation quality for forest fire detection. From the perspective of segmentation effectiveness, the MIEEFO-based algorithm can efficiently segment forest fire regions. In conclusion, this algorithm can solve optimization problems in various dimensions and effectively address complex engineering challenges.

Table 8. PSNR values for each method.

Image	Dim	MEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image7	2	9.8233	9.8233	9.8233	9.8233	9.8233	9.8233
	4	18.8473	18.8473	18.8082	18.7532	18.8473	18.8473
	8	24.4981	24.4536	24.4367	24.4486	24.4695	24.0293
	10	26.7583	26.7429	26.6805	25.8615	26.6948	26.5086
	12	28.1360	28.0948	27.8337	27.3201	28.0571	28.0438
Image8	2	10.3805	10.3805	10.3805	10.3805	10.3805	10.3805
	4	18.9104	18.9104	18.9104	18.0873	18.9104	18.9104
	8	24.9001	24.8117	24.7425	24.0358	24.7088	24.5550
	10	26.7528	26.6621	26.7145	25.6014	26.6089	26.4455
	12	27.8407	27.6935	27.7019	26.7616	27.5445	27.6708

Table 9. SSIM values for each method.

Image	Dim	MEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image7	2	0.2839	0.2839	0.2839	0.2839	0.2839	0.2839
	4	0.6474	0.6474	0.6474	0.6323	0.6474	0.6474
	8	0.8161	0.8128	0.8137	0.8134	0.8156	0.8123
	10	0.8659	0.8630	0.8630	0.8523	0.8638	0.8572
	12	0.8911	0.8898	0.8852	0.8844	0.8824	0.8877
Image8	2	0.2953	0.2953	0.2953	0.2953	0.2953	0.2953
	4	0.6554	0.6554	0.6554	0.6421	0.6554	0.6554
	8	0.8383	0.8375	0.8316	0.8346	0.8361	0.8365
	10	0.8816	0.8709	0.8790	0.8573	0.8748	0.8810
	12	0.9018	0.8909	0.8924	0.8755	0.8895	0.8991

Table 10. FSIM values for each method.

Image	Dim	MEEFO	EEFO	LHHO	NHHGWO	HSMAWOA	HVSFLA
Image7	2	0.6383	0.6383	0.6383	0.6360	0.6383	0.6383
	4	0.8139	0.8139	0.8117	0.8127	0.8100	0.8139
	8	0.9112	0.9109	0.9110	0.9072	0.9105	0.9012
	10	0.9491	0.9478	0.9488	0.9348	0.9488	0.9446
	12	0.9629	0.9619	0.9610	0.9544	0.9611	0.9602
Image8	2	0.6436	0.6436	0.6436	0.6436	0.6436	0.6436
	4	0.8256	0.8224	0.8224	0.8159	0.8224	0.8224
	8	0.9215	0.9195	0.9193	0.9174	0.9169	0.9112
	10	0.9514	0.9502	0.9505	0.9380	0.9496	0.9513
	12	0.9645	0.9625	0.9642	0.9465	0.9595	0.9604

6. Conclusions and Future Works

This paper proposes an improved Electric Eel Optimization Algorithm (MIEEFO) and tests it on 15 benchmark functions. MIEEFO is compared with EEFO, DE, DBO, HHO, ZOA, IDBO and MIHHO. The experimental results clearly demonstrate that MIEEFO exhibits superior exploration, exploitation, robustness and convergence accuracy. Additionally, MIEEFO is applied to the problem of color image segmentation. The test images include benchmark color images from the Berkeley database and forest fire images from real-world engineering problems. Using Kapur’s entropy as the fitness function, MIEEFO is compared with EEFO, LHHO, NHHGWO, HSMAWOA and HVSFA under different threshold levels. The experimental results show that the segmentation algorithm based on MIEEFO outperforms other algorithms across various threshold levels, proving the effectiveness of the model.

In future work, our research will focus on the following aspects: On the one hand, while the algorithm has already produced reliable results, additional strategies can be incorporated to further balance exploration and exploitation capabilities, thereby enhancing the convergence speed of EEFO. On the other hand, the improved MIEEFO can be applied to more complex domains, such as power systems, feature selection, data mining, artificial intelligence and other benchmark functions.