Low-Carbon Transport for Prefabricated Buildings: Optimizing Capacitated Truck–Trailer Routing Problem with Time Windows
Abstract
1. Introduction
2. Literature Review
2.1. The Truck–Trailer Routing Problem for Prefabricated Components
2.2. Existing Solution Methods for the TTRP
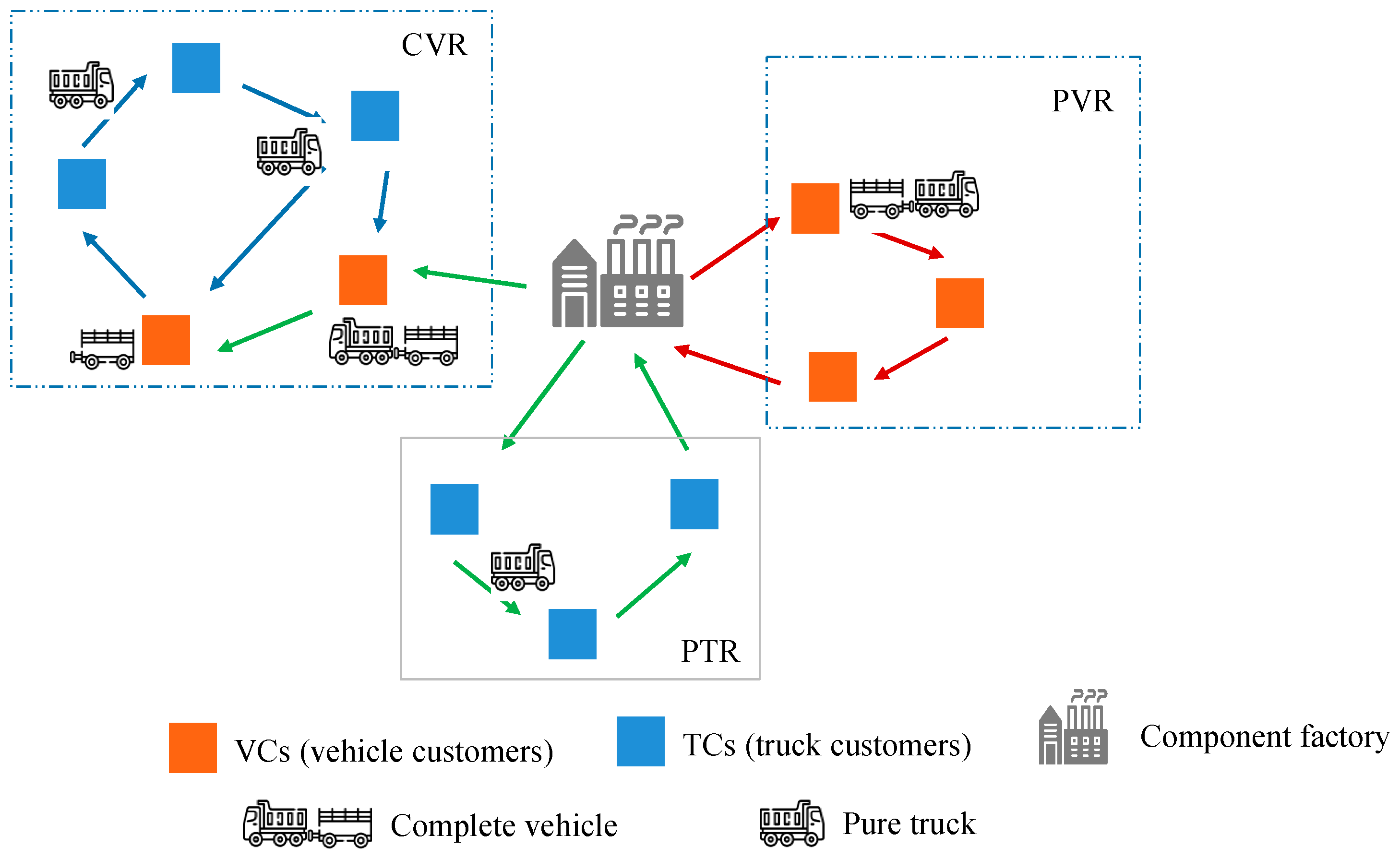
3. Problem Description and Model Formulation
3.1. Problem Description
3.2. The Mathematical Formulation for the CTTRPTW
3.2.1. Fixed Costs
3.2.2. Fuel Consumption Costs
3.2.3. Carbon Emissions Costs
3.2.4. Customer Satisfaction with Soft Time Windows
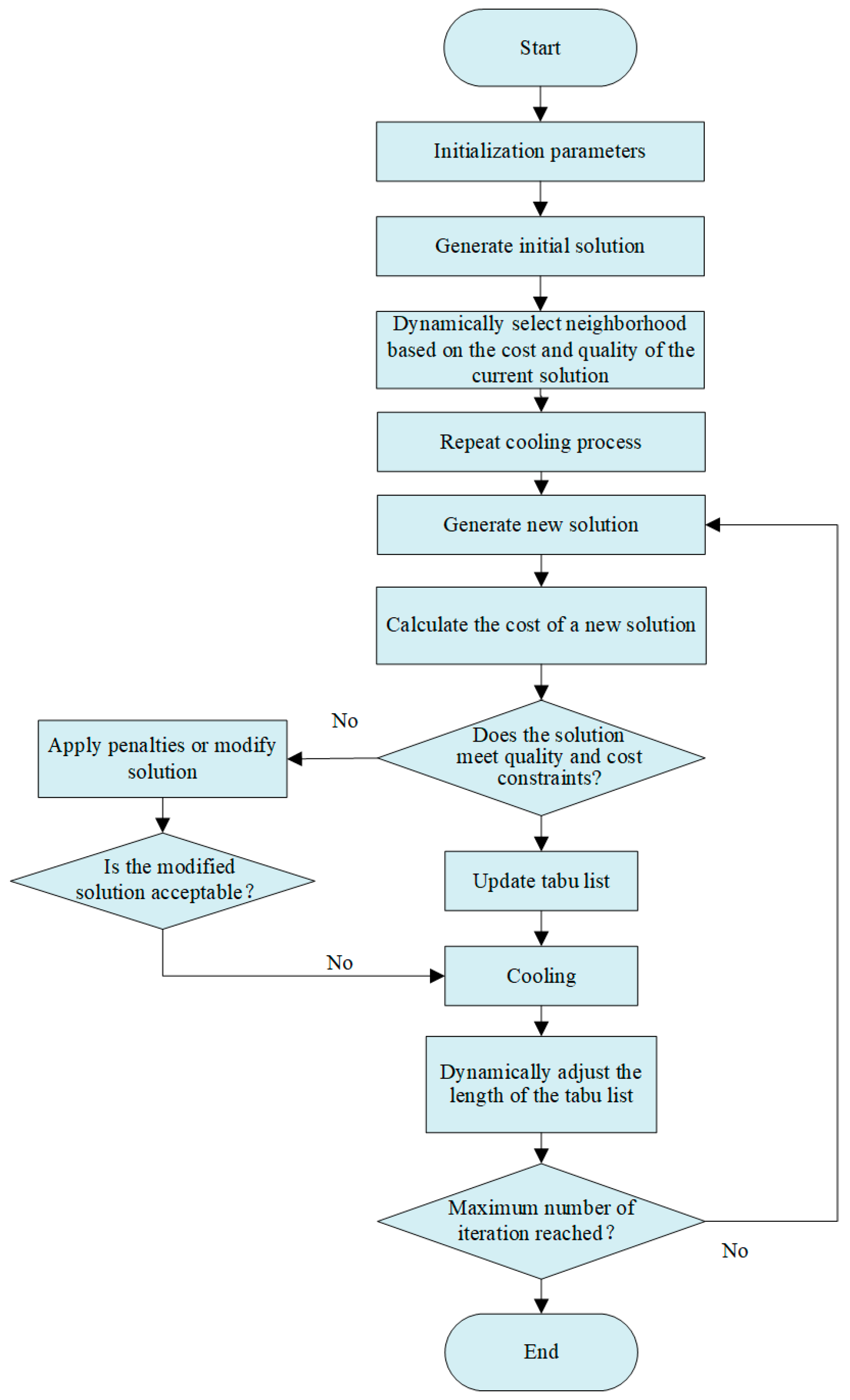
4. Solution Algorithm
5. Computational Experiments
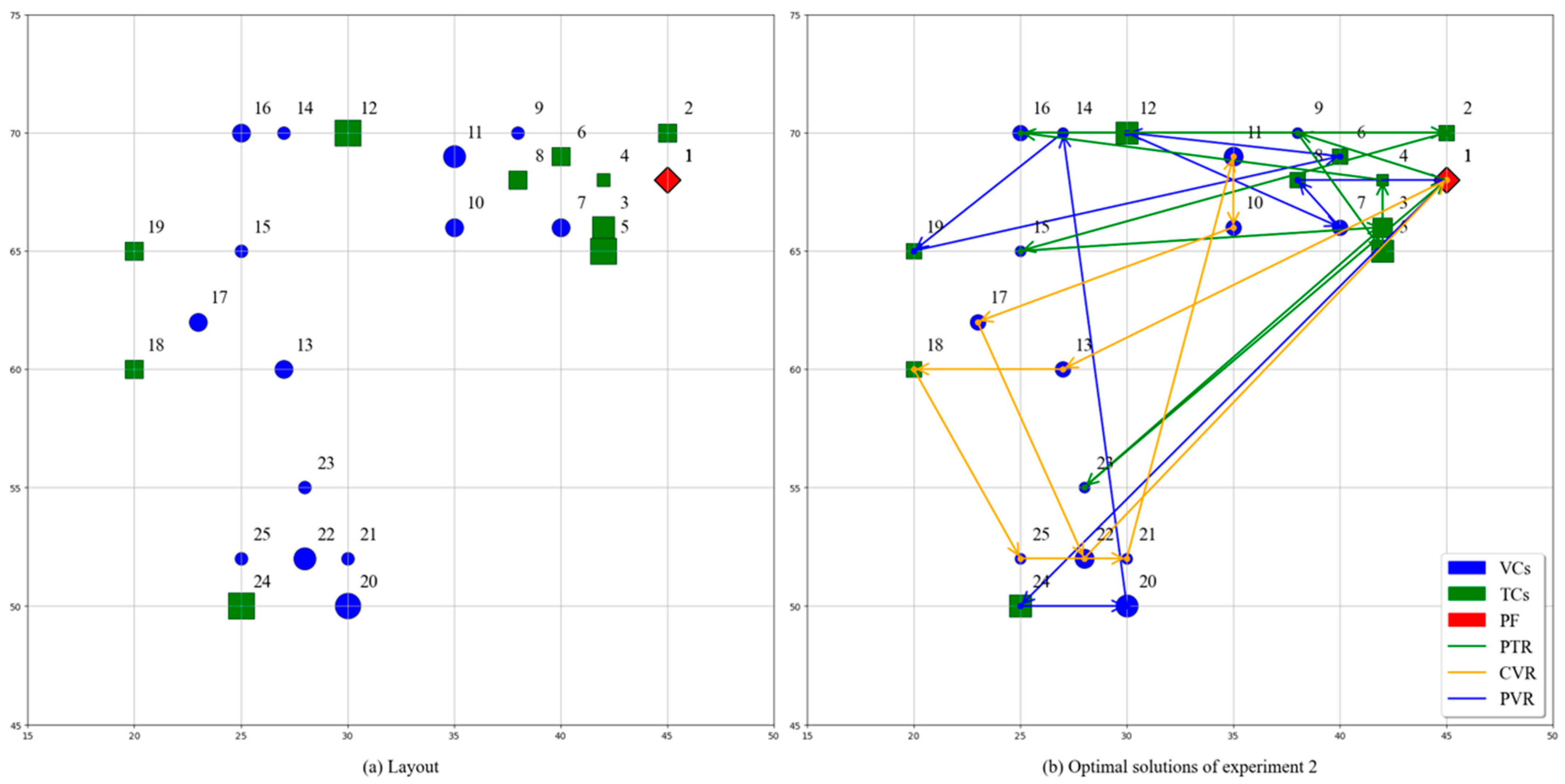
5.1. Description of the Test Instances
5.2. Computational Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mao, C.; Shen, Q.; Shen, L.; Tang, L. Comparative Study of Greenhouse Gas Emissions between Off-Site Prefabrication and Conventional Construction Methods: Two Case Studies of Residential Projects. Energy Build. 2013, 66, 165–176. [Google Scholar] [CrossRef]
- Xiang, Y.; Ma, K.; Mahamadu, A.-M.; Florez-Perez, L.; Zhu, K.; Wu, Y. Embodied Carbon Determination in the Transportation Stage of Prefabricated Constructions: A Micro-Level Model Using the Bin-Packing Algorithm and Modal Analysis Model. Energy Build. 2023, 279, 112640. [Google Scholar] [CrossRef]
- Bai, L.; Xie, Q.; Lin, J.; Liu, S.; Wang, C.; Wang, L. Dynamic Selection of Risk Response Strategies with Resource Allocation for Construction Project Portfolios. Comput. Ind. Eng. 2024, 191, 110116. [Google Scholar] [CrossRef]
- Lin, S.-W.; Yu, V.F.; Lu, C.-C. A Simulated Annealing Heuristic for the Truck and Trailer Routing Problem with Time Windows. Expert Syst. Appl. 2011, 38, 15244–15252. [Google Scholar] [CrossRef]
- Bac, U.; Erdem, M. Optimization of Electric Vehicle Recharge Schedule and Routing Problem with Time Windows and Partial Recharge: A Comparative Study for an Urban Logistics Fleet. Sustain. Cities Soc. 2021, 70, 102883. [Google Scholar] [CrossRef]
- Regnier-Coudert, O.; McCall, J.; Ayodele, M.; Anderson, S. Truck and Trailer Scheduling in a Real World, Dynamic and Heterogeneous Context. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 389–408. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, R.; Qiu, B.; Chen, W.; Xie, X. Drop-and-Pull Container Drayage with Flexible Assignment of Work Break for Vehicle Drivers. Comput. Oper. Res. 2024, 162, 106475. [Google Scholar] [CrossRef]
- Ehmke, J.F.; Campbell, A.M.; Thomas, B.W. Vehicle Routing to Minimize Time-Dependent Emissions in Urban Areas. Eur. J. Oper. Res. 2016, 251, 478–494. [Google Scholar] [CrossRef]
- Toro, E.M.; Franco, J.F.; Echeverri, M.G.; Guimarães, F.G. A Multi-Objective Model for the Green Capacitated Location-Routing Problem Considering Environmental Impact. Comput. Ind. Eng. 2017, 110, 114–125. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, B.; Hao, Y.; Chen, S.; Wen, Y.; Yang, Z. Quantification of CO2 Emissions in Transportation: An Empirical Analysis by Modal Shift from Road to Waterway Transport in Zhejiang, China. Transp. Policy 2024, 145, 177–186. [Google Scholar] [CrossRef]
- Wang, D.; Moon, I.; Zhang, R. Multi-Trip Multi-Trailer Drop-and-Pull Container Drayage Problem. IEEE Trans. Intell. Transport. Syst. 2022, 23, 19088–19104. [Google Scholar] [CrossRef]
- Li, H.; Lv, T.; Li, Y. The Tractor and Semitrailer Routing Problem with Many-to-Many Demand Considering Carbon Dioxide Emissions. Transp. Res. Part D Transp. Environ. 2015, 34, 68–82. [Google Scholar] [CrossRef]
- Cheng, C.; Qi, M.; Wang, X.; Zhang, Y. Multi-Period Inventory Routing Problem under Carbon Emission Regulations. Int. J. Prod. Econ. 2016, 182, 263–275. [Google Scholar] [CrossRef]
- Accorsi, L.; Vigo, D. A Hybrid Metaheuristic for Single Truck and Trailer Routing Problems. Transport. Sci. 2020, 54, 1351–1371. [Google Scholar] [CrossRef]
- Chao, I.-M. A Tabu Search Method for the Truck and Trailer Routing Problem. Comput. Oper. Res. 2002, 29, 33–51. [Google Scholar]
- Tan, K.C.; Chew, Y.H.; Lee, L.H. A Hybrid Multi-Objective Evolutionary Algorithm for Solving Truck and Trailer Vehicle Routing Problems. Eur. J. Oper. Res. 2006, 172, 855–885. [Google Scholar] [CrossRef]
- Niu, B.; Xie, T.; Tan, L.; Bi, Y.; Wang, Z. Swarm Intelligence Algorithms for Yard Truck Scheduling and Storage Allocation Problems. Neurocomputing 2016, 188, 284–293. [Google Scholar] [CrossRef]
- Li, H.; Jian, X.; Chang, X.; Lu, Y. The Generalized Rollon-Rolloff Vehicle Routing Problem and Savings-Based Algorithm. Transp. Res. Part B Methodol. 2018, 113, 1–23. [Google Scholar] [CrossRef]
- Bartolini, E.; Schneider, M. A Two-Commodity Flow Formulation for the Capacitated Truck-and-Trailer Routing Problem. Discret. Appl. Math. 2020, 275, 3–18. [Google Scholar] [CrossRef]
- Davila-Pena, L.; Penas, D.R.; Casas-Méndez, B. A New Two-phase Heuristic for a Problem of Food Distribution with Compartmentalized Trucks and Trailers. Int. Tran. Oper. Res. 2023, 30, 1031–1064. [Google Scholar] [CrossRef]
- Semet, F.; Taillard, E. Solving Real-Life Vehicle Routing Problems Efficiently Using Tabu Search. Ann. Oper. Res. 1993, 41, 469–488. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Cheng, B.; Zhou, M. Optimal Method for Allocation of Tractors and Trailers in Daily Dispatches of Road Drops and Pull Transport. J. Adv. Transp. 2022, 2022, 3017196. [Google Scholar] [CrossRef]
- Wu, W.; Li, Y. The Multi-Compartment Truck and Trailer Petrol Station Replenishment Problem with Domino Hazard Risks. Transp. Res. Part B: Methodol. 2024, 190, 103078. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Wang, C.-N.; Fu, H.-P.; Dang, T.-T. Joint Scheduling of Yard Crane, Yard Truck, and Quay Crane for Container Terminal Considering Vessel Stowage Plan: An Integrated Simulation-Based Optimization Approach. Mathematics 2021, 9, 2236. [Google Scholar] [CrossRef]
- Wang, W.F.; Yun, W.Y. Scheduling for Inland Container Truck and Train Transportation. Int. J. Prod. Econ. 2013, 143, 349–356. [Google Scholar] [CrossRef]
- Villegas, J.G.; Prins, C.; Prodhon, C.; Medaglia, A.L.; Velasco, N. A Matheuristic for the Truck and Trailer Routing Problem. Eur. J. Oper. Res. 2013, 230, 231–244. [Google Scholar] [CrossRef]
- Gerdessen, J.C. Vehicle Routing Problem with Trailers. Eur. J. Oper. Res. 1996, 93, 135–147. [Google Scholar] [CrossRef]
- Hoff, A.; Løkketangen, A. A Tabu Search Approach for Milk Collection in Western Norway Using Trucks and Trailers. In Proceedings of the 6th Triennial Symposium on Transportation Analysis, Phuket Island, Thailand, 11–15 June 2007. [Google Scholar]
- Lin, S.-W.; Yu, V.F.; Chou, S.-Y. A Note on the Truck and Trailer Routing Problem. Expert Syst. Appl. 2010, 37, 899–903. [Google Scholar] [CrossRef]
- Drexl, M. Branch-and-Price and Heuristic Column Generation for the Generalized Truck-and-Trailer Routing Problem. Rev. Métodos Cuantitativos Para Econ. Empresa 2011, 12, 5–38. [Google Scholar]
- Belenguer, J.M.; Benavent, E.; Martínez, A.; Prins, C.; Prodhon, C.; Villegas, J.G. A Branch-and-Cut Algorithm for the Single Truck and Trailer Routing Problem with Satellite Depots. Transport. Sci. 2016, 50, 735–749. [Google Scholar] [CrossRef]
- Parragh, S.N.; Cordeau, J.-F. Branch-and-Price and Adaptive Large Neighborhood Search for the Truck and Trailer Routing Problem with Time Windows. Comput. Oper. Res. 2017, 83, 28–44. [Google Scholar] [CrossRef]
- Rothenbächer, A.-K.; Drexl, M.; Irnich, S. Branch-and-Price-and-Cut for the Truck-and-Trailer Routing Problem with Time Windows. Transport. Sci. 2018, 52, 1174–1190. [Google Scholar] [CrossRef]
- Teng, Y.; Li, K.; Pan, W.; Ng, T. Reducing Building Life Cycle Carbon Emissions through Prefabrication: Evidence from and Gaps in Empirical Studies. Build. Environ. 2018, 132, 125–136. [Google Scholar] [CrossRef]
- Teng, Y.; Pan, W. Systematic Embodied Carbon Assessment and Reduction of Prefabricated High-Rise Public Residential Buildings in Hong Kong. J. Clean. Prod. 2019, 238, 117791. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, L.; Zhang, H.; Qian, Y.; Xiang, Y.; Luo, Z.; Wang, Z. Carbon Emission Analysis of Precast Concrete Building Construction: A Study on Component Transportation Phase Using Artificial Neural Network. Energy Build. 2023, 301, 113708. [Google Scholar] [CrossRef]
- Ehsani, M.; Ahmadi, A.; Fadai, D. Modeling of Vehicle Fuel Consumption and Carbon Dioxide Emission in Road Transport. Renew. Sustain. Energy Rev. 2016, 53, 1638–1648. [Google Scholar] [CrossRef]
- Santos, G. Road Transport and CO2 Emissions: What Are the Challenges? Transp. Policy 2017, 59, 71–74. [Google Scholar] [CrossRef]
- Turkensteen, M. The Accuracy of Carbon Emission and Fuel Consumption Computations in Green Vehicle Routing. Eur. J. Oper. Res. 2017, 262, 647–659. [Google Scholar] [CrossRef]
- Rauniyar, A.; Nath, R.; Muhuri, P.K. Multi-Factorial Evolutionary Algorithm Based Novel Solution Approach for Multi-Objective Pollution-Routing Problem. Comput. Ind. Eng. 2019, 130, 757–771. [Google Scholar] [CrossRef]
- Shi, Y.; Lin, Y.; Wang, S.; Wen, H.; Lim, M.K.; Li, Y. A Simultaneous Facility Location and Vehicle Routing Problem with Recyclable Express Packaging Consideration for Sustainable City Logistics. Sustain. Cities Soc. 2023, 98, 104857. [Google Scholar] [CrossRef]
- Baños, R.; Ortega, J.; Gil, C.; Fernández, A.; De Toro, F. A Simulated Annealing-Based Parallel Multi-Objective Approach to Vehicle Routing Problems with Time Windows. Expert Syst. Appl. 2013, 40, 1696–1707. [Google Scholar] [CrossRef]
- Asghari, M.; Al-e-hashem, S.M.J.M. Green Vehicle Routing Problem: A State-of-the-Art Review. Int. J. Prod. Econ. 2021, 231, 107899. [Google Scholar] [CrossRef]
- Wu, Z.; Lou, P.; Hu, J.; Zeng, Y.; Fan, C. An Adaptive Large Neighborhood Search for a Green Vehicle Routing Problem with Depot Sharing. Mathematics 2025, 13, 214. [Google Scholar] [CrossRef]
- Luo, L.; Jin, X.; Shen, G.Q.; Wang, Y.; Liang, X.; Li, X.; Li, C.Z. Supply Chain Management for Prefabricated Building Projects in Hong Kong. J. Manage. Eng. 2020, 36, 5020001. [Google Scholar] [CrossRef]
- Godbole, S.; Lam, N.; Mafas, M.; Fernando, S.; Gad, E.; Hashemi, J. Dynamic Loading on a Prefabricated Modular Unit of a Building during Road Transportation. J. Build. Eng. 2018, 18, 260–269. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, L. Dynamic Transportation Planning for Prefabricated Component Supply Chain. Eng. Constr. Archit. Manage. 2020, 27, 2553–2576. [Google Scholar] [CrossRef]
- Koskosidis, Y.A.; Powell, W.B.; Solomon, M.M. An Optimization-Based Heuristic for Vehicle Routing and Scheduling with Soft Time Window Constraints. Transp. Sci. 1992, 26, 69–85. [Google Scholar] [CrossRef]
- Dan, Y.; Liu, G. Integrated Scheduling Optimization of Production and Transportation for Precast Component with Delivery Time Window. Eng. Constr. Archit. Manag. 2024, 31, 3335–3355. [Google Scholar] [CrossRef]
- Liu, L.; He, A.; Tian, T.; Lee, L.S.; Seow, H.-V. Bi-Objective Mixed Integer Nonlinear Programming Model for Low Carbon Location-Inventory-Routing Problem with Time Windows and Customer Satisfaction. Mathematics 2024, 12, 2367. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Yang, T.; Chen, Z. Optimized Transportation Scheduling for Precast Concrete Components Considering Heterogeneous Vehicle-Size Matching. Adv. Eng. Inf. 2024, 62, 102658. [Google Scholar] [CrossRef]
- Tavares, V.; Gregory, J.; Kirchain, R.; Freire, F. What Is the Potential for Prefabricated Buildings to Decrease Costs and Contribute to Meeting EU Environmental Targets? Build. Environ. 2021, 206, 108382. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Hou, K.; Yao, G. Carbon Emissions Factor Evaluation for Assembled Building during Prefabricated Component Transportation Phase. Energy Explor. Exploit. 2021, 39, 385–408. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L. Transition towards Carbon Neutrality: Forecasting Hong Kong’s Buildings Carbon Footprint by 2050 Using a Machine Learning Approach. Sustain. Prod. Consum. 2023, 35, 633–642. [Google Scholar] [CrossRef]
- Han, Y.; Yan, X.; Piroozfar, P. An Overall Review of Research on Prefabricated Construction Supply Chain Management. ECAM 2023, 30, 5160–5195. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A General Heuristic for Vehicle Routing Problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Zachariadis, E.E.; Tarantilis, C.D.; Kiranoudis, C.T. A Hybrid Metaheuristic Algorithm for the Vehicle Routing Problem with Simultaneous Delivery and Pick-up Service. Expert Syst. Appl. 2009, 36, 1070–1081. [Google Scholar] [CrossRef]
- Andelmin, J.; Bartolini, E. An Exact Algorithm for the Green Vehicle Routing Problem. Transport. Sci. 2017, 51, 1288–1303. [Google Scholar] [CrossRef]
- You, G. Sustainable Vehicle Routing Problem on Real-Time Roads: The Restrictive Inheritance-Based Heuristic Algorithm. Sustain. Cities Soc. 2022, 79, 103682. [Google Scholar] [CrossRef]
- Lin, S.-W.; Yu, V.F.; Chou, S.-Y. Solving the Truck and Trailer Routing Problem Based on a Simulated Annealing Heuristic. Comput. Oper. Res. 2009, 36, 1683–1692. [Google Scholar] [CrossRef]
- Derigs, U.; Pullmann, M.; Vogel, U. Truck and Trailer Routing—Problems, Heuristics and Computational Experience. Comput. Oper. Res. 2013, 40, 536–546. [Google Scholar] [CrossRef]
- Baker, B.M.; Ayechew, M.A. A Genetic Algorithm for the Vehicle Routing Problem. Comput. Oper. Res. 2003, 30, 787–800. [Google Scholar] [CrossRef]
- Yu, V.F.; Redi, A.A.N.P.; Hidayat, Y.A.; Wibowo, O.J. A Simulated Annealing Heuristic for the Hybrid Vehicle Routing Problem. Appl. Soft Comput. 2017, 53, 119–132. [Google Scholar] [CrossRef]
- MirHassani, S.A.; Abolghasemi, N. A Particle Swarm Optimization Algorithm for Open Vehicle Routing Problem. Expert Syst. Appl. 2011, 38, 11547–11551. [Google Scholar] [CrossRef]
- Sluijk, N.; Florio, A.M.; Kinable, J.; Dellaert, N.; Van Woensel, T. Two-Echelon Vehicle Routing Problems: A Literature Review. Eur. J. Oper. Res. 2023, 304, 865–886. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Liu, B. Low-Carbon Routing for Cold-Chain Logistics Considering the Time-Dependent Effects of Traffic Congestion. Transp. Res. Part D Transp. Environ. 2022, 113, 103502. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Zhang, S.; Lee, C.K.M.; Choy, K.L.; Ho, W.; Ip, W.H. Design and Development of a Hybrid Artificial Bee Colony Algorithm for the Environmental Vehicle Routing Problem. Transp. Res. Part D Transp. Environ. 2014, 31, 85–99. [Google Scholar] [CrossRef]
- Zhou, M.; Jin, H.; Wang, W. A Review of Vehicle Fuel Consumption Models to Evaluate Eco-Driving and Eco-Routing. Transp. Res. Part D Transp. Environ. 2016, 49, 203–218. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Z.; Zhang, D.; Leung, S.C.H. A Simulated Annealing Algorithm for the Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints. Eur. J. Oper. Res. 2018, 265, 843–859. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Lin, Y.; Bian, Z.; Liu, X. Developing a Dynamic Neighborhood Structure for an Adaptive Hybrid Simulated Annealing—Tabu Search Algorithm to Solve the Symmetrical Traveling Salesman Problem. Appl. Soft Comput. 2016, 49, 937–952. [Google Scholar] [CrossRef]
- Küçükoğlu, İ.; Dewil, R.; Cattrysse, D. Hybrid Simulated Annealing and Tabu Search Method for the Electric Travelling Salesman Problem with Time Windows and Mixed Charging Rates. Expert Syst. Appl. 2019, 134, 279–303. [Google Scholar] [CrossRef]


| Reference | Solution Algorithm | Constraints | Carbon | ||
|---|---|---|---|---|---|
| C | T | O | |||
| Chao [15] | Tabu search algorithm | ✔ | |||
| Tan et al. [16] | Evolutionary algorithm | ✔ | |||
| Lin et al. [4] | Simulated annealing algorithm | ✔ | |||
| Niu et al. [17] | Particle swarm optimization algorithm | ✔ | |||
| Regnier-Coudert et al. [6] | Greedy algorithm | ✔ | |||
| Li et al. [18] | Benders decomposition algorithm | ✔ | ✔ | ||
| Bartolini and Schneider [19] | Branch-and-cut algorithm | ✔ | |||
| Wang et al. [11] | Adaptive large neighborhood search algorithm | ✔ | ✔ | ||
| Davila-Pena et al. [20] | Clarke–Wright algorithm | ✔ | |||
| Current paper | Tabu search and simulated annealing algorithm | ✔ | ✔ | ✔ | |
| Notations | Definitions |
|---|---|
| Decision Variables | |
| ) (1 if used, 0 otherwise) | |
| ) (1 if used, 0 otherwise) | |
| Binary variable, indicating whether truck k is used (1 if used, 0 otherwise) | |
| Integer variable, representing the number of deliveries made to node j | |
| Continuous decision variable, representing the transported load on arc (i,j) in truck k | |
| Parameters | |
| Departure costs for the driver | |
| Wages paid to the driver | |
| Driver’s reward for the number of successful deliveries | |
| Fuel consumption rate per unit distance when an empty truck is hauling an empty trailer (liters/km) | |
| Fuel consumption rate per unit distance of an empty truck running alone (liters/km) | |
| Fuel consumption per unit distance of full load complete vehicles (truck + trailer) (liters/km) | |
| Fuel consumption per unit distance of full load complete trucks without trailers (liters/km) | |
| Effective fuel consumption rate of vehicles on arc (i,j) | |
| Rated load capacity of a truck without a trailer (tons) | |
| Rated load capacity of a vehicle (truck + trailer) (tons) | |
| Unit fuel consumption costs (yuan/liter) | |
| Unit carbon emissions costs (yuan/kg) | |
| Carbon emissions produced per unit of fuel consumed | |
| Unit penalty costs for delays in the delivery | |
| The time for truck k arriving at the construction site s | |
| Demand at node i |
| No. | Coordinate (X, Y) | Demand | Earliest Time | Latest Time | Customer Type |
|---|---|---|---|---|---|
| 0 | 35, 54 | - | - | - | - |
| 1 | 45, 68 | 10 | 912 | 967 | 1 |
| 2 | 45, 70 | 30 | 825 | 870 | 1 |
| 3 | 42, 66 | 10 | 65 | 146 | 1 |
| 4 | 42, 68 | 10 | 727 | 782 | 1 |
| 5 | 42, 65 | 10 | 15 | 67 | 1 |
| 6 | 40, 69 | 20 | 621 | 702 | 0 |
| 7 | 40, 66 | 20 | 170 | 225 | 1 |
| 8 | 38, 68 | 20 | 255 | 324 | 0 |
| 9 | 38, 70 | 10 | 534 | 605 | 0 |
| 10 | 35, 66 | 10 | 357 | 410 | 0 |
| 11 | 35, 69 | 10 | 448 | 505 | 0 |
| 12 | 30, 70 | 20 | 652 | 721 | 0 |
| 13 | 27, 60 | 30 | 30 | 92 | 0 |
| 14 | 27, 70 | 10 | 567 | 620 | 0 |
| 15 | 25, 65 | 40 | 384 | 429 | 0 |
| 16 | 25, 70 | 40 | 475 | 528 | 1 |
| 17 | 23, 62 | 20 | 99 | 148 | 0 |
| 18 | 20, 60 | 20 | 179 | 254 | 1 |
| 19 | 20, 65 | 10 | 278 | 345 | 1 |
| 20 | 30, 50 | 10 | 10 | 73 | 0 |
| 21 | 30, 52 | 20 | 914 | 965 | 0 |
| 22 | 28, 52 | 20 | 812 | 883 | 0 |
| 23 | 28, 55 | 10 | 732 | 777 | 0 |
| 24 | 25, 50 | 10 | 65 | 144 | 0 |
| 25 | 25, 52 | 40 | 169 | 224 | 0 |
| Type | Problems | Characteristic |
|---|---|---|
| R | R1 | Customers are disperses with narrow time windows, limited vehicle capacities, and short route durations. |
| R2 | Customers are disperses with wider time windows, larger vehicle capacities, and longer route durations. | |
| C | C1 | Customers are clustered with narrow time windows, limited vehicle capacities, and short route durations. |
| C2 | Customers are clustered with wider time windows, larger vehicle capacities, and longer route durations. | |
| RC | RC1 | A mix of dispersed and clustered customers, characterized by narrow time windows, limited vehicle capacities, and short route durations. |
| RC2 | A mix of dispersed and clustered customers, characterized by narrow time windows, limited vehicle capacities, and short route durations. |
| Total Costs | Carbon Emissions Costs | Solution Time (Seconds) | |
|---|---|---|---|
| Initial solution | 63,311.144 | 9102.299 | 0.365 |
| CPLEX | 52,566.208 | 7120.329 | 0.498 |
| SA | 62,826.109 | 9002.213 | 0.330 |
| TS | 60,936.506 | 8612.295 | 0.366 |
| DASA-TS | 52,393.315 | 6909.462 | 0.306 |
| Original Problem | CPLEX | DASA-TS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case | VCs | TCs | Total Costs | Total Carbon Emissions Costs | Solution Time (Seconds) | Total Costs | Total Carbon Emissions Costs | Solution Time (Seconds) | ||
| Test 1 (25) | 1 | RC101 | 10 | 15 | 165,967.8361 | 27,020.0414 | 0.004 | 165,082.3034 | 26,769.6817 | 0.290 |
| 2 | RC101 | 15 | 10 | 166,253.2252 | 26,909.2786 | 0.004 | 164,213.5527 | 27,015.2373 | 0.274 | |
| 3 | RC201 | 10 | 15 | 167,080.2769 | 27,265.3359 | 0.005 | 166,784.0610 | 27,240.8108 | 0.234 | |
| 4 | RC201 | 15 | 10 | 168,250.7589 | 26,754.0413 | 0.005 | 168,413.3385 | 26,267.7567 | 0.213 | |
| Test 2 (50) | 5 | RC101 | 20 | 30 | 487,822.3078 | 92,160.1587 | 0.006 | 473,366.3021 | 91,477.1735 | 0.372 |
| 6 | RC101 | 20 | 30 | 484,050.9021 | 93,906.4925 | 0.680 | 479,588.2613 | 92,397.5703 | 0.413 | |
| 7 | RC201 | 20 | 30 | 474,065.1031 | 89,321.3705 | 0.705 | 473,366.3021 | 88,373.1735 | 0.376 | |
| 8 | RC201 | 37 | 13 | 498,091.0120 | 95,898.1453 | 0.604 | 497,410.7872 | 92,075.2418 | 0.432 | |
| Test 3 (100) | 9 | RC101 | 40 | 60 | 1,711,778.8260 | 321,391.4460 | 10.307 | 1,709,710.6087 | 318,306.7923 | 6.631 |
| 10 | RC101 | 60 | 40 | 2,431,076.3334 | 449,232.2015 | 8.135 | 2,289,416.4772 | 435,534.6520 | 6.583 | |
| 11 | RC201 | 40 | 60 | 1,785,390.2267 | 337,956.7135 | 12.307 | 1,751,653.6209 | 323,420.5884 | 7.598 | |
| 12 | RC201 | 60 | 40 | 2,200,800.9498 | 413,090.6721 | 9.110 | 2,061,096.9005 | 394,213.6461 | 8.309 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Du, Q.; Chen, Q.; Ye, Z.; Bai, L.; Li, Y. Low-Carbon Transport for Prefabricated Buildings: Optimizing Capacitated Truck–Trailer Routing Problem with Time Windows. Mathematics 2025, 13, 1210. https://doi.org/10.3390/math13071210
Zhou J, Du Q, Chen Q, Ye Z, Bai L, Li Y. Low-Carbon Transport for Prefabricated Buildings: Optimizing Capacitated Truck–Trailer Routing Problem with Time Windows. Mathematics. 2025; 13(7):1210. https://doi.org/10.3390/math13071210
Chicago/Turabian StyleZhou, Jiajie, Qiang Du, Qian Chen, Zhongnan Ye, Libiao Bai, and Yi Li. 2025. "Low-Carbon Transport for Prefabricated Buildings: Optimizing Capacitated Truck–Trailer Routing Problem with Time Windows" Mathematics 13, no. 7: 1210. https://doi.org/10.3390/math13071210
APA StyleZhou, J., Du, Q., Chen, Q., Ye, Z., Bai, L., & Li, Y. (2025). Low-Carbon Transport for Prefabricated Buildings: Optimizing Capacitated Truck–Trailer Routing Problem with Time Windows. Mathematics, 13(7), 1210. https://doi.org/10.3390/math13071210






