Low-Complexity Relay Selection for Full-Duplex Random Relay Networks
Abstract
1. Introduction
2. System Model
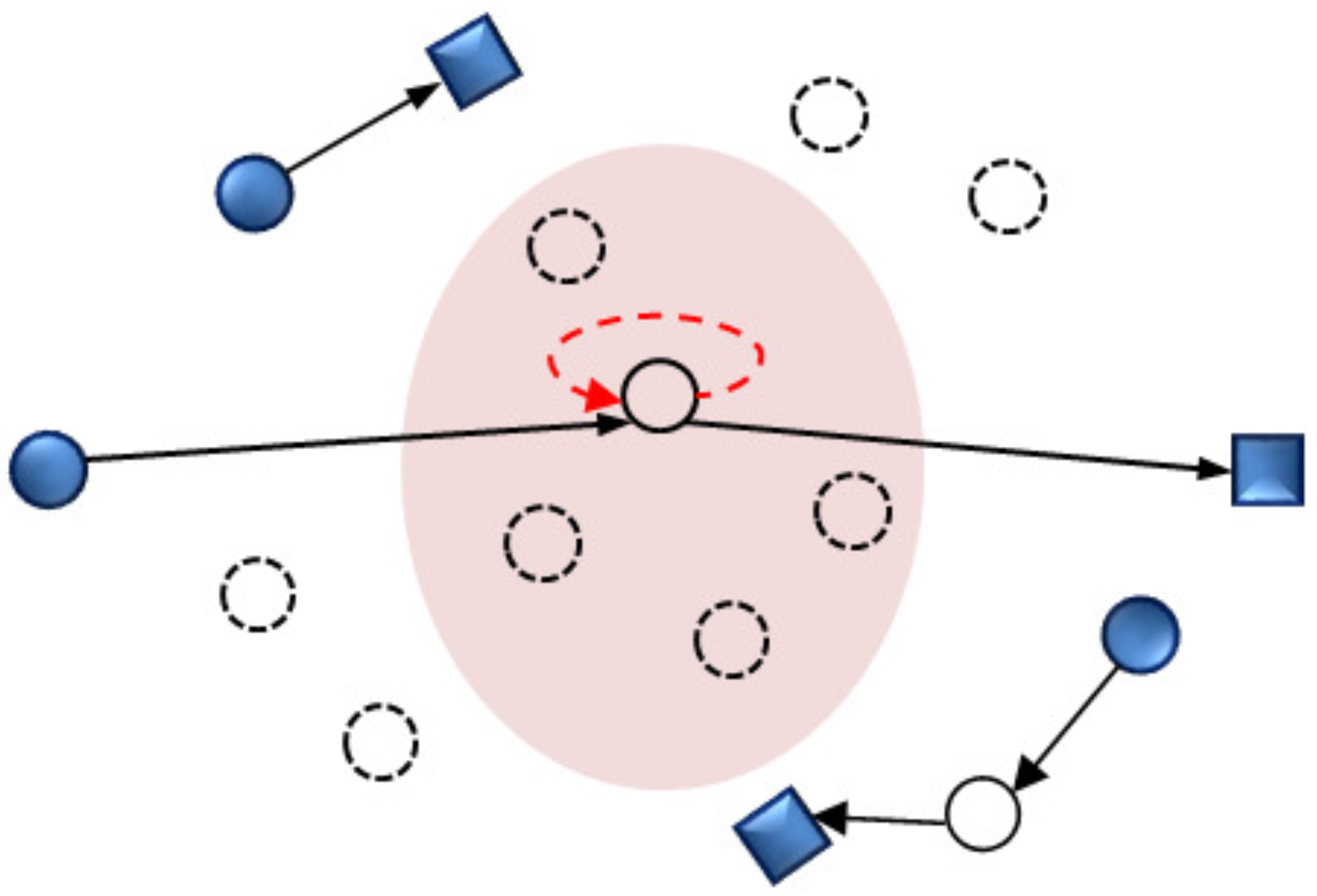
2.1. Description of FDRRN
2.2. Outage Probability of the FDRRN
3. Relay Selection Algorithms for the FDRRN
- Step 1: The transmitter and receiver determine the temporary number of candidate relay nodes, , that the system can accommodate for CSI feedback, considering the system resource constraints.
- Step 2: The transmitter and receiver compute the selection diversity gain for , . If exceeds a predefined threshold , the current number of candidate relay nodes is adopted, i.e., . Otherwise, the number of candidate relay nodes is reduced by one, i.e., , and the process repeats until the selection diversity gain satisfies the threshold condition. The detailed procedure for Step 2 is outlined below:
- Step 3: The J candidate relays are selected based on their proximity to the optimal relay location.
- Step 4: The transmitter and receiver acquire the CSI of the selected candidate relay nodes and finalize the relay selection using the max-min relay selection Algorithm 1.
| Algorithm 1 Determination of the number of candidate relay nodes |
|
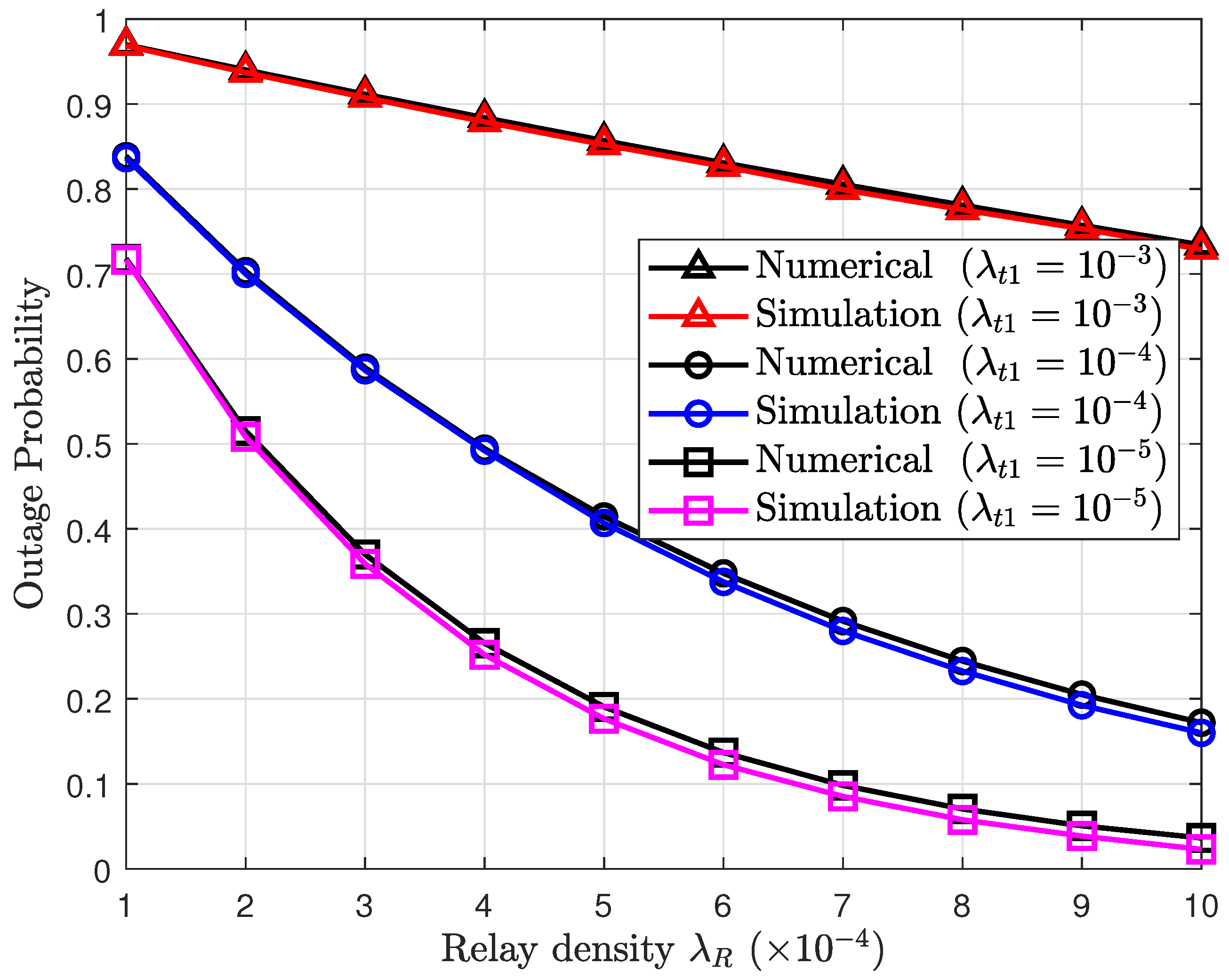
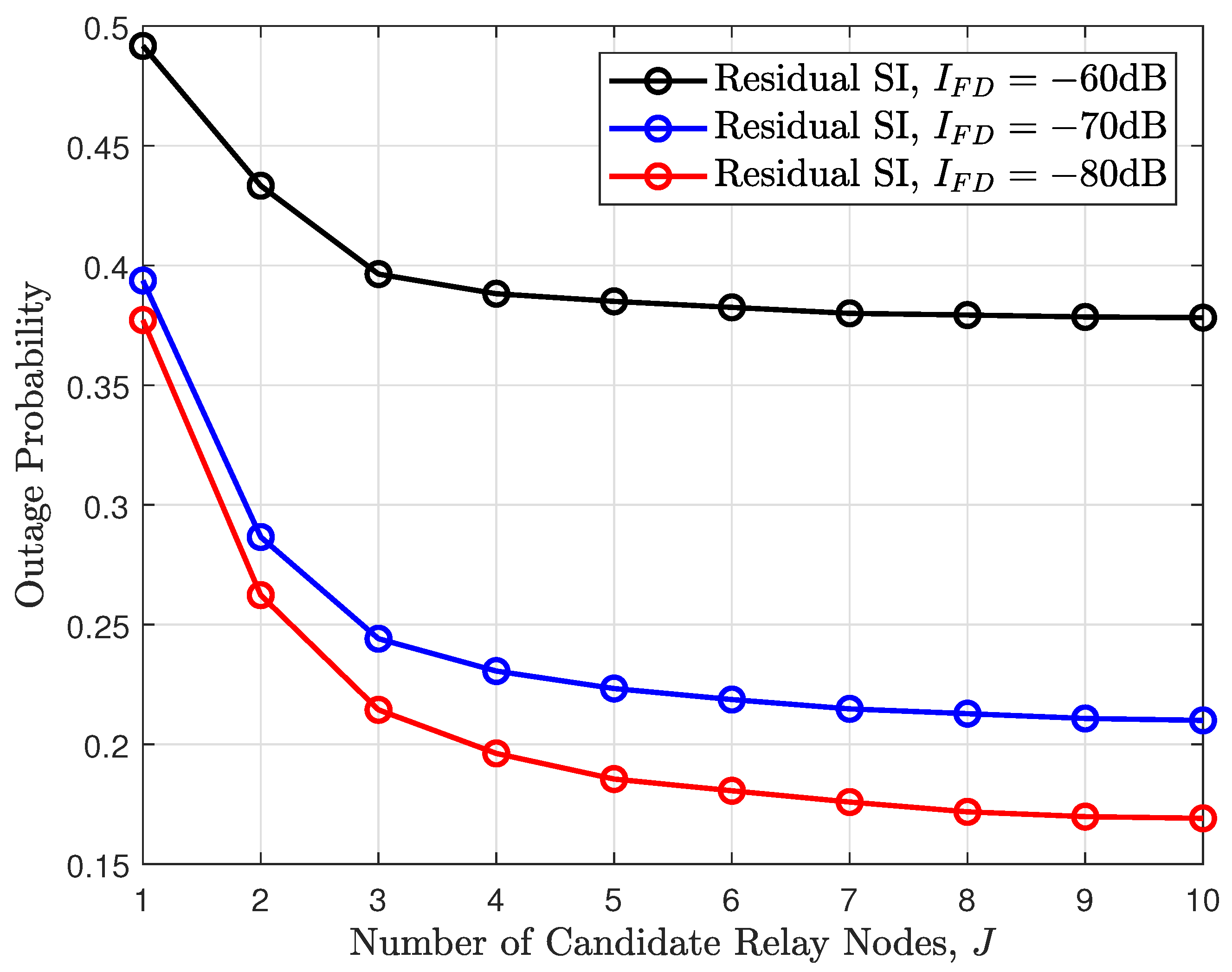
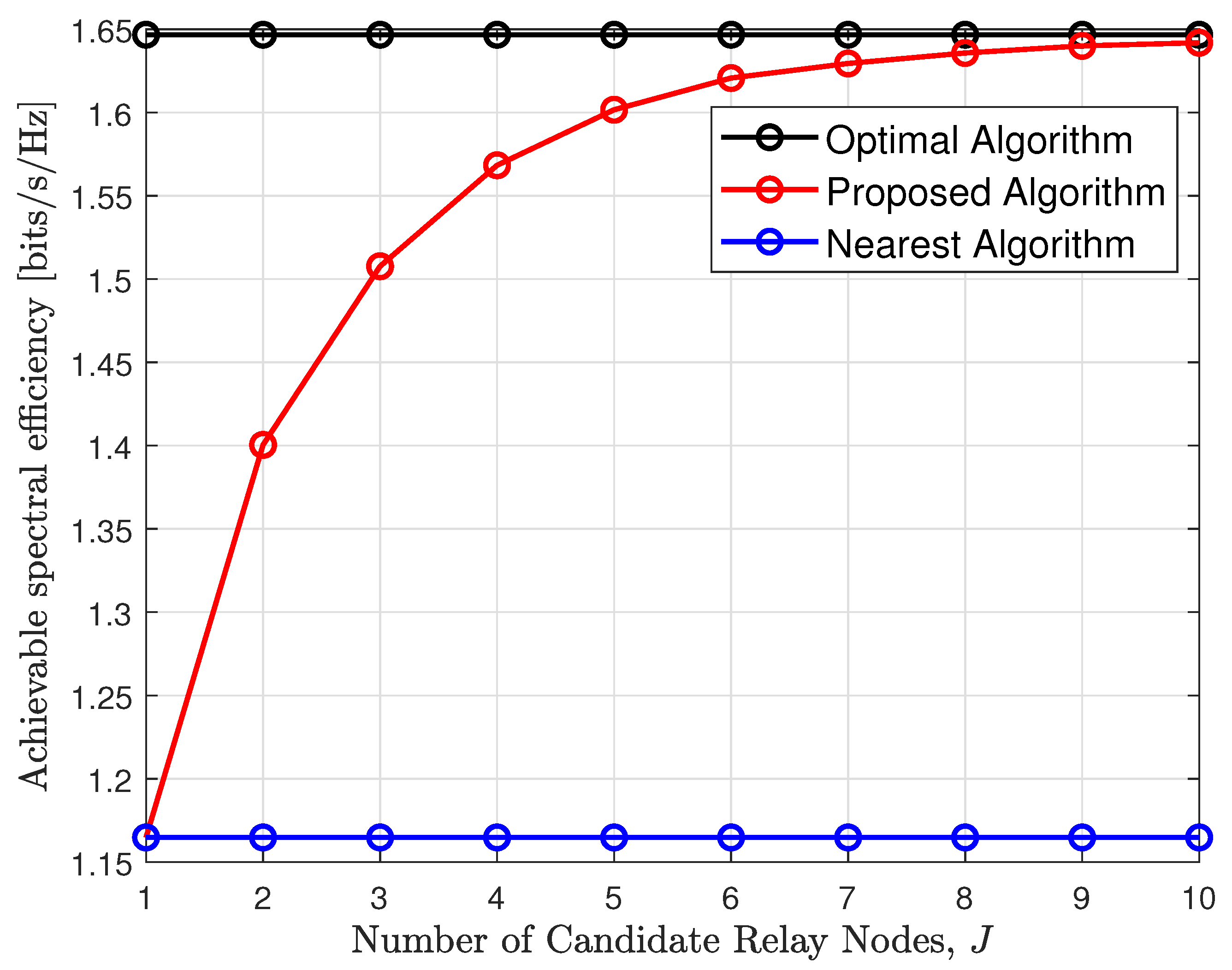
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Notation | Definition |
|---|---|
| Tx. power of each node | |
| Fading gain of the link between nodes x and y | |
| Distance between nodes x and y | |
| Distance of mth relay hop | |
| Residual SI | |
| SIR of mth relay hop | |
| Pathloss exponent | |
| Target SIR of the FDRRN | |
| PPP for interfering node of mth relay hop | |
| PPP for relay nodes | |
| Spatial density of interfering node of mth relay hop | |
| Spatial density of candidate relay nodes | |
| The outage probability of optimal relay seleciton | |
| The outage probability for a low-complexity scheme | |
| The lower bound of outage probability for low-complexity scheme | |
| Location of relay nodes | |
| Optimal relay location | |
| Relay located at a distance n from the optimal relay location |
References
- Kim, D.; Lee, H.; Hong, D. A survey of in-band full-duplex transmission: From the perspective of PHY and MAC layers. IEEE Commun. Surv. Tutor. 2015, 17, 2017–2046. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mobini, Z.; Galappaththige, D.; Tellambura, C. A comprehensive survey on full-duplex communication: Current solutions, future trends, and open issues. IEEE Commun. Surv. Tutor. 2023, 25, 2190–2244. [Google Scholar] [CrossRef]
- Kim, Y.; Moon, H.J.; Yoo, H.; Kim, B.; Wong, K.K.; Chae, C.B. A State-of-the-art Survey on Full-duplex Network Design. Proc. IEEE 2024, 112, 463–486. [Google Scholar] [CrossRef]
- Smida, B.; Wichman, R.; Kolodziej, K.E.; Suraweera, H.A.; Riihonen, T.; Sabharwal, A. In-Band Full-Duplex: The Physical Layer. Proc. IEEE 2024, 112, 322–462. [Google Scholar] [CrossRef]
- Mori, S.; Mizutani, K.; Harada, H. A digital self-interference cancellation scheme for in-band full-duplex-applied 5G system and its software-defined radio implementation. IEEE Open J. Veh. Technol. 2023, 4, 444–456. [Google Scholar] [CrossRef]
- Le, A.T.; Huang, X.; Ding, C.; Zhang, H.; Guo, Y.J. An In-Band Full-Duplex Prototype With Joint Self-Interference Cancellation in Antenna, Analog, and Digital Domains. IEEE Trans. Microw. Theory Tech. 2024, 4, 5540–5549. [Google Scholar]
- Dong, Q.; Austin, A.C.; Sowerby, K.W. Augmentation of Self-Interference Cancellation for Full-Duplex using NARX Neural Networks. IEEE Wirel. Commun. Lett. 2023, 13, 810–813. [Google Scholar] [CrossRef]
- Fukushima, K.; Mori, S.; Mizutani, K.; Harada, H. Throughput enhancement of dynamic full-duplex cellular system by distributing base station reception function. IEEE Open J. Veh. Technol. 2022, 4, 114–126. [Google Scholar] [CrossRef]
- Choi, D.; Byun, G. Circular polarization conversion using dual frequency selective surfaces for full-duplex satellite communications. IEEE Access 2024, 12, 120219–120225. [Google Scholar] [CrossRef]
- Cho, W.; Chang, K.; Shin, W.; Kim, Y.; Ko, Y.J. OFDM-Based In-Band Full-Duplex ISAC Systems. IEEE Wirel. Commun. Lett. 2025, 14, 365–369. [Google Scholar] [CrossRef]
- Liu, G.; Yu, F.R.; Ji, H.; Leung, V.C.; Li, X. In-band full-duplex relaying: A survey, research issues and challenges. IEEE Commun. Surv. Tutor. 2015, 17, 500–524. [Google Scholar] [CrossRef]
- Shen, H.; He, Z.; Xu, W.; Gong, S.; Zhao, C. Is full-duplex relaying more energy efficient than half-duplex relaying? IEEE Wirel. Commun. Lett. 2019, 8, 841–844. [Google Scholar] [CrossRef]
- Shao, Y.; Gulliver, T.A. Transceiver Optimization for Multiuser Multiple-Input Multiple-Output Full-Duplex Amplify-and-Forward Relay Downlink Communications. Telecom 2024, 5, 216–227. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, D.; Wei, H.; Liu, B.; Zhao, Y.; Zhang, Y.; Liu, X. Joint Hybrid Beamforming Design for Millimeter Wave Amplify-and-Forward Relay Communication Systems. Appl. Sci. 2024, 14, 3713. [Google Scholar] [CrossRef]
- Shim, Y.; Shin, W.; Vaezi, M. Relay power control for in-band full-duplex decode-and-forward relay networks over static and time-varying channels. IEEE Syst. J. 2021, 16, 33–40. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, L.; Xue, Y. Distributed alamouti protocol for full-duplex decode-and-forward relaying networks. IEEE Commun. Lett. 2021, 26, 182–186. [Google Scholar] [CrossRef]
- Siddig, A.A.; Ibrahim, A.S.; Ismail, M.H. A low-delay hybrid half/full-duplex link selection scheme for cooperative relaying networks. IEEE Trans. Veh. Technol. 2022, 71, 11174–11188. [Google Scholar] [CrossRef]
- Ma, J.; Huang, C.; Li, Q. Energy efficiency of full-and half-duplex decode-and-forward relay channels. IEEE Internet Things J. 2022, 9, 9730–9748. [Google Scholar] [CrossRef]
- Behnad, A.; Wang, X. Distance statistics of the communication best neighbor in a Poisson field of nodes. IEEE Trans. Commun. 2015, 63, 997–1005. [Google Scholar] [CrossRef]
- Sadeghi, M.; Rabiei, A.M. A fair relay selection scheme for a DF cooperative network with spatially random relays. IEEE Trans. Veh. Technol. 2017, 66, 11098–11107. [Google Scholar] [CrossRef]
- Bang, J.; Lee, J.; Kim, S.; Hong, D. An efficient relay selection strategy for random cognitive relay networks. IEEE Trans. Wirel. Commun. 2014, 14, 1555–1566. [Google Scholar] [CrossRef]
- Bang, J.; Kim, T. Location-Based Relay Selection in Full-Duplex Random Relay Networks. Appl. Sci. 2024, 14, 10626. [Google Scholar] [CrossRef]
- Smida, B.; Sabharwal, A.; Fodor, G.; Alexandropoulos, G.C.; Suraweera, H.A.; Chae, C.B. Full-duplex wireless for 6G: Progress brings new opportunities and challenges. IEEE J. Sel. Areas Commun. 2023, 14, 2729–2750. [Google Scholar] [CrossRef]
- Win, M.Z.; Pinto, P.C.; Shepp, L.A. A mathematical theory of network interference and its applications. Proc. IEEE 2009, 97, 205–230. [Google Scholar] [CrossRef]
- Haenggi, M.; Ganti, R.K. Interference in large wireless networks. Found. Trends® Netw. 2009, 3, 127–248. [Google Scholar] [CrossRef]
- Chiu, S.N.; Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lee, J.; Quek, T.Q. Hybrid full-/half-duplex system analysis in heterogeneous wireless networks. IEEE Trans. Wirel. Commun. 2015, 14, 2883–2895. [Google Scholar] [CrossRef]
- Baccelli, F.; Blaszczyszyn, B.; Muhlethaler, P. An Aloha protocol for multihop mobile wireless networks. IEEE Trans. Inf. Theory 2006, 52, 421–436. [Google Scholar] [CrossRef]
- Kingman, J. Poisson Process; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Luo, S.; Teh, K.C. Buffer state based relay selection for buffer-aided cooperative relaying systems. IEEE Trans. Wirel. Commun. 2015, 14, 5430–5439. [Google Scholar] [CrossRef]
- Moltchanov, D. Distance distributions in random networks. Ad Hoc Netw. 2012, 10, 1146–1166. [Google Scholar] [CrossRef]
- Ju, M.; Kim, I.M.; Kim, D.I. Joint relay selection and relay ordering for DF-based cooperative relay networks. IEEE Trans. Commun. 2012, 60, 908–915. [Google Scholar] [CrossRef]


| Parameters | Values |
|---|---|
| Pathloss exponent, | 4 |
| Target SIR threshold, | 3 |
| Spatial density of interference, , | |
| Spatial density of relay, | |
| Cell radius | 300 m |
| Distance between source and destination | 10 m |
| Residual SI, | −110 dB |
| Tx. power, | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bang, J.; Kim, T. Low-Complexity Relay Selection for Full-Duplex Random Relay Networks. Mathematics 2025, 13, 971. https://doi.org/10.3390/math13060971
Bang J, Kim T. Low-Complexity Relay Selection for Full-Duplex Random Relay Networks. Mathematics. 2025; 13(6):971. https://doi.org/10.3390/math13060971
Chicago/Turabian StyleBang, Jonghyun, and Taehyoung Kim. 2025. "Low-Complexity Relay Selection for Full-Duplex Random Relay Networks" Mathematics 13, no. 6: 971. https://doi.org/10.3390/math13060971
APA StyleBang, J., & Kim, T. (2025). Low-Complexity Relay Selection for Full-Duplex Random Relay Networks. Mathematics, 13(6), 971. https://doi.org/10.3390/math13060971





