Applied Mathematical Techniques for the Stability and Solution of Hybrid Fractional Differential Systems
Abstract
1. Introduction
2. Preliminaries
3. Main Results
- Assume that the functions are bounded and continuous, meaning there exist positive constant and such that
- Assume that and are continuous, and there exist positive constants and for such that
- ∃ positive constant and (for i = 0,1,2) such that
- Let be a bounded set, and such that
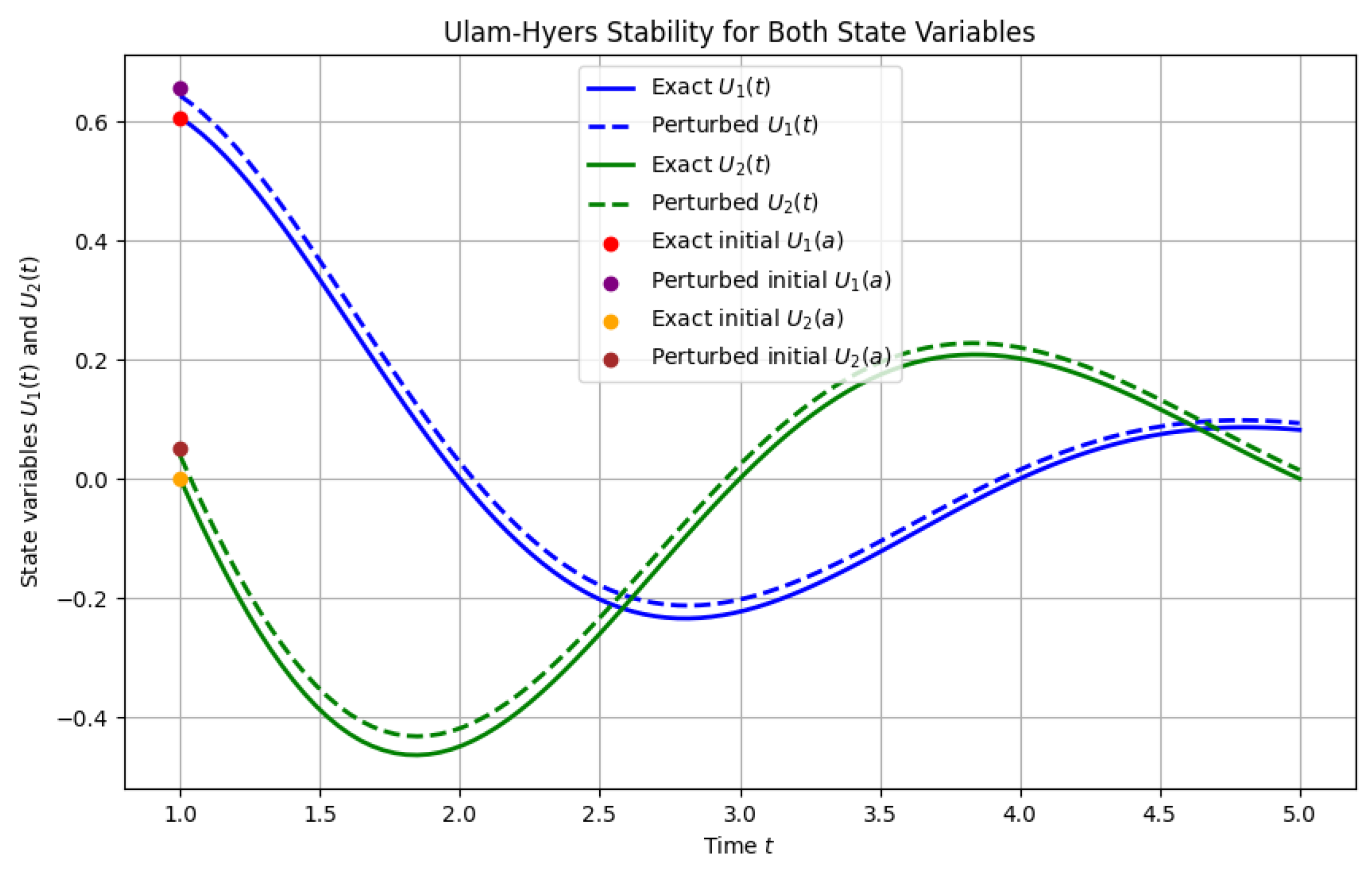
4. Stability Analysis
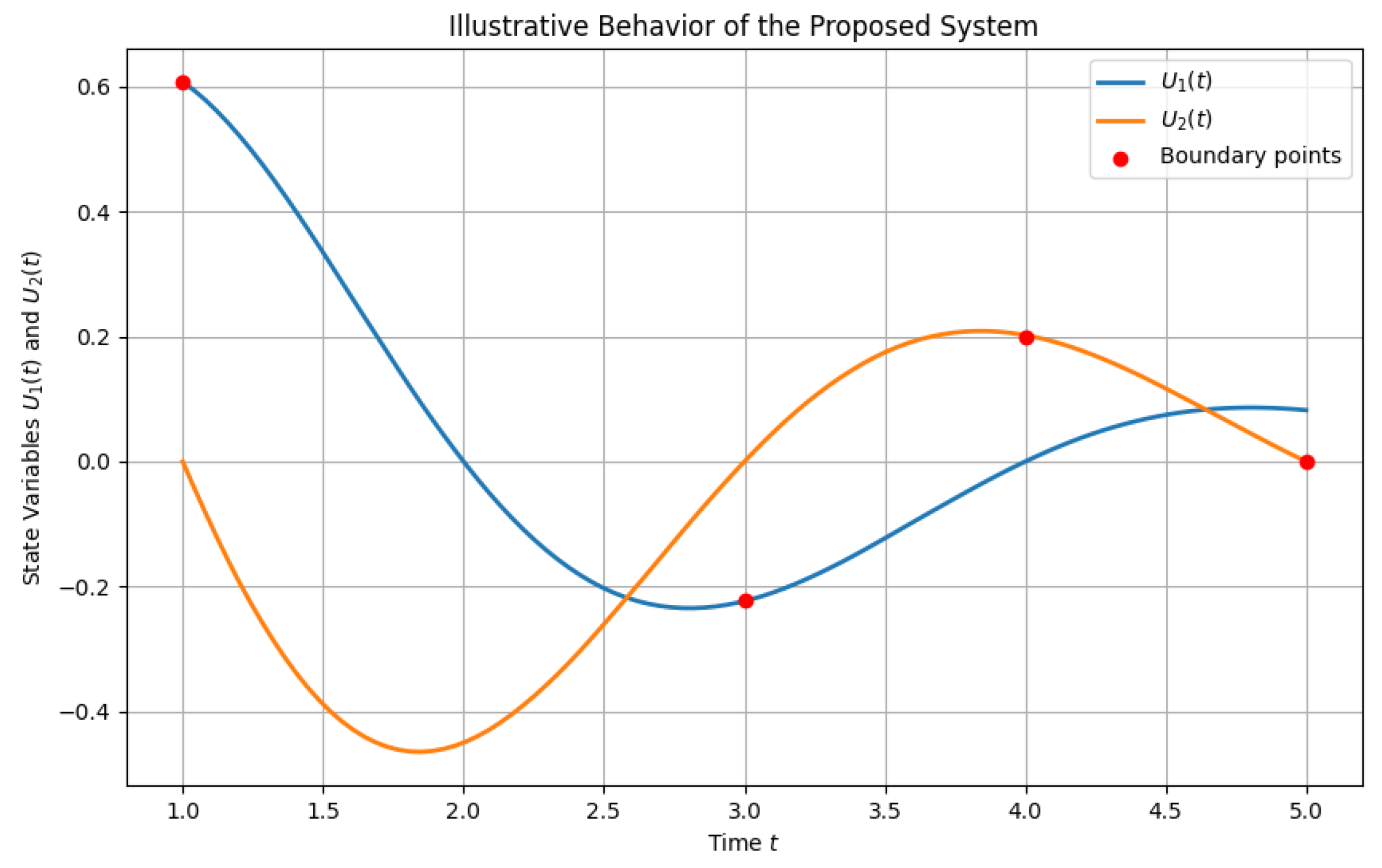
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Milici, C.; Drăgănescu, G.; Machado, J.T. Introduction to Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2018; Volume 25. [Google Scholar]
- Demirci, E.; Karakoç, F.; Kütahyalıoglu, A. Mittag-Leffler stability of neural networks with Caputo–Hadamard fractional derivative. Math. Methods Appl. Sci. 2024, 47, 10091–10100. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L. Properties of Hadamard fractional integral and its application. Fractal Fract. 2022, 6, 670. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; pp. 82–89. [Google Scholar]
- Debnath, P.; Srivastava, H.M.; Kumam, P.; Hazarika, B. Fixed Point Theory and Fractional Calculus: Recent Advances and Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 2012, 94. [Google Scholar] [CrossRef]
- Zafar, R.; Rehman, M.U.; Shams, M. On Caputo modification of Hadamard-type fractional derivative and fractional Taylor series. Adv. Differ. Equ. 2020, 2020, 219. [Google Scholar] [CrossRef]
- Balachandran, K.; Matar, M.; Annapoorani, N.; Prabu, D. Hadamard functional fractional integrals and derivatives and fractional differential equations. Filomat 2024, 38, 779–792. [Google Scholar] [CrossRef]
- Murugesan, M.; Muthaiah, S.; Alzabut, J.; Nandha Gopal, T. Existence and HU stability of a tripled system of sequential fractional differential equations with multipoint boundary conditions. Bound. Value Probl. 2023, 2023, 56. [Google Scholar] [CrossRef]
- Subramanian, M.; Manigandan, M.; Zada, A.; Gopal, T.N. Existence and Hyers–Ulam stability of solutions for nonlinear three fractional sequential differential equations with nonlocal boundary conditions. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 3071–3099. [Google Scholar] [CrossRef]
- Wang, J.; Li, X. A uniform method to Ulam–Hyers stability for some linear fractional equations. Mediterr. J. Math. 2016, 13, 625–635. [Google Scholar] [CrossRef]
- Zada, A.; Ali, W.; Farina, S. Hyers–Ulam stability of nonlinear differential equations with fractional integrable impulses. Math. Methods Appl. Sci. 2017, 40, 5502–5514. [Google Scholar] [CrossRef]
- Jakhar, J.; Sharma, S.; Jakhar, J.; Yousif, M.A.; Mohammed, P.O.; Chorfi, N.; Vivas-Cortez, M. Hyers–Ulam–Rassias Stability of Functional Equations with Integrals in B-Metric Frameworks. Symmetry 2025, 17, 168. [Google Scholar] [CrossRef]
- Rus, I.A. Ulam stabilities of ordinary differential equations in a Banach space. Carpathian J. Math. 2010, 26, 103–107. [Google Scholar]
- Khan, S.; Shah, K.; Debbouche, A.; Zeb, S.; Antonov, V. Solvability and Ulam-Hyers stability analysis for nonlinear piecewise fractional cancer dynamic systems. Phys. Scr. 2024, 99, 025225. [Google Scholar] [CrossRef]
- Subramanian, M.; Manigandan, M.; Gopal, T.N. Fractional differential equations involving Hadamard fractional derivatives with nonlocal multi-point boundary conditions. Discontin. Nonlinearity Complex. 2020, 9, 421–431. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. Representations of acting processes and memory effects: General fractional derivative and its application to theory of heat conduction with finite wave speeds. Appl. Math. Comput. 2019, 346, 531–544. [Google Scholar] [CrossRef]
- Vabishchevich, P.N. Numerical solution of the heat conduction problem with memory. Comput. Math. Appl. 2022, 118, 230–236. [Google Scholar] [CrossRef]
- Al Elaiw, A.; Awadalla, M.; Manigandan, M.; Abuasbeh, K. A novel implementation of Mönch’s fixed point theorem to a system of nonlinear Hadamard fractional differential equations. Fractal Fract. 2022, 6, 586. [Google Scholar] [CrossRef]
- Abuasbeh, K.; Awadalla, M.; Jneid, M. Nonlinear Hadamard fractional boundary value problems with different orders. Rocky Mountain J. Math. 2021, 51, 17–29. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Awadalla, M.; Abuassba, K. Hadamard and caputo-hadamard FDE’s with three point integral boundary conditions. Nonlinear Anal. Differ. Equ. 2017, 5, 271–282. [Google Scholar] [CrossRef]
- Agrawal, O. Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. Math. Theor. 2007, 40, 6287. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L. Existence of solutions for the initial value problem with hadamard fractional derivatives in locally convex spaces. Fractal Fract. 2024, 8, 191. [Google Scholar] [CrossRef]
- Almeida, R.; Torres, D.F. Necessary and sufficient conditions for the fractional calculus of variations with Caputo derivatives. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1490–1500. [Google Scholar] [CrossRef]
- Boutiara, A.; Guerbati, K.; Benbachir, M. Caputo Hadamard fractional differential equation with three-point boundary conditions in Banach spaces. Aims Math. 2019, 5, 259–272. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abazid, M.A.; Awadalla, M.; Manigandan, M.; Alahmadi, J. Applied Mathematical Techniques for the Stability and Solution of Hybrid Fractional Differential Systems. Mathematics 2025, 13, 941. https://doi.org/10.3390/math13060941
Abazid MA, Awadalla M, Manigandan M, Alahmadi J. Applied Mathematical Techniques for the Stability and Solution of Hybrid Fractional Differential Systems. Mathematics. 2025; 13(6):941. https://doi.org/10.3390/math13060941
Chicago/Turabian StyleAbazid, Mohammad Alakel, Muath Awadalla, Murugesan Manigandan, and Jihan Alahmadi. 2025. "Applied Mathematical Techniques for the Stability and Solution of Hybrid Fractional Differential Systems" Mathematics 13, no. 6: 941. https://doi.org/10.3390/math13060941
APA StyleAbazid, M. A., Awadalla, M., Manigandan, M., & Alahmadi, J. (2025). Applied Mathematical Techniques for the Stability and Solution of Hybrid Fractional Differential Systems. Mathematics, 13(6), 941. https://doi.org/10.3390/math13060941





