Abstract
In the container loading problem (CLP), the construction of packing patterns is driven by the maximization of the volume occupied, and comprises several constraints such as loading feasibility, weight balance, cargo stability, operational safety, material handling, and the prevention of cargo damage during container shipping. Previous works introduced dynamic stability indicators using simulation or statistical approaches. However, this firstly exponentially increases the computational burden, and secondly misrepresents the essential kinetic mechanical aspects. This paper presents a hybrid scheme to solve the CLP by embedding a mechanical model into a reactive GRASP algorithm, leading to two main novelties; namely, the substitution of the physics simulation engine to find the dynamic stability of the packing patterns, and a modified structure of the metaheuristic, guaranteeing specified minimum stability while achieving efficient packing patterns. The mechanical model dynamically analyzes the forces and accelerations acting on the cargo to predict loss of support, overturning, or critical velocity deltas that would damage it. At the same time, the reactive GRASP algorithm considers the dynamic stability indicators in the improvement steps. The stability indicators are obtained from the mechanical model, allowing the user to know the percentage of damaged boxes in a packing pattern. The effectiveness of the proposed approach is tested using a set of classical benchmark instances, obtaining adequately accurate solutions within a short computational time. The resulting scheme integrates real-world problem conditions and achieves dynamic stability solutions at an acceptable computational cost; it is programmed in C++ instead of relying on proprietary simulation tools.
MSC:
05B40
1. Introduction
Transportation, loading, and unloading of cargo are essential activities of the supply chain, as companies cannot operate without moving their raw materials or finished products [1]. Ensuring the product arrives undamaged is necessary for customer satisfaction, saving costs, and avoiding repeated work. The number of packages shipped in 2019 was 100 billion and is expected to reach 200 billion globally by 2025 [2]. As a consequence, in the specialized literature economic incentives have been a driving force behind the study of packaging problems where the issue of packing a set of small objects (e.g., boxes) into large objects (e.g., containers) needs to be solved. Consequently, there is a genuine interest in effectively using assets related to the transportation of goods to decrease costs while increasing customer satisfaction. Added to these interests, there is also the potential to reduce the environmental effects of logistics operations [3].
The above problem has been cataloged in the field of cutting and packing problems, such as the container loading problem, wherein the most basic version includes geometric constraints such as the fact that all boxes must be packed orthogonally to the container walls, all boxes must be completely contained within the container, and boxes must not overlap each other. However, these considerations are insufficient to deal with the logistical problems that companies face daily. Bischoff and Ratcliff [4] were the first to notice this and pointed out a set of constraints that would be applicable to the CLP. Later, Bortfeldt and Wäscher [5] took advantage of this set of conditions and developed a classification of these constraints, differentiating between container-related constraints, box-related constraints, cargo-related constraints, positioning constraints, and load-related constraints. Further, in [6] these constraints were grouped into two clusters named safety constraints and logistic constraints.
Safety constraints relate to the integrity of the cargo and the transport unit and the safety of personnel (most recently robots) during loading, handling, and transport operations; these constraints include weight, orientation, load-bearing, and stability constraints. Weight constraints are related to the upper limit that the container can support as well as cargo balance, which requires a uniform weight distribution of the load on the container floor. Orientation limitations determine the types of rotations that are allowed for the boxes and those that are not. The load-bearing restrictions limit the weight each box can support to avoid damage. There are two types of stability restrictions: static or vertical stability, which is ensured when the container does not move; and dynamic or horizontal stability, which must be shown when the cargo moves and is subject to acceleration, braking, and rotation [5,7,8].
Logistics constraints refer to operational decisions on how boxes are delivered to customers and involve delivery, multiple delivery, priority, and total shipment constraints. Delivery constraints require a set of boxes to be packed together or separately within a container. Multi-drop constraints consider the order in which boxes are delivered on a route to different customers, requiring boxes not to be rearranged along the route [9]. On the other hand, priority constraints assign degrees of importance to customer orders, which constrains those boxes or orders to be loaded first, before others of lower priority. Similarly, full-shipment constraints require that all boxes from a customer are packed in the same container; if this is not possible, no boxes from that customer are packed [6].
We address the CLP with six practical constraints: weight limit, vertical and horizontal load stabilities, load bearing, multi-drop, and multiple orientations. In particular, we study the effect of using a mechanical formulation to consider the dynamic stability constraints and their impact on the CLP solutions. The computational study shows that when an efficient strategy is used, the inclusion of these constraints produces only a small decrease in the container’s occupied volume. Thus, we propose a hybrid algorithm based on a Greedy Randomized Adaptive Search Procedure (GRASP) enhanced with a mechanical dynamic stability model that limits the exploration space and guarantees accepted levels of cargo damage in the solution.
2. Related Work
There is a vast body of literature on this topic, which has been extensively reviewed in [5,10], and more recently in [11]. Packing problems fall within the broader category of cutting and packing problems, which have been classified as NP-hard [12,13]. Due to the high dimensionality of the feasible space, as concluded in previous studies [14], it is virtually impossible to ensure that a general global random search algorithm will reach the global optimum.
In particular, in this paper, we focus on studying one of the variants of the problem in three dimensions, where the set of objects to be packed corresponds to boxes whose variety is weakly heterogeneous, the container dimensions are fixed, and only a single container is available. According to the classification proposed by [15], this problem instance corresponds to the 3D single-large-object placement problem (3D-SLOPP) and the 3D single-knapsack problem (3D-SKP). Given the inherent complexity of the 3D-SLOPP and 3D-SKP, different approaches have been proposed to solve them, including exact algorithms, heuristics, and metaheuristics.
A few exact methods directly related to the 3D-SLOPP or 3D-SKP are found in the literature, although they can find the optimal solution only for small and middle-sized instances of the problem [16]. It is expected that with the increase in computational capacity, this situation will improve and attract researchers to formulate exact algorithms, which are essential points of comparison to measure the quality of non-exact methods even if they are not computationally competitive. In [13], a dynamic programming algorithm to solve the 3D-SLOPP was proposed. Ref. [17] proposed the first mixed-integer linear programming (MILP) model that uses the relative position of the elements to address the non-overlap between the components for the 3D-SLOPP. Ref. [18] proposed an exact branch-bound algorithm that iteratively packs the boxes at the corner point.
Regarding the inclusion of practical constraints, in [19] an MILP model was proposed and solved employing a branch and cut algorithm, where they considered weight distribution constraints, load bearing, and vertical and horizontal stability. The numerical results showed that the proposed model could find optimal solutions for medium-sized instances. Similarly, the authors of [20] formulated an MILP model including load-bearing, weight distribution, orientation, and stability constraints. Recently, Ref. [21] proposed an MILP formulation where practical constraints of stability, fragility, weight distribution, and box loading priorities were addressed. Astonishingly, Ref. [22] presented an exact approach wherein integer linear programming and constraint programming models were used to solve the 3D-SLOPP while considering twelve practical constraints, such as complete shipment, cargo priority, weight limit, stability, and stacking. The approach was able to solve medium-sized instances optimally.
Due to the inherent difficulty of the 3D-SLOPP and 3D-SKP, heuristic algorithms are the most widely used in the literature. In particular, much attention has been given to developing constructive heuristics that arrange the boxes in layers or blocks and then follow simple packing rules. Common elements in heuristic algorithms are sequencing, empty space management, and loading patterns. Sequencing aims to sort or categorize the unpacked items effectively, frequently using the dimension of the boxes, the volume, or a combination of those measures as criteria. Space management tries to identify and represent possible free spaces in the container. The most relevant approaches are matrix representation, corner point representation, and maximal space representation.
The loading pattern aims to select a desired free space and pack chosen items based on specific rules or patterns. The work in [23] distinguishes five types of patterns: wall construction, stacking construction, horizontal layer construction, block construction, and guillotine cutting. Wall construction and layered construction patterns are the most common approaches to problems with weakly heterogeneous elements. Some works that consider layer packing include [4,24,25,26,27,28], while works considering block packing include [23,29,30,31].
Metaheuristics have been introduced in an attempt to improve the effectiveness of heuristic methods. Examples include [25,27,32], which used genetic algorithms; Refs. [33,34,35], which used tabu search; and Refs. [36,37,38], which used simulated annealing; among others. Regarding GRASP, Ref. [39] applied a version of metaheuristics in which the GRASP local search procedure improves the initial solution by creating and searching new neighborhoods. The work proposed in [40] combines a personalized heuristic based on wall construction with an MILP, including boundary and weight distribution constraints. Recently, GRASP has been used in the multi-container version in the work in [41,42,43]. In the first work, the constructive phase is composed of the following steps: first, one empty space is selected; second, an unpacked box is chosen to be the base of a stack, and then the construction of layers is performed on that base. The first and second phases are randomized to perform the exploration phase of the GRASP. The second paper noted that it was applied in a logistics company and applied a layered construction approach in the construction phase and a randomization phase to produce varied solutions.
As mentioned above, various practical considerations have been included to approximate real-life situations, which have recently been classified as safety and logistical constraints. The following describes how these constraints have been considered in the literature.
2.1. Security Constraints
One of the most common safety constraints is the weight limit, which requires that the packed boxes’ total weight does not exceed the upper limit that the container can support. This constraint has been included in [42,44,45,46,47,48,49]. Another weight-related constraint is the weight distribution, which generally has been addressed through the center of gravity of the cargo, seeking to locate it close to the geometric center of the container floor, as proposed in [6,40,50,51,52,53,54].
Regarding the box orientation constraints, some approaches allow all six orientations of a box for packaging [9,55,56], while other works do not allow rotation [19] or restrict the orientation to specific axes [41,57]. Moreover, in the case of load constraints, these are generally dictated by the size, weight, or contents of a box, and require that a specific item be placed (or not placed) in a particular position (e.g., large items must be placed on the floor of the container) or in a particular area of the container [25,58]. Additionally, stacking constraints minimize the probability of damage to the boxes by limiting how boxes can be placed on top of each other. The most common way to account for this restriction is to prohibit the placement of heavier boxes on top of lighter boxes and non-fragile boxes on top of fragile ones [20,47].
The approach related to loading and transportation emphasizes the properties of the final disposition of the items in the container, directly related to security constraints involving cargo stability. Cargo packaging represents a crucial factor in reducing the risks of damage in cargo transportation, which represents 28% of total damage [59], in which the cost of replacing damaged products can represent up to 17 times the original shipping cost [60]. These stability restrictions protect, as much as possible, the physical integrity of the boxes, reducing the risks in the operations of loading and unloading for logistics operators. In the literature, two types of stability have been distinguished: static and dynamic [5]. The first, also known as vertical, is called a strict constraint since it refers to the loading operations and the handling of materials involved [61,62]. The evaluation of compliance with this restriction focuses on the viability of the physical packing sequence, which is directly linked to how the charge is located in the container space. In this case, the impact of the approach to the construction of packing patterns is directly evaluated for the building approach: wall, stack, horizontal layer, block, or guillotine. Another crucial factor corresponds to the percentage of support that the box has, and this can be partial support or full support. In addition, authors such as those of [63] include the mechanical balance approach, in which the contact of the base of cargo is evaluated by means of the sum of the forces.
In the case of dynamic or horizontal stability, it is referred to as a soft restriction due to the level of difficulty in implementation, which is directly linked to what happens during transport with the cargo when the container is subjected to acceleration and braking forces. The first authors to propose an approach regarding a set of metrics that represent the degree of dynamic stability of a solution to evaluate what happens to the cargo during transport were [4]. They used indicators that refer to how much the geometric configuration of the cargo changes during transport, without considering the forces that the items withstand during transport. Trying to overcome the above issues, in [64] two metrics, based on the number of failed items and the number of items inside the damaged area of a damage curve limit, determined by means of a linear regression that does not consider kinetic factors, were introduced. Following these approaches, in [7] they tested these literature metrics in a simulation and found that the existing dynamic stability indicators were insufficient by themselves and proposed modifications to the indicators related to the number of failed boxes and the number of boxes likely to be damaged in case of acceleration, using a mechanical approach.
Finally, other authors have followed different approaches to justify the fact of not directly addressing dynamic stability in relation to kinematics in their solution methodologies. According to [63], vertical and horizontal stabilities are commonly handled with a support factor for the bottom faces (vertical stability) and the lateral faces (horizontal stability) of items. Then, the full support of the faces is required to guarantee stability; although, in horizontal stability, other conditions based on mechanical equilibrium may be necessary, showing that compliance with this restriction can be guaranteed using the support factor approach.
2.2. Logistic Constraints
When the container space is not sufficient, decisions must be made regarding the boxes to be packed. One of the scenarios is to determine the prioritization in the delivery of customer orders, either by cargo type or delivery time. In this regard, in [65] high and low priorities for boxes were considered, where the latter were only packed if the packing of high-priority boxes was not compromised. In [66], a condition was imposed that all high-priority boxes must be loaded first and, after that, the other boxes. A study that considers prioritization based on due dates is presented in [28], in which packing boxes with due dates are prioritized over those without.
A second scenario is to limit partial deliveries of customer orders, wherein either a customer’s boxes are completely packed in the container, or no boxes are packed. In some situations, this condition can be relaxed to allow partial deliveries to one or more customers. This type of constraint has been considered in [67,68], which highlight the realistic case addressed in [28], which solves an instance of the problem for a company that receives daily orders and the items of an order must go in the same container.
One of the constraints that also limits the way the packing is performed and has no relation to the customer is the pattern complexity constraint. This constraint has a significant connection with the difficulties that robots or loading personnel have in understanding and implementing the loading pattern [37,48,69,70]. It is noteworthy that complex patterns are unsuitable for both cases: in the first one because operators cannot visualize the pattern and require more time in the loading process. In the second, robots may not possess sufficient freedom to achieve complex packing patterns and may need human assistance.
Another scenario is the need to group the boxes so that their positions within the container are very close, known as relative positioning constraints. Either because it is required that boxes of the same customer remain as close together as possible, or in cases where boxes by their nature must remain together and separate from other types (e.g., detergents and foodstuffs) [70,71].
A set of constraints closely related to the previous one is multi-drop constraints, that require adherence to a delivery route for customer orders. Items with the same delivery location should be packed close together and placed in specific positions according to their destination to avoid unnecessary operations [72,73]. When applying these constraints, the primary purpose is to make the minimum rearrangements possible in the delivery task. One way to achieve this is to combine the vehicle routing problem and the SLOPP, so that the container cargo is linked to the route for delivery of the customers’ orders, as presented by [74] in their tabu search algorithm. When the issue is focused purely on packing, the order of dispatch to customers is a piece of input information to the problem. This constraint has been addressed by including visibility, accessibility, and reachability conditions. The visibility condition is the most common approach and imposes that when the boxes are packed, at least one side must be visible, or in case it is blocked, it is only by boxes for the same customer. This condition has been successfully applied by [26] through a local search procedure first implemented in [72] using a tree search algorithm. The accessibility condition classifies the boxes as reachable in terms of the position of the box concerning the worker performing the unloading task (or robots), employing a maximum distance [34]. The reachability condition defined by [19] uses the concept of virtual walls to separate the different orders of each customer by specifying a parameter that indicates the distance between each wall.
Table 1 summarizes the main differences between this work and the state of the art approaches to the SLOPP. In this table, the symbol “×” indicates whether a particular aspect is considered or not. As can be observed, logistic constraints are little considered in the literature, which is relevant given that, although the CLP is a problem widely studied in the literature, there is still room for exploration. Moreover, these constraints have the greatest applicability in realistic cases. Regarding safety constraints, there is a growing interest in addressing constraints related to dynamic stability, which is the framework in which this work is framed. As mentioned in the Introduction, the present work considers constraints related to the weight limit, orientation of the boxes, load-bearing strength, the stability of the cargo, and the multi-drop patterns.

Table 1.
Proposed approach versus the related literature.
3. Solution Approach
This paper introduces a novel hybrid scheme to solve the container loading problem (CLP) by integrating a mechanical model into a metaheuristic framework, resulting in two key innovations: (i) the replacement of physics-based simulation engines for evaluating the dynamic stability of packing patterns, and (ii) a metaheuristic structure designed to ensure an accepted cargo stability level.
The proposed approach follows the classical GRASP structure [83], but with a significant enhancement: it incorporates an adaptive self-calibration mechanism through a training phase for the alpha parameter—which governs the size of the restricted candidate list (RCL), thus controlling the balance between randomness and greediness in the construction phase. In addition, the algorithm, during the remaining phase, includes a mechanism to further refine the construction process.
A major distinction from the original GRASP approach is that the proposed algorithm leverages information from the mechanical model during the construction phase to perform a targeted local search on elements identified as critical, enhancing both the solution quality and stability performance.
The mechanical model dynamically analyzes the forces and accelerations acting on the cargo to predict the loss of support, overturning, or reaching the critical velocity that would damage it, while the structure of the metaheuristic includes the dynamic stability indicators in the improvement steps. It is important to mention that the stability indicators are obtained from the mechanical model, allowing the practitioner to know the percentage of damaged boxes for an efficient packing pattern. In this section, firstly the proposed approach is described, and secondly the mechanical model is presented.
3.1. Hybrid Approach
The CLP has been studied extensively by a lot of researchers with different objective functions and constraints by using diverse methods, as can be observed in Table 1, presented in Related Work. In real-world problems, a number of practical constraints and requirements need to be satisfied, such as loading feasibility, stability, weight balance, operational safety, product handling, and the prevention of cargo damage during container shipping, but only a few works have addressed these mentioned requirements. The GRASP algorithm has been widely used in packing problems and it was developed to solve difficult combinatorial optimization problems [83]. Different studies have demonstrated its quality and its robustness. It is often used alongside the concept of maximal spaces, initially introduced by [84]. These two elements allow for the incorporation of a large number of practical constraints in an appropriate and concise manner, while also enabling the evaluation of the objective function and secondary indicators clearly and precisely. The objective function of this work focuses on packing as much cargo as it is possible to fit inside the container (maximize volume utilization). The algorithm satisfies the constraints of the orientation of the boxes, load-bearing strength, the limit of the weight, the stability of the cargo, and the multi-drop patterns. In addition, the construction of the packing patterns is carried out in blocks, taking into account the multi-drop constraint approach of [26] (boxes that are visible from one side or blocked just by boxes for the same destination).
The proposed method integrates a constructive phase, an improvement phase, and a dynamic stability evaluation mechanism to ensure that the generated solutions are feasible and optimized with respect to the given constraints. Algorithm 1 describes the key components and steps of the hybrid approach in detail.
The algorithm accepts the following inputs: the sequence in which destinations are visited (denoted by ); the list of boxes for each destination (represented by , where each box is defined by a triple indicating its length, width, and height); and the container dimensions (X, Y, and Z, corresponding to its length, width, and height, respectively). It also requires GRASP-specific parameters, including the total number of iterations (), the set of alpha coefficients (), and the number of iterations for alpha training (N). The algorithm outputs the best solution () that satisfies the dynamic stability constraints.
In the constructive phase (lines 2–15), the algorithm starts by creating a residual space list E that represents the spaces available within the container (line 2). The list of boxes for each destination i is also initialized with the original demand (line 3) and the current packing pattern starts as empty for each iteration (line 4). For each destination (line 5), an attempt is made to introduce its box demand, following a procedure in which the residual space to be used is first selected and then the block of boxes is chosen. This procedure is carried out until the box demand is met or all available spaces within the container are exhausted (line 6). The algorithm selects the maximal space e from the list of residual spaces E (line 7), following a criterion that prioritizes selecting the residual spaces located deeper inside the container first. In case of ties, the residual space farthest from the container floor is selected (to encourage box stacking). If the tie persists, the smallest residual space is chosen first. Then, a list of all feasible blocks is generated for the selected space e and the remaining boxes (line 8). The restricted candidate list (RCL) is built by selecting the blocks in a process influenced by the alpha coefficients. This step introduces randomness to diversify the generated patterns (line 9). A block b is randomly selected from the RCL (line 10) and placed in the selected space e (line 11). Finally, the list of maximal spaces E (line 12) and the list of remaining boxes are updated accordingly (line 13).
After constructing a packing pattern P, the algorithm evaluates its dynamic stability using a mechanical model (line 16). The dynamic stability indicator () is calculated and, if it falls below a predefined threshold, the solution is considered feasible (line 17). The algorithm then checks if the current solution P improves the objective function compared to the incumbent solution (line 18). If so, P is updated as the new incumbent (line 19).
In the improvement phase, attempts are made to satisfy or improve the dynamic stability constraint while simultaneously seeking to enhance container utilization. The algorithm identifies and removes critical boxes from the packing pattern P (line 22). The lists E and are updated to reflect the changes (lines 23–24). The algorithm re-attempts to pack the remaining boxes into the container, this time using a deterministic approach to select the block that best fits into the maximal space (lines 25–34). This step seeks to enhance the packing efficiency while simultaneously refining the compliance with dynamic stability constraints. The dynamic stability of the updated packing pattern P is reevaluated (line 35). If the solution is feasible and improves the objective function, it is updated as the new incumbent (lines 36–38).
| Algorithm 1 Proposed Hybrid Approach |
Input: Vector order vector of destinations, List list of boxes for each destination i, Tuple : dimensions of the container (length, width, and height); Parameters: total GRASP iterations, set of coefficients for the reactive feature, number of iterations for training; Output: Solution .
|
The algorithm iterates through the constructive and improvement phases for a total of iterations. The best solution that satisfies the dynamic stability constraints is returned as the final output. The proposed GRASP algorithm incorporates a reactive feature in which the alpha coefficients are self-adjusted based on the performance of previous iterations. This adaptive mechanism enhances the algorithm’s ability to explore the solution space effectively. The integration of a mechanical model for dynamic stability evaluation ensures that the generated solutions are not only optimized for space utilization, but are also feasible in real-world scenarios, where dynamic forces are a concern. The use of a randomized greedy procedure in the constructive phase and the removal of critical boxes in the improvement phase introduce diversification, helping the algorithm escape local optima and explore a broader solution space.
The creation of the restricted candidate list (RCL) is a key component of the proposed methodology. The reactive feature of the GRASP algorithm is implemented within the function (Algorithm 2) and dynamically adjusts the number of candidate blocks in the RCL. This mechanism achieves a balance between small RCL sizes, which may result in excessively greedy behavior, and large RCL sizes, which compromise efficiency.
| Algorithm 2 Build RCL |
Input: list of feasible blocks, selected residual space, Current iteration; Parameters: set of alphas, number of iterations for training; Output: restricted candidates list of blocks for the space e
|
Algorithm 2 takes as input a list A containing a predefined set of coefficients (; ), where each coefficient determines a possible size for the RCL. For instance, results in an RCL containing half of the most promising blocks. The reactive mechanism aims to favor the selection of values that yield better outcomes by dynamically adjusting the probability of choosing each based on its cumulative performance.
Initially, all coefficients have no performance record (line 1) and are assigned equal selection probability (line 2). The core strategy (lines 3–7) involves selecting an based on a probability distribution , which is iteratively refined based on observed performance. During the first N iterations, a uniform distribution () is used to select due to the limited data available for estimating .
The list of blocks () must be processed to identify the best fits (residual linear distance between the block and the space) for each block within the selected space while simultaneously determining the volume represented by each block () (lines 8–11). One of two packing criteria is randomly selected: the block with the best fit or the block with the largest volume. Based on the chosen criterion, an auxiliary block list is generated and sorted to create the restricted candidate list (lines 12–16).
The is then constructed by selecting the first elements from the ordered auxiliary block list (lines 17–21). After each GRASP iteration, the objective function value is used to update the cumulative performance of the selected , where higher objective function values indicate better performance in the maximization process (line 22). Following the performance update, selection probabilities for the coefficients are normalized to maintain a valid discrete probability distribution (line 23). Finally, the is returned (line 24).
3.2. Mechanical Model for Dynamic Stability
The GRASP pseudocode invokes the function to assess dynamic stability indicators for solutions generated in both the constructive and improvement phases. This procedure describes an implementation of the mechanical model based on Newtonian mechanics.
The dynamic behavior of the cargo is analyzed with the assumption that boxes are perpendicular or parallel to the container dimensions as well as to the acting accelerations. The model presented in [85] defines two types of mechanical units (free boxes and columns of boxes; called in Algorithm 1) that are subjected to a standard set of accelerations. Their dynamic behavior in response to these accelerations is determined by Equation (1), where a is the acceleration of the container, g represents gravity, is the static coefficient of friction, h and b are the vertical and horizontal distances from the center of mass to the possible edge or pivot of the box while being tipped over, is the maximum velocity delta allowed by the damage boundary curve, and t is the time spent under acceleration. Based on the literature and the CTU code [85,86], the static friction coefficient for typical material pairings in cargo transportation ranges from 0.4 to 0.6. To simplify the modeling while maintaining reasonable accuracy, an average value of 0.5 was adopted for as an approximation.
However, these behaviors may only be exhibited if the box has enough leeway to fail. This information is obtained by projecting certain vertices of the box to test if collisions prevent the movements that result in a failure state.
Algorithm 3 receives a packing pattern as input. It utilizes stability parameters corresponding to static and kinetic friction variables, along with four maximum acceleration values that the cargo can withstand in different directions during transport, considering the acceleration duration (). The percentage of damaged boxes is calculated based on the analysis of each mechanical unit. Therefore, it is necessary to determine whether a box is part of a column or is a free-standing box (lines 1–10). To achieve this, the algorithm verifies box locations within the packing pattern by checking the vertices of each box through projected points, ensuring that no collision volume exists directly above.
| Algorithm 3 Calculate Dynamic Stability |
Input: set of boxes packed along with their respective allocated positions; Parameters: Static Mechanical Variables; Outputs: percentage of broken boxes, List free boxes and box columns
|
Once the list of mechanical units to analyze () is obtained, the algorithm iterates through each unit (line 11) to determine its stability. If a unit is capable of movement, the mechanical model must be checked. As a unit may move forward, backward, left, or right, possible instabilities must be assessed for the four directions (line 12), if a unit is capable of movement, the mechanical model must checked.
Initially, all boxes share the same velocity as the container, but their positions change due to inertial effects caused by accelerations. A box is considered to have fallen either by sliding (linear acceleration and motion) or tipping over (angular acceleration and motion). The function verifies these conditions by determining whether a unit (a single box or a column of boxes) slides during transport. If movement is detected, the algorithm proceeds to damage evaluation, assessing whether the displacement is sufficient to cause a fall and whether the velocity change places the unit within the damage curve. To evaluate tipping, equations of simple motion are used, incorporating collision volumes, acceleration magnitudes, friction coefficients, and simulation time parameters. Structural failure is assessed by projecting points (the adjacent two bottom corners of the unit) in the direction of potential movement by half the unit’s size (length or width). If the projection exceeds this threshold, the unit is deemed capable of falling, and the algorithm then checks whether it lies within the damage boundary curve ().
If a unit falls within the damage boundary curve, the number of affected boxes within that unit is recorded, and the total count of broken boxes is updated accordingly (line 17). Finally, the calculated stability indicator—defined as the percentage of broken boxes relative to the total boxes within the packing pattern (line 22)—is returned along with the set of critical boxes (line 23).
The values assumed for the calculations are based on the studies in [7,8,64] and on the information contained in [86], that presents the most common accelerations, in addition to gravity, that occur in the transportation of cargo on land roads, as defined by different regulations.
4. Computational Experiments and Result Analysis
This section presents a performance evaluation of the proposed hybrid approach for solving the container loading problem (CLP). To assess its effectiveness, we tested it on 23 real-world instances proposed in [26].
It is important to note that, since finding the optimal solution is highly unlikely for most instances, it is standard practice to evaluate the algorithm’s performance using statistical analysis on well-established benchmark test sets.
For the computational experiments, we used a Windows 10 Pro 64-bit system with an Intel(R) Core(TM) i5-7200U CPU (2.5 GHz). The algorithm was implemented in C++ to ensure efficiency and scalability.
Based on the results obtained in [7,8], the most significant parameters when assessing the impact of dynamic stability constraints on the CLP are the number of boxes, the degree of assortment homogeneity, and the accepted percentage of allowable damage (referred to as the threshold in this paper). Therefore, the selected instances include 19 input parameters related to customer information, container specifications, and box characteristics. Across the 23 instances considered, the total number of boxes ranges from 27 to 278, while the assortment of boxes—defined as the number of boxes with different sizes—varies between 5 and 71. Finally, threshold values of 1%, 5%, and 25% are analyzed.
As described in the methodology section, the proposed approach requires calibration of only two parameters ( and N), as the parameter alpha is automatically adjusted after the training period. For this reason, the total number of iterations was set to 50,000 and N was set to 1000 iterations, aiming to maximize the occupied volume while maintaining a reasonable computational time.
Figure 1 shows the results of the occupied volume for each of the considered instances, while Figure 2 shows the computational time spent on each instance for the three thresholds used. It is emphasized that the average occupancy is 66.7%, and the average computational time is 7.37 s.
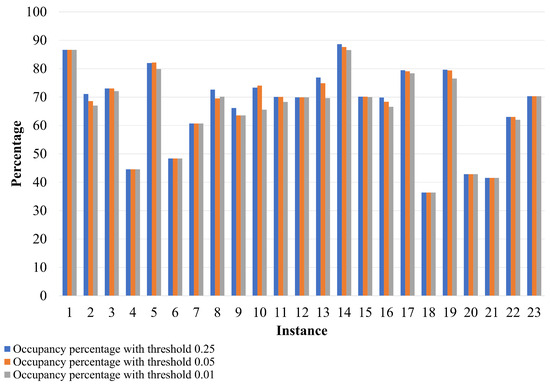
Figure 1.
Comparison of instances by threshold: occupancy percentage.
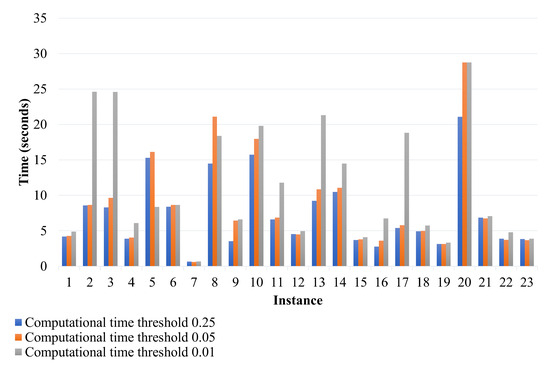
Figure 2.
Comparison of instances by threshold: Computational time.
As can be seen in Figure 1 and Figure 2, the percentage of container occupancy does not vary greatly for the different threshold values, implying that the hybrid approach’s loading patterns guarantee a high level of dynamic stability that even consistently exceeds the required value. Additionally, from the computational times, it is observed that including the dynamic stability model within GRASP leads to an increase in the computational expense, which is minimal, especially when compared to machine simulation-based approaches in the literature, such as [64] (Bullet®) and [7,8] (PhysX®).
The proposed approach was compared against the simulation-optimization method based on the GRASP algorithm presented in [8], which serves as the baseline approach. Figure 3, Figure 4 and Figure 5 summarize the results, comparing the occupancy percentages obtained for each instance across the different threshold values.
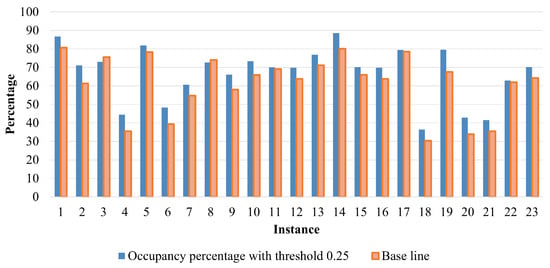
Figure 3.
Comparison of occupancy percentage between proposed and baseline approach: threshold equal to 1%.
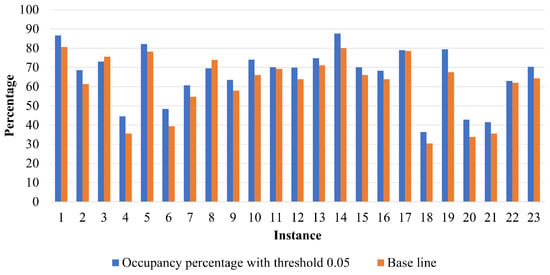
Figure 4.
Comparison of occupancy percentage between proposed and baseline approach: threshold equal to 5%.
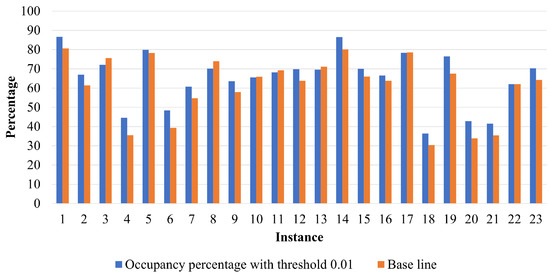
Figure 5.
Comparison of occupancy percentage between proposed and baseline approach: threshold equal to 25%.
A key achievement of this study is demonstrating that desired stability levels can be attained without compromising the primary objective of maximizing the utilized volume of packed boxes. This is made possible by an efficient hybrid algorithm structure that effectively balances solution quality and computational effort, avoiding the need for excessive computation to evaluate and detect instabilities, thanks to an optimized mathematical model.
From Figure 3, Figure 4 and Figure 5, it can be observed that the occupancy percentages exhibit a slight improvement, further reinforcing the intuitive relationship between dynamic stability constraints and occupied volume. Specifically, higher occupied volumes tend to correspond to greater dynamic stability in the cargo. This finding aligns with the conclusions presented in [22].
Finally, a factorial experiment was designed to determine the possible causes of the differences in occupancy of the different instances used. The test evaluated the statistical significance of the following factors concerning the percentage of container occupancy: the threshold, the number of boxes that could be stored in the container, and the number of different types of boxes to be stored. The number of boxes stored was classified into low, medium, and high levels: the low level corresponds to the number of boxes stored being between 1 and 100, the medium level between 101 and 199, while the large level has a number of boxes higher than 200. Two clusters were defined for the variable of the assortment of boxes: one with a number of types more than 21 and the other less or equal to 21. The groups were separated, as shown in Table 2, as well as by the average occupancy for each group.

Table 2.
Factorial design.
The results obtained by the ANOVA model show that the p-value for the factor Quantity_Boxes (number of boxes) is less than the significance level (typically 0.05), indicating that it is the only factor that significantly affects the percentage of occupation, as shown in Table 3. Moreover, the variation in the threshold does not significantly affect the occupancy percentage. The ANOVA was performed on a factorial design with 36 observations. The dependent variable was the occupancy percentage. The factors included in the model were Quantity_Boxes, the number of boxes, with three levels (“low”, “medium”, “large”); , the box fragility threshold, with three levels (0.01, 0.05, 0.25); and Dif_Boxes, the assortment of boxes of different sizes, with two levels (“<21”, “>20”).

Table 3.
ANOVA results.
Additionally, the interaction plots in Figure 6 show that the mean occupancy percentage (occupa_perc) always changes with the quantity of boxes stored, and there is not much change and no interaction with respect to the threshold and the assortment of boxes.
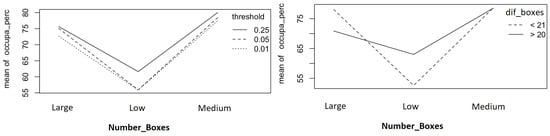
Figure 6.
Interaction plots.
Considering that the number of boxes factor is significant, a box plot was drawn in which the difference in the average of the different levels can be evidenced (see Figure 7). For this purpose, a Tukey test was carried out in order to find the level of the factor that maximizes the percentage of occupation (see Table 4). The result of this test is that there are alternate optima and both the large and the medium levels maximize the occupancy percentage.
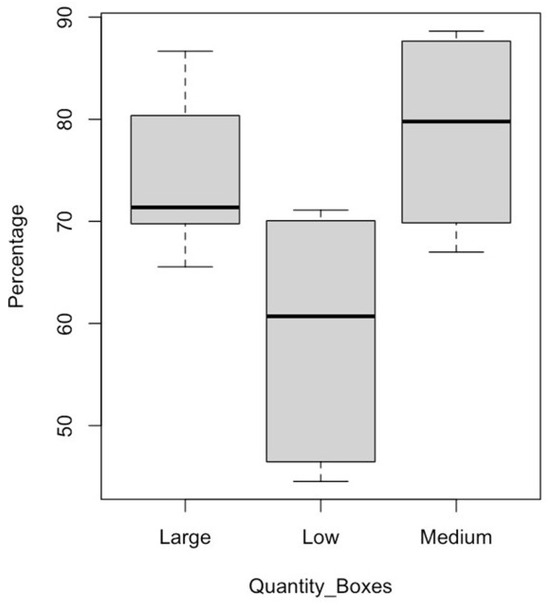
Figure 7.
Box plot.

Table 4.
Tukey multiple comparison means—quantity of boxes.
5. Conclusions and Future Work
This study addressed the container loading problem (CLP), with a focus on dynamic stability, by proposing a hybrid approach based on the GRASP algorithm. This approach integrates a mathematical model of dynamic stability that demonstrates a higher degree of kinetic fidelity compared to the regression-based methods commonly found in the literature.
The experimental results demonstrate a strong correlation between the percentage of occupied volume and dynamic stability, where higher occupied volumes lead to greater stability. Specifically, our approach achieves an average container occupancy of approximately 67% across the tested instances, with an average computational time of less than eight seconds. Moreover, the factorial experiment confirms that the number of boxes significantly impacts the occupancy percentage, while variations in box assortment and the fragility threshold have a minimal effect.
A key contribution of this work is that incorporating dynamic stability calculations does not significantly increase computational cost, making our method more competitive compared to traditional simulation-based approaches. For instance, while including dynamic stability constraints increases computational effort, the additional cost is negligible when compared to physics engine simulations such as Bullet® and PhysX®. Furthermore, when comparing our results to the baseline GRASP approach, we observe a slight improvement in occupancy percentages, reinforcing the relationship between occupied volume and stability.
From a bibliographic perspective, further research is needed on integrating functional logistic constraints into the CLP. This approach could be extended to incorporate full-shipment constraints, cargo prioritization, and pattern complexity. Notably, including full-shipment restrictions would provide deeper insights into the role of the dynamic stability model in the search space exploration. The literature suggests that these constraints typically reduce the occupied volume, consequently increasing the likelihood of movement for unsecured boxes. Addressing this aspect is crucial for real-world applications in logistics and automation. Additionally, further computational comparisons on more realistic instances are necessary to validate and refine the model.
Regarding the mechanical model, while significantly more efficient than physical simulations for the distances considered, its current implementation exhibits a worst-case computational complexity of . This is due to collision checks being performed between all paired boxes unless they are adjacent to the container walls or supported by another box. Optimizing this process could further enhance performance and scalability.
For future research, integrating the proposed hybrid approach into commercial [80] or open-source [8] decision support systems is recommended to assess its overall effectiveness for logistics-based companies. Such integration would facilitate real-world validation and promote its adoption in automated container loading and stability optimization processes.
Author Contributions
Formal analysis, D.Á.-M.; funding acquisition, D.Á.-M.; investigation, A.M.M.-F. and J.C.M.-F.; project administration, A.T. and D.Á.-M.; supervision, A.T. and D.Á.-M.; visualization, A.M.M.-F.; writing—original draft, A.M.M.-F. and J.C.M.-F.; writing—review and editing, A.T. and D.Á.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was made possible thanks to the funding from Patrimonio Autónomo Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación Francisco José de Caldas. The APC was funded by Universidad de los Andes.
Data Availability Statement
The original data presented in the study are openly available in CLPwithDynamicStablity at https://github.com/Anamontesf/CLPwithDynamicStablity (accessed on 3 March 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Santos, L.; Coutinho-Rodrigues, J.; Current, J.R. An improved heuristic for the capacitated arc routing problem. Comput. Oper. Res. 2009, 36, 2632–2637. [Google Scholar] [CrossRef][Green Version]
- Martin, P. Global Parcel Shipping Volume Between 2013 and 2026 (in Billion Parcels). 2022. Available online: https://www.statista.com/statistics/1139910/parcel-shipping-volume-worldwide/ (accessed on 12 April 2022).
- Li, Y.; Tang, X.; Cai, W. On dynamic bin packing for resource allocation in the cloud. In Proceedings of the 26th ACM Symposium on Parallelism in Algorithms and Architectures, Prague, Czech Republic, 23–25 June 2014; pp. 2–11. [Google Scholar]
- Bischoff, E.E.; Ratcliff, M. Issues in the development of approaches to container loading. Omega 1995, 23, 377–390. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Wäscher, G. Constraints in container loading–a state-of-the-art review. Eur. J. Oper. Res. 2013, 229, 1–20. [Google Scholar] [CrossRef]
- Ramos, A.G.; Silva, E.; Oliveira, J.F. A new load balance methodology for container loading problem in road transportation. Eur. J. Oper. Res. 2018, 266, 1140–1152. [Google Scholar] [CrossRef]
- Martínez-Franco, J.C.; Álvarez-Martínez, D. Physx as a middleware for dynamic simulations in the container loading problem. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 2933–2940. [Google Scholar]
- Martínez-Franco, J.; Céspedes-Sabogal, E.; Álvarez-Martínez, D. PackageCargo: A decision support tool for the container loading problem with stability. SoftwareX 2020, 12, 100601. [Google Scholar] [CrossRef]
- Martínez, D.A.; Alvarez-Valdes, R.; Parreño, F. A grasp algorithm for the container loading problem with multi-drop constraints. Pesqui. Oper. 2015, 35, 1–24. [Google Scholar] [CrossRef]
- Zhao, X.; Bennell, J.A.; Bektaş, T.; Dowsland, K. A comparative review of 3D container loading algorithms. Int. Trans. Oper. Res. 2016, 23, 287–320. [Google Scholar] [CrossRef]
- Ali, S.; Ramos, A.G.; Carravilla, M.A.; Oliveira, J.F. On-line three-dimensional packing problems: A review of off-line and on-line solution approaches. Comput. Ind. Eng. 2022, 168, 108122. [Google Scholar] [CrossRef]
- Hartmanis, J. Computers and intractability: A guide to the theory of np-completeness (michael r. garey and david s. johnson). Siam Rev. 1982, 24, 90. [Google Scholar] [CrossRef]
- Scheithauer, G. Algorithms for the container loading problem. In Operations Research Proceedings 1991; Springer: Berlin/Heidelberg, Germany, 1992; pp. 445–452. [Google Scholar]
- Pepelyshev, A.; Zhigljavsky, A.; Žilinskas, A. Performance of global random search algorithms for large dimensions. J. Glob. Optim. 2018, 71, 57–71. [Google Scholar] [CrossRef]
- Wäscher, G.; Haußner, H.; Schumann, H. An improved typology of cutting and packing problems. Eur. J. Oper. Res. 2007, 183, 1109–1130. [Google Scholar] [CrossRef]
- da Silva, E.F.; Leão, A.A.; Toledo, F.M.; Wauters, T. A matheuristic framework for the Three-dimensional Single Large Object Placement Problem with practical constraints. Comput. Oper. Res. 2020, 124, 105058. [Google Scholar] [CrossRef]
- Chen, C.; Lee, S.M.; Shen, Q. An analytical model for the container loading problem. Eur. J. Oper. Res. 1995, 80, 68–76. [Google Scholar] [CrossRef]
- Martello, S.; Pisinger, D.; Vigo, D. The three-dimensional bin packing problem. Oper. Res. 2000, 48, 256–267. [Google Scholar] [CrossRef]
- Junqueira, L.; Morabito, R.; Yamashita, D.S. Three-dimensional container loading models with cargo stability and load bearing constraints. Comput. Oper. Res. 2012, 39, 74–85. [Google Scholar] [CrossRef]
- Paquay, C.; Schyns, M.; Limbourg, S. A mixed integer programming formulation for the three-dimensional bin packing problem deriving from an air cargo application. Int. Trans. Oper. Res. 2016, 23, 187–213. [Google Scholar] [CrossRef]
- Ocloo, V.E.; Fügenschuh, A.; Pamen, O.M. A New Mathematical Model for a 3D Container Packing Problem; Brandenburgische Technische Universität Cottbus-Senftenberg, Fakultät 1/MINT: Cottbus, Germany, 2020. [Google Scholar]
- do Nascimento, O.X.; de Queiroz, T.A.; Junqueira, L. Practical constraints in the container loading problem: Comprehensive formulations and exact algorithm. Comput. Oper. Res. 2021, 128, 105186. [Google Scholar] [CrossRef]
- Fanslau, T.; Bortfeldt, A. A tree search algorithm for solving the container loading problem. INFORMS J. Comput. 2010, 22, 222–235. [Google Scholar] [CrossRef]
- George, J.A.; Robinson, D.F. A heuristic for packing boxes into a container. Comput. Oper. Res. 1980, 7, 147–156. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Gehring, H. A hybrid genetic algorithm for the container loading problem. Eur. J. Oper. Res. 2001, 131, 143–161. [Google Scholar] [CrossRef]
- Ceschia, S.; Schaerf, A.; Stützle, T. Local search techniques for a routing-packing problem. Comput. Ind. Eng. 2013, 66, 1138–1149. [Google Scholar] [CrossRef]
- Ramos, A.G.; Oliveira, J.F.; Gonçalves, J.F.; Lopes, M.P. A container loading algorithm with static mechanical equilibrium stability constraints. Transp. Res. Part B Methodol. 2016, 91, 565–581. [Google Scholar] [CrossRef]
- Sheng, L.; Xiuqin, S.; Changjian, C.; Hongxia, Z.; Dayong, S.; Feiyue, W. Heuristic algorithm for the container loading problem with multiple constraints. Comput. Ind. Eng. 2017, 108, 149–164. [Google Scholar] [CrossRef]
- Eley, M. Solving container loading problems by block arrangement. Eur. J. Oper. Res. 2002, 141, 393–409. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, Y.; Leung, S.C. A heuristic block-loading algorithm based on multi-layer search for the container loading problem. Comput. Oper. Res. 2012, 39, 2267–2276. [Google Scholar] [CrossRef]
- Zhu, W.; Oon, W.C.; Lim, A.; Weng, Y. The six elements to block-building approaches for the single container loading problem. Appl. Intell. 2012, 37, 431–445. [Google Scholar] [CrossRef]
- Gehring, H.; Bortfeldt, A. A genetic algorithm for solving the container loading problem. Int. Trans. Oper. Res. 1997, 4, 401–418. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Gehring, H.; Mack, D. A parallel tabu search algorithm for solving the container loading problem. Parallel Comput. 2003, 29, 641–662. [Google Scholar] [CrossRef]
- Liu, J.; Yue, Y.; Dong, Z.; Maple, C.; Keech, M. A novel hybrid tabu search approach to container loading. Comput. Oper. Res. 2011, 38, 797–807. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, F. An effective tabu search approach with improved loading algorithms for the 3L-CVRP. Comput. Oper. Res. 2015, 55, 127–140. [Google Scholar] [CrossRef]
- Mack, D.; Bortfeldt, A.; Gehring, H. A parallel hybrid local search algorithm for the container loading problem. Int. Trans. Oper. Res. 2004, 11, 511–533. [Google Scholar] [CrossRef]
- Egeblad, J.; Pisinger, D. Heuristic approaches for the two-and three-dimensional knapsack packing problem. Comput. Oper. Res. 2009, 36, 1026–1049. [Google Scholar] [CrossRef]
- Mostaghimi Ghomi, H.; St Amour, B.G.; Abdul-Kader, W. Three-dimensional container loading: A simulated annealing approach. Int. J. Appl. Eng. Res. 2017, 12, 1290. [Google Scholar]
- Moura, A.; Oliveira, J.F. A GRASP approach to the container-loading problem. IEEE Intell. Syst. 2005, 20, 50–57. [Google Scholar] [CrossRef]
- Lim, A.; Ma, H.; Qiu, C.; Zhu, W. The single container loading problem with axle weight constraints. Int. J. Prod. Econ. 2013, 144, 358–369. [Google Scholar] [CrossRef]
- Correcher, J.F.; Alonso, M.T.; Parreño, F.; Alvarez-Valdés, R. Solving a large multicontainer loading problem in the car manufacturing industry. Comput. Oper. Res. 2017, 82, 139–152. [Google Scholar] [CrossRef]
- Alonso, M.T.; Alvarez-Valdés, R.; Iori, M.; Parreño, F. Mathematical models for multi container loading problems with practical constraints. Comput. Ind. Eng. 2019, 127, 722–733. [Google Scholar] [CrossRef]
- Cuellar-Usaquen, D.; Camacho-Muñoz, G.; Quiroga-Gomez, C.; Álvarez-Martínez, D. An approach for the pallet-building problem and subsequent loading in a heterogeneous fleet of vehicles with practical constraints. Int. J. Ind. Eng. Comput. 2021, 12, 329–344. [Google Scholar] [CrossRef]
- Bortfeldt, A. A hybrid algorithm for the capacitated vehicle routing problem with three-dimensional loading constraints. Comput. Oper. Res. 2012, 39, 2248–2257. [Google Scholar] [CrossRef]
- Deplano, I.; Lersteau, C.; Nguyen, T.T. A mixed-integer linear model for the multiple heterogeneous knapsack problem with realistic container loading constraints and bins’ priority. Int. Trans. Oper. Res. 2021, 28, 3244–3275. [Google Scholar] [CrossRef]
- Iori, M.; Martello, S. Routing problems with loading constraints. TOP 2010, 18, 4–27. [Google Scholar] [CrossRef]
- Paquay, C.; Limbourg, S.; Schyns, M.; Oliveira, J.F. MIP-based constructive heuristics for the three-dimensional Bin Packing Problem with transportation constraints. Int. J. Prod. Res. 2018, 56, 1581–1592. [Google Scholar] [CrossRef]
- Toffolo, T.A.; Esprit, E.; Wauters, T.; Berghe, G.V. A two-dimensional heuristic decomposition approach to a three-dimensional multiple container loading problem. Eur. J. Oper. Res. 2017, 257, 526–538. [Google Scholar] [CrossRef]
- Wang, L.; Guo, S.; Chen, S.; Zhu, W.; Lim, A. Two natural heuristics for 3D packing with practical loading constraints. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Daegu, Repubic of Korea, 30 August–2 September 2010; pp. 256–267. [Google Scholar]
- Alonso, M.T.; Alvarez-Valdes, R.; Parreño, F.; Tamarit, J.M. Algorithms for pallet building and truck loading in an interdepot transportation problem. Math. Probl. Eng. 2016, 2016, 11. [Google Scholar] [CrossRef]
- Costa, M.d.G.; Captivo, M.E. Weight distribution in container loading: A case study. Int. Trans. Oper. Res. 2016, 23, 239–263. [Google Scholar] [CrossRef]
- Gehring, H.; Menschner, K.; Meyer, M. A computer-based heuristic for packing pooled shipment containers. Eur. J. Oper. Res. 1990, 44, 277–288. [Google Scholar] [CrossRef]
- Haessler, R.W.; Talbot, F.B. Load planning for shipments of low density products. Eur. J. Oper. Res. 1990, 44, 289–299. [Google Scholar] [CrossRef]
- Moon, I.; Nguyen, T.V.L. Container packing problem with balance constraints. Spectrum 2014, 36, 837–878. [Google Scholar] [CrossRef]
- Parreño, F.; Alvarez-Valdés, R.; Tamarit, J.M.; Oliveira, J.F. A maximal-space algorithm for the container loading problem. INFORMS J. Comput. 2008, 20, 412–422. [Google Scholar] [CrossRef]
- Mahvash, B.; Awasthi, A.; Chauhan, S. A column generation-based heuristic for the three-dimensional bin packing problem with rotation. J. Oper. Res. Soc. 2018, 69, 78–90. [Google Scholar] [CrossRef]
- Sharma, E. Harmonic algorithms for packing d-dimensional cuboids into bins. arXiv 2020, arXiv:2011.10963. [Google Scholar]
- Moura, A.; Bortfeldt, A. A two-stage packing problem procedure. Int. Trans. Oper. Res. 2017, 24, 43–58. [Google Scholar] [CrossRef]
- Reidy, S. The Basics that Everyone Must Know About CARGO DAMAGE. 2020. Available online: https://arviem.com/the-basics-that-everyone-must-know-about-cargo-damage/ (accessed on 28 May 2022).
- Jiang, Y. How Much a Damaged Pack Can Really Cost Your Business. 2020. Available online: https://www.amcor.com/insights/blogs/how-much-a-damaged-pack-can-really-cost-your-business#:~:text=Replacing%20a%20damaged%20product%20can,to%20research%20firm%20IHL%20Group (accessed on 16 May 2022).
- Techanitisawad, A.; Tangwiwatwong, P. A GA-based heuristic for the interrelated container selection loading problems. Ind. Eng. Manag. Syst. 2004, 3, 22–37. [Google Scholar]
- Fuellerer, G.; Doerner, K.F.; Hartl, R.F.; Iori, M. Metaheuristics for vehicle routing problems with three-dimensional loading constraints. Eur. J. Oper. Res. 2010, 201, 751–759. [Google Scholar] [CrossRef]
- Queiroz, T.A.; Bracht, E.C.; Miyazawa, F.K.; Bittencourt, M.L. An extension of Queiroz and Miyazawa’s method for vertical stability in two-dimensional packing problems to deal with horizontal stability. Eng. Optim. 2019, 51, 1049–1070. [Google Scholar] [CrossRef]
- Ramos, A.G.; Oliveira, J.F.; Gonçalves, J.F.; Lopes, M.P. Dynamic stability metrics for the container loading problem. Transp. Res. Part C Emerg. Technol. 2015, 60, 480–497. [Google Scholar] [CrossRef]
- Ren, J.; Tian, Y.; Sawaragi, T. A priority-considering approach for the multiple container loading problem. Int. J. Metaheuristics 2011, 1, 298–316. [Google Scholar] [CrossRef]
- Wang, N.; Lim, A.; Zhu, W. A multi-round partial beam search approach for the single container loading problem with shipment priority. Int. J. Prod. Econ. 2013, 145, 531–540. [Google Scholar] [CrossRef]
- Gimenez-Palacios, I.; Alonso, M.T.; Alvarez-Valdes, R.; Parreño, F. Logistic constraints in container loading problems: The impact of complete shipment conditions. TOP 2021, 29, 177–203. [Google Scholar] [CrossRef]
- Kurpel, D.V.; Scarpin, C.T.; Junior, J.E.P.; Schenekemberg, C.M.; Coelho, L.C. The exact solutions of several types of container loading problems. Eur. J. Oper. Res. 2020, 284, 87–107. [Google Scholar] [CrossRef]
- Amossen, R.R.; Pisinger, D. Multi-dimensional bin packing problems with guillotine constraints. Comput. Oper. Res. 2010, 37, 1999–2006. [Google Scholar] [CrossRef][Green Version]
- Olsson, J.; Larsson, T.; Quttineh, N.H. Automating the planning of container loading for Atlas Copco: Coping with real-life stacking and stability constraints. Eur. J. Oper. Res. 2020, 280, 1018–1034. [Google Scholar] [CrossRef]
- Elhedhli, S.; Gzara, F.; Yildiz, B. Three-Dimensional Bin Packing and Mixed-Case Palletization. INFORMS J. Optim. 2019, 1, 323–352. [Google Scholar] [CrossRef]
- Christensen, S.G.; Rousøe, D.M. Container loading with multi-drop constraints. Int. Trans. Oper. Res. 2009, 16, 727–743. [Google Scholar] [CrossRef]
- Silva, E.; Ramos, A.G.; Oliveira, J.F. Load balance recovery for multi-drop distribution problems: A mixed integer linear programming approach. Transp. Res. Part B Methodol. 2018, 116, 62–75. [Google Scholar] [CrossRef]
- Gendreau, M.; Iori, M.; Laporte, G.; Martello, S. A tabu search algorithm for a routing and container loading problem. Transp. Sci. 2006, 40, 342–350. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Gehring, H. Applying Tabu Search to Container Loading Problems. In Proceedings of the Operations Research Proceedings 1997: Selected Papers of the Symposium on Operations Research (SOR’97), Jena, Germany, 3–5 September 1997; pp. 533–538. [Google Scholar]
- Araújo, O.C.B.D.; Armentano, V.A. A multi-start random constructive heuristic for the container loading problem. Pesqui. Oper. 2007, 27, 311–331. [Google Scholar] [CrossRef]
- Gonçalves, J.F.; Resende, M.G. A parallel multi-population biased random-key genetic algorithm for a container loading problem. Comput. Oper. Res. 2012, 39, 179–190. [Google Scholar] [CrossRef]
- Saraiva, R.D.; Nepomuceno, N.; Pinheiro, P.R. A Two-Phase Approach for Single Container Loading with Weakly Heterogeneous Boxes. Algorithms 2019, 12, 67. [Google Scholar] [CrossRef]
- Nishiyama, S.; Lee, C.; Mashita, T. Designing a flexible evaluation of container loading using physics simulation. Commun. Comput. Inf. Sci. 2020, 1173 CCIS, 255–268. [Google Scholar]
- Pachon, J.C.; Martinez-Franco, J.; Alvarez-Martinez, D. SIC: An intelligent packing system with industry-grade features. SoftwareX 2022, 20, 101241. [Google Scholar] [CrossRef]
- de Azevedo Oliveira, L.; de Lima, V.L.; de Queiroz, T.A.; Miyazawa, F.K. The container loading problem with cargo stability: A study on support factors, mechanical equilibrium and grids. Eng. Optim. 2021, 53, 1192–1211. [Google Scholar] [CrossRef]
- Filella, G.B.; Trivella, A.; Corman, F. Modeling soft unloading constraints in the multi-drop container loading problem. Eur. J. Oper. Res. 2023, 308, 336–352. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. Greedy randomized adaptive search procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef]
- Parreño, F.; Alvarez-Valdés, R.; Oliveira, J.F.; Tamarit, J.M. Neighborhood structures for the container loading problem: A VNS implementation. J. Heuristics 2010, 16, 1–22. [Google Scholar] [CrossRef]
- Martínez, J.C.; Cuellar, D.; Álvarez Martínez, D. Review of Dynamic Stability Metrics and a Mechanical Model Integrated with Open Source Tools for the Container Loading Problem. Electron. Notes Discret. Math. 2018, 69, 325–332. [Google Scholar] [CrossRef]
- Naber, G. Container Handbook. Cargo Loss Prevention Information from German Marine Insurers. Chapter 2. 2018. Available online: https://www.containerhandbuch.de/chb_e/ (accessed on 12 April 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).